Parzen窗方法的分析和研究

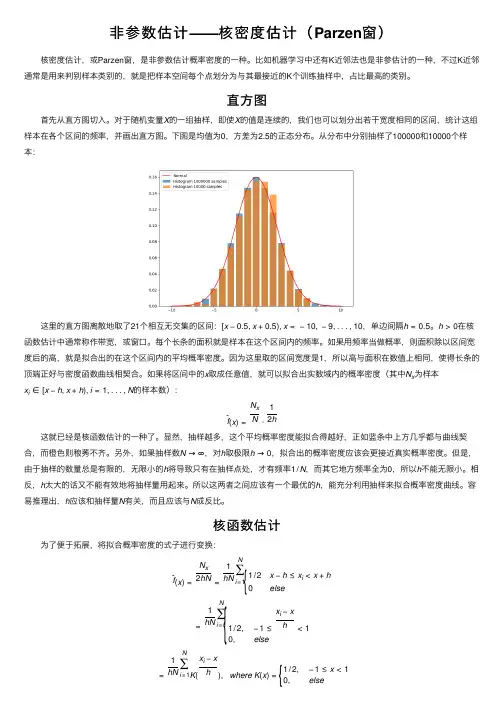
⾮参数估计——核密度估计（Parzen 窗） 核密度估计，或Parzen 窗，是⾮参数估计概率密度的⼀种。

⽐如机器学习中还有K 近邻法也是⾮参估计的⼀种，不过K 近邻通常是⽤来判别样本类别的，就是把样本空间每个点划分为与其最接近的K 个训练抽样中，占⽐最⾼的类别。

直⽅图 ⾸先从直⽅图切⼊。

对于随机变量X 的⼀组抽样，即使X 的值是连续的，我们也可以划分出若⼲宽度相同的区间，统计这组样本在各个区间的频率，并画出直⽅图。

下图是均值为0，⽅差为2.5的正态分布。

从分布中分别抽样了100000和10000个样本： 这⾥的直⽅图离散地取了21个相互⽆交集的区间：[x −0.5,x +0.5),x =−10,−9,...,10，单边间隔h =0.5。

h >0在核函数估计中通常称作带宽，或窗⼝。

每个长条的⾯积就是样本在这个区间内的频率。

如果⽤频率当做概率，则⾯积除以区间宽度后的⾼，就是拟合出的在这个区间内的平均概率密度。

因为这⾥取的区间宽度是1，所以⾼与⾯积在数值上相同，使得长条的顶端正好与密度函数曲线相契合。

如果将区间中的x 取成任意值，就可以拟合出实数域内的概率密度（其中N x 为样本x i ∈[x −h ,x +h ),i =1,...,N 的样本数）：ˆf (x )=N xN ⋅12h 这就已经是核函数估计的⼀种了。

显然，抽样越多，这个平均概率密度能拟合得越好，正如蓝条中上⽅⼏乎都与曲线契合，⽽橙⾊则稂莠不齐。

另外，如果抽样数N →∞，对h 取极限h →0，拟合出的概率密度应该会更接近真实概率密度。

但是，由于抽样的数量总是有限的，⽆限⼩的h 将导致只有在抽样点处，才有频率1/N ，⽽其它地⽅频率全为0，所以h 不能⽆限⼩。

相反，h 太⼤的话⼜不能有效地将抽样量⽤起来。

所以这两者之间应该有⼀个最优的h ，能充分利⽤抽样来拟合概率密度曲线。

容易推理出，h 应该和抽样量N 有关，⽽且应该与N 成反⽐。

Parzen窗估计及KN近邻估计实验报告总结计划装订线模式辨别实验报告题目：Parzen窗预计与KN近邻预计学院计算机科学与技术专业xxxxxxxxxxxxxxxx学号xxxxxxxxxxxx姓名xxxx指导教师xxxx20xx年xx月xx日1.Parzen窗预计与KN近邻预计一、实验目的本的目的是学Parzen窗估和k近来估方法。

在以前的模式研究中，我假概率密度函数的参数形式已知，即判函数J(.)的参数是已知的。

本使用非参数化的方法来理随意形式的概率散布而不用预先考概率密度的参数形式。

在模式中有在令人感趣的非参数化方法，Parzen窗估和k近来估就是两种典的估法。

二、实验原理非参数化概率密度的预计于未知概率密度函数的估方法，此中心思想是：一个向量x落在地区R中的概率可表示：此中，P是概率密度函数p(x)的光滑版本，所以能够通算P来估概率密度函数p(x)，假n个本x1,x2,⋯,xn，是依据概率密度函数p(x)独立同散布的抽取获得，，有k个本落在地区R中的概率听从以下散布：此中k的希望：概率k的散布在均邻近有着特别著的波峰，所以若本个数P的一个估将特别正确。

假p(x)是的，且地区n足大，使用R足小，有：k/n作以下所示，以上公式生一个特定的相概率，迫近一个δ函数，函数即是真的概率。

公式中的能够获得对于概率密度函数p(x)的估：当n近于无大，曲的形状V是地区R所包括的体。

上所述，在中，了估x的概率密度函数，需要结构包括点x的地区R1,R2,⋯,Rn。

第一个地区使用1个本，第二个地区使用2个本，以此推。

VnRn的体。

kn落在区Rn中的本个数，而pn(x)表示p(x)的第n次估：欲足pn(x)收：pn(x)→p(x)，需要足以下三个条件：有两种常采纳的得种地区序列的门路，以下所示。

此中“Parzen窗方法”就是根据某一个确立的体函数，比方Vn=1/√n来逐收一个定的初始区。

就要求随机量kn和kn/n能保pn(x)能收到p(x)。

parzen窗估计例题摘要：I.引言- 介绍Parzen 窗的概念和应用- 简述Parzen 窗估计的方法和步骤II.Parzen 窗的定义和性质- 定义Parzen 窗- 说明Parzen 窗的性质和特点III.Parzen 窗估计方法- 详细阐述Parzen 窗估计的步骤- 解释各步骤的意义和作用IV.Parzen 窗估计例题- 给出一个具体的Parzen 窗估计例题- 展示解决例题的过程和结果V.总结与展望- 总结Parzen 窗估计的主要内容- 展望Parzen 窗估计在实际应用中的前景正文：I.引言Parzen 窗是一种在机器学习中广泛应用的窗函数，主要用于估计密度函数和进行聚类分析等任务。

Parzen 窗估计是一种非参数估计方法，它通过计算样本数据邻域内数据的密度来估计总体密度。

本文将详细介绍Parzen 窗的概念、性质以及估计方法，并通过一个具体的例题展示Parzen 窗估计的过程。

II.Parzen 窗的定义和性质Parzen 窗，又称Parzen 核函数，是由德国数学家Wolfgang Parzen 在1960 年代提出的。

Parzen 窗是一个具有对称性的连续函数，定义为：f_h(x) = (1 / (h * sqrt(2 * pi))) * exp(-((x - μ)^2) / (2 * h^2))其中，h 是窗宽参数，μ是窗的中心。

Parzen 窗具有以下性质：1.具有对称性：f_h(x) = f_h(-x)2.具有局部性：当h 趋近于0 时，f_h(x) 趋于一个常数3.窗宽参数h 对函数形状的影响：当h 增大时，函数变得更为平缓；当h 减小时，函数波动加大，对局部特征更加敏感III.Parzen 窗估计方法Parzen 窗估计方法主要包括以下步骤：1.确定窗宽参数h：根据问题的实际需求和数据特点选择合适的窗宽参数h。

通常情况下，窗宽的选择需要通过交叉验证等方法进行优化。

k-最近邻（k-NN）估计和Parzen窗法是非参数估计方法，常用于密度估计和分类问题。

k-最近邻估计（k-NN）：
基本思想：
•对于一个给定的数据点，通过观察其邻近的k个数据点的标签（对于分类问题）或者值（对于回归问题），来预测该数据点的标签
或值。

算法步骤：
1.计算待预测点与所有训练数据点之间的距离（通常使用欧氏距离）。

2.选择与待预测点距离最近的k个训练数据点。

3.对于分类问题，通过多数投票确定待预测点的类别；对于回归问
题，取k个邻居的平均值作为预测值。

参数：
•k值的选择对算法的性能影响较大，选择一个合适的k值很重要。

Parzen窗法：
基本思想：
•将一个窗口（窗宽h）放在每个观测点上，通过计算落入窗口内的数据点的贡献来估计概率密度。

算法步骤：
1.对于每个数据点，定义以该点为中心的窗口。

2.计算落入窗口内的数据点的权重，通常使用核函数（如高斯核函
数）。

3.对所有窗口进行叠加，得到概率密度估计。

参数：
•窗口宽度h的选择影响估计的平滑程度，较小的h可能导致过拟合，较大的h可能导致欠拟合。

这两种方法都是基于样本的方法，没有对数据的分布进行明确的假设，因此在某些情况下可以更灵活地适应不同的数据分布。

选择适当的算法和参数是使用这些方法时需要注意的重要因素。

parzen窗估计例题一、引言Parzen窗估计作为一种非参数概率密度估计方法，广泛应用于统计学、信号处理、图像处理等领域。

本文将详细介绍Parzen窗估计的基本原理、计算步骤、优缺点以及在实际应用中的案例，帮助读者更好地理解和应用这一方法。

二、Parzen窗估计的基本原理1.Parzen窗的定义Parzen窗估计是一种基于数据点邻域的密度估计方法。

给定一组数据点X = {x1, x2, ..., xn}，Parzen窗宽度的函数h（宽度大于0）为数据点集的函数，那么在点x处的Parzen窗函数表示为：f(x) = (1/h^2) * Σ[K(x, xi)]，其中K为核函数，xi为数据点。

2.Parzen窗的性质（1）Parzen窗估计具有平滑性，可以有效地避免噪声对密度估计的影响。

（2）当窗口宽度h减小时，估计结果越接近真实密度；当h增大时，估计结果趋于平滑，但可能损失局部信息。

（3）Parzen窗估计是连续的，可以描述数据分布的连续性。

3.Parzen窗在概率密度估计中的应用Parzen窗估计可应用于一维和多维数据的概率密度估计。

通过调整窗口宽度和核函数，可以实现对不同数据类型的适应。

三、Parzen窗估计的计算步骤1.数据准备：收集一组数据点X = {x1, x2, ..., xn}。

2.确定Parzen窗的参数：选择合适的窗口宽度h和核函数K。

窗口宽度影响着估计结果的粗糙程度，核函数的选择依据数据类型和需求进行。

3.计算概率密度估计值：根据公式计算每个数据点的概率密度估计值，然后绘制概率密度函数图像。

四、Parzen窗估计的优缺点1.优点：（1）适应性强，可以应用于不同类型的数据。

（2）具有良好的平滑性，能有效减小噪声影响。

（3）计算简便，易于实现。

2.缺点：（1）对窗口宽度的选择敏感，较难确定最佳参数。

（2）在数据点分布稀疏的区域，估计结果可能不准确。

五、Parzen窗估计在实际应用中的案例1.信号处理：在信号处理领域，Parzen窗估计可以用于估计信号的概率密度，从而实现信号的参数估计、特征提取等任务。

Parze ‎n 窗mat ‎lab 仿真‎实验一、Parze ‎n 窗基本原‎理Parze ‎n 窗估计法‎是一种具有‎坚实理论基‎础和优秀性‎能的非参数‎函数估计方‎法，它能够较好‎地描述多维‎数据的分布‎状态。

其基本思想‎就是利用一‎定范围内各‎点密度的平‎均值对总体‎密度函数进‎行估计。

一般而言，设x 为d 维‎空间中任意‎一点，N 是所选择‎的样本总数‎，为了对x 处‎的分布概率‎密度进行估‎()^x p 计，以x 为中心‎作一个边长‎为的超立方‎h 体V ,则其体积为‎dV h =，为计算落入‎V 中的样本数‎k ，构造一个函‎数使得()11,,1,2,...,20,jj du uϕ⎧≤=⎪=⎨⎪⎩其他(1)并使满足条‎()u ϕ件()0u ϕ≥，且()1u du ϕ=⎰，则落入体积‎V 中的样本‎数为1Ni Ni x x kh ϕ=⎛⎫-= ⎪ ⎪⎝⎭∑，则此处概率‎密度的估计‎值是： ()^111Ni i x x Nx pVh ϕ=⎛⎫-=⎪ ⎪⎝⎭∑(2)式(2)是Parz ‎e n 窗估计‎法的基本公‎式，()1u Vϕ称为窗函数‎，或核函数。

在Parz‎e n 窗估计‎法的基本公‎式中，窗宽是一个‎h 非常重要的‎参数。

当样本数N ‎有限时，h对估计的效‎果有着较大‎的影响。

二、Matla ‎b 实现Pa ‎rzen 窗‎仿真实验为了编写P ‎a rzen ‎窗，首先要确定‎一个窗函数‎。

一般可以选‎择的窗函数‎有方窗、正态窗等。

接下来将分‎别用方窗、正态窗实现‎P a rze ‎n 窗法。

2.1、方窗1,1,2,...(,)2j ji d i h x x j d k x x h ⎧-≤=⎪=⎨⎪⎩若其他（3）其中，h 为超立方体‎的棱长。

因为编程中‎所用的信号‎是一维的正‎态信号，所以此处的‎d 取值为1。

2.1.1 方窗Par ‎zen 仿真‎实验流程图‎2.1.2 方窗Par‎zen仿真‎实验mta‎lab代码‎r=normr‎n d(0,1,1,10000‎);f=r(1:1000);f=sort(f);lth=1;h=[0.25,1,4];V1=h(1);V2=h(2);V3=h(3);V=[V1,V2,V3];a=zeros‎(1000,3);p=zeros‎(1000,3);b=0;for m=1:3for x=1:1000for n=1:lthif abs((r(:,n)-f(x))/h(:,m))<=1/2 q=1;elseq=0;endb=q+b;enda(x,m)=b;b=0;endendfor m=1:3for x=1:1000p(x,m)=1/(lth*V(m))* a(x,m);endsubpl‎o t(4,3,m)plot(f(1:1000),p(:,m))ylabe‎l('N=1')endhold onlth=16;b=0;for m=1:3for x=1:1000for n=1:lthif abs((r(:,n)-f(x))/h(:,m))<=1/2 q=1;elseq=0;endb=q+b;enda(x,m)=b;b=0;endendfor m=1:3for x=1:1000p(x,m)=1/(lth*V(m))* a(x,m);endsubpl‎o t(4,3,m+3)plot(f(1:1000),p(:,m))ylabe‎l('N=16')endhold onlth=256;b=0;for m=1:3for x=1:1000for n=1:lthif abs((r(:,n)-f(x))/h(:,m))<=1/2 q=1;elseq=0;endb=q+b;enda(x,m)=b;b=0;endendfor m=1:3for x=1:1000p(x,m)=1/(lth*V(m))* a(x,m);endsubpl‎o t(4,3,m+6)plot(f(1:1000),p(:,m))axis([-5,5,0,0.6]);ylabe‎l('N=256')endlth=10000‎;b=0;for m=1:3for x=1:1000for n=1:lthif abs((r(:,n)-f(x))/h(:,m))<=1/2 q=1;elseq=0;endb=q+b;enda(x,m)=b;b=0;endendfor m=1:3for x=1:1000p(x,m)=1/(lth*V(m))* a(x,m);endsubpl‎o t(4,3,m+9)plot(f(1:1000),p(:,m))axis([-5,5,0,0.5]);ylabe‎l('N=10000‎')end2.1.3 方窗Par‎zen仿真‎实验运行结‎果h=0.25 h=1 h=42.2正态窗正态窗函数‎为()211(,)e x p 2i k x x u V u ϕ⎧⎫==-⎨⎬⎩⎭（4）概率密度的‎估计式为()2^111112Ni Ni x x N x p hh =⎡⎤⎛⎫-⎢⎥=- ⎪ ⎪⋅⎢⎥⎝⎭⎣⎦（5）式中1h =。

parzen方法-回复什么是Parzen方法？Parzen方法，也被称为窗函数法或者核函数法，是一种非参数估计方法用于密度估计。

它通过对每个数据点周围的窗口或区域进行加权平均，来估计整个数据集的概率分布密度。

该方法通常可以应用于分类、聚类、异常检测等机器学习和统计问题中。

Parzen方法的基本原理是通过将样本空间中的每个数据点视为核心，然后计算该数据点的邻域内的密度值，最后将这些密度值进行加权平均来估计整个数据集的密度分布。

这个邻域的大小和形状由所选择的窗口函数来确定。

窗口函数通常使用高斯函数或矩形函数。

第一步：选择窗口函数在Parzen方法中，选择合适的窗口函数是非常重要的。

常见的窗口函数有高斯函数和矩形函数。

高斯函数是最常用的窗口函数之一，它在原点处有一个峰值，并随着距离的增加而逐渐减小。

而矩形函数则是一个常数函数，在指定的窗口范围内取值为1，其它地方都为0。

选择窗口函数需要考虑数据的分布情况以及希望实现的效果。

如果数据分布比较平滑，高斯函数可能是更好的选择；而如果数据分布比较离散，矩形函数可能更适合。

第二步：确定窗口大小和形状窗口的大小和形状决定了核密度估计的精确度和偏差。

过小的窗口大小会导致估计的密度函数不够平滑，过度拟合数据；而过大的窗口大小则会导致估计的密度函数过于平滑，丧失了对真实分布的敏感性。

可以使用交叉验证或根据经验规则来选择窗口大小和形状。

第三步：计算密度估计在确定了窗口函数、窗口大小和形状之后，可以开始计算密度估计了。

对于每个数据点，需要计算其邻域内的密度值。

这可以通过将窗口函数与各个数据点的距离结合起来得到。

距离可以使用欧氏距离或其他距离度量方法来计算。

在计算邻域内的密度值时，可以使用简单求和的方法，即对邻域内的所有数据点的窗口函数值进行加权求和。

具体计算方法会根据选择的窗口函数和距离度量方法而不同。

第四步：应用密度估计结果一旦得到了密度估计结果，就可以应用于各种机器学习和统计问题中。

对不起，无法提供具体的例题，但可以提供Parzen窗估计的基本概念和步骤。

Parzen窗估计是一种密度估计方法，用于估计一个数据集的密度函数。

它基于Parzen窗方法，通过使用核密度估计来估计数据集的密度。

步骤如下：
1. **选择核函数**：首先，需要选择一个合适的核函数。

常用的核函数包括高斯核、多项式核等。

在Parzen窗估计中，通常使用高斯核函数。

2. **计算核密度估计**：使用选择的核函数，对数据集中的每个点进行核密度估计。

这通常通过使用一个窗口（例如，一个矩形窗口或高斯窗口）来计算数据点周围的点的密度。

3. **计算Parzen窗**：根据核密度估计的结果，使用Parzen窗方法来估计数据集的密度。

Parzen窗方法通过计算数据点周围点的密度的加权平均值来估计密度。

权重由高斯函数决定，其中心点对应于数据点本身，而其宽度则决定了窗口的大小。

4. **平滑密度估计**：最后，通过平滑密度估计结果，可以减少噪声的影响，得到更平滑的密度估计。

需要注意的是，Parzen窗估计是一种非参数方法，不需要对数据进行任何先验假设或参数化。

此外，Parzen窗估计在处理连续数据时非常有效，因为它能够捕捉到数据的局部特性。

如果你需要更具体的例子或更深入的解释，可能需要查阅相关的数学和统计学教材或在线资源。

这些资源通常会提供更详细和具体的例子和算法实现。

2011，47（8）1引言聚类是将物理或抽象对象的集合分组成为由类似的对象组成的多个类的过程，它所生成的类的集合是一组数据对象的集合，同一个类中的对象彼此相似，与其他类中的对象却相异。

一个好的聚类算法应能识别任意数据形态，对数据的输入顺序不敏感，随输入数据的大小线性扩展，当数据维数增加时也具有良好的可伸缩性[1]。

聚类所具有的无指导学习能力使它具有广泛的应用空间，例如模式识别、图像处理等。

对高维数据的处理是聚类的一个重要应用领域。

生物信息学和电子信息化的加深，带来了越来越多的高维数据，除了“维灾问题”，高维数据中含有的大量随机噪声也会带来额外的效率问题，并且在实际的高维数据应用中，如果需要对某类具有上百个属性的对象进行聚类，很难得到理想的聚类结果。

至今，有很多文献对如何进行高维对象之间的聚类进行了研究[2]。

例如，专门针对各维属性取值为区间变量的高属性维稀疏聚类问题提出了SFC聚类方法和用于求解二态变量的高属性维稀疏聚类问题的CABOSFV算法[3-4]。

解决高维数据比较典型的有频繁模式挖掘、基于模式相似的聚类、特征选择/子空间聚类、特征转换法等。

高维数据的聚类算法逐步发展，近几年国内学者提出很多解决算法，例如具有输入知识的高维数据聚类算法、改进CLIQUE算法的并行高维聚类算法，以及高维空间球体的k-中心聚类等方法的研究[1-2，5]。

本文对Parzen窗估计法加权，通过多次仿真得到更优的加权函数，根据Parzen窗对一维数据的优良聚类效果的特性，将高维数据投影在低维空间，进行聚类，逐步投向高维数据，并对结果矩阵进行优化处理。

最后一章将所得的聚类效果与Parzen窗进行高维数据聚类的效果进行比较，并做了分析得出结论。

2方法思想Parzen窗估计法是一种具有坚实理论基础和优秀性能的非参数估计方法，能够较好地描述数据的分布状态。

使用Par-zen窗估计法求取每个分类的概率密度函数，从而建立其稳定性指标，使用该指标可以比较各个分类结果的好坏。

对Parzen窗/PNN算法的学习和研究报告姓名：吴潇学号：13337551、Parzen窗方法综述、发展历史及现状模式识别领域的非参数估计方法大致可以分为两类。

第一种类型是先估计出概率密度函数的具体形式，然后再利用这个估计出来的概率密度函数对样本进行分类。

第二种类型是，不估计具体的概率密度函数，而直接根据样本进行分类。

Parzen窗方法就是属于第一种类型的非参数估计方法，概率神经网络（PNN）是它的一种实现方式。

Parzen窗方法的基本思想是利用一定范围内的各点密度的平均值对总体密度函数进行估计。

Parzen窗（Parzen window）又称为核密度估计（kernel density estimation），是概率论中用来估计未知概率密度函数的非参数方法之一。

该方法由Emanuel Parzen于1962年在The Annals of Mathematical Statistics杂志上发表的论文“On Estimation of a Probability Density Function and Mode”中首次提出。

Nadaraya和Watson最早把这一方法用于回归法中。

Specht把这一方法用于解决模式分类的问题，并且在1990年发表的论文“Probabilistic neural networks”中提出了PNN网络的硬件结构。

Ruppert和Cline基于数据集密度函数聚类算法提出了修订的核密度估计方法，对Parzen窗做了一些改进。

Parzen窗方法虽然是在上个世纪60年代提出来的，已经过去了45年的时间，看上去是一种很“古老”的技术，但是现在依然有很多基于Parzen窗方法的论文发表。

这说明Parzen 窗方法的确有很强的生命力和实用价值，虽然它也存在很多缺点。

2、Parzen窗方法和概率神经网络Parzen窗方法就是基于当样本个数n非常大的时候，有公式成立这样的一个事实而提出的。

计算题3.6 已知三类训练样本为1ω：[ -1，-1 ]T ， 2ω：[ 0，0 ]T ， 3ω：[ 1，1 ]试用多类感知器算法求解判别函数。

解：采用多类情况3的方式分类，将训练样本写成增广向量形式，有X 1= [ -1，-1，1 ]T ， X 2= [ 0，0，1 ]T ， X 3= [ 1，1，1 ]T任取初始权向量为：W 1(1) = W 2(1) = W 3(1)= [ 0，0，0 ]T 取校正增量c = 1。

迭代过程如下：第一次迭代，k = 1，以X 1= [ -1，-1，1 ]T 作为训练样本，计算得 d 1(1) = W 1T (1) X 1= 0 d 2(1) = W 2T (1) X 1= 0 d 3(1) = W 3T (1) X 1= 0X 1∈1ω，但d 1(1)>d 2(1)且d 1(1)>d 3(1)不成立，故修改3个劝向量，即 W 1(2) = W 1(1) + X 1= [ -1，-1，1 ]T W 2(2) = W 2(1) – X 1= [ 1，1，-1 ]T W 3(2) = W 3(1) – X 1= [ 1，1，-1 ]T 第二次迭代，k = 2，以X 2=[ 0，0，1 ]T 作为训练样本，计算得 d 1(2) = W 1T (2)X 2= 1 d 2(2) = W 2T (2)X 2= -1 d 3(2) = W 3T (2)X 2= -1X 2∈2ω，但d 2(2)>d 1(2)且d 2(2)>d 3(2)不成立，故修改3个权向量，即W 1(3) = W 1(2) – X 2= [ -1，-1，0 ]T W 2(3) = W 2(2) + X 2= [ 1，1，0 ]T W 3(3) = W 3(2) – X 2= [ 1，1，-2 ]T 第三次迭代，k = 3，以X 3= [ 1，1，1 ]T 作为训练样本，计算得 d 1(3) = W 1T (3)X 3= -2 d 2(3) = W 2T (3)X 3= 2 d 3(3) = W 3T (3)X 3= 0X 3∈3ω，d 3(3)>d 1(3)成立，但d 3(3)>d 2(3)不成立，故仍需修改部分权向量，即 W 1(4) = W 1(3) = [ -1，-1，0 ]T W 2(4) = W 2(3) – X 3= [ 0，0，-1 ]T W 3(4) = W 3(3) + X 3= [ 2，2，-1 ]T以上经过一轮迭代运算后，三个样本还未正确分类，故进行下一轮迭代。

MATLAB下的Parzen函数Parzen窗法概率密度函数估计在基于熵的⾳频相似度度量中，⽤到Parzen窗法对所提取的MFCC参数进⾏概率密度函数估计，
其MATLAB实现如下：
function p=Parzen(xi,x,h1,f)
%xi为样本，x为概率密度函数的⾃变量的取值，
%h1为样本数为1时的窗宽，f为窗函数句柄
%返回x对应的概率密度函数值
if isempty(f)
%若没有指定窗的类型，就使⽤正态窗函数
f=@(u)(1/sqrt(2*pi))*exp(-0.5*u.^2);
end;
N=size(xi,2);
hn=h1/sqrt(N);
[X Xi]=meshgrid(x,xi);
p=sum(f((X-Xi)/hn)/hn)/N;
由于不知道如何在m语⾔中设置函数参数的默认值或设置可变参数，所以即使你使⽤默认的正态窗，也需要传⼊f参数，传⼊为‘[]’。

举例说明这个函数的⽤法：
>>xi=rand(1,1024);
>>x=linspace(-1,2,1024);
>>p=Parzen(xi,x,1,[]);
>>plot(x,p);
得到如下图形：
上⾯演⽰的是均匀分布，现在再试试正态分布：
>>xi=randn(1,1024);
>>x=linspace(-2,2,1024);
>>p=Parzen(xi,x,1,[]);
>>plot(x,p);
得到如下图形：
最好不要设置太⼤的N。