下载文档原格式
高三年级组第一次模拟考试成绩分析背景高三年级组第一次模拟考试是评估学生在高中阶段的学业成就的重要指标。
对学生成绩进行详细的分析有助于了解学生掌握知识的程度以及存在的问题，为后续教学和辅导提供依据。
成绩分布本次模拟考试共有150名学生参加，他们在五个学科的考试中取得了如下成绩分布：- 语文：- 平均分：80分- 最高分：95分- 最低分：60分- 数学：- 平均分：75分- 最高分：90分- 最低分：55分- 英语：- 平均分：85分- 最高分：98分- 最低分：70分- 物理：- 平均分：70分- 最高分：87分- 最低分：50分- 化学：- 平均分：77分- 最高分：93分- 最低分：62分不同学科之间的差异分析通过对各学科成绩的分析，我们可以发现以下趋势：- 语文和英语成绩普遍较高，说明学生对语言类学科有较好的掌握能力；- 数学和化学成绩偏中等水平，说明学生在数理化方面需要进一步加强研究和理解；- 物理成绩相对较低，需要重点关注学生对物理知识的理解和应用能力。
优秀学生的分析本次模拟考试中有10名学生取得了总成绩在90分以上，他们的表现如下：- 学科分布：3名学生在语文和英语两个学科表现出色，5名学生在数学和化学两个学科表现出色，2名学生在英语和物理两个学科表现出色；- 研究态度：8名学生积极参与课堂讨论和提问，主动完成作业，2名学生重点复并针对性地解决知识点上的困难；- 研究惯：9名学生定期复，制定了合理的研究计划，1名学生善于总结复方法和技巧。
低分学生的分析本次模拟考试中有15名学生总成绩在60分以下，他们的表现如下：- 学科分布：7名学生在数学和物理两个学科成绩较低，4名学生在语文和英语两个学科成绩较低，4名学生在化学成绩较低；- 研究态度：10名学生缺乏研究的主动性和积极性，对课堂内容漠不关心，5名学生对研究不够认真负责；- 研究惯：12名学生缺乏有效的研究方法和计划，研究效率较低，3名学生缺乏及时复和总结的惯。
合肥市2024年高三第一次教学质量检测地理试题（考试时间：90分钟满分：100分）注意事项：1.答题前，务必在答题卡和答题卷规定的地方填写自己的姓名，准考证号和座位号后两位。
2.答第I卷时，每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动，用橡皮擦干净后，再选涂其他答案标号。
3.答第II卷时，必须使用0.5毫米的黑色墨水签字笔在答题卷.上书写，要求字体工整、笔迹清晰。
作图题可先用铅笔在答题卷规定的位置绘出，确认后再用0.5毫米的黑色墨水签字笔猫清楚。
必须在题号所指示的谷题区城作，超出答题区域书写的答案无效，在试题卷、草稿纸上答题无效。
4.考试结束，务必将答题卡和答题卷一并上交。
第I卷选择题（共25小题，50分）下图示意南美大陆局部区域1月与7月平均气温差值分布。
据此完成1-2题。
1.M点的数值可能为A.-5℃B.-3℃C.1℃D.4℃2.造成M，N两地1月与7月平均气温差值不同的主要因素为A.纬度位置B.海陆分布C.洋流D.地形我回黄河流域古代劳动人民发明了世界上最早的时间测量工具——圭表，主是平放的尺，表为直立的标杆，圭与表垂直且固定。
古人通过测量当地正午的日影长度以定节令。
合肥市某中学地理兴趣小组利用自制的圭表模型（如下图所示）在校园内观测一年内正午日影的变化。
图中圭上的黑点表示二分二至日正午表影端点的位置。
据此完成3-5题。
3.古代劳动人民利用丰表测量正午日影时，表影位于表的A.正东方B.正西方C.正南方D.正北方4.该兴趣小组测得表影端点位于M位置时，此时的节气是A.春分B.夏至C.秋分D.冬至5.古代劳动人民利用圭表可以①辨识方向②判断节气③确定正午A.①②B.①③C.②③D.①②③尼亚加拉河全长56km，从伊利湖注入安大略湖。
研究发现：尼亚加拉瀑布从12000年前的尼亚加拉陡崖附近逐渐发育至现今位置（如下图所示）：目前尼亚加拉河入湖口三角洲发育缓慢。
据此完成6-7题。
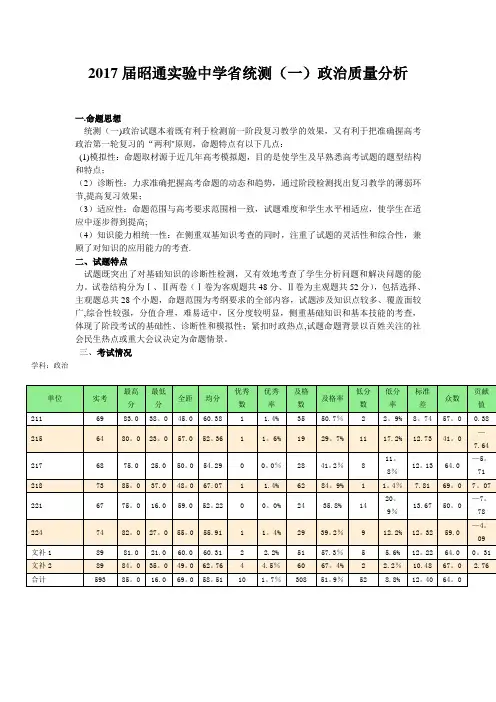
2017届昭通实验中学省统测（一）政治质量分析一.命题思想统测（一)政治试题本着既有利于检测前一阶段复习教学的效果，又有利于把准确握高考政治第一轮复习的“两利"原则，命题特点有以下几点：(1)模拟性：命题取材源于近几年高考模拟题，目的是使学生及早熟悉高考试题的题型结构和特点；（2）诊断性：力求准确把握高考命题的动态和趋势，通过阶段检测找出复习教学的薄弱环节,提高复习效果；（3）适应性：命题范围与高考要求范围相一致，试题难度和学生水平相适应，使学生在适应中逐步得到提高;（4）知识能力相统一性：在侧重双基知识考查的同时，注重了试题的灵活性和综合性，兼顾了对知识的应用能力的考查.二、试题特点试题既突出了对基础知识的诊断性检测，又有效地考查了学生分析问题和解决问题的能力。
试卷结构分为Ⅰ、Ⅱ两卷（Ⅰ卷为客观题共48分、Ⅱ卷为主观题共52分），包括选择、主观题总共28个小题，命题范围为考纲要求的全部内容，试题涉及知识点较多、覆盖面较广,综合性较强，分值合理，难易适中，区分度较明显，侧重基础知识和基本技能的考查，体现了阶段考试的基础性、诊断性和模拟性；紧扣时政热点,试题命题背景以百姓关注的社会民生热点或重大会议决定为命题情景。
三、考试情况学科：政治四、学生答题时存在的问题(1）基础知识不扎实：学生对双基知识掌握不够扎实,还没有将所学知识升华，形成完整的知识网络,所以综合运用知识解决问题的能力较弱.（2）解题思维不够严谨：思维的严密性、全面性不够,对题目设计的各种干扰因素不能作出清析准确的判断，逻辑推理能力和知识迁移能力较差。
（3）答题缺乏规范意识:政治学科用语使用不规范，主观题语言表述不简练,文字表达能力较差.（4）阅读审题能力较弱：读题不认真，审题不仔细,张冠李戴，答非所问,是造成学生失分很重要的一个原因，如：26题（3)问结合材料三，运用唯物辩证法的内容，分析大力推进生态文明的哲学依据，有很多考生对辩证唯物论和唯物辩证法分不清楚，答辩证唯物论的多，以至于偏离答题要求，答非所问,考生缺乏良好的答题习惯和应试策略。
一模考试后，我们要干什么？2017年3月13日星期一同学们：高三的考试，每一次都相当重要，这次的一模是高考前很重要的一次学习检验和阅兵。
一模成功，可以使自己信心倍增，但不要沾沾自喜；一模受挫，也不要恢心丧气，妄自菲薄。
应该为一模恰当定位：它是“加油站”而不是“终点站”。
一模考完了，我们能做些什么？我们该做些什么？我们应做出明智的选择。
在此，提醒同学们注意做好以下事情：一、做好考试以后的分析、反思一模后，我们应该重点关注考试中暴露出来的问题；明确自己的位次，对自己的学习状况作出清醒的判断。
充分地利用好成绩，把这次考试的真正意义落实到具体的学习中去。
学校建议：看到自己的成绩后我们首先要从以下几方面进行分析：1、正确地对自己的成绩进行横向比较。
所谓的横向比较就是发下卷子或是知道成绩后，首先与自己周围的同学或是与跟自己水平差不多的同学进行比较，看一看自己与别人的差距，差在那儿？差在那科上？差了多少分数？为什么？反思一下自己的学习付出与别人的付出是否成正比，找到自己与别人有差距的真正原因。
拿自己考前的学习状态、努力程度、学习方法、准备情况以及应试策略技巧等等各方面与别人进行对比反思，只有这样才能找到自己主观或客观上存在的问题，然后再看别人的学习是如何进行的，在此基础上，自己确定好下一步的复习重点与方法。
2、将自己的多次成绩进行纵向比较，做出一个自我成绩评价。
纵向比较就是根据本次考试试题的难易程度以及自己所得的成绩与上几次的成绩进行比较。
看一看有没有进步，进步了多少？下降了多少？我们把自己的每一次考试的年级名次做成一个曲线图，这样成绩变化就会一目了然，这样成绩分析是一个很奏效的方法。
然后再找单科试卷上的问题，相对其他同学是进步了还是下降了，我们都要有一个正确的评价。
反思一下你在考试之前，用在这一学科上的时间与我们取得的成绩是否成正比，如果用了很多的时间而没有好的成绩，就要看自己的学习方法是否合理，学习效率怎么样？是不是出工不出力，追求了形式而没有讲求实效等等。
姓名座位号(在此卷上答题无效)2024年合肥市高三第一次教学质量检测历史(考试时间: 75 分钟满分: 100 分)注意事项：1. 答卷前，务必将自己的姓名和座位号填写在答题卡和试卷上。
2. 回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动，务必擦净后再选涂其他答案标号。
回答非选择题时，将答案写在答题卡上。
写在本试卷上无效。
3. 考试结束后，将本试卷和答题卡一并交回。
一、选择题(本大题共16 小题，每小题 3 分，共48 分。
每小题只有一个正确答案，请把正确答案填在答题卷上。
)1. 考古发现，在距今约 7000 年姜寨遗址的公共墓地里，没有夫妻合葬墓，每个人都单独地按辈分高低、血缘关系远近以及去世的先后顺序埋葬。
这反映出A. 旧石器时代的生产力状况B. 按血缘关系分配政治权力C. 当时氏族聚落的社会风貌D. 国家的初始形态已经具备2. 汉武帝初平岭南时，其地“山川长远，习俗不齐，言语同异，重译乃通，民如禽兽，长幼无别”，后派官吏到岭南“教其耕犁，使之冠履；为设媒官，始知聘娶；建立学校，导之经义”。
这些措施A. 巩固了多民族国家统一B. 促进了南北经济的平衡C. 确立了儒学的正统地位D. 建立了完备的教育体系3. 陈寅恪认为，在北朝时代汉人与胡人的分别，“凡汉化之人即目为汉人，胡化之人即目为胡人，其血统如何，在所不论”。
这凸显出当时A. 少数民族的封建化B. 民族间的文化交融C. 世家大族逐渐瓦解D. 黄河流域走向统一历史试题第1页(共6页)4. 宋太宗派遣内侍八人携带诏书、金帛前往南海诸国，招谕各国来朝，博买香料、药材、犀角、象牙、龙脑。
南宋统治者更加留意此事，宋高宗曾说：“市舶之利，颇助国用，宜循旧法，以招徕远人，卑通货贿”。
这反映出宋朝A. 开辟了海上丝绸之路B. 抛弃厚往薄来的传统观念C. 中华文化圈开始形成D. 实行开放的海洋贸易政策5. 图1为明代画家陈洪绶创作的《水浒叶子》(叶子即纸牌，也用于行酒)。
肥东圣泉中学合肥市“一模”考试学科成绩分析汇报会
一、时间安排：
二、参加人员：高三应历届、14宏志班教师（含历届兼职教师）。
三、会议地点：行政楼二楼会议室，会议由教研员主持。
四、会议内容与流程：
内容：查找与一中差距，分析考试暴露出来的问题，列举每位教师的达标情况，进一步细化赶超目标，提出应对策略。
二、三轮复习的初步
安排与基本思路。
流程：先高三应届、历届和宏志班汇报，后学校领导提要求。
五、会议要求：
1、提前到会，不迟到，手机关闭或静音，会议期间不接听或拨打手机；
2、认真听会，不做与会议无关的事情，不玩手机。
3、准备两份纸质材料，用课件汇报，每人汇报时间10—15分钟。
高中教科室
2017年2月3日。
合肥一中2024—2025学年高三教学质量检测参考答案1.D【解析】A.由材料一史学与哲学关系可知，“史学”和“哲学”性质差异明显而不是相近，另外题干中的因果关系界定也是不当，应是转折关系。
B.“是研究历史根本问题的，要以史学研究结果为基础”错误，原文的表述是“哲学史亦是一种历史的研究，故亦需用历史的研究法以研究哲学史”“历史哲学是研究历史的根本问题的”，首先研究历史根本问题的是“历史哲学”，不是“哲学史”；此外“用历史的研究法”不是“以史学研究结果为基础”。
C.“也不能离开这些学科而独自存在”错误，原文的表述是“哲学在任何具体学科领域都无法与该学科一争高下，但它可以从事任何具体学科所无法完成的工作，它为学科的诞生准备条件。
数学在任何具体学科领域都有可能出色地工作，但它离开具体学科之后却无法作出贡献。
它必须利用具体学科为它创造的条件”，可见应是数学不能离开这些学科而独自存在。
2.C【解析】C.“哲学与数学的研究范畴呈此消彼长的态势”错误，原文的表述是“自然科学的大发展使哲学退出了一系列研究领域，哲学的中心问题从'世界是什么样的'变成'人怎样认识世界'。
这个时候，数学扩大了自己的领域，它开始研究运动与变化”,“自然科学的大发展使哲学退出了一系列研究领域，哲学的中心问题从'世界是什么样的'变成'人怎样认识世界'”不等于哲学的研究范畴缩小。
3.D【解析】依旧材料一“史学家的历史观每渊源于哲学。
但有人说史学家不应有历史观，应当虚怀若谷地去研究，不可有偏见或成见，以历史附会己说，才可算是好史学家。
也有人说史学家应有历史观，然后才有准绳去处置史料，不然便如迷离飘荡于洋海之中，茫无把握，很难寻出头绪来”可知，“历史观”是指史学家的主观观点。
D．是在陈述历史客观事实，无主观观点。
4.“望远镜”说明了哲学学科前瞻性、广泛性、模糊性等特点；（2分）“显微镜”说明了数学学科深刻性、具体性、精确性等特点。
2017年高考数学（理科）全国Ⅰ卷试卷分析合肥一中吴建平1.试卷题型稳定，难、易适中选择、填空、解答题基本是按照由易到难的顺序排列，数学的几大主要板块进行了重点考查，主要是数列、三角函数、立体几何、概率统计、解析几何、函数导数以及选考部分参数方程和不等式，试卷结构和往年保持不变，体现了高考的稳定性和延续性，注重基础知识，体现数学素养，考查计算能力，有利于学生的正常发挥。
2.试卷体现了对数学核心素养和数学文化的考查试卷体现了数学文化，如第2题把几何概型的考查揉合进了我国古代的八卦图中，弘扬了优秀的传统文化，体现了图形的对称美。
12题的数学抽象和推理、16题的数学建模、19题的数学应用和数学建模，都是对学生的核心素养进行了很好的考查。
3.体现了基础性和常规性选择题前11题和填空题前3题都比较基础和常规，解答题的17、18及选考题都是常规的考查，和往年的全国一卷及模考题相类似。
体现了通性、通法，学生如有较扎实的基本功和运算能力，解答这些题目应该完全没有问题。
4.体现了综合性、创新性和应用性如选择题12题考查数列的通项、求和及不等式问题，16题考查了平面图形的折叠、函数模型的建立、锥体体积公式和函数最值的求法。
19题数学应用问题贴近生活、贴近学生，具有浓厚的生活气息，体现了数学和实际的紧密结合，对学生阅读理解、提取信息和数据处理能力要求较高，20题考查运算能力、特殊和一般关系问题，第21题第（1）问要求考生求出导函数的零点，进而对参数进行分类讨论，掌握函数的单调性；在此基础上，第（2）问要求根据函数有两个零点的条件，确定参数的取值范围，试题层层深入，为考生解答提供广阔的想象空间。
在知识的交汇点处命题，对学生的理性思维进行了很好的考查。
总之，整份试卷加强对学生理性思维的考查，渗透了数学文化，突出对创新应用能力的考查。
试题关注社会发展，引导考生运用所学数学知识解决生活实际问题，富有时代气息。
试卷遵循考试大纲的各项规定，试卷结构保持稳定，难易适度，各种难度的试题比例适当。
