几何图形 五大模型

小学数学五大几何模型知识框架一、等积模型DC BA①等底等高的两个三角形面积相等；②两个三角形高相等，面积比等于它们的底之比； 两个三角形底相等，面积比等于它们的高之比；③夹在一组平行线之间的等积变形，如右图ACDBCD S S =△△；反之，如果ACD BCD S S =△△，则可知直线AB 平行于CD ．④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形)； ⑤三角形面积等于与它等底等高的平行四边形面积的一半；⑥两个平行四边形高相等，面积比等于它们的底之比；两个平行四边形底相等，面积比等于它们的高之比．二、共角定理（鸟头定理）两个三角形中有一个角相等或互补，这两个三角形叫做共角三角形． 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比．:():()ABC ADE S S AB AC AD AE =⨯⨯△△(1)(2)(3)(4)三、蝴蝶定理任意四边形中的比例关系(“蝴蝶定理”)： ①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径．通过构造模型，一方面可以使不规则四边形的面积关系与四边形内的三角形相联系；另一方面，也可以得到与面积对应的对角线的比例关系．S 4S 3S 2S 1O DC BA梯形中比例关系(“梯形蝴蝶定理”)：①2213::S S a b =②221324::::::S S S S a b ab ab =； ③S 的对应份数为()2a b +．A BC DO baS 3S 2S 1S 4四、相似模型(一)金字塔模型 (二) 沙漏模型GF E ABCD ABCDEF G①AD AE DE AFAB AC BC AG ===； ②22:ADE ABC S S AF AG =△△：．所谓的相似三角形，就是形状相同，大小不同的三角形(只要其形状不改变，不论大小怎样改变它们都相似)，与相似三角形相关的常用的性质及定理如下：⑴相似三角形的一切对应线段的长度成比例，并且这个比例等于它们的相似比； ⑵相似三角形的面积比等于它们相似比的平方； ⑶连接三角形两边中点的线段叫做三角形的中位线．三角形中位线定理：三角形的中位线长等于它所对应的底边长的一半． 相似三角形模型，给我们提供了三角形之间的边与面积关系相互转化的工具． 在小学奥数里，出现最多的情况是因为两条平行线而出现的相似三角形．五、共边定理（燕尾定理）有一条公共边的三角形叫做共边三角形。

平面几何五种模型 TYYGROUP system office room 【TYYUA16H-TYY-TYYYUA8Q8-平面几何五种模型等积，鸟头，蝶形，相似，共边1、等积模型等底等高的2个三角形面积相等2个三角形高相等，面积比=底之比2个三角形底相等，面积比=高之比夹在一组平行线之间的等积变形（方方模型）等积模型是基本应用应是烂熟于心的都是利用面积公式得到的推定比例如下：1等底等高的2个平行四边形面积相等2三角形面积等于它等底等高的平行四边形面积的一半3 2个平行四边形高相等，面积比=底之比；2个平行四边形底相等，面积比=高之比2、鸟头模型（共角定理）鸟头定理：2个三角形中，有一个角相等或互补，这2个三角形叫做共角三角形。

共角三角形的面积比等于对应角（相等角或互补角）两夹边的乘积之比（夹角2边）鸟头定理的使用要火眼金睛，经常需要自己补一条辅助线同时经过2次以上转换对应才能得到结果。

A B C DE如图，浅紫色的三角形ADE 跟大三角形ABC 是公用A 角的，等于浅紫色三角形是“嵌入”在大三角形ABC 里面，注意，鸟头定理用的是乘积比！不是单独的线段比~记忆上用夹角2边 最好记，这里等于鸟头定理的证明，写出来是因为很多题目的解题过程，都需要补这么一条辅助线来过度连接2个看起来无关的图形。

证明的途径其实跟我们日常解题途径重合，所以写出来，仔细看。

经由媒介的ABE ，联系了ADE 和大三角形ABCBE 辅助线很重要！鸟头定理是用等高（等于是用等积推算而得） 第二种的证明方式将对顶角压回来ABC 内，对顶角性质是相等的，所以压回来的新跟ADE 是全等，再做一条辅助线就能用共角的方式证明出对角的鸟头定理互补角的鸟头定理证明S△ADE=S△AD'E,因为同底等高AD=AD',高相等，所以面积相等D'A B C D E 写了这几个证明，其实说的目的只有一个：连接小三角形和大三角形过度的那条辅助线，特别重要！3蝴蝶模型 任意四边形中的比例关系（“蝴蝶定理”）任蝴蝶①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++ 【上下比】= = = 【上上比】 = ==由上述比例可以按数学运算原则推出很多规则：如面积交叉相乘的乘积相等 == 1324S S S S ⨯=⨯ 梯形蝴蝶定理（梯蝴蝶）①2213::S S a b =→上：下=22:a b②221324::::::S S S S a b ab ab =→上：下：左：右=22:::a b ab ab ③S 的对应份数为()2a b +→a 2+2ab+b 2=a 2+b 2+ab+ab 有木有↑4 相似三角形形状相同，大小不同的三角形，只要形状不变，无论大小怎么改变，他们都相似。

五、燕尾定理（共边定理、燕尾模型和风筝模型） 在三角形ABC中，AD，BE，CF相交于同一点O，那
么
．
上述定理给出了一个新的转化面积比与线段比的手段，因为和 的形状很象燕子的尾巴，所以这个定理被称为燕尾定理．该定理在许 多几何题目中都有着广泛的运用，它的特殊性在于，它可以存在于任 何一个三角形之中，为三角形中的三角形面积对应底边之间提供互相 联系的途径.
h
11
解法二：特殊点法．找H的特殊点，把H点与D点重合，那么 图形就这可样变阴成影右部图分：的面积就是
△DEF的面积， 根据鸟头定理，则有：
h
12
【巩固】
h
13
h
14
h
15
h
16
h
17
h
18
h
19
h
20
h
21
h
22
h
23
h
24
h
25
h
26
h
27
h
28
h
29
h
30
h
3
二、鸟头定理
两个三角形中有一个角相等或互补，这两个三角形叫做共
角三角形．
A
D
共角三角形的面积比等于对应角(相等角或互补角)两夹边
A 的乘积之比．D
E E
B
C
图⑴BΒιβλιοθήκη C图 (2)如图在
中，D、E分别是AB、AC上的点如图
⑴(或D在BA的延长线上，E在AC上)，则
h
4
三、蝴蝶定理 任意四边形中的比例关系(“蝴蝶定理”)： ① S1 : S2 = S4 : S3 或者 S1 ×S3 =S2 × S4 ② AO : OC = (S1 + S2 ) : ( S4 +S3 ) 蝴蝶定理为我们提供了解决不规则四边形的面积问题的 一个途径． 通过构造模型，一方面可以使不规则四边形的面积关系 与四边形内的三角形相联系；另一方面，也可以得到与面积 对应的对角线的比例关系． 梯形中比例关系(“梯形蝴蝶定理”)：

几何五大模型一、五大模型简介（1）等积变换模型1、等底等高的两个三角形面积相等；2、两个三角形高相等，面积之比等于底之比，如图①所示，S[sub]1[/sub]：S[sub]2[/sub]=a:b；3、两个三角形底相等，面积在之比等于高之比，如图②所示，S[sub]1[/sub]：S[sub]2[/sub]=a:b；4、在一组平行线之间的等积变形，如图③所示，S[sub]△ACD[/sub]=S[sub]△BCD[/sub]；反之，如果S[sub]△ACD[/sub]=S[sub]△BCD[/sub]，则可知直线AB平行于CD。

例、如图，三角形ABC的面积是24，D、E、F分别是BC、AC、AD的中点，求三角形DEF的面积。

（2）鸟头（共角）定理模型1、两个三角形中有一个角相等或互补，这两个三角形叫共角三角形；2、共角三角形的面积之比等于对应角（相等角或互补角）两夹边的乘积之比。

如图下图三角形ABC中，D、E分别是AB、AC上或AB、AC延长线上的点则有：S[sub]△ABC[/sub]：S[sub]△ADE[/sub]=（AB×AC）：（AD×AE）我们现在以互补为例来简单证明一下共角定理！如图连接BE，根据等积变化模型知，S[sub]△ADE[/sub]：S[sub]△ABE[/sub]=AD：AB、S[sub]△ABE[/sub]：S[sub]△CBE[/sub]=AE：CE，所以S[sub]△ABE[/sub]：S[sub]△ABC[/sub]=S[sub]△ABE[/sub]：（S[sub]△ABE[/sub]+S[sub]△CBE[/sub]）=AE：AC，因此S[sub]△ADE[/sub]：S[sub]△ABC[/sub]=（S[sub]△ADE[/sub]：S[sub]△ABE[/sub]）×（S[sub]△ABE[/sub]：S[sub]△ABC[/sub]）=（AD：AB）×（AE：AC）。

在学习小学数学的时候，几何模型算是比较新颖的 一个模块，学生们熟练掌握五大面积模型，并掌握五大 面积模型的各种变形，
今天就为大家推荐一篇小学数学几何五大模型的内容。
一、等积 模①型等底等高的两个三角形面积相等；
AB
②两个三角形高相等，面积比等于它们的底之比；
两个三角形底相等，面积比等于它们的高之S比1 ；S2
典型例题
【例1】如图，正方形ABCD的边长为6，AE= 1.5，CF= 2．长
方形EFGH的面积为？
H
H
A
D
A
D
E
E
G
G
B FC
B
FC
【解析】连接DE，DF，则长方形EFGH的面积是三角形DEF面 积的二倍．
三角形DEF的面积等于正方,所形以的长面方积形减E去FG三H面个积三为角33． 形的面积，
【巩固】如图所示，正方形ABCD的边长为8厘米，长方形EBGF 的长BG为10厘米，那么长方形的宽为几厘米？
【解析】本题主要是让学生会运用等底等高的两个平行四边形面积 相等(长方形和正方形可以看作特殊的平行四边形)．三角形面积等 于与它等底等高的平行四边形面积的一半．
【巩固】如图所示，正方形ABCD的边长为8厘米，长方形EBGF 的长BG为10厘米，那么长方形的宽为几厘米？
证明：连接AG（我们通过△ABG把这两个长方形和正方形联系在一起）
∴ 正方形ABCD与长方形EFGB面积相等。长方形的宽=8 ×8÷10=6.4（厘
【例2】长方形ABCD的面积为36cm2，E 、F、G为各边 中点，H为AD边上任意一点，问阴影部分面积是多少 ？
【解析解,】H法C 一，：如寻下找图可：利用的条件，连接BH
如右图

∵在正方形ABCD中，S△ABG=×AB × AB边上的高，
∴ S△ABG= S□ABCD（三角形面积等于与它等底等高的平行四边形面积的一半）
同理，S△ABG=

S
□EFGB
∴ 正方形ABCD与长方形EFGB面积相等。长方形的宽=8 ×8÷10=6.4（厘米）
【例2】长方形ABCD的面积为36cm2，E 、F、G为各边中点，H为AD边上
任意一点，问阴影部分面积是多少？
【解析】解法一：寻找可利用的条件，连接BH ,HC ，如下图：
解法二：特殊点法．找H的特殊点，把H点与D点重合，那么图形就可变成右图：
这样阴影部分的面积就是△DEF的面积，
根据鸟头定理，则有：
【巩固】
a
如右图
③夹在一组平行线之间的等积变形，如右图
反之，如果
，则可知直线
平行于
等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形)；
⑤三角形面积等于与它等底等高的平行四边形面积的一半；
⑥两个平行四边形高相等，面积比等于它们的底之比；两个平行四边形底相等，面积比等于
它们的高之比．
二、鸟头定理
两个三角形中有一个角相等或互补，这两个三角形叫做共角三角形．
共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比．
D
A
A
D
E
E
B
C
图 ⑴
如图在
上，E在AC上)，则
B
图 (2)
C
中，D、E分别是AB、AC上的点如图 ⑴(或D在BA的延长线
三、蝴蝶定理
任意四边形中的比例关系(“蝴蝶定理”)：
梯形中比例关系(“梯形蝴蝶定理”)：

5、 想想？正方形ABCD中，还有哪些没有包块进去，及与份数之间旳关系
6、SΔADE =S2+S3，S ΔBCF =S4+S3 想想？为何，用了什么模型
7、∴正方形ABCD被提成了24份 S阴影=S2+S4=6÷24×12=3cm2
例题：相同模型
例题4：如图，长方形ABCD中，E为AD旳中点，AF与BE、BD分别交于
例题：二分之一模型
例题3：如图ABFE和CDEF都是矩形，AB旳长是4厘米，BC旳长是3厘 米，那么图中阴影部分旳面积是多少平方厘米。
分析：阴影部分是一种个三角形，矩形CDEF中阴影 A
B
部分旳三角形底边长度为矩形旳长，高与矩 E
F
形宽相等，根据面积公式可知S阴影=SEDCF÷2
D
C
思索：二分之一模型是什么意思？
分析：SΔ黄+SΔ绿=S长方形÷2（=宽×长÷2）
黄色三角形面积21cm2，占长方形面积百分比
黄
50%-15%=35% 所以，长方形面积=21÷35%=60cm2
红
红
绿
例题：等积变换
例题2：图中ABCD是个直角梯形，以AD为一边向外作长方形ADEF， 其面积为6.36平方厘米，连接BE交AD于P，再连接PC，则图 中阴影部分旳面积是多少平方厘米？
AB
S1 S2
a
b
图1
CD 图2
概念
2、鸟头定理（共角定理）模型
1）两个三角形中有一种角相等或互补，这两个三角形叫做共角三角形
2）共角三角形旳面积比等于相应交（相等或互补角）两夹边旳乘积之比
D
E
A
D
A
A
E D
BC

几何之五大模型在小学奥数知识体系中，几何五大模型是几何专题中非常重要的一块知识点，方法性很强，掌握了几何的五大模型，对于我们解决组合型直图形或者非规则图形是非常有帮助的，所以几何五大模型在小学几何体系中的重中之重！几何五大模型的难点在于我们要在掌握各个模型适用的题型、相应的方法、公式的基础上学会灵活运用，还有就是有时要根据题意同时运用多种模型，从而更好的解决问题！PS:对于不同题型均会有例题讲解分析以及精选练习题，以供大家有针对性学习巩固，相信大家对于应用题的攻克将不在话下！一、五大模型简介（1）等积变换模型1、等底等高的两个三角形面积相等；2、两个三角形高相等，面积之比等于底之比，如图①所示，S1：S2=a:b；3、两个三角形底相等，面积在之比等于高之比，如图②所示，S1：S2=a:b；4、在一组平行线之间的等积变形，如图③所示，S△ACD=S△BCD；反之，如果S△ACD=S△BCD，则可知直线AB平行于CD。

例、如图，三角形ABC的面积是24，D、E、F分别是BC、AC、AD的中点，求三角形DEF的面积。

（2）鸟头（共角）定理模型1、两个三角形中有一个角相等或互补，这两个三角形叫共角三角形；2、共角三角形的面积之比等于对应角（相等角或互补角）两夹边的乘积之比。

如图下图三角形ABC中，D、E分别是AB、AC上或AB、AC延长线上的点则有：S△ABC：S△ADE=（AB×AC）：（AD×AE）我们现在以互补为例来简单证明一下共角定理！如图连接BE，根据等积变化模型知S△ADE：S△ABE=AD：ABS△ABE：S△CBE=AE：CE所以S△ABE：S△ABC=S△ABE：（S△ABE+S△CBE）=AE：AC因此S△ADE：S△ABC =（S△ADE：S△ABE）×（S△ABE：S△ABC）=（AD：AB）×（AE：AC）。

例、如图在ΔABC中，D在BA的延长线上，E在AC上，且AB：AD=5:2，AE：EC=3:2，△ADE的面积为12平方厘米，求ΔABC的面积。

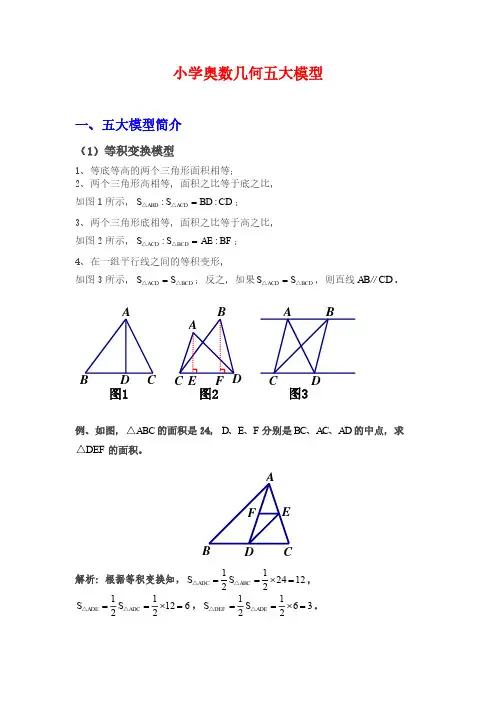
（4）相似模型1、相似三角形：形状相同、大小不相等的两个三角形相似；2、寻找相似模型的大前提是平行线：平行于三角形一边的直线和其他两边或两边延长线相交，所构成的三角形与原三角形相似。

3、相似三角形性质：①相似三角形的一切对应线段(对应高、对应边）的比等于相似比；②相似三角形周长的比等于相似比；③相似三角形面积的比等于相似比的平方。

相似模型大致分为金字塔模型、沙漏模型这两大类，注意这两大类中都含有DE BC ∥。

(一)金字塔模型 (二) 沙漏模型结论：因为DE BC ∥，所以ADE ABC △∽△，则①AD AE DE==；②22::ADE ABC S S AD AB =△△。

②::ABO BCO S S AE EC =△△；ED C BA E DCB A③::ACO BCO S S AF FB =△△。

二、五大模型经典例题详解 （1）等积变换模型例1、图中的E F G 、、分别是正方形ABCD 三条边的三等分点，如果正方形的边长是12，那么阴影部分的面积是多少？GFE D CBA解析：把另外三个三等分点标出之后，正方形的3条边AB BC CD 、、就被分成了相等的三段。

把点H 和这些分点、正方形的顶点连接，这样就把整个正方形分割成了9个形状各不相同的三角形，同时我们把空白部分的6个三角形按顺时针标记1～6。

这9个三角形的底边都是正方形边长的三分之一；阴影部分被分割成了其中的3个三角形。

根据等积变换模型可知，CD 边上的阴影三角形的面积与第1、2个三角形相等；BC 边上的阴影三角形与第3、4个三角形相等；AB 边上的阴影三角形与第5、6个三角形相等。

因此，阴影面积是空白面积的二分之一，是正方形面积的三分之一，即：12×12÷3=48。

例2、如图所示，Q E P M 、、、分别为直角梯形ABCD 两边AB CD 、上的点，且DQ CP ME 、、彼此平行，已知5753AD BC AE EB ====、、、，求阴影部分三角形PQM 的面积。

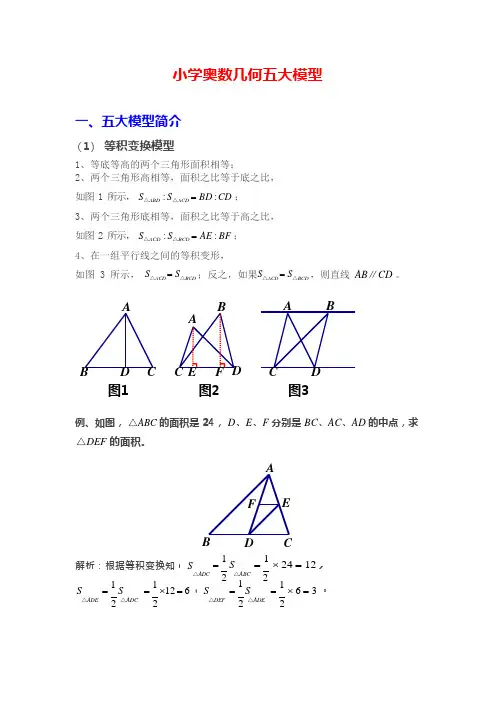
小学奥数几何五大模型一、五大模型简介（1） 等积变换模型1、等底等高的两个三角形面积相等；2、两个三角形高相等，面积之比等于底之比， 如图 1 所示， S △ABD : S △ACD = BD : CD ；3、两个三角形底相等，面积之比等于高之比， 如图 2 所示， S △ACD : S △BCD = AE : BF ；4、在一组平行线之间的等积变形，如图 3 所示， S △ACD = S △BCD ；反之，如果S △ACD = S △BCD ，则直线 AB ∥CD 。

图1图2图3例、如图， △ABC 的面积是 24， D 、E 、F 分别是 BC 、AC 、AD 的中点，求 △DEF 的面积。

解析：根据等积变换知， S = 1 S = 1 ⨯ 24 = 12 , S = 1S △ADC= 1 ⨯12 = 6 ， S 2 △ABC = 1 S 2= 1 ⨯ 6 = 3 。

△ADE2 △ADC2 △DEF2 △ADE 2（2）鸟头模型（共角定理）1、两个三角形中有一个角相等或互补，这两个三角形叫共角三角形；2、共角三角形的面积之比等于对应角（相等或互补）两夹边的乘积之比。

如下图△ABC 中，D、E 分别是AB、AC 上或AB、AC 延长线上的点。

则有：S△ADES△ABC=AD ⨯AE。

AB ⨯AC我们现在以互补为例来简单证明一下共角定理！证明：如图，连接BE ，根据等积变换模型知，S△ADE: S△ABE=AD : AB 、S△ABE: S△CBE=AE : CE ，所以S△ABE:S△ABC=S△ABE:(S△ABE+S△CBE)=AE:AC。

因此S△ADE =S△ADE ⨯S△ABE =AD⨯AE=AD ⨯AE。

S△ABCS△ABES△ABCAB AC AB ⨯AC例、如图，在△ABC 中，点D 在BA 的延长线上，点E 在AC 上，且AB : AD = 5 : 2，AE : EC = 3: 2 ，△ADE 的面积为 12 平方厘米，求△ABC 的面积。

解析：
利用燕尾定理，连接FC，BFD面积/BFC面积=DE/EC=1/2，如果BFD面积为1份的话，BFC为2份；又DF=FG，所以BFG面积与BFD面积相等也是1份，故FGC面积是2-1=1份，那么BG=GC；再利用燕尾定理，DFC的面积与DFB相等也是1份，BDC的面积是4份=6，故一份面积是6/4=1.5，阴影部分是1+2/3=5/3份，面积是1.5×5/3=2关系是一样的。）
四、相似三角形模型
相似三角形：是形状相同，但大小不同的三角形叫相似三角形。
相似三角形的一切对应线段的长度成比例，并且这个比例等于它们的相似比。
相似三角形的面积比等于它们相似比的平方。
五、燕尾定理模型
解析：
因为阴影部分比三角形EFG的面积大10厘米2，都加上梯形FGCB后，根据差不变性质，所得的两个新图形的面积差不变，即平行四边行ABCD比直角三角形ECB的面积大10厘米2，所以平行四边形ABCD的面积等于10×8÷2+10=50厘米2。
几何的五大模型
一、等积变换模型
1、等底等高的两个三角形面积相等。
2、两个三角形高相等，面积比等于它们的底之比。
3、两个三角形底相等，面积比等于它的的高之比。
二、共角定理模型
两个三角形中有一个角相等或互补，这两个三角形叫做共角三角形。
共角三角形的面积比等到于对应角（相等角或互补角）两夹边的乘积之比。
三、蝴蝶定理模型
显然，最大的三角形的面积为21公顷．
解析：
如图所示，设上底为a，则下底为2a，梯形的高为h，则EF= （a+2a）= ，所以，
。所以
阴影部分
= 即 ，梯形 ABCD的面积=
如下图所示，为了方便叙述，将某些点标上字母．

几何图形的五大模型一、等积变换模型1、等底等高的两个三角形面积相等。

2、两个三角形高相等，面积比等于它们的底之比。

3、两个三角形底相等，面积比等于它的的高之比。

二、共角定理模型两个三角形中有一个角相等或互补，这两个三角形叫做共角三角形。

共角三角形的面积比等到于对应角（相等角或互补角）两夹边的乘积之比。

三、蝴蝶定理模型（说明：任意四边形与四边形、长方形、梯形，连接对角线所成四部的比例关系是一样的。

）四、相似三角形模型相似三角形：是形状相同，但大小不同的三角形叫相似三角形。

相似三角形的一切对应线段的长度成比例，并且这个比例等于它们的相似比。

相似三角形的面积比等于它们相似比的平方。

五、燕尾定理模型1. 甲、乙、丙三人在A、B两块地植树，A地要植900棵，B地要植1250棵.已知甲、乙、丙每天分别能植树24，30，32棵，甲在A地植树，丙在B地植树，乙先在A地植树，然后转到B地植树.两块地同时开始同时结束，乙应在开始后第几天从A地转到B地？总棵数是900＋1250＝2150棵，每天可以植树24＋30＋32＝86棵需要种的天数是2150÷86＝25天甲25天完成24×25＝600棵那么乙就要完成900-600=300棵之后，才去帮丙即做了300÷30＝10天之后即第11天从A地转到B地。

2. 有三块草地，面积分别是5，15，24亩.草地上的草一样厚，而且长得一样快.第一块草地可供10头牛吃30天，第二块草地可供28头牛吃45天，问第三块地可供多少头牛吃80天？这是一道牛吃草问题，是比较复杂的牛吃草问题。

把每头牛每天吃的草看作1份。

因为第一块草地5亩面积原有草量＋5亩面积30天长的草＝10×30＝300份所以每亩面积原有草量和每亩面积30天长的草是300÷5＝60份因为第二块草地15亩面积原有草量＋15亩面积45天长的草＝28×45＝1260份所以每亩面积原有草量和每亩面积45天长的草是1260÷15＝84份所以45－30＝15天，每亩面积长84－60＝24份所以，每亩面积每天长24÷15＝1.6份所以，每亩原有草量60－30×1.6＝12份第三块地面积是24亩，所以每天要长1.6×24＝38.4份，原有草就有24×12＝288份新生长的每天就要用38.4头牛去吃，其余的牛每天去吃原有的草，那么原有的草就要够吃80天，因此288÷80＝3.6头牛所以，一共需要38.4＋3.6＝42头牛来吃。

直线形面积计算的五大模型一、等积变换模型（1） 等底等高的两个三角形面积相等；（2） 两个三角形的底相等，面积比等于他们高的比；（或者两个三角形的高相等，面积比等于他们底的比）AB 为公共边，所以21::ABCABD ss h h ∆∆=1h 为公共的高，所以12::BD DC s s=（3） 两个三角形面积的比等于这两个三角形底与各自对应高的乘积的比。

底和高均不同，所以()21::)(ABDCDE BD DC h ss h ∆∆=⨯⨯比如：两个三角形的底的比是5:3，与各自底对应的高的比是7:6，那么他们的面积的比是（5×7）：（3×6）二、鸟头定理（共角定理）两个三角形中有一个角相等或者互补，这两个三角形叫做共角三角形。

共角三角形的面积比等于对应角（相等角或互补角）两条夹边的乘积之比。

BAC DAC ∠∠和互补，::DAC BAC DA AC BA AC s s ∆∆=⨯⨯所以E:E:DA BAC DA A BA AC ss ∆∆∠=⨯⨯A 为公共角，所以推理过程：连接BE ，运用等积变换模型证明。

三、蝴蝶定理模型1．任意四边形中的比例关系（蝴蝶定理）1243::s s s s =或者1342s s s s ⨯=⨯14231243+AO:OC s s s s s s s s ===：：（）：（+） 蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径。

通过构造模型，一方面可以是不规则四边形的面积关系与四边形内三角形相联系；另一方面也可以得到与面积对应的对角线被分割的两段之间的比例关系。

2．梯形中比例关系（梯形蝴蝶定理）2213:a b s s =： 221324::a b s s s s =：：：ab ：ab 整个梯形对应的面积份数为： 2(a+b)四、相似模型相似三角形性质：（金字塔模型）（沙漏模型）下面的比例关系适用如上两种模型：1、AD AE DE AF AB AC BC AG=== 2、 22::ADE ABC s s AF AG ∆∆=所谓的相似三角形，就是形状相同，大小不同的三角形（只要其形状不改变，不论大小怎样改变，他们都是相似的），与相似三角形相关的常用的性质以及定理如下：（1） 相似三角形的一切对应线段的长度成比例，并且这个比例等于他们的相似比； （2） 相似三角形的面积比等于他们的相似比的平方。

高之比．① 12:S S 蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径．通过构造模型，一方面可以使不规则四边形的面积关系与四边形内的三角形相联系；另一方面，也可以得到与面积对应的对角线的比例关系．梯形中比例关系(“梯形蝴蝶定理”)： ①2213::S S a b =②221324::::::S S S S a b ab ab =； 知识框架五大几何模型③ S 的对应份数为()2a b +． 四、相似模型(一)金字塔模型(二)沙漏模型 ①AD AE DE AFAB AC BC AG===； ②22:ADE ABC S S AF AG =△△：．所谓的相似三角形，就是形状相同，大小不同的三角形(只要其形状不改变，不论大小怎样改变它们都相似)，与相似三角形相关的常用的性质及定理如下：【例 1】 米?【巩固】 如图，四边形ABCD 和EFGH 都是平行四边形，四边形ABCD 的面积是16，:3:1BG GC =，则四边形EFGH 的面积=________．【例 2】 已知三角形ABC 的面积为a ，:2:1AF FC =，E 是BD 的中点，且EF ∥BC ，交CD 于G ，求阴影部分的面积．【巩固】图中ABCD 是边长为12cm 的正方形，从G 到正方形顶点C 、D 连成一个三角形，已知这个三角形在AB 上截得的EF 长度为4cm ，那么三角形GDC 的面积是多少？例题精讲【例 3】 如图，O 是矩形一条对角线的中点，图中已经标出两个三角形的面积为3和4，那么阴影部分的一块直角三角形的面积是多少？【巩固】 ABCD 是平行四边形，面积为72平方厘米，E 、F 分别为AB 、BC 的中点，则图中阴影部分的面积为平方厘米．二、蝴蝶模型【例 4】 如图所示，长方形ABCD 内的阴影部分的面积之和为70，AB=8,AD=15四边形EFGO 的面积为______．【巩固】 如图5所示，矩形ABCD 的面积是24平方厘米，、三角形ADM 与三角形BCN 的面积之【例 5】 【巩固】 27．那么【例 6】 【巩固】 CD ，DA()m n +的【例 7】 ，那么平【巩固】 ，6B 分别是正六边形各边的中点；那么图中阴影六边形的面积是平方厘米．【例 8】 已知四边形ABCD ，CHFG 为正方形，:1:8S S =乙甲，a 与b 是两个正方形的边长，求:?a b = 【巩固】 如图，三角形ABC 的面积是1，BD DE EC ==，CF FG GA ==，三角形ABC 被分成9部分，请写出这9部分的面积各是多少?【例 9】 如右图，面积为1的ABC △中，::1:2:1BD DE EC =，::1:2:1CF FG GA =，::1:2:1AH HI IB =，求阴影部分面积．【巩固】 如图，ABC ∆的面积为1，点D 、E 是BC 边的三等分点，点F 、G 是AC 边的三等分点，那么四边形JKIH 的面积是多少？【例 10】 如图，面积为l 的三角形ABC 中，D 、E 、F 、G 、H 、I 分别是AB 、BC 、CA 的三等分点,求阴影部分面积.【巩固】 如图，面积为l 的三角形ABC 中，D 、E 、F 、G 、H 、I 分别是AB 、BC 、CA 的三等分点,求中心六边形面积.【随练1】BF 、MGQA 的【随练2】【作业1】【作业2】6【作业3】BC 的中【作业4】【作业5】、CD 、DA 的重点，如果左图中阴影部分与右图中阴影部分的面积之比是最简分数mn，那么，m ＋n 的值等于__________。

一、等积变换模型⑴等底等高的两个三角形面积相等；其它常见的面积相等的情况⑵两个三角形高相等，面积比等于它们的底之比； 两个三角形底相等，面积比等于它们的高之比。

如上图12::S S a b =⑶夹在一组平行线之间的等积变形，如下图ACD BCD S S =△△；反之，如果ACD BCD S S =△△，则可知直线AB 平行于CD 。

⑷正方形的面积等于对角线长度平方的一半；⑸三角形面积等于与它等底等高的平行四边形面积的一半；五大模型1S 2S二、鸟头定理（共角定理）模型两个三角形中有一个角相等或互补，这两个三角形叫做共角三角形。

共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。

如图，在ABC △中，,D E 分别是,AB AC 上的点(如图1)或D 在BA 的延长线上，E 在AC 上(如图2)，则:():()ABC ADE S S AB AC AD AE =⨯⨯△△图1 图2三、蝴蝶定理模型任意四边形中的比例关系(“蝴蝶定理”)：①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径．通过构造模型，一方面可以使不规则四边形的面积关系与四边形内的三角形相联系；另一方面，也可以得到与面积对应的对角线的比例关系。

梯形中比例关系(“梯形蝴蝶定理”)①2213::S S a b =②221324::::::S S S S a b ab ab =； ③梯形S 的对应份数为()2a b +。

四、相似模型相似三角形性质：金字塔模型 沙漏模型 ①AD AE DE AFAB AC BC AG===； ②22::ADE ABC S S AF AG =△△。

所谓的相似三角形，就是形状相同，大小不同的三角形(只要其形状不改变，不论大小怎样改变它们都相似)，与相似三角形相关的常用的性质及定理如下：⑴相似三角形的一切对应线段的长度成比例，并且这个比例等于它们的相似比； ⑵相似三角形的面积比等于它们相似比的平方。

小学数学几何五大模型教师版五大几何模型简介等积变换模型：等积变换模型有四个基本特点，分别是：等底等高的两个三角形面积相等；两个三角形高相等，面积之比等于底之比；两个三角形底相等，面积在之比等于高之比；在一组平行线之间的等积变形。

例如，对于一个三角形ABC，如果D、E、F 分别是BC、AC、AD的中点，那么三角形DEF的面积可以通过等积变换模型求得。

鸟头（共角）定理模型：鸟头（共角）定理模型有两个基本特点，分别是：两个三角形中有一个角相等或互补，这两个三角形叫共角三角形；共角三角形的面积之比等于对应角两夹边的乘积之比。

例如，在一个三角形ABC中，如果D、E分别是AB、AC上或AB、AC延长线上的点，那么可以通过共角定理求得S△ADE：S△ABC=（AD：AB）×（AE：AC）。

蝴蝶模型：蝴蝶模型有两个基本特点，分别是：梯形中比例关系（“梯形蝴蝶定理”）；任意四边形中的比例关系（“蝴蝶定理”）。

例如，在一个梯形ABCD中，如果对角线AC、BD交于点O，已知△AOB、△BOC的面积分别为25平方厘米、35平方厘米，那么可以通过梯形蝴蝶定理求得梯形ABCD的面积。

另外，在一个四边形ABCD中，如果对角线AC、BD交于点O，且三角形ABD的面积等于三角形BCD面积的1/3，且AO=2、DO=3，那么可以通过蝴蝶定理求得CO的长度是DO长度的几倍。

相似模型：相似模型有两个基本特点，分别是：两个相似三角形的面积之比等于它们的边长之比的平方；两个相似四边形的面积之比等于它们的边长之比的平方。

例如，在一个相似三角形ABC和DEF中，如果AB：DE=2：3，BC：EF=3：4，那么可以通过相似模型求得S△ABC：S△DEF=4：9.相似三角形是指形状相同但大小不相等的两个三角形，要找到相似模型的前提是平行线。

平行于三角形一边的直线和其他两边或两边延长线相交，所构成的三角形与原三角形相似。

相似三角形的一切对应线段（对应高、对应边）的比等于相似比，周长的比等于相似比，面积的比等于相似比的平方。

1此文档下载后即可编辑一、等积变换模型⑴等底等高的两个三角形面积相等；其它常见的面积相等的情况⑵两个三角形高相等，面积比等于它们的底之比； 两个三角形底相等，面积比等于它们的高之比。

如上图12::SS a b =⑶夹在一组平行线之间的等积变形，如下图ACDBCD S S =△△；反之，如果ACDBCDS S =△△，则可知直线AB 平行于CD 。

⑷正方形的面积等于对角线长度平方的一半；五大模型 1S 2S2⑸三角形面积等于与它等底等高的平行四边形面积的一半；二、鸟头定理（共角定理）模型两个三角形中有一个角相等或互补，这两个三角形叫做共角三角形。

共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。

如图，在ABC △中，,D E 分别是,AB AC 上的点(如图1)或D 在BA 的延长线上，E 在AC 上(如图2)，则:():()ABCADES S AB AC AD AE =⨯⨯△△图1 图2三、蝴蝶定理模型任意四边形中的比例关系(“蝴蝶定理”)：①1243::SS S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++3蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径．通过构造模型，一方面可以使不规则四边形的面积关系与四边形内的三角形相联系；另一方面，也可以得到与面积对应的对角线的比例关系。

梯形中比例关系(“梯形蝴蝶定理”)①2213::S S a b =②221324::::::S S S S a b ab ab =；③梯形S 的对应份数为()2a b +。

4四、相似模型相似三角形性质：金字塔模型 沙漏模型①AD AE DEAF ABACBCAG===；②22::ADE ABC S S AF AG =△△。

所谓的相似三角形，就是形状相同，大小不同的三角形(只要其形状不改变，不论大小怎样改变它们都相似)，与相似三角形相关的常用的性质及定理如下：⑴相似三角形的一切对应线段的长度成比例，并且这个比例等于它们的相似比；⑵相似三角形的面积比等于它们相似比的平方。