第六章回顾与思考——变量之间的关系[上学期]--北师大版-

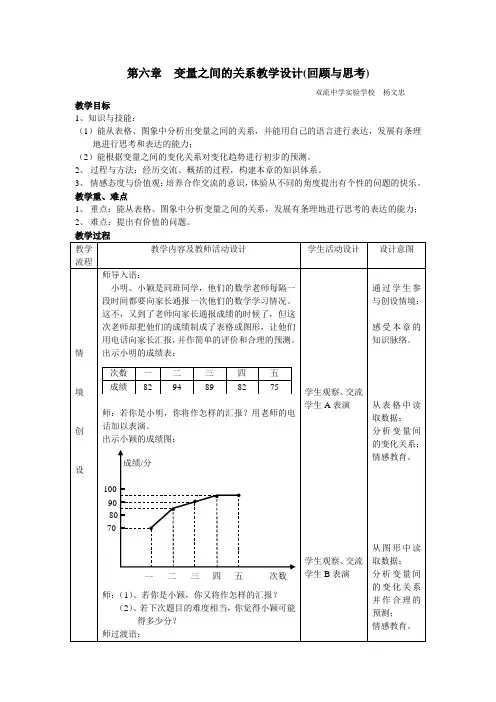
第六章变量之间的关系教学设计(回顾与思考)
双流中学实验学校杨文忠
教学目标
1、知识与技能：
（1）能从表格、图象中分析出变量之间的关系，并能用自己的语言进行表达，发展有条理地进行思考和表达的能力；
（2）能根据变量之间的变化关系对变化趋势进行初步的预测。

2、过程与方法：经历交流、概括的过程，构建本章的知识体系。

3、情感态度与价值观：培养合作交流的意识，体验从不同的角度提出有个性的问题的快乐。

教学重、难点
1、重点：能从表格、图象中分析变量之间的关系，发展有条理地进行思考的表达的能力；
2、难点：提出有价值的问题。

教学过程。

北师大版初中数学目录七年级上册第一章丰富的图形世界1．生活中的立体图形2．展开与折叠3．截一个几何体4．从不同方向看5．生活中的平面图形回忆与思考复习题第二章有理数及其运算1．数怎么不够用了2．数轴3．绝对值4．有理数的加法5．有理数的减法6．有理数的加减混合运算7．水位的变化8．有理数的乘法9．有理数的除法10．有理数的乘方11．有理数的混合运算12．计算器的使用回忆与思考复习题第三章字母表示数1．字母能表示什么2．代数式3．代数式求值4．合并同类项5．去括号6．探索规律回忆与思考复习题第四章平面图形及其位置关系1．线段、射线、直线2．比拟线段的长短3．角的度量与表示4．角的比拟5．平行6．垂直7．有趣的七巧板8．图案设计回忆与思考复习题第五章一元一次方程1．你今年几岁了2．解方程3．日历中的方程4．我变胖了5．打折销售6．“希望工程〞义演7．能追上小明吗8．教育储蓄回忆与思考复习题第六章生活中的数据1．100万有多大2．科学记数法3．扇形统计图4．月球上有水吗5．统计图的选择回忆与思考复习题第七章可能性1．一定摸到红球吗2．转盘游戏3．谁转出的四位数大回忆与思考复习题课题学习制成一个尽可能大的无盖长方体总复习七年级下册第一章整式的运算1．整式2．整式的加减3．同底数幂的乘法4．幂的乘方与积的乘方5．同底数幂的除法6．整式的乘法7．平方差公式8．完全平方公式9．整流器式的除法回忆与思考复习题第二章平行线与相交线1．台球桌面上的角2．探索直线平行的条件3．平行线的特征4．用尺规作线段和角回忆与思考复习题第三章生活中的数据1．认识百万分之一2．近似数和有效数字3．世界新生儿图回忆与思考复习题课题学习制作“人口图〞第四章概率1．游戏公平吗2．摸到红球的概率3．停留在黑砖上的概率回忆与思考复习题第五章三角形1．认识三角形2．图形的全等3．图案设计4．全等三角形5．探索三角形全等的条件6．作三角形7．利用三角形全等测距离8．探索直角三角形全等的条件回忆与思考复习题第六章变量之间的关系1．小车下滑的时间2．变化中的三角形3．温度的变化4．速度的变化回忆与思考复习题第七章生活中的轴对称1．轴对称现象2．简单的轴对称图形3．探索轴对称的性质4．利用轴对称设计图案5．镜子改变了什么6．镶边与剪纸回忆与思考复习题总复习八年级上册第一章勾股定理1．探索勾股定理2．能得到直角三角形吗3．蚂蚁怎样走最近回忆与思考复习题课题学习拼图与勾股定理第二章实数1．数怎么又不够用了2．平方根3．立方根4．公园有多宽5．用计算器开方6．实数回忆与思考复习题第三章图形的平移与旋转1．生活中的平移2．简单的平移作图3．生活中的旋转4．简单的旋转作图5．它们是怎样变过来的6．简单的图案设计回忆与思考复习题第四章四边形性质探索1．平行四边形的性质2．平行四边形的判别3．菱形4．矩形、正方形5．梯形6．探索多边形的内角和与外角和7．平面图形的密铺8．中心对称图形回忆与思考复习题第五章位置确实定1．确定位置2．平面直角坐标系3．变化的鱼回忆与思考复习题第六章一次函数1．函数2．一次函数3．一次函数的图象4．确定一次函数表达式5．一次函数图象的应用回忆与思考复习题第七章二元一次方程组1．谁的包裹多2．解二元一次方程组3．鸡兔同笼4．增收节支5．里程碑上的数6．二元一次方程与一次函数回忆与思考复习题第八章数据的代表1．平均数2．中位数与众数3．利用计算器求平均数回忆与思考复习题总复习八年级下册第一章一元一次不等式和一元一次不等式组1．不等关系2．不等式的根本性质3．不等式的解集4．一元一次不等式5．一元一次不等式与一次函数6．一元一次不等式组回忆与思考复习题第二章相似图形1．线段的比2．黄金分割3．形状相同的图形4．相似多边形5．相似三角形6．探索三角形相似的条件7．测量旗杆的高度8．相似多边形的周长比和面积比9．图形的放大与缩小回忆与思考复习题课题学习制作视力表第三章分解因式1．分解因式2．提公因式法3．运用公式法回忆与思考复习题第四章分式1．分式2．分式的乘除法3．分式的加减法4．分式方程回忆与思考复习题第五章数据的收集与处理1．每周干家务活的时间2．数据的收集3．频数与频率4．数据的波动回忆与思考复习题课题学习吸烟的危害第六章证明〔一〕1．你能肯定吗2．定义与命题3．为什么它们平行4．如果两条直线平行5．三角形内角和定理的证明6．关注三角形的外角回忆与思考复习题总复习九年级上册第一章证明〔二〕1．你能证明它们吗2．直角三角形3．线段的垂直平分线4．角平分线回忆与思考复习题第二章一元二次方程1．花边有多宽2．配方法3．公式法4．分解因式法5．为什么是1.618回忆与思考复习题第三章证明〔三〕1．平行四边形2．特殊平行四边形回忆与思考复习题第四章视图与投影1．视图2．太阳光与影子3．灯光与影子回忆与思考复习题第五章反比例函数1．反比例函数2．反比例函数的图象与性质3．反比例函数的应用回忆与思考复习题课题学习猜测、证明与拓广第六章频率与概率1．频率与概率2．投针实验3．池塘里有多少条鱼回忆与思考复习题总复习九年级下册〔培训用书〕第一章直角三角形的边角关系1．从梯子的倾斜程度谈起2．30o，45o，60o角的三角函数值3．三角函数的有关计算4．船有触礁的危险吗回忆与思考复习题第二章二次函数1．二次函数所描述的关系2．结识抛物线3．刹车距离与二次函数4．二次函数的图象5．用三种方式表示二次函数6．何时获得最大利润7．最大面积是多少8．二次函数与一元二次方程回忆与思考复习题课题学习拱桥设计第三章圆1．车轮为什么做成圆形2．圆的对称性3．圆周角和圆心角的关系4．确定圆的条件5．直线和圆的位置关系6．圆和圆的位置关系7．弧长及扇形的面积8．圆锥的侧面积回忆与思考复习题课题学习设计庶阳棚第四章统计与概率1．50年的变化2．哪种方式更合算3．游戏公平吗回忆与思考复习题课题学习媒体中的数学总复习。

版权申明本文部分内容，包括文字、图片、以及设计等在网上搜集整理.版权为个人所有This article includes some parts, including text, pictures, and design. Copyright is personal ownership.b5E2R。

用户可将本文地内容或服务用于个人学习、研究或欣赏，以及其他非商业性或非盈利性用途，但同时应遵守著作权法及其他相关法律地规定，不得侵犯本网站及相关权利人地合法权利.除此以外，将本文任何内容或服务用于其他用途时，须征得本人及相关权利人地书面许可，并支付报酬.p1Ean。

Users may use the contents or services of this article for personal study, research or appreciation, and other non-commercial or non-profit purposes, but at the same time, they shall abide by the provisions of copyright law and other relevant laws, and shall not infringe upon the legitimate rights of this website and its relevant obligees. In addition, when any content or service of this article is used for other purposes, written permission and remuneration shall be obtained from the person concerned and the relevant obligee.DXDiT。

第六章概率的进一步认识回顾与思考一、学生知识状况分析在以前概率学习的基础上，本章进一步研究了理论概率与实验概率之间的关系，并通过几个现实生活模型介绍了随机事件的概率的实验估算方法和涉及两步及两步以上实验的随机事件理论概率计算的又一种方法——列表法.本节引导学生回顾本章内容，梳理知识结构，同时，到本章为止，学生基本完成了义务教育阶段有关概率知识的学习.二、教学任务分析在学生充分思考和交流的基础上，教师可引导学生共同回忆有关概率的知识框架图. 本节课的任务是在本章知识讲完后，需要学生将知识系统化，进一步理解概率与频率的关系；能进一步体会应用试验的方法估计一些事件的概率；归纳总结求概率的一般方法；合理运用概率的思想，解决生活中的实际问题.三、教学过程分析本节课设计了五个教学环节.第一环节：问题引入，复习旧知；第二环节：重点知识回顾，建立知识架构；第三环节：课堂练习；第四环节：课堂小结；第五环节：作业布置。

第一环节：问题引入，复习旧知活动内容：把本章知识习题化，从而引入新课.活动目的：抽象问题具体化，引入新课，同时对全章知识的系统回顾提供了铺垫.活动过程：在有一个10万人的小镇,随机调查了2000人,其中有250人看中央电视台的早间新闻.在该镇随便问一个人,他看早间新闻的概率大约是多少?该镇看中央电视台早间新闻的大约是多少人?解:根据概率的意义,可以认为其概率大约等于250/2000=0.125.该镇约有100000×0.125=12500人看中央电视台的早间新闻.活动效果：学生通过对本环节设计问题的解答，激活学生头脑中原有的知识.第二环节：重点知识回顾，建立知识架构活动内容：帮助学生回顾♦ 1.某个事件发生的概率是1/2,这意味着在两次重复试验中该事件必有一次发生吗?♦ 2.你能用试验的方法估计那些事件发生的概率?举例说明.♦ 3.有时通过试验的方法估计一个事件发生的概率有一定的难度,你能否通过模拟试验估计该事件发生的概率?♦ 4.你掌握了哪些求概率的方法?举例说明.活动目的：通过本环节的学习使学生的知识系统化条理化.实现知识目标，使学生系统地掌握本章所学的知识，建立有关概率知识的框架图.活动过程：引导学生对上述四个问题，进行回顾，在过程中可以通过具体的例子加以解释和说明，同时安排练习。

八年级数学第六章回顾与思考——变量之间的关系一、教学目标：1、知识与技能目标：使学生感受现实世界中的变量和变量之间存在各式各样的关系及变量之间的规律，了解表示这些关系的基本方法。

2、过程与方法目标：让学生经历探索具体情景中两个变量之间关系的过程，进一步发展符号感和抽象思维的能力。

3、情感与态度目标：引导学生能从运动变化的角度解释生活中的数学现象，体验成就感，获得学习的快乐，发展对数学更高层次的认识。

二、重点与难点：重点：感受和体验从运动变化的角度来认识数学对象的过程。

难点：根据具体问题选取不同的方式来表示变量之间的关系，能解决简单的现实问题。

三、教学过程与设计：通过对第六章的学习，我们知道了如何用数学的方法去理解现实生活中的变化问题。

下面我们来看一个事例。

活动一、再次认识变量之间的关系事例：一天，在全长267千米的沪宁高速公路上，一辆轿车早上6：00从某某出发以80千米/时的速度匀速行驶开往某某，随着时间t的变化汽车行驶的路程s也相应发生着变化。

●我们思考：事例中哪些量是变量？他们之间的相互地位如何？（时间t和路程s是变量; 其中s随t的变化而变化，所以t是自变量，s是因变量）回忆我们学过的知识，大家思考：你怎样来表示它们之间的变化关系？用什么方法？（图象、表格、关系式）●此时板书设计：●幻灯片打出图像:表格：关系式：s = 80t●提问：1、填表2、通过图像、关系式、表格预测轿车几点能到某某。

（大约9：20到）●在黑板上勾勒出知识结构图。

●总结：通过对本章知识体系的整理，我们知道要用变量的思想去分析问题，首先找出问题中存在的变量，确定自变量与因变量，尽可能多的从图像，表格，和表达式中得到有用信息，来分析变量之间的关系。

活动二、观察与思考1、下列各情景分别可以用哪一幅图来近似的刻画？（1） 汽车紧急刹车（速度与时间的关系） （D ） （2） 人的身高变化（身高与年龄的关系） （B ） （3） 跳高运动员跳跃横杆（高度与时间的关系） （C ） （4） 一面冉冉上升的红旗（高度与时间的关系） （A ）2、某种油箱容量为60升的汽车，加满汽油后，汽车行驶时油箱的油量Q （升）随汽车行驶时间t （时）变化的关系式如下：Q ＝60－6t（1）请完成下表（2） 汽车行驶5小时后，油箱中油量是升（3）若汽车行驶过程中，油箱的油量为12升，则汽车行驶了小时(C) (D)(A)(B)（4）贮满60升汽油的汽车，最多行驶小时（5）下面哪个图像能够反映变量Q 与t 的关系：（ ）活动三、应用与解释1、沪宁高速公路是某某省第一条高速公路。

初一数学第六章变量之间的关系北师大版【本讲教育信息】一. 教学内容：第六章变量之间的关系［教学要求］1、能分清实际问题中的常量与变量、自变量与因变量，并能举出反映变量之间关系的例子。

2、通过对某种图形中变量之间关系的探索，进一步体验一个变量的变化对另一个变量的影响，发展符号感。

能根据具体问题，用关系式表示某些变量之间的关系。

3、经历从图像中分析变量之间关系的过程进一步感受变量之间的关系。

4、进一步经历从图中分析变量之间关系的过程，从而加深对图像表示自变量与因变量关系的理解，逐步培养从图像中获取信息的能力。

［重点及难点］1、重点是对常量、自变量及因变量等概念的理解。

难点是根据表格中的数据尝试对变化趋势进行初步的预测。

2、重点是根据具体问题求自变量与因变量之间的关系式，并能用关系式求因变量的值。

难点是建立实际问题中自变量与因变量之间的关系式。

3、从熟悉的情景出发用图像直观的表示两个变量之间的关系，并获得对图像反映变量之间关系的体验。

4、重点是从图像中获取信息，难点是用语言描述图像所表示的变化过程。

［知识要点］一、小车下滑的时间1、如果用h 表示支撑物的高度，t 表示小车下滑时间，随着h 逐渐变大，t 的变化趋势是什么？在表中，支撑物高度h 和小车下滑时间t 都在变化，它们都是变量，其中t 随h 的变化而变化，h 是自变量，t 是因变量。

二、变化中的三角形（1）关系式：表示自变量与因变量之间关系的数学式子叫做关系式。

△ABC 底边BC 上的高是6厘米，当三角形的顶点C 沿所在直线向点B 运动时，三角形的面积发生了什么变化？如果三角形的底边长为x 厘米，那么三角形的面积y 可以表示为（y ＝3x ）圆锥的高是4厘米，当圆锥的底面半径由小到大变化时，圆锥的体积也随之发生了变化。

如果圆锥底面半径为r （厘米），那么圆锥的体积V 与r 的关系式为（V ＝43πr 2）圆锥的底面半径是2厘米，当圆锥的高由小到大变化时，圆锥的体积也随之发生了变化，如果圆锥的高为h （厘米），那么圆锥的体积V 与h 的关系式为（V ＝43πh ）（2）因变量的值：对于每一个确定的自变量值，例如x＝a时，因变量有一个唯一确定的对应值，这个对应值，叫做当自变量x＝a时的因变量的值。