中考数学难题汇总

数学难题一 •填空题(共2小题)1如图，矩形纸片 ABCD 中，AB= I ., BC=」丨.第一次将纸片折叠，使点 B 与点D 重合，折痕与 BD 交于点 01; O 1D 的中点为D 1，第二次将纸片折叠使点 B 与点D 1重合，折痕与 BD 交于点02；设O 2D 1的中点为D 2，第 三次将纸片折叠使点 B 与点D 2重合，折痕与BD 交于点03,….按上述方法折叠，第 n 次折叠后的折痕与 BD 交 于点 O n ,贝廿 B01=, BO n = .二.解答题(共28小题)23 .已知：关于 x 的一元二次方程 kx +2x+2 - k=0 ( k 昌). (1) 求证：方程总有两个实数根；(2) 当k 取哪些整数时，方程的两个实数根均为整数.24. 已知：关于 x 的方程 kx 2+ (2k - 3) x+k - 3=0. (1) 求证：方程总有实数根；(2) 当k 取哪些整数时，关于 x 的方程kx 2+ (2k - 3) x+k - 3=0的两个实数根均为负整数?335.在平面直角坐标系中，将直线 I : 丁--二了-二沿x 轴翻折，得到一条新直线与 x 轴交于点A ，与y 轴交于点B ,将抛物线C 1：尸沿x 轴平移，得到一条新抛物线 C 2与y 轴交于点D ，与直线AB 交于点E 、点F .(1) 求直线AB 的解析式；(2) 若线段DF // x 轴，求抛物线 C 2的解析式；(3) 在(2)的条件下，若点F 在y 轴右侧，过F 作FH 丄x 轴于点G ,与直线I 交于点H ，—条直线 m( m 不过△ AFH 的顶点)与AF 交于点M ，与FH 交于点N ，如果直线 m 既平分△ AFH 的面积，又平分 △ AFH 的周长，求直线 m 的解析式.2.如图，在平面直角坐标系 xoy 中，A (- 3, 0), B (0, 1),形状相同的抛物线C n (n=1 , 2, 3, 4,…)的顶点 x 轴的交点的横坐标依次为 2, 3, 5, 8, 13 ,…，根据上述规律，抛物线 C 2的顶点坐标第一次折萱第二対斤磐 第三次折査在直线AB 上，其对称轴与26. 已知：关于x的一元二次方程-x+ (m+4) x - 4m=0，其中0 v m v4.(1)求此方程的两个实数根(用含m的代数式表示)；(2)设抛物线y= - x + ( m+4) x-4m与x轴交于A、B两点(A在B的左侧)，若点D的坐标为(0,- 2),且AD?BD=10，求抛物线的解析式；(3)已知点E (a, y i)、F (2a, y2)、G (3a, y3)都在(2)中的抛物线上，是否存在含有y i、y2、y3，且与a无关的等式？如果存在，试写出一个，并加以证明；如果不存在，说明理由.7. 点P为抛物线y=x2-2mx+m2(m为常数，m>0) 上任一点，将抛物线绕顶点G逆时针旋转90°后得到的新图象与y轴交于A、B两点(点A在点B的上方)，点Q为点P旋转后的对应点.(1)当m=2，点P横坐标为4时，求Q点的坐标；(2)设点Q (a, b)，用含m、b的代数式表示a；(3)如图，点Q在第一象限内，点D在x轴的正半轴上，点C为OD的中点，QO平分/ AQC , AQ=2QC ,当QD=m&关于x的一元二次方程x2- 4x+c=0有实数根，且c为正整数.(1)求c的值；(2)若此方程的两根均为整数，在平面直角坐标系xOy中，抛物线y=x2- 4x+c与x轴交于A、B两点(A在B左侧)，与y轴交于点C .点P为对称轴上一点，且四边形OBPC为直角梯形，求PC的长；(3)将(2)中得到的抛物线沿水平方向平移，设顶点D的坐标为(m, n),当抛物线与(2)中的直角梯形OBPC只有两个交点，且一个交点在PC边上时，直接写出m的取值范围.29.如图，已知AD ABC的角平分线，EF为AD的垂直平分线.求证：FD =FB?FC.10 .如图，AD是厶ABC的角平分线，EF是AD的垂直平分线. 求证：(1) Z EAD= / EDA .(2) DF // AC .211 .已知：关于x的一元二次方程(m - 1) x + (m - 2) x -仁0 ( m为实数)(1)若方程有两个不相等的实数根，求m的取值范围；(2)在(1)的条件下，求证：无论m取何值，抛物线y= (m - 1) x2+ (m - 2) x - 1总过x轴上的一个固定点；2 2(3)关于x的一兀二次方程(m- 1) x + (m - 2) x -仁0有两个不相等的整数根，把抛物线y= (m- 1) x + (m -2) x - 1向右平移3个单位长度，求平移后的解析式.12. 已知△ ABC，以AC为边在△ ABC外作等腰△ ACD，其中AC=AD .(1) ____________________________________________________________________________________ 如图1,若Z DAC=2 Z ABC , AC=BC，四边形ABCD是平行四边形，则Z ABC= _________________________________ ;(2)如图2,若Z ABC=30 ° △ ACD是等边三角形，AB=3 , BC=4 .求BD的长；(3)如图3,若Z ACD为锐角，作AH丄BC于H .当BD2=4AH 2+BC2时，Z DAC=2 Z ABC是否成立？若不成立, 请说明你的理由；若成立，证明你的结论.213. 已知关于x 的方程mx2+ (3- 2m) x+ ( m- 3) =0，其中m>0.(1)求证：方程总有两个不相等的实数根；(2)设方程的两个实数根分别为x1,x2，其中x1> x2, y=-求y与m的函数关系式;(3)在(2)的条件下，请根据函数图象，直接写出使不等式yw- m成立的m的取值范围.14. 已知：关于 x 的一元二次方程 x+ (n -2m ) x+m - mn=O ① (1) 求证：方程 ① 有两个实数根；(2) 若m - n -仁0,求证：方程 ① 有一个实数根为1;(3) 在(2)的条件下，设方程 ①的另一个根为a .当x=2时，关于m 的函数y i =nx+am 与y 2=x 2+a (n -2m ) x+m 2 -mn 的图象交于点 A 、B (点A 在点B 的左侧)，平行于y 轴的直线L 与y i 、y 2的图象分别交于点 C 、D .当L 沿 AB 由点A 平移到点B 时，求线段CD 的最大值.J1 1 1 Ly■y= ( 3- m ) x 2+2 ( m - 3) x+4m - m 2的顶点A 在双曲线yj 上，直线y=mx+b 经过点A , 与y 轴交于点B ，与x 轴交于点C .(1) 确定直线AB 的解析式；(2) 将直线 AB 绕点O 顺时针旋转90°与x 轴交于点D ，与y 轴交于点E ,求sin / BDE 的值； (3)过点B 作x 轴的平行线与双曲线交于点 G ,点M 在直线BG 上，且到抛物线的对称轴的距离为6.设点N 在16.如图，AB 为O O 的直径，AB=4，点C 在O O 上，CF 丄OC ,且CF=BF .15.如图，已知抛物线 N 的坐标. / ANB=45。

初中中考数学难题1. 几何题：例如，已知一个等边三角形ABC，边长为6cm，点D是BC边的中点，连接AD并延长到E，使得AE=AB，求三角形ADE的面积。

解答，首先，连接AC和BE，得到一个平行四边形ABEC。

由于AE=AB，所以AEBC是一个菱形，且AC是对角线。

又因为AC是等边三角形ABC的边长，所以AC=6cm。

根据菱形的性质，对角线的垂直平分线相交于菱形的顶点，所以AD是AC的垂直平分线。

因此，三角形ADE是一个直角三角形，且AD=3cm，DE=6cm。

根据直角三角形的面积公式，三角形ADE的面积为(1/2) AD DE = (1/2) 3cm 6cm = 9cm²。

2. 代数题：例如：已知方程组：2x + y = 7。

3x 2y = 4。

求解x和y的值。

解答，可以使用消元法或代入法来解这个方程组。

首先，将第一个方程的系数乘以2，得到4x + 2y = 14。

然后将第二个方程的系数乘以3，得到9x 6y = 12。

将这两个方程相加，消去y的项，得到13x = 26，即x = 2。

将x的值代入第一个方程，得到22 + y = 7，解得y = 3。

所以，方程组的解为x = 2，y = 3。

3. 概率题：例如，一个标准的扑克牌中，从中随机抽取5张牌，求抽到一对（即两张点数相同的牌）的概率。

解答，首先计算一副扑克牌中一对的可能情况。

有13种点数，对于每种点数，有4张牌。

所以一对的可能情况有13（C(4,2)）= 78种。

接下来计算抽取5张牌的总的可能情况。

一副扑克牌中共有52张牌，抽取5张的组合数为C(52,5) = 2598960。

所以，抽到一对的概率为78/2598960，约为0.00003。

以上是我从几个不同的角度给出的初中中考数学难题的例子和解答。

希望能对你有所帮助。

中考数学中的常见难题解析在中考数学中，有一些常见的难题经常困扰着学生。

本文将对其中的一些难题进行解析，帮助同学们更好地应对这些问题。

一、分数问题分数问题是中考数学中常见的难题之一。

很多同学对分数的四则运算不够熟练，容易出错。

要解决这个问题，首先需要掌握分数的基本运算规则。

例如，两个分数相加时，需要找到它们的公共分母，然后将分子相加，并保持分母不变。

另外，同学们还需要掌握将分数转化为小数或百分数的方法，以及将小数或百分数转化为分数的方法。

二、图形问题图形问题也是中考数学中常见的难题之一。

同学们对于图形的性质和相关知识了解不深，容易在解题过程中迷失方向。

要解决这个问题，同学们需要掌握常见图形的特征和性质，例如矩形的对角线相等、平行四边形的对角线互相平分等。

此外，同学们还需要学会根据已知图形的特征画出几何图形，帮助他们更好地理解和解决问题。

三、方程问题方程问题也是中考数学中常见的难题之一。

同学们在解方程的过程中经常出现代数计算错误和方程变形错误的情况。

要解决这个问题，同学们需要加强对代数计算规则和方程变形法则的掌握，例如加减消元法、倍增法、变形法等。

同时，同学们还需要多做一些方程问题的练习，提高解题能力。

四、几何证明问题几何证明问题是中考数学中常见的难题之一。

同学们对于几何证明的思路和方法不够清晰，容易在证明过程中出现错误。

要解决这个问题，同学们需要掌握几何证明的基本思路，例如利用已知条件引出待证结论、利用图形的对称性等。

此外，同学们还需要多做一些几何证明的练习，提高证明的能力。

总之，中考数学中的常见难题需要同学们掌握一定的解题技巧和方法。

对于分数问题，需要熟练掌握分数的四则运算规则；对于图形问题，需要掌握图形的特征和性质；对于方程问题，需要掌握代数计算和方程变形的方法；对于几何证明问题，需要掌握证明的基本思路。

只有通过大量的练习和巩固，才能在中考数学中取得好成绩。

希望同学们能够认真学习，并且勇于挑战这些难题，取得优异的成绩！。

初三数学中考难题总结1.如图1所示，四边形ABCD 中，M ，N 分别为AB ，CD 的中点，且AD=BC ，延长MN ，AD 交与E 点，延长BC ，MN 交与F 点。

求证：∠DEN ＝∠F ．ABCDMNF E图 12.如图2平行四边形ABCD 中，AB=5，BC=10，BC 边上的高AM=4，E 为BC 边上的一个动点，且不与B ，C 两点重合，过E 作AB 的垂线，垂足为F ，FE 与DC 的延长线交与G ，连接DE ，DF 。

（1）求证：BE*CG=BF*CE 。

（2）当点E 在BC 上运动时，三角形BEF 和三角形CEG 的周长之间有什么关系？并说明理由。

（3）设BE 为x ，三角形DEF 的面积为y ，求出y 与x 之间的函数关系式，并求出x 为什么值得时候，y 有最大值，最大值为多少？DCBA F MEG图 23.在数学工具中，三角板经常用到，如图3.1所示，将三角板ABC与三角板DEF摆放在一起，A与D重合，C与E重合，然后将三角板DEF的一个直角顶点放在边AC上，如图3.2所示，旋转一定角度，使DE与AB边交与P，DF与AC边交与Q，若CE：AE=1:1，连接PQ，判定三角形EPQ的形状，并说明理由。

A，DB C，EFD F CAB QPE图3.1图3.24.如图4所示，在梯形ABCD中，AB//CD，AB=7，CD=1，AD=BC=5，点M，N分别在AD，BC上移动，保持MN//AB，ME垂直ＡＢ于Ｅ，ＮＦ垂直于ＡＢ于Ｆ。

（１）求梯形ＡＢＣＤ的面积。

（2）求四边形MEFN面积的最大值。

（3）试判断MEFN能否为正方形，若能，求出面积，若不能，说明理由。

D CA BE FM N图 45.如图5所示，AB 是半圆O 上的直径，E 是 ⌒BC 的中点，OE 交弦BC 于点D ，过点C 作⊙O 切线交OE 的延长线于点F. 已知BC=8，DE=2. ⑴求⊙O 的半径；⑵求CF 的长；⑶求tan ∠BAD 的值。

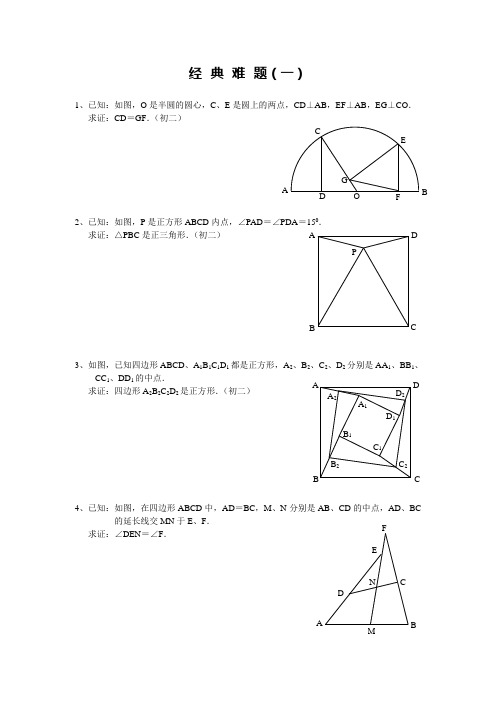
1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ． 求证：CD ＝GF ．（初二）2、已知：如图，P 是正方形ABCD 内点，∠PAD ＝∠PDA ＝150． 求证：△PBC 是正三角形．（初二）3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二）4、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ．A P C DB A F G CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 BF1、已知：△ABC 中，H 为垂心（各边高线的交点），O（1）求证：AH ＝2OM ； （2）若∠BAC ＝600，求证：AH ＝AO ．（初二）2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A ，自A 及D 、E ，直线EB 及CD 分别交MN 于P 、Q ． 求证：AP ＝AQ ．（初二）3、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN 于P 、Q ． 求证：AP ＝AQ ．（初二）4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．（初二）2、如图，四边形ABCD 为正方形，DE ∥AC ，且CE ＝CA ，直线EC 交DA 延长线于F ．求证：AE ＝AF ．（初二）3、设P 是正方形ABCD 一边BC 上的任一点，PF ⊥AP ，CF 平分∠DCE ．求证：PA ＝PF ．（初二）4、如图，PC 切圆O 于C ，AC 为圆的直径，PEF 为圆的割线，AE 、AF 与直线PO 相交于B 、D ．求证：AB ＝DC ，BC ＝AD ．（初三）1、已知：△ABC 是正三角形，P 是三角形内一点，PA ＝3，PB ＝4，PC ＝5．求：∠APB 的度数．（初二）2、设P 是平行四边形ABCD 内部的一点，且∠PBA ＝∠PDA ． 求证：∠PAB ＝∠PCB ．（初二）3、设ABCD 为圆内接凸四边形，求证：AB ·CD ＋AD ·BC ＝AC ·4、平行四边形ABCD 中，设E、F 分别是BC 、AB 上的一点，AE 与CF 相交于P ，且 AE ＝CF ．求证：∠DPA ＝∠DPC ．（初二）1、设P 是边长为1的正△ABC 内任一点，L ＝PA ＋PB ＋PC ，求证：≤L ＜2．2、已知：P 是边长为1的正方形ABCD 内的一点，求PA ＋PB ＋PC 的最小值．3、P 为正方形ABCD 内的一点，并且PA ＝a ，PB ＝2a ，PC ＝3a ，求正方形的边长．4、如图，△ABC 中，∠ABC ＝∠ACB ＝800，D 、E 分别是AB 、AC 上的点，∠DCA ＝300，∠EBA ＝200，求∠BED 的度数．APCBACBPDEDCB A A CBPD1.如下图做GH⊥AB,连接EO。

上海初中数学中考难题精选近年来，上海初中数学中考难题备受关注。

数学作为一门基础学科，对学生的逻辑思维和数学能力的培养起着重要的作用。

在中考中，难题的出现不仅考察了学生的数学知识运用能力，更重要的是考察学生的解决问题的能力和创新思维。

下面将选取几道上海初中数学中考难题进行精选，帮助学生们更好地备战中考。

1. 题目：设集合A={x | 2x^2 - 5x + 3 ≤ 0}，集合B={x | x^2 + 4x + 3 ≥ 0}，则A∪B=？解析：首先，我们分别解析集合A和集合B的含义。

对于集合A，2x^2 - 5x + 3 ≤ 0，我们可以将其转化为二次方程的根的判断形式，即找出2x^2 - 5x + 3 = 0的根，然后判断根的区间。

通过求解，我们可以得到x = 1或x = 1.5，因此集合A中的元素为x ∈ [1, 1.5]。

对于集合B，x^2 + 4x + 3 ≥ 0，我们同样可以将其转化为二次方程的根的判断形式。

通过求解，我们可以得到x = -1或x = -3，因此集合B中的元素为x ∈ (-∞,-3] ∪ [-1, +∞)。

然后，我们求A∪B，即求出集合A和集合B的并集。

根据集合的定义，A∪B的元素为既属于集合A又属于集合B的元素。

通过观察可知，集合A与集合B的交集为空集，因此A∪B的元素为x ∈ [1, 1.5] ∪ (-∞, -3] ∪ [-1, +∞)。

综上所述，A∪B的答案为x ∈ [1, 1.5] ∪ (-∞, -3] ∪ [-1, +∞)。

2. 题目：甲、乙、丙三个人合伙做某项工程，合同规定按工程投入的资金比例分享工程利润，甲投入3000元，乙投入5000元，丙投入7000元，利润分成比例为甲：乙：丙 = 2：5：7，若工程利润为20000元，甲的分得的利润为多少元？解析：根据题意，甲、乙、丙三个人的利润分成比例为2：5：7。

利润总额为20000元。

设甲的分得利润为2x元，乙的分得利润为5x元，丙的分得利润为7x元。

矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。

如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。

㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。

(2 列出开发利用方案编制所依据的主要基础性资料的名称。

如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。

对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。

二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。

2、国内近、远期的需求量及主要销向预测。

㈡产品价格分析
1、国内矿产品价格现状。

2、矿产品价格稳定性及变化趋势。

三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。

2、矿区矿产资源概况。

3、该设计与矿区总体开发的关系。

㈡该设计项目的资源概况
1、矿床地质及构造特征。

2、矿床开采技术条件及水文地质条件。