第9章-密码协议(不经意传输和掷硬币协议)电子教案

密码学报 I S S N 2095-7025 C N 10-1195/T NJournal of Cryptologic Research^ 2021, 8(2): 282-293◎《密码学报》编辑部版权所有.E-mail:jcr@ http://w w Tel/F a x:+86-10-82789618概率型2选1不经意传输协议的方案设计*张艳硕'赵瀚森\陈H1，杨亚涛31.北京电子科技学院密码科学与技术系，北京1000702.密码科学技术国家重点实验室，北京1008783.北京电子科技学院电子与通信工程系，北京100070通信作者：张艳硕，E~mail: zhang_***************摘要：目前的2选1不经意传输协议可以分为两类：一类是接收方有50%的概率可以获取自己想得到的消息，另一类是接收方有100%的概率可以获取自己想得到的消息.考虑到复杂网络情形，以固定概率获取所需信息的接收方受到限制.本文分别在E v e n、Bellare和N a o r的2选1不经意传输协议的基础上，对接收方成功恢复所需的秘密信息的概率进行了一般化处理，使得接收方可以以一般的概率来成功恢复自己想得到的秘密信息，并分析了协议的安全性及正确性.由于概率可以根据需求进行设置，因此可以在应用方面更加灵活.关键词：不经意传输；协议；2选1;概率型；安全中图分类号：T P309.7 文献标识码：A D O I: 10.13868/ki.jcr.000437中文引用格式：张艳硕，赵瀚森，陈辉焱，杨亚涛.概率型2选1不经意传输协议的方案设计1J1.密码学报，2021, 8(2): 282-293. [DOI：10.13868/ki.jcr.000437]英文引用格式：ZHANG Y S, ZHAO H S, CHEN H Y, YANG Y T. On scheme design of probabilistic 1out of 2 oblivious transfer protocol[J]. Journal of Cryptologic Research, 2021, 8(2): 282-293. [DOI: 10.13868/ki.jcr.000437]O n S ch em e D esig n o f P rob ab ilistic 1 ou t o f 2 O b liviou s TransferP ro to co lZ H A N G Y a n-S h u o1’2，Z H A O H a n-S e n1,C H E N Hui-Y a n1,Y A N G Y a-T a o31. Department of Cryptology Science and Technology, Beijing Electronic Science & Technology Institute, Beijing 100070, China2. State Key Laboratory of Cryptology, Beijing 100878, China3. Department of Electronic and Communication Engineering, Beijing Electronic Science Technology Institute, Beijing 100070, ChinaCorresponding author: ZHANG Yan-Shuo, E-mail: **********************基金项目：国家重点研发计划（2017Y FB0801803);国家自然科学基金面上项目（61772047);中央高校基本科研业务费 (3282〇19〇2);密码科学技术国家重点实验室开放课题（M M KFKT；201804); “十三五”国家密码发展基金（MMJJ20170110) Foundation: Key Research and Development Program of China (2017YFB0801803); General Program of National N atural Science Foundation of China (61772047); Fundamental Research Funds for the Central Universities (328201902); Open Fund of State Key Laboratory of Cryptology (MMKFKT201804); National Cryptography Development Fund of T hirteenth Five-Year Plan (MMJJ20170110)收稿日期：2020-05-21 定稿日期：2020-07-27张艳碩等：概率型2选1不经意传输协议的方案设计283A b stra ct:At present,l-out-of-2 oblivious transfer protocols can be divided into two categories:one is that the receiver has a50%probability of getting the message he wants,another is that the receiver has a 100% probability to get the message he wants.Considering complex networks,the receiver who can only obtain the required information with a fixed probability will be limited.In this paper,on the basis of Even,Bellare and Naor’s l-out-of-2oblivious transfer,we generalize the probability of the receiver's successful recovery of the secret information needed,so that the receiver can recover the secret information he wants with a general probability.The security and correctness of the protocols are analyzed.Because the probability of the protocols can be set according to the needs,the protocols have more flexible applications.Key w ords:oblivious transfer;protocol;l-out-of-2; probabilistic;securityi引言不经意传输协议（oblivious transfer,O T)是密码学的一个基本协议，是一种可保护隐私的双方通信协议，通信双方可以以一种模糊化的方式传送消息.他使得服务的接收方以不经意的方式得到服务发送方输入的某些消息，这样就可以在保证接收者在不知道发送者隐私的前提下，保护接受者的隐私不被发送者所知道.因此不经意传输协议也经常作为一种基本的密码模块来实现许多密码协议的构造，如安全多方计算、零知识证明和电子合同等.不经意传输协议最初是由R a b i n M在1981年提出的，在R a b i n的方案中实现了 1选1不经意传输协议，接收方有50%的概率可以成功获取秘密信息，从此不经意传输协议逐渐成为密码学的一个重要组成部分，随着学者们的不断深入研宄，不经意传输协议也在不断的发展和完善，逐渐应用到我们生活的各个领域，如安全多方计算、电子交易、公平拍卖协议等.目前，不经意传输协议主要分为以下四个研宄方向:经典1选1不经意传输协议M、2选1不经意传输协议W、…选i不经意传输协议W和…选不经意传输协议[51.其中，2选1不经意传输协议是由E v e n W在1985年最先提出的，并随之涌现出许多基于该协议的研宄设计，如Bellare W提出的非交互式2选1不经意传输协议、N a o r M基于Bellare的协议所提出的改进方案和H u a n g基于E D D H(extended decisional Diffe-H e l l m a n)假设而设计出的2选1不经意传输协议等等，均是对2选1不经意传输协议的很好的应用扩展.我们对经典的E v e n方案…U Bellare方案和N a o r方案间研究后发现，这三个典型的2选1不经意传输协议可以根据接收方成功获取所需秘密信息的概率分为两类：一类是接收方有50%的概率可以获取自己所需的秘密信息，如E v e n方案和Bellare方案；另一类是接收方有100%的概率可以获取自己所需的秘密信息，如N a o r方案.因此，本文分别对E v e n Bellare W和N a o r的2选1不经意传输协议进行了一般化推广，提出了三个接收方可以以一般概率接受信息的概率型2选1不经意传输协议，针对三个基本方案中接收方获取信息的概率进行了一般化改进，使得接收方可以以一定的概率获取信息，且经过分析，本文所提出的三个概率型2选1不经意传输协议方案是安全、可行的.原来的E v e n方案、Bellare方案和N a o r方案中接收方获取所需信息的概率是固定的，而在我们所提出的三个概率型2选1不经意传输协议方案中，概率可以根据实际需要灵活调整，可以说，我们用一种可变换概率的方式将三个—在复杂网经典方案在概率上实现了统一的P =f的形式，而这种形式也就可以实现我们统一的目的—络中根据实际需要进行概率的灵活变化和调整，更好得适应目前复杂网络环境中不经意传输协议的信息传输需求.2不经意传输协议不经意传输协议经过多年的研究发展，逐渐成为密码学的一个重要组件.目前不经意传输协议的研究主要分为四类：经典1选1不经意传输协议i21、2选1不经意传输协议M、n选1不经意传输协议W和n选fc不经意传输协议这四类不经意传输协议在后续的研究中均有很大的进展.284JowrnaZ 〇/CVyp<oZogic i?esearc/i 密码学报 Vol.8，No.2,A pr.2021经典1选1不经意传输协议在1981年由R abin121第一次提出，在R a b i n的方案中，接收方有50%的概率可以成功获取发送方所持有的唯一的秘密信息，且发送方并不知道接收方到底是否得到了秘密信息，此方案是基于二次剩余计算的.在2009年，郑天翔等人[31将R a b i n方案中的二次剩余替换成三次剩余，对R a b i n方案进行了改进.2选1不经意传输协议首先由E v e n W在1985年提出，是结合电子商务通信时代的背景所构建的一种通信协议，这种方案是由发送方向接收方秘密传送两个秘密消息，而接收方只能接收其中一个秘密消息，且发送方也不知道接收方所接收的是哪一个秘密消息，这样就保证了双方的隐私性.1987年，Goldreich等人用2选1不经意传输协议构造了一种安全多方计算方案；2008年，P a r a k h [111基于Diffie-Hellman 方案，为实现不经意传输的传统方法提供了一种有用的替代方案；1989年，C M p e a u等人1121用2选1不经意传输协议实现了对未察觉电路的评估和比特的公平交换；1995年，Stadler等人I13)基于2选1不经意传输协议构造了一种公平的盲签名方案；1999年，N a o r等人1141用2选1不经意传输协议构造了一个用于公平安全拍卖的体系结构；2000年，C a c h i n等人1151基于2选1不经意传输协议实现了一轮的安全多方计算；2010年，J a i n等人[161对P a r a k h的2选1不经意传输协议进行推广.在J a i n所提出的协议中，相关各方不经意地生成Diffie-H e l l m a n密钥，然后将它们用于秘密的不经意传输；2015年，K u m a r 等人1171提出了一种非自适应的，并且是完全可模拟的2选1不经意传输协议方案；2017年，P l e s c h等人[181提出了一种更为简化的2选1不经意传输协议.n选1不经意传输协议在1986年由Brassard141第一次提出，通过调用n次2选1的不经意传输协议来实现.接着，在1987年，Brassard141进一步改进了 n选1的方案，仅需调用log2n次2选1不经意传输协议，大大提高了协议的效率.2000年，G e r t n e r等人提出了一种分布式ri选1不经意传输协议；2004年，Tzeng等人基于判定性Diffie Heilman困难性假设，设计出了一个新的不经意传输协议;接着在2005年，赵春明等人1211在Tzeng等人的方案的基础上加以改进，提出了增强的n选1不经意传输协议；2006年，叶君耀等人1221提出了一个基于门限思想并且可复用的n选1不经意传输协议，在效率方面优于以往的N ao r协议和Tzeng协议；2007年，朱健东等人f231在N ao r协议的基础上，基于现有公钥体制同态性设计出了一个在计算上更简单的不经意传输协议的构造方法；2007年，Camenisch等人1241基于一些基础的密码学原件设计出了不经意传输协议方案；2008年，张京良等人p5l对N aor协议进行改进并应用到群签名中；2019年，M i等人1261提出了一种基于N T R U密码原语的更适合在异构和分布式环境中部署的后量子轻量级n选1不经意传输协议.n选A:不经意传输协议首次提出是在1989年由Bellare所构建的一类提出非交互式n选A:不经意传输，第一次实现了接收方可以一次选择接收多个秘密信息.1999年，N a o r W在2选1不经意传输协议的基础上，提出了一个只针对某种特殊情况可以使用的n选fc不经意传输协议，到了 2001年，N a o r 又接着W提出了具有普适性的ri选A;不经意传输协议，成为以后不经意传输协议研究的基础之一；2009年，C h a n g等人提出一种基于C R T的鲁棒《选fc的不经意传输协议；2014年，L o u等人在椭圆曲线密码体制的基础上，提出了一种新的用于私人信息检索的n选fc不经意传输协议，该协议更适合于智能卡或移动设备；2018年，L a i等人1291提出了一个以最小通讯成本的n选fc不经意传输方案；2019年，D o t t l i n g等人I#提出了一种构造恶意安全的两轮不经意转移的新方法，在可计算Diffie-Hellman (computational Diffie-H e l l m a n,C D H)假设或学习等价噪声（Learning Parity with Noise,L P N)假设下给出了基本O T的简单构造，得到了恶意两轮O T的第一个构造；2020年，G o y a l等人[31】给出了三轮不经意传输协议的第一个构造-在普通模型中-基于多项式时间假设，实现接收者的统计隐私和发送者对抗恶意对手的计算隐私.3经典2选1不经意传输协议的对比研究3.1 2选1不经意传输协议2选1不经意传输协议是一种能保护通信双方隐私的通信协议，信息的持有者将自己所拥有的两个秘密信息加密后发送给接收方，接收方只能成功恢复其中一个消息，而信息持有者并不知道接收方恢复的是哪一个秘密消息.张艳硕等：概率型2选1不经意传输协议的方案设计285本节所列举了三个典型的2选1不经意传输协议，分别是1985年E v e n丨6丨首次提出的2选1不经 意传输协议、1990年Bellare [71提出的非交互式2选1不经意传输协议和2001年N a o r间针对Bellare 方案提出的改进2选1不经意传输协议方案，而这三个方案也是后续2选1不经意传输协议的基础，后 续各位学者所提出的各个新的方案及各个领域的应用，有相当一部分与这三个方案密切相关，是对这三个 方案中的某一个的改进扩展，因此我们也将基于这三个基础方案进行概率的一般化扩展，提出三个概率型 2选1不经意传输协议方案.3.2 E v e n的2选1不经意传输协议本节将对E v e n间的2选1不经意传输协议方案进行简单描述，方案如下：(1) 设和分别为A l i c e的公钥加解密函数.A l i c e从自己的公钥系统的消息空间中随机选择勿而.A l i c e将加密函数和z0,发送给B o b.(2) B o b随机选择r e {0,1}，并从A l i c e的公钥系统的消息空间中随机选择f c.计算9 =私㈨®将g发送给Alice.(3) 对于 i =0,1，Alice 计算 f c; =ArQ—4).Alice 随机选择 s € {0,1}.将（M〇+fc:，Mi发送给Bob.⑷最终B o b可以成功得到3.3 B e lla r e的2选1不经意传输协议本节将对Bellare I7]的2选1不经意传输协议方案进行简单描述，方案如下：初始化：选择一个素数p,且定义g为■^的生成元，从Z纟中选择C1(其中C =汰x并公开.B o b随机选择i e {0,1},再随机选择灼€ {0,1, —，p-2},接着计算爲=0和魚-i =C x (广广1,得到B o b自己的公钥03,，/^和私钥（i,).传输阶段：(1) Alice随机选择如，e {0,1，…，p-2}，计算a〇 =g110和如=分yi.A lice接着计算7〇 = /^。

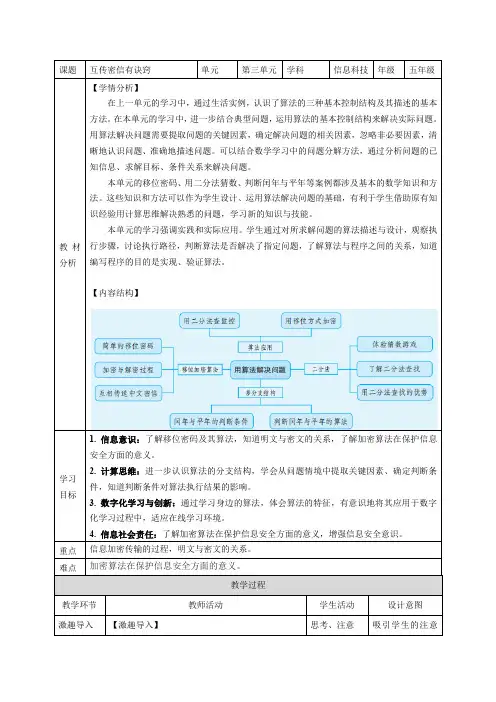
课题互传密信有诀窍单元第三单元学科信息科技年级五年级教材分析【学情分析】在上一单元的学习中，通过生活实例，认识了算法的三种基本控制结构及其描述的基本方法。

在本单元的学习中，进一步结合典型问题，运用算法的基本控制结构来解决实际问题。

用算法解决问题需要提取问题的关键因素，确定解决问题的相关因素，忽略非必要因素，清晰地认识问题、准确地描述问题。

可以结合数学学习中的问题分解方法，通过分析问题的已知信息、求解目标、条件关系来解决问题。

本单元的移位密码、用二分法猜数、判断闰年与平年等案例都涉及基本的数学知识和方法。

这些知识和方法可以作为学生设计、运用算法解决问题的基础，有利于学生借助原有知识经验用计算思维解决熟悉的问题，学习新的知识与技能。

本单元的学习强调实践和实际应用。

学生通过对所求解问题的算法描述与设计，观察执行步骤，讨论执行路径，判断算法是否解决了指定问题，了解算法与程序之间的关系，知道编写程序的目的是实现、验证算法。

【内容结构】学习目标1. 信息意识：了解移位密码及其算法，知道明文与密文的关系，了解加密算法在保护信息安全方面的意义。

2. 计算思维：进一步认识算法的分支结构，学会从问题情境中提取关键因素、确定判断条件，知道判断条件对算法执行结果的影响。

3. 数字化学习与创新：通过学习身边的算法，体会算法的特征，有意识地将其应用于数字化学习过程中，适应在线学习环境。

4. 信息社会责任：了解加密算法在保护信息安全方面的意义，增强信息安全意识。

重点信息加密传输的过程，明文与密文的关系。

难点加密算法在保护信息安全方面的意义。

教学过程教学环节教师活动学生活动设计意图激趣导入【激趣导入】思考、注意吸引学生的注意同学们，今天老师要给大家讲一个发生在很久很久以前的有趣故事。

【提问】同学们，你们想不想知道恺撒是怎么做到的呢？【建构】这背后其实隐藏着一门很有趣的知识——密码学。

今天，我们就一起来学习神秘又有趣的凯撒密码。