重要极限的证明
- 格式:doc
- 大小:252.50 KB
- 文档页数:5

两个重要的极限1.证明:0sin lim 1x x x→= 证明:如图(a )作单位圆。
当0<x<2π时,显然有ΔOAD 面积<扇形OAD 面积<ΔOAB 面积。
即111sin 222x x <<tgx ,sinx<x<tgx 。
除以sinx ,得到11sin cos x x x<< 或sin 1cos x x x >>。
(1) 由偶函数性质,上式对02x π-<<时也成立。
故(1)式对一切满足不等式0||2x π<<的x 都成立。
由0lim x →cosx=1及函数极限的迫敛性定理立刻可得0lim x →sin 1x x=。
函数f(x)=sin x x的图象如图(b )所示。
2.证明:1lim(1)n n n →∞+存在。
证明:先建立一个不等式,设b>a>0,于是对任一自然数n 有 11(1)n n n b a n b b a++-<+-或11(1)()n n n b a n b b a ++-<+-,整理后得不等式1[(1)]n n a b n a nb +>+-。
(1) 令a=1+11n +,b=1+1n ,将它们代入(1)。
由于11(1)(1)(1)(1)11n a nb n n n n +-=++-+=+, 故有111(1)(1)1n n n n ++>++,这就是说1{(1)}n n+为递增数列。
再令a=1,b=1+12n代入(1)。
由于11(1)(1)(1)22n a nb n n n +-=+-+=,故有111(1)22n n >+,12(1)2n n >+。
不等式两端平方后有214(1)2n n >+,它对一切自然数n 成立。
联系数列的单调性,由此又推得数列1{(1)}n n +是有界的。
于是由单调有界定理知道极限1lim(1)n n n→∞+是存在的。

两个重要的极限1.证明:0sin lim 1x x x→= 证明:如图(a )作单位圆。
当0<x<2π时,显然有ΔOAD 面积<扇形OAD 面积<ΔOAB 面积。
即111sin 222x x <<tgx ,sinx<x<tgx 。
除以sinx ,得到11sin cos x x x<< 或sin 1cos x x x >>。
(1) 由偶函数性质,上式对02x π-<<时也成立。
故(1)式对一切满足不等式0||2x π<<的x 都成立。
由0lim x →cosx=1及函数极限的迫敛性定理立刻可得0lim x →sin 1x x=。
函数f(x)=sin x x的图象如图(b )所示。
2.证明:1lim(1)n n n →∞+存在。
证明:先建立一个不等式,设b>a>0,于是对任一自然数n 有 11(1)n n n b a n b b a++-<+-或11(1)()n n n b a n b b a ++-<+-,整理后得不等式1[(1)]n n a b n a nb +>+-。
(1) 令a=1+11n +,b=1+1n ,将它们代入(1)。
由于11(1)(1)(1)(1)11n a nb n n n n +-=++-+=+, 故有111(1)(1)1n n n n ++>++,这就是说1{(1)}n n+为递增数列。
再令a=1,b=1+12n代入(1)。
由于11(1)(1)(1)22n a nb n n n +-=+-+=,故有111(1)22n n >+,12(1)2n n >+。
不等式两端平方后有214(1)2n n >+,它对一切自然数n 成立。
联系数列的单调性,由此又推得数列1{(1)}n n +是有界的。
于是由单调有界定理知道极限1lim(1)n n n→∞+是存在的。



第一重要极限证明极限是微积分中的重要概念之一,它在数学和科学中具有广泛的应用。
而第一重要极限证明则是极限理论中最基础的证明之一。
本文将从人类视角出发,详细描述第一重要极限的证明过程,使读者能够更好地理解并感受这一数学原理的美妙。
我们先来介绍一下第一重要极限的概念。
在微积分中,当自变量趋向于某个特定值时,函数的极限就是函数在该特定值附近的行为。
第一重要极限是指当自变量趋向于某个常数a时,函数f(x)的极限。
具体来说,如果对于任意给定的正数ε,存在一个正数δ,使得当0 < |x - a| < δ时,有|f(x) - L| < ε成立,那么我们就说函数f(x)在x趋近于a时的极限为L。
接下来,我们将通过一个实例来说明第一重要极限的证明过程。
考虑函数f(x) = 2x + 1,我们需要证明当x趋近于2时,函数f(x)的极限为5。
我们给定一个任意的正数ε,我们需要找到一个正数δ,使得当0 < |x - 2| < δ时,有|f(x) - 5| < ε成立。
我们可以先尝试通过代入一些近似值来判断可能的δ的取值范围。
当我们令x = 1.9时,可以得到f(1.9) = 2(1.9) + 1 = 3.8 + 1 = 4.8,而当x = 2.1时,可以得到f(2.1) = 2(2.1) + 1 = 4.2 + 1 = 5.2。
可以看出,当x在1.9和2.1之间时,f(x)的值在4.8和5.2之间变化。
根据这一观察,我们可以猜测当0 < |x - 2| < 0.1时,有|f(x) - 5| < 0.2成立。
接下来,我们需要证明这一猜测的正确性。
假设存在一个正数δ,使得当0 < |x - 2| < δ时,有|f(x) - 5| < 0.2成立。
我们可以取δ = 0.1,根据我们的猜测,这个δ是满足条件的。
现在,我们可以证明当0 < |x - 2| < 0.1时,有|f(x) - 5| < 0.2成立。




第三章函数极限4 两个重要的极限一、证明:limx→0sin xx=1.证:∵sinx<x<tanx(0<x<π2),∴1<xsin x<1cos x(0<x<π2),∴cosx<sin xx<1(0<x<π2),又cos-x=cosx,sin−x−x =sin xx,∴对0<|x|<π2,有cosx<sin xx<1.由limx→0cosx=1,根据极限的迫敛性,limx→0sin xx=1.例1:求limx→πsin x π−x.解:令t=π-x,则sinx=sin(π-t)=sint,且当x→π时,t→0,∴limx→πsin xπ−x=limt→0sin tt=1.例2:求limx→01−cos xx2.解:limx→01−cos xx2=limx2→012sin x2x22=12,二、证明limx→∞1+1xx=e.证:设f(x)=1+1n+1n, g(x)=1+1nn+1, n≤x<n+1, n=1,2,…,则f(x)递增且有上界,g(x)递减且有下界,∴limx→+∞f x与limx→+∞g x都存在,取{x n}={n},由归结原则得lim x→+∞f x=limn→+∞1+1n+1n=e,limx→+∞g x=limn→+∞1+1nn+1=e,又1+1n+1<1+1x≤1+1n,则1+1n+1n<1+1xx<1+1nn+1,根据迫敛性定理得limx→+∞1+1xx= e.设x=-y,则1+1x x=1−1y−y=1+1y−1y,且当x→-∞,y→+∞,从而有lim x→−∞1+1xx=limy→+∞1+1y−1y−1·1+1y−1=e.∴limx→∞1+1xx=e.注:e的另一种形式:lima→01+a1a=e.证:令a=1x ,则当a→0时,1x→∞,∴lima→01+a1a=lim1x→∞1+1xx=e.例3:求limx→01+2x1x.解:limx→01+2x1x=lim12x→∞1+2x12x2=e2.例4:求limx→01−x1x.解:limx→01−x1x=lim−1x→∞1[1+(−x)]−1x=1e.例5:求limn→∞1+1n−1n2n.解:1+1n −1n2n<1+1nn→e(n→∞),又当n>1时有1+1n −1n2n=1+n−1n2n2n−1−nn−1≥1+n−1n2n2n−1−2→e(n→∞,即n−1n2→0).由迫敛性定理得:limn→∞1+1n−1n2n=e.习题1、求下列极限: (1)lim x →0sin 2x x;(2)limx →0sin x 3 (sin x)2;(3)lim x →π2cos xx −π2;(4)limx →0tan x x;(5)limx →0tan x −sin xx 3;(6)limx →0arctan xx;(7)lim x →+∞x sin 1x;(8)limx →asin 2 x −sin 2 ax −a;(9)limx → x +1−1(10)limx →0 1−cos x 21−cos x.解:(1)limx →0sin 2x x=lim2x →02sin 2x 2x=2;(2)lim x →0sin x 3(sin x)2=limx →0 x 3sin x 3x 3(sin x )2=limx 3→0sin x 3x3·lim x 2→0xsin x 2·lim x →0x =0; (3)lim x →π2cos x x −π2=lim x −π2→0−sin x −π2x −π2= -1;(4)limx →0tan x x=limx →0sin x x·limx →01cos x=1;(5)lim x →0tan x −sin xx 3=limx →0sinx 1cos x −1x 3=limx →0sin x·1−cos xcos x x 3=limx →02sinx 2cos x 2·2 sin x 2 2cos xx3=limx →04 sinx 2 3·cos x2cos x x3=limx →0sin x 2 3·cos x2cos x 2 x 23=lim x2→0sinx 2x 23·lim x 2→0cosx 22lim x →0cos x =12;(6)令arctan x=y ,则x=tany ,且x →0时,y →0, ∴limx →0arctan xx=limy →0ytan y =limy →0cos ysin y y=1;(7)lim x →+∞x sin 1x =lim 1x→0sin1x1x =1;(8)lim x →asin 2 x −sin 2 ax −a =limx →a sin x −sin a (sin x+sin a)x −a=limx →a2cosx +a 2 sin x −a2x −a·2sin a=limx −a2→0sinx −a2x −a 2·cos a ·2sin a= sin2a ;(9)limx →x +1−1lim x →0( x+1+1)sin 4xx=8lim4x →0sin 4x 4x=8;(10)lim x →0 1−cos x 21−cos x=limx →0 2sin x 222 sin x 22= 2limx →0sinx 22 x 22 sinx 2x 22= 2.2、求下列极限:(1)limx→∞1−2x−x;(2)limx→01+ax1x(a为给定实数);(3)limx→01+tan x cot x;(4)limx→01+x1−x1x;(5)limx→+∞3x+23x−12x−1;(6)limx→+∞1+αxβx(α,β为给定实数)解:(1)limx→∞1−2x−x=lim−x2→∞1+1−x2−x22=e2;(2)limx→01+ax1x=lima x→01+ax1axa=e a;(3)limx→01+tan x cot x=limtan x→01+tan x1tan x=e;(4)limx→01+x1−x1x=limx→01+x1x1−x1x=limx→01+x1xlim−x→0[1+−x]1−x−1=e2;(5)limx→+∞3x+23x−12x−1=limx→+∞1+33x−16x−33=lim33x−1→0+1+33x−123x−1−13=lim33x−1→0+1+33x−123x−13lim33x−1→0+1+33x−113=e2;(6)limx→+∞1+αxβx=limx→+∞1+αxαβxα=limαx→0+1+αxxααβ=eαβ.3、证明:limx→0limn→∞cos xcos x2cos x22…cos x2n=1.证:∵cos xcos x2cos x22…cos x2n=2n+1cos xcos x2cos x22…cos x2nsin x2n2n+1sin x2n=sin 2x2n+1sin x2n=sin 2x2xsin x2nx2n=x2nsin x2n·sin 2x2x;∴当x≠0时,limn→∞ cos xcos x2cos x22…cos x2n=limx2n→0x2nsin x2n·sin 2x2x=sin 2x2x;lim x→0limn→∞cos xcos x2cos x22…cos x2n=lim2x→0sin 2x2x=1.当x=0时,cos xcos x2cos x22…cos x2n=1,∴limx→0limn→∞cos xcos x2cos x22…cos x2n=1.4、利用归结原则计算下列极限:(1)limn→∞n sinπn;(2)limn→∞1+1n+1n2n.解:(1)∵limx→∞x sinπx=limx→∞sinπxπx·x=limπx→0sinπxπx·limx→∞x=0根据归结原则,limn→∞n sinπn=0.(2)∵当x>0时,1+1x +1x2x>1+1xx→e(x→+∞),又1+1x +1x2x=1+x+1x2x2x+1+xx+1<1+x+1x2x2x+1→e(x→+∞,即x+1x2→0),∴limx→+∞1+1x+1x2x=e根据归结原则,limn→∞1+1n+1n2n=e.。

准则1:若数列}{n x 、}{n y 、}{n z 满足以下条件:(i ) N n ∈∃0,当0n n >时,有n n n z y x ≤≤; (ii )a y n n =∞→lim ,a z n n =∞→lim 。
那么数列}{n x 极限存在,且a x n n =∞→lim 。
证明:因为a z y n n n n ==∞→∞→lim lim ,所以对0,01>∃>∀N ε,当1N n >时,有ε<-a y n ,即εε+<<-a y a n ,对2N ∃,当2N n >时,有ε<-a z n ,即εε+<<-a z a n ,又因为n n n z x y ≤≤,所以当},{21N N Max N n =>时,有εε+<≤≤<-a z x y a n n n ,即有:εε+<<-a x a n ,即ε<-a x n ,所以 a x n n =∞→lim 。
准则1′如果函数)(),(),(x h x g x f 满足下列条件:(i )当))(,(0M x r x U x >∈∧时,有)()()(x h x f x g ≤≤。
(ii )当)(0∞→→x x x 时,有A x h A x g →→)(,)(。
那么当)(0∞→→x x x 时,)(x f 的极限存在,且等于A 。
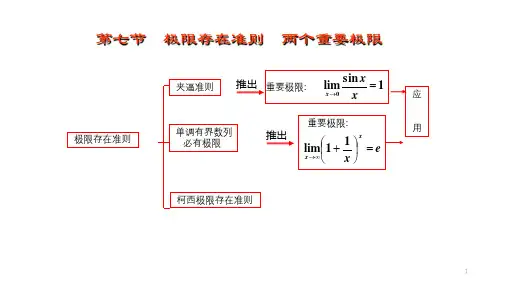
第一个重要极限:1sin lim0=→xxx作为准则I ′的应用,下面将证明第一个重要极限:1sin lim 0=→xxx 。
证明:作单位圆,如下图: 设x 为圆心角AOB ∠,并设20π<<x 见图不难发现:AOD AOB AOB S S S ∆∆<<扇形,即:x x x tan 2121sin 21<<,即 x x x tan sin <<, (因为20π<<x ,所以上不等式不改变方向,若02<<-x π,不等式也成立)当x 改变符号时,x x x sin ,cos 及1的值均不变,故对满足20π<<x 的一切 x ,有1si n co s <<x xx 。
重要极限的证明极限是ea>0在n比较大时,(1+(1-a)/n)^n<=原式<=(1+1/n)^n取极限后,e》=原式的上极限》=原式的下极限》=e^(1-a)由a的任意性,得极限为e利用极限存在准则证明:(1)当x趋近于正无穷时,(Inx/x^2)的极限为0;(2)证明数列{Xn},其中a>0,Xo>0,Xn=[(Xn-1)+(a/Xn-1)]/2,n=1,2,…收敛,并求其极限。
1)用夹逼准则:x大于1时,lnx>0,x^2>0,故lnx/x^2>0且lnx1),lnx/x^2<(x-1)/x^2.而(x-1)/x^2极限为0故(Inx/x^2)的极限为02)用单调有界数列收敛:分三种情况,x0=√a时,显然极限为√ax0>√a时,Xn-X(n-1)=[-(Xn-1)+(a/Xn-1)]/2<0,单调递减且Xn=[(Xn-1)+(a/Xn-1)]/2>√a,√a为数列下界,则极限存在.设数列极限为A,Xn和X(n-1)极限都为A.对原始两边求极限得A=[A+(a/A)]/2.解得A=√a同理可求x0<√a时,极限亦为√a综上,数列极限存在,且为√(一)时函数的极限:以时和为例引入.介绍符号: 的意义, 的直观意义.定义 ( 和 . )几何意义介绍邻域其中为充分大的正数.然后用这些邻域语言介绍几何意义.例1验证例2验证例3验证证……(二)时函数的极限:由考虑时的极限引入.定义函数极限的“ ”定义.几何意义.用定义验证函数极限的基本思路.例4 验证例5 验证例6验证证由 =为使需有为使需有于是, 倘限制 , 就有例7验证例8验证 ( 类似有 (三)单侧极限:1.定义:单侧极限的定义及记法.几何意义: 介绍半邻域然后介绍等的几何意义.例9验证证考虑使的 2.单侧极限与双侧极限的关系:Th类似有: 例10证明: 极限不存在.例11设函数在点的某邻域内单调. 若存在, 则有= §2 函数极限的性质(3学时)教学目的:使学生掌握函数极限的基本性质。
重要极限公式推导摘要:1.极限公式概述2.重要极限公式推导3.极限公式的应用4.结论正文:极限是数学中一个重要的概念,它在很多实际问题中都有着广泛的应用。
本文将介绍一些重要的极限公式及其推导过程,并探讨如何在实际问题中运用这些极限。
一、极限公式概述极限公式是用来描述一个变量在某一点附近变化趋势的数学表达式。
在极限公式中,通常用字母x表示自变量,y表示因变量。
当自变量x趋近于某个值a时,极限公式可以表示为:lim (x->a) y(x)二、重要极限公式推导1.指数函数极限当x趋近于0时,e^x的极限为1。
证明如下:lim (x->0) e^x = 12.对数函数极限当x趋近于1时,log_2(x)的极限为0。
证明如下:lim (x->1) log_2(x) = 03.三角函数极限(1)正弦函数极限当x趋近于0时,sin(x)的极限为0。
证明如下:lim (x->0) sin(x) = 0(2)余弦函数极限当x趋近于0时,cos(x)的极限为1。
证明如下:lim (x->0) cos(x) = 14.反三角函数极限(1)反正弦函数极限当x趋近于1时,arcsin(x)的极限为π/4。
证明如下:lim (x->1) arcsin(x) = π/4(2)反余弦函数极限当x趋近于1时,arccos(x)的极限为0。
证明如下:lim (x->1) arccos(x) = 0三、极限公式的应用极限公式在实际问题中有广泛的应用,如求解极限问题、求解导数和积分等。
以下举一个求解极限的例子:求极限:lim (x->0) (e^x - 1) / x解:根据极限公式,我们有:lim (x->0) (e^x - 1) / x = lim (x->0) e^x / x - lim (x->0) 1 / x由于lim (x->0) e^x / x = 1,lim (x->0) 1 / x = 0,所以:lim (x->0) (e^x - 1) / x = 1 - 0 = 1四、结论极限公式是数学中一个重要的概念,掌握这些极限公式有助于解决实际问题。
两个重要极限的应用探讨两个重要极限的应用探讨一、引言微积分学是现代数学的重要组成部分,而极限理论则是微积分学的理论基础。
在极限理论中,两个重要极限扮演着至关重要的角色。
它们不仅是微积分学的基础,而且在解决实际问题中也具有广泛的应用。
本文将对这两个重要极限的应用进行深入探讨。
二、两个重要极限的概述第一个重要极限是:当x趋近于0时,sinx/x的极限为1。
这个极限可以用几何解释和代数解释两种方法来理解。
几何解释是将sinx表示为一个三角形的斜边,x表示三角形的底边,当底边无限缩短时,斜边与底边的比值趋近于1。
代数解释则是利用泰勒级数展开sinx,得到sinx/x的极限为1。
第二个重要极限是:当x趋近于无穷大时,(1+1/x)^x的极限为e。
这个极限可以通过二项式定理和夹逼定理来证明。
二项式定理将(1+1/x)^x展开为多项式,夹逼定理则证明了当x趋近于无穷大时,多项式的极限为e。
三、两个重要极限的应用1.三角函数的应用第一个重要极限在三角函数中有广泛的应用。
例如,在求解三角函数的极限问题时,可以利用第一个重要极限将问题转化为求sinx或cosx的极限。
此外,在求解三角函数的导数时,也需要利用第一个重要极限。
例如,在求解sinx的导数时,可以将sinx表示为(sinx/x)x,然后利用第一个重要极限和导数的定义求解。
2.复利计算的应用第二个重要极限在复利计算中有广泛的应用。
例如,在求解连续复利的极限问题时,可以利用第二个重要极限将问题转化为求(1+r/n)^(nt)的极限,其中r为年利率,n为每年计息次数,t为投资时间。
此外,在求解连续复利的导数时,也需要利用第二个重要极限。
例如,在求解连续复利函数e^(rt)的导数时,可以利用第二个重要极限和导数的定义求解。
3.经济学中的应用两个重要极限在经济学中也有广泛的应用。
例如,在求解经济增长率和折现率的问题时,可以利用第二个重要极限将问题转化为求(1+r)^(-t)的极限,其中r为折现率,t为时间。
e的两个重要极限公式证明在数学的奇妙世界里,e 这个神秘的数字就像一位隐藏在迷雾中的精灵,总是让人充满好奇和探索的欲望。
而 e 的两个重要极限公式,更是数学大厦中极为关键的基石。
先来说说第一个重要极限公式:$\lim\limits_{x \to 0} \frac{\sin x}{x} = 1$。
这个公式看似简单,但其证明过程却蕴含着深刻的数学思想。
咱们从几何的角度来瞧瞧。
想象一个单位圆,圆心在原点,半径为1 。
以原点为顶点,x 轴正半轴为一条边,角 x 的终边与单位圆相交于点 P 。
过点 P 作 x 轴的垂线,垂足为 M 。
那么,$\sin x$ 就是线段 PM 的长度,而 x 对应的弧长就是线段弧 PQ 的长度。
当 x 非常非常小的时候,也就是角 x 接近 0 时,弧 PQ 的长度和线段 PM 的长度几乎相等。
因为在很小的范围内,圆弧可以近似看作直线段。
所以,$\frac{\sin x}{x}$ 的值就趋近于 1 啦。
再看第二个重要极限公式:$\lim\limits_{x \to \infty} (1 +\frac{1}{x})^x = e$ 。
为了更好地理解这个公式,咱们来做一个有趣的思想实验。
假设你有一笔钱,初始本金为 1 元,年利率为 100% 。
如果一年结算一次利息,那么年底你将拥有 2 元。
但如果把一年分成 n 等份,每过 1/n 年就结算一次利息并把利息加入本金,那么到年底你的钱数就会变成$(1 +\frac{1}{n})^n$ 元。
当 n 越来越大,也就是结算利息的次数越来越多,越来越频繁时,到年底你拥有的钱数就会越来越接近一个固定的值,这个值就是 e 。
记得我当年读高中的时候,刚开始接触这两个重要极限公式,那叫一个头疼啊!老师在讲台上讲得口沫横飞,我在下面听得云里雾里。
特别是那些复杂的推导过程,感觉就像一团乱麻,怎么也理不清。
但是,我没有放弃。
课后,我拿着书本,对着那些图形和式子,一遍又一遍地琢磨。
几个重要极限公式
1. 欧拉公式:
欧拉公式是数学中的一项重要极限公式,由著名数学家欧拉提出,在数学中具有重要的应用价值。
具体来说,欧拉公式表示为:e^(iπ)+1=0
其中,e是自然对数的底数,i表示虚数单位,π表示圆周率。
2. 格朗沃尔定理:
格朗沃尔定理是微积分中的一项重要极限公式,由法国数学家格
朗沃尔提出。
格朗沃尔定理表示为∫_{a}^{b}f'(x)dx=f(b)-f(a)
其中,∫表示积分符号,f(x)表示被积函数,f'(x)表示其导数,
a和b为积分区间。
3. 斯特林公式:
斯特林公式是组合数学中的一项经典极限公式,由苏格兰数学家
斯特林提出并证明。
斯特林公式表示为:n!=sqrt(2πn)*(n/e)^n
其中,n!表示n的阶乘,e表示自然对数的底数,π表示圆周率。
这三个极限公式都是数学中的重要定理,广泛应用于各个领域。
欧拉公式与电工学有关,格朗沃尔定理与微积分有关,斯特林公式与组合数学和统计学有关。
掌握这些公式的应用方法不仅有助于我们深入了解数学的本质,也能够帮助我们更好地应用数学知识解决实际问题。
1.求证:sin(π/(2n+1))sin(2π/(2n+1))sin(3π/(2n+1))……sin(nπ
/(2n+1))=√(2n +1)/2^n,
Sol:复数方法:
复数方程 z^(2n+1)=1的根是 a1,a2,a3,...,a(2n),1。
其中,ak=cos(2kπ/(2n+1))+i sin(2kπ/(2n+1)),k=1,2,...,2n。
所以,ak=(a1)^k
所以,z^(2n+1)-1=(z-a1)(z-a2)...(z-a(2n))(z-1),即
(z-a1)(z-a2)...(z-a(2n))=(z^(2n+1)-1)/(z-1)=z^(2n)+z^(2n-1)+...+z+1。
两边令z=1,并取模,则:
|1-a1|×|1-a2|×......×|1-a2n|=2n+1.........(*)
因为,|1-ak|=√|(cos(2kπ/(2n+1))-1))+i sin(2kπ/(2n+1))|=2×
sin(kπ/(2n+1)),所以由(*)式得:
2^n×sin(π/(2n+1))sin(2π/(2n+1))sin(3π/(2n+1))……sin(nπ/(2n+1))
=2n+1。
所以,sin(π/(2n+1))sin(2π/(2n+1))sin(3π/(2n+1))……sin(nπ/(2n+1))=√(2n+1)/2^n
2.三角函数
求证:sin(π/(2n+1))sin(2π/(2n+1))sin(3π/(2n+1))……sin(nπ
/(2n+1))=√(2n +1)/2^n.
证:sin(π/(2n+1))sin(2π/(2n+1))sin(3π/(2n+1))........sin(nπ
/(2n+1))=√(2n +1)/2^n
设Z=cos2π/(2n+1)+ isin2π/(2n+1)
则x^(2n+1)=1的根为1,z,...z^2n
得x^2n+...+x+1=(x-z)(x-z^2)...(x-z^2n)
2n+1=|(1-z)||(1-z^2)|...|(1-z^2n)| (1)
又|(1-z^k)|=2sinkπ/(2n+1) (2)
|1-z^k| = |1-(cos(2kπ/(2n+1)) +sin(2kπ/(2n+1)) )|
=|1-cos(2kπ/(2n+1))) -sin(2kπ/(2n+1)) )|
=√((1-2cos(2kπ/(2n+1)) +cos^2 (2kπ/(2n+1))) + sin^2 (2kπ/(2n+1))) =√(2-2cos(2kπ/(2n+1)) )
=√(4sin^2(kπ/(2n+1))
=2sin(kπ/(2n+1)
故
2n+1 =( n(π/(2n+1)). n(2π/(2n+1)) n(3π/(2n+1))........ n(2nπ/(2n+1)) 两边开方,得
sin(π/(2n+1))sin(2π/(2n+1))sin(3π/(2n+1))........sin(nπ/(2n+1)) =√(2n+1) / 2^n
另外那个类似,可以尝试自己证一下.
3.为什么sinπ/n+sin2π/n......+sin(n-1)π/n=cotπ/2n?
解:2 sin [π/(2n)]·sin(π/n)= cos [π/n -π/(2n)]- cos [π/n +π/(2n)]= cos [π/(2n)]- cos [3π/(2n)]2 sin [π/(2n)]·sin(2π/n)= cos [2π/n -π/(2n)]- cos [2π/n+π/(2n)]= cos [3π/(2n)]- cos
[5π/(2n)]2 sin [π/(2n)]·sin(3π/n)= cos [3π/n -π/(2n)]- co s [3π/n +π/(2n)]= cos [5π/(2n)]- cos [7π/(2n)]……2 sin [π/(2n)]·sin[(n-1)π/n]= cos [(n-1)π/n -π/(2n)]- cos [(n-1)π/n +π/(2n)]= cos [(2n-3)π/(2n)]- cos [(2n-1)π/(2n)]
故:2 sin [π/(2n)] ·{sin(π/n)+sin(2π/n)+......+sin[(n-1)π/n]}= cos [π/(2n)]- cos [(2n-1)π/(2n)]= cos [π/(2n)]- cos [π-π/(2n)]=2 cos [π/(2n)]
故:sin(π/n)+sin(2π/n)+......+sin[(n-1)π/n]= cos[π/(2n)]/ sin
[π/(2n)]= cot [π/(2n)]
4.级数sin n/(n+1)收敛还是发散,如果收敛,是绝对收敛还是条件收敛,为什么? Sol:收敛,Dirichlet 判别法.这是最典型的一个用Dirichlet 判别法判别收敛的例子.sinn 的部分和=[sin1/2(sin1+sin2+...+sinn)]/sin1/2(积化和差公式)=[cos1/2-cos(2n+1)/2)]/sin1/2,于是有界,1/(n+1)单调递减趋于0,收敛.不绝对收敛.|sinn/(n+1)|>=sin^2n/(n+1)=[1-cos(2n)]/2(n+1).类似用Dirichl et 判别法知道级数cos2n/(n+1)收敛,但级数1/(n+1)发散,于是易知不绝对收敛.建议记住这个典型例子.
1
2122ln ln ...ln lim .2ln ln ln ...ln n ln 2ln 1:ln 2ln =ln 2
o n n n n x n
o n n n n c c c I n
n c c c n n sol n n n n n
I →∞+++=+++-≤==-求
5.求sin π/n*sin2π/n*…*sin(n-1)π/n 的值,用复数思想
6.三角函数连乘(正弦)求证:sin[π/(2n+1)]*sin[2π/(2n+1)]*sin[3π/(2n+1)]*……*sin[nπ/(2n+1)]=(根号下2n-1)/2^n
Sol:
7.证一般项级数∑sin√(n^2+1)π条件收敛
Sol:∵sin√(n²+1)π
=[(-1)^n]sin[√(n²+1)π-nπ]
=[(-1)^n]sin[√(n²+1)-n]π
=[(-1)^n]sin{1/[√(n²+1)+n]}π
lim(n→∞)[sin{1/[√(n²+1)+n]}π]/(1/n)
=lim(n→∞)nπ/[√(n²+1)+n]
=π/2
∴∑sin{1/[√(n²+1)+n]}与∑1/n有相同的敛散性,即∑sin{1/[√(n²+1)+n]}π发散
lim(n→∞)sin{1/[√(n²+1)+n]}π=0,且sin{1/[√[(n+1)²+1]+(n+1)]}π≤sin{1/[√(n ²+1)+n]}π
由莱布尼兹判别法知lim[(-1)^n]sin{1/[√(n²+1)+n]}π收敛
∴原级数条件收敛
其他回答:sin√(n^2+1)π=(-1)^n sin(√(n^2+1)π+nπ)
再利用分子有理化可得:(-1)^n sin(π/[根号(n^2+1)+n])
利用 Dirichlet判别法可知级数收敛。
而它的绝对值级数可以等价为:sin(π/[根号(n^2+1)+n])~π/[根号(n^2+1)+n]~1/n即发散。
9.Sin(π/n) ×sin(2π/n) ×sin(3π/n) ×…×sin[(n-1)π/n]=n×2^(1-n) 这等式怎么证?大概要从哪个方面入手?
sin(π/n) ×sin(2π/n) ×sin(3π/n) ×…×sin[(n-1)π/n]=n×2^(1-n)
用复数
w=cos(2π/n)+isin(2π/n)
w'=cos(2π/n)-isin(2π/n)
z^n=1
(z-1)(z^(n-1)+z^(n-2)+……+z+1)=0
z^(n-1)+z^(n-2)+……+z+1=(z-w)(z-w^2)(z-w^3)……(z-w^(n-1))
令
z=1
n=(1-w)(1-w^2)(1-w^3)…(1-w^(n-1))
1-w^k=2sinkπ/n(sinkπ/n+icoskπ/n)
|1-w^k|=|2sinkπ/n(sinkπ/n+icoskπ/n)|=|2sinkπ/n||(sinkπ/n+icoskπ
/n)|=|2sinkπ/n|=2sin(kπ/n)
取模
|n|=|(1-w)(1-w^2)(1-w^3)…(1-w^(n-1))|
|n|=|(1-w)||(1-w^2)||(1-w^3)|…|(1-w^(n-1))|
n=2^(n-1)sin(π/n)sin(2π/n)……sin[(n-1)π/n]
得证。