下载文档原格式
大作业（一）一、填空题1、仅受（两个）力作用且处于（平衡）状态的构件称为二力构件。
2、力对物体有两种效应：（外效应）和（内效应）3、柔索的约束反力沿（柔索本身）且（背向）被约束物体。
4、光滑接触面的约束反力通过接触点沿（接触面的公法线），（指向）被约束物体。
5、平面汇交力系具有（2 ）个独立平衡方程。
6、度量力对物体的转动效应的物理量是（力矩）7、力偶在任意坐标轴上的投影的代数和恒等于（零）。
力偶对任一点之矩为（常量）8、在保持（力偶矩）不变的条件下，可任意改变力和力偶臂，并可在作用面内任意转移。
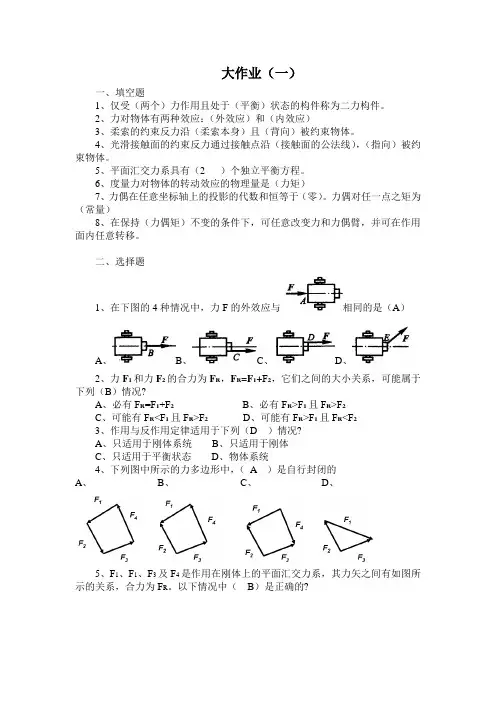
二、选择题1、在下图的4种情况中，力F的外效应与相同的是（A）A、B、C、D、2、力F1和力F2的合力为F R，F R=F1+F2，它们之间的大小关系，可能属于下列（B）情况?A、必有F R=F1+F2B、必有F R>F1且F R>F2C、可能有F R<F1且F R>F2D、可能有F R>F1且F R<F23、作用与反作用定律适用于下列（D ）情况?A、只适用于刚体系统B、只适用于刚体C、只适用于平衡状态D、物体系统4、下列图中所示的力多边形中，（A ）是自行封闭的A、B、C、D、5、F1、F1、F3及F4是作用在刚体上的平面汇交力系，其力矢之间有如图所示的关系，合力为F R。
以下情况中（B）是正确的?A、F R=F4B、F R=2F4C、F R=-F4D、F R=-2F46、三铰刚架ABC如图所示，不计自重，仅受力F作用，铰链A反力FA的方位必满足（ C ）?A、通过B点B、通过D点C、通过E点D、通过C点7、在图中，如果两力偶均作用在杆AC上，铰链A或B的反力方位（ C ）?A、垂直于ACB、垂直于BCC、垂直于ABD、不确定三、画受力图1、重为P的均质圆轮在边缘A点用绳AB系住，绳AB通过轮心C，圆轮边缘D点靠在光滑的固定曲面上，试画圆轮的受力图解：（1）选圆轮为研究对象，画出其分离体图（2）在分离体圆轮上画出作用其上的主动力P（3）在分离体的每处约束，画出其约束力。
大作业（一）一、填空题1、杆件变形的基本形式有（轴向拉伸和压缩）、（剪切）、（扭转）和（弯曲）2、材料力学所研究的问题是构件的（强度）、（刚度）和（稳定性）。
3、脆性材料的抗压能力远比抗拉能力（强）。
4、同一种材料，在弹性变形范围内，横向应变ε/和纵向应变ε之间有如下关系：（ε/= -με）5、（弹性模量E ）是反映材料抵抗弹性变形能力的指标。
6、（屈服点σs ）和（抗拉强度σb ）是反映材料强度的两个指标7、(伸长率δ)和(断面收缩率ψ)是反映材料塑性的指标，一般把（δ>5%）的材料称为塑性材料，把（δ<5%）的材料称为脆性材料。
8、应力集中的程度可以用（应力集中因数K ）来衡量 9、（脆性材料）对应力集中十分敏感，设计时必须考虑应力集中的影响 10、挤压面是外力的作用面，与外力（垂直），挤压面为半圆弧面时，可将构件的直径截面视为（挤压面）11、如图所示，铆接头的连接板厚度t=d ，则铆钉剪应力τ=（ 22d P πτ= ） ，挤压应力σbs =（ td Pbs2=σ ）。
P/2P/2二、选择题1、构成构件的材料是可变形固体，材料力学中对可变形固体的基本假设不包括（C ）A 、均匀连续性B 、各向同性假设C 、平面假设D 、小变形假设 2、下列力学性能指标中，（B ）是强度指标A 、弹性模量EB 、屈服强度s σC 、伸长率δD 、许用应力σ 3、下列力学性能指标中，（C ）是反映塑性的指标A 、比例极限p σB 、抗拉强度b σC 、断面收缩率ψD 、安全系数n 4、下列构件中，（ C ）不属于轴向拉伸或轴向压缩 A 、 B 、 C 、 D 、5、强度计算时，引入安全系数的原因不包括（A）A、力学性能指标测定方法都不是太科学B、对构件的结构、尺寸和受力等情况都作了一定程度的简化C、加工工艺对构件强度的影响考虑的不全面D、构件需有必要的强度储备6、一直杆受外力作用如图所示，此杆各段的轴力图为（C）A、B、C、D、7、一直杆受外力作用如图所示，此杆各段的轴力为（A）A、+6（拉力），- 4（压力），4（拉力）B、-6（压力），- 4（压力），4（拉力）C、+6（拉力），+ 4（拉力），4（拉力）D、-6（压力），+ 4（拉力），4（拉力）8、图所示为两端固定的杆。
作业一说明：本次作业对应于平面体系的几何组成分析和静定结构的受力分析，应按相应教学进度完成。
一、选择题（每小题2分，共20分）1．三刚片组成几何不变体系的规则是（B ）A 三链杆相联，不平行也不相交于一点B 三铰两两相联，三铰不在一直线上C 三铰三链杆相联，杆不通过铰D 一铰一链杆相联，杆不过铰2．在无多余约束的几何不变体系上增加二元体后构成（C ）A 可变体系B 瞬变体系C 无多余约束的几何不变体系D 有多余约束的几何不变体系3．瞬变体系在一般荷载作用下，（C ）A产生很小的内力B不产生内力C产生很大的内力D不存在静力解答4．已知某体系的计算自由度W=-3，则体系的（C ）A自由度为3 B自由度等于0C 多余约束数等于3D 多余约束数大于等于35．不能作为建筑结构使用的是（D ）A无多余约束的几何不变体系B有多余约束的几何不变体系C 几何不变体系D几何可变体系6．图示桁架有几根零杆（ D ）9A 折线B 圆弧C 双曲线D 抛物线二、判断题（每小题2分，共20分）1．多余约束是体系中不需要的约束。
（×）2．如果体系的计算自由度大于零，那么体系一定是几何可变体系。
（√）3．两根链杆的约束作用相当于一个单铰。
（×）4．一个体系是有n个自由度的几何可变体系，那么加入n个约束后就成为无多余约束的几题2-7图题2-10图四、绘制下图所示各结构的弯矩图。
（每小题10分，共30分）（3）参考答案：40单位：m kN ⋅五、计算图示桁架中指定杆件的内力。
（10分）参考答案：4/2P N 1F F -=，P N2F F -=，2/3P N3F F =。
《工程力学》第1次作业解答（静力学基本概念与公理）2010-2011学年第二学期一、填空题1．力是物体间相互的相互机械作用，这种作用能使物体的运动状态和形状发生改变。
2．力的基本计量单位是牛顿（N）或千牛顿（kN）。
3．力对物体的作用效果取决于力的大小、方向和作用点（作用线）三要素。
4．若力F对某刚体的作用效果与一个力系对该刚体的作用效果相同，则称F为该力系的合力，力系中的每个力都是F的分力。
5．平衡力系是合力（主矢和主矩）为零的力系，物体在平衡力系作用下，总是保持静止或作匀速直线运动。
6．力是既有大小，又有方向的矢量，常用带有箭头的线段画出。
7．刚体是理想化的力学模型，指受力后大小和形状始终保持不变的物体。
8．若刚体受二力作用而平衡，此二力必然大小相等、方向相反、作用线重合。
9．作用力和反作用力是两物体间的相互作用，它们必然大小相等、方向相反、作用线重合，分别作用在两个不同的物体上。
10．约束力的方向总是与该约束所能限制运动的方向相反。
11．受力物体上的外力一般可分为主动力和约束力两大类。
12．柔性约束限制物体绳索伸长方向的运动，而背离被约束物体，恒为拉力。
13．光滑接触面对物体的约束力，通过接触点，沿接触面公法线方向，指向被约束的物体，恒为压力。
14．活动铰链支座的约束力垂直于支座支承面，且通过铰链中心，其指向待定。
15．将单独表示物体简单轮廓并在其上画有全部外力的图形称为物体的受力图。
在受力图上只画受力，不画施力；在画多个物体组成的系统受力图时，只画外力，不画内力。
二、选择题1．约束力的方向必与（B）的方向相反。
A．主动力；B．物体被限制运动；C．重力；D．内力。
2．柔性约束的约束力方向总是（C）受约束物体。
A．铅垂指向；B．沿绳索指向；C．沿绳索背离；D．水平指向。
3．光滑面约束的约束力总对受力物体形成（A）作用。
A．压力；B．拉力；C．牵引力；D．摩擦力。
4．凡能使物体运动或有运动趋势的力称为（A）。
2014-2015学年第二学期期末《工程力学（工）》大作业1、槽形铸铁梁受力如图所示，槽形截面对中性轴z 的惯性矩I z ＝40×106mm 4，材料的许用拉应力[]MPa 40=t σ，材料的许用压应力[]MPa 150=c σ。
试 （1）画出梁的剪力图和弯矩图；（2）校核此梁的强度。
（10分）C答：（1）支座反力,0=A F kN F B 60=（2） m kN M M B ⋅==30max][10510104014.0103014.01263max max c zc MPa I M σσ<=⨯⨯⨯⨯=⨯=-][4510104006.0103006.01263max max t zt MPa I M σσ>=⨯⨯⨯⨯=⨯=- ∴此梁不安全。
2、两端铰支压杆，材料为Q235A 钢，200E GPa =，长1l m =，直径为25d mm =，承受25kN 压力，规定稳定安全系数[]3=n w，校核此压杆的稳定性。
(15分）m kN 30⋅M kN30kN 30s F解：（1）mm d i 4254==λμλp i l 1604/2510001=⨯== 采用欧拉公式计算临界力()()KN EI l F cr79.376414.320014.3100012510243222=⨯⨯⨯⨯⨯==⨯μϕ[]351.12579.37====n Fn wcrw F稳定性不足3、一端外伸梁如图所示，已知q,a ,3a 。
试求梁的约束反力。
（15分）解答：以外伸梁ABC 为研究对象，画受力图，如下图所示。
其中A 为固定铰链支座，故R A 的方向未定，将其分解为X A 、Y A ；B为可动铰链支座，R B 的方向垂直于支撑面，q 为主动力，列出平衡方程：0)(=∑F m A 032)3()3(=⋅-+⋅+a R a a a a q B 0=∑X0=A X0=∑Y 04=-+qa R YB A最后解得：Y A =（4/3）qa ,R B =(8/3)qa4、已知：拉杆AB 为圆截面，直径d=20mm ，许用应力[σ]=160MPa 试求：校核拉杆AB 的强度。
大作业（一）一、填空题1、杆件变形的基本形式有（轴向拉伸和压缩）、（剪切）、（扭转）和（弯曲）2、材料力学所研究的问题是构件的（强度）、（刚度）和（稳定性）。
3、脆性材料的抗压能力远比抗拉能力（强）。
4、同一种材料，在弹性变形范围内，横向应变ε/和纵向应变ε之间有如下关系：（ε/= -με）5、（弹性模量E ）是反映材料抵抗弹性变形能力的指标。
6、（屈服点σs ）和（抗拉强度σb ）是反映材料强度的两个指标7、(伸长率δ)和(断面收缩率ψ)是反映材料塑性的指标，一般把（δ>5%）的材料称为塑性材料，把（δ<5%）的材料称为脆性材料。
8、应力集中的程度可以用（应力集中因数K ）来衡量 9、（脆性材料）对应力集中十分敏感，设计时必须考虑应力集中的影响 10、挤压面是外力的作用面，与外力（垂直），挤压面为半圆弧面时，可将构件的直径截面视为（挤压面）11、如图所示，铆接头的连接板厚度t=d ，则铆钉剪应力τ=（ 22dP πτ= ） ，挤压应力σbs =（ td Pbs 2=σ ）。
P/2P/2二、选择题1、构成构件的材料是可变形固体，材料力学中对可变形固体的基本假设不包括（C ）A 、均匀连续性B 、各向同性假设C 、平面假设D 、小变形假设 2、下列力学性能指标中，（B ）是强度指标A 、弹性模量EB 、屈服强度s σC 、伸长率δD 、许用应力σ 3、下列力学性能指标中，（C ）是反映塑性的指标A 、比例极限p σB 、抗拉强度b σC 、断面收缩率ψD 、安全系数n 4、下列构件中，（ C ）不属于轴向拉伸或轴向压缩 A 、 B 、 C 、 D 、5、强度计算时，引入安全系数的原因不包括（A）A、力学性能指标测定方法都不是太科学B、对构件的结构、尺寸和受力等情况都作了一定程度的简化C、加工工艺对构件强度的影响考虑的不全面D、构件需有必要的强度储备6、一直杆受外力作用如图所示，此杆各段的轴力图为（C）A、B、C、D、7、一直杆受外力作用如图所示，此杆各段的轴力为（A）A、+6（拉力），- 4（压力），4（拉力）B、-6（压力），- 4（压力），4（拉力）C、+6（拉力），+ 4（拉力），4（拉力）D、-6（压力），+ 4（拉力），4（拉力）8、图所示为两端固定的杆。
(一) 单选题1.二同向平行力简化的最终为一合力FR，则___。
(A)(B)(C)(D)参考答案：(A)2.水平梁受三角形载荷作用，分布载荷的最大值为，梁长为，与之等效合力的大小和位置分别是___。
(A)，合力作用的位置距分布载荷的最大值距离是(B)，合力作用的位置距分布载荷的最大值距离是(C)，合力作用的位置距分布载荷的最大值距离是(D)，合力作用的位置距分布载荷的最大值距离是参考答案：(B)3.作用在图示支架上点A的三个力的合力为___。
(A)，指向左上方，与水平线夹角(B) ，指向左下方，与水平线夹角(C) ，指向左上方，与水平线夹角(D) ，指向左下方，与水平线夹角参考答案：(B)4. 图所示水平力F作用在刚架的B点，不计刚架重量，支座A和D的约束力为___。
(A)(B)(C)(D)参考答案：(A)5. 已知某平面力系简化的最后结果为一合力，若将此平面力系向作用面内其它任一点O简化，则主矢和主矩___。
(A)必有，必有(B) 必有，可能有(C) 可能有，可能有(D) 可能有，可能有参考答案：(B)6. 重为W的物块放置在光滑水平面上，物块对支承面的压力为P，支承面对物块的约束力为N，则三个力大小之间的关系是___。
(A)(B)(C)(D)参考答案：(C)7.图所示外伸梁，不计自重，力单位为kN，力偶矩单位为，分布载荷单位为kN/m，长度单位为m，支座A和B的约束力为___。
(A)(B)(C)(D)参考答案：(A)8. 曲柄连杆活塞机构的活塞上受力F=400N。
如不计所有构件的重量，在曲柄上应加多大的力偶矩M是___才能使机构在图示位置平衡。
(A)(B)(C)(D)参考答案：(C)9. 某平面力系向A、B两点简化的主矩皆为零，则___。
(A)力系必平衡(B) 力系可能简化为力偶(C) 力系可能平衡(D) 力系向任意点简化的主矩必等于零参考答案：(C)10. 活动铰支座的约束力___。
(A)用两个互相垂直的约束分力表示(B) 用一个垂直于支承面且过铰心的力表示，指向可任意设置(C) 用一个垂直于支承面且过铰心的力表示，指向被约束的物体(D) 用一个垂直于支承面且过铰心的力表示，背离被约束的物体参考答案：(B)11.图所示___力对z轴之矩等于零。
大作业（一）一、填空题1、杆件变形的基本形式有（轴向拉伸和压缩）、（剪切）、（扭转）和（弯曲）2、材料力学所研究的问题是构件的（强度）、（刚度）和（稳定性）。
3、脆性材料的抗压能力远比抗拉能力（强）。
4、同一种材料，在弹性变形范围内，横向应变ε/和纵向应变ε之间有如下关系：（ε/= -με）5、（弹性模量E ）是反映材料抵抗弹性变形能力的指标。
6、（屈服点σs ）和（抗拉强度σb ）是反映材料强度的两个指标7、(伸长率δ)和(断面收缩率ψ)是反映材料塑性的指标，一般把（δ>5%）的材料称为塑性材料，把（δ<5%）的材料称为脆性材料。
8、应力集中的程度可以用（应力集中因数K ）来衡量 9、（脆性材料）对应力集中十分敏感，设计时必须考虑应力集中的影响 10、挤压面是外力的作用面，与外力（垂直），挤压面为半圆弧面时，可将构件的直径截面视为（挤压面）11、如图所示，铆接头的连接板厚度t=d ，则铆钉剪应力τ=（ 22dP πτ= ） ，挤压应力σbs =（ td Pbs 2=σ ）。
P/2P/2二、选择题1、构成构件的材料是可变形固体，材料力学中对可变形固体的基本假设不包括（C ）A 、均匀连续性B 、各向同性假设C 、平面假设D 、小变形假设 2、下列力学性能指标中，（B ）是强度指标A 、弹性模量EB 、屈服强度s σC 、伸长率δD 、许用应力σ 3、下列力学性能指标中，（C ）是反映塑性的指标A 、比例极限p σB 、抗拉强度b σC 、断面收缩率ψD 、安全系数n 4、下列构件中，（ C ）不属于轴向拉伸或轴向压缩 A 、 B 、 C 、 D 、5、强度计算时，引入安全系数的原因不包括（A）A、力学性能指标测定方法都不是太科学B、对构件的结构、尺寸和受力等情况都作了一定程度的简化C、加工工艺对构件强度的影响考虑的不全面D、构件需有必要的强度储备6、一直杆受外力作用如图所示，此杆各段的轴力图为（C）A、B、C、D、7、一直杆受外力作用如图所示，此杆各段的轴力为（A）A、+6（拉力），- 4（压力），4（拉力）B、-6（压力），- 4（压力），4（拉力）C、+6（拉力），+ 4（拉力），4（拉力）D、-6（压力），+ 4（拉力），4（拉力）8、图所示为两端固定的杆。
在C、D两端处有一对力P作用，杆的横截面面积为A ，弹性模量为E ， A 、B 处支座反力（C ）A 、F A =FB =2F/3 B 、 F A =F B =F/3C 、F A =F/3 F B =2P/3D 、F A =2F/3 F B =F/39、一钢制阶梯杆如图所示，已知轴向外力P 1=5KN ，P 2=2KN ，各段杆长为l 1=15mm ，l 2=l 3=12mm ，横截面面积A 1=A 2=6mm 2，A 3=3mm 2，钢的弹性模量E=200Gpa ，各段杆的线应变分别为1ε、2ε、3ε，下列选项正确的是（B ）A 、||1ε>||2ε>||3εB 、||3ε>||1ε>||2εC 、 ||2ε>||3ε>||1εD 、||2ε>||1ε>||3ε11、在研究材料的力学性能时，出现过σ0.2，下列( C )说法是正确的? A 、σ0.2是塑性材料的屈服强度 B 、σ0.2是脆性材料的屈服强度C 、σ0.2是指试件在卸载后产生数值为0.2％的塑性应变时的应力值D 、σ0.2是指试件在加载后产生数值为0.2％的应变时的应力值 12、对于脆性材料，下列说法（ C ）是错误的? A 、试件在受拉过程中，不出现屈服和颈缩现象。
B 、压缩强度极限比拉伸强度极限高出许多 C 、抗冲击性能好D 、脆性材料拉伸断裂前的变形很少 13、齿轮与轴由平键（b ×h ×L =20 ×12 ×100）连接，它传递的扭矩m =2KNm ，轴的直径d =70mm ，键的许用切应力为[τ]= 60M Pa ，许用挤压应力为[]bs σ= 100M Pa ，则键的（B ）。
A 、剪切强度和挤压强度都不足B 、剪切强度和挤压强度都足够2LLPFBCF BF A AC 、剪切强度不足D 、挤压强度不足 三、计算题1、一直杆受外力作用如图所示，求此杆各段的轴力，并作轴力图解：（1）AB 段：用截面1-1假想将杆截开，取左段研究，设截面上的轴力为正方向，受力如图所示。
列平衡方程式：0=∑xF061=-N F61=N F （拉力）（2）BC 段，取2-2截面左段研究，FN2设为正向，受力如图所示，列平衡方程式：0=∑xF06102=-+N F42-=N F （压力）；（3）CD 段，取3-3截面右段研究，FN3设为正，受力如图所示，列平衡方程式：0=∑xF043=-N F43=N F （拉力）（4）画轴力图2、如图所示空心圆截面杆，外径D=20mm ，内径d=15mm ，承受轴向载荷F=20kN ，材料的屈服应力σs=235MPa ，安全因数n=1.5，试问该杆的强度解：杆件横截面上的正压力MPa Pa d D F 5.14510455.1)15.002.0(10204)(4822322=⨯=-⨯⨯=-=ππσ 材料的许用应力[]MPa n ss1565.1235===σσ []杆件能够安全工作∴<σσ3、如图所示吊环，由圆截面斜杆AB ，AC 与横梁BC 所组成。
已知吊环的最大吊重F=500kN ，斜杆用锻钢制成，其许用应力[σ]=120MPa ，斜杆与拉杆轴线的夹角α=20°，试确定斜杆的直径。
解：（1）斜杆轴力分析节点A 的受力如图，设轴力F N ，则有平衡方程0cos 20=-=∑αN yF F FN F F N 531066.220cos 210500cos 2⨯=⨯==α （2）截面设计[]σNF A ≥42d A π=m m F d N 2651031.5101201066.24][4-⨯=⨯⨯⨯⨯=≥πσπ 取斜杆的截面直径mm d 0.53=4、如图所示桁架，由杆1与杆2组成，在节点B 承受载荷F 作用。
试计算载荷F 的最大允许值即所谓许用载荷。
已知杆1与杆2的横面积A=100mm 2，许用拉应力为[σt]=200MPa ，许用压应力[σc]=150MPa.解： （1）轴力分析设杆1和杆2轴向受拉，杆1与2的轴力分别为F N1和F N2，节点B 的受力图如图所示。
列节点B 的平衡方程得045sin 01=-=∑F F F N y)(21拉F F N = 045cos 012=--=∑ N N xF F F)(2压F F N -=（2）计算许用载荷 杆1的强度条件][2t AFσ≤ N A F 46610414.1210200101002][⨯=⨯⨯⨯≤≤-σ 杆2的强度条件][c AFσ≤- N A F 466105.11015010100][⨯=⨯⨯⨯=≤-σ可见，桁架所能承受的最大载荷即许用载荷为 kN F 14.14][=5、如图所示结构中，梁AB 可视为刚体，其弯曲变形可忽略不计，杆1为钢质圆杆，直径d 1=20mm ，其弹性模量E 1=200Gpa ，杆2为铜杆，其直径d 2=25mm ，弹性模量E 2=100Gpa ，不计刚梁AB 的自重，试求：（1）载荷P 加在何处，才能使刚梁AB 受力后保持水平？ （2）若此时P=30KN ，求两杆内横截面上的正应力？解：（1）、选取刚梁AB 为研究对象，画出其受力图。
∑F y =0：N A -P+N B =0。
………….(1) ∑m A (F)=0：-P X+N B ×2=0……………(2) 变形谐调条件为：△l 1=△l 2。
即：221115.1A E N A E N B A ⋅⨯=⋅⨯（虎克定律） 解得：N A =0.8533N B ………………(3) 由（1）和（2）得：x=2N B /（N A +N B ）。
由（3）代入上式得：x=1.08m 。
（2）、由（2）式得：N B =PX/2=30×1.08/2=16.2KN 。
N A =P - N B =13.8KN 。
∴σ1=N A /A 1=13.8×4/π×(0.02)2=43.9Mpa 。
σ2=N B /A 2=16.2×4/π×(0.025)2=33Mpa 。
6、齿轮与轴由平键（b ×h ×L =20 ×12 ×100）连接，它传递的扭矩m =2KNm ，轴的直径d =70mm ，键的许用切应力为[τ]= 60M Pa ，许用挤压应力为[]bs σ= 100M Pa ，试校核键的强度。
解：(1)键的受力分析如图, kN 5707.02222=⨯==∴=•d m P m d P (2)切应力和挤压应力的强度校核 P F s =剪切面bL A =,挤压面2h L A bs =[]ττ≤=⨯⨯===MPa 6.281002010573bL P A F s[]bs bs bs h L P A P σσ≤=⨯⨯===MPa 3.956100105723综上，键满足强度要求。
7、一铆接头如图所示，受力F=110kN ，已知钢板厚度为 t =1cm ，宽度 b =8.5cm ，许用应力为[σ ]= 160M Pa ；铆钉的直径d =1.6cm ，许用切应力为[τ]= 140M Pa ，许用挤压应力为[σbs ]= 320M Pa ，试校核铆接头的强度。
（假定每个铆钉受力相等。
）解：（1）取下面钢板为研究对象，受力分析如图每个孔受销轴的约束反力为 4F P F == （2）销轴的剪切强度和挤压强度计算每个销轴的剪切力为：4FP F s ==剪切面面积：42dA π=则[]τπτ≤=⨯⨯===MPa 8.136106.114.311044722d F A F s 每个销轴的挤压力为：4F P = 挤压面面积：td A bs = 则[]bs bs bs td F A P σσ≤=⨯⨯⨯===MPa 9.171106.11411047 （3）钢板的拉伸强度计算 截面1—1的轴力为：41FF N = ，面积：)(1d b t A -= 截面2—2的轴力为：432FF N =，面积：)2(2d b t A -= 截面3—3的轴力为：F F N =3，面积：)(3d b t A -= 所以，钢板的2--2和3—3截面为危险面[]σσ≤=⨯⨯-⨯⨯=-==MPa 7.15510)6.125.8(41103)2(437222d b t F A F N []σσ≤=⨯-⨯=-==MPa 4.15910)6.15.8(1110)(7333d b t F A F N 综上，接头安全。
