第十讲 行程问题(1)
- 格式:doc
- 大小:35.00 KB
- 文档页数:5

学习目标本讲主要通过例题加深对行程问题的三个基本数量关系的理解。
在历年小升初与各类小学竞赛试卷中,行程问题的试题占的比值是相当大的,所以学好行程问题不但对于应对小升初考试和各类数学竞赛有着举足轻重的关键性作用,而且也为初中阶段的学习打下良好的基础。
我们把研究路程、速度、时间以及这三者之间关系的一类问题,总称为行程问题. 行程问题主要涉及时间 (t)、速度 (v)和路程 (.s)这三个基本量,它们之间的关系如下: 路程 = 速度×时间 可简记为:s vt = 速度 = 路程÷时间 可简记为:/v s t = 时间 = 路程÷速度 可简记为:/t s v = 路程一定,速度与时间成反比 速度一定,路程与时间成正比时间一定,路程与速度成正比显然,知道其中的两个量就可以求出第三个量.【例 1】 一段路程分为上坡、平路、下坡三段,各段路程的长度之比是 1:2:3,某人走这三段路所用的时间之比是 4:5:6,已知他上坡时每小时行2.5千米,路程全长为 20千米,此人走完全程需多少时间?【例 2】甲、乙两地相距60千米,自行车队 8点整从甲地出发到乙地去,前一半时间每分钟行 1千米,后一半时间每分钟行0.8千米。
自行车队到达乙地的时间是几点几分几秒?【例3】某人上山时每走30分钟休息10分钟,下山时每走30分钟休息5分钟,已知下山的速度是上山速度的1.5倍,如果上山用了3 时50分钟,那么下山用多少时间?【例4】汽车以72千米/时的速度从甲地到乙地,到达后立即以48千米/时的速度返回甲地,求该车的平均速度。
【例5】甲、乙两车往返于A、B两地之间,甲车去时的速度为60千米/时,返回时的速度为40千米/时,乙车往返的速度都是50千米/时,求甲、乙两车往返一次所用的时间比.【例6】从甲地到乙地全部是山路,其中上山路程是下山路程的23,一辆汽车上山速度是下山速度的一半,从甲地到乙地共行7时,这辆汽车从乙地返回甲地需要多少时间?【例7】一辆车从甲地行往乙地,如果把车速提高20%,那么可以比原定时间提前1 小时到达;如果以原速度行驶100千米后再将车速提高30%,那么也比原定时间提前 1 小时到达,求甲、乙两地的距离。

行程问题(一)这一讲在相遇问题和追及问题的基础上学习一些综合性的问题。
【例1】 甲、乙两辆汽车同时从A 、B 两地相向开出。
甲车每小时行56千米,乙车每小时行48千米。
两车在离中点32千米处相遇。
求A 、B 两地间的距离是多少?分析 这题要求路程,题中已知两车速度,但缺少两车相遇所用时间,可先求出甲车比乙车多行多少千米,用多少时间。
解 如图(1)相遇时甲车比乙车多行64232=⨯(千米)(2)甲车比乙车多行64千米要8485664=-÷)((小时) (3)A 、B 两地间的距离是83284856=⨯+)((千米) 答:A 、B 两地相距832千米。
说明 1. 不能错误地认为甲车只比乙车多行32千米。
应当是甲多行32千米的2倍。
2. 这里两车相遇的时间即用多少时间甲车才能比乙车多行64千米。
【例2】 甲每分钟走50米,乙每分钟走60米,丙每分钟走70米,甲、乙两人从A 地。
丙一人从B 地同时相向出发,丙遇到乙后2分钟又遇到甲,A 、B 两地相距多少米?分析 在已知速度的情况下,要求A 、B 两地间距离必须求出丙和乙相遇所用的时间。
丙遇到乙后2分钟又遇到甲。
丙、甲这两分钟合行的路程,实际上就是乙与丙相遇时,乙比甲多行的路程。
而乙比甲多行这段路所用的时间就是乙与丙相遇所用的时间。
解 设乙、丙在D 相遇,甲、丙在C 相遇(如图)(1)甲、丙2分钟合行路程CD24027050=⨯+)((米) (2)乙比甲多行CD 所需时间245060240=-÷)((分钟) (3)A 、B 两地的距离为3120247060=⨯+)((米) 答:A 、B 两地相距3120米。
说明 本题与例1有类似的地方,请加以比较。
【例3】 一列慢车在上午9点钟以每小时40千米的速度由甲城开往乙城。
另有一列32千米 A 甲车 乙车 B 中点 C D甲、丙2分钟 合行的路程A BC D 甲 乙, 丙快车在上午9点30分以每小时56千米的速度也由甲城开往乙城。

三年级科学第十讲简单的行程问题三年级科学第十讲简单的行程问题
引言
本次课程旨在教授三年级学生如何解决简单的行程问题。
行程问题是指计算在规定的时间内,一个物体根据给定的速度和时间间隔的移动情况。
通过研究本课程,学生将能够理解行程问题的基本概念和解决方法。
目标
本课程的目标是使学生能够:
- 理解行程问题的定义和基本要素
- 学会根据给定速度和时间间隔计算物体的行程
- 解决简单的行程问题
课程内容
1. 行程问题的定义
- 行程是指一个物体在一段时间内的移动距离。
- 行程问题需要知道物体的速度和经过的时间间隔。
2. 计算行程的公式
- 行程等于速度乘以时间间隔。
3. 解决简单的行程问题
- 根据给定的速度和时间间隔计算行程。
- 使用行程公式求解行程问题的一般步骤:
1. 确定已知量,包括速度和时间间隔。
2. 使用行程公式进行计算。
3. 得出行程结果。
4. 例题演练
- 提供几个简单的行程问题的例题,供学生练。
结论
通过本课程的研究,学生已经掌握了解决简单的行程问题的基本方法。
他们能够理解行程的定义和基本要素,并能够使用行程公式计算物体的行程。
接下来,他们可以通过练更多的行程问题来提高他们的解决能力。

第10讲综合行程问题(一)【例1】甲乙两车站相距3.5千米,A车速为每分钟180米,B车速为每分钟170米,A、B两车分别从甲、乙两站相向开出,两车到站后都要停留7分钟,它们第一次相遇后要经过多少时间第二次相遇?【LX1】甲乙两人分别从AB两地同时出发相向而行,甲每小时行6千米,乙每小时行4千米。
在离A 两地3千米的地方相遇,求AB两地的距离。
【例2】甲每分钟走50米,乙每分钟走60米,丙每分钟走70米,甲、乙两人从A地,丙从B地三人同时相向出发,丙先遇乙,再经过2分钟后遇到甲,问A、B两地相距多远?【LX2】甲乙两人分别从A,B两地骑车同时出发相向而行,2小时后相遇,相遇后乙继续向A地前进,甲则返回。
当甲到达A地时,乙距离A地还有4千米。
已知AB两地相距80千米。
求甲乙两个人各自的速度。
【例3】A、B两城相距420千米,一辆轿车和一辆货车分别从两城相向而行,货车上午8点出发,轿车上午9点出发,轿车速度是货车速度的2倍,两车在11点时相遇,求两车的速度。
【LX3】甲、乙两车从A、B两站同时相向开出,已知甲车的速度是乙车速度的9倍,甲、乙到达途中C 站的时刻依次为5:00和15:00,这两车相遇是什么时刻?【例4】甲乙两人同时分别从两地骑车相向而行,甲每小时行20千米,乙每小时行18千米,两人相遇时距全程中点3千米,求全程长多少千米?【LX4】快慢两列火车同时从甲、乙两地相向开出,3小时后两车在距中点12公里处相遇,快车每小时比慢车每小时快多少公里?【例5】骑自行车从同一地点出发,沿周长900公里的环形路,若反向而行2分钟就相遇,若同向而行经过18分快者追上慢者,求慢者的速度?【LX5】甲、乙两架飞机从一个机场起飞,向同一方向飞行,甲、乙速度为每小时300公里和340公里,飞行4小时后,甲机要提速,2小时后追上乙,问甲的速度【例6】兄妹同时从家出发上学,兄妹的速度为每分钟90公尺和60公尺,兄到达校门时发现忘带语文书,立即按原速原路返回,在离学校180公尺处与妹妹相遇,他们家距学校多远?【LX6】甲、乙两人练习跑步,若甲让乙先跑10公尺,则甲跑5秒钟追上乙,若甲让乙先跑2秒,则甲跑4秒钟就追上乙,求甲的速度?【例7】狗追狐狸,狗跳一次前进18公尺,狐狸跳一次前进11公尺,狗每跳2次时狐狸恰好跳3次,如果开始时狗离狐狸有30公尺,那么狗跳多少公尺才能追上狐狸?【LX7】一只狗追赶一只野兔,狗跳5次的时间兔子能跳6次,狗跳4次的距离与兔子跳7次的距离相等.兔子跳出550米后狗子才开始追赶.问狗跳了多远才能追上兔子?【例8】小明以每分钟 50 米的速度从学校步行回家,12分钟后小强从学校出发骑自行车以每分钟150米的速度去追小明,结果小明到家时,小强还差100米才追上,求小强骑自行车追了多少时间?【LX8】甲、乙两架飞机同时从一个机场起飞,向同一方向飞行,甲机每小时行300千米,乙机每小时行340千米,飞行4小时后它们相隔多少千米?这时候甲机提高速度用1小时还差80千米追上乙机,甲机每小时要飞行多少千米?思维训练1. 甲乙两人分别从相距800千米的两地同时出发相向而行,甲车每小时行52千米,乙车每小时行48千米,问:(1)几小时后两车还相距200千米?(2)几小时后两车相遇?(3)几小时后两车相遇又相距400千米?2.大客车在公路上每小时行60千米,小客车每小时行48千米,两辆汽车从甲乙两城相对开出,在离公路中点24公里处相遇,甲、乙两城的公路长多少公里?3.甲比乙每小时多走1公里,甲、乙同时从A、B两地相向而行,5小时后相遇,A、B间距离为45公里,求甲的速度?4.王明回家,距家门300公尺,妹妹和小狗一起向他奔来,王明和妹妹的速度都是每分钟50公尺,小狗的速度是每分钟200公尺,小狗遇到王明和妹妹,立即调头往回跑,用同样的速度不停往返王明与妹妹之间,当王明与妹妹相距10公尺时,小狗一共跑多少公尺?5.小明步行上学,每分钟行70米.离家12分钟后,爸爸发现小明的文具盒忘在家中,爸爸带着文具盒,立即骑自行车以每分钟280米的速度去追小明.问爸爸出发几分钟后追上小明?当爸爸追上小明时他们离家多远?6.哥哥和弟弟在同一所学校读书.哥哥每分钟走65 米,弟弟每分钟走40 米,有一天弟弟先走5 分钟后,哥哥才从家出发,当弟弟到达学校时哥哥正好追上弟弟也到达学校,问他们家离学校有多远?思维拓展:甲、乙两人在相距50米的A、B两端的水池里沿直线来回游泳。

训练点21——行程问题例1:甲乙两人分别从相距20千米的两地同时出发相向而行,甲每小时走6千米,乙每小时走4千米。
两人几小时后相遇?分析与解答:这是一道相遇问题。
所谓相遇问题就是指两个运动物体以不同的地点作为出发地作相向运动的问题。
根据题意,出发时甲乙两人相距20千米,以后两人的距离每小时缩短6+4=10千米,这也是两人的速度和。
所以,求两人几小时相遇,就是求20千米里面有几个10千米。
因此,两人20÷(6+4)=2小时后相遇。
练习一1,甲乙两艘轮船分别从A、B两港同时出发相向而行,甲船每小时行驶18千米,乙船每小时行驶15千米,经过6小时两船在途中相遇。
两地间的水路长多少千米?2,一辆汽车和一辆摩托车同时分别从相距900千米的甲、乙两地出发,汽车每小时行40千米,摩托车每小时行50千米。
8小时后两车相距多少千米?3,甲乙两车分别从相距480千米的A、B两城同时出发,相向而行,已知甲车从A城到B城需6小时,乙车从B城到A城需12小时。
两车出发后多少小时相遇?例2:王欣和陆亮两人同时从相距2000米的两地相向而行,王欣每分钟行110米,陆亮每分钟行90米。
如果一只狗与王欣同时同向而行,每分钟行500米,遇到陆亮后,立即回头向王欣跑去;遇到王欣后再回头向陆亮跑去。
这样不断来回,直到王欣和陆亮相遇为止,狗共行了多少米?分析与解答:要求狗共行了多少米,一般要知道狗的速度和狗所行的时间。
根据题意可知,狗的速度是每分钟行500米,关键是要求出狗所行的时间,根据题意可知:狗与主人是同时行走的,狗不断来回所行的时间就是王欣和陆亮同时出发到两人相遇的时间,即2000÷(110+90)=10分钟。
所以狗共行了500×10=5000米。
练习二1,甲乙两队学生从相隔18千米的两地同时出发相向而行。
一个同学骑自行车以每小时15千米的速度在两队之间不停地往返联络。
甲队每小时行5千米,乙队每小时行4千米。

行程问题(一)【教学目标】1、掌握行程问题的应用题的结构,掌握简单实际问题中的数量关系。
2、会解答已知两地的距离和两物体的运行速度,求相遇或追及时间的实际问题。
3、掌握解行程问题的一般方法和特有方法。
重点:掌握相遇及追及问题的数量关系。
难点:用方程解决相遇问题中求相遇时间的问题。
【知识回顾】路程、时间、速度是行程问题的三个基本量,它们之间的关系如下:路程=时间×速度,时间=路程÷速度,速度=路程÷时间。
【知识要点】1、本讲重点讲相遇问题及追及问题。
两个物体从两地出发,相向而行,经过一段时间,必然在途中相遇,这类题型我们把它称为相遇问题,相遇问题是研究速度、时间和路程三量之间关系的问题。
2、相遇、追及问题和一般行程问题区别:不是一个物体的运动,而是两个物体的相向或运动,所以,它研究的速度包含两个物体的速度,也就是速度和或速度差。
基本公式:路程=速度×时间基本类型:相遇问题:速度和×相遇时间=相遇路程;追及问题:速度差×追及时间=路程差;流水问题:关键是抓住水速对追及和相遇的时间不产生影响;顺水速度=船速+水速逆水速度=船速-水速静水速度=(顺水速度+逆水速度)÷2水速=(顺水速度-逆水速度)÷2(也就是顺水速度、逆水速度、船速、水速4个量中只要有2个就可求另外2个)其他问题:利用相应知识解决,比如和差分倍和盈亏;复杂的行程:1、多次相遇问题;2、环形行程问题;3、运用比例、方程等解复杂的题;【典型例题】例1、甲乙两辆汽车同时从A 、B 两城出发,相向而行,在离A 城75千米处相遇,两车各自到达对方城市后,都立即以原速沿原路返回,又在离A 城33千米处相遇。
AB 两城间的距离是多少千米?思路导航:甲乙第一次相遇,共行1个全程,其中甲行了75千米,甲乙第二次相遇,共行3个全程,其中甲行了2个全程减去33千米。
甲乙共行3个全程,所用时间是共行1个全程的3倍。

行程问题(1)行程应用题是专门讲物体运动的速度、时间、路程三者关系的应用题。
行程问题按所行方向的不同可分为三种:(1)相遇问题;(2)相离问题;(3)追及问题。
行程问题的主要数量关系是:距离=速度×时间。
它大致分为以下三种情况:(1)相向而行:相遇距离=相遇时间×速度和(2)相背而行:相背距离=速度和×时间。
(3)同向而行:速度慢的在前,快的在后。
追及时间=追及距离×速度差 解决行程问题的主要方法:行程图;将复杂行程问题分解成我们熟悉的类型。
一、过中点相遇例1 甲乙二人同时从两地骑自行车相向而行,甲每小时行15千米,乙每小时行11千米,两人在距中点4千米处相遇,求两地的距离。
练习:(1)甲乙两车分别从A 、B 两地同时出发相向而行,相遇点距中点320米,已知甲的速度是乙的速度的65,甲每分钟行800米。
求AB 的距离。
(2)快车和慢车同时从甲、乙两地相向开出,乙车每小时行40千米,经过3小时,快车已驶过中点25千米,这时快车与慢车还相距7千米。
慢车每小时行多少千米?二、追及问题例2 甲乙两人同时从东村到西村,甲每分钟行120米,乙每分钟行100米,结果甲比乙早五分钟到达西村。
东村到西村的路程是多少米?练习:(1)甲乙两人上午甲乙两人上午8时同时从东村去西村,甲每小时比乙快6千米,中午12时甲到西村后立即返回东村,在距西村15千米处和乙相遇。
求东西两村相距多少千米?(2)汽车从甲地开往乙地,每小时行32千米。
4小时后,剩下的路比全程的一半少8千米,如果改用每小时56千米的速度行驶,再行几小时到达乙地?例3一辆汽车从甲地开往乙地,要行360千米。
开始按计划以每小时45千米的速度行驶,途中因汽车故障修车2小时。
因为要按时到达乙地,修好车后必须每小时多行30千米。
汽车是在离甲地多远处修车的?练习:(1)小王家离工厂3千米,他每天骑车以每分钟200米的速度上班,正好准时到工厂。

第10讲行程问题(一)[教学内容]春季六年级精英版,第10讲“行程问题(一)”。
[教学目标]知识与技能利用行程问题中的路程、速度、时间的关系,并结合分数、比、比例等的知识解行程类应用题,感知数学在实际生活中的用途。
数学思考理解数学的数形结合的思想,发展学生的抽象概括能力。
问题解决获得分析较复杂的行程问题和解决这类问题的一些基本方法,体验解决行程问题方法的多样性,发展创新意识。
情感与态度在学习过程中,体验获得成功的乐趣,锻炼克服困难的意志,建立自信心;在合作与交流中学会肯定自己和倾听他人的意见。
[教学重点和难点]教学重点:结合分数、比、比例等知识解决行程问题。
教学难点:寻找解决较复杂的行程问题的方法。
[教学准备]动画多媒体语言课件第一课时教学过程:第二课时教学过程:本讲内容参考答案:自主探究例1:2420米例2:1.75小时例3: 39千米/时例4: 126分例5: 315千米例6: 150千米大胆闯关1、675米2、308千米3、10分钟4、7时40分5、11秒本讲内容的补充习题及答案:1、邮递员去送信,已知回来时沿原路返回,但速度提高了25%。
并且来、回的时间差是小时。
求往返一次用多少小时?路程速度时间去 1 1 5回 1 125% 4÷(5-4)×(5+4)=小时2、甲、乙两人分别从A、B两地同时出发,相向而行。
出发时他们的速度比是3:2,他们第一次相遇后,甲的速度提高了20%,乙的速度提高了30%。
这样,当甲到达B地时,乙离A地还有280km。
那么A、B两地的路程是多少千米?3×(1+20%)=3.62×(1+30%)=2.6280÷(-÷3.6×2.6)=900千米3、甲、乙两辆汽车同时从A去B,出发后,甲、乙两车的速度的比是5:4。
当甲车行至中点时,乙离中点还差60千米。
当乙车到达中点后,速度提高50%。
当甲到达B地时,乙离B地还有多少千米?÷5×4=—=60÷=600千米-÷4×5=4×(1+50%)=6÷5×6=600×(-)=30千米4、甲、乙两车同时从A、B两地相向而行,两车第一次在距A地32千米处相遇,相遇后两车继续行驶各自到达B、A两地后,立即沿原路返回,第二次在距A地64千米处相遇。

小升初——行程问题行程问题(一)行程问题是小学、初中的重难点,行程问题关系复杂,而多数小学生的分析能力还未能达到理想的水平。
体会相遇、追及问题的特点,并灵活运用列方程、比例等方法解行程问题,训练假设法、守恒等数学思维。
行程问题的三个基本量是距离、速度和时间。
其互逆关系可用乘、除法计算,方法简单,但应注意行驶方向的变化,按所行方向的不同可分为三种:(1)相遇问题;(2)相离问题;(3)追及问题。
行程问题的主要数量关系是:距离=速度×时间。
它大致分为以下三种情况:(1)相向而行:相遇时间=距离÷速度和(2)相背而行:相背距离=速度和×时间。
(3)同向而行:速度慢的在前,快的在后。
追及时间=追及距离÷速度差在环形跑道上,速度快的在前,慢的在后。
追及距离=速度差×时间。
解决行程问题时,要注意充分利用图示把题中的情节形象地表示出来,有助于分析数量关系,有助于迅速地找到解题思路。
1.一辆客车和一辆货车同时分别从A、B两城相对开出,客车每小时行9 5千米,货车每小时行8 5千米,相遇时客车比货车多行了3 0千米,求A、B两城相距多少千米?2.甲、乙二人在同一条公路上,他们相距100米,二人同时出发,朝各自的方向前进,甲的速度为每分钟100米,乙的速度为每分钟80米,问:经过多长时间两人相距200米?3.ABCD是一个边长为6米的正方形模拟跑道,甲玩具车从A出发顺时针行进,速度是每秒5厘米,乙玩具车从CD的中点出发逆时针行进,结果两车第二次相遇恰好是在B点,求乙车每秒走多少厘米?4.小明去学校,去时速度为15千米/小时,返回时速度为10千米/小时,那么平均速度为多少?5.已知甲车速度为每小时90千米,乙车速度为每小时60千米,甲乙两车分别从A,B两地同时出发相向而行,在途经C地时乙车比甲车早到10分钟;第二天甲乙分别从B,A两地出发同时返回原来出发地,在途经C地时甲车比乙车早到1个半小时,那么AB距离时多少?6.甲、乙、丙三人步行的速度分别是:每分钟甲走90米,乙走75米,丙走60米。

第十讲 行程(一)在历年“小升初”与各类小学竞赛试卷中,我们不难发现,“行程问题” 的试题占应用题的比值是相当大的,所以,学好行程问题不但对应对小升初考试和各类数学竞赛有着举足重轻的关键性作用而且也为我们初中的学习打下好的基础。
本讲着重介绍行程问题中的两人及多人的相遇和追及问题。
(1) 相遇问题涉及到:速度和=甲速+乙速、相遇时间和路程和三个量,三者之间的关系为:路程和=速度和×相遇时间。
(2) 追问题涉及到:速度差=甲速-乙速(甲速>乙速)、追及时间和路程差三个量,三者之间的关系为:路程差=速度差×追及时间。
显然,知道其中的两个量,就可以求出第三个量,这是我们在小学课堂中经常解决的问题。
所以大家在做题时一定要仔细分析题中都给了那个量,让我们求什么?,例如:让我们求相遇时间,那我们的做题目的就出来了,找所求相遇时间对应的路程和及速度和。
其实行程问题并没有有同学们想象的那么复杂,只要大家善于总结,其实行程问题是一类很好玩的问题。
希望大家在做题时好好体会做题心得,这对大家分析题会有很好的帮助。
分析:这个地点能找到,假设和尚在打完水上山时候,正好有另外一个和尚(可称之为影子和尚)仿照他下山的速度和速度变化从山顶下山,那么这个和尚与“影子和尚”相遇的地点便是符合条件的地点。
I 、两个人的相遇和追及【例1】 (★★★)甲车每小时行40千米,乙车每小时行60千米。
两车分别从A ,B 两地同时出发,相向而行,相遇后3时,甲车到达B 地。
求A ,B 两地的距离。
分析:相遇后甲行驶了120340=⨯千米,即相遇前乙行驶了120千米,说明甲乙二人的相遇时间是260120=÷小时,则两地相距2002)6040(=⨯+千米。
专题精讲 知识说明想挑战吗?从前有座山,山上有座庙,庙里有个和尚,和尚每天下山打水,打了水再挑上山,为了保证效率,他在下山前点一根香,挑水上山前再点一根同样的香,和尚每次都能保证在第一根香烧完之前下到山脚,但他不能保证在第二根香烧完之前回到山顶。
做行程问题时要做到以下※三点☆⏹行程问题:⏹1、画图理解⏹2、分辨如何计算⏹★3、细心认真计算专题简析:在行程问题中,与环行有关的行程问题的解决方法与一般的行程问题的方法类似,但有两点值得注意:一是两人同地背向运动,从第一次相遇到下次相遇共行一个全程;二是同地、同向运动时,甲追上乙时,甲比乙多行了一个全程。
基本数量关系:速度×时间=路程路程÷速度=时间路程÷时间=速度知道三者中的任意两个,就可以求出第三个。
早晨,小明和小芳同时从家里出发走向学校(如图),经过4分两人在校门口相遇。
他们两家相距多少米?我每分钟走70米我每分钟走60米70米70米70米70米60米60米60米60米?米我画图整理小明家小芳家第一讲行程问题(相遇)1.什么是相遇?两个人相向而行+70米70米70米70米60米60米60米60米小明家小芳家小明从家到学校小芳从家到学校每分走70米走了4分每分走60米走了4分根据整理的结果,想一想可以先算什么??米70×4+60×4=420速度1×时间1+速度2×时间2=总路程路程1 + 路程2 = 总路程(70+60)×4=420(速度1+速度2)×相遇时间=总路程(速度和)×相遇时间=总路程第一讲行程问题(相遇)1.什么是相遇?两个人路程=速度×时间相向而行+共行路程=速度和×相遇时间2.相遇问题基本公式共行路程÷相遇时间=速度和共行路程÷速度和=相遇时间出发点?米小芳小明55米55米55米60米60米60米中午放学了,小明和小芳同时从学校出发。
小明向东走去新华书店,每分走60米;小芳向西走去文具店,每分走55米。
经过3分,两人相距多少米?解:(60+55) ×3=345(米)答:两人相距345米。
小试牛刀——目的:熟记公式1、小兔住在东村,小虎住在西村,某日,二人同时从家出发,打算到对方家抄作业,2小时后在途中相遇,小兔的速度是1千米每小时,小虎的速度是4千米每小时,问:东、西两村相距多少千米?速度和×相遇时间=共行路程共行路程÷相遇时间=速度和共行路程÷速度和=相遇时间小试牛刀——目的:熟记公式2、小明和小牛两家相距20千米,某日,二人同时从家出发,打算到对方家抄作业,2小时后在途中相遇,小明的速度是4千米每小时,问:小牛的速度是多少?速度和×相遇时间=共行路程共行路程÷相遇时间=速度和共行路程÷速度和=相遇时间•1、甲乙两地之间的距离是420千米。
《佳一数学思维训练教程》教案第二课时本讲教材及练习册答案:教材:探究类型1:100÷(1.5+1)=40秒 2×40=80(米) 探究类型2:640÷(100+60)=4(分)100×4=400(米)60×4=240(米)400-240=160(米)探究类型3:250-100=150(米)18×100=1800(米)1800÷150=12(分钟)探究类型4:180÷60=3(分)(90×3+180)÷2=225(米)探究类型5:75×3-55=170(千米)大胆闯关:1.(100+80)×5÷(100-80)=45(分钟)(45+5)×100=5000(米)2. 2400×3÷(70+50)=60(分)3. 相遇时间:108×2÷(54-48)=36(分钟)两地距离:(54+48)×36÷3=1224(千米)练习册:1. 两车路程差:32×2=64(千米)相遇时间:64÷(56-48)=8(时)两地距离:8×(56+48)=832(千米)2. 两车相遇时间:480÷(35+45)=6(时)燕子飞行路程:6×50=300(千米)3. 相反方向两人第一次相遇需要时间:3000÷(160+240)=7.5(分)同向出发乙追上甲所用时间:3000÷(240-160)=37.5(分钟)4. 小明准时到校所需时间:3÷15=0.2(时)逆风开始1千米所用时间:1÷10=0.1(时)所剩时间:0.2-0.1=0.1(时)剩下2千米的速度:2÷0.1=20(千米/时)5. 第一次相遇两人合走一个全程各需40分钟,第二次相遇两人合走3个全程各需40×3=120(分)B的速度:(6000+2000)÷(40×3)=66.7(米/分钟)A的速度:(6000+4000)÷(40×3)=83.3(米/分钟)。
行程问题(一)导读这一讲我们来研究行程问题中的另一种典型的应用题——同向追及问题。
同向追及问题的特点是:两个物体同时沿同一方向运动,慢者在前面,快者在后面。
他们之间的距离不断缩短,直到快者追上慢者。
它有三个基本的数量:追及时间、速度差以及路程差。
其基本的数量关系式是:追及时间=路程差(即相隔路程)/速度差(快行速度-慢行速度)速度差=路程差/追及时间路程差=速度差*追及时间我们来具体看几个例子。
例题1小强和小英从相距80米的两地同时同向行走,小英在前面每分钟走50米,小强在后面每分钟走70米。
两分钟后小强和小英还相隔多少米?解法一:以小强出发的地点为起点,那么2分钟后,小英与起点相隔的距离就是80米加上她两分钟行走的路程:80+50*2=180(米0,同理可以求出2分钟后,小强与起点相隔的路程,这样再来求他们相隔的距离就不难了。
解法二:这一题还可以这样来分析:小强每分钟比小英多走70-50=20(米),即每分钟他们的距离可以缩短20米,两分钟他们的距离就可以缩短20*2+40(米),那么他们还相距80-40+40(米)解:解法一:(80+50*2)-70*2=40(米)解法二:80-(70-50)*2=40(米)答:两分钟后小强和小英还相隔40米。
即时练习1甲、乙两艘轮船从相距60千米的码头同时出发相向而行,甲轮船每小时行驶25千米,乙轮船在后每小时行38千米,几小时后两轮船还相距21千米?例题2小强和小英从相距80米的两地同时同向而行,小英在前面每分钟走50米,小强在后面每分钟走70米,几分钟后小强可以追上小英?思路启迪小强比小英每分钟多行的路程是70-50=20(米),通过例1的分析,可知,他们每分钟的距离可缩短20米,要求几分钟后小强追上小英,也就是求80米里面有多少个20米,这就是第一个数量关系式的道理。
解:80/(70-50)=4(分钟)答:4分钟后小强追上小英。
即时练习2娟子和小平从相距140米的两地同时同向而行,小平在前每分钟走45米,娟子在后每分钟走65米,即分钟后娟子可以追上小平?例题3一辆汽车从甲地出发,速度是每小时50千米,在汽车开出1小时后,一辆摩托车以每小时75千米的速度从同一地点出发沿同一行驶路线去追这辆汽车,几小时可以追上?追上时距出发地的距离是多少?思路启迪当摩托车出发时,汽车已经开出了1小时,距离摩托车50*1=50(千米)而摩托车1小时可以追上汽车75-50=25(千米),用相距的路程除以每小时的路程就可算出几小时可以追上。
初中数学二元一次方程组的应用题型分类汇编——行程问题1(附答案)1.小颖家离学校1200米,其中有一段为上坡路,另一段为下坡路,她去学校共用了16分钟,假设小颖上坡路的平均速度是3千米/小时,下坡路的平均速度是5千米/小时,若设小颖上坡用了min x ,下坡用了min y ,根据题意可列方程组( )A .35120016x y x y +=⎧⎨+=⎩B .35 1.2606016x y x y ⎧+=⎪⎨⎪+=⎩ C .35 1.216x y x y +=⎧⎨+=⎩D .351200606016x y x y ⎧+=⎪⎨⎪+=⎩ 2.小颖家离学校1200米,其中有一段为上坡路,另一段为下坡路.她去学校共用了16分钟.假设小颖上坡路的平均速度是3千米/时,下坡路的平均速度是5千米/时.若设小颖上坡用了x 分钟,下坡用了y 分钟,根据题意可列方程组为( )A .3x 5y 1200x y 16+=⎧+=⎨⎩B .35x y 1.26060x y 16⎧+=⎪⎨⎪+=⎩C .3x 5y 1.2x y 16+=⎧+=⎨⎩D .35x y 12006060x y 16⎧+=⎪⎨⎪+=⎩ 3.甲、乙两人练习跑步.如果乙先跑10米,则甲跑5秒就可追上乙;如果乙先跑2秒,则甲跑4秒就可追上乙.若设甲的速度为x 米/秒,乙的速度为y 米/秒,则下列方程组中正确的是( )A .5510,442x y x y y =+⎧⎨=+⎩B .5510,424x y x x y -=⎧⎨-=⎩C .5105,442x y x y +=⎧⎨-=⎩D .5510,424x y x y -=⎧⎨-=⎩4.小刚去距县城28千米的旅游点游玩,先乘车,后步行.全程共用了1小时,已知汽车速度为每小时36千米,步行的速度每小时4千米,则小刚乘车路程和步行路程分别是( )A .26千米,2千米B .27千米,1千米C .25千米,3千米D .24千米,4千米5.一辆汽车在公路上行驶,看到里程表上是一个两位数,1小时后其里程表还是一个两位数,且刚好它的十位数字与个位数字与第一次看到的两位数的十位数字与个位数字颠倒了位置,又过了1小时后看到里程表是一个三位数,它是第一次看到的两位数中间加一个0,则汽车的速度是( )千米/小时.A .35B .40C .45D .506.甲乙两人在一环形跑道上同时从A 点匀速跑步,已知甲的速度比乙的速度快,若两人同向出发,则两人在6分钟时第1次相遇;若两人背向出发,两人在3分钟时第1次相遇,则甲的速度是乙的速度的( )倍. A .2B .3C .4D .57.李明同学早上骑自行车上学,中途因道路施工需步行一段路,到学校共用时15分钟.他骑自行车的速度是250米/分钟,步行的速度是80米/分钟.他家离学校的距离是2900米.若他骑车和步行的时间分别为x 分钟和y 分钟,则列出的方程组是( )A .1{4250802900x y x y +=+= B .15{802502900x y x y +=+= C .15{250802900x y x y +=+=D .1{4802502900x y x y +=+= 8.甲、乙两人练习跑步,如果甲让乙先跑10米,那么甲跑5秒就能追上乙;如果甲让乙先跑2秒,那么甲跑4秒就能追上乙.若甲、乙每秒分别跑x y 、米,则列出方程组应是( )A .5105442x y x y +=⎧⎨-=⎩B .5510424x y x y =+⎧⎨-=⎩C .()551042x y x y y -=⎧⎨-=⎩D .()()51042x y x y ⎧-=⎪⎨-=⎪⎩9.甲.乙二人从同一地点出发,同向而行,甲骑车乙步行,若乙先行12千米,那么甲1小时追上乙;如果乙先走1小时,甲只用12小时追上乙,则乙的速度是( ) A .6千米/时B .12千米/时C .18千米/时D .36千米/时10.一艘船从甲码头到乙码头顺流行驶,用了2小时,从乙码头返回到甲码头逆流行驶,用了2.5小时.已知水流的速度是3千米/时,船在静水中的速度为千米/时,则可列方程为( ) A .B .C .D .11.一艘轮船顺流从重庆到上海需5天,而逆流从上海到重庆要7天,那么有一木排从重庆顺流漂到上海要________天.12.A 、B 、C 三地在同一直线上,甲、乙两车分别从A ,B 两地相向匀速行驶,甲车先出发2小时,甲车到达B地后立即调头,并将速度提高10%后与乙车同向行驶,乙车到达A地后,继续保持原速向远离B的方向行驶,经过一段时间后两车同时到达C地,设两车之间的距离为y(千米),甲行驶的时间x(小时).y与x的关系如图所示,则B、C两地相距_____千米.13.A、B两地相距20千米,甲乙两人分别从A、B两地相向而行,2小时后在途中相遇,然后甲立即返回A地,乙继续向A地走,当甲回到A地时,乙距离A地还有2千米,则甲的速度为____千米/时,乙的速度为_____千米/时.14.A、B两地相距80千米,一艘船从A地出发顺水航行4小时到达B地,而它从B 地出发逆水航行5小时才能到达A地.已知船顺水航行、逆水航行的速度分别为船在静水中的速度与水流速度的和与差,则船在静水中的速度是________,水流速度是________.15.某体育场的环行跑道长400米,甲、乙同时从同一起点分别以一定的速度练习长跑和骑自行车.如果反向而行,那么他们每隔30秒相遇一次.如果同向而行,那么每隔80秒乙就追上甲一次.甲、乙的速度分别是多少?设甲的速度是x米/秒,乙的速度是y米/秒.则列出的方程组是_____.16.在一条笔直的公路上有A、B两地,甲、乙两车均从A地匀速驶向B地,甲车比乙车早出发2小时,出发后,甲车出现了故障停下来维修,半小时后继续以原速向B地行驶.当乙车到达B地后立刻提速50%返回,在返回途中第二次与甲车相遇.下图表示甲乙两车之间的距离y(千米)与甲车行驶的时间x(小时)之间的函数关系.则当乙车第二次与甲车相遇时,甲车距离B地_____千米.17.已知A、B两地之间的距离为20千米,甲步行,乙骑车,两人沿着相同路线,由A地到B地匀速前行,甲、乙行进的路程s与x(小时)的函数图象如图所示.(1)乙比甲晚出发___小时;(2)在整个运动过程中,甲、乙两人之间的距离随x的增大而增大时,x的取值范围是___.18.小蒲家与学校之间是一条笔直的公路,小蒲从家步行前往学校的途中发现忘带作业本,便向路人借了手机打给妈妈,妈妈接到电话后,带上作业本马上赶往学校,同时小蒲沿原路返回,两人相遇后,小蒲立即赶往学校,妈妈沿原路返回家,小蒲到达学校刚好比妈妈到家晩了2分钟.若小蒲步行的速度始终不变,打电话和交接作业本的时间忽略不计,小蒲和妈妈之间的距离y米与小蒲打完电话后步行的时间x分钟之间的函数关系如图所示;则相遇后妈妈返回家的速度是每分钟_____米.19.一辆汽车要在规定的时间内从甲地赶往乙地,如果每小时行驶45千米,就要迟到0.5小时;如果每小时行驶50千米,就会早0.5小时.若设甲、乙两地间的距离为x千米,规定的时间为y小时,则可列方程组为________.20.已知铁路桥长500米,现有一列火车从桥上通过测得火车从开始上桥到完全离开桥共用30秒,而整列火车在桥上的时间为20秒,则火车的长度________.21.甲、乙两人同时绕400米的环形跑道行走,如果他们同时从同一起点背向而行,2.5分钟可以相遇;如果他们同时从同一点同向而行,12.5分钟甲能追上乙.求甲、乙每人每分钟各走多少米?22.一条船顺流航行,每小时行20千米;逆流航行,每小时行16千米.求船在静水中的速度与水流的速度.23.从甲地到乙地有一段下坡路与一段平路,如果保持下坡路每小时走5千米,平路每小时走4千米,上坡路每小时走3千米,那么从甲地到乙地需要36分钟,从乙地返回甲地需要48分钟.求甲地到乙地的全程是多少?24.某学校组织学生乘汽车去自然保护区野营,先以60km/h的速度走平路,后又以30km/h的速度爬坡,共用了6.5h;原路返回时,汽车以40km/h的速度下坡,又以50km/h 的速度走平路,共用了6 h.问平路和坡路各有多远?25.小华从家里到学校的路是一段平路和一段下坡路.假设他始终保持平路每分钟走60米,下坡路每分钟走80米,上坡路每分钟走40米,从家里到学校需10分钟,从学校到家里需15分钟.请问小华家离学校多远?26.小明从家里到学校先是走一段平路然后走一段下坡路,假设他始终保持平路每分钟走80m,下坡路每分钟走90m,上坡路每分钟走60m,则他从家里到学校需20min,从学校到家里需25min.问:从小明家到学校有多远?27.“滴滴出行”改变了传统打车方式,最大化节省了司机与乘客双方的资源与时间.该打车方式的总费用由里程费和耗时费组成,其中里程费按x元/公里计算,耗时费按y元/分钟计算.甲、乙两乘客用该打车方式出行,按上述计价规则,其打车总费用、行驶里程数与平均车速等信息如下表:平均速度(公里/时)里程数(公里)车费(元)甲乘客60812乙乘客501016(1)求x,y的值;(2)如果你采用“滴滴出行”的打车方式,保持平均车速45公里/时,行驶了9公里,那么你是否能够计算出打车的总费用?如果能,总费用为多少元?如果不能,请说明理由.28.小李骑电动自行车,预计用相同的时间往返于甲、乙两地,去时电动自行车的车速是18km/h,结果早到20min;返回时,以每小时15km的速度行进,结果晚到4min.求甲、乙两地间的距离和预计时间.29.“铁路建设助推经济发展”,近年来我国政府十分重视铁路建设.渝利铁路通车后,从重庆到上海比原铁路全程缩短了320千米,列车设计运行时速比原铁路设计运行时速提高了120千米/小时,全程设计运行时间只需8小时,比原铁路设计运行时间少用16小时.(1)渝利铁路通车后,重庆到上海的列车设计运行里程是多少千米?(2)专家建议:从安全的角度考虑,实际运行时速要比设计时速减少m%,以便于有充分时间应对突发事件,这样,从重庆到上海的实际运行时间将增加110m 小时,求m 的值.30.从A 地到B 地全程290千米,前一路段为国道,其余路段为高速公路.已知汽车在国道上行驶的速度为60/km h ,在高速公路上行驶的速度为100/km h ,一辆客车从A 地开往B 地一共行驶了3.5h .求A 、B 两地间国道和高速公路各多少千米.(列方程组,解应用题)参考答案1.B 【解析】 【分析】根据路程=时间乘以速度得到方程35 1.26060x y +=,再根据总时间是16分钟即可列出方程组. 【详解】∵她去学校共用了16分钟, ∴x+y=16,∵小颖家离学校1200米, ∴351.26060x y +=, ∴35 1.2606016x y x y ⎧+=⎪⎨⎪+=⎩, 故选:B. 【点睛】此题考查二元一次方程组的实际应用,正确理解题意列出方程组,注意时间单位,这是解题中容易出现错误的地方. 2.B 【解析】 【分析】两个等量关系为:上坡用的时间+下坡用的时间=16;上坡用的时间×上坡的速度+下坡用的时间×下坡速度=1200,把相关数值代入即可求解. 【详解】小颖上坡用了x 分钟,下坡用了y 分钟,根据题意得35x y 1.26060x y 16⎧+=⎪⎨⎪+=⎩, 故选B . 【点睛】本题考查了二元一次方程组的应用,弄清题意,找准合适的等量关系列出方程组是解题的关键. 3.A 【解析】 【分析】根据甲跑的路程等于相同时间乙跑的路程加上乙先跑的路程即可解答. 【详解】设甲的速度为x 米/秒,乙的速度为y 米/秒,根据题意得:5510442x y x y y =+⎧⎨=+⎩故选:A 【点睛】此题主要考查了由实际问题抽象出二元一次方程组,此题是追及问题,注意:无论是哪一个等量关系中,总是甲跑的路程=乙跑的路程. 4.B 【解析】 【详解】试题分析:利用方程的思想进行求解,设乘车的路程为x 千米,则步行的路程为(28-x)千米,根据时间=路程÷时间求出乘车的时间和步行的时间,根据两个时间之和为1小时列出方程进行求解.设乘车的路程为x 千米,则步行的路程为(28-x)千米,281364x y x y +=⎧⎪⎨+=⎪⎩ 解得:x=27,y=1 故选:B 5.C 【解析】 【分析】设第一次他看到的两位数的个位数为x ,十位数为y ,汽车行驶速度为v ,第一次看到的两位数为10y+x ,行驶一小时后看到的两位数为10x+y ,第三次看到的三位数为100y+x ,由汽车均速行驶可得三段时间的路程相等,即可列出两个方程求解即可.由速度=总里程时间,求得答案. 【详解】设第一次他看到的两位数的个位数为x ,十位数为y ,汽车行驶速度为v ,根据题意得:()()10101100101x y y x v y x x y v ⎧+-+=⨯⎪⎨+-+=⨯⎪⎩, 解得:6x y =, ∵xy 为1-9内的自然数, ∴61x y =⎧⎨=⎩;即两位数为16.即:第一次看到的两位数是16. 第二次看到的两位数是61. 第三次看到的两位数是106. 则汽车的速度是:10616452-=(千米/小时). 故选:C. 【点睛】本题考查了二元一次方程组的应用,解题关键是弄清题意,合适的等量关系,列出方程组.本题涉及一个常识问题:两位数=10×十位数字+个位数字,并且在求两位数或三位数时,一般是不能直接设这个两位数或三位数的,而是设它各个数位上的数字为未知数. 6.B 【解析】 【分析】设乙的速度为x 米/分钟,甲的速度为y 米/分钟,根据同向出发相遇和背向出发相遇列出方程组求解即可. 【详解】设乙的速度为x 米/分钟,甲的速度为y 米/分钟,根据题意得:1613y x y x⎧=⎪-⎪⎨⎪=⎪+⎩ 解方程得:3yx=,即甲的速度是乙的速度的3倍. 故选:B 【点睛】本题考查了列二元一次方程组解环形问题的运用,二元一次方程组的解法的运用,解答时运用环形问题的数量关系建立方程是关键. 7.C 【解析】 【分析】根据关键语句“到学校共用时15分钟”可得方程:x+y=15,根据“骑自行车的平均速度是250米/分钟,步行的平均速度是80米/分钟.他家离学校的距离是2900米”可得方程:250x+80y=2900,两个方程组合可得方程组. 【详解】设骑车和步行的时间分别为x 分钟,y 分钟,由题意得:15{250802900x y x y +=+=, 故选C. 【点睛】本题考查了二元一次方程组的应用,根据题意找到等量关系式是解题的关键. 8.C 【解析】 【分析】等量关系:(1)乙先跑10米,甲跑5秒就追上乙;(2)如果让乙先跑2秒,那么甲跑4秒就追上乙,可以列出方程组. 【详解】设甲、乙每秒分别跑x 米,y 米,由题意知:()551042x y x y y -=⎧⎨-=⎩. 故选:C. 【点睛】此题考查由实际问题抽象出二元一次方程组,解题关键在于理解题意列出方程., 9.A 【解析】 【分析】这里给了两个信息,我们可以设两个未知数,列两个等式,给出二元一次方程组,只需求解二元一次方程组即可. 【详解】解:设甲的速度为每小时x 千米,乙的速度为每小时y 千米121122x y x y y -=⎧⎪⎨-=⎪⎩ ,解得186x y =⎧⎨=⎩, 故选A 【点睛】本题考查了二元一次方程组的应用,学会利用题目给的信息列等量关系式是关键. 10.B 【解析】 【分析】顺水行船的路程=逆水行船的路程,再根据流水行船问题的公式求出顺水路程以及逆水路程,即可得到答案. 【详解】∵顺水路程=顺水速度×顺水时间=2(x+3) 逆水路程=逆水速度×逆水时间=2.5(x-3) 又顺水路程=逆水路程∴2.5(x-3)=2(x+3),因此答案选择B. 【点睛】本题主要考查的是一元一次方程的应用,需要熟悉流水行船问题的公式.11.35 【解析】 【分析】设重庆到上海的路程为单位“1”,根据1V V V 5=+=顺流船水以及1=7V V V =-逆流船水 ,即可求出水流的速度,从而求出木排从重庆顺流漂到上海的天数. 【详解】解:设船的速度为V 船,顺流的速度为V 顺流,逆流速度为V 逆流,水流速度为V 水,则1=51=7V V V V V V ⎧=+⎪⎪⎨⎪=-⎪⎩顺流船水逆流船水①②, 由①-②得:1122=5735V -=水 ∴1=35V 水, ∴有一木排从重庆顺流漂到上海要35天 故答案为:35 【点睛】本题考查了方程组的实际应用,当一些必须的量没有时,应设为未知数,在计算过程中消除即可. 12.1320. 【解析】 【分析】根据题意和函数图象中的数据,可以求得甲乙两车的速度,再根据“路程=速度×时间”,即可解答本题. 【详解】解:设甲车的速度为a 千米/小时,乙车的速度为b 千米/小时,(62)()560(62)(96)a b b a -⨯+=⎧⎨-=-⎩,解得8060a b =⎧⎨=⎩,∴A 、B 两地的距离为:80×9=720千米, 设乙车从B 地到C 地用的时间为x 小时, 60x =80(1+10%)(x+2﹣9), 解得,x =22,则B 、C 两地相距:60×22=1320(千米) 故答案为:1320. 【点睛】本题考查一次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答. 13.5.5 4.5 【解析】 【分析】设甲的速度为x km/h ,乙的速度为y km/h ,根据行程问题的数量关系建立方程解出方程即可. 【详解】解:设甲的速度为x km/h ,乙的速度为y km/h ,由题意得:2()20222x y x y +=⎧⎨-=⎩ ,解得: 5.54.5x y =⎧⎨=⎩ 故甲的速度为5.5千米/时,乙的速度为4.5千米/时. 【点睛】本题考查了列二元一次方程组解决实际问题的运用,二元一次方程组的解法的运用,相遇问题和追及问题的数量关系,解答时由行程问题的数量关系建立方程组是关键. 14.18千米/时 2千米/时 【解析】 【分析】设船在静水中的速度为x 千米/时,水流速度为y 千米/时,根据题意列出二元一次方程组即可求解. 【详解】设船在静水中的速度为x 千米/时,水流速度为y 千米/时. 根据题意,得4()805()80x y x y +=⎧⎨-=⎩,解得182x y =⎧⎨=⎩.即船在静水中的速度为18千米/时,水流速度为2千米/时.【点睛】此题主要考查二元一次方程组的应用,解题的关键根据题意找到等量关系列方程求解.15.30()400 80()400x yy x+=⎧⎨-=⎩【解析】【分析】此题中的等量关系有反向而行,则两人30秒共走400米;②同向而行,则80秒乙比甲多跑400米【详解】解:①根据反向而行,得方程为30(x+y)=400;②根据同向而行,得方程为80(y﹣x)=400.那么列方程组30()400 80()400x yy x+=⎧⎨-=⎩.【点睛】此题考查由实际问题抽象出二元一次方程组,解题关键在于列出方程组16.90【解析】【分析】设甲的速度a千米/时,乙的速度b千米/时,由图象可列方程组,求出甲,乙速度,即可求解.【详解】解:设甲的速度a千米/时,乙的速度b千米/时,由图象可知,甲,乙第一次相遇是甲出发3.5小时时,乙到达B地是甲出发6.5小时时,∴3 1.5 6120 4.5a ba b=⎧⎨+=⎩,解得:4080 ab=⎧⎨=⎩,∴甲的速度40千米/时,乙的速度80千米/时,∴A、B两地距离=80×4.5=360千米,∴从B地返回到相遇时间=12034080(150%)4=+⨯+小时,∴当乙车第二次与甲车相遇时,甲车距离B地=120﹣40×34=90千米,故答案为:90.【点睛】本题考查了一次函数的应用,以及二元一次方程组,理解图象,正确进行求解是本题的关键.17.1,0≤x≤1或43≤x≤2.【解析】【分析】(1)由图象直接可得答案;(2)根据图象求出甲乙的函数解析式,再求出方程组的解集即可解答【详解】(1)由函数图象可知,乙比甲晚出发1小时.故答案为1.(2)在整个运动过程中,甲、乙两人之间的距离随x的增大而增大时,有两种情况:一是甲出发,乙还未出发时:此时0≤x≤1;二是乙追上甲后,直至乙到达终点时:设甲的函数解析式为:y=kx,由图象可知,(4,20)在函数图象上,代入得:20=4k,∴k=5,∴甲的函数解析式为:y=5x①设乙的函数解析式为:y=k′x+b,将坐标(1,0),(2,20)代入得:202k bk b=+⎧⎨=+⎩,解得2020kb=⎧⎨=-⎩,∴乙的函数解析式为:y=20x﹣20 ②由①②得52020y xy x=⎧⎨=-⎩,∴43203xy⎧=⎪⎪⎨⎪=⎪⎩,故43≤x≤2符合题意.故答案为0≤x≤1或43≤x≤2.【点睛】此题考查函数的图象和二元一次方程组的解,解题关键在于看懂图中数据18.50.【解析】【分析】由图像得出相向而行和背向而行行走的路程和时间,然后列出方程组,即可求解.【详解】解:设相遇后妈妈返回家的速度是每分钟x米,小蒲的速度为每分钟y米,由题意得:16+10y=2000 16+18y=2960xx⎧⎨⎩解得:x=50 y=120⎧⎨⎩∴相遇后妈妈返回家的速度是每分钟50米.【点睛】本题考查了函数图象的识别,二元一次方程组的应用,列出方程组解题的关键.19.0.5450.550x yx y⎧+=⎪⎪⎨⎪-=⎪⎩【解析】【分析】设规定时间是y小时,甲、乙两地相距x千米,根据45×(规定时间+0.5)=两地距离;50×(规定时间-0.5)=两地距离,列出方程组即可.【详解】设甲、乙两地间的距离为x千米,规定的时间为y小时,由题意得0.5450.550x y x y ⎧+=⎪⎪⎨⎪-=⎪⎩. 故答案为:0.5450.550x y x y ⎧+=⎪⎪⎨⎪-=⎪⎩.【点睛】此题考查了二元一次方程组的运用,解答此题的关键是读懂题意,找出之间的等量关系,列出方程组. 20.100米. 【解析】 【分析】设火车长为x,火车速度为y ,根据题意得方程:500+x=30y 和500-x=20y ,根据等式性质求解. 【详解】解: 设火车长为x,火车速度为y根据题意得方程: 500+x=30y 和500-x=20y 解得 x=100,y=20所以火车的速度是20米/秒,火车的长度是100米. 故答案为:100米. 【点睛】考核知识点:列方程解应用题.理解题意列出方程,根据等式性质求解是关键. 21.甲每分钟走96米,乙每分钟走64米. 【解析】 【分析】设甲每分钟x 米,乙每分钟y 米 ,根据题目中相遇问题和追及问题的等量关系可得: ,解方程组即可. 【详解】设甲每分钟x 米,乙每分钟y 米 ,根据题意可得:2.540012.5400x y x y +=⎧⎨-=⎩()(), 解得:9664x y =⎧⎨=⎩.答:甲每分钟走96米,乙每分钟走64米. 【点睛】本题主要考查列二元一次方程组解决行程问题,解决本题的关键是要熟练掌握行程问题中追及和相遇问题的等量关系. 22.18/km h ,2/km h 【解析】 【分析】直接根据题意结合静水速度+水速度=顺水速度,静水速度-水速度=逆水速度,进而列出方程组,求出答案. 【详解】解:设船在静水中的速度为/xkm h ,水流的速度为/ykm h .根据题意可得:2016x y x y +=⎧⎨-=⎩, 解得:182x y =⎧⎨=⎩答:船在静水中的速度为18/km h ,水流的速度为2/km h . 【点睛】此题主要考查了二元一次方程组在路程问题中的应用,根据题意正确得出等量关系是解题关键.23.甲地到乙地的全程是2.7千米. 【解析】 【分析】设从甲地到乙地的下坡路为xkm ,平路为ykm ,根据保持下坡每小时走5km ,平路每小时走4km ,上坡每小时走3km ,然后根据从甲地到乙地用36分钟,从乙地返回甲地用48分钟列出方程组进行求解即可.设从甲地到乙地的下坡路为xkm ,平路为ykm ,由题意得:365460483460x y x y ⎧+=⎪⎪⎨⎪+=⎪⎩,解得: 1.51.2x y =⎧⎨=⎩,所以:x+y=2.7千米答:甲地到乙地的全程是2.7千米. 【点睛】本题考查了二元一次方程组的应用,根据实际问题中的条件列方程组时,要注意抓住题目中的一些关键性词语,找出等量关系,列出方程组. 24.平路有150 km ,坡路有120 km . 【解析】 【分析】设平路有x km ,坡路有y km ,根据题意列出方程组求解即可. 【详解】解:设平路有x km ,坡路有y km ,根据题意,得x y+=6.56030{x y +=65040, 解得x=150{y=120. 答:平路有150 km ,坡路有120 km . 【点睛】本题考查了二元一次方程组的应用(行程问题).方程(组)的应用解题关键是找出等量关系,列出方程求解. 25.小华家离学校700米. 【解析】设出平路和坡路的路程,由题意从家里到学校需10分钟,从学校到家里需15分钟,列方程即可得出答案. 【详解】设平路有x 米,坡路有y 米,根据题意列方程得,106080{156040x y x y +=+=, 解这个方程组,得300{400x y ==,所以x +y =700.所以小华家离学校700米. 【点睛】本题考查二元一次方程的应用,此题主要利用时间、速度、路程三者之间的关系进行解答,注意来回坡路的变化是解题的关键. 26.1700m 【解析】 【分析】设出平路和坡路的路程,从家里到学校走平路和下坡路一共用10分钟,从学校到家里走上坡路和平路一共用15分钟,利用这两个关系式列出方程组解答即可. 【详解】解:设平路有x 米,坡路有y 米,根据题意列方程得,208090258060x y x y ⎧+=⎪⎪⎨⎪+=⎪⎩ 解得:800900x y =⎧⎨=⎩总路程:8009001700m += 答:小明家到学校有1700m .【点睛】此题考查二元一次方程组的应用,主要利用时间、速度、路程三者之间的关系解答,解答时注意来回坡路的变化,由此找出关系式,列方程组解决问题.27.(1)112xy=⎧⎪⎨=⎪⎩;(2)能,总费用是15元.【解析】【分析】(1)由表中数据可列出二元一次方程组,求解即可得到x,y的值;(2)设平均车速为a公里/时,行驶时间为b分钟,车费为w元,则w=a+12b,将a=45,b=945代入,即可得总费用.【详解】解:(1)由题意得886012601010601650x yx y⎧+⨯=⎪⎪⎨⎪+⨯=⎪⎩.解得112 xy=⎧⎪⎨=⎪⎩(2)能.设平均车速为a公里/时,行驶时间为b分钟,车费为w元,则w=a+12 b,将a=45,b=945代入,可得总费用w=91916015452⨯+⨯⨯=(元)答:总费用是15元.【点睛】本题考查二元一次方程组和一次函数的应用,灵活运用一次函数解决问题是解题的关键.28.36km,7 3 h【解析】【分析】设预计时间为t h,甲、乙两地间的距离为s km,根据时间=路程÷速度,即用去时的时间加上早到的20min (即13h )等于t ,返回的时间减去晚到的4min (115h )等于t ,即可列方程组解答.【详解】 解:设预计的时间为t h ,甲、乙两地间的距离为s km , 据题意得118311515s t s t ⎧+=⎪⎪⎨⎪-=⎪⎩,解得7336t s ⎧=⎪⎨⎪=⎩.答:甲、乙两地间的距离为36km ,预计时间为73h . 【点睛】本题考查二元一次方程组的实际应用,解答此题的关键是明白去时所用的时间加上早到的时间与返回时所用的时间减去迟到的时间相等;二是时间的单位换算.29.(1)1600;(2)20.【解析】【分析】(1)利用“从重庆到上海比原铁路全程缩短了320千米,列车设计运行时速比原铁路设计运行时速提高了l20千米/小时,全程设计运行时间只需8小时,比原铁路设计运行时间少用16小时”,分别得出等式组成方程组求出即可;(2)根据题意得出:1(80120)(1%)(8)160010m m +-+=进而求出即可. 【详解】 试题解析:(1)设原时速为xkm/h ,通车后里程为ykm ,则有:8(120){(816)320x y x y+=+=+, 解得:80{1600x y ==,答:渝利铁路通车后,重庆到上海的列车设计运行里程是1600千米;(2)由题意可得出:1(80120)(1%)(8)160010m m +-+=, 解得:120=m ,20m =(不合题意舍去),答:m 的值为20.考点:1.一元二次方程的应用;二元一次方程组的应用.30.A、B两地国道为90千米,高速公路为200千米.【解析】【分析】首先设A、B两地间国道和高速公路分别是x、y千米,根据题意可得等量关系:国道路程+高速路程=290,在国道上行驶的时间+在高速公路上行驶的时间=3.5,根据等量关系列出方程组,再解即可.【详解】解:设A、B两地国道为x千米,高速公路为y千米.则方程组为:2903.5 60100x yx y+=⎧⎪⎨+=⎪⎩,解得:90200 xy=⎧⎨=⎩,答:A、B两地间国道和高速公路分别是90、200千米.【点睛】此题考查了二元一次方程组的应用,关键是设出未知数,表示出每段行驶所花费的时间,得出方程组,难度一般.。
行程问题综合(1)基本模式(一)相遇问题和相离问题:(1)相遇问题:“两物体分别从两地出发,相向而行”,注意关键词“相向”,如果两物体同时出发,相遇时所用时间一定相同,注意对速度和的理解图示:关系式:相遇时间=总路程÷速度和总路程=速度和×相遇时间例1:甲、乙两车的速度比是3:4,两车同时从两地相向而行,在离中点6千米处相遇,求两地相距多少千米?巩固:1、甲乙两车同时从AB两地出发相向而行。
甲车每小时行45千米,两车相遇后乙车再行135千米到A地,甲车再行2小时到B地。
求乙车行全程共用了几小时?2、甲乙两队学生从相隔17km的两地出发,相向而行,一个同学骑自行车以每刻钟3.5km的速度在两队之间往返联络,如果甲队每小时走4.5km,乙队每小时走4km,问:两队相遇时骑自行车的同学一共行了多少千米?<4>某轮船公司较长时间以来,每天中午有一只轮船从哈佛开往纽约,并且在每天的同一时间也有一只轮船从纽约开往哈佛,轮船在途中所花的时间,来去是六昼夜,问今天中午从哈佛开出的轮船,在整个航运途中,将会遇到只同一公司的轮船从对面开来。
<5>甲乙分别从A、B两地同时出发,相向而行,甲在早上9点到达C地,而乙到达C地时已经是下午5点了,已知甲乙速度比为5:3,则甲乙相遇时间时是几点?(2)相离问题:“两物体(从同一地点)同时出发,相背而行”,注意对“速度和”的理解,注意时间的因素图示:A B关系式:相离距离=速度和×相背而行的时间例2:甲乙两人上午8时分别从AB两地同时相向出发,到10时两车相距112.5km两车继续行驶到下午1时,两车还是相距112.5千米,求AB两地之间的距离?基本模式(二)追及问题和领先问题(1)追及问题:“两物体同向而行,一快一慢,慢者先行,快者追之”图示:基本数量关系式:追及时间=需要追及的距离÷速度差;追及距离=速度差×追及时间速度差=追及距离÷所用时间,近而再根据其他已知条件求出各自速度,从而解决问题。
行程问题(一)相遇问题追及问题【基本公式】1、路程=速度×时间2、相遇问题:相遇路程=速度和×相遇时间3、追及问题:相差路程=速度差×追及时间行程问题(一)-----相遇问题【典型例题】1、老李和老刘同时从两地相对出发,老李步行每分钟走8米,老刘骑自行车的速度是老李步行的3倍,经过5分钟后两人相遇,问这两地相距多少米2、在一条笔直的公路上,王辉和李明骑车从相距900米的A、B两地同时出发,王辉每分钟行200米,李明每分钟行250米,经过多少时间两人相距2700米(分析各种情况)3、客货两车同时从甲、乙两地相对开出,客车每小时行44千米,货车每小时行52千米,两车相遇后继续以原速度前进,到达乙、甲两地后立即返回,第二次相遇时,货车比客车多行60千米。
问甲、乙两地相距多千米4、小冬从甲地向乙地走,小青同时从乙地向甲地走,当各自到达终点后,又迅速返回,各自速度不变,两人第一次相遇在距甲地40米处,第二次相遇在距乙地15米处,问甲、乙两地相距多少米5、甲村、乙村相距6千米,小张与小王分别从甲、乙两村出发,在两村之间往返行走(到达另一村后就马上返回)。
在出发后40分钟两人第一次相遇。
小王到达甲村后返回,在离甲村2千米的地方两人第二次相遇。
问小张和小王两人的速度各是多少6、小张与小王分别从甲、乙两村出发,在两村之间往返行走(到达另一村后就马上返回)。
他们离甲村千米处第一次相遇,在离乙村2千米处第二次相遇。
问他们两人第四次相遇的地点离乙村有多远(相遇指迎面相遇)7、甲、乙两辆汽车同时从东西两地相向开出,甲每小时行56千米,乙每小时行48千米,两车在离两地中点32千米处相遇。
问:东西两地间的距离是多少千米8、甲、乙两地相距15千米,小聪和小明分别从甲、乙两地同时相向而行,2小时后在离中点千米处相遇,求小聪和小明的速度。
9、甲、乙两人同时从相距50千米的两地同时出发相向而行,甲每小时行3千米,乙每小时行2千米,与甲同时同向而行的一条小狗,每小时行5千米,小狗在甲、乙之间不停往返,直到两人相遇为止。
十、行程问题在关于走路、行车等匀速运动中,已知距离、时间和速度三个数量中两个量的值,求第三个量的值,这类问题叫行程问题。
行程问题大致上说有以下情形,其解法要点是:(1)同时相向而行:相遇的时间=距离÷速度和;(2)同时同地背向而行:距离=速度和×时间;(3)同时同向而行,慢前快后:追及时间=距离÷速度差;(4)同时同地同向而行,慢后快前:距离=速度差×时间;注;这类问题的特点数量带有方向性,速度均匀无变化,而且行程问题是具有代表性的问题,它可以包括平均问题,和差问题,盈亏问题,鸡兔问题等各种问题,所以在解答复杂的行程问题时要掌握各种问题的特点。
1.甲乙两地相距98千米,某人2小时前以每小时8千米的速度自甲地去乙地,而乙地另一人以每小时12千米的速度向甲地行进,几小时后二人相距2千米?2.一飞机从甲地飞往乙地,计划每分钟飞行9千米,现将速度提到每分钟飞行12千米,结果比计划早到30分钟。
甲乙两地相距多少?3.某人骑摩托车从甲地到乙地,每小时行46千米,行了2.5小时恰好走了全程的一半,然后速度比原来增加4千米,还需几小时可到乙地?4.甲乙二人从相距60千米的两地同时出发相向而行,5小时相遇,若从同地同时同向而行,6小时甲在乙前12千米,求二人的速度。
5.甲乙两地相距180千米,客货二车同时从甲地开往乙地,货车速度每小时30千米,客车速度每小时20千米,货车到达乙地后停留0.5小时后返回甲地,从甲地出发后经几小时两车相遇?6.甲乙二人同时从两地骑车相向而行,甲时速20千米,乙时速18千米,二人相遇时距中点3千米。
求全程。
7.自行车时速15千米,汽车所用的时间是自行车的5倍,而所行使的路程是自行车的18倍,求汽车时速。
8.甲以一定的速度走完一段路需3小时,乙所走的路程是甲的5倍,而速度是甲的一半,求乙所用的时间。
9.一架飞机飞出时每小时950千米,飞回时每小时850千米,往返只需4小时,问最远飞出多远就应飞回?10.某人骑车从甲地到乙地去时每小时30千米,回时每小时75千米,回时比去时少用6小时。
第十讲行程问题(1)
【基础练习】
1、甲、乙两地相距720千米,一辆客车和一辆货车从甲、乙两地同时相向而行,客车的速度是70千米/小时,货车的速度是50千米/小时,问两车多长时间后相遇?
2、甲、乙两地相距720千米,一辆客车和一辆货车从甲、乙两地同时相向而行,客车的速度是65千米/小时,货车的速度是55千米/小时,问两车相遇是客车比货车多行多少千米?
3、甲、乙两人相距600米,甲的速度是60米/分钟,乙的速度是40米/分钟,两人同时同向而行,甲在乙的后面,经过多长时间,甲才可以追上乙?
4、A、B两地相距300千米,甲车从A到B需要5小时,乙车从B到A需要6小时,两车从A、B两地同时相向而行,多久可以相遇?
5、甲、乙两辆汽车同时从东西两地相向开出,甲每小时行56千米,乙每小时行48千米,两车在离两地中点32千米处相遇。
问:东西两地间的距离是多少千米?
【精讲精练】
1,货车距【例题1】客车从甲地,货车从乙地同时相对开出5小时后,客车距离乙地还有全程的
6
离甲地还有142千米。
已知客车每小时比货车多行12千米,求甲乙两地的距离多少千米?
1,小明【练习1】小军从A地,小明从B地同时相对行走8分钟后,小军距离B地还有全程的
10
距离A地还有15千米。
已知小军比小明每分钟少走5米,问A、B两地相距多少米?
【练习2】客车和货车同时从A、B两地相向而行,6小时后客车距离B地的路程是全程的12.5%,货车过终点54千米。
已知货车每小时比客车少行15千米,求A、B两地间的距离。
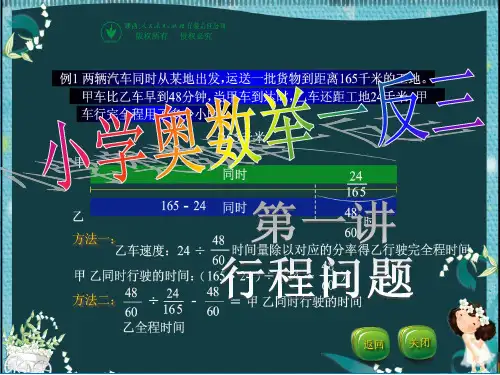
【例题2】两辆汽车同时从某地出发,运送一批货物到距离165千米的工地。
甲车比乙车早到48分钟,当甲车到达时,乙车距离工地还有24千米。
甲车完成全程用多少小时?
【练习1】甲、乙两地间的距离是420千米。
两辆汽车同时从甲地开往乙地,第一辆车每小时行42千米,第二辆汽车每小时行28千米。
第一辆车到达乙地后立即返回。
两辆汽车从出发到相遇共用多少小时?
【练习2】甲、乙两人进行60米赛跑,甲离终点还有10米时,甲领先乙10米。
如果两人按原速度冲向终点,那么当甲到达终点时,乙距离终点还有多少米?
【例题3】A、B两车同时从甲、乙两地相对开出,5小时后A车到达中点,B车距离终点还有60
2,求甲、乙两地相距多少千米?
千米。
已知B车的速度是A车的
3
【练习1】A、B两车同时从甲、乙两地相对开出,4小时候B车到达中点,A车距离中点还有50
4,求甲乙两地间的距离。
千米。
已知A车的速度是B车的
5
【练习2】小红以每分钟50米的速度从A地出发向B地行走40米后,小燕以每分钟60米的速度从B地出发向A地行走,两人恰好在A、B两地的中点相遇,求A、B两地的距离。
【例题4】A、B两地相距960米,甲、乙两人分别从A、B两地同时出发。
若相向而行,6分钟相遇,若同向而行,80分钟甲可以追上乙。
甲从A地到B地需要多少分钟?
【练习1】A、B两地相距1800米,甲、乙两人同时从AB两地出发,若相向而行,18分钟相遇,若同向而行90分钟,甲追上乙。
求甲从A地出发到B地需要多少分钟?
【练习2】甲、乙两人在400米长的环形跑道上散步,如果他们同时从同一地点出发,背向而行,4分钟相遇,如果同向而行,20分钟甲追上乙。
在跑道上走一圈,甲、乙各需多少分钟?
【例题5】甲、乙、丙三人,每分钟分别走68米、70.5米、72米。
现甲、乙从东镇去西镇,丙从西镇去东镇,三人同时出发,丙和乙相遇后,又过了2分钟与甲相遇,东、西两镇的距离是多少千米?
【练习1】有甲乙丙三人,甲每分钟走70米,乙每分钟走60米,丙每分钟走75米,甲乙从A地去B 地,丙从B地去A地,三人同时出发,丙遇到甲8分钟后遇到乙。
甲乙两地相距多少千米?
【练习2】甲、乙、丙三人过桥,甲乙从桥南往北走,丙从桥北往南走,甲每分钟走45米,乙每分钟走50米,丙每分钟走55米。
丙与乙相遇2分钟后又与甲相遇,求桥长多少?
【课后作业】
5,乙距离终点还有5 1、甲、乙两人骑自行车同时从AB两地相对而行,3小时后甲行了全程的
8
千米。
已知乙每小时比甲少行4千米,甲、乙两地相距多少千米?
2、甲、乙两车同时从A地开往B地,乙车6小时可以到达,甲车每小时比乙车慢8千米,因此比乙车迟到1小时,求甲、乙两地相距多少千米?
3、甲、乙两车同时从A、B两地相对开出,3小时后甲车距离终点还有40千米,乙车正好到达中
5。
问AB两地的距离是多少?
点,已知甲车的速度是乙车速度的
9
4、A、B两地相距240米,甲、乙两人同时从A、B两地出发,若相向而行,12分钟相遇,若同向而行,分钟后甲落后在乙后面272米。
求甲、乙两人的速度分别是多少?
5、甲、乙两人从东镇,丙从西镇同时相向而行,当丙遇到乙10分钟后,又遇到甲。
已知甲乙丙三人每分钟的速度分别是20米、25米、30米,东、西两镇相距多少米?。