电路原理总复习题1

《电路理论》 一、填空题1 .对称三相电路中，负载Ｙ联接，已知电源相量︒∠=•0380AB U （V ），负载相电流︒∠=•305A I （A ）；则相电压=•C U （V ），负载线电流=•Bc I （A ）。

2 .若12-=ab i A ，则电流的实际方向为 ，参考方向与实际方向 。

3 .若10-=ab i A ，则电流的实际方向为 ，参考方向与实际方向 。

4 .元件在关联参考方向下，功率大于零，则元件 功率，元件在电路中相当于 。

5 .回路电流法自动满足 定律，是 定律的体现6 .一个元件为关联参考方向，其功率为―100W ，则该元件 功率，在电路中相当于 。

7 .在电路中，电阻元件满足两大类约束关系，它们分别是 和 。

8 .正弦交流电的三要素是 、 和 。

9 .等效发电机原理包括 和 。

10.回路电流法中自阻是对应回路 ，回路电流法是 定律的体现。

11.某无源一端口网络其端口电压为)302sin(240)(︒+=t t u (V)，流入其端口的电流为)602cos(260)(︒-=t t i (A)，则该网络的有功功率 ，无功功率 ，该电路呈性。

若端口电压电流用相量来表示，则其有效值相量=•U ,=•I 。

12.无源二端电路N 的等效阻抗Z=(10―j10) Ω，则此N 可用一个 元件和一个 元件串联组合来等效。

13 .LC 串联电路中，电感电压有效值V 10U L =，电容电压有效值V 10U C =，则LC 串联电路总电压有效值=U ，此时电路相当于 。

15.对称三相星形连接电路中，线电压超前相应相电压 度，线电压的模是相电压模的 倍。

16 .RLC 并联谐振电路中，谐振角频率0ω为 ，此时电路的阻抗最 。

17 .已知正弦量))(402sin()(1A t t i ︒+=，))(1102cos()(2A t t i ︒+-=，则从相位关系来看，•1I •2I ，角度为 。

Zi
ZL
图 2-22
) 的方法。 D. 并联电容。 )。 D．160 Ω
V1
A. 串联电感； B. 串联电容； C. 并联电感； 2-24 若某电感的基波感抗为 40 Ω ，则其 4 次谐波感抗为( D Ａ．10 Ω B．20 Ω C．40 Ω
2-25 已知图 2-25 所示的正弦稳态电路中，电压表读数 （电压表的读数为正弦电压的有效值）为：V1 为 30V； V2 为 40V，则图中电源电压有效值 US 为（ B ） 。 A. 40V ； B. 50V； C. 70V； D. 30V。
－10t －t/τ
10kΩ ＋ 20V － 10kΩ
5kΩ iC
10µF
＋ uC －
图3
(时间单位 ms)
4.如图 4 所示电路在 t = 0 时 S 闭合，求 uC(t )。
＋ 126V －
3kΩ
3kΩ ＋ uC －
100µF
图4
解：在开关 S 闭合后属于零输入响应，利用三要素公式，响应的一般形式为：
2-14 如图 2-14 所示电路，电压 u1 和电压 u0 之间 满足以下哪个关系式（ C ） 。 R1 R A． u 0 = − B． u 0 = 1 u1 u1 R2 R2 C． u 0 = −
R1 ＋ u1 －
R2 － ＋ ∞ ＋ ＋ u0 － 图 2-14
R2 u1 R1
D． u 0 =
R2 u1 R1
电路原理复习资料
一、填空题
1-1 根据换路定律，在一阶电路中，换路前后 RL 电路中电感的 电路中电容的 电压 不可能突变。 电流 不可能突变，RC
1-2 为提高感性负载电路的功率因数，通常采用 并联电容 的方法。 1-3 某有源二端网络开路电压为 12V，短路电流 0.5A，则其等效内阻为 24 欧。

XX 大学继续教育学院 电路原理 试卷（A ） 学年： 学期:年级： 专业： 学习形式： 层次：（本试题满分100分，时间90分钟）一、单项选择题(每题8分，总计40分)1、电路如图所示，其中电流I 1为( )A 、0.6 A B 、0.4 AC 、3.6 A D 、2.4 A3Ω6Ω2、电路如图示，U ab 应为( )A 、0 VB 、-16 VC 、0VD 、4V3、图示电路中，7 V 电压源吸收功率为( )A 、14 WB 、-7 WC 、-14 W D 、7 W4、图示电路在t =0时开关闭合，t ≥0时u t C ()为( )A 、---1001100(e )V tB 、(e )V -+-505050tC 、--100100e V tD 、---501100(e )V tu5、若负载所取的功率P 为72kW ，负载的功率因数角为︒4.41(电感性，滞后)，则其视在功率为A 、54kVAB 、96kVAC 、47.6kVAD 、108.9kVA 二、非客观题(共10分)图示三角形联接对称三相电路中，已知对称三相电源线电压l U =380V ，三相负载功率P =2.4kW ，功率因数ϕλcos ==0.6(滞后，感性)，求负载阻抗Z 。

C B A Z三、非客观题(共10分)求：图示网络ab 二端间的戴维南等效电路。

1ab四、非客观题(共10分)将一只150 uA 、1 k Ω的表头改制为0.5mA 与5 mA 的两量程电流表,其电路如图所示，求：电阻R 1与R 2的数值。

05.mA五、非客观题(共10分)试用叠加定理求图示电路中的电压U 。

4Ω六、非客观题(共10分)图示电路在换路前已达稳态。

当t =0时开关断开，求：t ≥0的u t C ()。

100u C七、非客观题(共10分)图示正弦交流电路中，R=12Ω，L ω=9Ω，C ω=25Ω，t u ωcos 2150=V ，求：1i ，2i ，i 及电路功率P 。

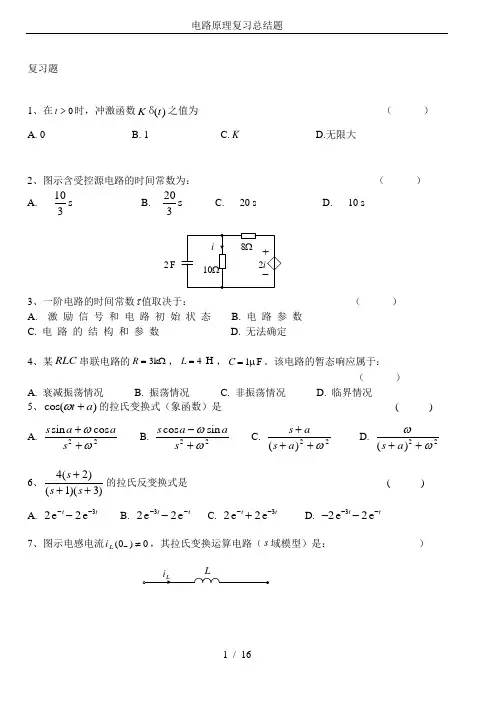
复习题1、在t >0时，冲激函数)(t K δ之值为 （ ） A. 0 B. 1 C. K D.无限大2、图示含受控源电路的时间常数为： （ ） A.s 310 B. s 320 C. 20 s D. 10 s2F3、一阶电路的时间常数τ值取决于： （ ） A. 激 励 信 号 和 电 路 初 始 状 态 B. 电 路 参 数C. 电 路 的 结 构 和 参 数D. 无法确定4、某RLC 串联电路的R =3k Ω，L =4H ，C =1μF 。

该电路的暂态响应属于： （ ）A. 衰减振荡情况B. 振荡情况C. 非振荡情况D. 临界情况 5、cos()ωt a +的拉氏变换式（象函数）是 ( ) A.s a a s sin cos ++ωω22 B. s a as cos sin -+ωω22C. s a s a +++()22ωD. ωω()s a ++22 6、4213()()()s s s +++的拉氏反变换式是 ( )A. 223e e ---ttB. 223e e ---ttC. 223e e --+ttD. ----223e e tt7、图示电感电流i L ()00-≠，其拉氏变换运算电路（s 域模型）是： ）︒︒i L8、e sin -att ω的拉氏变换式（象函数）是 ( )A.a s a ()++22ω B. ωω()s a -+22 C. s a s a +++()22ω D. ωω()s a ++229、图示电感的拉氏变换运算电路（s 域模型）是： （ ）︒︒i L ()-Li ()0-Li ()0-Li s()0-Li s()0-A.B.C.D.10、图示电路中电压比U s U s o S ()()的形式应是： ( )+_+_u Su OA. s s as b 22++B. as s as b 2++C. bs as b2++ D.s b s as b 22+++11、图示网络是： （ ）A ．二端口网络B ．三端网络C ．四端网络D ．以上都不是12、图示二端口网络Y 参数中y 12等于： （ ）A.110 S B. 115 S C. 120S D. 以上皆非13、)3)(2(1++s s 的拉氏反变换式是: 答（ ）A. e e ---23t tB. e e ---32t tC. 223e e ---t tD. 232e e ---t t14、图示电路，在开关S 断开时，电容C 两端的电压为: （ ） A 、10V B 、0V C 、按指数规律增加μF15、图示电路转移电压比U s U s L ()()S 的极零点分布应是 ( )A. B.C. D.u16、图示电路的图中，可写出独立的KCL 、KVL 方程数分别为 （ ）A. 3个，3个B. 3个，4个C. 4个，3个D. 4个，4个17、图G 如图所示，现以{1，3，5}支路集合为树，则单连支回路（基本回路）是（ ）A.{1，4，6} B. {1，2，4，5} C. {1，3，5，6} D. {2，3，4，6}18、图示桥形电路中，构成割集的支路集合是 （ ）A.{1，2} B. {1，3，5} C. {1，3，4，5} D. {1，2，4，5}19、图示二端口网络Z 参数中z 11等于： ( ) A. 0Ω B. 2Ω C. 无穷大 D. 以上皆非20.图示电路在开关S 断开之前电路已达稳态，若在t=0时将开关S 断开，则电路中L 上通过的电流)0(+L i 为: A.2A B. 0A C.－2A10μF( ) 二、填充题：1、（本小题2分）图示电路的转移电压比U sU sC()()S=_________________________。

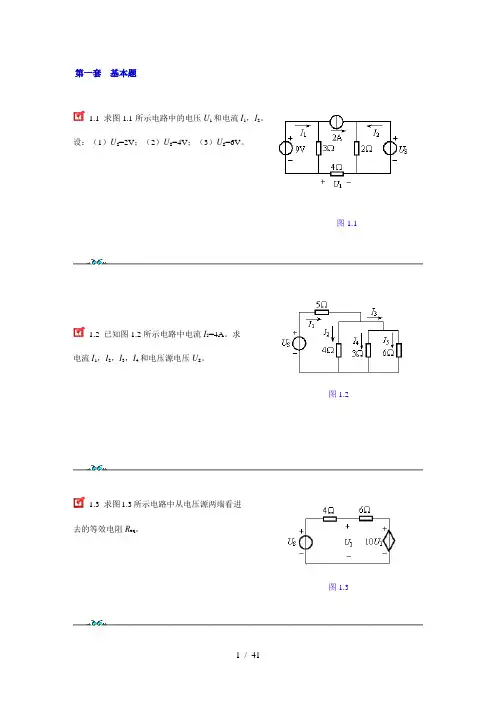
第一套基本题1.1 求图1.1所示电路中的电压U1和电流I1，I2。

设：（1）U S=2V；（2）U S=4V；（3）U S=6V。

图1.11.2 已知图1.2所示电路中电流I5=4A。

求电流I1，I2，I3，I4和电压源电压U S。

图1.21.3 求图1.3所示电路中从电压源两端看进去的等效电阻R eq。

图1.31.4 求图1.4所示电路中各元件的功率，并校验功率守恒。

图1.4 第二套提高题1.1 已知图1.1所示电路中电压U=3V。

求由电源端看进去的电阻R eq和电阻R1的值。

图1.11.2 图1.2所示电路中，已知3A电流源两端电压为40V。

求负载吸收的功率。

图1.21.3 已知图1.3所示电路中，R1=40W，R e=27W，R b=150W，R L=1500W， =0.98。

求电压增益u2/u1和功率增益p2/p1。

其中p1是u1供出的功率，p2是R L吸收的功率。

图1.3 第一套基本题2.1 求图2.1所示各电路的入端电阻R AB、R ab。

图2.12.2 试求图2.2所示电路中的电压U。

图2.22.3 试将图2.3所示电路化成最简单形式。

图2.32.4 图2.4所示电路中，设输入电压为U i，试求U o/ U i。

图2.4 第二套提高题2.1 求图2.1所示各电路的入端电阻R AB，R ab。

图中各电阻值均为1 。

图2.1答案：2.2 求图2.2所示电路中的电压U L。

设I S，R，R L为已知。

图2.22.3 求图2.3所示电路中的电流i。

图2.32.4 图2.4所示电路由许多单元构成，每个单元包含R1图2.4和R2两个电阻。

设单元数极多，视作无穷大。

（1）设R1=2Ω，R2=1Ω。

求A，B处的入端电阻。

（2）以B点为电位参考点，若每个节点电压是前一个节点电压的一半，问此时R1/R2是多少？第一套基本题3.1 在图3.1所示电路中，试用支路电流法求图示电路的各支路电流。

图3.13.2 试用回路电流法求图3.2所示电路中电流源两端电压U S。

、选择题图示电路中负载电阻R L 获得的最大功率为(1) 2W 2) 4W 3) 8W 4) 16W4. 图示电路中电压U 等于() 1) 2V 2) -2V 3) 6V 4) -6V5. 图示电路中5V 电压源发出的功率P 等于()电路原理的题库1. 图示电路中电流i s等于()1) 1.5 A 2) -1.5A 3) 3A 4) -3A2. 图示电路中电流I 等于() 1) 2A 2) -2A 3) 3A 4) -3Ais Ai =1A2'J6'J 2门4 J16V 'O'2'1) 15W 2) -15W 3) 30W 4) -30W6.对于具有b 条支路，n 个结点的连通电路来说，可以列出线性无关的KVL 方程的最大数目是()。

A. b — 1B.n — 1C.b — n+1D.b — n — 1下述的特点()。

10. 图示网络端口的电压电流关系为4U =40-81，则该网络诺顿等效电路是7.不含受控源线性电阻网络的节点电压方程中般来说互电导(g ij和g jj )具有A.互电导为负，且 g ij = g j iB. 有的互电导为正，且 g m = g jiC.有的互电导为正，且g j = gjiD.互电导为负,g j = gji8.图示电路，用一个等效电源代替, 应该是一个 2A 的理想电流源 B 、 ()2V 的理想电压源C 、 不能代替，仍为原电路4V 的理想电压源9. 图示电路在换路前处于稳定状态，在( )。

t=0瞬间将开关 S 闭合，则i(0 )为C. 0.3AD. 1Aa+U b11. 设电路的电压与电流参考方向如图示，已知 U .0 , I ::: 0，贝U 电压与电流的 实际方向为（）。

A. a 点为高电位,电流由a 至bB. a 点为高电位,电流由b 至aC. b 点为高电位，电流由a 至bD. b 点为高电位,电流由b 至aI ——a 令—►—--- 住b+ -U12. 如图示电路，下面的说法正确的是（）。

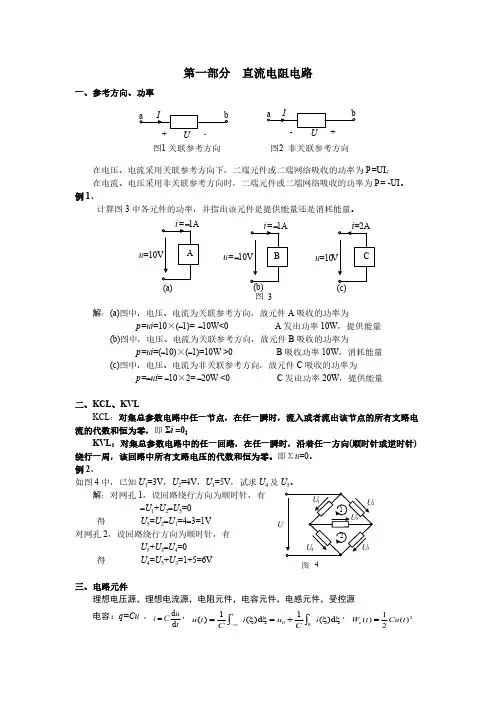
第一部分 直流电阻电路一、参考方向、功率U图1 关联参考方向图2 非关联参考方向在电压、电流采用关联参考方向下，二端元件或二端网络吸收的功率为P =UI ；在电流、电压采用非关联参考方向时，二端元件或二端网络吸收的功率为P = -UI 。

例1、计算图3中各元件的功率，并指出该元件是提供能量还是消耗能量。

u u = -u =10(a)图3解：(a)图中，电压、电流为关联参考方向，故元件A 吸收的功率为 p=ui =10×(-1)= -10W<0 A 发出功率10W ，提供能量 (b)图中，电压、电流为关联参考方向，故元件B 吸收的功率为 p=ui =(-10)×(-1)=10W >0 B 吸收功率10W ，消耗能量 (c)图中，电压、电流为非关联参考方向，故元件C 吸收的功率为 p=-ui = -10×2= -20W <0 C 发出功率20W ，提供能量二、KCL 、KVLKCL ：对集总参数电路中任一节点，在任一瞬时，流入或者流出该节点的所有支路电流的代数和恒为零，即Σi =0；KVL ：对集总参数电路中的任一回路，在任一瞬时，沿着任一方向(顺时针或逆时针)绕行一周，该回路中所有支路电压的代数和恒为零。

即Σu =0。

例2、如图4中，已知U 1=3V ，U 2=4V ，U 3=5V ，试求U 4及U 5。

解：对网孔1，设回路绕行方向为顺时针，有 -U 1+U 2-U 5=0得 U 5=U 2-U 1=4-3=1V 对网孔2，设回路绕行方向为顺时针，有 U 5+U 3-U 4=0得 U 4=U 5+U 3=1+5=6V 三、电路元件理想电压源，理想电流源，电阻元件，电容元件，电感元件，受控源电容：q=Cu ，，，tu C i d d =ξξ+=ξξ=⎰⎰∞-d )(1d )(1)(00i Cu i Ct u tt2c )(21)(t Cu tW =图4电感：ΨL =Li ，，，t i L t Ψu d d d d L ==ξξ+=ξξ=⎰⎰∞-d )(1d )(1)(00u L i u L t i tt 2)(21)(t Li t W L =例3、电路如图5所示，试写出各图中U 与I 之间的关系式。

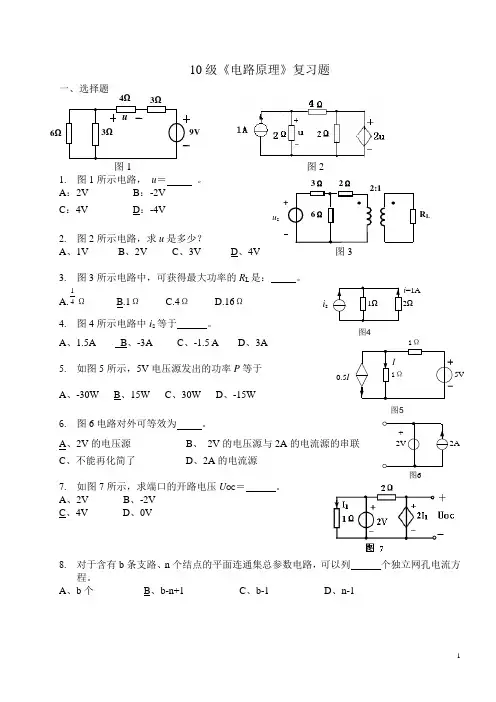
10级《电路原理》复习题一、选择题图1 图2 1. 图1所示电路， u ＝ 。

A ：2V B ：-2VC ：4VD ：-4V2. 图2所示电路，求u 是多少？A 、1VB 、2VC 、3VD 、4V 图33. 图3所示电路中，可获得最大功率的R L 是： 。

A.41Ω B.1Ω C.4Ω D.16Ω4. 图4所示电路中i s 等于 。

A 、1.5AB 、-3AC 、-1.5 AD 、3A5. 如图5所示，5V 电压源发出的功率P 等于A 、-30WB 、15WC 、30WD 、-15W6. 图6电路对外可等效为 。

A 、2V 的电压源B 、 2V 的电压源与2A 的电流源的串联C 、不能再化简了D 、2A 的电流源7. 如图7所示，求端口的开路电压U OC ＝ 。

A 、2V B 、-2V C 、4V D 、0V8. 对于含有b 条支路、n 个结点的平面连通集总参数电路，可以列 个独立网孔电流方程。

A 、b 个B 、b-n+1C 、b-1D 、n-1R Lu s6Ω 1Ω5V0.5I图5i s 2Ωi =1A图42A图69. 图8所示电路中,u S (t)=4Sin （2t ） V,则单口网络相量模型的等效阻抗为 。

A 、 (2-j2)Ω B 、 (2-j1)Ω C 、 (2+j2)Ω D 、 (2+j1)Ω10. 图9所示正弦稳态单口的端口等效电感是： 。

A. 3HB.32H C. 5H D.54H图911. 图10中所示电流源i 在不违反电路的基本定律的前提下允许的取值为 。

A 、1.2AB 、-1.2AC 、0.6AD 、-0.6A图10 12. 图11所示电路中，受控源实际上 。

A 、发出功率 B 、吸收功率C 、功率为零D 、时而吸收时而发出功率图11图13 图14 13. 图13所示电路，问受控源吸收的功率是： 。

A 、2W B 、-2W C 、0W D 、 4W14. 图14所示单口网络，其端口的VCR 关系是： 。

电路原理的题摘要：一、电路原理概述1.电路原理基本概念2.电路元件及性质3.电路分析方法二、基本电路定理1.基尔霍夫定律2.欧姆定律3.诺顿定理三、交流与直流电路分析1.直流电路分析2.交流电路分析3.电路的频率响应四、电路设计与应用1.电路设计基本原则2.实际电路应用案例3.电路原理在现代科技中的应用正文：电路原理是电子工程、电气工程等领域的基础知识，涉及到电路的组成、性质、分析以及设计与应用等方面。

本文将对电路原理进行简要概述。

一、电路原理概述电路原理主要包括电路的基本概念、电路元件的性质以及电路分析方法等内容。

电路是由导线、电源、电阻、电容、电感等元件组成的电流路径。

电路分析方法主要有节点分析法、单元法、超定电路分析法等。

二、基本电路定理电路分析中有很多基本定理，如基尔霍夫定律、欧姆定律和诺顿定理等。

基尔霍夫定律包括基尔霍夫电流定律（KCL）和基尔霍夫电压定律（KVL）。

欧姆定律是描述电阻中电流与电压之间关系的定律。

诺顿定理则是在基尔霍夫定律基础上推导出的一个重要定理，用于简化复杂电路的分析。

三、交流与直流电路分析电路分析中，直流电路和交流电路有不同的分析方法。

直流电路主要依据基尔霍夫定律进行分析，而交流电路则需要考虑电流的相位差，通常采用复数法进行分析。

此外，电路的频率响应也是交流电路分析中的一个重要内容。

四、电路设计与应用电路设计是电子工程师和电气工程师的重要工作之一。

在进行电路设计时，需要遵循一定的原则，如安全性、可靠性、经济性等。

实际电路应用案例包括家用电器、通信设备、交通工具等。

此外，电路原理在现代科技领域中有着广泛的应用，如计算机、手机、物联网等。

总之，电路原理作为电子工程和电气工程的基础知识，对于从事相关领域工作的人员具有重要的指导意义。

复习题一一、判断题（将判断结果用“√”或“×”填入括号内。

每小题1分，共5分）（ ）1.电路中，当电流控制电压源的控制量为零时，被控制量所在处相当于短路。

（ ）2.当含源一端口网络输入电阻R in=0 时，该一端口网络的等效电路为理想电压源。

（ ）3.理想电容元件在某时刻的电流值为零，则该时刻电容上的储能一定为零。

（ ）4.已知A，V，则u与i的相位差为（ ）5.对称三相四线制 Y-Y 电路中线上无电流。

二、选择题（将正确答案填入下面对应位置内。

每小题3分，共21分）题号1234567答案1．电路如图1所示，电压u=？图1 图2 图3（A）5V （B）3V （C）1V （D）-2V2.电路如图2所示，电压U=？（A）4V （B）8V （C）12V （D）16V3.电路如图3所示，ab端的戴维南等效电路中u oc和R eq分别为（A)-20V，16Ω （B）20V，16Ω （C）-12V，4Ω （D）12V，4Ω图4 图5 图64.电路如图4所示，已知A，并以作为参考相量，则为（A）A （B）A （C）A （D）A5.电路如图5所示，已知，，，, 则电路的驱动点阻抗为（A） （B）（C） （D）6.以结点(4)为参考,写出图6示有向图的关联矩阵 A=（A） （B） （C） （D）7.在对称三相三线制Y-Y电路中，已知线电压V，则当A相负载短路和开路时，B相负载两端的电压分别为（A）220V ， 220V （B）220V ， 190V （C）380V ， 220V （D）380V ， 190V三、填空题（将正确答案填入对应的位置。

每小题3分，共21分）1. 电路如图7所示，ab端的输入电阻R in为图7 图8图92. 电路如图8所示，结点①的结点电压方程为：3. 电容C1与C2串联，其等效电容C= 。

4. 图9所示的电流用阶跃函数表示为：。

5. 电路如图10所示，已知，则 V。

图10 图116. 图11中的等效电感为L= 。

总复习题及解总复习题及解一、问 答第一章答题1. 电流与电压为关联参考方向是指什么？答：电流参考方向（箭头方向）与电压降参考方向（“+”到“-”的方向）一致的方向。

第二章答题1. 应用叠加定理时，理想电压源不作用时视为短路，理想电流源不作用时视为 开路。

2、求含有受控源单口网络的戴维南（诺顿）等效电路的内阻时，屏蔽掉电源后须用 外施电压、电流 法求得。

第三章答题1、对于电容C 和电感L ，电压和电流间的关系为：，2、换路定律是指： 3、全响应解的两种表达式：（1）全响应=（零输入响应）+（零状态响应） （2）三要素法： 第四章答题1、直流电路中，感抗为0，容抗为无穷大。

2、正弦电压u(t) =2U cos (?t + ?u )对应的相量表示为uUUθ∠=•。

3、任意一个相量乘以j相当于该相量逆时针旋转90o 。

4、三相对称电源星型联结，相、线电压的关系为相电压是线电压的31倍，且相电压滞后对应线电压30°。

对称电源△接线时，线电流、相电流之间关系为线电流等于3倍相电流，相位滞后对应相电流30°。

5、电阻元件的电压电流的有效值满足：U=IR，关联参考方向下电压和电流同相位，即第五章答题无第六章答题1、本征半导体电子浓度等于空穴浓度；N型半导体的电子浓度大于空穴浓度；P型半导体的电子浓度小于空穴浓度。

2、场效应管属于电压控制型器件，晶体三极管则属于电流控制器件。

3、晶体三极管工作在放大状态时，应使发射结正向偏置；集电结反向偏置。

4、稳定二极管稳压时是处于反向偏置状态，而二极管导通时是处于正向偏置状态。

5、 PN结的单向导电性，就是PN结正偏时导通，反偏时截止。

6、当温度升高时，三极管的集电极电流Ic 增加，发射结压降U BE减小。

第七章答题1、共模抑制比K CMR是差模放大倍数与共模放大倍数（绝对值）之比。

2、抑制温漂（零漂）最常用的方法是采用差放电路。

3、差分放大电路能够抑制共模信号，放大差模信号。

电路理论基础复习题一、判断题1．线性电阻是阻值不随其两端电压或电流数值变化。

（）2．伏安关系是电流与电阻之间的关系。

（）3．当电流、电压的实际值远小于额定值时，电气设备功耗增大，效率降低。

（）4．电气设备只有在轻载状态下工作，才最经济合理、安全可靠。

（）5．应用KCL定律解题事先标出的是结点电流的实际方向。

（）6．电路的参考点可以任意选取，参考点选得不同，电路中各点的电位是不变的。

（）7．当电压、电流和功率的实际值大于其额定值时电气设备为过载运行状态。

（）8．电压定律是用来确定回路中各段电压之间关系的电路定律。

（）9．任一瞬间流入节点电流的代数和恒等于零。

（）10．在电路等效的过程中，与理想电压源并联的电流源不起作用。

（）11．如果需要调节电路中的电流时，一般也可以在电路中串联一个变阻器来进行调节。

（）12．负载并联运行时，任何一个负载的工作情况基本上不受其他负载的影响。

（）13．并联的负载电阻越多，每个负载的电流和功率越大。

（）14．为了某种需要，可将电路中的某一段与电阻或变阻器并联，以起分流或调节电流的作用。

（）15．回路电流法适用于支路数较多但网孔数较少的复杂电路。

（）16．节点电压法适用于支路数较多但节点数较少的复杂电路。

（）17．计算功率时可以应用叠加原理。

（）18. 叠加定理不只适用于线性电路求电压和电流，还适用于非线性电路。

（）19．零输入响应是电路发生换路前，动态元件中已储有原始能量。

（）20．零状态响应是动态元件的原始储能为零，仅在外部输入激励的作用下引起的电路响应。

（）二、填空题1．将电源提供的电能转换为其他形式能量的设备叫（）。

2．构成电路的三要素是（）。

3．只消耗电能，不存储能量的元件叫（）。

4．对外提供恒定的或随时间变化的电压，而与流过它的电流无关的电源是（）源。

5．对外提供恒定的或随时间变化的电流，而与加在它两端的电压无关的电源叫（）源。

6．在电路等效的过程中，与理想电流源相（）联的电压源不起作用。

电路原理复习题(总24页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--2电路原理复习题单项选择题：在下列各题中，有四个备选答案，请将其中唯一正确的答案写在题后的括号内。

（共10小题，总共 30 分）1题2图所示电路的I 和U 分别为I = A ；U = V 。

A. -2；3 ；-3 C. 1；3 D. 2；32. 图示电路中a 、b 端的等效电阻R ab 为 。

A. 100ΩB. 50ΩC. 150ΩD. 200Ω 3 电路如图所示，其中I = A 。

A. 6B. 1C. 2D. 4、4 电路电压与电流参考方向如题1图所示，已知U <0，I >0，则电压与电流的实际方向为A. a 点为高电位，电流由a 至bB. a 点为高电位，电流由b 至aC. b 点为高电位，电流由a 至bD. b 点为高电位，电流由b 至a题1图 题2图5. 如图所示，u 、i 的参考方向 ，则ui 的乘积表示 功率。

A. 关联，吸收B. 关联，发出C. 非关联，吸收D. 非关联，发出答（ ）题1图6. 在如图所示电路中，电流I 的数值应该为a3A. -2AB. -1AC. 1AD. 2A答（ ）题2图3. 如图所示直流电路中电流I 等于A. I U U R =-S 12B. I U R =-11C. I U U R U R =--S 1211D. I U R UR =-S 211答（ ）7 电路如图所示，其中I = A 。

A. -6AB. -5AC. 6AD. 5A答（ ）题3图 题4图8. 由图（a ）得其诺顿等效电路（b ），其中，I = ，R = 。

A ，Ω B. 4 A ，5Ω C. 8 A ，5Ω D. 4 A ， Ω答（ ）+U 1 -4（a ） （b ）题5图9. 图6电路中，R L 可变，R L 获得最大功率条件为R L = ，此时P max = 。

解：(1) 由 t = 0-电路求 uC(0–)、iL (0–) 换路前电路已处于稳态：电容元件视为开路； 由 t = 0-电路可求得：电感元件视为短路。
iL (0 )
R1 R1 R3
R
U R1R3
4
4
4
2
U 4
4
1A
R1 R3
44
(1) iL (0 ) 1 A
uC (0 ) R3iL (0 ) 4 1 4 V
I1
解：
I2
E1 R1 R2
1A
I3＝0
VA ＝R3I3－E2＋R2I2
＝0－4＋2 ×1＝ -2V
或
VA＝R3I3－E2－R1I1＋E1 ＝0－4－4 ×1＋6＝-2V
7. 计算 A 点的电位 VA
8. 电路如图。U1＝10V，IS＝2A，R1＝1Ω，R2＝2Ω，R3＝5 Ω ，R＝1 Ω。求电阻 R 中的电流 I；(2)计算理想电压源 U1 中的电流 IU1 和理想电流 源 IS 两端的电压 UIS；(3)分析功率平衡。 解： （1）
1.2A
I 34
E R3 R4
12 10 5
0.8A
UO I12R2 I34R4 1.25 0.85 2V
(2) 求等效电源的内阻 R0
R0 R1 // R2 R3
R4
(3) 画出等效电路求电流
IG
UO RO RG
2 5.8 10
0.126A
17.
18. 用诺顿原理计算图中电阻 R3 上的电流 I3.已知 R1=6Ω,R2=2 Ω,R3=3Ω,Is=10A,E=6V 解：(1) 求短路电流
(b) E 单独作用 将 IS 断开
I 2

I 1
U 1
I 2
+
N
R 2
U 2
(a)
S
+
6V
N
C
u (t) C
(b)
答案： uC (t) （6 1 et / ) V t 0 ( 3 10-5s)
十二、题示电路中，非线性电阻元件的伏安特性关系式为 u(t)
3i2 (t) 3i2 (t)
，i(t) 0 ，i(t) 0
其 中 ， 电 压 、 电 流 的 单 位 分 别 为 伏 和 安 。 电 阻 R=6Ω ， 电 感 L=16mH ， 电 压 源
1
+ 18V
N
1 (a)
2
1
2
+ 7.2V
+ 18V
N
2.4A
2
1
2
(b)
答案： T
2.5 0.7S
72.5.5， IS 15.9A。
1
2 2 I=1A
IN S
3 6
1
2
(c)
八、已知图示电路在 t<0 时已达稳态(其中开关 S1、S2 闭合，S3、S4 断开)。当 t=0 时，四个开 关同时动作，即开关 S1、S2 断开，S3、S4 闭合。求开关动作经过多长时间电压 u(t)达到零伏。
u
1V
1
+
12 3iFra biblioteku1
2
u1 1
答案：
uiL2
1.5 1
0 0.5 1
F 1 u1 1
0.5
u2
1.5
2 iL 0
F
十、电路如图所示。已知 uC(0)=1V，iL(0)=2A。电压源电压 uS(t)＝2(t)V。

《电工原理》自考复习题一. 填空题1.任何一个元件的电压u与电流i取关联参考方向时，该元件吸收的功率为p= 。

当流经元件的电流电压实际方向时,元件吸收功率，电流电压实际方向时，元件发出功率。

2.一个恒定电压15V与内阻3Ω串联的电压源可以等效变换成内阻为Ω与一个恒定电流为A并联的电流源。

3.已知正弦电压u=100sin(314t+60°）V，电压的有效值为 V，初相位为 ,频率为。

4.对于RLC串联电路发生谐振时的条件为，电路的谐振频率f o= ,电路的阻抗值达到最，谐振电流达到最 ,此时电路呈性。

5.电路中负载大是指负载大，而负载电阻。

当负载电阻等于时负载可获得最大功率.6。

三相对称电动势瞬时值的代数和等于。

相量和等于。

7.任何一个元件的电压u与电流i取非关联参考方向时，该元件吸收的功率p= 。

当流经元件的电流电压实际方向一致时，元件功率，电流电压实际方向相反时，元件功率。

8.一个恒定电流5A与内阻4Ω并联的电流源可以等效变换成内阻为Ω与一个恒定电压为 v串联的电压源。

9。

已知正弦电流的有效值相量为=10∠—45°A，则其幅值为 A,有效值为 A，初相位为 .10.对于RLC串联电路发生谐振时，又称为谐振,此时电路的总电压与总电流相位。

11。

在电力系统中常采用在感性负载两端并联的方法来提高功率因数，但电路的有功功率。

12.一阶RL电路的时间常数为τ= .13。

电容元件电流的大小与方向取决于的变化率，其表达式为。

14.叠加原理只适用于电路,任一瞬间各支路中的电流或电压恒等于各独立电源单独作用时在该支路产生响应的和。

15。

已知正弦量=220sin（ωt+30°）V,=100sin（ωt-45°）V，则其相位差为，其相位关系为角。

16。

对于RLC并联电路发生谐振时，电路的阻抗值达到最，电路的谐振电流达到最，此时电路呈现性。

17.电路中电容的一般不能跃变，其换路定则为 .18。

《电路原理》复习资料一、填空题1、 图1-1所示电路中，I 1 = 4 A ，I 2 = 1 A 。

2、 图1-2所示电路， U 1 = 4 V ，U 2 =10 V 。

3、 图1-3所示电路，开关闭合前电路处于稳态，()+0u =4 V ，+0d d tu C = 20000V/s 。

4、 图1-4（a ）所示电路，其端口的戴维南等效电路图1-4（b ）所示，其中u OC = 8 V ，R eq = 2。

5、图1所示电路中理想电流源的功率为 -60W图1-13A6Ω3ΩI 1I 2图1-3＋ u － ＋ u C －2A2Ω2Ω 100FS (t =0)1eq＋ u OC － 12+ 10V图1-4+ 4ii(a)(b)1＋ U 1 －图1-2＋U －2Ω 2A ∞ + +6、图2所示电路中电流I为－1.5A 。

7、图3所示电路中电流U为115V 。

二、单选题（每小题2分，共24分）1、设电路元件的电压和电流分别为u和i，则( B ).（A）i的参考方向应与u的参考方向一致（B）u和i的参考方向可独立地任意指定（C）乘积“u i”一定是指元件吸收的功率（D）乘积“u i”一定是指元件发出的功率2、如图所示，在指定的电压u和电流i的正方向下，电感电压u和电流i的约束方程为(A).（A）0.002didt-（B）0.002didt（C）0.02didt-（D）0.02didt图题2图3、电路分析中所讨论的电路一般均指( A ).（A）由理想电路元件构成的抽象电路（B）由实际电路元件构成的抽象电路（C）由理想电路元件构成的实际电路（D）由实际电路元件构成的实际电路4、图所示电路中100V电压源提供的功率为100W，则电压U为( C ).（A）40V （B）60V （C）20V （D）-60V图题4图图题5图5、图所示电路中I的表达式正确的是（ A ）.（A）SUI IR=-（B）SUI IR=+（C）UIR=-（D）SUI IR=--6、下面说法正确的是（ A ）.（A）叠加原理只适用于线性电路（B）叠加原理只适用于非线性电路（C）叠加原理适用于线性和非线性电路（D）欧姆定律适用于非线性电路7、图所示电路中电流比ABII为（B ）.（A）ABRR（B）BARR（C）ABRR-（D）BARR-图 题7图8、与理想电流源串联的支路中电阻R （ C ）.（A ）对该支路电流有影响 （B ）对该支路电压没有影响 （C ）对该支路电流没有影响 （D ）对该支路电流及电压均有影响9、图所示电路中N 为有源线性电阻网络，其ab 端口开路电压为30V ，当把安培表接在ab 端口时，测得电流为3A ，则若把10Ω的电阻接在ab 端口时，ab 端电压为：（ D ）. （A ）–15V （B ）30V （C ）–30V （D ）15VNIab图 题9图10、一阶电路的全响应等于( B ).（A ）稳态分量加零输入响应 （B ）稳态分量加瞬态分量 （C ）稳态分量加零状态响应 （D ）瞬态分量加零输入响应11、动态电路换路时，如果在换路前后电容电流和电感电压为有限值的条件下，换路前后瞬间有：（ D ）. （A ）()()+-=00C C i i （B ）()()+-=00L L u u（C ）()()+-=00R R u u （D ）()()+-=00C C u u12、已知()015cos 31460i t A =-+，()0210sin 31460i t A =+，则1i 与2i 的相位差为( A ).（A ）090- （B ）090 （C ）00 （D ）0180 三、计算题（每小题10分，共80分）（作业共8题）1、求图中各二端网络的等效电阻。