三次抛物线超高计算公式

⾼中数学：抛物线公式总结，快快收藏抛物线顶点坐标公式
y=ax²+bx+c（a≠0）的顶点坐标公式是（-b/2a，（4ac-b²）/4a)
y=ax²+bx的顶点坐标是（-b/2a，-b²/4a)
抛物线标准⽅程
右开⼝抛物线：y^2=2px
左开⼝抛物线:y^2= -2px
上开⼝抛物线：x^2=2py y=ax^2（a⼤于等于0）
下开⼝抛物线:x^2= -2py y=ax^2（a⼩于等于0）
[p为焦准距（p>0）]
特点
在抛物线y^2=2px中，焦点是(p/2，0），准线的⽅程是x= -p/2，离⼼率e=1，范围：x≥0；
在抛物线y^2= -2px 中，焦点是( -p/2，0），准线的⽅程是x=p/2，离⼼率e=1，范围：x≤0；
在抛物线x^2=2py 中，焦点是（0，p/2），准线的⽅程是y= -p/2,离⼼率e=1，范围：y≥0；
在抛物线x^2= -2py中，焦点是（0，-p/2），准线的⽅程是y=p/2，离⼼率e=1，范围：y≤0；
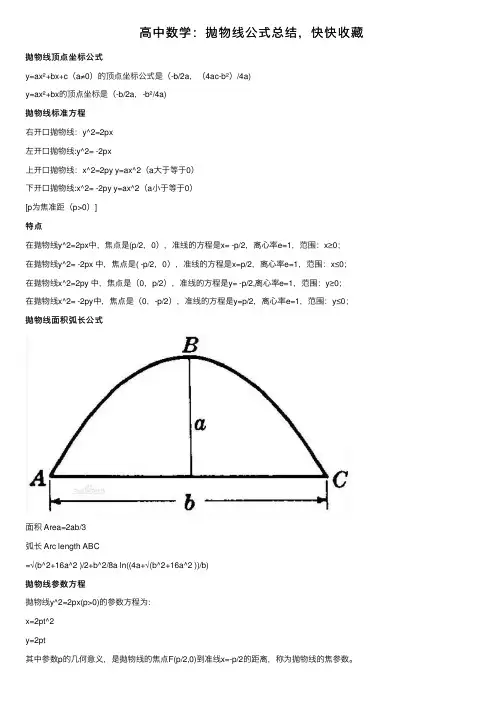
抛物线⾯积弧长公式
⾯积 Area=2ab/3
弧长 Arc length ABC
=√(b^2+16a^2 )/2+b^2/8a ln((4a+√(b^2+16a^2 ))/b)
抛物线参数⽅程
抛物线y^2=2px(p>0)的参数⽅程为:
x=2pt^2
y=2pt
其中参数p的⼏何意义，是抛物线的焦点F(p/2,0)到准线x=-p/2的距离，称为抛物线的焦参数。

抛物线公式抛物线是一种常见的二次函数图形，其数学表达式为抛物线公式。

抛物线公式可以通过一些参数来控制抛物线的位置、形状和方向。

在数学和物理学中，抛物线公式被广泛应用于描述和解决各种问题。

抛物线的基本概念抛物线是由平面上的一系列点构成的曲线，其特点是对称性。

抛物线可以打开向上或向下。

当抛物线开口向上时，其顶点位于抛物线的最低点，并且曲线向上弯曲。

当抛物线开口向下时，其顶点位于抛物线的最高点，并且曲线向下弯曲。

抛物线公式表示了抛物线上的点的坐标，其一般形式为：y = ax^2 + bx + c其中： - a是控制抛物线开口方向和形状的常数，决定了抛物线的曲率。

- b是抛物线的线性项，决定了抛物线在 x 轴方向的平移。

- c是抛物线的常数项，决定了抛物线在 y 轴方向的平移。

抛物线的顶点抛物线的顶点是其曲线的最高或最低点，可以通过抛物线公式直接计算出来。

顶点的 x 坐标可以通过以下公式计算：x = -b / (2a)将 x 坐标带入抛物线公式，可以计算出顶点的 y 坐标。

抛物线的焦点焦点是抛物线上的一个特殊点，具有特殊的几何性质。

焦点的坐标可以通过以下公式计算：x = -b / (2a)y = (4ac - b^2) / (4a)抛物线的对称轴抛物线的对称轴是与抛物线的曲线相切且通过抛物线的顶点的直线。

对称轴的方程可以通过以下公式计算：x = -b / (2a)抛物线的判别式抛物线的判别式决定了抛物线的类型和性质。

抛物线的判别式可以通过以下公式计算：D = b^2 - 4ac根据判别式的值，我们可以判断抛物线的类型： - 当D > 0时，抛物线开口向上，有两个不同的 x-intercepts。

- 当D =0时，抛物线开口向上，有一个 x-intercept。

- 当D < 0时，抛物线开口向上，没有实数解。

抛物线的图形表示我们可以使用各种工具和方法来绘制和表示抛物线的图形。

在数学中，可以使用二维坐标系和抛物线公式来绘制抛物线的图像。

抛物线的四种标准方程公式
抛物线，即参数方程，在建筑中体现的非常明显，著名的几何体之声，也就是
抛物线的发展，系几何学的一种抽象化的发展，一般有三种形式存在。

其中，四种标准抛物线的公式是：
第一种：y= ax^2 +bx+c，其中a可以大于0也可以小于0，如果a>0，该抛物
线是翻出，如果a<0，该抛物线是翻入；
第二种：y= a(x-h)^2+k，其中a可以大于0也可以小于0，如果a>0，该抛物
线是翻出，如果a<0，该抛物线是翻入；
第三种：x= ay^2+by+c，其中a可以大于0也可以小于0，如果a>0，该抛物
线是翻出，如果a<0，该抛物线是翻入；
最后一种：x= a(y-h)^2 +K，其中a可以大于0也可以小于0，如果a>0，该
抛物线是翻出，如果a<0，该抛物线是翻入。

以上四种抛物线，是建筑中最基本的几何体，它们经常在建筑物中呈现，而一
些拥有非常令人惊叹的建筑作品便是基于这些抛物线原理才能营造出如此震撼的空间感。

举个例子，早期的拱顶，当时人们通过抛物线的参数公式，将多边形表面张开，就形成了一个完美的拱顶，而它的几何体也就凝结成了抛物线的形式。

因此，抛物线参数方程的高级应用，使建筑领域有了一定的蓬勃发展，可以运
用到多边形，穹顶，立体几何，甚至到三维空间中都是被做到的，它是建筑发展过程中最重要的几何加工机制。

在建筑专业中，抛物线参数方程被广泛用于建筑设计，艺术形象分析等方面，使建筑设计更加精致独特，更加丰富多彩。

抛物线公式大全
抛物线方程是指抛物线的轨迹方程，是一种用方程来表示抛物线的方法。

在几何平面上可以根据抛物线的方程画出抛物线。

抛物线在合适的坐标变换下，也可看成二次函数图像。

抛物线方程公式
一般式:ax²+bx+c(a、b、c为常数，a≠0）
顶点式:y=a(X-h）2+k（a、h、k为常数，a≠0）
交点式（两根式）：y=a（x-x1）（x-x2）（a≠0）
其中抛物线y=aX2+bX+c(a、b、c为常数，a≠0）与x轴交点坐标，即方程
aX2+bX+c=0的两实数根。

抛物线标准方程
右开口抛物线：y^2=2px
左开口抛物线:y^2= -2px
上开口抛物线：x^2=2py y=ax^2（a大于等于0）
下开口抛物线:x^2= -2py y=ax^2（a小于等于0）
[p为焦准距（p>0）]
抛物线四种方程的异同
共同点：
①原点在抛物线上，离心率e均为1；
②对称轴为坐标轴；
③准线与对称轴垂直，垂足与焦点分别对称于原点，它们与原点的距离都等于一次项系数的绝对值的1/4。

不同点：
①对称轴为x轴时，方程右端为±2px，方程的左端为y^2；对称轴为y轴时，方程的右端为±2py，方程的左端为x^2；
②开口方向与x轴（或y轴）的正半轴相同时，焦点在x轴（y轴）的正半轴上，方程的右端取正号；开口方向与x（或y轴）的负半轴相同时，焦点在x轴（或y轴）的负半轴上，方程的右端取负号。

线性超高公式：I=(Z-C)*(N-M)÷S+M
I=(( Ls -A)*(E+D))/(B-A)-D B为超高渐变段终点桩号 A为超高渐变段起点桩号 E为直线段横坡 D为全超过横坡 Ls为超高渐变段长度
N为超高段终点横坡，无则不输，M为超高起点横坡，Z待求桩号，C超高渐变段起点桩号，无则不输
S为超高渐变段长度。

三次抛物线超高公式：I=（3K²-2K³)*(N-M)+M K=(Z-C)÷S
N为超高段终点横坡，无则不输，M为超高起点横坡，Z待求桩号，C超高渐变段起点桩号，无则不输
S为超高渐变段长度。

线性加宽公式：BX=（Z-C）*(B-A)÷S+A
B为加宽段终点宽度，无则不输，A为加宽段起点宽度，Z待求桩号，C渐变段起点桩号，无则C=Z
S为加宽渐变段长度，无则不输。

三次抛物线加宽公式：BX=（3K²-2K³)*(B-A)+A K=(Z-C)÷S
B为加宽段终点宽度，无则不输，A为加宽段起点宽度，Z待求桩号，C加宽渐变段起点桩号，无则C=Z
S为加宽渐变段长度，无则不输。

三次抛物线超高计算公式抛物线的标准方程为：y = ax² + bx + c其中，a、b和c是常数。

通过给定的三个点，我们可以确定这三个常数的值。

假设这三个点的坐标分别为(x₁,y₁)，(x₂,y₂)和(x₃,y₃)，我们可以通过联立三个方程来解这些常数。

这三个方程是：y₁ = ax₁² + bx₁ + cy₂ = ax₂² + bx₂ + cy₃ = ax₃² + bx₃ + c我们可以使用这三个方程来求解a、b和c的值。

例如，我们可以通过消去c来解这个方程组，得到：a=((y₂-y₃)(x₁-x₃)+(y₃-y₁)(x₂-x₃))/((x₁-x₂)(x₁-x₃)(x₂-x₃))b=((y₂-y₃)(x₁²-x₃²)+(y₃-y₁)(x₂²-x₃²))/((x₁-x₂)(x₁-x₃)(x₂-x₃))c = y₁ - ax₁² - bx₁现在，我们已经得到了抛物线的标准方程。

接下来，我们将使用这个方程来计算三次抛物线的超高。

在抛物线的最高点，它的切线垂直于横轴。

这意味着横轴上的斜率为零。

根据抛物线的标准方程，斜率可以通过求导来计算。

我们将方程求导，得到：y' = 2ax + b将斜率为零代入方程，我们可以解得最高点的横坐标x值为：x=-b/(2a)将此值代入抛物线方程，我们可以计算出最高点的纵坐标：y = ax² + bx + c现在，我们已经得到了抛物线的最高点的坐标，我们可以计算出三次抛物线的超高。

超高可以通过减去抛物线两个端点的纵坐标来计算：超高 = y - min(y₁, y₃)其中，y是抛物线最高点的纵坐标，min(y₁, y₃)表示抛物线的两个端点的纵坐标的最小值。

综上所述，三次抛物线的超高计算公式为：a=((y₂-y₃)(x₁-x₃)+(y₃-y₁)(x₂-x₃))/((x₁-x₂)(x₁-x₃)(x₂-x₃))b=((y₂-y₃)(x₁²-x₃²)+(y₃-y₁)(x₂²-x₃²))/((x₁-x₂)(x₁-x₃)(x₂-x₃))c = y₁ - ax₁² - bx₁x=-b/(2a)y = ax² + bx + c超高 = y - min(y₁, y₃)通过这个公式，我们可以根据给定的三个点的坐标来计算三次抛物线的超高。

抛物线运动计算公式
在竖直方向上，抛物线运动的公式可以表示为：
s = s0 + v0t + 0.5gt^2
其中，s为物体的竖直方向位移，s0为初始位置，v0为初始速度，t
为时间，g为重力加速度。

这个公式可以用来计算物体在竖直方向上的任意时刻的位置。

根据这
个公式，我们可以知道，当物体开始运动时，位移s等于初始位置s0。

随着时间的增加，重力加速度g的作用使得物体的位移增大。

当物体达到
最高点时，位移等于0，并且速度v等于0。

之后，物体开始下落，位移
s又开始增大，速度v也开始增大。

可以使用这个公式计算物体任意时刻
的位置。

在水平方向上，抛物线运动的公式可以表示为：
s=v0t
其中，s为物体的水平方向位移，v0为水平方向上的速度，t为时间。

这个公式表明，在水平方向上，物体的速度是恒定的，所以物体的位
移是速度乘以时间。

物体在水平方向上的速度不会受到任何外力的影响，
所以速度保持不变。

总结一下，抛物线运动可以使用竖直方向和水平方向的运动公式来描
述物体的运动规律。

在竖直方向上，物体受到重力的影响，位移随时间增加。

在水平方向上，物体的速度恒定，位移等于速度乘以时间。

通过这些
公式，我们可以计算物体在抛物线运动中的任意时刻的位置、速度和加速
度等重要参数，从而更好地理解和分析抛物线运动的特性和规律。

抛物线运动计算公式
抛物线运动计算公式是描述物体在重力作用下沿着抛物线轨迹
运动的公式。

它可以用来计算物体在抛出时的速度、发射角度、飞行时间、到达最高点的高度、到达落地点的位置等重要参数。

抛物线运动计算公式的核心是二次函数方程，形式为y = ax2 + bx + c，其
中y是物体的高度，x是运动时间，a是重力加速度的一半，b是发
射速度在水平方向上的分量，c是抛出高度。

如果将抛出点作为坐标原点，则c为零。

根据这个公式，可以通过解方程来确定物体的各种运动参数，也可以通过将参数代入方程来计算特定的数值。

抛物线
运动计算公式是物理学中基础而重要的知识，被广泛应用于各个领域，例如设计投掷物、计算轨道弹道、优化空间飞行器轨迹等。

掌握这个公式，不仅能够深入理解抛物线运动的本质，还能够为实际问题的解决提供有力的工具和思路。

- 1 -。