第一学期高三数学期末质检复习题.doc

甘肃省白银市靖远县第一中学2024学年高三数学第一学期期末质量检测试题 请考生注意：1．请用2B 铅笔将选择题答案涂填在答题纸相应位置上，请用0．5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。

写在试题卷、草稿纸上均无效。

2．答题前，认真阅读答题纸上的《注意事项》，按规定答题。

一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．执行如图所示的程序框图，如果输入2[2]t e ∈-，，则输出S 属于（ ）A ．[32]-，B ．[42]-，C ．[0]2，D ．2[3]e -，2．已知等比数列{}n a 的各项均为正数，设其前n 项和n S ，若14+=n n n a a （n *∈N ），则5S =（ ）A ．30B ．312C ．2D ．623．高斯是德国著名的数学家，近代数学奠基者之一，享有“数学王子”的称号，用其名字命名的“高斯函数”为：设x ∈R ，用[]x 表示不超过x 的最大整数，则[]y x =称为高斯函数，例如：[]0.51-=-，[]1.51=，已知函数12()4324x x f x -=-⋅+（02x <<），则函数[]()y f x =的值域为（ ） A ．13,22⎡⎫-⎪⎢⎣⎭ B ．{}1,0,1- C ．1,0,1,2 D ．{}0,1,24．已知n S 是等差数列{}n a 的前n 项和，若312S a S +=，46a =，则5S =（ ） A ．5 B ．10 C ．15D ．20 5．已知正三角形ABC 的边长为2，D 为边BC 的中点，E 、F 分别为边AB 、AC 上的动点，并满足2AE CF =，则DE DF ⋅的取值范围是（ ）A ．11[,]216-B ．1(,]16-∞C ．1[,0]2- D ．(,0]-∞6．已知3log 74a =，2log b m =，52c =，若a b c >>，则正数m 可以为（ ） A ．4 B ．23 C ．8 D ．17 7．已知函数()()3sin f x x ωϕ=+，()0,0πωϕ><<，若03f π⎛⎫-= ⎪⎝⎭，对任意x ∈R 恒有()3f x f π⎛⎫≤ ⎪⎝⎭，在区间ππ,155⎛⎫ ⎪⎝⎭上有且只有一个1x 使()13f x =，则ω的最大值为（ ） A ．1234 B ．1114 C ．1054 D ．1174 8．若直线不平行于平面，且，则（ ） A ．内所有直线与异面B ．内只存在有限条直线与共面C ．内存在唯一的直线与平行D ．内存在无数条直线与相交9．已知i 为虚数单位，若复数z 满足5i 12i z =-+，则z =（ ） A ．1i + B ．1i -+C ．12i -D ．12i + 10．若函数()2ln f x x x ax =-有两个极值点，则实数a 的取值范围是（ ）A ．10,2⎛⎫ ⎪⎝⎭ B ．1,12⎛⎫ ⎪⎝⎭C ．1,2D ．()2,e 11．已知12log 13a =131412,13b ⎛⎫= ⎪⎝⎭，13log 14c =，则,,a b c 的大小关系为（ ） A ．a b c >> B ．c a b >>C ．b c a >>D ．a c b >> 12．过直线0x y +=上一点P 作圆()()22152x y ++-=的两条切线1l ，2l ，A ，B 为切点，当直线1l ，2l 关于直线0x y +=对称时，APB ∠=（ ）A ．30B ．45︒C ．60︒D ．90︒二、填空题：本题共4小题，每小题5分，共20分。

2025届辽宁省沈阳市二十中学数学高三第一学期期末质量检测试题注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。

回答非选择题时，将答案写在答题卡上，写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．抛物线的准线与双曲线的两条渐近线所围成的三角形面积为，则的值为 ( )A ．B ．C ．D ．2．某中学有高中生1500人，初中生1000人为了解该校学生自主锻炼的时间，采用分层抽样的方法从高生和初中生中抽取一个容量为n 的样本.若样本中高中生恰有30人，则n 的值为（ ） A ．20B ．50C ．40D ．603．已知双曲线C 的一个焦点为()0,5，且与双曲线2214x y -=的渐近线相同，则双曲线C 的标准方程为( )A ．2214y x -=B ．221520y x -=C ．221205x y -=D ．2214x y -=4．如图是函数sin()R,A 0,0,02y A x x πωφωφ⎛⎫=+∈>><< ⎪⎝⎭在区间5,66ππ⎡⎤-⎢⎥⎣⎦上的图象，为了得到这个函数的图象，只需将sin (R)y x x =∈的图象上的所有的点( )A ．向左平移3π个长度单位，再把所得各点的横坐标变为原来的12，纵坐标不变 B ．向左平移3π个长度单位，再把所得各点的横坐标变为原来的2倍，纵坐标不变C ．向左平移6π个长度单位，再把所得各点的横坐标变为原来的12，纵坐标不变 D ．向左平移6π个长度单位，再把所得各点的横坐标变为原来的2倍，纵坐标不变 5．()cos sin xe f x x=在原点附近的部分图象大概是（ ）A ．B ．C ．D ．6．设α为锐角，若3cos 45πα⎛⎫+= ⎪⎝⎭，则sin 2α的值为（ ） A ．1725B ． 725-C ． 1725-D ．7257．中国古代中的“礼、乐、射、御、书、数”合称“六艺”.“礼”，主要指德育；“乐”，主要指美育；“射”和“御”，就是体育和劳动；“书”，指各种历史文化知识；“数”，数学.某校国学社团开展“六艺”课程讲座活动，每艺安排一节，连排六节，一天课程讲座排课有如下要求：“乐”不排在第一节，“射”和“御”两门课程不相邻，则“六艺”课程讲座不同的排课顺序共有（ ）种. A ．408B ．120C ．156D ．2408．某人用随机模拟的方法估计无理数e 的值，做法如下：首先在平面直角坐标系中，过点1,0A 作x 轴的垂线与曲线x y e =相交于点B ，过B 作y 轴的垂线与y 轴相交于点C （如图），然后向矩形OABC 内投入M 粒豆子，并统计出这些豆子在曲线xy e =上方的有N 粒()N M <，则无理数e 的估计值是（ ）A ．NM N-B ．MM N-C ．M NN- D ．M N9．已知1sin 243απ⎛⎫+= ⎪⎝⎭，则sin α的值等于（ ） A ．79-B ．29-C ．29D ．7910．已知,a b 为非零向量，“22a b b a =”为“a a b b =”的（ ） A ．充分不必要条件 B ．充分必要条件C ．必要不充分条件D ．既不充分也不必要条件11．在ABC ∆中，60BAC ∠=︒，3AB =，4AC =，点M 满足2B M M C =，则AB AM ⋅等于（ ） A ．10B ．9C ．8D ．712．某市政府决定派遣8名干部（5男3女）分成两个小组，到该市甲、乙两个县去检查扶贫工作，若要求每组至少3人，且女干部不能单独成组，则不同的派遣方案共有（ ）种 A ．240B ．320C ．180D ．120二、填空题：本题共4小题，每小题5分，共20分。

广西桂林市中山中学2025届高三数学第一学期期末学业质量监测试题注意事项1．考生要认真填写考场号和座位序号。

2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。

第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。

3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。

一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

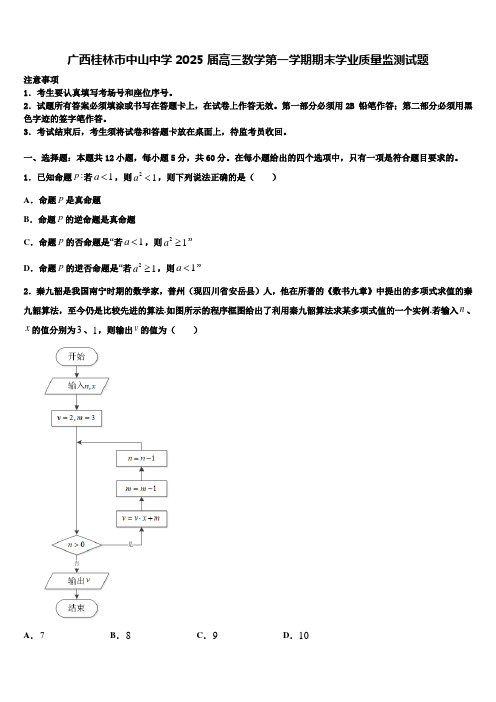
1．已知命题:p 若1a <，则21a <，则下列说法正确的是（ ）A ．命题p 是真命题B ．命题p 的逆命题是真命题C ．命题p 的否命题是“若1a <，则21a ≥”D ．命题p 的逆否命题是“若21a ≥，则1a <”2．秦九韶是我国南宁时期的数学家，普州（现四川省安岳县）人，他在所著的《数书九章》中提出的多项式求值的秦九韶算法，至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例.若输入n 、x 的值分别为3、1，则输出v 的值为（ ）A ．7B ．8C ．9D ．103．已知函数log ()a y x c =+（a ，c 是常数，其中0a >且1a ≠）的大致图象如图所示，下列关于a ，c 的表述正确的是（ ）A ．1a >，1c >B ．1a >，01c <<C ．01a <<，1c >D ．01a <<，01c <<4．在直角坐标平面上，点(),P x y 的坐标满足方程2220x x y -+=，点(),Q a b 的坐标满足方程2268240a b a b ++-+=则y b x a--的取值范围是（ ） A ．[]22-, B ．474733⎡--+⎢⎣⎦C ．13,3⎡⎤--⎢⎥⎣⎦D ．676733⎡+⎢⎣⎦ 5．若点(3,4)P -是角α的终边上一点，则sin 2α=（ ）A ．2425-B ．725-C ．1625D ．856．已知三棱锥P ABC -中，ABC ∆是等边三角形，43,25,AB PA PC PA BC ===⊥，则三棱锥P ABC -的外接球的表面积为（ ）A ．25πB ．75πC ．80πD ．100π7．已知定义在R 上的函数()f x 满足()()f x f x =-，且在(0,)+∞上是增函数，不等式()()21f ax f +≤-对于[]1,2x ∈恒成立，则a 的取值范围是A ．3,12⎡⎤--⎢⎥⎣⎦B ．11,2⎡⎤--⎢⎥⎣⎦C ．1,02⎡⎤-⎢⎥⎣⎦D ．[]0,18．5G 网络是一种先进的高频传输技术，我国的5G 技术发展迅速，已位居世界前列.华为公司2019年8月初推出了一款5G 手机，现调查得到该款5G 手机上市时间x 和市场占有率y （单位：%）的几组相关对应数据.如图所示的折线图中，横轴1代表2019年8月，2代表2019年9月……，5代表2019年12月，根据数据得出y 关于x 的线性回归方程为0.042y x a =+.若用此方程分析并预测该款手机市场占有率的变化趋势，则最早何时该款5G 手机市场占有率能超过0.5%（精确到月）（ ）A ．2020年6月B ．2020年7月C ．2020年8月D ．2020年9月9．小王因上班繁忙，来不及做午饭，所以叫了外卖.假设小王和外卖小哥都在12：00~12：10之间随机到达小王所居住的楼下，则小王在楼下等候外卖小哥的时间不超过5分钟的概率是（ ）A ．12B ．45C ．38D ．3410．若直线不平行于平面，且，则（ ）A ．内所有直线与异面B ．内只存在有限条直线与共面C ．内存在唯一的直线与平行D ．内存在无数条直线与相交 11．已知复数z 满足32i z i ⋅=+（i 是虚数单位），则z =（ ）A ．23i +B ．23i -C ． 23i -+D ． 23i --12．《易·系辞上》有“河出图，洛出书”之说，河图、洛书是中华文化，阴阳术数之源，其中河图的排列结构是一、六在后，二、七在前，三、八在左，四、九在右，五、十背中，如图，白圈为阳数，黑点为阴数，若从阴数和阳数中各取一数，则其差的绝对值为5的概率为A ．15B ．625C ．825D ．25二、填空题：本题共4小题，每小题5分，共20分。

北京市朝阳区2023-2024学年度第一学期期末质量检测高三数学答案及评分参考 2024.1一、选择题（共10小题，每小题4分，共40分） （1）A （2）B （3）B （4）D （5）D （6）C（7）A（8）B（9）D（10）C二、填空题（共5小题，每小题5分，共25分）（11）40（12）28n n + （13）（14）43（答案不唯一）（15）① ④三、解答题（共6小题，共85分） （16）（共13分）解：（Ⅰ）由(0)10f m =+=得1m =−．所以2()cos cos 1f x x x x =+−cos2111212cos222222x x x x +=+−=+−π1sin(2)62x =+−．所以()f x 的最小正周期为2π2πT ==． ················································· 7分（Ⅱ）由πππ2π22π262k x k −++≤≤（k ∈Z ），得ππππ36k x k −+≤≤（k ∈Z ）．所以()f x 的单调递增区间为ππ[π,π]36k k −+（k ∈Z ）．因为()f x 在区间[0,]t 上单调递增，且ππ0[,]36∈−，此时0k =，所以π6t ≤，故t 的最大值为π6． ······················································· 13分（17）（共14分）解：（Ⅰ）取PB 的中点F ，连接,CF EF ．因为E 是PA 的中点，所以//,2EF AB AB EF =． 又因为//,2AB DC AB DC =， 所以//EF DC 且EF DC =．所以四边形CDEF 为平行四边形． 所以//DE CF ．又因为DE ⊄平面PBC ，CF ⊂平面PBC ，所以//DE 平面PBC ． ······································································ 5分 （Ⅱ）取BC 的中点O ，连接PO ．因为PB PC =，所以PO BC ⊥． 又因为侧面PBC ⊥底面ABCD ， 且平面PBC平面ABCD BC =，所以PO ⊥平面ABCD ．如图，在平面ABCD 中，作//Oy BA ， 则,,PO BC PO Oy Oy BC ⊥⊥⊥， 建立空间直角坐标系O xyz −．选条件①：连接AO ，在Rt ABO △中，因为2AB =，1BO =，所以AO 在Rt PAO △中，因为AP =，AO =PO ．所以1(1,2,0),(1,0,0),(1,0,0),(1,1,0),(2A B C D P E −−−．所以13(,1,),(2,1,0)22BE BD ==．设平面EDB 的法向量是(,,)x y z =m ，则 0,0,BE BD ⎧⋅=⎪⎨⋅=⎪⎩m m 即10,220.x y z x y ⎧+=⎪⎨⎪+=⎩令1x =，则2,y z =−=． 于是(1,=−m ．因为PO ⊥平面ABCD ，所以(0,0,1)=n 是平面BDC 的法向量．所以cos ,||||〈〉⋅==m n m n m n ．由题知，二面角E BD C −−为钝角，所以其余弦值为． ···················· 14分选条件③：连接AO ，因为PO ⊥平面ABCD ， 所以PAO ∠是直线AP 与平面ABCD 所成角．所以tan PO PAO AO ∠==．在Rt ABO △中，因为2,1AB BO ==，所以AO在Rt PAO △中，因为PO AO AO =，所以PO =．下同选条件①． ··············································································· 14分（18）（共13分）解：（Ⅰ）设“甲比乙的步数多”为事件A ．在11月4日至11月10日这七天中，11月5日与11月9日这两天甲比乙步数多，所以2()7P A =． ··············································································· 3分（Ⅱ）由图可知，7天中乙的步数不少于20000步的天数共2天．X 的所有可能取值为0,1,2，321255230127277533(0),(1),(2)777241C C C C C P X P X C C C C =========．所以X 的分布列为2416()0127777E X =⨯+⨯+⨯=． ························································· 10分（Ⅲ）11月6日． ···················································································· 13分 （19）（共15分）解：（Ⅰ）由()ln 1()R f x x a x a =−−∈得()1af x x '=−，依题意，(1)10f a '=−=，得1a =．经验证，()ln 1f x x x =−−在点(1,0)处的切线为0y =，所以1a =． ··········· 4分（Ⅱ）由题得()1a x a f x x x −'=−=．（1）若1a ≤，当(1,)x ∈+∞时，()0f x '>恒成立，所以()f x 在区间(1,)+∞上单调递增，所以()f x 无极值点． （2）若1a >，当(1,)x a ∈时，()0f x '<，故()f x 在区间(1,)a 上单调递减， 当(,)x a ∈+∞时，()0f x '>，故()f x 在区间(,)a +∞上单调递增．所以x a =为()f x 的极小值点，且()f x 无极大值点． 综上，当1a ≤时，()f x 在区间(1,)+∞内的极值点个数为0；当1a >时，()f x 在区间(1,)+∞内的极值点个数为1． ····················· 9分（Ⅲ）由（Ⅱ）知当1a ≤时，()f x 在区间(1,)+∞上单调递增，所以()(1)0f x f >=．所以()f x 在区间(1,)+∞内无零点．当1a >时，()f x 的单调递减区间为(1,)a ，单调递增区间为(,)a +∞． 所以()(1)0f a f <=．若()f x 在区间(1,)+∞内有零点t ，则(,)t a ∈+∞．而22()2ln 1f a a a a =−−，设2()2ln 1(1)g x x x x x =−−>， 则()22(1ln )1ln )g x x x x x '=−+=−−．设()2(1ln )(1)h x x x x =−−>，则12(1)()2(1)0x h x x x −'=−=>，所以()h x 在区间(1,)+∞上单调递增． 所以()(1)0h x h >=，即()0g x '>．所以()g x 在区间(1,)+∞上单调递增．所以()(1)0g a g >=，即2()0f a >． 又2()0,f t a a =>， 所以2t a <． ··················································································· 15分（20）（共15分）解：（Ⅰ）由题可知(,0),(0,),||A a B b AB −=因为AOB △的面积为1，所以112AOB S ab ==△．因为点O 到直线AB的距离为，所以1||12AOB S AB ===△．所以222,5,,ab a b a b =⎧⎪+=⎨⎪>⎩得2,1.a b =⎧⎨=⎩所以椭圆E 的方程为2214x y +=． ························································ 5分（Ⅱ）点N 为线段CM 的中点，理由如下：由题知直线l 的斜率存在，设过点(2,1)P −的直线l 的方程为1(2)y k x −=+，即(2)1y k x =++． 由22(2)1,44,y k x x y =++⎧⎨+=⎩得2222(14)(168)16160k x k k x k k +++++=．由2222(168)4(14)(1616)640k k k k k k ∆=+−++=−>，得0k <． 设11)(,C x y ，22)(,D x y ，则221212221681616,1414k k k k x x x x k k +++=−=++． 直线AD 的方程为22(2)2y y x x =++，令1x x =，得点M 的纵坐标212(2)2M y x y x +=+．直线AB 的方程为1(2)2y x =+，令1x x =，得点N 的纵坐标11(2)2N y x =+．要证点N 为线段CM 的中点，只需证明1)1(2N M y y y =+，即112M N y y y +=．因为2211112(2)(2)(2)(2)2M N y y y y y x x x x +++++=+121121121222222222222222(2)(2)(4)(2)(2)422()4168414216161682()41414(168)416216162(168)4(14)48242121,k x x x x x x x x k x x x x k k k k k k k kk k k k k k k k k k k k k k k+++++=++++=+++++−++=++++−+++−+++=++−+++−=+=+−=所以点N 为线段CM 的中点． ····························································· 15分（21）（共15分）解：（Ⅰ）10b =，20b =，31b =，103b =； ························································ 3分 （Ⅱ）由题可知11a ≥，所以1B =∅，所以10b =．若12a m =≥，则2B =∅，1{1}m B +=， 所以20b =，11m b +=，与{}n b 是等差数列矛盾． 所以11a =．设*1)(n n n d a a n +−∈=N ，因为{}n a 是各项均为正整数的递增数列，所以*n d ∈N ．假设存在*k ∈N 使得2k d ≥．设k a t =，由12k k a a +−≥得12k a t ++≥．由112k k a t t t a +=<+<+≤得t b k <，21t t b b k ++==，与{}n b 是等差数列矛盾．所以对任意*n ∈N 都有1n d =．所以数列{}n a 是等差数列，1(1)n a n n =+−=． ······································ 8分（Ⅲ）因为对于*n ∈N ，1n n B B +⊆，所以1n n b b +≤．所以111n n n n b n b n b ++++<++≤，即数列{}n n b +是递增数列． 先证明S T =∅．假设ST ∅≠，设正整数p ST∈．由于p S ∈，故存在正整数i p <使得i p i a =+，所以i a p i =−． 因为{}n a 是各项均为正整数的递增数列，所以11i a p i +−+≥．所以1p i b i −=−，1p i b i−+=．所以()11p i p i b p i i p −−+=−+−=−，1(1)11p i p i b p i i p −+−++=−++=+．又因为数列{}n n b +是递增数列，所以p T ∈/，矛盾． 所以S T =∅．再证明*ST =N ． 由题可知*ST ⊆N ．设*q ∈N 且q S ∈/，因为数列{}n n a +是各项均为正整数的递增数列， 所以存在正整数j ，使得jq j a <+．令0min{|}j j j q j a =<+．若01j =，则11q a <+，即11a q >−，所以1a q ≥． 所以q b =，所以q q b q T+=∈．若01j >，则000101j j j a q j a −−+<<+，所以00101j j a q j a −<−+≤．所以0101q j b j −+=−，所以00100(1)11q j q j b q j j q−+−++=−++−=．因为001(1)q j q j b T−+−++∈，所以q T ∈．所以*S T ⊆N ．综上，*ST =N 且ST =∅．·························································· 15分。

辽宁省辽河油田第二中学2024学年数学高三第一学期期末质量跟踪监视试题注意事项:1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。

2．答题时请按要求用笔。

3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。

4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。

5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．如图，正方体的底面与正四面体的底面在同一平面α上，且//AB CD ，若正方体的六个面所在的平面与直线CE EF ，相交的平面个数分别记为m n ，，则下列结论正确的是（ ）A ．m n =B ．2m n =+C ．m n <D ．8m n +<2．设x ∈R ，则“327x <”是“||3x <”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件3．设复数z 满足()117i z i +=-，则z 在复平面内的对应点位于（ ） A ．第一象限B ．第二象限C ．第三象限D ．第四象限4．等比数列{}n a 的各项均为正数，且384718a a a a +=，则3132310log log log a a a +++=( )A ．12B ．10C ．8D ．32log 5+5．设全集U =R ，集合2{|340}A x x x =-->，则UA =（ ）A ．{x |-1 <x <4}B ．{x |-4<x <1}C ．{x |-1≤x ≤4}D ．{x |-4≤x ≤1}6．为得到的图象，只需要将的图象（ ）A ．向左平移个单位B ．向左平移个单位C ．向右平移个单位D ．向右平移个单位7．若函数32()2()f x x mx x m R =-+∈在1x =处有极值，则()f x 在区间[0,2]上的最大值为（ ）A ．1427B ．2C ．1D ．38．已知复数z 满足()1z i i =-，(i 为虚数单位)，则z =( )A ．2B ．3C ．2D ．39．已知抛物线22(0)y px p =>上一点(5,)t 到焦点的距离为6，P Q 、分别为抛物线与圆22(6)1x y -+=上的动点，则PQ 的最小值为（ ）A ．211-B ．525-C ．25D ．251-10．为比较甲、乙两名高中学生的数学素养，对课程标准中规定的数学六大素养进行指标测验（指标值满分为100分，分值高者为优），根据测验情况绘制了如图所示的六大素养指标雷达图，则下面叙述不正确的是（ ）A ．甲的数据分析素养优于乙B ．乙的数据分析素养优于数学建模素养C ．甲的六大素养整体水平优于乙D ．甲的六大素养中数学运算最强11．执行如图所示的程序框图，若输入的3t =，则输出的i =( )A ．9B ．31C ．15D ．6312．已知函数()2331x x f x x ++=+，()2g x x m =-++，若对任意[]11,3x ∈，总存在[]21,3x ∈，使得()()12f x g x =成立，则实数m 的取值范围为（ ） A ．17,92⎡⎤⎢⎥⎣⎦B ．[)17,9,2⎛⎤-∞+∞ ⎥⎝⎦C ．179,42⎡⎤⎢⎥⎣⎦D ．4179,,2⎛⎤⎡⎫-∞+∞ ⎪⎥⎢⎝⎦⎣⎭二、填空题：本题共4小题，每小题5分，共20分。

2025届北京市清华大学附属中学高三数学第一学期期末检测试题注意事项1．考生要认真填写考场号和座位序号。

2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。

第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。

3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。

一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．集合{}2,A x x x R =>∈，{}2230B x x x =-->，则A B =（ ）A ．(3,)+∞B ．(,1)(3,)-∞-+∞C ．(2,)+∞D ．(2,3)2．若双曲线E ：22221x y a b-=（0,0a b >>）的一个焦点为(3,0)F ，过F 点的直线l 与双曲线E 交于A 、B 两点，且AB 的中点为()3,6P --，则E 的方程为（ ）A ．22154x y -=B ．22145x y -=C ．22163x y -=D ．22136x y -=3．高三珠海一模中，经抽样分析，全市理科数学成绩X 近似服从正态分布()285,N σ，且(6085)0.3P X <≤=．从中随机抽取参加此次考试的学生500名，估计理科数学成绩不低于110分的学生人数约为（ ） A ．40B ．60C ．80D ．1004．已知函数()()()2sin 0,0f x x ωϕωϕπ=+><<，8f π⎛⎫= ⎪⎝⎭02f ⎛⎫= ⎪⎝⎭π且在()0,π上是单调函数，则下列说法正确的是（ ）A ．12ω=B ．8f π⎛⎫-= ⎪⎝⎭C ．函数()f x 在,2ππ⎡⎤--⎢⎥⎣⎦上单调递减D ．函数()f x 的图像关于点5,04π⎛⎫⎪⎝⎭对称 5．已知F 为抛物线24y x =的焦点，点A 在抛物线上，且5AF =，过点F 的动直线l 与抛物线,B C 交于两点，O 为坐标原点，抛物线的准线与x 轴的交点为M .给出下列四个命题： ①在抛物线上满足条件的点A 仅有一个；②若P 是抛物线准线上一动点，则PA PO +的最小值为 ③无论过点F 的直线l 在什么位置，总有OMB OMC ∠=∠；④若点C 在抛物线准线上的射影为D ，则三点B O D 、、在同一条直线上.其中所有正确命题的个数为（ ） A ．1B ．2C ．3D ．46．已知函数()2sin()(0,0)3f x x A ωωπ=->>，将函数()f x 的图象向左平移3π个单位长度，得到函数()g x 的图象，若函数()g x 的图象的一条对称轴是6x π=，则ω的最小值为A ．16B ．23 C ．53D ．567．二项式522x x ⎛⎫- ⎪⎝⎭的展开式中，常数项为（ ）A ．80-B ．80C ．160-D ．1608．设α，β是方程210x x --=的两个不等实数根，记n nn a αβ=+（n *∈N ）.下列两个命题（ ）①数列{}n a 的任意一项都是正整数； ②数列{}n a 存在某一项是5的倍数. A ．①正确，②错误 B ．①错误，②正确 C ．①②都正确D ．①②都错误9．如图，用一边长为2的正方形硬纸，按各边中点垂直折起四个小三角形，做成一个蛋巢，将体积为43π的鸡蛋（视为球体）放入其中，蛋巢形状保持不变，则鸡蛋中心（球心）与蛋巢底面的距离为（ ）A ．22B ．32C ．212D ．31210．若双曲线E ：221x y m n-=(0)mn >绕其对称中心旋转3π后可得某一函数的图象，则E 的离心率等于（ ）A 23B 3C ．223D ．2311．已知抛物线()220y px p =>经过点(2,22M ，焦点为F ，则直线MF 的斜率为（ ）A ．22B ．24C ．22D ．22-12．关于函数()cos cos 2f x x x =+，有下列三个结论:①π是()f x 的一个周期；②()f x 在35,44ππ⎡⎤⎢⎥⎣⎦上单调递增；③()f x 的值域为[]22-,.则上述结论中，正确的个数为（） A ．0B ．1C ．2D ．3二、填空题：本题共4小题，每小题5分，共20分。

北京市海淀区北京师大附中2024年数学高三第一学期期末复习检测试题注意事项1．考生要认真填写考场号和座位序号。

2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。

第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。

3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。

一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．设向量a ，b 满足2=a ，1b =，,60a b =，则a tb +的取值范围是 A ．)2,⎡+∞⎣B ．)3,⎡+∞⎣C ．2,6⎡⎤⎣⎦D ．3,6⎡⎤⎣⎦2．已知集合{}|1A x x =>-，集合(){}|20B x x x =+<，那么A B 等于（ ）A ．{}|2x x >-B ．{}1|0x x -<<C ．{}|1x x >-D ．{}|12x x -<<3．如图所示，用一边长为2的正方形硬纸，按各边中点垂直折起四个小三角形，做成一个蛋巢，将体积为43π的鸡蛋（视为球体）放入其中，蛋巢形状保持不变，则鸡蛋（球体）离蛋巢底面的最短距离为（ ）A ．212 B ．212C ．612D ．3124．若复数z 满足2312z z i -=+，其中i 为虚数单位，z 是z 的共轭复数，则复数z =（ ） A ．35B ．25C ．4D ．55．已知集合A ＝{﹣2，﹣1，0，1，2}，B ＝{x |x 2﹣4x ﹣5＜0}，则A ∩B ＝（ ） A ．{﹣2，﹣1，0}B ．{﹣1，0，1，2}C ．{﹣1，0，1}D ．{0，1，2}6．甲在微信群中发了一个6元“拼手气”红包,被乙､丙､丁三人抢完,若三人均领到整数元,且每人至少领到1元,则乙获得“最佳手气”(即乙领到的钱数多于其他任何人)的概率是（ ）A ．13B ．310C ．25D ．347．如图，正四面体P ABC -的体积为V ，底面积为S ，O 是高PH 的中点，过O 的平面α与棱PA 、PB 、PC 分别交于D 、E 、F ，设三棱锥P DEF -的体积为0V ，截面三角形DEF 的面积为0S ，则（ ）A ．08V V ≤，04S S ≤B ．08V V ≤，04S S ≥C ．08V V ≥，04S S ≤D ．08V V ≥，04S S ≥8．在复平面内，复数z a bi =+（a ，b R ∈）对应向量OZ （O 为坐标原点），设OZ r =，以射线Ox 为始边，OZ 为终边旋转的角为θ，则()cos sin z r i θθ=+，法国数学家棣莫弗发现了棣莫弗定理：()1111cos sin z r i θθ=+，()2222cos sin z r i θθ=+，则()()12121212cos sin z z rr i θθθθ=+++⎡⎤⎣⎦，由棣莫弗定理可以导出复数乘方公式：()()cos sin cos sin nn r i r n i n θθθθ+=+⎡⎤⎣⎦，已知)43z i =，则z =（ ）A ．23B ．4C ．83D ．169．已知函数()3cos f x x m x =+，其图象关于直线3x π=对称，为了得到函数2()3g x m x =+的图象，只需将函数()f x 的图象上的所有点（ ） A ．先向左平移6π个单位长度，再把所得各点横坐标伸长为原来的2倍，纵坐标保持不变 B ．先向右平移6π个单位长度，再把所得各点横坐标缩短为原来的12，纵坐标保持不变 C ．先向右平移3π个单位长度，再把所得各点横坐标伸长为原来的2倍，纵坐标保持不变 D ．先向左平移3π个单位长度，再把所得各点横坐标缩短为原来的12，纵坐标保持不变 10．已知{}n a 为正项等比数列，n S 是它的前n 项和，若116a =，且4a 与7a 的等差中项为98，则5S 的值是( )A ．29B ．30C ．31D ．3211．若干年前，某教师刚退休的月退休金为6000元，月退休金各种用途占比统计图如下面的条形图.该教师退休后加强了体育锻炼，目前月退休金的各种用途占比统计图如下面的折线图.已知目前的月就医费比刚退休时少100元，则目前该教师的月退休金为（ ）.A ．6500元B ．7000元C ．7500元D ．8000元12．已知定义在R 上函数()f x 的图象关于原点对称，且()()120f x f x ++-=，若()11f =，则()1(2)(3)(2020)f f f f ++++=（ ）A ．0B ．1C ．673D ．674二、填空题：本题共4小题，每小题5分，共20分。

河南省濮阳市范县一中2024学年数学高三第一学期期末质量检测试题考生须知：1．全卷分选择题和非选择题两部分，全部在答题纸上作答。

选择题必须用2B 铅笔填涂；非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。

2．请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。

3．保持卡面清洁，不要折叠，不要弄破、弄皱，在草稿纸、试题卷上答题无效。

一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．设i 是虚数单位，若复数5i2i()a a +∈+R 是纯虚数，则a 的值为（ ） A ．3-B ．3C ．1D ．1-2．我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”，用现代式子表示即为：在ABC ∆中，角,,A B C 所对的边分别为,,a b c ，则ABC ∆的面积S =根据此公式，若()cos 3cos 0a B b c A ++=，且2222a b c --=，则ABC ∆的面积为（ ）AB ．CD ．3．已知集合{}2{|23,},|1=-<<∈=>A x x x N B x x A ，则集合A B =（ ）A ．{2}B ．{1,0,1}-C ．{2,2}-D ．{1,0,1,2}-4．著名的斐波那契数列{}n a ：1，1，2，3，5，8，…，满足121a a ==，21n n n a a a ++=+，*N n ∈，若2020211n n k a a-==∑，则k =( ) A ．2020B ．4038C ．4039D ．40405．点O 在ABC ∆所在的平面内，OA OB OC ==，2AB =，1AC =，AO AB ACλμ=+(),R λμ∈，且()420λμμ-=≠，则BC =（ ）A ．73B C ．7D 6．某高中高三（1）班为了冲刺高考，营造良好的学习氛围，向班内同学征集书法作品贴在班内墙壁上，小王，小董，小李各写了一幅书法作品，分别是：“入班即静”，“天道酬勤”，“细节决定成败”，为了弄清“天道酬勤”这一作品是谁写的，班主任对三人进行了问话，得到回复如下： 小王说：“入班即静”是我写的；小董说：“天道酬勤”不是小王写的，就是我写的；小李说：“细节决定成败”不是我写的.若三人的说法有且仅有一人是正确的，则“入班即静”的书写者是（ ） A ．小王或小李B ．小王C ．小董D ．小李7．若[]x 表示不超过x 的最大整数(如[]2.52=，[]44=，[]2.53-=-)，已知2107n n a ⎡⎤=⨯⎢⎥⎣⎦，11b a =，()*110,2n n n b a a n n -=-∈≥N ，则2019b =（ ）A ．2B ．5C ．7D ．88．已知函数()2x f x x x ln a ⎛⎫=- ⎪⎝⎭，关于x 的方程f （x ）＝a 存在四个不同实数根，则实数a 的取值范围是（ ）A ．（0，1）∪（1，e ）B ．10e ⎛⎫ ⎪⎝⎭，C ．11e ⎛⎫ ⎪⎝⎭， D ．（0，1）9．设i 为虚数单位，则复数21z i=-在复平面内对应的点位于( ) A ．第一象限B ．第二象限C ．第三象限D ．第四象限10．()f x 是定义在()0,∞+上的增函数，且满足：()f x 的导函数存在，且()()f x x f x '<，则下列不等式成立的是（ ） A ．()()221f f < B ．()()3344ff <C ．()()2334f f <D ．()()3223f f <11．设实数满足条件则的最大值为（ ） A ．1B ．2C ．3D ．412．中国古代中的“礼、乐、射、御、书、数”合称“六艺”.“礼”，主要指德育；“乐”，主要指美育；“射”和“御”，就是体育和劳动；“书”，指各种历史文化知识；“数”，指数学.某校国学社团开展“六艺”课程讲座活动，每艺安排一节，连排六节，一天课程讲座排课有如下要求：“数”必须排在第三节，且“射”和“御”两门课程相邻排课，则“六艺”课程讲座不同的排课顺序共有（ ） A ．12种B ．24种C ．36种D ．48种二、填空题：本题共4小题，每小题5分，共20分。

2025届陕西咸阳市高三数学第一学期期末检测试题注意事项1．考试结束后，请将本试卷和答题卡一并交回．2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置． 3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．4．作答选择题，必须用2B 铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效． 5．如需作图，须用2B 铅笔绘、写清楚，线条、符号等须加黑、加粗．一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知函数()cos sin 2f x x x =，下列结论不正确的是（ ） A ．()y f x =的图像关于点(),0π中心对称 B ．()y f x =既是奇函数，又是周期函数C ．()y f x =的图像关于直线2x π=对称D ．()y f x =的最大值是22．小张家订了一份报纸，送报人可能在早上6:307:30-之间把报送到小张家，小张离开家去工作的时间在早上7.008:00-之间.用A 表示事件：“小张在离开家前能得到报纸”，设送报人到达的时间为x ，小张离开家的时间为y ，(,)x y 看成平面中的点，则用几何概型的公式得到事件A 的概率()P A 等于（ ）A ．58B ．25C ．35D ．783．已知函数2()(2)g x f x x =+为奇函数，且(2)3f =，则(2)f -=（ ） A ．2B ．5C ．1D ．34．设平面α与平面β相交于直线m ，直线a 在平面α内，直线b 在平面β内，且b m ⊥则“αβ⊥”是“a b ⊥”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．即不充分不必要条件5．已知双曲线()222210,0x y a b a b-=>>的左、右焦点分别为12F F 、，圆222x y b +=与双曲线在第一象限内的交点为M ，若123MF MF =．则该双曲线的离心率为A ．2B ．3C D6．已知函数()cos (0)f x x x ωωω->，()y f x =的图象与直线2y =的两个相邻交点的距离等于π，则()f x 的一条对称轴是（ ）A ．12x π=-B ．12x π=C ．3x π=-D ．3x π=7．设()11i a bi +=+，其中a ，b 是实数，则2a bi +=（ ） A ．1B ．2C ．3D ．58．设函数()f x 的定义域为R ，满足(2)2()f x f x +=，且当2(]0,x ∈时，()(2)f x x x =--.若对任意(,]x m ∈-∞，都有40()9f x ≤，则m 的取值范围是（ ）. A ．9,4⎛⎤-∞ ⎥⎝⎦B ．19,3⎛⎤-∞ ⎥⎝⎦C ．(,7]-∞D ．23,3⎛⎤-∞ ⎥⎝⎦9．在等差数列{}n a 中，若n S 为前n 项和，911212a a =+，则13S 的值是（ ） A ．156B ．124C ．136D ．18010．在三棱锥P ABC -中，5AB BC ==，6AC =，P 在底面ABC 内的射影D 位于直线AC 上，且2AD CD =，4PD =.设三棱锥P ABC -的每个顶点都在球Q 的球面上，则球Q 的半径为（ ）A ．6898B ．6896C ．5268D ．526611．设复数z 满足|3|2z -=，z 在复平面内对应的点为(,)M a b ，则M 不可能为（ ） A ．(2,3)B ．(3,2)C ．(5,0)D ．(4,1)12．函数2sin cos ()20x x xf x x =+在[2,0)(0,2]ππ-⋃上的图象大致为( ) A ． B ．C ．D ．二、填空题：本题共4小题，每小题5分，共20分。

2025届浙江省温岭中学高三数学第一学期期末质量检测试题考生请注意：1．答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内，不得在试卷上作任何标记。

2．第一部分选择题每小题选出答案后，需将答案写在试卷指定的括号内，第二部分非选择题答案写在试卷题目指定的位置上。

3．考生必须保证答题卡的整洁。

考试结束后，请将本试卷和答题卡一并交回。

一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．如图，设P 为ABC ∆内一点，且1134AP AB AC =+，则ABP ∆与ABC ∆的面积之比为A ．14 B ．13 C ．23D ．162．给定下列四个命题：①若一个平面内的两条直线与另一个平面都平行，则这两个平面相互平行； ②若一个平面经过另一个平面的垂线，则这两个平面相互垂直； ③垂直于同一直线的两条直线相互平行；④若两个平面垂直，那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直． 其中，为真命题的是( )A ．①和②B ．②和③C ．③和④D ．②和④3．做抛掷一枚骰子的试验，当出现1点或2点时，就说这次试验成功，假设骰子是质地均匀的.则在3次这样的试验中成功次数X 的期望为（ ） A ．B ．C ．1D ．24．已知过点(1,1)P 且与曲线3y x =相切的直线的条数有（ ）． A ．0B ．1C ．2D ．35．已知函数()()f x x R ∈满足(1)1f =，且()1f x '<，则不等式()22lg lg f x x <的解集为（ ）A ．10,10⎛⎫⎪⎝⎭B ．10,10,10C ．1,1010⎛⎫⎪⎝⎭D ．()10,+∞6．已知集合{}21|A x log x =<，集合{|B y y ==，则A B =（ ）A ．(),2-∞B ．(],2-∞C ．()0,2D ．[)0,+∞7．已知曲线cos(2)||2C y x πϕϕ⎛⎫=+<⎪⎝⎭：的一条对称轴方程为3x π=，曲线C 向左平移(0)θθ>个单位长度，得到曲线E 的一个对称中心的坐标为,04π⎛⎫⎪⎝⎭，则θ的最小值是（ ） A ．6π B ．4π C ．3π D ．12π8．已知函数()32,0log ,0x x f x x x ⎧≤=⎨>⎩，则=3f f ⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭（ ） A．2B ．12C ．3log 2-D ．3log 29．设f (x )是定义在R 上的偶函数，且在(0,+∞)单调递减，则（ ）A ．0.30.43(log 0.3)(2)(2)f f f -->> B ．0.40.33(log 0.3)(2)(2)f f f -->> C ．0.30.43(2)(2)(log 0.3)f f f -->>D ．0.40.33(2)(2)(log 0.3)f f f -->>10．在ABC 中，12BD DC =，则AD =（ ） A ．1344+AB AC B ．21+33AB ACC ．12+33AB ACD ．1233AB AC -11．已知函数()[]010x x f x x x ⎧≥⎪=⎨⎪⎩，，＜（[]x 表示不超过x 的最大整数），若()0f x ax -=有且仅有3个零点，则实数a的取值范围是（ ）A ．12,23⎛⎤ ⎥⎝⎦B ．12,23⎡⎫⎪⎢⎣⎭C ．23,34⎡⎫⎪⎢⎣⎭D ．23,34⎛⎤ ⎥⎝⎦12．已知不重合的平面,,αβγ 和直线l ，则“//αβ ”的充分不必要条件是（ ） A ．α内有无数条直线与β平行 B ．l α⊥ 且l β⊥C ．αγ⊥ 且γβ⊥D ．α内的任何直线都与β平行二、填空题：本题共4小题，每小题5分，共20分。

第一学期高三数学期末质检复习题一、选择题1．若集合M={2，3}，}{Zx x N xx ∈<=-,1232，又集合P=MUN ，则集合P 的真子集的个数共有（ ）A ．6个 B.7个 C.8个 D.以上答案都不正确2．已知映射f ：A →B ，使集合B 中元素y=x+1与集合A 中元素x 对应，要使映射f ：A →B 是一一映射，那么集合A ，B 可以是（ ） A ．A=R ，B=R B.A=R ，B={y |y ≧0}C.A={x |x ≧0}，B=RD.A={x |x ≧0}，B={y |y ≧0}3．已知f(x)是定义在R 上的偶函数，且周期为2，当x ∈[2，3]时，f(x)=x ，则f （23）的值为（ ） A. 211-B. 25-C. 25D. 2114．已知θ是第三象限角，且,95cos sin 44=+θθ那么θ2sin 等于（ ）A.232-B. 232C. 32-D. 325．{a n }是等差数列，S 10>0，S 11<0则使a n <0最小的n 的值为（ ） A ．5 B. 6 C. 7 D. 86．若|a+b|=|a-b|，则向量a 与b 的关系是（ ）A. a=→0或b=→0 B.|a|=|b| C. a•b=0 D.以上都不对 7．简单随机抽样，系统抽样，分层抽样之间的共同点是（ ） A ．都是从总体中逐个抽取B ．将总体分成n 个部分，按事先确定的规则在各部分抽取C ．将总体分成几层，然后各层按比例抽取D ．抽样过程中每个个体被抽到的概率相等8．已知直线l 垂直于平面α，直线m ⊂平面β内，给出下列四个命题： ①若α∥β，则l ⊥m ②若l ∥m ，则α⊥β ③若α⊥β，则若l ∥m ④若l ⊥m ，则α∥β 其中正确的命题是（ ）A ．③与④B .①与③C .②与④D .①与②9．已知双曲线)0,0(12222 b a by a x =-与x 轴的正半轴交于A 点，F 是它的左焦点，设B 点的坐标为（0，b ），且AB ⊥BF ，则双曲线的离心率是（ ） A ．231+ B. 251+ C. 452+ D. 462+ 10．过抛物线y 2=4x 的焦点作直线交抛物线于A （x 1，y 1），B （x 2，y 2），若x 1+x 2=6，则AB的中点M 到抛物线的准线的距离等于（ ） A ．5 B. 4 C. 3 D. 2 11．定义运算a*b 为：a*b=⎩⎨⎧≤)()(b a b b a a 则关于x 的函数f(x)=x 21*的取值范围是（ ）A ．(]1,∞- B.（0，1） C. (]1,0 D.[1，+∞）12．四面体的顶点和各棱中点共10个点，从其中取4个不同的点，不共面的取法共有（ ）A ．150种 B.147种 C.144种 D.141种 二、填空题13．（理）设复数z 满足=+=+-z i z z 则,2_______（文）曲线y=24x 上有一点P ，曲线在点P 处的切线的倾斜角为135°，则P 点坐标为_______________14．设nx x ⎪⎪⎭⎫ ⎝⎛+21313展开式中的各项的系数之和为A ，各项的二项式系数和为B ，若A+B=272，则展开式中的2x 项的系数是________15．将一个直角三角形沿斜边上的高折成直二面角后两直角边的夹角为ϑ，则ϑ的最小值是_______________16．已知函数y=f(x)满足f(4)=2 ，f ’(4)= —2，则4)(424lim--→x x f x x 的值等于__________三、解答题17．已知向量a=（cos23x ，sin 23x ），b=（cos 2x ，—sin 2x ）且x ∈[0，2π] （1）求a ·b 及∣a+b∣（2）若f （x ）=λ2-⋅b a ∣a+b∣的最小值是-23，求实数入的值18．15名新生中有3名特长生，随机将15名新生平均分配到3个班组中去 （1）每班级各分配到一名特长生的概率是多少？ （2）3名特长生分配到同一班级的概率是多少？19．已知函数f（x）=16x3-20ax2+8a2x-a3，其中a≠0，求f（x）的极大值与极小值。

第一学期高三期末质量检测数学试题数 学 试 题第Ⅰ卷（选择题）一、选择题 (本大题共12小题，每小题5分，共60分；在每小题给出的四个选项中，只有一项是正确的) 1、命题|2:|-x p ≤3是命题x q :≥1-或x ≤5A ：充分非必要条件B ：必要非充分条件C ：充分必要条件D ：既非充分又非必要条件2、设)1,0()(≠>=a a a x f x为增函数，那么1log )(=x g 的图象是A B C D3、从分别写有A 、B 、C 、D 、E 的5张卡片中，任取2张，这2张卡片上的字母恰好按字母顺序相邻的概率是A ：51 B ：52C ：103D ：1074、要得到)42cos(π-=x y 的图象，只需将2sin xy =的图象A ：向左平移2πB ：向右平移2πC ：向左平移4πD ：向右平移4π5、若复数z 满足z i z i z z ⋅-⋅+⋅≤0，则复数|1|i z ++的最大值是 A ：526+ B ：15+ C ：15- D ：36、已知函数)(x f 的导数为x x x f 44)(3'-=，且图象过点)5,0(-，当函数)(x f 取得极大值5-时，x 的值为A ：1±B ：1-C ：0D ：17、下列命题中正确结论的个数有1） 若=，则ABCD 是平行四边形。

数学试题 第1页 (共9页)2） 与不共线⇔对任何实数λ都有λ≠ 3） ||||0)()(b a b a b a =⇔=-⋅+4） 在上的投影等于在上的投影⇒||||b a =A ：0个B ：1个C ：2个D ：3个8、 已知)32sin(1)12(cos )(2ππ++-=x x x f ，那么A ：)(x f 既是奇函数又是偶函数B ： )(x f 没有最小正周期C ：)(x f 没有最大值也没有最小值D ：)(x f 不是偶函数且最大值是21 9、已知定义在R 上的偶函数)(x f 在),0[+∞上是增函数，且0)31(=f ，则0)(log 81>x f 的x 的取值范围A ：),0(+∞B ：),2()21,0(+∞⋃C ：)2,21()81,0(⋃D ：)21,0(10、在等差数列{}n a 中，2511=a ，从第10项开始比1大，记t S a n n n n =+∞→)(1lim 2，则t 的取值范围是A ：754>t B ：t <758≤253C ：503754<<tD ：t <754≤50311、若不等式0log 32<-x x a 在)31,0(∈x 时恒成立，则实数a 的取值范围是A ：]271,0(B ：)1,271(C ：)271,0(D ：)1,271[12、如下图所示，教室的墙壁上挂着一块黑板，它的上、下边缘分别在学生的水平视线上方 2.4米和1.2米，现要求看黑板的竖直方向视角尽可能大些，则学生选择到墙壁的最佳距离为A ：1.3米B ：1.5米C ：1.7米D ：2.0米数学试题 第2页 (共9页)P 水平视线第一学期高三期末质量检测数 学 试 题第Ⅱ卷注意事项：1、 第Ⅰ卷答案填写在第Ⅱ卷的指定位置上2、 用蓝色(或黑色)钢笔和圆珠笔将答案直接写在试卷上3、 答卷前将密封线内的项目填写清楚，并在试卷右上角填上座位号13、一批灯泡共400只，其中20W ，40W ，60W 的数目比为1:3:4，现用分层抽样产生一个容量为40的样本，三种灯泡依次抽取的个数为_____ _____ ______。

高三第一学期期末质量抽查数学试题上海市浦东新区_届高三第一学期期末质量抽查数学试题_.1一.填空题:1. .2.函数的定义域为 .3.不等式的解集为 .4.已知,则= .5.计算: .6.函数的反函数的图像经过,则 .7.若,则 .8.(理)在极坐标系中,是极点,,则的形状为等腰直角三角形 . (文)某工程由下列工序组成,则工程总时数为天.9.有4条线段,长度分别为3,5,7,8,从这4条线段中任取3条,则所取3条线段能构成一个三角形的概率是 .10.在中,,,,则边长为 .11.方程的解的个数是个.12.有穷数列,为其前项和,定义为数列的〝凯森和〞.如果有99项的数列的〝凯森和〞为,则有项的的〝凯森和〞 .二.选择题:13.〝〞是〝〞的( )A. 充分而不必要条件B.必要而不充分条件C. 充要条件D.既不充分也不必要条件14.复数,则在复平面内的对应点位于( D )A.第一象限B. 第二象限C. 第三象限D. 第四象限15.函数的部分图象如图,则.可以取的一组值是( C )A.B.C.D.16.已知命题:函数的值域为,命题:是减函数,若或为真命题,且为假命题,求实数的取值范围是( D )A. B.C.D.或三.解答题:17.关于的方程有一实根为,设复数,求的值及复数的模.解:将代入方程,可知,∴, ,∴.18.已知集合,求解:A＝(－,),B＝,∴=.19.先阅读下列不等式的证法,再解决后面的问题: 已知,,求证:证明:构造函数,因为对一切,恒有成立,所以,从而证得.(1)若,,请写出上述结论的推广形式;(2)参考上述解法,对你推广的结论加以证明. 解:(1)若,,则.(2)证明:构造函数,∵,即恒成立,∴,即.20.现有一批货物用轮船从上海洋山深水港运往青岛,已知该船航行的最大速度为35海里/小时,上海至青岛的航行距离约为500海里,每小时运输成本由燃料费用和其余费用组成.轮船每小时使用的燃料费用与轮船速度的平方成正比(比例系数为0.6),其余费用每小时960元.(1)把全程运输成本y(元)表示为速度(海里/小时)的函数;(2)为了使全程运输成本最小,轮船应以多大速度行驶.解:(1) ()(2)先证明其在上为减函数,则时,取得最小值.答:略.21.已知在数列中,()(1)若,求;(2)(理)若是等比数列,且是等差数列,求满足的条件;(文),若是等比数列,且是等差数列,求满足的关系式;(3)一个质点从原点出发,依次按向右.向上.向左.向下的方向交替地运动,第次运动的位移是,质点到达点,设点的横坐标为,若,求.解:(1)∵,∴,,猜测.(2)(理),当＝0,显然成立;当0,,则;,当,显然成立;当,.(文),,.(3),则,∵,∴,由.22.已知函数,(1)若函数,求函数的解析式;(2)(理)若函数,函数的定义域是,求的值;(文)若函数,求函数的定义域;(3)设是定义在上的周期为4的奇函数,且函数的图像关于直线对称,当,求正数的最小值及函数在上的解析式.解:(1)∵,,∴,,(2) (理),∴的定义域是,∴,即. (文),函数的定义域是. (3) 据题意,作图如下:可知正数.函数在上的解析式了.。

高三数学第一学期期末统测试卷高 三 数 学命题人：周凯本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）部分。

满分150分，时间120分钟。

参考公式： 正棱锥、圆锥的侧面积公式 如果事件A 、B 互斥，那么 cl S 21=锥侧 P （A+B ）=P （A ）+P （B ）如果事件A 、B 相互独立，那么 其中，c 表示底面周长、l 表示斜高或 P （A ·B ）=P （A ）·P （B ） 母线长 如果事件A 在1次实验中发生的概率是 球的体积公式 P ，那么n 次独立重复实验中恰好发生k 334R V π=球 次的概率 其中R 表示球的半径k n k kn n P P C k P --=)1()(第I 卷（选择题，共60分）一． 选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的，把所选项前的字母填在题后的括号内。

1．已知集合{},22≤≤-∈=x N x A 则必有 ------------------------------------( )A A ∈-1. AB ∈0. AC ∈2. AD ∈2.2．函数a x y =的图象经过点),41,2(则该函数的图象 ------------------------- ( )A. 关于原点对称B. 关于x 轴对称C. 关于y 轴对称D. 关于直线x y =对称 3．函数)0()1lg(<-=x x y 的反函数是 ----------------------------------- ( ) )0(101.>-=x y A x )0(101.<-=x y B x )0(10.1>=-x y C x )0(10.1<=-x y D x4．在10)3(-x 的展开式中，6x 的系数为 --------------------------------------- ( )41027.C A 61027.C B - 4109.C C 6109.C D -5．将函数1)3cos(3+--=πx y 的图象沿向量)1,3(-=πa 平移后所得图象的函数表达式为 ------------------------------------ ---- ( ) 2c o s 3.A +-=x y x y B cos 3.-= )32c o s (3.π--=x y C 2)32c o s (3.+--=πx y D 6．双曲线的焦距为4，两准线间的距离为3，则双曲线的离心率为 ------------( ) 332.A 33.B 36.C 2.D 7．将5本不同的书全部分给4位同学，每人至少1本，则不同的分法种数为-----( )A. 480B. 240C. 120D. 968．111.02lg <>x x 是的 ----------------------------------------------------------( ) A ．充分而不必要条件 B. 必要而不充分条件 C. 充要条件 D. 既不充分也不必要条件 9．设b a ,为直线，γβα,,为平面，给出下列命题：① βαγβγα//,⇒⊥⊥ ② βαβα//,⇒⊥⊥a a ③ b a b a ////,,⇒⊂⊂βαβα ④ βαβα//,//a a ⇒⊂ 其中，正确的命题是------------------------------（ ） A. ①② B. ①③ C. ②④ D. ③④10．设四面体ABCD 的各棱长均相等，E ，F 分别为AC ，AD 的中点（如图所示），则△BEF 在该四面体的面ABC 上的射影是-----------------------------------( )11．若曲线x x x f -=4)(在点P 处的切线平行于直线,03=-y x 则点P 的坐标为BC ADE F (A) (B) (C) (D)-------（ ）A. (－1,3)B. (1,3)C. (－1,0)D. (1,0)12．设A ，B 是两个独立事件，“A 和B 同时不发生”的概率为，91“A 发生且B 不发生”的概率与“B 发生且A 不发生”的概率相等，则事件A 发生的概率为------------------( )181.A 92.B C. 31 D. 32第II 卷（非选择题，共90分）二． 填空题：本大题共4小题，每小题4分，共16分，把答案填在题中的横线上。

2021～2021学年度第一学期期末教学质量调研监测制卷人：歐陽文化、歐陽理複；制卷時間：二O二二年二月七日理科数学2021～2021学年度第一学期期末教学质量调研监测高三数学试题〔B〕参考答案及评分HY一、选择题 1. C2. B 【解析】(3.5)(2.51)(2.5)(1.51)(1.5)(0.51)f f f f f f =+=-=-+==+(0.5)0.5f =-=-.3. D 【解析】242pp =⇒=.4. C5. C6. B 【解析】因为26n m =，24q p π=，所以22266644n m m q p p πππ⎛⎫=== ⎪⎝⎭. 7. A()()20AB AC AO AB AO AC AO OB OC +=⇒-+-⇒+=，所以BC 为圆O 的直径. 又1AC AO ==，所以∠60C =°，∠30B =°，3BA =，所以向量BA 在BC方向上的投影为3cos 2BA B =.8. A 【解析】232015sinsinsin sin03333S ππππ=++++=.9. B 【解析】设公比为q ，因为11223412a a a ===，那么2112a q =，23112a q =，3212a q=. 由31a ，32a ，33a ，34a 成等差数列，有343132313()a a a a =+-，得1q =〔舍〕或者12q =.所以121a =，1111211(1)()2n n a a n a a =+--=，11222n nn n n n a -⎛⎫=⨯=⎪⎝⎭，所以1122339923912392222a a a a ++++=++++，由错位相减法可得112233*********a a a a ++++=.10. D 【解析】由1x =-为函数()x f x e 的一个极值点可得a c =，∴2()f x ax bx a =++.假设()f x 有两个零点1x ，2x ，那么121x x =，显然D 不合适.二、填空题11. 假设0x ≠且0y ≠，那么0xy ≠. 12. 9 13. 214. 【解析】由2sin sin sin a c bA CB ===，得 2sin a A =，2sin cC =，所以24sin 2sin 4sin 2sin(120)5sin a c A C A A A A +=+=+︒-=+， 所以2a c +=. 15 ① ③ ④ 【解析】作出两个函数的图象. 三、解答题16. 【解析】〔1〕211()cos cos 22f x a b x x x ωωω=⋅-=--11(1cos 2)2cos 2223x x x πωωω⎛⎫=+-=+ ⎪⎝⎭. 因为直线3x π=是()y f x =图象的一条对称轴，所以233k ππωπ⋅+=，31()2k k z ω-=∈，当1k =时，正数ω获得最小值1. ………6分〔2〕当1ω=时，()cos 23f x x π⎛⎫=+ ⎪⎝⎭. 由2223k x k ππππ-+≤≤，得236k x k ππππ--≤≤.所以()f x 的单调增区间236k k ππππ⎡⎤--⎢⎥⎣⎦，(Z k ∈). …………12分 17. 【解析】〔1〕取1AA 中点D ，连接BD 、1C D、1AC ，因为11A B AB AA ==，所以△1ABA 是正三角形，所以1BD AA ⊥.根据侧面11ABB A ⊥侧面11ACC A ，有BD ⊥侧面11ACC A .由12AA AC ==，平行四边形11ACC A 的面积为23，∠11AAC 为锐角，可得∠1160AAC =°，所以△11AAC 为正三角形，有11C D AA ⊥.所以1AA ⊥平面1BC D ，从而1AA ⊥1BC . …………6分〔2〕因为112A B AB AA ===，所以3BD =，所以四棱锥11B AAC C -的体积为123323V =⨯⨯= .又三棱锥111B A B C -的体积为三棱柱111ABC A B C -体积的13，所以四棱锥11B AAC C -的体积为三棱柱111ABC A B C -体积的23.从而所求的斜三棱柱111ABC A B C -的体积为3. …………12分18. 【解析】〔1〕甲答错题目数的平均数为32011.54x +++==，所以答对题目数的平均数为10 1.58.5-=，所以甲第一卷的平均得分为8.5542.5⨯=. …………6分〔2〕根据题意知点()P x y ，一共有16个：(34)，、(33)，、(32)，、(30)，、(24)，、(23)，、(22)，、(20)，、(04)，、(03)，、(02)，、(00)，、(14)，、(13)，、(12)，和(10)，. 因为2221y k y x x +=⇒+≥≥，所以符合2k ≥的点P 一共有8个：(24)，、(04)，、(03)，、(02)，、(10)，、(12)，、(13)，、(14)，.故所求的概率为81P 162==. …………12分19. 【解析】〔1〕由2211112(2)()0n n n n n n n n a a a a a a a a ++++=+⇒-+=. 因为0n a >，*N n ∈，所以120n n a a +-=，即12n n a a +=，所以数列{}n a 是首项为2，公比为2的等比数列.故2n n a =，*N n ∈. …………5分 〔2〕22(1)(1)(12)(12)n nnn n b a a a a =---=---. 1n n b b +>，即1212(12)(12)(12)(12)n n n n a a ++--->---，化简得232n a >-⋅.因为2322324n -⋅-⋅=-≤，所以4a >-时，有1n n b b +>. …………12分 20. 【解析】〔1〕由直线2y =+与圆222x y b +=相切，得1b =.由c a=222a b c =+，得2a =. 所以椭圆C 的方程为2214x y +=. …………5分〔2〕设11()P x y ，，22()T x y ，，12x x ≠，那么直线PT 的方程为122212()y y y y x x x x --=--.令0y =，得122112221212x x x y x y x x y y y y y --=-=--，所以211212x y x y OM y y -=-.因为P 、Q 两点关于x 轴对称，所以11()Q x y -，.同理可得211212x y x y ON y y --=--，所以222221122112211222121212x y x y x y x y x y x y OM ON y y y y y y ----⋅=⋅=----.因为221114x y +=，222214x y +=，所以22114(1)x y =-，22224(1)x y =-，从而 2222222221122112222212124(1)4(1)4x y x y y y y y OM ON y y y y ----⋅===--为定值. …13分21. 【解析】〔1〕32()()()(3)(2)()F x f x f x x b x c b x d c '=-=+-+-+-. 因为()F x 为奇函数，所以()()0F x F x +-=恒成立，得22(3)2()0b x d c -+-=，R x ∈.所以3b =，d c =.又(1)F t =，所以1(6)c t +-=，故5d c t ==+.所以3()(1)F x x t x =+-，2()3(1)F x x t '=+-. …………3分 ① 当1t ≥时，()0F x '≥，从而()F x 在()-∞+∞，上单调递增，无极值；② 当1t <时，221113(1)0333t t t x t x x ---+-<⇔<⇔-<<，所以()F x 在1133t t⎛⎫--- ⎪ ⎪⎝⎭，上单调递减，在13t ⎛⎫--∞- ⎪ ⎪⎝⎭，和13t⎛⎫-+∞ ⎪ ⎪⎝⎭，上单调递增，12()=(1)3(1)39t F x F t t ⎛⎫-=--- ⎪ ⎪⎝⎭极大， 12()=(1)3(1)39t F x F t t ⎛⎫-=--- ⎪ ⎪⎝⎭极小. ………7分〔2〕当26t =-时，3()27F x x x =-，根据〔1〕可知()F x 在()33-，上单调递减，在()3-∞-，和()3+∞，上单调递增，()()354F x F =-=极大，()()354F x F ==-极小.作函数()y F x =的图象，如下图. 由图可知当5454m -<<时，方程()F x m =有三个不同的实数解. …………14分制卷人：歐陽文化、歐陽理複；制卷時間：二O二二年二月七日。

2021-2021学年〔上〕高三期末质检考试制卷人：歐陽文化、歐陽理複；制卷時間：二O 二二年二月七日数 学〔文〕〔试卷满分是：150分 考试时间是是：120分钟〕一、选择题：本大题一一共12小题，每一小题5分，一共60分．在每一小题所给出的四个备选项里面，只有一项是哪一项符合题目要求的．1．集合{}5,4,3,2,1=A ，{}3≤=x x B ，那么=B A 〔 〕 A ．{}3 B ．{}21， C ．{}32，D ．{}321，，2．命题p ：假设b a >，那么22b a >；命题q ：21,0≥+>∀xx x .那么以下为真命题的是〔 〕A ．q p ∨B ．q p ∧C ．()q p ⌝∨D ．()q p ⌝∧3．函数()⎪⎩⎪⎨⎧-=,2,22xx x x f ，，00≤>x x 那么()()=1f f 〔 〕A ．0B ．21C ．1D ．24．假设y x ,满足约束条件101030x y x y x +-≤⎧⎪--≤⎨⎪+≥⎩，那么y x z 2+=的最大值为〔 〕A ．11-B ．1C ．5D ．115．锐角α满足536cos =⎪⎭⎫⎝⎛+πα，那么=⎪⎭⎫ ⎝⎛+32sin πα〔 〕 A ．2512B ．2512±C ．2524 D ．2524±6．抛物线()02:2>=p px y C 的焦点为F ，点A 在C 上，AF 的中点坐标为()2,2，那么C 的方程为〔 〕A ．x y 42=B ．x y 82=C ．xy 102=D ．x y 162=7．在长方体1111D C B A ABCD -中，2=AB ，1=BC ，11=AA ，E ，F 分别为棱11B A ，11D C 的中点，那么异面直线AF 与BE 所成角的余弦值为〔 〕A ．0B ．55 C ．23 D ．5528．在ABC ∆中，3=AB ，2=AC ，D 为BC 的中点，那么AD BC ⋅=〔 〕A ．5-B ．52-C ．25 D ．59．函数()()()33log 3log 3f x x x x =--++的局部图像大致为〔 〕A ．B ．C ．D ．10．数列{}n a 满足21=a ，221++=+n a a n n ，那么=+++2021111a a a 〔 〕 A ．1019B ．2019 C ．2110 D ．212011．双曲线()0,01:2222>>=-b a by a x E 的左，右焦点分别为21,F F ，过1F 作一条直线与两条渐近线分别相交于B A ,两点，假设A F B F 112=，OB F F 221=，那么双曲线的离心率为〔 〕A ．2B ．3C ．2D ．312．函数()()⎪⎭⎫⎝⎛≤++=212sin 2πϕϕx x f ，当⎪⎭⎫ ⎝⎛∈125,0πx 时，()0>x f ，那么⎪⎭⎫⎝⎛4πf 的最小值是〔 〕A ．1B ．2C ．12+D ．13+二、填空题：本大题4小题，每一小题5分，一共20分．13．复数32iz i-=+的一共轭复数是 ．14．直线10x y --=与圆225x y +=交于,A B 两点，那么||AB = ．15．?九章算术?将底面为矩形且有一条侧棱与底面垂 直的四棱锥称之为“阳马〞．如下图，网格纸上的小 正方形的边长为1，粗实线画出的是某一阳马的正视图 和侧视图，那么该阳马中，最长的棱的长度为 ．16．函数3()f x x x =+，对于[]0,2x ∈，都有|(1)|2xf ax e -+≤，那么实数a 的取值范围是 ．三、解答题：本大题一一共6小题，一共70分．解容许写出文字说明、证明过程或者演算步骤．17．〔此题满分是12分〕在ABC ∆中，角A 、B 、C 所对的边分别为a 、b 、c ，且222sin sin 2sin sin A B A B C +=．〔1〕求角C ；〔2〕假设cos A =，3b =，求ABC ∆的面积．18．〔此题满分是12分〕{}n a 是首项为1的等差数列，{}n b 是公比为2的等比数列，且23a b =，3123a b b b =++．〔1〕求{},{}n n a b 的通项公式；〔2〕记{}n a 的前n 项和为n S ，{}n b 的前n 项和为n T ，求满足5n T S ≤的最大正整数n 的值．19．〔此题满分是12分〕如图，在ABC ∆中，BC AC ⊥，,D E 分别为,AB AC 的中点．将ADE ∆沿DE 折起到PDE ∆的位置．〔1〕证明：BC ⊥平面PEC ；〔2〕假设22BP =BC CD =，直线BP 与平面PEC 所成的角为45︒，求四棱锥P BCED -的体积．20．〔此题满分是12分〕在平面直角坐标系中，点()2,0M -，()2,0N ，P 是平面内一点，直线PM ，PN 的斜率之积为34-． 〔1〕求点P 的轨迹方程；〔2〕设点P 的轨迹曲线为Γ，过点(1,0)E -的直线l 与Γ相交于,A B 两点，以线段AB 为直径的圆过点()1,0F ，求直线l 的方程．21．〔此题满分是12分〕 函数()2ln f x x ax =-． 〔1〕求()f x 的极值； 〔2〕当1x ≥时，()af x x≤-，求a 的取值范围．请考生在22、23题中任选一题答题，假如多做，那么按所做的第一题计分，做答时请写清题号．22．[选修44-:坐标系与参数方程]〔此题满分是10分〕在同一直角坐标系中，经过伸缩变换12x x y y⎧'=⎪⎨⎪'=⎩后，曲线C 变为曲线221x y ''+=．以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，直线l的极坐标方程为sin 3πρθ⎛⎫-= ⎪⎝⎭〔1〕求C 和l 的直角坐标方程；〔2〕过点()1,0P 作l 的垂线交C 于,A B 两点，点A 在x 轴上方，求11||||PA PB -．23．[选修45-:不等式选讲]〔此题满分是10分〕函数()|2|f x ax =+，不等式()f x a ≤的解集为{|20}x x -≤≤． 〔1〕求a 的值；〔2〕求证：对任意x R ∈，存在1m >，使得不等式1(2)(2)1f x f x m m -+≥+-成立．制卷人：歐陽文化、歐陽理複；制卷時間：二O二二年二月七日。

卜人入州八九几市潮王学校2021届高三数学上学期期末考试教学质量监测试题理〔含解析〕本卷须知：1.本套试卷分第一卷〔选择题〕和第二卷〔非选择题〕两局部.2.考试时间是是120分钟，总分值是150分.3..4全部答案在答题卡上完成，答在套本套试卷上无效第一卷〔选择题一共60分〕一、选择题：此题一共12小题，每一小题5分，一共60分.在每一小题给出的四个选项里面，只有一项为哪一项哪一项符合题目要求的. 1.全集U Z =，集合{}15A x x x =∈><-Z |或，集合{}2,1,0,1,2B =--，那么集合()U A B =〔〕 A.{}5,4,0,1--B.{}2,1,0,1,2--C.{}2,1,0,1--D.{}2,1,0--【答案】C 【解析】 【分析】根据补集和交集的求法直接求解即可. 【详解】{}51UA x Z x =∈-≤≤|，{}2,1,0,1,2B =--，所以(){}2,1,0,1U A B --=.应选：C.【点睛】此题考察补集和交集的求法，属于根底题.2.i 为虚数单位，复数z 满足()1234i z i -=-，那么复数z 在复平面内对应的点位于〔〕A.第二象限B.第三象限C.直线2110x y -=上D.直线2110x y +=上【答案】C 【解析】 【分析】 将()1234i z i -=-变形为3412i z i-=-，化简得11255z i =+，根据复数的几何意义即可判断.【详解】()12i 34i z -=-，∴34(34)(12)11212(12)(12)251155i i i i i z i i i --++====--++， 所以复数z 在复平面内对应的点的坐标为112,55⎛⎫⎪⎝⎭， 112211055⨯-⨯=，∴复数z 在复平面内对应的点在直线2110x y -=上. 应选：C.【点睛】此题考察复数的化简，考察复数的几何意义，考察运算才能，属于根底题. 3.矩形ABCD 中，2AB =，4=AD ，E ，F 分别为BC ，DC 的中点，那么AE BF ⋅=〔〕A.4B.6C.8D.10【答案】B 【解析】 【分析】首先建立平面直角坐标系，进一步利用向量的数量积的应用求出结果。