下载文档原格式
传输线的基本知识传输射频信号的线缆泛称传输线，常用的有两种:双线与同轴线。
频率更高则会用到微 带线与波导，虽然结构不同，用途各异，但其基本传输特性都由传输线公式所表征。
不妨先让我们作一个实验，在一台PNA3620上测一段同轴线的输入阻抗。
我们会发现 在某个频率上同轴线末端开路时其输入阯抗却呈现短路，而末端短路时入端反而呈现开路。
通过这个实验可以得到儿个结论或想法：首先，这个现象按低频常规电路经验看是想不通 的，因此一段线或一个网络必须在使用频率上用射频仪器进行测试才能反映其真实情况。
其二，出现这种现象时同轴线的长度力测试频率下的X/ 4或其奇数倍；因此传输线的特 性通常是与长度的波长数有关，让我们习惯用波长数来描述传输线长度，而不是绝对长度, 这样作就更通用更广泛一些。
最后，这种现象必须通过传输线公式来计算（或阯抗圆图来 查出），熟悉传输线公式或圆阁是射频、天馈线工作者的基本功。
传输线公式是由著名的电报方程导出的，在这里不作推导而直接引用其公式。
对于一 般工程技术人员，只耑会利用公式或圆图即可。
这里主要讲无耗传输线，有耗的用得较少，就不多提了。
射频器件（包括天线）的性能是与传输线（也称馈线）有关的，射频器件的匹配过程 是在传输线上完成的，可以说射频器件是离不幵传输线的。
先熟悉传输线是合理的，而电 路的东西是比较具体的。
即使是天线，作者也尽量将其看成是个射频器件来处理，这种作 法符合一般基层工作者的实际水平。
1.1传输线基本公式1. 电报方程对于一段均匀传输线，在有关书上可 查到，等效电路如图1-1所示。
根据线的 微分参数可列出经典的电报方程，解出的 结果为：• x 为距离或长度，由负载端起算，即负载端的x 为0• r= a + j 3 , r 为传播系数，a 为袞减系数，P 为相移系数。
无耗时r = jf3. —般 情况不常用无耗线來进行分析，这样公式简单一些，也明确一些，或者说理想化一些。
传输线阻抗和介电常数（实用版）目录1.传输线的基本概念2.传输线阻抗的定义和计算方法3.介电常数的定义和影响因素4.传输线阻抗和介电常数对信号传输的影响5.应用实例正文1.传输线的基本概念传输线（Transmission line）是电子工程中一种用于信号传输的电路，通常由两个平行的导线组成，分别是信号线和地线。
在信号传输过程中，导线电阻和电感等因素会导致信号衰减和失真，因此研究传输线的性质对于保证信号质量至关重要。
2.传输线阻抗的定义和计算方法传输线阻抗（Impedance）是指信号在传输线上遇到的阻力，用 Z 表示。
阻抗是电阻（R）和电感（XL）的复合，即 Z=R+jXL，其中 j 是虚数单位。
阻抗的单位是欧姆（Ω）。
传输线阻抗的计算方法通常采用波动方程法。
对于一条均匀传输线，波动方程可以表示为：Z = √(L/C) * exp(-j * β * l)，其中 L 是传输线的电感，C 是传输线的电容，β是相速，l 是传输线的长度。
3.介电常数的定义和影响因素介电常数（Dielectric constant）又称相对电介质常数，是用来描述绝缘材料在电场中极化程度的物理量。
介电常数的大小反映了介质在电场作用下产生极化的能力。
介电常数的单位是真空介电常数，通常用 K 表示。
介电常数的大小受多种因素影响，如材料性质、温度、电场强度等。
不同材料的介电常数差异很大，例如空气的介电常数约为 1，而硅的介电常数约为 10000。
4.传输线阻抗和介电常数对信号传输的影响传输线阻抗和介电常数对信号传输有重要影响。
首先，阻抗会影响信号的衰减和传输速率。
当传输线阻抗与信号源阻抗不匹配时，会导致信号反射，从而降低信号传输的质量。
其次，介电常数会影响传输线的电容和电感，进而影响阻抗。
对于高频信号传输，介电常数较小的绝缘材料具有更好的传输性能。
5.应用实例在实际应用中，传输线阻抗和介电常数的研究对于设计和优化通信系统、射频电路和信号传输线路具有重要意义。
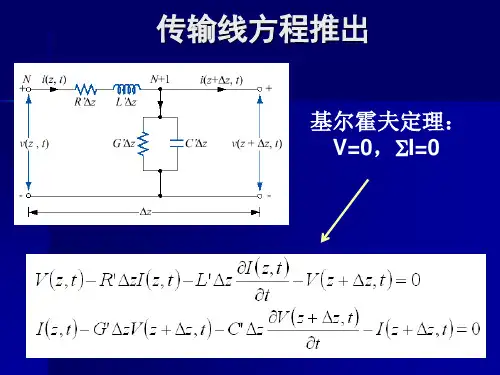
传输线方程（Transmission Line Equations），也被称为电报方程（Telegrapher's Equations），是一组描述传输线上任意点电压和电流与传输线一次参数之间关系的微分方程组。
在均匀传输线的情况下，传输线方程的一般形式为：
- dV/dz = -R*I - L*dI/dt （电压对距离的微分等于负的电阻乘以电流减去电感乘以电流对时间的微分）
- dI/dz = -G*V - C*dV/dt （电流对距离的微分等于负的电导乘以电压减去电容乘以电压对时间的微分）
其中，V 是电压，I 是电流，z 是传输线的长度，R、L、G、C 分别是传输线单位长度的电阻、电感、电导和电容，t 是时间。
这两个方程分别描述了电压和电流在传输线上的变化情况。
第一个方程表示电压沿传输线方向的变化率与电流和电流的变化率有关，第二个方程表示电流沿传输线方向的变化率与电压和电压的变化率有关。
传输线方程是研究传输线上电压、电流的变化规律以及电压
和电流之间关系的重要工具。
通过解这组微分方程，可以得到传输线上任意点的电压和电流随时间变化的规律，以及电压和电流之间的相位关系等信息。
传输线公式整理1.传输线方程传输线方程 波动方程 通解⎪⎪⎩⎪⎪⎨⎧-=-=)()()()(11z U C j dz z dI z I L j dz z dU ωω ⎪⎪⎩⎪⎪⎨⎧=+=+0)()(0)()(222222z I dz z I d z U dz z U d ββ ⎪⎩⎪⎨⎧-=+=--)(1)()(21021z j z j z j z j e A e A Z z I e A e A z U ββββ终端边界条件()()⎪⎪⎩⎪⎪⎨⎧-=+=-l j lj e I Z U A e I Z U A ββ202220212121 ⎪⎪⎩⎪⎪⎨⎧+=--+=+=-++=--)'()'(22)'()'()'(22)'('0202'0202'202'202z I z I e Z I Z U e Z I Z U z I z U z U e I Z U e I Z U z U r i z j z j r i z j z j ββββ ⎪⎩⎪⎨⎧+=+='cos 'sin )'('sin 'cos )'(202202z I z Z U j z I z I jZ z U z U ββββ 始端边界条件()()⎪⎪⎩⎪⎪⎨⎧-=+=101210112121I Z U A I Z U A ⎪⎪⎩⎪⎪⎨⎧+=--+=+=-++=--)()(22)()()(22)('0101'0101'101'101z I z I e Z I Z U e Z I Z U z I z U z U e I Z U e I Z U z U r i z j z j r i z j z j ββββ ⎪⎩⎪⎨⎧+-=-=zI z Z U j z I z I jZ z U z U ββββcos sin )(sin cos )(1011012.特性参数传输线公式整理相位常数 相速度 相波长11C L ωβ= 111C L dt dz v p ===βω rp p T v ελβπλ02===特性阻抗 驻波系数 行波系数110)()()()(C L z I z U z I z U Z r r i i =-== Γ-Γ+===11min max min max I I U U ρ ρ1=K 输入阻抗'cos 'sin 'sin 'cos )'()'((202202z I z Z U j z I jZ z U z I z U Z in ββββ++==输入阻抗与负载阻抗的关系'')'(000z tg jZ Z z tg jZ Z Z z Z L L in ββ++= 周期性：)'()2/'(z Z m z Z in g in =+λ反射系数(反射系数与该参考面的输入阻抗有一一对应的关系）电压、电流反射系数：)'()'()'(z U z U z i r V =Γ ； )'()'()'(z I z I z i r I =Γ )'()'(z z I V Γ-=Γ)]'(1)['()'()]'(1)['()'(z z I z I z z U z U Γ-=Γ+=++终端、任意点反射系数：'2)'(z j L e z β-Γ=Γ； 20ϕj L L L L e Z Z Z Z Γ=+-=Γ )'2(2)'(z j L e z βϕ-Γ=Γ周期性： )'()2'(z mz gΓ=+Γλ反射系数与驻波系数关系：ρρ+-=Γ11 反射系数与阻抗关系⎪⎪⎩⎪⎪⎨⎧+-=ΓΓ-Γ+=000)'()'()'()'(1)'(1)'(Z z Z Z z Z z z z Z z Z z'=0时，负载情况 ⎪⎪⎩⎪⎪⎨⎧+-=ΓΓ-Γ+=00011Z Z Z Z Z Z L LLL L L传输功率传输线公式整理())()()(12)()(22z P z P z Z z U z P rii -=Γ-=电压波腹点 K Z U IU z P 02max minmax2121)(==传输线功率容量 K Z U P brbr 0221=3。
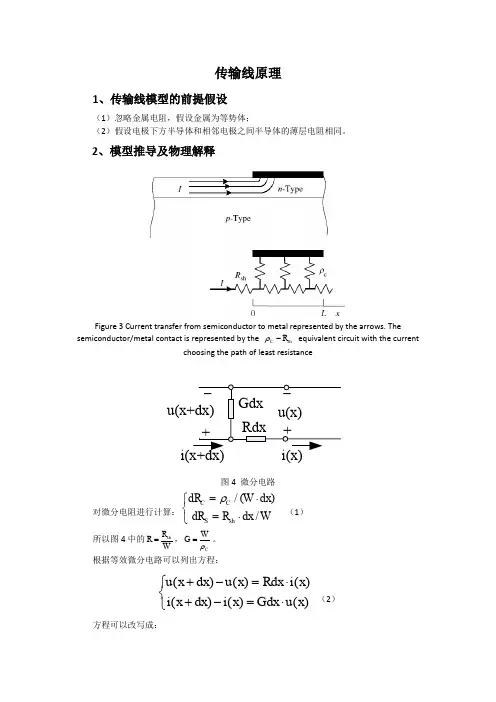
传输线原理1、传输线模型的前提假设（1）忽略金属电阻，假设金属为等势体；（2）假设电极下方半导体和相邻电极之间半导体的薄层电阻相同。
2、模型推导及物理解释Figure 3 Current transfer from semiconductor to metal represented by the arrows. Thesemiconductor/metal contact is represented by the C sh R ρ- equivalent circuit with the currentchoosing the path of least resistance图4 微分电路对微分电阻进行计算：/()/C C S sh dR W dx dR R dx Wρ=⋅⎧⎨=⋅⎩ （1）所以图4中的sh R R W=，C W G ρ=。
根据等效微分电路可以列出方程：()()()()()()u x dx u x Rdx i x i x dx i x Gdx u x +-=⋅⎧⎨+-=⋅⎩ （2） 方程可以改写成：()()()()du x Ri x dxdi x Gv x dx⎧=⎪⎪⎨⎪=⎪⎩ （3） 写成二阶常微分方程的形式：222222()()0()()0d u x u x dx d i x i x dx αα⎧-=⎪⎪⎨⎪-=⎪⎩ （4） 该常微分方程组的通解形式为：12120()()x x x x u x A e A e A e A e i x Z αααα--⎧=+⎪-⎨=⎪⎩（5）其中，0Z ==1、当给定边界条件0x =处电压、电流分别为1U 、1I 时，代入通解中求出系数得出最终解（部分文献给出这样的形式）：11011011011000()22()22x x x x U I Z U I Z u x e e U I Z U I Z i x e e Z Z αααα--+⋅-⋅⎧=+⎪⎪⎨+⋅-⋅⎪=-⎪⎩（6） 将解的形式改写成双曲函数的形式：110110()cosh sinh ()cosh sinh u x U x I Z x U i x I x x Z αααα=+⋅⎧⎪⎨=+⎪⎩（7）2、如果给定边界条件0x =处电流为(0)0i =，x L =处电流为()i L I =，可以求得系数为0122sinh I Z A A Lα⋅==，最终解为（部分文献给出这样的形式）：0()cosh sinh I Z u x x Lαα⋅= （8）由于图4中的x 坐标定在接触电极的右端，改成接触电极的左端，上述方程应该变成：()cosh ()sinh I Z u x L x Lαα⋅=- （9）电压曲线在图5中画出，可以看出当电流从半导体流入金属时，接触电极下方的电压随着x 轴的方向而衰减，当电压衰减到1/e 时的位置称为电流的扩散长度，有1T L α==扩散长度可以看成电流从半导体流入金属时，在电极下方大部分电流扩散的距离。
传输线基本公式1、电报方程对于一段均匀传输线，在有关书上可查到，等效电路如下图所示。
Z i V1V2Z2等效电路根据线的微分参数可列出经典的电报方程，解出的结果为：V1=21(V2+I2Z0)eγχ+21(V2－I2Z0)e-γχI1=Z21(V2+I2Z0)eγχ-0Z21(V2－I2Z0) e-γχ式中，x是传输线上距离的坐标，它由负载端起算，即负载端的x为0。
γ为传输线的传输系统，γ=α+jβ，α为衰减常数，β为相移常数。
无耗时γ=jβ。
一般情况下常用无耗线来进行分析，这样公式简单一些，也明确一些，或者说理想化一些。
而这样做实际上是可行的，真要计算衰减时，再把衰减常数加上。
Z0为传输线的特性阻抗。
Z i为源的输出阻抗（或源内阻），通常假定亦为Z0；若不是Z0，其数值仅影响线上电压的幅度大小，并不影响其分布曲线形状。
上述两式中，前一项x 越大值越大，相位也越领先，即为入射波。
后一项x 越大值越小，相位也越落后，即为反射波。
由于一般只对线上的电压、电流的空间分布感兴趣，因此上式中没有写时间因子e j ωt(下同)。
2、无耗线上的电压电流分布上面式（1.1）和式（1.2）中，下标2为负载端，下标1为源端，而x 可为任意值，那么V 1、I 1可以泛指线上任意一点的电压与电流，因此下面将V 1、I 1的下标1字省掉。
V=21(V 2+I 2Z 0)ej βχ+21(V 2－I 2Z 0) e-j βχ=21(V 2+I 2Z 0)ej βχ｛1+Γe-j (2βχ－ψ)｝I=21｛ (V 2+I 2Z 0)/ Z 0｝ej βχ｛1－Γe-j (2βχ－ψ)｝式中，发射系数Γ＝Γ∠ψ＝22022Z I V Z I V +-＝202Z Z Z Z +-Γ≤1，要想反射为零，只要Z 2 =Z 0即成。
上式中，首项不是x 的函数，而e j βχ为相位因子，不影响幅度。
只是末项影响幅度分布。
现在让我们看看电压分布：V x ＝V(1+Γe-j (2βχ－ψ)显然：2βx －ψ＝０或２Ｎπ时，电压最大，V MAX =V （1+Γ） 2βx －ψ＝π或（２Ｎ－1）π时，电压最小，V MIN =V （1－Γ）驻波比 ρ=MINMAX V V =T-T +11当Γ＜＜ 1时，ρ=1+2Γ，有时也会用到Γ=(ρ-1)/2。
驻波比ρ是天馈线中最常见的一个技术指标，英文缩写为SWR ，也有用VSWR ，即强调是电压之比。
线上电压因反射的存在而出现有高有低的现象并不是我们希望的，我们希望Γ→0，也就是ρ→1。
一般应用时ρ≤1.5即可，有的场合要求ρ≤1.1。
也有人用行波系数（即驻波比的倒数）来描述线上的反射状态，应该说是很合理的，因为它避免了∞的出现，但由于传输线上电压最小点的输入阻抗为Z 0/ρ（见式（1.16）），而最大点的输入阻抗为ρZ 0（见式（1.15）），因此用ρ还是有实际意义的。
至于真正驻波比与行波的概念请参见本章1.4节之5，一般只要求知道指标所代表的含义以及合格范围即可。
作为运算，用反射系数Γ更合适一些。
也有人定义返回损失（回损）RL 为： RL=20㏒Γ (dB)返回损失（Return Loss,RL ）也有人译成回波损耗。
由于Γ≤1，因此为负值，但习惯上不管这个负号，有时会讲出驻波比多少dB 之类的话，其实是在讲回损。
不同行业有不同的习惯用语，驻波比ρ、回损RL 与反射系数Γ的常用数值见附录D 。
3、对特性阻抗Z 0的理解 （1）Z 0的定义 在解电报方程中令 Z 0=Lj G L j R ωω++式中R 为传输线单位长度的电阻（导体本身电阻与长度的比值）；L 为传输线单位长度的电感（导体本身电感与长度的比值）；G 为传输线单位长度的电导（两导体间的电导与长度的比值）； C 为传输线单位长度的电容（两导体间的电容与长度的比值）。
在频率较低时，Z 0随频率而变化，频率高时（射频） Z 0≈CL /Z 0就与频率关系不大了。
通常Z 0在射频端是用测一段传输线的电感与电容后算出的，直接测Z 0是测不出来的。
（2）Z 0是一种结构尺寸决定的电参数 如同轴线的Z 0为 Z 0=rε60㏑dD式中，εr 为同轴线内充填介质的相对介电常数；D 为外导体内径；d 为内导体外径，如上图所示。
双线的Z 0为Z 0=120㏑⎥⎦⎤⎢⎣⎡-+1)/(2d D dD ≈120㏑(2D/d)式中，D 为两导线之间的中心距；d 为导线直径，如上图所示。
其他形状的传输线的Z0可查其他书如[2]得到其计算公式或图表。
尺寸均匀的传输线本身不产生反射，只是在尺寸不连续处才会产生反射。
2、常用同轴电缆的型号代码²第一个字母一般为S，即同轴射频电缆之意。
²第二个字母代表绝缘种类：Y为聚乙烯，F为氟塑料，D为稳定聚乙烯支撑的空心电缆，U为聚四氟乙烯等。
²第三个字母表示护套材料：V为聚氯乙烯，B为编织套，T为半硬铜管等。
其他最好见产品说明。
字母后为用连接号（口语称扛，也有称划的）分开的数字。
Δ第一组数字一般不是50就是75，表示特性阻抗。
Δ第二组数字表示外导体内径（或绝缘支撑的外径）。
Δ第三组数字为结构序号。
如一般最常用的电缆为实心聚乙稀绝缘的SYV-50-3，它比较便宜，比较软，但屏蔽性能不太好。
好一些的为氟塑料的SFF-50-3，但价格贵10倍。
内部连线在频率较高时（比如2GHz以上）最好采用半硬同轴线SFT系列或半软SM系列。
功率较大时只好用皱纹铜管SDY系列。
电缆越粗，损耗越小，但不能粗到同轴线平均周长等于使用波长(请见下式)，此时将出现搞次模，破坏正常工作。
πeε(D+d)/2=λ式中，eε为有效相对介电常数；d与D分别为内外导体直径。
3.1 辐射的基本知识 1.电流元的远区电场强度由麦氏方程可解出一小段电流元在远区的场强为 E θ=jλrπIdl 60Sin θe-j βrH Φ= E θ/120π式中，假定电流元强度为I ，长度为dl →0（用箭头→表示趋于，下同），放在球坐标原点Z 轴上。
由于性能与方位角φ无关，为绘图简单起见，只在Y0Z 平面内来看上式说明电场方向为θ方向，而磁场只有φ分量，在远区磁场与电场只差一个常数，因此只需要研究电场即可。
上式中无e j ωt 项，因为研究天线时只对空间特性感兴趣，故省去了时间项。
上式说明只要有一小段线上有电流在来回流动，则远处某一点不但有电场，而且大小都可用公式算出。
两点之间不用线即可联系，这就是无线电的基础，这就叫辐射。
这里我们直接有文献[10]中引用了电流线元辐射公式，它是个基础。
任何线天线都可看成是一小段一小段连成的；正如面天线式面电流元组成的一样。
线元与面元是基础，经过数学处理，可以进行多种天线的理论设计。
但这里只是引出个辐射概念，由此引出天线的基本参数。
按实验研究的方法对常规天线进行开发或研制，不涉及过多的理论。
2.为什么双线传输线基本不辐射双线示意图一段开路的双线传输线，若长度为λ/4，则其输入阻抗Z ab→0，它上面有电流，为什么辐射不大呢？由于双线对称，两根线上的电流幅度相等，但方向相反。
在远区P点，由于距离很远，可简化为r2=r1+DSinθ，而DSinθ很小，因此不影响幅度，只影响相位。
这一项叫程差或路径差，假若D〈〈λ的话，则两根线在远区的辐射基本相消（或者就说基本不辐射）。
假如D继续增大，或频率继续增高，再用双线传输线就不行了，双线仅用于较低频段。
3.半波振子的出现作为传输线希望辐射越小越好，但作为天线就希望加强辐射。
假如我们将前述λ/4开路线掰开成180°（共线），即形成了一个半波振子（也称偶极子dipole），上下两段电流原本式反向的，现在变成同方向了，如下图，因此两段电流在远区的电场叠加了起来。
若线很细，上面电流分布为正弦波。
通过电流元辐射公式对Idl积分可得半波振子场强为E (θ)=j rI 60³θθπsin )cos 2cos(e-jβr此公式可参见文献[10]入阻抗Z ab 约73Ω左右，这可以由计算得到，计算得出的数据差别不大，而由于引出得结构不同，实测结果会大相径庭。
实用中以测试为准。
半波振子时对称线天线中得以种最基本的结构，经常会用到它。
3.收发互易性一个常规的天线（即其中并未加入开关器件，或不可逆器件），它在作发射与作接收时，所表现出的特性时相同的，这叫收发互易性，譬如测一个天线的方向图，可以在作发射天线时测，也可在作接收天线时测，看怎样作方便怎样有利于测试精度即可。
下面对天线的描述通常是当成发射天线来讲的。
3.2天线方向图 1.什么叫天线方向图天线向各个方向的辐射通常都是不同的，在自由空间形成了一个立体波束，譬如半波振子的立体波束就像一个苹果形，沿振子方向的辐射凹进去，甚至小到零。
可是用立体波束表示是不方便的，因此用两个剖面来表示是适宜的。
让我们采用常用的球坐标而让半波振子与Z 轴重合，中心落在原点上，这时两个剖面就很好画了；在方位面上（即XOY 面上，或θ=90°面上）立体波束的剖面为一个圆。
而沿Z 轴剖开垂直方向图为8字形，如下图。
由于垂直方向图不是φ的函数，立体波束是绕Z轴的旋转对称体。
假如半波振子水平放置，则水平面为8字形，而垂直在自由空间为圆。
实际上，由于脱离不了地球，不管怎样放置由地面反射干涉会形成多种花瓣，实际的垂直方向图是比较复杂的，而水平方向图与自由空间差别不大。
方向图又称波瓣图，有时称为场型。
用公式来表示的话，对于简单可分离变量情况F(θ,φ)=F(θ) ³F(φ)式种，F（θ,φ）为立体波束；F(θ)为垂直波束；F(φ)为水平波束。
对于不好分离变量情况F(θ)=F(θ,φ=CF(φ)=F(θ=C，φ)式中，C表示某一常数，一般为0或90°，通常是取最大值方向。
垂直方向图是不太好测的，办得到的话只需将天线转90°来测试即可。
水平方向图式比较容易测的，但θ=0的条件不易满足，尤其是有地面影响以后，因为真正θ=0时是收不到信号的，只好用θ为某一角度的锥面来替代，雷达天线的实际情况就是如此。
由于方向图绘制在极坐标上类似花瓣，常称波瓣图，方向图在极坐标上是很直观的，但不太好画，常用直角坐标来绘制。
2.方向图的基本类型（1）水平方向图主要有两大类：²全向波束所谓全向即方位面3600内基本是均匀的；一般用于电视、广播或中心基地台。
通常场强不均匀性在±3dB以内是足够的，更高要求，似无必要。
²定向类对于某些系统，服务可能是分区的，而对于雷达类则由于要求定位精度高，则希望方位面内波束尽量窄，甚至为了跟踪还会要求同时存在差波束（利用差波束的零点附近很尖锐，来提高定向精度）。
