【有理数概念复习(期中复习)
- 格式:ppt
- 大小:1.16 MB
- 文档页数:60
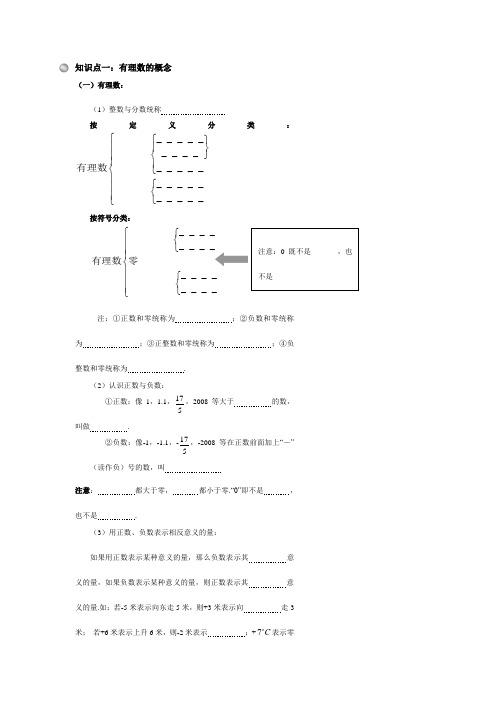
知识点一:有理数的概念(一)有理数:(1)整数与分数统称按定义分类:_______________⎧⎧⎫⎪⎪⎬⎨⎭⎪⎪⎪⎨⎩⎪⎧⎪⎨⎪⎩⎩_ _ _ _ _ _ _ _ _有理数 _ _ _ _ __ _ _ _ _ _ _ _ _ _ 按符号分类:__________⎧⎧⎨⎪⎩⎪⎪⎨⎪⎧⎪⎨⎪⎩⎩_ _ _ _ _ _ _ _有理数零_ _ _ _ _ _ _ _注:①正数和零统称为 ;②负数和零统称为 ;③正整数和零统称为 ;④负整数和零统称为 .(2)认识正数与负数:①正数:像1,1.1,175,2008等大于 的数,叫做 .②负数:像-1,-1.1,-175,-2008等在正数前面加上“-”(读作负)号的数,叫注意: 都大于零, 都小于零.“0”即不是 ,也不是 .(3)用正数、负数表示相反意义的量:如果用正数表示某种意义的量,那么负数表示其 意义的量,如果负数表示某种意义的量,则正数表示其 意义的量.如:若-5米表示向东走5米,则+3米表示向 走3米; 若+6米表示上升6米,则-2米表示 ;+7C 表示零注意:0既不是_______,也不是____上7C ,-7C 则表示.(4)有理数“0”的作用:作用举例表示数的性质0是自然数、是有理数、是整数表示没有3个苹果用+3表示,没有苹果用0表示表示某种状态00C表示冰点表示正数与负数的界点0非正非负,是一个中性数(二)数轴(1)概念:规定了、和的直线注:①、、称为数轴的三要素,三者缺一不可.②单位长度和长度单位是两个不同的概念,前者指所取度量单位的,后者指所取度量单位的,即是一条人为规定的代表“1’的线段,这条线段,按实际情况来规定,同一数轴上的单位长度一旦确定,则不能再改变.(2)数轴的画法及常见错误分析①画一条水平的;②在这条直线上适当位置取一实心点作为:③确定向右的方向为,用表示;④选取适当的长度作单位长度,用细短线画出,并对应标注各数,同时要注意同一数轴的要一致.⑤数轴画法的常见错误举例:错例原因不统一没有 (3)有理数与数轴的关系一切有理数都可以用数轴上的 表示出来.在数轴上,右边的点所对应的数总比左边的点所对应的数 ,正数都大于 ,负数都小于 ,正数大于一切负数.注意:数轴上的点不都是有理数,如π.(三)相反数(1)相反数:只有 的两个数互称为相反数.特别地,0的相反数是;若a 与b 互为相反数,则___a b += ,反之亦然 .(2)相反数的性质:①代数意义:只有 的两个数叫做互为相反数,特别地,O 的相反数是0.相反数必须 出现,不能单独存在.例如+5和 互为相反数,或者说+5是 的相反数,-5是 的相反数,而单独的一个数不能说是 .另外,定义中的“只有”指除 以外,两个数 ,注意应与“只要符号不同”区分开.例如+3与-3互为相反数,而+3与-2虽然不同,但它们不是相反数.②几何意义:一对相反数在数轴上应分别位于 两侧,并且到原点的 相等.这两点是关于 对称的.③求任意一个数的相反数,只要在这个数的前面添上“”号即可.一般地,数a的相反数是;这里以a表示任意一个数,可以为、、负数,也可以是任意一个代数式.注意-a不一定是.注意:当a>0时,-a 0(正数的相反数是数);当a=0时,-a O(0的相反数是);当a<0时, a O (负数的相反数是).④互为相反数的两个数的和为,即若a与b互为,则a+b=0,反之,若a+b=O,则a与b互为.⑤多重符号的化简:一个正数前面不管有多少个“+”号,都可以全部;一个正数前面有个“-”号,也可以把“-”号全部去掉;一个正数前面有个“-”号,则化简后只保留一个“-”号,即“负正”(其中“奇偶”是指正数前面的“”号的个数的,“负正”是指化简的最后结果的.(四)绝对值(1)绝对值的代数意义及几何意义①绝对值的代数意义:一个正数的绝对值是;一个负数的绝对值是它的;0的绝对值是.②绝对值的几何意义:一个数a的绝对值就是数轴上表示数a的与的距离.数a的绝对值记作.注意:①取绝对值也是一种 ,这个 符号是“ ”,求一个数的绝对值,就是根据性质 绝对值符号.②绝对值具有 性,取绝对值的结果总是 .③任何一个有理数都是由 部分组成: 和它的 ,如:-5,符号是 ,绝对值是 .(2)字母a 的绝对值的分类___,()___,(0)___,(0)a o a a a >⎧⎪==⎨⎪<⎩ 或___,(0)___,(0)a a a ≥⎧=⎨<⎩ 或___,(0)___,(0)a a a >⎧=⎨≤⎩ (3)利用绝对值比较两个负有理数的大小规则:两个负数,绝对值大的反而 .步骤:①计算两个负数的 .②比较这两个 的大小.③写出正确的判断结果.④如果若干个非负数的和为0,那么这若干个非负数都必为 .例如:若0,____,_a b c a b c ++====则 知识点二:有理数运算(一)有理数比较大小(1)数轴上的数,右边的数总 左边的数.(2)正数大于0,负数小于0,正数大于负数;(3)两个负数,绝对值大的反而 ;(4)两数比较大小,可按符号情况分类:0⎧⎧⎨⎪⎩⎪⎪⎨⎪⎧⎪⎨⎪⎩⎩同正:__________大的数大两数同号同负:__________大的反而小比较大小两数异号(一正一负):______大于_______正数与0:_______大于0其中有时负数与0:_______小于0(二)有理数的加减法(1)有理数加法法则①同号两数相加,取相同的 ,并把绝对值 .②绝对值不相等的异号两数相加,取 的加数的符号,并用较大的 减去较小的 .③一个数同0相加,仍得 .(2)有理数加法的运算步骤法则是运算的依据,根据有理数加法的运算法则,可以得到加法的运算步骤:①确定和的 ;②求和的绝对值,即确定是两个加数的绝对值的 .(3)有理数加法的运算律①两个加数相加,交换加数的位置, 不变.即a+b=b+a(加法律)②三个数相加,先把前两个数相加,或者先把后两个数相加,不变.即(a+b)+c=a+(b+c)(加法律)(4)有理数加法的运算技巧①分数与小数均有时,应先化为形式.②带分数可分为与两部分参与运算.③多个加数相加时,若有互为相反数的两个数,可先结合得④若有可以凑整的数,即相加得整数时,可先结合.⑤若有同分母的分数或易通分的分数,应先结合在一起.⑥相同的数可以先结合在一起.(5)有理数减法法则减去一个数,等于,即a-b=a+( )(6)有理数减法的运算步骤①把减号变为加号(改变运算符号)②把减数变为它的相反数(改变性质符号)③把减法转化为加法,按照加法运算的步骤进行运算.(7)有理数加减混合运算的步骤①把算式中的减法转化为加法;②省略加号与括号;③利用运算律及技巧简便计算,求出结果.注意:根据有理数减法法则,减去一个数等于加上,因此加减混合运算可以依据上述法则转变为只有的运算,即变为求几个正数,负数和0的和,这个和称为代数和.为了书写简便,可以把加号与每个加数外的括号均省略,写成省略加号和的形式,例如:(+3)+(-0.15)+(-9)+(+5)+(-11)=3-0.15-9+5-11,它的含义是正3,负0.15,负9,正5,负11的和。

人教版八年级上册数学期中复习知识点总结一、数与式1. 有理数- 概念:有理数是可以表示为两个整数比值的数,包括整数、分数、小数。
- 分类:正有理数、负有理数、零。
- 运算:加法、减法、乘法、除法。
2. 实数- 概念:实数包括有理数和无理数。
- 分类:正实数、负有实数、零。
- 运算:同有理数。
3. 代数式- 概念:代数式是由数字、字母和运算符组成的式子。
- 分类:单项式、多项式。
- 运算:加法、减法、乘法、除法。
二、方程与不等式1. 一元一次方程- 概念:未知数的最高次数为1的方程。
- 解法:移项、合并同类项、化简。
2. 不等式- 概念:表示两个数大小关系的式子。
- 解法:同方程,但需要考虑符号。
3. 二元一次方程组- 概念:含有两个未知数的一次方程组。
- 解法:代入法、消元法。
三、图形与几何1. 平面几何- 点、线、面的基本概念。
- 直线、射线、线段的性质。
- 平行线、垂线的性质。
- 三角形、四边形、圆的性质。
2. 立体几何- 平面、直线、点在立体几何中的扩展。
- 三视图。
- 柱体、锥体、球体的性质。
四、统计与概率1. 统计- 数据收集、整理、描述。
- 平均数、中位数、众数、方差。
2. 概率- 随机事件、必然事件、不可能事件。
- 概率的计算。
以上为八年级上册数学期中复习的知识点总结,希望能帮助同学们更好地复习和掌握数学知识。

初一数学期中复习,有理数专题基础是关键,计算要细心期中考试已经陆续开始了,作为初一的学生来说,是升入初中第一次比较大型的考试,对于学生和家长而言也是非常的重视,由于刚进入初中,课程进度相对而言还是比较轻松的,本次考试大部分地方的重点还是在第一章有理数,对于有理数的这一章,考察最多的还是对于概念等基础知识的考察,不管是绝对值的应用,还是有理数的运算,都必须掌握基础,因此复习有理数这一章,一定要抓住基本的概念,法则,运算律,然后进行综合的运用。
有理数的相关概念有:有理数、数轴、相反数、绝对值、倒数等。
对于有理数要特别注意的是0既不是正数也不是负数。
对于有理数的分类要掌握扎实,按照定义看清楚是按照正负数分类还是按照整数、分数分类,这部分常考的题型一般是选择题进行判断选择,填空题根据给定的数,写到相应的集合中,因此同学们一定要分清楚,不漏解不多写。
对于数轴、相反数和绝对值,经常会结合起来考察,而考察的根源还是在与对于概念的掌握。
数轴作为数形结合思想比较重要的工具,同学们在做题的时候一定要善于运用,不管是有理数比较大小,还是计算距离,借助于数轴都会非常的简单,而在相反数中,对于题目中给定a与b互为相反数,一般会写成a+b=0,进行使用,特别注意,0的相反数是0.绝对值的判断法则和性质绝对是本章的重点和难点,更是考点,正数的绝对值是它本身;负数的绝对值是它的相反数;0的绝对值是0。
(互为相反数的两个数的绝对值相等。
)而在有理数的运算中,首先要掌握加法和乘法的运算法则,对于减法只需要转变成加法、除法转变成乘法来进行运算即可,而不管是什么运算,引入负数之后,首先要做的就是先判断结果的符号,然后进行绝对值的计算,判断符号这点尤其重要,很多同学由于开始的时候不是非常的熟练,符号经常会弄错了,因此现阶段一定要细心仔细,这类题目并不是很难,要做的就是细心计算,熟练掌握法则,而对于运算律的运用,则可以让运算过程变得简便。


有理数全章复习理解有理数的概念和性质:有理数是指可以表示为两个整数的比值的数,这里的整数可以是正整数、负整数或零。
有理数的性质主要包括有理数的加减乘除运算性质、有理数大小的比较,以及有理数的乘方、开方运算等。
一、有理数的加减乘除运算性质:1.有理数的加法性质:-交换律:a+b=b+a-结合律:(a+b)+c=a+(b+c)-存在零元素:a+0=a-存在相反元素:a+(-a)=02.有理数的减法性质:-减法的定义:a-b=a+(-b)-减法与加法的关系:a-b=a+(-b)3.有理数的乘法性质:-交换律:a*b=b*a-结合律:(a*b)*c=a*(b*c)-分配律:a*(b+c)=a*b+a*c4.有理数的除法性质:-除法的定义:a÷b=a*(1/b)二、有理数的大小比较:1.同号比大小:正数大于负数,负数小于正数;正数之间、负数之间,绝对值大的数大。
2.异号比大小:两个数绝对值相比,绝对值大的数小。
三、有理数的乘方和开方运算:1.有理数的乘方:-正数的指数性质:a^m*a^n=a^(m+n)-负数的指数性质:a^(-m)=1/a^m-零的指数性质:a^0=1(a≠0)- 乘方的分配律:(ab)^n = a^n * b^n2.有理数的开方:-非负数的开方:√a*√a=a(a≥0)- 开方的分配律:√(ab) = √a * √b有理数的应用:1.在数轴上表示有理数:-正数表示:从0向右的数轴上的点表示,数值与点的位置对应。
-负数表示:从0向左的数轴上的点表示,数值与点的位置对应。
-零的表示:数轴上的0点表示。
2.数与有理数的运算:-数的加减法:将数转换为有理数进行运算。
-有理数与有理数的加减法:按照有理数的加减法规则进行运算。
3.比例与比例运算:-比例的定义:两个比例相等叫做比例,表示为a:b=c:d。
- 比例的性质:比例的两个比值相等,乘法性质:a:b = ac:bd。
-比例方程的解法:根据比例的性质,设置比例方程求解。

期中复习 第二章 有理数 1.有理数的概念班级:____________ 姓名:____________ 学号:____________ 评价:________【随堂练习】1、收入200元记作+200,那么-100表示_____________________2、2、)2(--, 3.5 , 54, -.35, 5.2-- , 22-,0 这些数中 正数有________________ 负数有___________分数有__________________整数有_______________________非正整数____________________,非负整数有_________________3、下面给出四条数轴,有错误的有 ( )4, 221, -|-4|, 0,3.55、 在数轴上,原点右边的点表示______,左边的点表示______.6、正数的绝对值是________,负数的绝对值是______,零的绝对值是_____绝对值最小的数是_______绝对值等于本身的是______绝对值是其相反数的是_______ 2-的相反数是____ 若x =5,那么x=_____7、用“﹤”“﹥”或“=”填空:-6 6,-1 -10 ,-︱-0.4︱ (-4) 8、=--)3( , 3--= ,2)3(-= , 23-=2)32(= 322= 2)32(-= 10科学记数法表示250 200 000 00011、把101022.1⨯还原成原数为 .12、若2-x +2)5(-y =0,求2y【课后巩固】1、检查商店出售的袋装白糖,白糖加袋按规定重g 503,一袋白糖重g 502,就记作g 1-,如果一袋白糖重g 506,应记作 。
2、地图上标有甲、乙、丙三地的海拔高度分别为米米、米、2003001886--+, 其中最低处是 地,最高处是 地,它们相差 。
3、在数轴上表示5-的点与表示的点的距离是 ,表示5-的点与表示1的点的距离是 ,原点与表示 点的距离是2.5。
有理数复习课一、有理数的基本概念1.正数和负数2.有理数3.数轴4.互为相反数5.互为倒数6.有理数的绝对值7.有理数大小的比较8.科学记数法、近似数.二、有理数的运算加、减、乘、除、乘方运算正数和负数1.大于0的数叫做正数。
例如:3,1.8%,3.5……2.在正数前面加上“-”号的数叫做负数。
例如:-3,-2.7%,-4.5……3.0既不是正数,也不是负数。
4.在同一个问题中,分别用正数和负数表示两个具有相反意义的量。
有理数1、统称整数,试举例说明。
2、统称分数,试举例说明。
3、_____________统称有理数。
4、统称非负数。
5、统称非正数。
有理数的分类说明:①分类的标准不同,结果也不同;②分类的结果应无遗漏、无重复;③有限小数、无限循环小数属于分数。
④π是无理数。
0的性质:(1)0是整数,是自然数,是有理数。
(2)0既不是正数,也不是负数。
自然数一定是整数吗?自然数一定是正整数吗?整数一定是自然数吗?自然数一定是整数;自然数不一定是正整数,因为零也是自然数;整数不一定是自然数,因为负整数不是自然数。
1.判断:(1)不带“-”号的数都是正数。
( )(2)带“-”号的数都是负数()(3)如果a是正数,那么-a一定是负数( )(4)在一个数前加上“-”号,这个数变为负数()(5)一个数如果不是正数,那么这个数是负数。
()2.增加-20%,实际的意思是.3.甲比乙大-3表示的意思是.4.小明的妈妈在超市买了一瓶消毒液,发现在瓶子上印有这样一段文字:“净含量(750±5)ml”,这瓶消毒液的标准含量是,这瓶消毒液至少有。
5. 把下列各数填在相应额大括号内:1,-0.1,-789,|-25|,0,-(+20),-3.14,-590,正整数集{…}负整数集{…}正分数集{…}负分数集{…}正有理数集{…}负有理数集{…}自然数集{…}6. 以下说法中正确的是()A.“向东5米”与“向西10米”不是相反意义的量;B.如果汽球上升25米记作+25米,那么-15米的意义就是下降-15米;C.如果气温下降6℃记作-6℃,那么+8℃的意义就是零上8℃;D.若将高1米设为标准0,高1.20米记作+0.20米,那么-0.05米所表示的高是0.95米.7.正数、负数在实际生活中的应用我校对七年级女生进行了仰卧起坐的测试,以能做36个为标准,超过的次数用正数表示,不足的次数用负数表示,其中8名女生的成绩如下:(1)这8名女生的成绩分别是多少?(2)这8名女生有百分之几达到标准?(3)她们共做了多少个仰卧起坐?8. 某检修队从A 地出发,在东西方向的公路上检修线路,如果规定向东行驶为正,向西行驶为负,这个检修队一天中行驶的距离记录如下(单位千米):-4,+7,-9,+8,+6,-5,-3。