中考数学试题分类汇编 规律探索(含详解答案)

中考数学复习专题——规律探索一.选择题1. （2018·湖北随州·3 分）我们将如图所示的两种排列形式的点的个数分别称作“三角形数”（如 1，3， 6，10…）和“正方形数”（如 1，4，9，1，在小于 200 的数中，设最大的“三角形数”为 m ，最大的 “正方形数”为 n ，则 m +n 的值为（ ）A ．33B ．301C ．386D ．5712.（2018•山东烟台市•3 分）如图所示，下列图形都是由相同的玫瑰花按照一定的规律摆成的，按此规律摆 下去，第 n 个图形中有 120 朵玫瑰花，则 n 的值为（ ）3.（2018•山东济宁市•3 分）如图，小正方形是按一定规律摆放的，下面四个选项中的图片， 适合填补图中空白处的是（ ）A ．B ． B.C ．D ．4. （2018 湖南张家界 3.00 分）观察下列算式：21=2，22=4，23=8，24=16，25=32，26=64，27=128，28=256…， 则 2+22+23+24+25+…+21018 的末位数字是（ ）A ．8B ．6C ．4D ．0二、填空题 1. （2018·湖北江汉油田、潜江市、天门市、仙桃市·3 分）如图，在平面直角坐标系中，△P 1OA 1，△P 2A 1A 2， △P3A2A3，…都是等2.（2018•江苏淮安•3 分）如图，在平面直角坐标系中，直线l为正比例函数y=x 的图象，点A1的坐标为（1，，过点A1作x轴的垂线交直线l于点D1，以A1D1为边作正方形A1B1C1D1；过点C1作直线l的垂线，垂足为A2，交x 轴于点B2，以A2B2为边作正方形A2B2C2D2；过点C2作x 轴的垂线，垂足为A3，交直线l 于点D3，以A3D3为边作正方形A3B3C3D3，…，按此规律操作下所得到的正方形A n B n C n D n的面积是（92）n﹣1 ．3.（2018•山东东营市•3分）如图，在平面直角坐标系中，点A1，A2，A3，…和B1，B2，B3，…分别在直线y=15x+b和x轴上．△OA1B1，△B1A2B2，△B2A3B3，…都是等腰直角三角形．如果点A1（1，那么点A2018的纵坐标是20173()2．4.（2018•临安•3 分.）已知：2+23=22×23，3+38=32×38，4+415=42×415，5+524=52×524，…，若10+ba=102×ba符合前面式子的规律，则a+b= ．5. （2018•广西桂林•3分）将从1开始的连续自然数按如图规律排列：规定位于第m行，第n列的自然记为6. （2018•广西南宁•3 分）观察下列等式：30=1，31=3，32=9，33=27，34=81，35=243，…，根据其中规律可 得 30+31+32+…+32018 的结果的个位数字是 ．7. （2018·黑龙江龙东地区·3 分）如图，已知等边△A BC 的边长是 2，以 B C 边上的高 AB 1 为边作等边三角 形，得到第一个等边△AB 1C 1；再以等边△AB 1C 1 的 B 1C 1边上的高 AB 2 为边作等边三角形，得到第二个等边△AB 2C 2；再以等边△A B 2C 2 的B 2C 2边上的高 A B 3 为边作等边三角形，得到第三个等边△AB 3C 3；…，记△B 1CB 2 的面积为 S 1，△B 2C 1B 3 的面积为 S 2，△B 3C 2B 4 的面积为 S 3，如此下去，则 S n = ．8.（2018·黑龙江齐齐哈尔·3 分）在平面直角坐标系中，点 A （3，1）在射线 O M 上，点 B （3，3）在 射线 ON 上，以 AB 为直角边作 Rt △A BA 1，以 BA 1 为直角边作第二个 Rt △BA 1B 1，以A 1B 1 为直角边作第三个 Rt△A 1B 1A 2，…，依次规律，得到 R t △B 2017A 2018B 2018，则点 B 2018 的纵坐标为 ． 9.（2018•广东•3 分）如图，已B 1 作 B 1A 2∥OA 1 交双曲线于点 A 2，过 A 2 作 A 2B 2∥A 1B 1 交 x 轴于点 B 2，得到第二个等边△B 1A 2B 2；过 B 2 作 B 2A 3∥B 1A 2 交双曲线于点 A 3，过 A 3 作 A 3B 3∥A 2B 2 交 x 轴于点 B 3，得到第三个等边△B 2A 3B 3；以此类推，…，则点 B 6 的坐标 为 （ ） ．nn201810. （2018•广西北海•3 分）观察下列等式： 30 = 1， 31 = 3， 32 = 9 ， 33 = 27 ， 34 = 81， 35= 243，…，根据其中规律可得 01220183+3+3+...3+的结果的个位数字是 。

规律研究一.1.〔2021·湖北随州· 3分〕我将如所示的两种排列形式的点的个数分称作“三角形数〞〔如1、3、6、10⋯〕和“正方形数〞〔如1、 4、 9、16⋯〕、在小于200 的数中、最大的“三角形数〞m、最大的“正方形数〞n、 m+n的〔〕A． 33 B． 301C． 386D． 571【解析】由形知第n 个三角形数 1+2+3+⋯ +n=、第 n 个正方形数 n2、据此得出最大的三角形数和正方形数即可得．【解答】解：由形知第n 个三角形数 1+2+3+⋯ +n=、第 n 个正方形数n2、当 n=19 、=190＜ 200、当 n=20 、=210＞ 200、所以最大的三角形数m=190；22当 n=14 、 n =196＜ 200、当 n=15 、 n =225＞ 200、所以最大的正方形数n=196、m+n=386、故： C．【点】本主要考数字的化律、解的关是由形得出第n 个三角形数1+2+3+⋯ +n=、第 n 个正方形数 n2．2.〔 2021?山烟台市? 3 分〕如所示、以下形都是由相同的玫瑰花依照必然的律成的、按此律下去、第n 个形中有120 玫瑰花、n 的〔〕A． 28 B．29 C． 30 D． 31【解析】依照目中的形化律、可以求得第个形中玫瑰花的数量、尔后令玫瑰花的数量120、即可求得相的n 的、从而可以解答本．【解答】解：由可得、第 n 个形有玫瑰花：4n、令 4n=120、得 n=30、故： C．【点】本考形的化、解答本的关是明确意、找出目中形的化律．3. 〔 2021?山宁市? 3 分〕如、小正方形是按必然律放的、下面四个中的片、适合填中空白的是〔〕A．B．C．D．【解答】解：由意知、原形中各行、各列中点数之和10、吻合此要求的只有故： C．4. 〔 2021 湖南家界 3.00 分〕察以下算式：21=2、22=4、23=8、24=16、25=32、 26=64、27=128、 28=256⋯、2+22+23+24+25+⋯+21018的末位数字是〔〕A．8B．6C． 4D． 0【解析】通察：2n的个位数字是2、4、 8、 6 四个一循、所以依照2021÷4=504⋯2、得出22021 的个位数字与 22的个位数字相同是4、而得出答案．【解答】解：∵ 2n的个位数字是2、 4、 8、 6 四个一循、 2021÷4=504⋯2、∴22021的个位数字与22的个位数字相同是4、故 2+22+23+24+25+⋯+21018的末位数字是 2+4+8+6+⋯+2+4 的尾数、2+22+23+24+25+⋯+21018的末位数字是： 2+4=6．故： B．【点二. 填空1. 〔 2021 ·湖北江油田、潜江市、天市、仙桃市· 3 分〕如、在平面直角坐系中、△ P1OA1、△ P2A1A2、△P3A2A3、⋯都是等腰直角三角形、其直角点P〔1 3、3〕、P2、P3、⋯均在直y=x+4 上．△ P1OA1、△ P2A1A2、△P3A2A3、⋯的面分S1、 S2、 S3、⋯、依照形所反响的律、S2021=．【解析】分点P1. P2. P3作 x 的垂段、先依照等腰直角三角形的性求得前三个等腰直角三角形的底和底上的高、而求得三角形的面、得出头的律即可得出答案．【解答】解：如、分点P1. P2. P3作 x 的垂段、垂足分点 C.D.E 、∵P1〔 3、 3〕、且△ P1OA1是等腰直角三角形、∴OC=CA1=P1C=3、A1D=a、 P2D=a、∴OD=6+a、∴点 P2坐〔 6+a、 a〕、将点 P2坐代入y=x+4、得：〔6+a〕+4=a、解得： a=、∴A1A2=2a=3、 P2D=、同理求得P3E=、A2A3=、∵S1=×6× 2=×3×=、S3=××=、⋯⋯∴S2021 =、故答案：．【点】本考律型：点的坐、等腰直角三角形的性等知、解的关是从特别到一般、研究律、利用律解决、属于中考常考型．2.〔 2021?江淮安? 3 分〕如、在平面直角坐系中、直 l 正比率函数 y=x 的象、点 A 的坐〔 1、10〕、点 A1作 x 的垂交直 l 于点 D1、以 A1D1作正方形A1B1C1D1；点 C1作直 l 的垂、垂足A2、交 x 于点 B2、以 A2B2作正方形 A2B2C2D2；点 C2作 x 的垂、垂足A3、交直 l 于点 D3、以A3 D3作正方形 A3B3C3D3、⋯、按此律操作下所获取的正方形A n B n C n D n的面是〔〕n﹣1．【解析】依照正比率函数的性获取∠D1OA1=45°、分求出正方形A1 B1C1D1的面、正方形A2B2C2D2的面、律解答．【解答】解：∵直l 正比率函数y=x 的象、∴∠ D1OA1=45°、∴D1A1=OA1=1、∴正方形A1B1C1D1的面 =1=〔〕1﹣1、由勾股定理得、OD1=、D1A2=、∴A2B2=A2O=、∴正方形A2B2C2D2的面 = =〔〕2﹣1、同理、 A3D3=OA3=、∴正方形 AB CD 的面 ==〔〕3﹣ 1、3333⋯由律可知、正方形A n B n C n D n的面 =〔〕n﹣1、故答案：〔〕n﹣1．【点】本考的是正方形的性、一次函数象上点的坐特色、依照一次函数解析式获取∠ D1OA1=45°、正确找出律是解的关．3.〔 2021?山市? 3 分〕如、在平面直角坐系中、点A1、A2、A3、⋯和B1、B2、B3、⋯分在直y= x+b 和 x 上．△ OA1B1、△ B1A2B2、△ B2A3B3、⋯都是等腰直角三角形．若是点A1〔 1、1〕、那么点A2021的坐是．【解析】因每个 A 点等腰直角三角形的直角点、每个点 A 的坐等腰直角三角形的斜一半．故先出各点 A 的坐、可以表示 A 的横坐、代入解析式可求点 A 的坐、律可求．【解答】解：分点 A1、A2、 A3、⋯向 x 作垂、垂足 C1、C2、 C3、⋯∵点 A1〔 1、1〕在直 y= x+b 上∴代入求得： b=∴y= x+∵△ OA1B1等腰直角三角形∴OB1=2点 A2坐〔 a、 b〕∵△ B1A2B2等腰直角三角形∴A2C2=B1C2=b∴a=OC2=OB1+B1C2=2+b把 A2〔 2+b、b〕代入 y= x+解得 b=∴OB2=5同理点A3坐〔 a、 b〕∵△ B2A3B3等腰直角三角形∴A3C3=B2C3=b∴a=OC3=OB2+B2C3=5+b把 A2〔 5+b、b〕代入 y= x+解得 b=以此推、每个 A 的坐依次是前一个的倍A2021的坐是故答案：【点】本一次函数象背景下的律研究、合了等腰直角三角形的性、解答程中注意比每个点 A 的坐化律．22、4+222×4.〔 2021?安?3 分. 〕：2+ =2 ×、3+ =3 ×=4 ×、5+ =5 ×、⋯、假设 10+ =10吻合前面式子的律、a+b=109．【解析】要求a+b 的、第一真仔地察目出的 4 个等式、找到它的律、即中、b=n+1、a=〔 n+1〕21．【解答】解：依照中资料可知=、∵10+ =102×、∴b=10、 a=99、a+b=109．【点】解关是要懂目的意思、依照目出的条件、找出式子的律．4.〔 2021?广西桂林?3 分〕将从 1 开始的自然数按如律排列：定位于第 m行、第 n 列的自然数10 〔 3、 2〕、自然数15 〔 4、 2〕......按此律、自然数 2021 __________【答案】〔 505、 2〕【解析】解析：由表格数据排列可知、 4 个数一、奇数行从左向右数字逐增大、偶数行从右向左数字逐增大、用2021 除以 4、商确定所在的行数、余数确定所行家的序数、尔后解答即可．解： 2021÷4=504 ??2.∴2021 在第 505 行、第 2 列、∴自然数 2021 〔 505、 2〕 .故答案：〔 505、 2〕 .点睛：本是数字化律的考、察出有 4 列、但每行数字的排列序是解的关、要注意奇数行与偶数行的排列序正好相反．5.〔 2021?广西南宁?3 分〕察以低等式： 30=1、 31=3、 32=9、 33=27、34=81、 35=243、⋯、依照其中律可得 30+31+32+⋯+3 2021的果的个位数字是 3 ．【解析】第一得出尾数化律、而得出01220213 +3 +3 +⋯+3的果的个位数字．【解答】解：∵30=1、31 =3、 32=9、33=27、 34=81、 35=243、⋯、∴个位数 4 个数一循、∴〔 2021+1〕÷ 4=504 余 3、∴1+3+9=13、∴30+31+32+⋯+32021的果的个位数字是： 3．故答案： 3．【点】此主要考了尾数特色、正确得出尾数化律是解关．6.〔2021·黑江地区· 3 分〕如、等△ABC的是2、以 BC上的高AB1作等三角形、获取第一个等△AB1C1；再以等△ AB1C1的 B1C1上的高AB2作等三角形、获取第二个等△AB2C2；再以等△ AB2C2的 B2C2上的高AB3作等三角形、获取第三个等△AB3C3；⋯、△ B1CB2的面 S1、2 1 3的面2324的面3n〔〕n．△BCB S、△ BCB S 、这样下去、S =【解析】由 AB1 2 的等三角形ABC的高、利用三合一获取B1 BC的中点、求出BB1的、利用勾股定理求出AB 的、而求出第一个等三角形ABC 的面、同理求出第二个等三角形ABC 的面、11122依此推、获取第n 个等三角形 AB C 的面．n n【解答】解：∵等三角形ABC的2、 AB ⊥BC、1∴BB1=1、 AB=2、依照勾股定理得：AB1=、∴第一个等三角形AB1C1的面×〔〕2 =〔〕1；∵等三角形 AB1C1的、AB⊥B C、211∴B1B2=、AB1=、依照勾股定理得：AB2=、∴第二个等三角形AB2C2的面×〔〕2=〔〕2；依此推、第n 个等三角形ABC 的面〔n．〕n n故答案：〔〕n．【点】此考了等三角形的性、属于律型、熟掌握等三角形的性是解本的关．7.〔2021·黑江哈· 3 分〕在平面直角坐系中、点A〔、1〕在射OM上、点 B〔、3〕在射ON上、以AB 直角作Rt △ ABA1、以BA1直角作第二个Rt △ BA1B1、以A1B1直角作第三个Rt△ A1B1A2、⋯、依次律、获取Rt△ B2021A2021B2021、点 B2021的坐32021．【解析】依照意、分找到1B1. A2B2⋯⋯及 BA1. B1A2. B2A3⋯⋯段度增律即可【解答】解：由可知点 A.A 1. A2. A3⋯⋯A2021各点在正比率函数y=的象上点 B.B 1. B2. B3⋯⋯B2021各点在正比率函数y=的象上两个函数相减获取横坐不的情况下两个函数象上点的坐的差：①由、 Rt△ A1B1A2、⋯、到Rt △ B2021A2021B2021都有一个角30°∴当 A〔 B〕点横坐、由① AB=2、BA1=2、点A1横坐、B1点坐9=32当 A1〔 B1〕点横坐3、由① A1B1=6、B1A2=6、点A2横坐、B2点坐327=3当 A2〔 B2〕点横坐9、由① A2B2=18、B2A3=18、点A3横坐、B3点4坐 81=32021点 B2021的坐 3 故答案： 32021【点】本是平面直角坐系律研究、考了含有特别角的直角三角形各数量关系、解答注意数形合．8.〔2021?广 ?3 分〕如、等△ OA1B1、点 A1在双曲y=〔x＞0〕上、点B1的坐〔2、0〕．B1作 B1A2∥ OA1交双曲于点A2、 A2作 A2B2∥ A1B1交 x 于点 B2、获取第二个等△B1A2B2； B2作 B2A3∥ B1A2交双曲于点A3、 A3作 A3B3∥ A2B2交 x 于点 B3、获取第三个等△B2A3B3；以此推、⋯、点B6的坐〔2、0〕．【解析】依照等三角形的性以及反比率函数象上点的坐特色分求出B2. B3. B4的坐、得出律、而求出点 B6的坐．【解答】解：如、作A2C⊥ x 于点 C、 B1C=a、 A2C=a、OC=OB+B C=2+a、 A 〔 2+a、a〕．112∵点 A 在双曲 y=〔x＞ 0〕上、2∴〔 2+a〕?a=、解得 a=1、或 a=1〔舍去〕、∴OB2=OB1+2B1C=2+22=2 、∴点 B 的坐〔 2、0〕；2作 A3D⊥ x 于点 D、 B2D=b、 A3D= b、OD=OB2+B2D=2 +b、 A2〔 2+b、b〕．∵点 A3在双曲 y=〔x＞ 0〕上、∴〔 2+b〕?b=、解得 b=+、或 b=〔舍去〕、∴OB=OB+2B D=22+2=2、322∴点 B3的坐〔 2、0〕；同理可得点 B4的坐〔 2、 0〕即〔 4、 0〕；⋯、∴点 B n的坐〔 2、0〕、∴点 B6的坐〔 2、0〕．故答案〔 2、 0〕．【点 】本 考 了反比率函数 象上点的坐 特色、等 三角形的性 、正确求出 B 2. B 3. B 4 的坐 而得出点 B n 的 律是解 的关 ．9. 〔2021?广西北海? 3 分〕 察以低等式：、 313、 32 9、 3327、 4、5243、⋯、313 81 3依照其中 律可得1 2 · · ·2021的 果的个位数字是 。

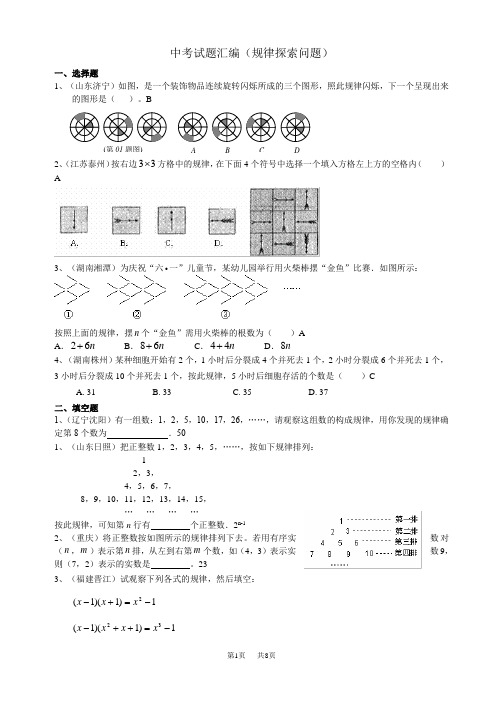
中考试题汇编（规律探索问题）一、选择题1、（山东济宁）如图，是一个装饰物品连续旋转闪烁所成的三个图形，照此规律闪烁，下一个呈现出来的图形是（ ）。

B2、（江苏泰州）按右边33⨯方格中的规律，在下面4个符号中选择一个填入方格左上方的空格内（ ）A3、（湖南湘潭）为庆祝“六一”儿童节，某幼儿园举行用火柴棒摆“金鱼”比赛．如图所示：按照上面的规律，摆n 个“金鱼”需用火柴棒的根数为（ ）A A ．26n + B ．86n + C ．44n + D ．8n4、（湖南株州）某种细胞开始有2个，1小时后分裂成4个并死去1个，2小时分裂成6个并死去1个，3小时后分裂成10个并死去1个，按此规律，5小时后细胞存活的个数是（ ）C A. 31 B. 33 C. 35 D. 37二、填空题 1、（辽宁沈阳）有一组数：1，2，5，10，17，26，……，请观察这组数的构成规律，用你发现的规律确定第8个数为 ．501、（山东日照）把正整数1，2，3，4，5，……，按如下规律排列： 1 2，3， 4，5，6，7，8，9，10，11，12，13，14，15，… … … …按此规律，可知第n 行有 个正整数．2n-12、（重庆）将正整数按如图所示的规律排列下去。

若用有序实数对（n ，m ）表示第n 排，从左到右第m 个数，如（4，3）表示实数9，则（7，2）表示的实数是 。

233、（福建晋江）试观察下列各式的规律，然后填空：1)1)(1(2-=+-x x x 1)1)(1(32-=++-x x x x(第01题图) A B C D11235...1)1)(1(423-=+++-x x x x x ……则=++++-)1)(1(910x x xx _______________。

111-x 。

4、（内蒙古赤峰）观察下列各式：22151(11)1005225=⨯+⨯+= 22252(21)1005625=⨯+⨯+= 22353(31)10051225=⨯+⨯+=……依此规律，第n 个等式（n 为正整数）为 ．22(105)(1)1005n n n +=+⨯+5、（浙江温州）意大利著名数学家斐波那契在研究兔子繁殖问题时，发现有这样一组数：1，1，2，3，5，8，13，…，其中从第三个数起，每一个数都等于它前面两上数的和。

规律探究一、1.（2019 年山东省菏泽市）在平面直角坐系中，一个智能机器人接到的指令是：从原点O 出，按“向上→向右→向下→向右”的方向挨次不停移，每次移1个位度，其移路如所示，第一次移到点A1，第二次移到点A2⋯⋯第n次移到点 A n，点 A2019的坐是（）A ．（ 1010 ， 0 ）B．（ 1010 ， 1）C．（ 1009 ， 0）D．（ 1009 ， 1）【考点】坐、平移、律探究【解答】解： A1（0，1）， A2（1，1）， A3（1，0）， A4（2，0）， A5（2，1），A6（3，1），⋯，2019 ÷ 4 ＝ 504 ⋯ 3 ，因此 A2019的坐（504 × 2+10），，A2019的坐是（1009，0）．故： C．2. （2019年山东省济宁市）已知有理数a≠ 1，我把称a的差倒数，如：2的差倒数是＝ 1， 1 的差倒数是＝．假如a1＝2，a2是a1的差倒数，a3是a2的差倒数， a4是 a3的差倒数⋯⋯依此推，那么a1+ a2+⋯+a100的是（）A ．B．C．D．【考点】律探究【解答】解：∵ a1＝2，∴a2＝＝，a3＝＝，a4＝＝2，⋯⋯∴ 个数列以 2，，挨次循，且2++＝，∵100 ÷ 3 ＝ 33 ⋯ 1 ，∴a1+ a2+⋯+a100＝33×（）2＝＝ 7.5 ，故： A．3.（2019 年山东省枣庄市）如，小正方形是按必定律放的，下边四个中的片，合适填中空白的是（）A ．B．C．D．【考点】律探究、形的化律【解答】解：由意知，原形中各行、各列中点数之和10 ，切合此要求的只有故： D．4. （2019年四川省达州市）a是不1的有理数，我把称a的差倒数，如2的差倒数＝ 1， 1 的差倒数＝，已知a1＝5，a2是a1的差倒数，a3是a2的差倒数， a4是 a3的差倒数⋯，依此推，a2019的是（）A ．5B．C．D．【考点】律探究、数字的化律【解答】解：∵ a1＝5，a2＝＝＝，a3＝＝＝，a4＝＝＝5，⋯∴数列以5 ，，三个数挨次不停循，∵2019 ÷ 3673＝，∴a2019＝ a3＝，故： D．5.（ 2019 年云南省）按必定律摆列的式：x3，－x5，x7，－x9，x11，⋯⋯第n 个式是（）A. （－ 1）n－1x2n－1B.（－ 1 ）n x2n－1C.（－ 1 ）n－1x2n＋1D.（－ 1）n x2n＋1【考点】律探究、数字的化律【解答】察可知，奇数系数正，偶数系数，∴能够用( 1)n 1或 ( 1)n 1，（n 大于等于 1 的整数）来控制正，指数从第3开始的奇数，因此指数部分律2n 1，故 C6. （2019年广西贺州市）算++++ ⋯+的果是（）A ．B．C．D．【考点】律探究、数字的化律、有理数的混淆运算【解答】解：原式＝＝＝．故： B．7.（2019年河南省）如，在△OAB中，点O（ 0，0），A（ 3，4 ），B（3， 4），将△OAB 与正方形 ABCD成的形点 O 旋，每次旋90 ° ，第 70 次旋束，点 D的坐（）A ．（ 10 ， 3）B．（ 3 ，10 ）C．（ 10 ， 3 ）D．（ 3， 10 ）【考点】律探究、旋【解答】解：∵ A（3，4）， B（3，4），∴AB＝3+3＝6，∵四形ABCD 正方形，∴AD＝ AB＝6，∴D（3，10），∵70 ＝ 4 × 17+2 ，∴每4 次一个循，第 70 次旋束，相当于△OAB与正方形ABCD成的形点 O旋2次，每次旋90 °，∴点D 的坐（3，10）．故： D．8. （2019年湖北省十堰市）一列数按某律摆列以下：，，，，，，，，，，⋯，若第n个数，n＝（）A ．50B． 60C．62D． 71【考点】律探究、数字的化【解答】解：，，，，，，，，，，⋯，可写：，（，），（，，），（，，，），⋯，∴分母11 开到分母 1 的数有 11 个，分，∴第n个数， n＝1+2+3+4+ ⋯ +10+5 ＝60 ，故： B．9. （ 2019 年内蒙古赤峰市）如，小用一面1的正方形片，按以下方式操作：①将正方形片四角向内折叠，使四个点重合，睁开后沿折痕剪开，把四个等腰直角三角形抛弃；②在余下片上挨次重复以上操作，当达成第2019 次操作，余下片的面（）A ．2 2019B．C．D．【考点】律探究、中点四形【解答】解：正方形片四角向内折叠，使四个点重合，睁开后沿折痕剪开，第一次：余下边，第二次：余下边，第三次：余下边，当达成第 2019 次操作，余下片的面，故： C．二、填空1.（2019 年山东省滨州市）察以下一数：a1＝，a2＝，a3＝，a4＝，a5＝，⋯，它是按必定律摆列的，利用此中律，写出第n个数 a n＝（用含n的式子表示）【考点】律探究、同底数的乘法n +1 ，【解答】解：察分母，3，5 ， 9， 17 ，33 ，⋯，可知律 2察分子的， 1 ，3 ， 6，10 ，15 ，⋯，可知律，∴a n＝＝；故答案；2.（ 2019 年山东省枣庄市）察以下各式：＝1+＝1+（1），＝1+＝1+（），＝1+＝1+（），⋯利用你的律，算：+++ ⋯+，其果．【考点】律探究、二次根式的化【解答】解：+ + + ⋯+＝ 1+ （ 1 ） +1+ （） + ⋯ +1+ （）＝ 2018+1 + + + ⋯+＝ 2018 ，故答案： 2018．3.（ 2019 年四川省广安市）如，在平面直角坐系中，点A1的坐（1，0），以OA 1直角作Rt OA△1A2，并使∠A1OA2＝ 60 °，再以OA2直角作Rt OA△2A3，并使∠A2 OA 3＝60°，再以OA 3直角作Rt OA△3A4，并使∠A3OA4＝ 60 °⋯按此律行下去，点 A2019的坐．【考点】解直角三角形、律探究【解答】解：由意得，A1的坐（1，0），A2的坐（1，），A3的坐（ 2 ， 2 ），A4的坐（8 ， 0 ），A5的坐（8 ， 8 ），A6的坐（16，16 ），A7的坐（64，0），⋯由上可知， A点的方向是每 6 个循，与第一点方向同样的点在x正半上，其横坐2n ﹣1，其坐 0，与第二点方向同样的点在第一象限内，其横坐 2n﹣2，坐 2n﹣2，与第三点方向同样的点在第二象限内，其横坐 2n﹣2，坐 2 n﹣2，与第四点方向同样的点在x半上，其横坐 2 n ﹣1，坐 0，与第五点方向同样的点在第三象限内，其横坐 2n﹣2，坐 2n﹣2，与第六点方向同样的点在第四象限内，其横坐 2n﹣2，坐 2 n﹣2，∵ 2019 ÷ 6 ＝ 336 ⋯ 3 ，∴点A 2019 的方向与点 A 23 的方向同样，在第二象限内， 其横坐 2n﹣2＝ 22017，坐22017，故答案 ：（22017 ， 22017）．4.（ 2019 年江 省 州市）如 ，在△ABC 中， AB=5 ，AC=4 ，若 行一下操作，在BC 上从左到右一次取点 D 1、 D 2 、 D 3、D 4 ⋯； 点 D1 作 AB 、 AC 的平行 分 交于 AC 、 AB 与点 E 1、F 1； 点 D 2作AB 、AC 的平行 分 交于 AC 、AB 于点 E 2 、F 2； 点 D 3 作AB 、 AC 的平行 分 交于AC 、AB 于点 E 3 、F 3 ⋯，4（ D 1 E 1 +D 2E 2+ ⋯ +D 2019 E 2019 ）+5 （ D 1F 1+D 2 F 2 + ⋯ +D 2019 F 2019 ）= ．【考点】 相像三角形，比率性质、 律探究【解答】 ∵D 1E 1∥ABD 1 F 1 ∥AC∴D 1E1CD 1 D 1 F BD 1 ABCBAC BC∵ AB=5AC=4∴D 1E1CD 1 D 1F BD 1 5CB 4 BCD 1E 1 D 1F CD 1 BD 1 BC ∴4CB BC15BC∴ 4D 1E+5D 1 F=20有 2019 组，即 2019 × 20=403805. （ 2019 年浙江省衢州市）如 ，由两个 2 ， 1 的 方形 成“ 7 ”字 形。

中考数学真题《规律探究题》专项测试卷(附答案)学校:___________班级：___________姓名：___________考号：___________（26题）一 、单选题1．（2023·重庆·统考中考真题）用长度相同的木棍按如图所示的规律拼图案 其中第①个图案用了9根木棍 第①个图案用了14根木棍 第①个图案用了19根木棍 第①个图案用了24根木棍 …… 按此规律排列下去，则第①个图案用的木棍根数是（ ）A ．39B ．44C ．49D ．542．（2023·重庆·统考中考真题）用圆圈按如图所示的规律拼图案 其中第①个图案中有2个圆圈 第①个图案中有5个圆圈 第①个图案中有8个圆圈 第①个图案中有11个圆圈 … 按此规律排列下去，则第①个图案中圆圈的个数为（ ）A ．14B ．20C ．23D ．263．（2023·云南·统考中考真题）按一定规律排列的单项式：23452345,a a a a a 第n 个单项式是（ ）A nB 11n n a --C n naD 1n na -4．（2023·山东烟台·统考中考真题）如图，在直角坐标系中 每个网格小正方形的边长均为1个单位长度 以点P 为位似中心作正方形123PA A A 正方形456,PA A A ⋯ 按此规律作下去 所作正方形的顶点均在格点上 其中正方形123PA A A 的顶点坐标分别为()()()123,0,2,1,1,0P A A --- ()32,1A --，则顶点100A 的坐标为（ ）A ．()31.34B ．()31,34-C ．()32,35D ．()32,05．（2023·山东·统考中考真题）已知一列均不为1的数123n a a a a ，，，，满足如下关系：1223121111a a a a a a ++==--， 34131111nn na a a a a a +++==--，， 若12a =，则2023a 的值是（ ） A ．12-B ．13C ．3-D ．26．（2023·四川达州·统考中考真题）如图，四边形ABCD 是边长为12的正方形 曲线11112DA B C D A 是由多段90︒的圆心角的圆心为C 半径为1CB 11C D 的圆心为D 半径为11111111,DC DA A B B C C D 、、、的圆心依次为A B C D 、、、循环，则20232023A B 的长是（ ）A ．40452πB ．2023πC ．20234πD ．2022π7．（2023·湖南常德·统考中考真题）观察下边的数表（横排为行 竖排为列） 按数表中的规律 分数202023若排在第a 行b 列，则a b -的值为( ) 11122113 22 31 1423 32 41…… A ．2003 B ．2004C ．2022D ．20238．（2023·四川内江·统考中考真题）对于正数x 规定2()1x f x x =+ 例如：224(2)213f ⨯==+ 1212212312f ⨯⎛⎫== ⎪⎝⎭+ 233(3)312f ⨯==+ 1211313213f ⨯⎛⎫== ⎪⎝⎭+ 计算：11111(1)1011009932f f f f f f ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+++++++⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭(2)(3)(99)(100)(101)f f f f f +++++=（ ）A ．199B ．200C ．201D ．2029．（2023·山东日照·统考中考真题）数学家高斯推动了数学科学的发展 被数学界誉为“数学王子” 据传 他在计算1234100+++++时 用到了一种方法 将首尾两个数相加 进而得到100(1100)12341002⨯++++++=．人们借助于这样的方法 得到(1)12342n n n ++++++=（n 是正整数）．有下列问题 如图，在平面直角坐标系中的一系列格点(),i i i A x y 其中1,2,3,,,i n = 且,i i x y 是整数．记n n n a x y =+ 如1(0,0)A 即120,(1,0)a A = 即231,(1,1)a A =- 即30,a =以此类推．则下列结论正确的是（ ）A ．202340a =B ．202443a =C ．2(21)26n a n -=-D ．2(21)24n a n -=-二 填空题10．（2023·四川成都·统考中考真题）定义：如果一个正整数能表示为两个正整数m n 的平方差 且1m n ->，则称这个正整数为“智慧优数”．例如 221653=- 16就是一个智慧优数 可以利用22()()m n m n m n -=+-进行研究．若将智慧优数从小到大排列，则第3个智慧优数是 第23个智慧优数是 ．11．（2023·四川遂宁·统考中考真题）烷烃是一类由碳 氢元素组成的有机化合物 在生产生活中可作为燃料 润滑剂等原料 也可用于动 植物的养护．通常用碳原子的个数命名为甲烷 乙烷 丙烷 …… 癸烷（当碳原子数目超过10个时即用汉文数字表示 如十一烷 十二烷……）等 甲烷的化学式为4CH 乙烷的化学式为26C H 丙烷的化学式为38C H …… 其分子结构模型如图所示 按照此规律 十二烷的化学式为 ．12．（2023·湖南岳阳·统考中考真题）观察下列式子：21110-=⨯ 22221-=⨯ 23332-=⨯ 24443-=⨯ 25554-=⨯ …依此规律，则第n （n 为正整数）个等式是 ．13．（2023·湖北随州·统考中考真题）某天老师给同学们出了一道趣味数学题：设有编号为1-100的100盏灯 分别对应着编号为1-100的100个开关 灯分为“亮”和“不亮”两种状态 每按一次开关改变一次相对应编号的灯的状态 所有灯的初始状态为“不亮”．现有100个人 第1个人把所有编号是1的整数倍的开关按一次 第2个人把所有编号是2的整数倍的开关按一次 第3个人把所有编号是3的整数倍的开关按一次 …… 第100个人把所有编号是100的整数倍的开关按一次．问最终状态为“亮”的灯共有多少盏？几位同学对该问题展开了讨论：甲：应分析每个开关被按的次数找出规律：乙：1号开关只被第1个人按了1次 2号开关被第1个人和第2个人共按了2次 3号开关被第1个人和第3个人共按了2次 ……丙：只有按了奇数次的开关所对应的灯最终是“亮”的状态．根据以上同学的思维过程 可以得出最终状态为“亮”的灯共有 盏．14．（2023·湖北十堰·统考中考真题）用火柴棍拼成如下图案 其中第①个图案由4个小等边三角形围成1个小菱形 第①个图案由6个小等边三角形围成2个小菱形 …… 若按此规律拼下去，则第n 个图案需要火柴棍的根数为 （用含n 的式子表示）．15．（2023·山西·统考中考真题）如图是一组有规律的图案 它由若干个大小相同的圆片组成．第1个图案中有4个白色圆片 第2个图案中有6个白色圆片 第3个图案中有8个白色圆片 第4个图案中有10个白色圆片 …依此规律 第n 个图案中有 个白色圆片（用含n 的代数式表示）16．（2023·黑龙江绥化·统考中考真题）在求123100++++的值时 发现：1100101+= 299101+=从而得到123100++++=101505050⨯=．按此方法可解决下面问题．图（1）有1个三角形 记作11a =分别连接这个三角形三边中点得到图（2） 有5个三角形 记作25a = 再分别连接图（2）中间的小三角形三边中点得到图（3） 有9个三角形 记作39a = 按此方法继续下去，则123n a a a a ++++= ．（结果用含n 的代数式表示）17．（2023·湖南怀化·统考中考真题）在平面直角坐标系中 AOB 为等边三角形 点A 的坐标为()1,0．把AOB 按如图所示的方式放置 并将AOB 进行变换：第一次变换将AOB 绕着原点O 顺时针旋转60︒ 同时边长扩大为AOB 边长的2倍 得到11A OB △ 第二次旋转将11A OB △绕着原点O 顺时针旋转60︒ 同时边长扩大为11A OB △ 边长的2倍 得到22A OB △ …．依次类推 得到20332033A OB ，则20232033A OB △的边长为点2023A 的坐标为 ．18．（2023·山东临沂·统考中考真题）观察下列式子 21312⨯+=22413⨯+= 23514⨯+=……按照上述规律 2n =．19．（2023·山东枣庄·统考中考真题）如图，在反比例函数8(0)y x x=>的图象上有1232024,,,P P P P 等点 它们的横坐标依次为1 2 3 … 2024 分别过这些点作x 轴与y 轴的垂线 图中所构成的阴影部分的面积从左到右依次为1232023,,,,S S S S ，则1232023S S S S ++++= ．20．（2023·山东聊城·统考中考真题）如图，图中数字是从1开始按箭头方向排列的有序数阵．从3开始 把位于同一列且在拐角处的两个数字提取出来组成有序数对：()3,5 ()7,10 ()13,17 ()21,26 ()31,37…如果单把每个数对中的第一个或第二个数字按顺序排列起来研究 就会发现其中的规律．请写出第n 个数对： ．21．（2023·湖南张家界·统考中考真题）如图，在平面直角坐标系中 四边形ABOC 是正方形 点A 的坐标为(1,1) 1AA 是以点B 为圆心 BA 为半径的圆弧 12A A 是以点O 为圆心 1OA 为半径的圆弧 23A A 是以点C 为圆心 2CA 为半径的圆弧 34A A 是以点A 为圆心 3AA 为半径的圆弧 继续以点B O C A 为圆心按上述作法得到的曲线12345AA A A A A 称为正方形的“渐开线”，则点2023A 的坐标是 ．22．（2023·山东东营·统考中考真题）如图，在平面直角坐标系中 直线l ：33y x =x 轴交于点1A 以1OA 为边作正方形111A B C O 点1C 在y 轴上 延长11C B 交直线l 于点2A 以12C A 为边作正方形2221A B C C 点2C 在y 轴上 以同样的方式依次作正方形3332A B C C … 正方形2023202320232022A B C C ，则点2023B 的横坐标是 ．23．（2023·湖北恩施·统考中考真题）观察下列两行数 探究第①行数与第①行数的关系：2- 4 8- 16 32- 64 ……①0 7 4- 21 26- 71 ……①根据你的发现 完成填空：第①行数的第10个数为 取每行数的第2023个数，则这两个数的和为 ．24．（2023·山东泰安·统考中考真题）已知 12345678,,,OA A A A A A A A △△△都是边长为2的等边三角形 按下图所示摆放．点235,,,A A A 都在x 轴正半轴上 且2356891A A A A A A ====，则点2023A 的坐标是 ．25．（2023·四川广安·统考中考真题）在平面直角坐标系中 点1234A A A A 、、、在x 轴的正半轴上 点123B B B 、、在直线()0y x =≥上 若点1A 的坐标为()2,0 且112223334A B A A B A A B A △、△、△均为等边三角形．则点2023B 的纵坐标为 ．26．（2023·黑龙江·统考中考真题）如图，在平面直角坐标系中 ABC 的顶点A 在直线13:l y x =上 顶点B 在x 轴上 AB 垂直x 轴 且22OB = 顶点C 在直线2:3l y x 上 2BC l ⊥ 过点A 作直线2l 的垂线 垂足为1C 交x 轴于1B 过点1B 作11A B 垂直x 轴 交1l 于点1A 连接11A C 得到第一个111A B C △ 过点1A 作直线2l 的垂线 垂足为2C 交x 轴于2B 过点2B 作22A B 垂直x 轴 交1l 于点2A 连接22A C 得到第二个222A B C △ 如此下去 ……，则202320232023A B C 的面积是 ．参考答案一 单选题1．（2023·重庆·统考中考真题）用长度相同的木棍按如图所示的规律拼图案 其中第①个图案用了9根木棍 第①个图案用了14根木棍 第①个图案用了19根木棍 第①个图案用了24根木棍 …… 按此规律排列下去，则第①个图案用的木棍根数是（ ）A ．39B ．44C ．49D ．54【答案】B【分析】根据各图形中木棍的根数发现计算的规律 由此即可得到答案． 【详解】解：第①个图案用了459+=根木棍 第①个图案用了45214+⨯=根木棍 第①个图案用了45319+⨯=根木棍 第①个图案用了45424+⨯=根木棍 ……第①个图案用的木棍根数是45844+⨯=根 故选：B ．【点睛】此题考查了图形类规律的探究正确理解图形中木棍根数的变化规律由此得到计算的规律是解题的关键．2．（2023·重庆·统考中考真题）用圆圈按如图所示的规律拼图案其中第①个图案中有2个圆圈第①个图案中有5个圆圈第①个图案中有8个圆圈第①个图案中有11个圆圈… 按此规律排列下去，则第①个图案中圆圈的个数为（）A．14B．20C．23D．26【答案】B【分析】根据前四个图案圆圈的个数找到规律即可求解.=⨯-【详解】解：因为第①个图案中有2个圆圈2311=⨯-第①个图案中有5个圆圈5321=⨯-第①个图案中有8个圆圈8331=⨯-第①个图案中有11个圆圈11341…⨯-=所以第①个图案中圆圈的个数为37120故选：B.n-是解题的【点睛】本题考查了图形类规律探究根据前四个图案圆圈的个数找到第n个图案的规律为31关键.3．（2023·云南·统考中考真题）按一定规律排列的单项式：2345,a第n个单项式是（）B1n-C n D1n-A【答案】C字母为a指数为1开始的自然数据此即可求解．【分析】根据单项式的规律可得【详解】解：按一定规律排列的单项式：2345,a第n n故选：C．【点睛】本题考查了单项式规律题找到单项式的变化规律是解题的关键．4．（2023·山东烟台·统考中考真题）如图，在直角坐标系中每个网格小正方形的边长均为1个单位长度以点P 为位似中心作正方形123PA A A 正方形456,PA A A ⋯ 按此规律作下去 所作正方形的顶点均在格点上 其中正方形123PA A A 的顶点坐标分别为()()()123,0,2,1,1,0P A A --- ()32,1A --，则顶点100A 的坐标为（ ）A ．()31.34B ．()31,34-C ．()32,35D ．()32,0【答案】A【分析】根据图象可得移动3次完成一个循环 从而可得出点坐标的规律()323n A n n --，．【详解】解：①()121A -， ()412A -， ()703A ， ()1014A ，①()323n A n n --，①1003342=⨯-，则34n =①()1003134A ， 故选：A ．【点睛】本题考查了点的规律变化 解答本题的关键是仔细观察图象 得到点的变化规律． 5．（2023·山东·统考中考真题）已知一列均不为1的数123n a a a a ，，，，满足如下关系：1223121111a a a a a a ++==--， 34131111nn na a a a a a +++==--，， 若12a =，则2023a 的值是（ ） A ．12-B ．13C ．3-D ．2【答案】A【分析】根据题意可把12a =代入求解23a =-，则可得312a =- 413a = 52a =…… 由此可得规律求解．【详解】解：①12a =①212312a +==-- 3131132a -==-+ 411121312a -==+51132113a +==- ……. 由此可得规律为按2 3- 12- 13四个数字一循环①20234505.....3÷= ①2023312a a ==- 故选A ．【点睛】本题主要考查数字规律 解题的关键是得到数字的一般规律．6．（2023·四川达州·统考中考真题）如图，四边形ABCD 是边长为12的正方形 曲线11112DA B C D A 是由多段90︒的圆心角的圆心为C 半径为1CB 11C D 的圆心为D 半径为11111111,DC DA A B B C C D 、、、的圆心依次为A B C D 、、、循环，则20232023A B 的长是（ ）A ．40452πB ．2023πC ．20234πD ．2022π【答案】A【分析】曲线11112DA B C D A …是由一段段90度的弧组成的 半径每次比前一段弧半径12+ 得到1114(1)22n n AD AA n -==⨯-+ 14(1)12n n BA BB n ==⨯-+ 得出半径 再计算弧长即可．【详解】解：由图可知 曲线11112DA B C D A …是由一段段90度的弧组成的 半径每次比前一段弧半径12+∴112AD AA ==111BA BB == 1132CB CC == 112DC DD ==12122AD AA ==+2221BA BB ==+ 22322CB CC ==+ 2222DC DD ==+ ⋯⋯1114(1)22n n AD AA n -==⨯-+ 14(1)12n n BA BB n ==⨯-+故20232023A B 的半径为()202320231420231140452BA BB ==⨯⨯-+=∴20232023A B 的弧长90404540451802ππ=⨯=． 故选A【点睛】此题主要考查了弧长的计算 弧长的计算公式：180n rl π= 找到每段弧的半径变化规律是解题关键． 7．（2023·湖南常德·统考中考真题）观察下边的数表（横排为行 竖排为列） 按数表中的规律 分数202023若排在第a 行b 列，则a b -的值为( ) 11122113 22 31 1423 32 41…… A ．2003 B ．2004 C ．2022 D ．2023【答案】C【分析】观察表中的规律发现 分数的分子是几，则必在第几列 只有第一列的分数 分母与其所在行数一致．【详解】观察表中的规律发现 分数的分子是几，则必在第几列 只有第一列的分数 分母与其所在行数一致 故202023在第20列 即20b = 向前递推到第1列时 分数为201912023192042-=+ 故分数202023与分数12042在同一行．即在第2042行，则2042a =． ①2042202022.a b -=-= 故选：C ．【点睛】本题考查了数字类规律探索的知识点 解题的关键善于发现数字递变的周期性和趋向性．8．（2023·四川内江·统考中考真题）对于正数x 规定2()1x f x x =+ 例如：224(2)213f ⨯==+ 1212212312f ⨯⎛⎫== ⎪⎝⎭+ 233(3)312f ⨯==+ 1211313213f ⨯⎛⎫== ⎪⎝⎭+ 计算：11111(1)1011009932f f f f f f ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+++++++⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭(2)(3)(99)(100)(101)f f f f f +++++=（ ）A ．199B ．200C ．201D ．202【答案】C【分析】通过计算11(1)1,(2)2,(3)223f f f f f ⎛⎫⎛⎫=+=+= ⎪ ⎪⎝⎭⎝⎭⋯可以推出11111(1)(2)(3)(99)(100)(101)1011009932f f f f f f f f f f f ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫++++++++++++ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭结果． 【详解】解：2(1)1,11f ==+ 12441212(2),,(2)2,112323212f f f f ⨯⎛⎫⎛⎫====+= ⎪ ⎪+⎝⎭⎝⎭+ 122331113(3),,(3)2,113232313f f f f ⨯⨯⎛⎫⎛⎫====+= ⎪ ⎪+⎝⎭⎝⎭+ …2100200(100)1100101f ⨯==+ 1212100()11001011100f ⨯==+1(100)()2100f f += 11111(1)(2)(3)(99)(100)(101)1011009932f f f f f f f f f f f ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫++++++++++++ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭21001=⨯+ 201=故选：C ．【点睛】此题考查了有理数的混合运算 熟练掌握运算法则 找到数字变化规律是解本题的关键． 9．（2023·山东日照·统考中考真题）数学家高斯推动了数学科学的发展 被数学界誉为“数学王子” 据传 他在计算1234100+++++时 用到了一种方法 将首尾两个数相加 进而得到100(1100)12341002⨯++++++=．人们借助于这样的方法 得到(1)12342n n n ++++++=（n 是正整数）．有下列问题 如图，在平面直角坐标系中的一系列格点(),i i i A x y 其中1,2,3,,,i n = 且,i i x y 是整数．记n n n a x y =+ 如1(0,0)A 即120,(1,0)a A = 即231,(1,1)a A =- 即30,a = 以此类推．则下列结论正确的是（ ）A ．202340a =B ．202443a =C ．2(21)26n a n -=-D ．2(21)24n a n -=-【答案】B【分析】利用图形寻找规律()211,1n A n n --- 再利用规律解题即可． 【详解】解：第1圈有1个点 即1(0,0)A 这时10a = 第2圈有8个点 即2A 到()91,1A 第3圈有16个点 即10A 到()252,2A 依次类推 第n 圈 ()211,1n A n n ---由规律可知：2023A 是在第23圈上 且()202522,22A ，则()202320,22A 即2023202242a =+= 故A 选项不正确 2024A 是在第23圈上 且()202421,22A 即2024212243a =+= 故B 选项正确第n 圈 ()211,1n A n n --- 所以2122n a n -=- 故C D 选项不正确 故选B ．【点睛】本题考查图形与规律 利用所给的图形找到规律是解题的关键．二 填空题10．（2023·四川成都·统考中考真题）定义：如果一个正整数能表示为两个正整数m n 的平方差 且1m n ->，则称这个正整数为“智慧优数”．例如 221653=- 16就是一个智慧优数 可以利用22()()m n m n m n -=+-进行研究．若将智慧优数从小到大排列，则第3个智慧优数是 第23个智慧优数是 ． 【答案】 15 45【分析】根据新定义 列举出前几个智慧优数 找到规律 进而即可求解．【详解】解：依题意 当3m = 1n =，则第1个一个智慧优数为22318-= 当4m = 2n =，则第2个智慧优数为224214-= 当4m = 1n =，则第3个智慧优数为224115-= 当5m = 3n =，则第5个智慧优数为225316-= 当5m = 2n =，则第6个智慧优数为225221-= 当5m = 1n =，则第7个智慧优数为225324-= ……6m =时有4个智慧优数 同理7m =时有5个 8m =时有6个12345621+++++=第22个智慧优数 当9m =时 7n = 第22个智慧优数为2297814932-=-= 第23个智慧优数为9,6m n ==时 2296813645-=-= 故答案为：15 45．【点睛】本题考查了新定义 平方差公式的应用 找到规律是解题的关键．11．（2023·四川遂宁·统考中考真题）烷烃是一类由碳 氢元素组成的有机化合物 在生产生活中可作为燃料 润滑剂等原料 也可用于动 植物的养护．通常用碳原子的个数命名为甲烷 乙烷 丙烷 …… 癸烷（当碳原子数目超过10个时即用汉文数字表示 如十一烷 十二烷……）等 甲烷的化学式为4CH 乙烷的化学式为26C H 丙烷的化学式为38C H …… 其分子结构模型如图所示 按照此规律 十二烷的化学式为 ．【答案】1226C H【分析】根据碳原子的个数 氢原子的个数 找到规律 即可求解． 【详解】解：甲烷的化学式为4CH 乙烷的化学式为26C H 丙烷的化学式为38C H ……碳原子的个数为序数 氢原子的个数为碳原子个数的2倍多2个十二烷的化学式为1226C H 故答案为：1226C H ．【点睛】本题考查了规律题 找到规律是解题的关键． 12．（2023·湖南岳阳·统考中考真题）观察下列式子：21110-=⨯ 22221-=⨯ 23332-=⨯ 24443-=⨯ 25554-=⨯ …依此规律，则第n （n 为正整数）个等式是 ．【答案】()21n n n n -=-【分析】根据等式的左边为正整数的平方减去这个数 等式的右边为这个数乘以这个数减1 即可求解． 【详解】解：①21110-=⨯ 22221-=⨯ 23332-=⨯ 24443-=⨯ 25554-=⨯ …①第n （n 为正整数）个等式是()21n n n n -=-故答案为：()21n n n n -=-．【点睛】本题考查了数字类规律 找到规律是解题的关键．13．（2023·湖北随州·统考中考真题）某天老师给同学们出了一道趣味数学题：设有编号为1-100的100盏灯 分别对应着编号为1-100的100个开关 灯分为“亮”和“不亮”两种状态 每按一次开关改变一次相对应编号的灯的状态 所有灯的初始状态为“不亮”．现有100个人 第1个人把所有编号是1的整数倍的开关按一次 第2个人把所有编号是2的整数倍的开关按一次 第3个人把所有编号是3的整数倍的开关按一次 …… 第100个人把所有编号是100的整数倍的开关按一次．问最终状态为“亮”的灯共有多少盏？几位同学对该问题展开了讨论：甲：应分析每个开关被按的次数找出规律：乙：1号开关只被第1个人按了1次 2号开关被第1个人和第2个人共按了2次 3号开关被第1个人和第3个人共按了2次 ……丙：只有按了奇数次的开关所对应的灯最终是“亮”的状态．根据以上同学的思维过程 可以得出最终状态为“亮”的灯共有 盏． 【答案】10【分析】灯的初始状态为“不亮” 按奇数次，则状态为“亮” 按偶数次，则状态为“不亮” 确定1-100中 各个数因数的个数 完全平方数的因数为奇数个 从而求解．【详解】所有灯的初始状态为“不亮” 按奇数次，则状态为“亮” 按偶数次，则状态为“不亮”因数的个数为奇数的自然数只有完全平方数 1-100中 完全平方数为1 4 9 16 25 36 49 64 81 100 有10个数 故有10盏灯被按奇数次 为“亮”的状态 故答案为：10．【点睛】本题考查因数分解 完全平方数 理解因数的意义 完全平方数的概念是解题的关键． 14．（2023·湖北十堰·统考中考真题）用火柴棍拼成如下图案 其中第①个图案由4个小等边三角形围成1个小菱形 第①个图案由6个小等边三角形围成2个小菱形 …… 若按此规律拼下去，则第n 个图案需要火柴棍的根数为 （用含n 的式子表示）．【答案】66n +/66n +【分析】当1n =时 有()2114+=个三角形 当2n =时 有()2216+=个三角形 当3n =时 有()2318+=个三角形 第n 个图案有()2122n n +=+个三角形 每个三角形用三根计算即可．【详解】解：当1n =时 有()2114+=个三角形 当2n =时 有()2216+=个三角形 当3n =时 有()2318+=个三角形 第n 个图案有()2122n n +=+个三角形 每个三角形用三根故第n 个图案需要火柴棍的根数为66n +． 故答案为：66n +．【点睛】本题考查了整式的加减的数字规律问题 熟练掌握规律的探索方法是解题的关键．15．（2023·山西·统考中考真题）如图是一组有规律的图案 它由若干个大小相同的圆片组成．第1个图案中有4个白色圆片 第2个图案中有6个白色圆片 第3个图案中有8个白色圆片 第4个图案中有10个白色圆片 …依此规律 第n 个图案中有 个白色圆片（用含n 的代数式表示）【答案】()22n +【分析】由于第1个图案中有4个白色圆片4221=+⨯ 第2个图案中有6个白色圆片6222=+⨯ 第3个图案中有8个白色圆片8223=+⨯ 第4个图案中有10个白色圆片10224=+⨯ ⋯ 可得第(1)n n >个图案中有白色圆片的总数为22n +．【详解】解：第1个图案中有4个白色圆片4221=+⨯ 第2个图案中有6个白色圆片6222=+⨯ 第3个图案中有8个白色圆片8223=+⨯ 第4个图案中有10个白色圆片10224=+⨯⋯①第(1)n n >个图案中有()22n +个白色圆片． 故答案为：()22n +．【点睛】此题考查图形的变化规律 通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素 然后推广到一般情况．解题关键是总结归纳出图形的变化规律． 16．（2023·黑龙江绥化·统考中考真题）在求123100++++的值时 发现：1100101+= 299101+=从而得到123100++++=101505050⨯=．按此方法可解决下面问题．图（1）有1个三角形 记作11a =分别连接这个三角形三边中点得到图（2） 有5个三角形 记作25a = 再分别连接图（2）中间的小三角形三边中点得到图（3） 有9个三角形 记作39a = 按此方法继续下去，则123n a a a a ++++= ．（结果用含n 的代数式表示）【答案】22n n -/22n n -+【分析】根据题意得出()14143n a n n =+-=- 进而即可求解． 【详解】解：依题意 ()1231,5,9,14143n a a a a n n ===⋅⋅⋅=+-=-， ①123n a a a a ++++=()21432122n n n n n n +-==-=- 故答案为：22n n -．【点睛】本题考查了图形类规律 找到规律是解题的关键．17．（2023·湖南怀化·统考中考真题）在平面直角坐标系中 AOB 为等边三角形 点A 的坐标为()1,0．把AOB 按如图所示的方式放置 并将AOB 进行变换：第一次变换将AOB 绕着原点O 顺时针旋转60︒ 同时边长扩大为AOB 边长的2倍 得到11A OB △ 第二次旋转将11A OB △绕着原点O 顺时针旋转60︒ 同时边长扩大为11A OB △ 边长的2倍 得到22A OB △ …．依次类推 得到20332033A OB ，则20232033A OB △的边长为 点2023A 的坐标为 ．【答案】 20232 ()202220222,2【分析】根据旋转角度为60︒ 可知每旋转6次后点A 又回到x 轴的正半轴上 故点2023A 在第四象限 且202320232OA = 即可求解．【详解】解：①AOB 为等边三角形 点A 的坐标为()1,0 ①1OA =①每次旋转角度为60︒ ①6次旋转360︒第一次旋转后 1A 在第四象限 12OA =第二次旋转后 2A 在第三象限 222OA =第三次旋转后 3A 在x 轴负半轴 332OA =第四次旋转后 4A 在第二象限 442OA =第五次旋转后 5A 在第一象限 552OA =第六次旋转后 6A 在x 轴正半轴 662OA =……如此循环 每旋转6次 点A 的对应点又回到x 轴正半轴①202363371÷=点2023A 在第四象限 且202320232OA =如图，过点2023A 作2023A H x ⊥轴于H在2023Rt OHA 中 202360HOA ∠=︒①202320232022202320231cos 2cos60222OH OA HOA =⋅∠=⨯︒=⨯=202320222023202320233sin 232A H OA HOA =⋅∠= ①点2023A 的坐标为()202220222,32．故答案为：20232 ()202220222,32．【点睛】本题考查图形的旋转 解直角三角形的应用．熟练掌握图形旋转的性质 根据旋转角度找到点的坐标规律是解题的关键．18．（2023·山东临沂·统考中考真题）观察下列式子 21312⨯+=22413⨯+= 23514⨯+=……按照上述规律 2n =． 【答案】()()111n n -++【分析】根据已有的式子 抽象出相应的数字规律 进行作答即可． 【详解】解：①21312⨯+= 22413⨯+=23514⨯+=……①()()2211n n n ++=+①()()2111n n n -++=．故答案为：()()111n n -++【点睛】本题考查数字类规律探究．解题的关键是从已有的式子中抽象出相应的数字规律． 19．（2023·山东枣庄·统考中考真题）如图，在反比例函数8(0)y x x=>的图象上有1232024,,,P P P P 等点 它们的横坐标依次为1 2 3 … 2024 分别过这些点作x 轴与y 轴的垂线 图中所构成的阴影部分的面积从左到右依次为1232023,,,,S S S S ，则1232023S S S S ++++= ．【答案】2023253【分析】求出1234,,,P P P P …的纵坐标 从而可计算出1234,,,S S S S …的高 进而求出1234,,,S S S S … 从而得出123n S S S S +++⋯+的值．【详解】当1x =时 1P 的纵坐标为8 当2x =时 2P 的纵坐标为4 当3x =时 3P 的纵坐标为83当4x =时 4P 的纵坐标为2当5x =时 5P 的纵坐标为85…则11(84)84S =⨯-=- 2881(4)433S =⨯-=-3881(2)233S =⨯-=-481(2)2558S =⨯-=- (881)n S n n =-+ 1238888888844228335111n n S S S S n n n n +++⋯+=-+-+-+-++-=-=+++ ①12320238202320242532023S S S S ⨯+++⋯+==． 故答案为：2023253． 【点睛】本题考查了反比例函数与几何的综合应用 解题的关键是求出881n S n n =-+． 20．（2023·山东聊城·统考中考真题）如图，图中数字是从1开始按箭头方向排列的有序数阵．从3开始 把位于同一列且在拐角处的两个数字提取出来组成有序数对：()3,5 ()7,10 ()13,17 ()21,26 ()31,37…如果单把每个数对中的第一个或第二个数字按顺序排列起来研究 就会发现其中的规律．请写出第n 个数对： ．【答案】()221,22n n n n ++++【分析】根据题意单另把每个数对中的第一个或第二个数字按顺序排列起来研究 可发现第n 个数对的第一个数为：()11n n ++ 第n 个数对的第二个位：()211n ++ 即可求解．【详解】解：每个数对的第一个数分别为3 7 13 21 31 … 即：121⨯+ 231⨯+ 341⨯+ 451⨯+ 561⨯+ … 则第n 个数对的第一个数为：()2111n n n n ++=++ 每个数对的第二个数分别为5 10 17 26 37 … 即：221+ 231+ 241+ 251+ 261+… 则第n 个数对的第二个位：()221122n n n ++=++①第n 个数对为：()221,22n n n n ++++ 故答案为：()221,22n n n n ++++．【点睛】此题考查数字的变化规律 找出数字之间的排列规律 利用拐弯出数字的差的规律解决问题． 21．（2023·湖南张家界·统考中考真题）如图，在平面直角坐标系中 四边形ABOC 是正方形 点A 的坐标为(1,1) 1AA 是以点B 为圆心 BA 为半径的圆弧 12A A 是以点O 为圆心 1OA 为半径的圆弧 23A A 是以点C 为圆心 2CA 为半径的圆弧 34A A 是以点A 为圆心 3AA 为半径的圆弧 继续以点B O C A 为圆心按上述作法得到的曲线12345AA A A A A 称为正方形的“渐开线”，则点2023A 的坐标是 ．【答案】()2023,1-【分析】将四分之一圆弧对应的A 点坐标看作顺时针旋转90︒ 再根据A 1A 2A 3A 4A 的坐标找到规律即可．【详解】①A 点坐标为()1,1 且1A 为A 点绕B 点顺时针旋转90︒所得 ①1A 点坐标为()2,0又①2A 为1A 点绕O 点顺时针旋转90︒所得 ①2A 点坐标为()0.2-又①3A 为2A 点绕C 点顺时针旋转90︒所得 ①3A 点坐标为()3,1-又①4A 为3A 点绕A 点顺时针旋转90︒所得 ①4A 点坐标为()1,5由此可得出规律：n A 为绕B O C A 四点作为圆心依次循环顺时针旋转90︒ 且半径为1 2 3 n每次增加1． ①202355053÷=故2023A 为以点C 为圆心 半径为2022的2022A 顺时针旋转90︒所得 故2023A 点坐标为()2023,1-． 故答案为：()2023,1-．【点睛】本题考查了点坐标规律探索 通过点的变化探索出坐标变化的规律是解题的关键．22．（2023·山东东营·统考中考真题）如图，在平面直角坐标系中 直线l ：33y x =x 轴交于点1A 以1OA 为边作正方形111A B C O 点1C 在y 轴上 延长11C B 交直线l 于点2A 以12C A 为边作正方形2221A B C C 点2C 在y 轴上 以同样的方式依次作正方形3332A B C C … 正方形2023202320232022A B C C ，则点2023B 的横坐标是 ．【答案】20221⎛ ⎝⎭【分析】分别求出点点1B 的横坐标是1 点2B 的横坐标是1 点3B 2413⎛+= ⎝⎭找到规律 得到答案见即可．【详解】解：当0y = 0= 解得1x = ①点()11,0A ,①111A B C O 是正方形 ①11111OA A B OC === ①点()11,1B ①点1B 的横坐标是1当1y =时 1 解得1x =+①点21A ⎛⎫⎪ ⎪⎝⎭①2221A B C C 是正方形①2212211A B C C A C ===①点212B ⎛ ⎝⎭即点2B 的横坐标是1当2y =时 2= 解得)223x =①点34,23A ⎝⎭①3332A B C C 是正方形①33233243A B C C A C ===①点3B 2413⎛= ⎝⎭……以此类推，则点2023B 的横坐标是202231⎛ ⎝⎭故答案为：202231⎛ ⎝⎭【点睛】此题是点的坐标规律题 考查了二次函数的图象和性质 正方形的性质等知识 数形结合是是解题的关键．23．（2023·湖北恩施·统考中考真题）观察下列两行数 探究第①行数与第①行数的关系：2- 4 8- 16 32- 64 ……①0 7 4- 21 26- 71 ……①根据你的发现 完成填空：第①行数的第10个数为 取每行数的第2023个数，则这两个数的和为 ．【答案】 1024 202422024-+【分析】通过观察第一行数的规律为(2)n - 第二行数的规律为(2)1n n -++ 代入数据即可. 【详解】第一行数的规律为(2)n - ①第①行数的第10个数为10(2)1024-= 第二行数的规律为(2)1n n -++①第①行数的第2023个数为2023(2)- 第①行数的第2023个数为2023(2)2024-+ ①202422024-+故答案为：1024 202422024-+．【点睛】本题主要考查数字的变化 找其中的规律 是今年考试中常见的题型. 24．（2023·山东泰安·统考中考真题）已知 12345678,,,OA A A A A A A A △△△都是边长为2的等边三角形 按下图所示摆放．点235,,,A A A 都在x 轴正半轴上 且2356891A A A A A A ====，则点2023A 的坐标是 ．。

规律探索一.选择题1. （2019•山东省济宁市 •3分）已知有理数a ≠1，我们把称为a 的差倒数，如：2的差倒数是＝﹣1，﹣1的差倒数是＝．如果a 1＝﹣2，a 2是a 1的差倒数，a 3是a 2的差倒数，a 4是a 3的差倒数……依此类推，那么a 1+a 2+…+a 100的值是（ ） A ．﹣7.5B ．7.5C ．5.5D ．﹣5.5【考点】数字的变化【分析】求出数列的前4个数，从而得出这个数列以﹣2，，依次循环，且﹣2++＝﹣，再求出这100个数中有多少个周期，从而得出答案． 【解答】解：∵a 1＝﹣2， ∴a 2＝＝，a 3＝＝，a 4＝＝﹣2，……∴这个数列以﹣2，，依次循环，且﹣2++＝﹣， ∵100÷3＝33…1，∴a 1+a 2+…+a 100＝33×（﹣）﹣2＝﹣＝﹣7.5，故选：A ．【点评】本题考查了规律型：数字的变化类：通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素，然后推广到一般情况． 2. （2019•广东深圳•3分）定义一种新运算：⎰-=⋅-abn n n b a dx x n 1，例如：⎰-=⋅khh k xdx 222，若⎰-=--m522mdx x ，则m =（ ）A. -2B. 52-C. 2D.52【答案】B 【解析】⎰-=-=-=----m51122511)5(mmm m m dx x ，则m =52-，故选B.3.（2019，山东枣庄，3分）如图，小正方形是按一定规律摆放的，下面四个选项中的图片，适合填补图中空白处的是（ ）A．B．C．D．【分析】根据题意知原图形中各行、各列中点数之和为10，据此可得．【解答】解：由题意知，原图形中各行、各列中点数之和为10，符合此要求的只有故选：D．【点评】本题主要考查图形的变化规律，解题的关键是得出原图形中各行、各列中点数之和为10．4. （2019•湖北十堰•3分）一列数按某规律排列如下：，，，，，，，，，，…，若第n个数为，则n＝（）A．50 B．60 C．62 D．71【分析】根据题目中的数据可以发现，分子变化是1，（1，2），（1，2，3），…，分母变化是1，（2，1），（3，2，1），…，从而可以求得第n个数为时n的值，本题得意解决．【解答】解：，，，，，，，，，，…，可写为：，（，），（，，），（，，，），…，∴分母为11开头到分母为1的数有11个，分别为，∴第n个数为，则n＝1+2+3+4+…+10+5＝60，故选：B．【点评】本题考查数字的变化类，解答本题的关键是明确题意，发现题目中数字的变化规律．5. （2019•湖北武汉•3分）观察等式：2+22＝23﹣2；2+22+23＝24﹣2；2+22+23+24＝25﹣2…已知按一定规律排列的一组数：250、251.252.…、299.2100．若250＝a，用含a的式子表示这组数的和是（）A．2a2﹣2a B．2a2﹣2a﹣2 C．2a2﹣a D．2a2+a【分析】由等式：2+22＝23﹣2；2+22+23＝24﹣2；2+22+23+24＝25﹣2，得出规律：2+22+23+…+2n＝2n+1﹣2，那么250+251+252+…+299+2100＝（2+22+23+…+2100）﹣（2+22+23+…+249），将规律代入计算即可．【解答】解：∵2+22＝23﹣2；2+22+23＝24﹣2；2+22+23+24＝25﹣2；…∴2+22+23+…+2n＝2n+1﹣2，∴250+251+252+…+299+2100＝（2+22+23+...+2100）﹣（2+22+23+ (249)＝（2101﹣2）﹣（250﹣2）＝2101﹣250，∵250＝a，∴2101＝（250）2•2＝2a2，∴原式＝2a2﹣a．故选：C．【点评】本题是一道找规律的题目，要求学生通过观察，分析、归纳发现其中的规律，并应用发现的规律解决问题．解决本题的难点在于得出规律：2+22+23+…+2n＝2n+1﹣2．二.填空题1. （2019•江苏连云港•3分）如图，将一等边三角形的三条边各8等分，按顺时针方向（图中箭头方向）标注各等分点的序号0、1.2.3.4.5.6.7.8，将不同边上的序号和为8的两点依次连接起来，这样就建立了“三角形”坐标系．在建立的“三角形”坐标系内，每一点的坐标用过这一点且平行（或重合）于原三角形三条边的直线与三边交点的序号来表示（水平方向开始，按顺时针方向），如点A的坐标可表示为（1，2，5），点B的坐标可表示为（4，1，3），按此方法，则点C的坐标可表示为（2，4，2）．【分析】根据点A的坐标可表示为（1，2，5），点B的坐标可表示为（4，1，3）得到经过点的三条直线对应着等边三角形三边上的三个数，依次为左、右，下，即为该点的坐标，于是得到结论．【解答】解：根据题意得，点C的坐标可表示为（2，4，2），故答案为：（2，4，2）．【点评】本题考查了规律型：点的坐标，等边三角形的性质，找出题中的规律是解题的关键．2.（2019•浙江衢州•4分）如图，由两个长为2，宽为1的长方形组成“7”字图形。

中考数学《规律(Lv)探索》专题复习试题含解析一(Yi)、选择题1. 如图，将一张等边(Bian)三角形纸片沿中位线剪成4个小三角形，称为第一次操作；然后，将其中的一个三角形按(An)同样方式再剪成4个小三(San)角形，共得到7个小(Xiao)三角形，称为第二次操作；再将其中一个三角形按同样方式再剪成4个小三角形，共得(De)到10个小三角形，称为第三次操(Cao)作；…根据以上操作，若要得到100个小三角形，则需要操作的次数是（）A．25 B．33 C．34 D．50【考点】规律型：图形的变化类．【分析】由第一次操作后三角形共有4个、第二次操作后三角形共有（4+3）个、第三次操作后三角形共有（4+3+3）个，可得第n次操作后三角形共有4+3（n﹣1）=3n+1个，根据题意得3n+1=100，求得n的值即可．【解答】解：∵第一次操作后，三角形共有4个；第二次操作后，三角形共有4+3=7个；第三次操作后，三角形共有4+3+3=10个；…∴第n次操作后，三角形共有4+3（n﹣1）=3n+1个；当3n+1=100时，解得：n=33，故选：B．2.观察图中正方形四个顶点所标的数字规律，可知，数2016应标在（）A．第504个正方形的左下角B．第504个正方形的右下角C．第505个正方形的左上角D．第505个正方形的右下角【考点】规律型：点的坐标．【分(Fen)析】根据图形中对应的数字和各个(Ge)数字所在的位置，可以推出数2016在第多少个正方形和它所在的位置，本(Ben)题得以解决．【解(Jie)答】解(Jie)：∵2016÷4=504，又(You)∵由题目中给出的几个(Ge)正方形观察可知，每个正方形对应四个数，而第一个最小的数是0，0在(Zai)右下角，然后按逆时针由小变大，∴第504个正方形中最大的数是2015，∴数2016在第505个正方形的右下角，故选D．3．（2016.山东省临沂市，3分）用大小相等的小正方形按一定规律拼成下列图形，则第n个图形中小正方形的个数是（）A．2n+1 B．n2﹣1 C．n2+2n D．5n﹣2【考点】规律型：图形的变化类．【分析】由第1个图形中小正方形的个数是22﹣1、第2个图形中小正方形的个数是32﹣1、第3个图形中小正方形的个数是42﹣1，可知第n个图形中小正方形的个数是（n+1）2﹣1，化简可得答案．【解答】解：∵第1个图形中，小正方形的个数是：22﹣1=3；第2个图形中，小正方形的个数是：32﹣1=8；第3个图形中，小正方形的个数是：42﹣1=15；…∴第n个图形中，小正方形的个数是：（n+1）2﹣1=n2+2n+1﹣1=n2+2n；故选：C．【点评】本题主要考查图形的变化规律，解决此类题目的方法是：从变化的图形中发现不变的部分和变化的部分及变化部分的特点是解题的关键．二、填空题1．如图，①是一个三角形，分别连接这个三角形三边中点得到图②，再连接图②中间小三角形三边的中点得到图③，按这样的方法进行下去，第n个图形中共有三角形的个数为4n﹣3 ．【考点】规律型：图形的变化类．【分析】结合题意，总结可知，每(Mei)个图中三角形个数比图形的编号的(De)4倍(Bei)少(Shao)3个三角形，即可(Ke)得出结果．【解(Jie)答】解：第(Di)①是(Shi)1个三角形，1=4×1﹣3；第②是5个三角形，5=4×2﹣3；第③是9个三角形，9=4×3﹣3；∴第n个图形中共有三角形的个数是4n﹣3；故答案为：4n﹣3．【点评】此题主要考查了图形的变化，解决此题的关键是寻找三角形的个数与图形的编号之间的关系．2．如图，直线l：y=－x，点A1坐标为（－3，0）. 过点A1作x轴的垂线交直线l于点B1，以原点O为圆心，OB1长为半径画弧交x轴负半轴于点A2，再过点A2作x 轴的垂线交直线l于点B2，以原点O为圆心，OB2长为半径画弧交x轴负半轴于点A 3，…，按此做法进行下去，点A2016的坐标为 .【考点】一次函数图像上点的坐标特征，规律型：图形的变化类．【分析】由直线l：y=－x的解析式求出A1B1的长，再根据勾股定理，求出OB1的长，从而得出A2的坐标；再把A2的横坐标代入y=－x的解析式求出A2B2的长，再根据勾股定理，求出OB2的长，从而得出A3的坐标；…，由此得出一般规律．【解(Jie)答】解(Jie)：∵点(Dian)A1坐(Zuo)标为（－3，0），知(Zhi)O A1=3，把(Ba)x=－3代入(Ru)直线(Xian)y=－x中，得y= 4 ，即A1B1=4.根据勾股定理，OB1===5，∴A2坐标为（－5，0），O A2=5；把x=－5代入直线y=－x中，得y=，即A2B2=.根据勾股定理，OB2====，∴A3坐标为（－3512，0），O A3=3512；把x=－3512代入直线y=－x中，得y=，即A3B3=.根据勾(Gou)股定理，OB 3====，∴A 4坐标(Biao)为（－3523，0），O A 4=3523；……同理(Li)可得(De)A n 坐(Zuo)标为（－，0），O A n =3521--n n ；∴A 2016坐(Zuo)标为（－，0）故(Gu)答案为：（− 3520142015，0）【点(Dian)评】本题是规律型图形的变化类题是全国各地的中考热点题型，考查了一次函数图像上点的坐标特征. 解题时，要注意数形结合思想的运用，总结规律是解题的关键. 解此类题时，要得到两三个结果后再比较、总结归纳，不要只求出一个结果就盲目的匆忙得出结论。

中考数学必考题型《规律探索》分类专项练习类型一 数式规律1. 我国战国时期提出了“一尺之棰，日取其半，万世不竭”这一命题，用所学知识来解释可理解为：设一尺长的木棍，第一天折断一半，其长为12尺，第二天再折断一半，其长为14尺，…，第n 天折断一半后得到的木棍长应为________尺． 12n2. 如图，是按一定规律排成的三角形数阵，按图中数阵的排列规律，第9行从左至右第5个数是________．第2题图41【解析】由图形可知，第n 行最后一个数为1＋2＋3＋…＋n ＝n （n ＋1）2，∴第8行最后一个数为8×92＝36＝6，则第9行从左至右第5个数是36＋5＝41.3. 观察下列关于自然数的式子：第一个式子：4×12－12 ① 第二个式子：4×22－32 ② 第三个式子：4×32－52 ③ …根据上述规律，则第2019个式子的值是______．8075 【解析】∵4×12－12＝3①，4×22－32＝7②，4×32－52＝11③，…，4n 2－(2n －1)2＝4n －1，∴第2019个式子的值是4×2019－1＝8075. 4. 将数1个1，2个12，3个13，…，n 个1n (n 为正整数)顺次排成一列：1，12，12，13，13，13，…，1n ，1n ，…，记a 1＝1，a 2＝12，a 3＝12，…，S 1＝a 1，S 2＝a 1＋a 2，S 3＝a 1＋a 2＋a 3，…，S n ＝a 1＋a 2＋…＋a n ，则S 2019＝________．63364 【解析】根据题意，将该数列分组，1个1的和为1，2个12的和为1，3个13的和为1，…；∵1＋2＋3＋…＋63＝2016个数，则第2019个数为64个164的第3个数，则此数列中，S 2019＝1×63＋3×164＝63364. 类型二 图形规律5. 如图，在平面直角坐标系中，第一次将△OAB 变换成△OA 1B 1，第二次将△OA 1B 1变换成△OA 2B 2，第三次将△OA 2B 2变换成△OA 3B 3，…，已知A (1，3)，A 1(2，3)，A 2(4，3)，A 3(8，3)，B (2，0)，B 1(4，0)，B 2(8，0)，B 3(16，0)．观察每次变换前后的三角形的变化，按照变换规律，则点A n 的坐标是________．第5题图(2n，3)【解析】∵A(1，3)，A1(2，3)，A2(4，3)，A3(8，3)，…，∴纵坐标不变，为3，横坐标都和2有关，为2n，即点An的坐标是(2n，3)．6. 如图，把正方形铁片OABC置于平面直角坐标系中，顶点A的坐标为(3，0)，点P(1，2)在正方形铁片上，将正方形铁片绕其右下角的顶点按顺时针方向依次旋转90°，第一次旋转至图①位置，第二次旋转至图②位置，…，则正方形铁片连续旋转2019次后，点P的坐标为________．第6题图(6058，1)【解析】∵铁片OABC为正方形，A(3，0)，P(1，2)，∴正方形铁片OABC 的边长为3，如解图第一个循环周期内的点P1，P2，P3，P4的坐标分别为(5，2)，(8，1)，(10，1)，(13，2)，每增加一个循环，对应的点的横坐标就增加12.而2019÷4＝504……3，即504个循环周期后点P2016的横坐标为504×12＋1＝6049，纵坐标为2，所以点P2019的横坐标为6049＋9＝6058，纵坐标为1.故P2019(6058，1)．第6题解图7. 如图，在平面直角坐标系中，半径均为1个单位长度的半圆O 1，O 2，O 3，…，组成一条平滑的曲线，点P 从原点O 出发，沿这条曲线向右运动，速度为每秒π2个单位长度，则第2019秒时，点P 的坐标是________．第7题图(2019，－1) 【解析】∵圆的半径都为1，∴半圆的周长＝π，以时间为点P 的下标．观察发现规律：P 0(0，0)，P 1(1，1)，P 2(2，0)，P 3(3，－1)，P 4(4，0)，P 5(5，1)，…，∴P 4n (4n ，0)，P 4n ＋1(4n ＋1，1)，P 4n ＋2(4n ＋2，0)，P 4n ＋3(4n ＋3，－1)．∵2019÷4＝504……3，∴第2019秒时，点P 的坐标为(2019，－1)．8. 如图，已知菱形OABC 的顶点O (0，0)，B (2，2)，若菱形绕点O 逆时针旋转，每秒旋转45°，则第60秒时，菱形的对角线交点D 的坐标为________．第8题图(－1，－1) 【解析】∵菱形OABC 的顶点O (0，0)，B (2，2)，∴BO 与x 轴的夹角为45°，∵菱形的对角线互相垂直平分，∴点D是线段OB的中点，∴点D的坐标是(1，1)，∵菱形绕点O逆时针旋转，每秒旋转45°，360°÷45°＝8，∴每旋转8秒，菱形的对角线交点就回到原来的位置(1，1)，∵60÷8＝7……4，∴第60秒时是把菱形绕点O 逆时针旋转了7周回到原来位置后，又旋转了4秒，即又旋转了4×45°＝180°，∴点D 的对应点落在第三象限，且对应点与点D关于原点O成中心对称，∴第60秒时，菱形的对角线交点D的坐标为(－1，－1)．9. 如图，∠MON＝60°，作边长为1的正六边形A1B1C1D1E1F1，边A1B1、F1E1分别在射线OM、ON上，边C1D1所在的直线分别交OM、ON于点A2、F2，以A2F2为边作正六边形A2B2C2D2E2F2，边C2D2所在的直线分别交OM、ON于点A3、F3，再以A3F3为边作正六边形A3B3C3D3E3F3，…，依此规律，经第n次作图后，点B n到ON的距离是________．第9题图3n－13【解析】由题可知，∠MON＝60°，设B n到ON的距离为h n，∵正六边形A1B1C1D1E1F1的边长为1，∴A1B1＝1，易知△A1OF1为等边三角形，∴A1B1＝OA1＝1，∴OB1＝2，则h1＝2×32＝3，又∵OA2＝A2F2＝A2B2＝3，∴OB2＝6，则h2＝6×32＝33，同理可得：OB3＝18，则h3＝18×32＝93，…，依此可得OB n＝2×3n－1，则h n＝2×3n －1×32＝3n －1 3.∴B n 到ON 的距离h n ＝ 3n －1 3.10. 如图，正方形AOBO 2的顶点A 的坐标为A (0，2)，O 1为正方形AOBO 2的中心；以正方形AOBO 2的对角线AB 为边，在AB 的右侧作正方形ABO 3A 1，O 2为正方形ABO 3A 1的中心；再以正方形ABO 3A 1的对角线A 1B 为边，在A 1B 的右侧作正方形A 1BB 1O 4，O 3为正方形A 1BB 1O 4的中心；再以正方形A 1BB 1O 4的对角线A 1B 1为边，在A 1B 1的右侧作正方形A 1B 1O 5A 2，O 4为正方形A 1B 1O 5A 2的中心；…；按照此规律继续下去，则点O 2018的坐标为________．第10题图(21010－2，21009) 【解析】由A (0，2)和A 1(2，4)可知直线AA 1的解析式为y ＝x ＋2，由图可知点A 1，A 2，…，A n 的纵坐标分别为22，23，…，2n ＋1，将y ＝2n ＋1代入y ＝x ＋2，得2n ＋1＝x ＋2，∴x ＝2n ＋1－2，∴点A n 的坐标为(2n ＋1－2，2n ＋1)，由图可知O 2n 横坐标与A n 的横坐标相同，O 2n 纵坐标是A n 的纵坐标的12，∴O 2n 的坐标为(2n ＋1－2，2n)，∴当n ＝1009时，O 2018的坐标为(21010－2，21009)． 真题反馈：1. 观察下列一组数：，，，，，…，它们是按一定规律排列的，那么这一组数的第n个数是．2. 如图，用黑白两种颜色的菱形纸片，按黑色纸片数逐渐增加1的规律拼成下列图案，若第n个图案中有2017个白色纸片，则n的值为( )A．671 B．672 C．673 D．6743. 观察下列一组图形，其中图形①中共有2颗星，图形②中共有6颗星，图形③中共有11颗星，图形④中共有17颗星，…，按此规律，图形⑧中星星的颗数是( )A．43 B．45 C．51 D．534. 请你计算:(1-x)(1+x),(1-x)(1+x+x2),…,猜想(1-x)(1+x+x2+…+x n)的结果是( ).A. 1-x n+1B. 1+x n+1C. 1-x nD. 1+x n5. 如图,已知正方形ABCD,顶点A(1,3),B(1,1),C(3,1).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换,如此这样,连续经过2019次变换后,正方形ABCD的对角线交点M的坐标变为().A. (-2012,2)B. (-2012,-2)C. (-2013,-2)D. (-2013,2)6. 观察下列数据：－2，52，－103，174，－265，…，它们是按一定规律排列的，依照此规律，第11个数据是．7. 观察下列数据：－2，52，－103，174，－265，…，它们是按一定规律排列的，依照此规律，第11个数据是．8. 正方形A1B1C1O，A2B2C2C1，A3B3C3C2，…按如图的方式放置．点A1，A2，A3，…和点C1，C2，C3，…分别在直线y＝x＋1和x轴上，则点B6的坐标是．9. 如图,将若干个正三角形、正方形和圆按一定规律从左向右排列,那么第2015个图形是.10. 如图,弹性小球从点P(0,3)出发,沿所示方向运动,每当小球碰到矩形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到矩形的边时的点为P1,第2次碰到矩形的边时的点为P2,…,第n 次碰到矩形的边时的点为P n,则点P3的坐标是;点P2 019的坐标是.11.观察下列关于自然数的等式：32-4×12=5 ①52-4×22=9 ②72-4×32=13 ③…根据上述规律解决下列问题：（1）完成第四个等式：（2）写出你猜想的第n个等式（用含n的式子表示），并验证其正确性．12.(1)证明三角形中位线定理:三角形的中位线平行于第三边,且等于第三边的一半;[要求根据图(1)写出已知、求证、证明;在证明过程中,至少有两处写出推理依据(“已知”除外)(2)如图(2),在▱ABCD中,对角线焦点为O,A1,B1,C1,D1分别是OA,OB,OC,OD的中点,A2,B2,C2,D2分别是OA1,OB1,OC1,OD1的中点,…,以此类推.若▱ABCD的周长为1,直接用算式表示各四边形的周长之和l;(3)借助图形(3)反映的规律,猜猜l可能是多少?(1)(2) (3)。

类型一数字规律探索1.(2016.济宁)按一定规律排列的一列数：，1，1，□，，，，…请你仔细观察，按照此规律方框内的数字应为.2.观察下列等式：71=7,72=49,73=343,74=2401,75=16807,76=117649，...则71+72+73+ (72017)末位数是——————。

3.观察下列等式：31=3，32=9，33=27，34=81，35=243，36=729，…，试猜想，32017的个位数字是4.（2015•孝感）观察下列等式：1 2 =1，1+3=2 2 ，1+3+5=3 2 ，1+3+5+7=4 2 ，…，则1+3+5+7+…+2015=____________．5.（2016.南宁）观察下列等式：在上述数字宝塔中，从上往下数，2016在第层．类型二数式规律探索．6.古希腊数学家把数 1，3，6，10，15，21，······叫做三角数，它有一定的规律性，则第30个三角数减去第28个三角数的值为______7.古希腊数学家把数1，3，6，10，15，21……叫做三角形数，它有一定的规律性.若把第一个三角形数记为，第二个三角形数记为，……，第个三角形数记为，计算……，由此推算，____________，__________.8.（2015•武威）古希腊数学家把数1，3，6，10，15，21，…叫做三角形数，其中1是第一个三角形数，3是第2个三角形数，6是第3个三角形数，…依此类推，那么第9个三角形数是，2016是第个三角形数．类型三图形规律探索9. （2016.重庆）观察下列一组图形，其中图形①中共有2颗星，图形②中共有6颗星，图形③中共有11颗星，图形④中共有17颗星，…，按此规律，图形⑧中星星的颗数是（）A ．43B ．45C ．51D ．5310. 如图，正方形ABCD 的边长为2，其面积标记为S 1，以CD 为斜边作等腰直角三角形，以该等腰直角三角形的一条直角边为边向外作正方形，其面积标记为S 2，…，按照此规律继续下去，则S 9的值为（ ）A ．（）6B ．（）7C ．（）6 D ．（）711. 如图，下列各图形中的三个数之间均具有相同的规律，依此规律，那么第4个图形中的x= ，一般地，用含有m ，n 的代数式表示y ，即y=12．（2015.河南）在平面直角坐标系中，半径均为1个单位长度的半圆O 1,O 2,O 3…组成一条平滑的曲线，点P 从原点O 出发，沿这条曲线向右运动，速度为每秒2π个单位长度，则2015秒时，点P 的坐标是（ ）A.（2014，0）B.（2015，-1）C.（2015，1）D.（2015，0）13.（2015•宜宾）如图，以点O 为圆心的20个同心圆，它们的半径从小到大依次是1、2、3、4、…、20，阴影部分是由第1个圆和第2个圆，第3个圆和第4个圆，…，第19个圆和第20个圆形成的所有圆环，则阴影部分的面积为（ ）A．231πB．210πC．190πD．171π类型四坐标中的规律探索14. （2016•聊城）如图，在平面直角坐标系中，边长为1的正方形OA1B1C1的两边在坐标轴上，以它的对角线OB1为边作正方形OB1B2C2，再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3，以此类推…、则正方形OB2015B2016C2016的顶点B2016的坐标是14题图15题图15. 如图，在平面直角坐标系中，△A1A2A3，△A3A4A5，△A5A6A7，△A7A8A9，…，都是等边三角形，且点A1，A3，A5，A7，A9的坐标分别为A1（3，0），A3（1，0），A5（4，0），A7（0，0），A9（5，0），依据图形所反映的规律，则A100的坐标为．16.（2015•丹东，）如图，直线OD与x轴所夹的锐角为30°，OA1的长为1，△A1A2B1、△A2A3B2、△A3A4B3…△AnAn+1Bn均为等边三角形，点A1、A2、A3…An+1在x轴的正半轴上依次排列，点B1、B2、B3…Bn在直线OD上依次排列，那么点Bn的坐标为.答案1.【解答】解：把整数1化为，得，，，（），，，…可以发现后一个数的分子恰是前面数的分母，所以，第4个数的分子是2，分母是3，故答案为：．2.答案73.观察下列等式：31=3，32=9，33=27，34=81，35=243，36=729，…，试猜想，32017的个位数字是3.【解答】解：设n为自然数，∵34n+1的个位数字是3，与31的个位数字相同，34n+2的个位数字是9，与32的个位数字相同，34n+3的个位数字是7，与33的个位数字相同，34n的个位数字是1，与34的个位数字相同，∴32016=3504×4的个位数字与34的个位数字相同，应为1，故答案为：34.（2015•孝感）观察下列等式：1 2 =1，1+3=2 2 ，1+3+5=3 2 ，1+3+5+7=4 2 ，…，则1+3+5+7+…+2015= ——————————．4.解答：解：因为 1=1 2 ；1+3=2 2 ；1+3+5=3 2 ；1+3+5+7=4 2 ；…，所以 1+3+5+…+2015=1+3+5+…+（2×1008﹣1）=1008 2=1016064故答案为：1016064．【解答】解：第一层：第一个数为12=1，最后一个数为22﹣1=3，第二层：第一个数为22=4，最后一个数为23﹣1=8，第三层：第一个数为32=9，最后一个数为24﹣1=15，∵442=1936，452=2025，又∵1936＜2016＜2025，∴在上述数字宝塔中，从上往下数，2016在第44层，故答案为：44类型二数式规律探索．由三角数规律可知，可知三角数的每一项中后一项比前一项多的点数为后一项最底层的点数，因而可知第30项比第29个项点数多30个，而第29项比第28项多29个，故可求出第30个三角数比第28个三角数多的点数59个7.解答：解：a 2-a1=3-1=2；a 3-a2=6-3=3；a 4-a3=10-6=4；…；a n -an-1=n．所以a100-a99=100．∵（a2-a1）+（a3-a2）+（a4-a3）+…+（an-an-1）=2+3+4+…+n=-1=an -a1，∴a100==5050．类型三图形规律探索9.【解答】解：设图形n中星星的颗数是a n（n为自然是），观察，发现规律：a1=2，a2=6=a1+3+1，a3=11=a2+4+1，a4=17=a3+5+1，…，∴a n=2+．令n=8，则a8=2+=51．10.【解答】解：在图中标上字母E，如图所示．∵正方形ABCD 的边长为2，△CDE 为等腰直角三角形， ∴DE 2+CE 2=CD 2，DE=CE ， ∴S 2+S 2=S 1．观察，发现规律：S 1=22=4，S 2=S 1=2，S 3=S 2=1，S 4=S 3=，…，∴S n =（）n ﹣3．当n=9时，S 9=（）9﹣3=（）6， 故选：A ．11.【解答】解：观察，发现规律：3=1×（2+1），15=3×（4+1），35=5×（6+1）， ∴x=7×（8+1）=63，y=m （n +1）． 故答案为：63；m （n +1）． 12.【解析】：一个半圆的周长是πr=π，速度×时间=2π×2015， 设点P 走了n 个半圆，则有2π×2015=n π，所以n=20152个2，即100712个2，1007个2时正好是上半圆弧，还有12半圆弧，正好在下半圆弧的中点，因此的P 在（2015，-1）处。