当前位置：文档之家 › 课件--模型预测控制

课件--模型预测控制

  • 格式：ppt
  • 大小：1.20 MB
  • 文档页数：96

下载文档原格式

  / 96

合集下载

模型预测控制ppt

模型预测控制ppt

令
02 动态矩阵控制
动态矩阵控制以优化确定控制策略，在优化过程中， 同时考虑输出跟踪期望值和控制量变化来选择最优化准
则。往往不希望控制增量 Δ ｕ 变化过于剧烈，这一因
素在优化性能指标中加入软约束予以考虑。
02 动态矩阵控制
02 动态矩阵控制
02 动态矩阵控制
02 动态矩阵控制
02 动态矩阵控制
01预测控制概述
工业过程的特点 多变量高维度复杂系统难以建立精确的数学模型 工业过程的结构、参数以及环境具有不确定性、时变性、 非线性、强耦合，最优控制难以实现
预测控制产生
基于模型的控制，但对模型要求不高 采用滚动优化策略，以局部优化取代全局优化 利用实测信息反馈校正，增强控制的鲁棒性
限时域优化策略。优化过程不是一次离线进行，而是在线反
复进行优化计算，滚动实施，从而使模型失配、时变、干扰 等引起的不确定性能及时得到弥补，提高系统的控制效果。
02滚动优化
03反馈校正
模型失配
实际被控过程存在非线性、时变性、不确定性等原因，使基于模型的预测不可能准确地与实 际被控过程相符
反馈校正
从图中可以看出： 第一根曲线是模型失配时的输出 曲线，其快速性较差，超调量小；
第二根曲线是模型未失配时的输 出曲线，其快速性较好，但超调量 略大。
这验证了预测控制对于模型精度 要求不高的优势，即使模型失配， 也能取得不错的控制效果，
05
总结
总结
模型预测控制
预测控制：不仅利用当前和过去的偏差值，而且还利用预测模 型来预测过程未来的偏差值。以滚动优化确定当前的最优控制 策略，使未来一段时间内被控变量与期望值偏差最小
增大P： 系统的快速性变差，稳定性增强； 减小P： 快速性变好，稳定性变差。

模型预测控制MIMOExamplePPT课件

模型预测控制MIMOExamplePPT课件

Amplitude
0.5
0
0
10
20 0
10
20 0
Time (sec)
第22页/共37页
10
20
动态矩阵控制---例子
• 阶跃响应模型 • S=step(model) ？ • S=[S(:,:,1),S(:,:,2),S(:,:,3)] ？ • S(k,j,i), 时间k，输出j，输入i
第23页/共37页
• [A,B,C,D]=ssdata(sys);
第27页/共37页
动态矩阵控制---例子
• Now simulate closed-loop MPC in Simulink • Tstop=30; % Simulation time • mpc_miso • 解释：t=10,20时加入可测/不可测系统输入的动态特性
• %% • % We also revised the MPC design • MPCobj.Model.Disturbance=.1; % Model for unmeasured
• % measurement noise of frequency 0.1 Hz. We want to inform the MPC object
• % about this so that state estimates can be improved
• omega=2*pi/10; • MPCobj.Model.Noise=0.5*tf(omega^2,[1 0 omega^2]);
pulatedVariables; • ServoMPC.OutputVariables=OutputVar
第15页/共37页
Se r vo m o to r- 参 数 设 置 对 性 能 作用

模型预测控制讲解

模型预测控制讲解
? 系统的线性性
– 则保证了可用线性系统的迭加性等
2019/6/9
第五讲 模型预测控制
16
计算机控制系统理论与应用
5-2 DMC的预测模型(1)
----Coperight by SEC----
t/T 12
计算机控制系统理论与应用
5-1 反馈校正(1)
----Coperight by SEC----
? 每到一个新的采样时刻，都要通过实际 测到的输出信息对基于模型的预测输出 进行修正，然后再进行新的优化。不断 根据系统的实际输出对预测输出值作出 修正使滚动优化不但基于模型，而且利 用了反馈信息，构成闭环优化。
----Coperight by SEC----
2019/6/9
第五讲 模型预测控制
2
计算机控制系统理论与应用
----Coperight by SEC----
模型预测控制的发展背景(1)
? 现代控制理论及应用的发展与特点
– 要求 ? 精确的模型 ? 最优的性能指标 ? 系统的设计方法
– 应用 ? 航天、航空 ? 军事等领域
4
计算机控制系统理论与应用
预测控制的特点（1）
----Coperight by SEC----
? 建模方便,不需要深入了解过程内部机理 ? 非最小化描述的离散卷积和模型,有利于
提高系统的鲁棒性 ? 滚动的优化策略,较好的动态控制效果 ? 不增加理论困难,可推广到有约束条件、
大纯滞后、非最小相位及非线性等过程 ? 是一种计算机优化控制算法
第五讲 模型预测控制
11
计算机控制系统理论与应用
----Coperight by SEC----
5-1 滚动优化(在线优化) (2)

预测控制-课件

预测控制-课件

学习交流PPT
16
滤波、预测与控制
❖ 预测：
▪ 已知信号的过去测量值： y(k), y(k-1), ……,y(k-n) ▪ 求解未来时刻期望值：y(k+1|k) , y(k+2|k) , ……
y(k)
预估器
y(k+d|k)
▪ 预估器：y(k+1|k)＝ b1y(k)+b2y(k-1)+……+any(k-n)
反馈
学习交流PPT
19
预测控制
❖ 预测控制：
▪ 不仅利用当前及过去测量值： u(k-1), ……,u(k-m), y(k), y(k1), ……,y(k-n)
▪ 也利用未来预测值： y(k+1|k), y(k+2|k), ……,
▪ 优点：利用预测的变化趋势，超前调节
学习交流PPT
20
预测控制的基本原理
预测控制的三要素
❖ 预测控制算法的核心内容：
▪ 建立内部模型、确定参考轨迹、设计控制算法、在线优化
❖ 预测控制算法的三要素为：
▪ 预测模型 ▪ 滚动优化 ▪ 反馈校正
学习交流PPT
13
预测控制的三要素
❖ 预测模型：对未来一段时间内的输出进行预测； ❖ 滚动优化：滚动进行有限时域在线优化； ❖ 反馈校正：通过预测误差反馈，修正预测模型，提
t/T 1─k时刻的预测输出 2─k＋１时刻实际输出 3─预测误差 4─k＋１时刻校正后的预测输出
学习交流PPT
34
反馈校正
y(k) e (k)
y (k+j| k)
y(k-j)
ym(k )
ym (k+j| k-1)
u (k+j )

第7章 模型预测控制4MIMOExample ppt课件

第7章 模型预测控制4MIMOExample ppt课件
y(t) = Cx(t) + Du(t)
2020/12/27
12
MPC Control of a DC Servomotor模型描述
sys
a=
x1 x2 x3 x4
x1 0 1 0 0
x2 -51.21 -1 2.56 0
x3 0 0 0 1
x4 128 0 -6.401 -10.2
b=
u1
x1 0
备注：下面文件单独键入运行界面 ManipulatedVariables=struct('Min',umin,'Max',umax,'Units','V'); OutputVariables(1)=struct('Min',-Inf,'Max',Inf,'Units','rad'); OutputVariables(2)=struct('Min',Vmin,'Max',Vmax,'Units','Nm'); Weights=struct('Input',uweight,'InputRate',duweight,'Output',yw
2020/12/27
7
动态矩阵控制---参数设置对性能 作用
A single input, V, one measured and fead back to the controller, qL, and one unmeasured, T.
2020/12/27
8
动态矩阵控制---参数设置对性能 作用
eight);

模型预测控制 PPT课件

模型预测控制 PPT课件

现代典型过程对象的控制系统层次图
Unit1 为 传 统 结构 Unit2 为 MPC 结构
模型预测控制的基本特点
预测控制算法的核心内容：
建立内部模型 确定参考轨迹 设计控制算法 实行在线优化
预测控制算法的三要素为：
预测模型 滚动优化 反馈校正
模型预测控制的三要素
预测模型
对未来一段时间内的输出进行预测
工业自动化工具的发展（仪表）
年代 1950
1960
工业发展状况
仪表技术
化工、钢铁、纺织、造纸等，规 气动仪表，标准信号：20～100kPa
模较小；电子管时代
采用真空电子管；自动平衡型
记录仪
半导体技术；石油化工；计算机； 电动仪表，标准信号：0～10mA
大型电站；过程工业大型化
仪表控制室；模拟流程图；DDC
反馈校正
y (k+j|k)= ym(k+j|k) +e(k+j|k) e (k+j|k)= y (k|k) - ym (k|k)
反馈校正
2 3 y
u
4
yˆ(k 1) ym (k
e(k 1) yˆ(k
1
k k+1
t/T
1─k时刻的预测输出ym(k)
2─k＋１时刻实际输出y (k+1)
3─预测误差e(k+1)
预测模型形式
➢ 参数模型：如微分方程、差分方程、状态方程、 传递函数等
➢ 非参数模型：如脉冲响应、阶跃响应、模糊模型、 智能模型等
预测模型
基于模型的预测示意图（P=M）
过去
未来
3
y
4
1u2ຫໍສະໝຸດ k 时刻1—控制策略Ⅰ 2—控制策略Ⅱ 3—对应于控制 策略Ⅰ的输出 4—对应于控制策略Ⅱ的输出

模型预测控制

模型预测控制

专题1作业
（1）简要介绍一下模型预测控制的原理、模型预测控制与基础PID控制回路的闭环实现框图；动态矩阵控制采用什么内部模型？
●模型预测控制原理：模型预测控制不仅利用当前和过去的偏差值，而且还利用预测模型
来预测过程未来的偏差值。

通过滚动优化来确定当前的最优控制策略，使未来一段时间内被控变量与期望值偏差最小。

系统输出的反馈校正用于补偿模型预测误差和其他扰动。

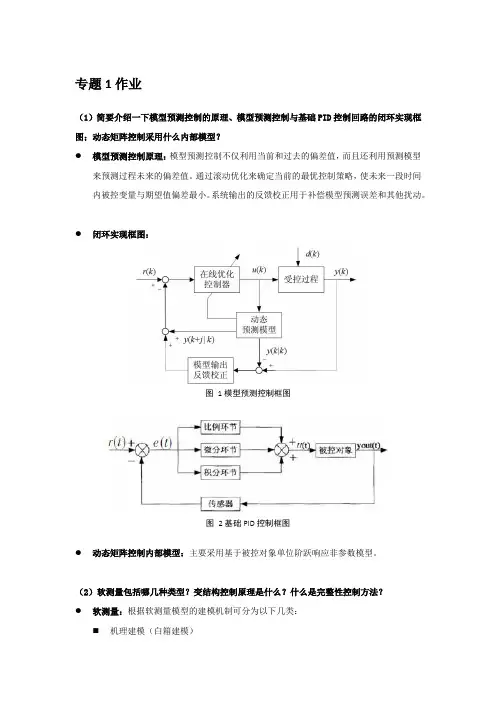
●闭环实现框图：
图1模型预测控制框图
图2基础PID控制框图
●动态矩阵控制内部模型：主要采用基于被控对象单位阶跃响应非参数模型。

（2）软测量包括哪几种类型？变结构控制原理是什么？什么是完整性控制方法？
●软测量：根据软测量模型的建模机制可分为以下几类：
⏹机理建模（白箱建模）
⏹数据驱动建模（黑箱建模）
⏹混合建模
⏹非线性动态软测量建模
●变结构控制原理：在动态控制中，根据系统当时状态，以跃变方式有目的地不断变换，
迫使系统按预定的“滑动模态”的状态轨迹运动。

变结构是通过切换函数实现的。

当系统的状态向量所决定的切换函数值，随着它的运动达到某特定值时，系统中一种结构（运动微分方程）转变成另一种结构。

其系统结构图如下所示。

图3变结构控制系统框图
●完整性控制方法：完整性控制是容错控制的研究热点，所谓完整性是指当系统中某些部
件失效后，系统仍能够稳定工作的特性。

基于该特性的控制方法即为完整性控制方法。

第5章 模型预测控制

第5章 模型预测控制

对象的历史信息和未来输入，预测系统未来响应。
2. 滚动优化
(i) 优化目的 按照某个目标函数确定当前和未来控制作用的大小，这些控制作用 将使未来输出预测序列沿某个参考轨迹“最优地”达到期望输出设定 值 . (ii) 优化过程
不是采用一成不变的全局最优化目标，而是采用滚动式的有限时域 优化策略。优化过程不是一次离线进行，而是在线反复进行优化计 算、滚动实施，从而使模型失配、时变、干扰等引起的不确定性能及 时得到弥补，提高了系统的控制效果。
5.2 模型预测控制基本原理
一 模型预测控制的分类 1. 基于非参数模型的预测控制算法
代表性的算法有模型算法控制 (MAC) 和动态矩阵控制(DMC)。这 类算法适合处理开环稳定多变量过程约束间题的控制；
2. 基于ARMA或CARIMA等输入输出参数化模型预测控制算法
代表性的算法为广义预测控制算法(GPC)。这类算法可用于开环不 稳定、非最小相位和时变时滞等较难控制的对象，并对系统的时滞和 阶次不确定有良好的鲁棒性。但对于多变量系统，算法实施较困难。
闭环预测模型为： 目标函数可取为：
目标函数写成矩阵形式为： 极小化性能指标，即令 ，得最优控制率：
根据滚动优化原理，只实施当前控制量u2(k)：
式中： 多步优化MAC的特点: 优点: (i)控制效果和鲁棒性优于单步MAC算法简单; (ii)适用于有时滞或非最小相位对象。 缺点: (i)算法较单步MAC复杂; (ii)由于以u作为控制量, 导致MAC算法不可避免地出现稳态误差.
商品化预测控制软件产品：
(i). 第一代：以Adersa的IDCOM和She11 Oil的DMC为代表，算法针 对无约束多变量过程; (ii). 第二代：以Shell Oil的QDMC为代表，处理约束多变量过程的控 制问题; (iii). 第三代：产品包括Adersa的HIECOM和PFC，DMC的DMC plus 和Honeywell的RMPCT，算法增加了摆脱不可行解的办法，并具有容 错和多个目标函数等功能。

课件--模型预测控制

课件--模型预测控制

h1
h1
h2
PM 1
hi
i1
PM
第三节 模型算法控制(MAC) 二. 反馈校正
以当前过程输出测量值与模型计算值之差修正模型预测值
yP (k j) ym (k j) jy(k) ym (k)
N
ym (k) hiu(k i) i 1
对于P步预测
j 1, 2, , P
YP (k) Ym (k) βe(k)
主要内容 预测模型 反馈校正 参考轨迹 滚动优化
第四节 动态矩阵控制(DMC) 一. 预测模型
DMC的预测模型
渐近稳定线性被控对象的单位阶跃响应曲线
和给定值的偏差来确定当前的控制输入 预测控制：不仅利用当前的和过去的偏差值，
而且还利用预测模型来预测过程未来的偏差值。 以滚动优化确定当前的最优控制策略，使未来 一段时间内被控变量与期望值偏差最小 从基本思想看，预测控制优于PID控制
第二节 预测控制的基本原理
r(k)
+_
d(k)
在线优化 控制器
u(k)
y(k) 受控过程
+ y(k+j| k)
+
模型输出 反馈校正
动态 预测模型
y(k|k)
_ +
三要素：预测模型 滚动优化 反馈校正
第二节 预测控制的基本原理 一.预测模型（内部模型）
预测模型的功能 根据被控对象的历史信息{ u(k - j), y(k - j) |
j≥1 }和未来输入{ u(k + j - 1) | j =1, …, m} ，预测 系统未来响应{ y(k + j) | j =1, …, p} 预测模型形式 参数模型：如微分方程、差分方程 非参数模型：如脉冲响应、阶跃响应

模型预测控制ppt课件

模型预测控制ppt课件

……
多步输出预测
……
未
已
知
知
当前时刻k以后的控制量
当前时刻k以 前的控制量
多步输出预测
矩阵形式（P = M）：
PP维矩阵
P1维矩阵
未知
P(N－1)维
矩阵
已知
(N－1) 1
维矩阵
多步输出预测
当P>M时：
优化控制序列
保持不变
多步输出预测
矩阵形式（P>M）：
当 j > M 时， 保持不变，但控制输入仍保持u (k+M-1)，所以必须考 虑脉冲响应的作用。
制：
单步MAC的等效控制结构
ysp
w(k) +
参考轨迹
－
u(k)
Gc(z-1)
h
(k)
g(z-1) z-
1
g^(z-1) z-1
+ +
－
ym(k)
y(k)
+
e(k)
标准的内模控制结构!
纯滞后对象单步MAC
纯滞后对象：
一步输出预测：
闭环预测：
纯滞后对象单步MAC
参考轨迹：
性能指标：
制，完成整个动作循环。
模型算法控制－MAC
参考轨迹 输入
u(k)
优化计算
受控对象
y(k)
Z-1
预测输出
内部模型
e(k)
模型算法控制原理框图
离散脉冲响应模型
y
gi：脉冲响应系数
g11 g2
gN
0 12
t /T N
开环稳定系统的离散脉冲响应曲线
离散脉冲响应模型
适宜对象：线性、定常、自衡系统 在输入端加入控制量

模型预测控制

模型预测控制

先进控制技术”第二章第二章模型测控制模型预测控制—MPC Model PredictiveC lControl) )本讲内容要点))))))模型预测控制在工业中的应用举例模型预测控制的发展背景)))预测控制的特点（1）))))有约束条件、大纯滞后、非最小相位及)预测控制的发展)))国内外先进控制软件包开发所走的道路212.1 预测控制的基本原理))现在一般则更清楚地表述为：模型、滚动优化、反馈反馈2112.1.1.预测模型(内部模型) ))差分方程阶跃响应2112.1.1.预测模预测型(内部模型)3未来过去y 14u2k 时刻1—控制策略Ⅰ;2—控制策略Ⅱ;3—对应于控制策略Ⅰ的输出;的输出4—对应于控制策略Ⅱ的输出。

图2-1 基于模型的预测2.1.2. 滚动优化(在线优化）212))212K 时刻优化2.1.2.滚动优化(在线优化）.y ry213uk +1时刻优化y r21yu31─参考轨迹(虚线)y r ; 2─最优预测输出y (实线);─k +1`k t/T 3最优控制作用u 。

图2-2滚动优化2.1.3. 反馈校正213)实际测到的输出信息对基于模型的预测输出进行修正，然后再进行新对预测输出值作出修正使滚动优化不但基于模型，而且利用了反馈信息构成闭环优化息，构成闭环优化。

2.1.3.反馈校正(误差校正)2413yu k k +1时刻的测输出时刻实输出t/T2-31─k 时刻的预测输出;2─k ＋１时刻实际输出;3─预测误差；４─k ＋１时刻校正后的预测输出。

图23 误差校正222.2 动态矩阵控制(DMC) )a≈a)(∞N221DMC 2.2.1. DMC的预测模型(1)模型截断ya Na N-10123a 3a 2a 1N N-1t/T 图2-4 系统的单位阶跃采样数据示意图2.2 动态矩阵控制(DMC)22)))则保证了可用线性系统的迭加性等2.2.1. DMC的预测模型(2)221DMC, t=k T时刻预测未来N个时刻))+M 1y PM (k)a P-M+1Δu(k +M-1)+3/y M (k 3/k)y M (k +2/k)a 1Δu(k +2)a P-1Δu(k +1)y M (k +1/k)a 1Δu(k +1)a 2Δu(k +1)a P Δu(k)y P0(k)y 0(k +1/k)a 1Δu(k)a 2Δu(k)a 3Δu(k)y 0(k +2/k)k k+1k+2k+3k+P t/T y M (k +3/k)图2-5 根据输入控制增量预测输出的示意图2.2.1. DMC的预测模型(3)221DMC))是滚动优是控制时域长度。

模型预测控制

模型预测控制

模型预测控制模型预测控制（Model Predictive Control，MPC）是一种现代控制方法，被广泛应用于工业过程和汽车控制等领域。

MPC基于数学模型对未来系统行为进行预测，并通过优化算法计算当前时刻的最优控制动作。

本文将全面讲解MPC的原理、应用以及优缺点等方面。

MPC的基本原理是通过使用系统数学模型对未来一段时间内的系统行为进行预测，然后通过一个优化算法计算当前时刻的最优控制动作。

MPC的控制器与传统的PID控制器不同，它不仅仅根据当前系统状态进行控制，而是根据预测模型对未来的系统行为进行优化调整。

MPC的核心是系统模型。

对于一个要进行MPC控制的系统，需要建立一个准确的系统模型，该模型包括系统的动态方程以及输入和输出的关系。

系统模型可以基于物理原理、统计学方法或者机器学习等方式进行建立。

对于复杂的系统，模型的表示可能是非线性的，并且可能包含未知参数。

针对这种情况，可以使用非线性模型预测控制（NMPC）或者递归模型预测控制（RMPC）等方法。

MPC的控制周期可以根据具体的应用场景进行选择，例如在汽车控制中可以选择10ms的控制周期。

在每个控制周期内，MPC首先对当前状态进行估计，然后根据模型预测未来一段时间内的系统行为，并通过一个优化算法计算出当前时刻的最优控制动作。

最后，控制器将最优控制动作发送给执行机构，并等待下个控制周期的到来。

MPC的优点之一是可以对系统的限制条件进行灵活处理。

在优化算法中可以加入对输入和输出的限制条件，例如电流限制、速度限制等。

这可以确保系统在正常工作范围内进行控制，并且可以防止系统因超过限制条件而导致的事故或者损坏。

另一个优点是MPC可以考虑未来系统行为的不确定性。

通过对未来一段时间内的系统行为进行预测，MPC可以在控制过程中主动调整以应对不确定因素，例如外部干扰、传感器噪声等。

这使得MPC在不确定环境下更加鲁棒可靠。

MPC在许多领域都有广泛的应用。

在化工领域，MPC被用于优化生产过程中的控制策略，以提高生产效率和质量。

模型预测控制（MPC）

模型预测控制（MPC）

模型预测控制（MPC）预测控制预测控制或称为模型预测控制（MPC）是仅有的成功应用于工业控制中的先进控制方法之一。

各类预测控制算法都有一些共同的特点，归结起来有三个基本特征：（1）预测模型，（2）有限时域滚动优化，（3）反馈校正。

这三步一般由计算机程序在线连续执行。

预测控制是一种基于预测过程模型的控制算法，根据过程的历史信息判断将来的输入和输出。

它强调模型的函数而非模型的结构，因此，状态方程、传递函数甚至阶跃响应或脉冲响应都可作为预测模型。

预测模型能体现系统将来的行为，因此，设计者可以实验不同的控制律用计算机仿真观察系统输出结果。

预测控制是一种最优控制的算法，根据补偿函数或性能函数计算出将来的控制动作。

预测控制的优化过程不是一次离线完成的，是在有限的移动时间间隔内反复在线进行的。

移动的时间间隔称为有限时域，这是与传统的最优控制最大的区别，传统的最优控制是用一个性能函数来判断全局最优化。

对于动态特性变化和存在不确定因素的复杂系统无需在全局范围内判断最优化性能，因此这种滚动优化方法很适用于这样的复杂系统。

预测控制也是一种反馈控制的算法。

如果模型和过程匹配错误，或者是由于系统的不确定因素引起的控制性能问题，预测控制可以补偿误差或根据在线辨识校正模型参数。

虽然预测控制系统能控制各种复杂过程，但由于其本质原因，设计这样一个控制系统非常复杂，要有丰富的经验，这也是预测控制不能预期那样广泛得到应用的主要原因。

预测控制适用于先进过程控制（APC）和监督控制场合，其控制输出作用主要是跟踪设定值的变化。

但预测控制并不能很好地处理调节控制难题。

模型预测控制是一种基于模型的闭环优化控制策略，已在炼油、化工、冶金和电力等复杂工业过程控制中得到广泛的应用。

模型预测控制具有控制效果好、鲁棒性强等优点，可有效地克服过程的不确定性、非线性和关联性，并能方便处理过程被控变量和操纵变量中的各种约束。

预测控制算法种类较多，表现形式多种多样，但都可以用以下三条基本原理加以概括：①模型预测：预测控制的本质是在对过程的未来行为进行预测的基础上，对控制量加以优化，而预测是通过模型来完成的。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
d(k) r(k)
+ _
在线优化 控制器
u(k) 受控过程
y(k)
动态 预测模型
+ +
y(k+j| k)
_
y(k|k)
+
模型输出 反馈校正
三要素：预测模型
滚动优化
反馈校正
第二节 预测控制的基本原理 一.预测模型（内部模型）

预测模型的功能
根据被控对象的历史信息{ u(k - j), y(k - j) | j≥1 }和未来输入{ u(k + j - 1) | j =1, …, m} ，预测 系统未来响应{ y(k + j) | j =1, …, p}
k
k+1
t/T
1─k 时刻的预测输出 2─k +1时刻实际输出
3─ k +1 时刻预测误差 4─k +1时刻校正后的预测输出
第三节 模型算法控制(MAC)

模型算法控制（Model Algorithmic Control）：
基于脉冲响应模型的预测控制，又称模型预测 启发式控制(MPHC)


60年代末，Richalet等人在法国工业企业中应用 于锅炉和精馏塔的控制
第三节 模型算法控制(MAC) 三. 设定值与参考轨迹
预测控制并不是要求输出迅速跟踪设定值，而 是使输出按一定轨迹缓慢地跟踪设定值
过去 yd y(k) yr(k) yP(k) u(t) 未来
k
k+1
k+P
t/T
第三节 模型算法控制(MAC) 三. 设定值与参考轨迹
根据设定值和当前过程输出测量值确定参考轨迹 最广泛使用的参考轨迹为一阶指数变化形式

反馈校正
在每个采样时刻，都要通过实际测到的输出信息对基于 模型的预测输出进行修正，然后再进行新的优化

闭环优化
不断根据系统的实际输出对预测输出作出修正，使滚动 优化不但基于模型，而且利用反馈信息，构成闭环优化
第二节 预测控制的基本原理 三.反馈校正（误差校正）

反馈校正示意图
2 3 y u 4
1

MAC算法中的模型参数

有限脉冲响应(Finite Impulse Response，FIR) hT={h1，h2，…，hN} 可完全描述系统的动态特性 N称为建模时域 保证了模型可用有限的脉冲响应描述 保证了可用线性系统的迭加性


系统的渐近稳定性


系统的线性

第三节 模型算法控制(MAC) 一. 预测模型


u (k N 1) h1 h u (k N 2) 2 u (k N M ) u (k N M 1) u (k M 2) u (k M 3) u (k P N ) hN
主要内容 预测模型 反馈校正 参考轨迹 滚动优化
第三节 模型算法控制(MAC) 一. 预测模型

MAC的预测模型 渐近稳定线性被控对象的单位脉冲响应曲线
y
有限个采样周期后
lim h j 0
1 1 h2 h 0 hN
j
1
2
N
t/T
系统的离散脉冲响应示意图
第三节 模型算法控制(MAC) 一. 预测模型
第二节 预测控制的基本原理 二.滚动优化（在线优化）

滚动优化示意图
yr
y
k 时刻优化 2 1 3
1─参考轨迹yr (虚线) 2─最优预测输出y(实线) 3─最优控制作用u
u
k+1 时刻优化
yr
y
2 1 3
u
k k+1 t/T
第二节 预测控制的基本原理 三.反馈校正（误差校正）

模型失配
实际被控过程存在非线性、时变性、不确定性等原因， 使基于模型的预测不可能准确地与实际被控过程相符
U1 (k ) u(k N 1) u(k N 2) u(k 1)1( N 1)
U2 (k ) u(k ) u(k 1) u(k M 1)1M
第三节 模型算法控制(MAC) 二. 反馈校正
以当前过程输出测量值与模型计算值之差修正模型预测值
yP (k j) ym (k j) j y(k ) ym (k )
第三节 模型算法控制(MAC) 一. 预测模型
Ym (k ) H1U1 (k ) H 2U 2 (k )
h1 h 2 h2 h3 H2 hM h M 1 hP 1 P( N 1) hP
预测控制有关公司及产品 SetPoint : IDCOM DMC : DMC AspenTech : SetPoint Inc : SMC- IDCOM DMC Corp : DMCplus Profimatics: PCT Honeywell : Profimatics : RMPCT Adersa(法) : HIECON Invensys : Predictive Control Ltd : Connoisseur DOT(英) : STAR
yr (k j) j y(k ) (1 j ) yd
Ts ——采样周期
j 1, 2, , P
e

Ts T
T ——参考轨迹的时间常数
y(k)——当前时刻过程输出 yd ——设定值
T
Yr (k ) yr (k 1) yr (k 2) yr (k P)1P

最优控制
通过使某一性能指标最优化来确定其未来的控制作用的

局部优化
不是采用一个不变的全局最优目标，而是采用滚动式的 有限时域优化策略。在每一采样时刻，根据该时刻的优 化性能指标，求解该时刻起有限时段的最优控制率

在线滚动
计算得到的控制作用序列也只有当前值是实际执行的， 在下一个采样时刻又重新求取最优控制率
ym (k ) hi u (k i)
i 1 N

YP (k ) Ym (k ) βe(k )
e(k ) y(k ) ym (k )
β β1
β2 βP
T
T
YP (k ) yP (k 1) yP (k 2) yP (k P)1P
T
h2 hM 1 hM hP 1
T
0 hP M 2
hN 0 H1
hN 1 hN 0 hN
h1 h1 h2 P M 1 hi i 1 P M
ym (k j ) hi u (k j i)
i 1 N
j 1, 2, , M 1
N
ym ( k j )
j M 1 i 1
h u(k M 1) h u(k j i)
i i i j M 2
j M , M 1, , P
第一节 预测控制的发展
预测控制的特点

建模方便，对模型要求不高 滚动的优化策略，具有较好的动态控制效果


简单实用的反馈校正，有利于提高控制系统的 鲁棒性
不增加理论困难，可推广到有约束条件、大纯 滞后、非最小相位及非线性等过程 是一种计算机优化控制算法
第二节 预测控制的基本原理
模型预测控制与PID控制
1987年，Clarke 提出了基于时间序列模型和在线辨识的 广义预测控制(Generalized Predictive Control， GPC) 1988年，袁璞提出了基于离散状态空间模型的状态反馈预 测控制(State Feedback Predictive Control， SFPC)
第一节 预测控制的发展

要求
精确的数学模型
第一节 预测控制的发展

工业过程的特点

多变量高维复杂系统难以建立精确的数学模型 工业过程的结构、参数以及环境具有不确定性、 时变性、非线性，最优控制难以实现
基于模型的控制，但对模型的要求不高

预测控制的产生



采用滚动优化策略，以局部优化取代全局最优
利用实测信息反馈校正，增强控制的鲁棒性
第一节 预测控制的发展
1978年，Richalet 、Mehra提出了基于脉冲响应的模型预 测启发控制(Model Predictive Heuristic Control ， MPHC)，后转化为模型算法控制(Model Algorithmic Control，MAC)
1979年，Cutler提出了基于阶跃响应的动态矩阵控制 (Dynamic Matrix Control，DMC)
t/T
N
0 u
1
2
0.8 5 6
y (k ) hi u (k i )
i 1
2 1 u(0) u(1)
y(t ) g ( )u(t )d
0

t/T
第三节 模型算法控制(MAC) 一. 预测模型

采用脉冲响应模型对未来时刻输出进行预测
ym (k j ) hi u (k j i)

预测模型形式

参数模型：如微分方程、差分方程 非参数模型：如脉冲响应、阶跃响应
第二节 预测控制的基本原理 一.预测模型（内部模型）

基于模型的预测示意图
过去 未来 3 y 4
1
u k 时刻 2
1—控制策略Ⅰ 2—控制策略Ⅱ
3—对应于控制策略Ⅰ的输出 4—对应于控制策略Ⅱ的输出
第二节 预测控制的基本原理 二.滚动优化（在线优化）