初二数学-反比例函数难题拓展(学生版)

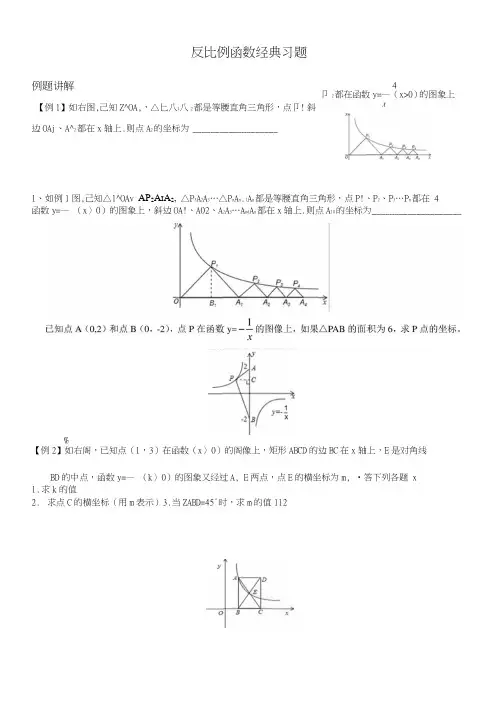
反比例函数经典习题例题讲解【例1】如右图,己知Z^OA,，△匕八|八2都是等腰直角三角形，点卩! 斜边OAj 、A^2都在x 轴上.则点A 2的坐标为 ___________________ 1、如例1图,己知△l^OAv AP 2A I A 2, △P 3A 2A 3…△P n A n .1A n 都是等腰直角三角形，点P!、P 2、P 3…P n 都在 4 函数y=— （x 〉0）的图象上，斜边OA!、A02、A 2A 3…A nd A n 都在x 轴上.则点A 10的坐标为 ____________________%【例2】如右阁，已知点（1，3）在函数（x 〉0）的阁像上，矩形ABCD 的边BC 在x 轴上，E 是对角线BD 的中点，函数y=— （k 〉0）的图象又经过A, E 两点，点E 的横坐标为m, •答下列各题 x1. 求k 的值2. 求点C 的横坐标（用m 表示）3.当ZABD=45°时，求m 的值1124 卩2都在函数y=— （x>0）的图象上， x21、已知：如图，矩形ABCD的边BC在x轴上，E是对角线AC、BD的交点，反比例函数y= —（x〉0）的图 x 象经过A, E两点，点E的纵坐标为m.（1）求点A坐标（用m表示）2、如图1,矩形ABCD的边BC在x轴的正半轴上，点E （m, 1）是对角线BD的中点,点A、E在反比例函数的阉象上.（1）求AB的长；b k（2）当矩形ABCD是正方形时，将反比例函数—的图象沿y轴翻折，得到反比例函数y= 2的图象（如图2），求卜的值；（3）直线y=-x上有一长为^动线段MN,作MH、NP都平行y轴交在条件（2）下，第一象限A的双曲线ky=—于点H、P,问四边形MHPN能否为平行四边形（如阁3） ?若能，请求出点M的坐标；若不能，请说明 x理由.【例3】在平面直角坐标系中，已知A（1，0），B（0，1）,矩形OMPN的相邻两边OM, ON分别在x, y轴的正半轴上，O为原点，线段AB与矩形OMPN的两边MRNP的交点分别为E,F,AAOF^ ABOE （顶点依次对应）（1）求ZFOE;（2）求证：矩形OPMN的顶点P必在某个反比例函数图像上，并写出该函数的解析式。

反比例函数难题拓展填空题1.（2011 浙江金华，16，4 分）如图，将一块直角三角板OAB 放在平面直角坐标系中， Bk（2 ，0），∠AOC ＝60°，点A 在第一象限，过点 A 的双曲线为y=x，在x 轴上取一点P，过点P 作直线OA 的垂线l，以直线l 为对称轴，线段OB 经轴对称变换后的像是O′B′. （1））当点O′与点A 重合时，点P 的坐标是.（2））设P（t，0）当O′B′与双曲线有交点时，t 的取值范围是.2.（2011 广东东莞，6，4 分）已知反比例函数y k的图象经过（1，－2）．则k ．x3.（2011 山东滨州，18 ，4 分）若点A(m，－2)在反比例函数y y≥－2 时，自变量x 的取值范围是. 4的图像上，则当函数值x4.（2011 四川南充市，14，3 分）过反比例函数y= k(k≠0)图象上一点A，分别作x 轴，y x轴的垂线，垂足分别为B,C，如果⊿ABC 的面积为 3.则k 的值为.2 5.（2011 宁波市，18 ，3 分）如图，正方形A1B1P1 P2 的顶点P1 、P2 在反比例函数y＝（xx＞0 ）的图像上，顶点A1、B1 分别在x 轴和y 轴的正半轴上，再在其右侧作正方形P2 P3A2B2，顶点P3 在反比例函数y＝2（x＞0）的图象上，顶点A3 在x 轴的正半轴上，则点P3 的坐标x为6.（2011 浙江衢州,5,4 分）在直角坐标系中，有如图所示的Rt ABO, AB x轴于点B ，斜边AO 10，sin AOB 3,反比例函数y5k( xx0) 的图像经过AO的中点C ，且与AB 交于点D ,则点D 的坐标为.yICDO B x（第15 题）7. (2011 浙江绍兴，13 ，5 分) 若点A(1, y ), B(2, y ) 是双曲线y 3上的点，则1 2xy1 y2 （填“>”,“<“”=”）.8. （2011 浙江丽水，16，4 分）如图，将一块直角三角板OAB 放在平面直角坐标系中，B(2 ，0) ，∠AOC ＝60° ，点A 在第一象限，过点 A 的双曲线为y= k，在x 轴上取一点P，过点P x作直线OA 的垂线l，以直线l 为对称轴，线段OB 经轴对称变换后的像是O′B′.（1））当点O′与点A 重合时，点P 的坐标是.（2））设P(t，0)当O′B′与双曲线有交点时，t 的取值范围是.9. （2011 湖南常德，5，3 分）如图1 所示的曲线是一个反比例函数图象的一支，点 A 在此曲线上，则该反比例函数的解析式为.y3 AO 1 x图 110 ．（2011 江苏苏州，18,3 分）如图，已知点 A 的坐标为（ 3 ，3），AB ⊥x 轴，垂足为B，连接OA，反比例函数y= k（k>0 ）的图象与线段OA、AB 分别交于点C、D.若AB=3BD ，x以点C 为圆心，CA 的5倍的长为半径作圆，则该圆与4x 轴的位置关系是（填“相离、”“相切”或“相）交”11.（2011 山东济宁，11，3 分）反比例函数y 范围是．m 1的图象在第一、三象限，则m 的取值x12.（2011 四川成都，25,4 分）在平面直角坐标系xOy 中，已知反比例函数y 2k(kx0) 满足：当x 0 时，y 随x 的增大而减小．若该反比例函数的图象与直线y x3k 都经过点P，且OP 7 ，则实数k= .13.（2011 安徽芜湖，15 ，5 分）如图，在平面直角坐标系中有一正方形AOBC ，反比例函数y kx经过正方形AOBC 对角线的交点，半径为（ 4 2 2 ）的圆内切于△ABC，则k 的值为．14.（2011 广东省，6，4 分）已知反比例函数y k的图象经过（1，－2）．则k ．x1 5. (2011 江苏南京，15，2 分)设函数y的值为．2与y xx1 11 的图象的交战坐标为（a，b），则a b16.（2011 上海，11，4 分）如果反比例函数y k（k 是常数，k≠0）的图像经过点(－1，x2) ，那么这个函数的解析式是．17.（2011 湖北武汉市，16 ，3 分）如图，□ABCD 的顶点A，B 的坐标分别是A（－1，0），B（0，－2），顶点C，D 在双曲线y= △ABE 面积的 5 倍，则k= ．k上，边AD 交y 轴于点E，且四边形BCDE 的面积是x18.（2011 湖北黄冈，4，3 分）如图：点 A 在双曲线y面积S△AOB =2，则k=．k上，AB ⊥x轴于B，且△AOB 的xBO xA第 4 题图19.（2011 湖北黄石，15 ，3 分）若一次函数y=kx+1 的图象与反比例函数y=公共点，则实数k 的取值范围是。

反比例函数难题拓展填空题1. （2011浙江金华，16，4分）如图，将一块直角三角板OAB 放在平面直角坐标系中，B （2，0），∠AOC ＝60°，点A 在第一象限，过点A 的双曲线为y= kx ，在x 轴上取一点P ，过点P作直线OA 的垂线l ，以直线l 为对称轴，线段OB 经轴对称变换后的像是O ′B ′. （1）当点O ′与点A 重合时，点P 的坐标是.（2）设P （t ，0）当O ′B ′与双曲线有交点时，t 的取值范围是 .2. （2011广东东莞，6，4分）已知反比例函数ky x=的图象经过（1，－2）．则k = ． 3. （2011山东滨州，18，4分）若点A(m ，－2)在反比例函数4y x=的图像上，则当函数值y ≥－2时，自变量x 的取值范围是___________. 4. （2011四川南充市，14，3分）过反比例函数y=xk(k ≠0)图象上一点A ，分别作x 轴，y 轴的垂线，垂足分别为B,C ，如果⊿ABC 的面积为3.则k 的值为 .5. （2011宁波市，18，3分）如图，正方形A 1B 1P 1P 2的顶点P 1、P 2在反比例函数y ＝2x （x ＞0）的图像上，顶点A 1、B 1分别在x 轴和y 轴的正半轴上，再在其右侧作正方形P 2P 3A 2B 2，顶点P 3在反比例函数y ＝2x（x ＞0）的图象上，顶点A 3在x 轴的正半轴上，则点P 3的坐标为6. （2011浙江衢州,5,4分）在直角坐标系中，有如图所示的t ,R ABO AB x ∆⊥轴于点B ，斜35=(0)ky xx=>的图像经过AO的中点C，且与AB交于的坐标为 .7. (2011浙江绍兴，13，5分) 若点12(1,),(2,)A yB y是双曲线3yx=上的点，则1y2y（填“>”,“<”“=”）.8. （2011浙江丽水，16，4分）如图，将一块直角三角板OAB放在平面直角坐标系中，B(2，0)，∠AOC＝60°，点A在第一象限，过点A的双曲线为y=kx，在x轴上取一点P，过点P 作直线OA的垂线l，以直线l为对称轴，线段OB经轴对称变换后的像是O′B′.（1）当点O′与点A重合时，点P的坐标是.（2）设P(t，0)当O′B′与双曲线有交点时，t的取值范围是 .9. （2011湖南常德，5，3分）如图1所示的曲线是一个反比例函数图象的一支，点A在此曲线上，则该反比例函数的解析式为_______________.10．（2011江苏苏州，18,3分）如图，已知点A的坐标为（3，3），AB⊥x轴，垂足为B，（第15题）xyCDBOIy1OAx3图1连接OA ，反比例函数y=xk（k>0）的图象与线段OA 、AB 分别交于点C 、D.若AB=3BD ，以点C 为圆心，CA 的45倍的长为半径作圆，则该圆与x 轴的位置关系是___________（填“相离”、“相切”或“相交”）11. （2011山东济宁，11，3分）反比例函数1m y x-=的图象在第一、三象限，则m 的取值范围是 ．12. （2011四川成都，25,4分）在平面直角坐标系xOy 中，已知反比例函数2(0)ky k x=≠满足：当0x <时，y 随x 的增大而减小．若该反比例函数的图象与直线3y x k =-+都经过点P ，且7OP =，则实数k=_________.13. （2011安徽芜湖，15，5分）如图，在平面直角坐标系中有一正方形AOBC ，反比例函数ky x=经过正方形AOBC 对角线的交点，半径为（422-）的圆内切于△ABC ，则k 的值为 ．14. （2011广东省，6，4分）已知反比例函数ky x=的图象经过（1，－2）．则k = ． 15. (2011江苏南京，15，2分)设函数2y x =与1y x =-的图象的交战坐标为（a ，b ），则11a b-的值为__________．16. （2011上海，11，4分）如果反比例函数k yx=（k是常数，k≠0）的图像经过点(－1，2)，那么这个函数的解析式是__________．17. （2011湖北武汉市，16，3分）如图，□ABCD的顶点A，B的坐标分别是A（－1，0），B（0，－2），顶点C，D在双曲线y=xk上，边AD交y轴于点E，且四边形BCDE的面积是△ABE 面积的5倍，则k=_____．18. （2011湖北黄冈，4，3分）如图：点A在双曲线kyx=上，AB⊥x轴于B，且△AOB的面积S△AOB=2，则k=______．19. （2011湖北黄石，15，3分）若一次函数y=kx+1的图象与反比例函数y=x1的图象没有公共点，则实数k的取值范围是。

《反比例函数》拓展题(含答案)知识点回顾由于反比例函数解析式及图象的特殊性，很多中考试题都将反比例函数与面积结合起来进行考察。

这种考察方式既能考查函数、反比例函数本身的基础知识内容，又能充分体现数形结合的思想方法，考查的题型广泛，考查方法灵活，可以较好地将知识与能力融合在一起。

下面就反比例函数中与面积有关的问题的四种类型归纳如下：一、利用反比例函数中|k|的几何意义求解与面积有关的问题设P为双曲线上任意一点，过点P作x轴、y轴的垂线PM、PN，垂足分别为M、N，则两垂线段与坐标轴所围成的的矩形PMON的面积为S=|PM|×|PN|=|y|×|x|=|xy|∴xy=k 故S=|k| 从而得结论1：过双曲线上任意一点作x轴、y轴的垂线，所得矩形的面积S为定值|k| 对于下列三个图形中的情形，利用三角形面积的计算方法和图形的对称性以及上述结论，可得出对应的面积的结论为：结论2：在直角三角形ABO中，面积S=结论3：在直角三角形ACB中，面积为S=2|k|结论4：在三角形AMB中，面积为S=|k|例题讲解【例1】如右图，已知△P10A1，△P2A1A2都是等腰直角三角形，点P1、P2都在函数y=4x（x＞0）的图象上，斜边OA1、A1A2都在x轴上．则点A2的坐标为 .1、如例1图，已知△P1OA1，△P2A1A2，△P3A2A3…△P n A n-1A n都是等腰直角三角形，点P1、P2、P3…P n都在函数y=4x（x＞0）的图象上，斜边OA1、A1A2、A2A3…A n-1A n都在x轴上．则点A10的坐标为2、已知点A（0,2）和点B（0，-2），点P在函数y=1x的图像上，如果△PAB的面积为6，求P点的坐标。

【例2】如右图，已知点（1,3）在函数y=kx（x＞0）的图像上，矩形ABCD的边BC在x轴上，E是对角线BD的中点，函数y=kx（k＞0）的图象又经过A,E两点，点E的横坐标为m，解答下列各题1.求k的值2.求点C的横坐标（用m表示）3.当∠ABD=45°时，求m的值1121、已知：如图，矩形ABCD的边BC在x轴上，E是对角线AC、BD的交点，反比例函数y=2 x（x＞0）的图象经过A，E两点，点E的纵坐标为m．（1）求点A坐标（用m表示）（2）是否存在实数m，使四边形ABCD为正方形，若存在，请求出m的值；若不存在，请说明理由2、如图1，矩形ABCD的边BC在x轴的正半轴上，点E（m，1）是对角线BD的中点，点A、E在反比例函数y=kx的图象上．（1）求AB的长；（2）当矩形ABCD是正方形时，将反比例函数y=kx的图象沿y轴翻折，得到反比例函数y=1kx的图象（如图2），求k1的值；（3）直线y=-x上有一长为2动线段MN，作MH、NP都平行y轴交在条件（2）下，第一象限内的双曲线y=kx于点H、P，问四边形MHPN能否为平行四边形（如图3）？若能，请求出点M的坐标；若不能，请说明理由．【例3】在平面直角坐标系中，已知A(1,0),B(0,1)，矩形OMPN的相邻两边OM，ON分别在x，y轴的正半轴上，O为原点，线段AB与矩形OMPN的两边MP,NP的交点分别为E,F,△AOF∽△BOE（顶点依次对应）（1）求∠FOE；（2）求证：矩形OPMN的顶点P必在某个反比例函数图像上，并写出该函数的解析式。

专题10 反比例函数的综合训练(数形结合)1．如图，一次函数4y x =-+的图象与反比例函数()0k y k x=≠在第一象限内的图象交于()1,A n 和()3,B m 两点．(1)求反比例函数的表达式．(2)在第一象限内，当一次函数4y x =-+的值大于反比例函数()0k y k x=≠的值时，写出自变量x 的取值范围(3)求△AOB 面积．2．如图，反比例函数2y x=的图象与一次函数y x b =+的图象交于(1, )A m ，(2, )B n -两点，一次函数图象与y 轴交于点C ，与x 轴交于点D ．（1）求一次函数的表达式；（2）观察图象，写出2kx b x>+时自变量x 的取值范围； （3）连接OA ，在第三象限的反比例函数图象上是否存在一点P ，使得2OCP OCA S S =△△？若存在，请求出点P 的坐标；若不存在，请说明理由.3．如图，在平面直角坐标系xOy 中，已知正比例函数y ＝12x 的图象与反比例函数y ＝k x的图象交于A （a ，﹣2），B 两点．（1）求反比例函数的表达式和点B 的坐标；（2）P 是第一象限内反比例函数图象上一点，过点P 作y 轴的平行线，交直线AB 于点C ，连接PO ，若△POC 的面积为3，求点P 的坐标．4．如图，等腰Rt ABO 的直角顶点O 与平面直角坐标系的原点重合，反比例函数()0m y x x=<的图象经过点A ，反比例函数()0n y x x =>的图象经过点B ．(1)试猜想m 与n 的数量关系，并说明理由；(2)若2n =，求当点B 的纵坐标分别为1和2时，等腰Rt ABO 的面积；(3)请直接写出当2n =时，等腰Rt ABO 的面积的最小值_________．5．如图，一次函数()=+0y mx n m ≠的图象与反比例函数()0k y k x =≠的图象相交于第二、四。

专题16反比例函数与几何图形综合问题【中考考向导航】目录【直击中考】 (1)【考向一反比例函数中K值的几何意义】 (1)【考向二反比例函数与三角形的综合问题】 (4)【考向三反比例函数与矩形的综合问题】 (6)【考向四反比例函数与菱形的综合问题】 (9)【考向五反比例函数与正方形的综合问题】 (11)【考向六反比例函数与圆的综合问题】 (15)【直击中考】【考向一反比例函数中K值的几何意义】【变式训练】1．（2023·安徽宿州·统考一模）如图，若反比例函数______在反比例函数3．（2022·黑龙江绥化·校考二模）如图，在过点A、C两点，点B在4．（2023秋·安徽池州·九年级统考期末）AC交y轴于点B，若点B是=【考向二反比例函数与三角形的综合问题】(1)求反比例函数的解析式；(2)过点A作AP垂直OA，交反比例函数的图象于点①求直线AC的解析式；②求点P的坐标．【变式训练】(1)求反比例函数的解析式；(2)坐标平面内有一点D，若以A(1)求反比例函数的表达式；(2)求等边△ACD的边长．【考向三反比例函数与矩形的综合问题】(1)直接写出B，C，D三点的坐标；(2)若将矩形向下平移，矩形的两个顶点值．【变式训练】上两点，的顶点【考向四反比例函数与菱形的综合问题】（1）求k的值及AB所在直线的函数表达式；（2）将这个菱形沿x轴正方向平移，当顶点【变式训练】是菱形，点(1)求一次函数与反比例函数的解析式；(2)设点P是直线AB上一动点，且ABCD(1)求双曲线y2的函数关系式及(2)判断点B是否在双曲线上，并说明理由；(3)若BA的延长线与双曲线【考向五反比例函数与正方形的综合问题】(1)求反比例函数的解析式；(2)若将正方形ABCD沿x轴向右平移得到正方形标，并判断点B′是否在该反比例函数的图象上，说明理由．【变式训练】在平面直角坐标系中，点(1)求反比例函数的解析式；(2)求四边形OAFM 的面积．2．（2022·山东济南·校考一模）如图，四边形35AE OE =．中点，以备用图4．（2022春·江苏苏州·八年级星海实验中学校考期中）如图，在平面直角坐标系中，四边形ABCD 为正方形，已知点()6,0A -、()7,3D -，点B 、C 在第二象限内．(1)点B 的坐标_________；(2)将正方形ABCD 以每秒2个单位的速度沿x 轴向右平移t 秒，若存在某一时刻t ，使在第一象限内点B 、D 两点的对应点B '、D ¢正好落在某反比例函数的图像上，请求出此时t 的值以及这个反比例函数的解析式；(3)在（2）的情况下，问是否存在y 轴上的点P 和反比例函数图像上的点Q ，使得以P 、Q 、B '、D ¢四个点为顶点的四边形是平行四边形？若存在，请直接写出符合题意的点Q 的坐标；若不存在，请说明理由．【考向六反比例函数与圆的综合问题】【变式训练】在反比例函数。

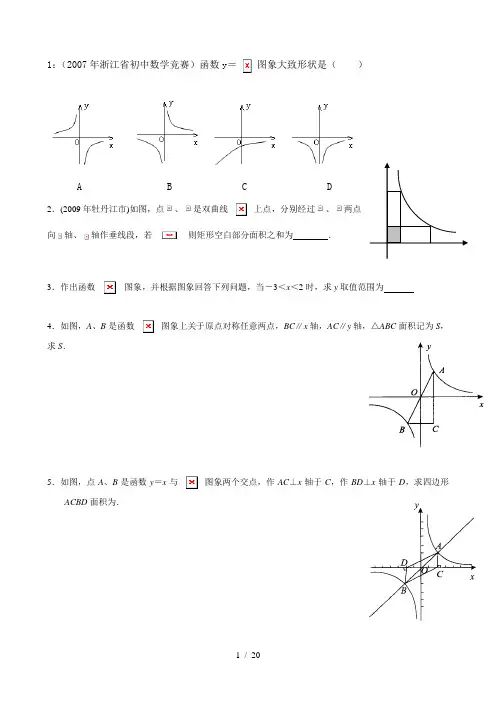
1：（2007年浙江省初中数学竞赛）函数y＝图象大致形状是（）A B C D2．(2009年牡丹江市)如图，点、是双曲线上点，分别经过、两点向轴、轴作垂线段，若则矩形空白部分面积之和为．3．作出函数图象，并根据图象回答下列问题，当－3＜x＜2时，求y取值范围为4．如图，A、B是函数图象上关于原点对称任意两点，BC∥x轴，AC∥y轴，△ABC面积记为S，求S．5．如图，点A、B是函数y＝x与图象两个交点，作AC⊥x轴于C，作BD⊥x轴于D，求四边形ACBD面积为．6．已知：如图，在平面直角坐标系xOy中，Rt△OCD一边OC在x轴上，∠C＝90°，点D在第一象限，OC＝3，DC＝4，反比例函数图象经过OD中点A．(1)求该反比例函数解析式；(2)若该反比例函数图象与Rt△OCD另一边交于点B，求过A、B两点直线解析式．7．如图，A、B两点在函数图象上．(1)求m值及直线AB解析式；(2)如果一个点横、纵坐标均为整数，那么我们称这个点是格点．请直接写出图中阴影部分(不包括边界)所含格点坐标．8．如图，已知点A在反比例函数图象上，AB⊥x轴于点B，点C(0，1)，若△ABC面积是3，则反比例函数解析式为____________．9．如图，双曲线(k＞0)经过矩形OABC边BC中点E，交AB于点D。

若梯形ODBC面积为3，求双曲线解析式为．10．如图，直线y＝kx＋b与反比例函数(x＜0)图象交于点A，B，与x轴交于点C，其中点A坐标为(－2，4)，点B横坐标为－4．(1)试确定反比例函数关系式；(2)求△AOC面积．11．如图，已知A(－4，n)，B(2，－4)是一次函数y＝kx＋b图象和反比例函数图象两个交点．(1)求反比例函数和一次函数解析式；(2)求直线AB与x轴交点C坐标及△AOB面积；(3)求方程解(请直接写出答案)；(4)求不等式解集(请直接写出答案)．12．如图，已知点A，B在双曲线上，AC⊥x轴于点C，BD⊥y轴于点D，AC与BD交于点P，P是AC中点，若△ABP面积为3，求k值．13（2010 山东济南）如图,已知直线与双曲线交A ，B 两点，且点A 横坐标为4.（1）求k 值； （2）若双曲线上一点C 纵坐标为8，求△AOC 面积；（3）过原点O 另一条直线l 交双曲线于P ，Q 两点（P 点在第一象限），若由点A ，B ，P ，Q 为顶点组成四边形面积为24，求点P 坐标．14（2010 河北）如图13，在直角坐标系中，矩形OABC 顶点O 与坐标原点重合，顶点A ，C 分别在坐标轴上，顶点B 坐标为（4，2）．过点D （0，3）和E （6，0）直线分别与AB ，BC 交于点M ，N ． （1）求直线DE 解析式和点M 坐标；（2）若反比例函数（x ＞0）图象经过点M ，求该反比例函数解析式，并通过计算判断点N 是否在该函数图象上；（3）若反比例函数（x ＞0）图象与△MNB 有公共点，请直接．．写出m 取值范围．xMNyD AB CEO图1321．（2010四川）一次函数y=kx+b 图象与反比例函数y=图象交于点A （2，1），B （－1，n ）两点。

11：（2007年浙江省初中数学竞赛）函数y= —」图象的大致形状是（x2 （2009年牡丹江市）如图，点A、B是双曲线y=3上的点，分别经过A、B两点向X轴、y轴作垂线x骰，若Spn® =人则S +$£ =3. 已知y与2x-3成反比例，且时，y=- 2,求y与x的函数关系式.44. 已知函数y= y i- y2,且屮为x的反比例函数，y为x的正比例函数，且x--和x= 1时，y的值都21?求y 关于x 的函数关系式.边形ACBD 勺面积为（).6.如图，A 、B 是函数y2BC // x 轴，AC 〃 y 轴,7.x△ ABC 的面积记为 S,贝V （s=AC 丄x 轴于C,作BD 丄x 轴于D ，则四的图象上关于原点对称的任意两点，8.已知：如图，在平面直角坐标系xOy中，Rt △ OCD勺一边0C在x轴上，/ C= 90°,点D在第一象限，4，反比例函数的图象经过0D的中点A(1) 求该反比例函数的解析式；⑵若该反比例函数的图象与Rt △ OCD勺另一边交于点B求过A B两点的直线的解析式9.如图，A. B两点在函数y=—(XA0)的图象上.⑴求m的值及直线AB的解析式；⑵如果一个点的横、纵坐标均为整数，那么我们称这个点是格点？请直接写出图中阴影部分边界)所含格点的个数.(不包括12.如图，已知点A在反比例函数的图象上，AB丄x轴于点B,点C(0, 1)，若△ ABC的面积是3则反0C = 3, DC=x)OKI)Cy BxyjkA 0 B占 八4 ,点B 的横坐标为D r ------ Bm的图象的两个交交于A B 两点，过点A 作AM 丄x 轴，垂足为M,连结BM 若13?如图，直线 y = mx 与双曲线y k S ^ABM = 2,贝U k 的值是(15.如图，直线y=坐标为(一Z kx+ b 与反比例函数k (X V 0)的图象交于点 A, B,与x 轴交于点C,其中点A 的xk14.如图，双曲线y(k> 0)经过矩形xOABC 的边BC 的中点E ，交AB 于点D 。

1：（2007年浙江省初中数学竞赛）函数y ＝1x-图象的大致形状是（ ）A B C D3．已知y 与2x －3成反比例，且41=x 时，y ＝－2，求y 与x 的函数关系式．4．已知函数y ＝y 1－y 2，且y 1为x 的反比例函数，y 2为x 的正比例函数，且23-=x 和x ＝1时，y 的值都是1．求y 关于x 的函数关系式．5．作出反比例函数xy 12=的图象，并根据图象解答下列问题： (1)当x ＝4时，求y 的值；(2)当y ＝－2时，求x 的值；(3)当y ＞2时，求x 的范围．6．作出反比例函数xy 4-=的图象，结合图象回答： (1)当x ＝2时，y 的值；(2)当1＜x ≤4时，y 的取值范围；(3)当1≤y ＜4时，x 的取值范围．7．作出函数xy 12=的图象，并根据图象回答下列问题： (1)当x ＝－2时，求y 的值；(2)当2＜y ＜3时，求x 的取值范围； (3)当－3＜x ＜2时，求y 的取值范围．8．如图，A 、B 是函数xy 2=的图象上关于原点对称的任意两点，BC ∥x 轴，AC ∥y 轴， △ABC 的面积记为S ，则(s= )．9．如图，点A 、B 是函数y ＝x 与xy 1=的图象的两个交点，作AC ⊥x 轴于C ，作BD ⊥x 轴于D ，则四边形ACBD 的面积为( )．10．已知：如图，在平面直角坐标系xOy 中，Rt △OCD 的一边OC 在x 轴上，∠C ＝90°，点D 在第一象限，OC ＝3，DC ＝4，反比例函数的图象经过OD 的中点A ． (1)求该反比例函数的解析式；(2)若该反比例函数的图象与Rt △OCD 的另一边交于点B ，求过A 、B 两点的直线的解析式．11．如图，A 、B 两点在函数)0(>=x xmy 的图象上．(1)求m 的值及直线AB 的解析式；(2)如果一个点的横、纵坐标均为整数，那么我们称这个点是格点．请直接写出图中阴影部分(不包括边界)所含格点的个数．12．如图，已知点A 在反比例函数的图象上，AB ⊥x 轴于点B ，点C (0，1)，若△ABC 的面积是3，则反比例函数的解析式为____________．13．如图，直线y ＝mx 与双曲线xky =交于A ，B 两点，过点A 作AM ⊥x 轴，垂足为M ，连结BM ，若S △ABM ＝2，则k 的值是( )．14．如图，双曲线xky =(k ＞0)经过矩形OABC 的边BC 的中点E ，交AB 于点D 。

反比例函数难题拓展(含答案)————————————————————————————————作者：————————————————————————————————日期：反比例函数经典专题知识点回顾由于反比例函数解析式及图象的特殊性，很多中考试题都将反比例函数与面积结合起来进行考察。

这种考察方式既能考查函数、反比例函数本身的基础知识内容，又能充分体现数形结合的思想方法，考查的题型广泛，考查方法灵活，可以较好地将知识与能力融合在一起。

下面就反比例函数中与面积有关的问题的四种类型归纳如下：一、利用反比例函数中|k|的几何意义求解与面积有关的问题设P为双曲线上任意一点，过点P作x轴、y轴的垂线PM、PN，垂足分别为M、N，则两垂线段与坐标轴所围成的的矩形PMON的面积为S=|PM|×|PN|=|y|×|x|=|xy|∴xy=k 故S=|k| 从而得结论1：过双曲线上任意一点作x轴、y轴的垂线，所得矩形的面积S为定值|k| 对于下列三个图形中的情形，利用三角形面积的计算方法和图形的对称性以及上述结论，可得出对应的面积的结论为：结论2：在直角三角形ABO中，面积S=结论3：在直角三角形ACB中，面积为S=2|k|结论4：在三角形AMB中，面积为S=|k|例题讲解【例1】如右图，已知△P10A1，△P2A1A2都是等腰直角三角形，点P1、P2都在函数y=4x（x＞0）的图象上，斜边OA1、A1A2都在x轴上．则点A2的坐标为 .1、如例1图，已知△P1OA1，△P2A1A2，△P3A2A3…△P n A n-1A n都是等腰直角三角形，点P1、P2、P3…P n都在函数y=4x（x＞0）的图象上，斜边OA1、A1A2、A2A3…A n-1A n都在x轴上．则点A10的坐标为2、已知点A（0,2）和点B（0，-2），点P在函数y=1x的图像上，如果△PAB的面积为6，求P点的坐标。

【例2】如右图，已知点（1,3）在函数y=kx（x＞0）的图像上，矩形ABCD的边BC在x轴上，E是对角线BD的中点，函数y=kx（k＞0）的图象又经过A,E两点，点E的横坐标为m，解答下列各题1.求k的值2.求点C的横坐标（用m表示）3.当∠ABD=45°时，求m的值1121、已知：如图，矩形ABCD的边BC在x轴上，E是对角线AC、BD的交点，反比例函数y=2 x（x＞0）的图象经过A，E两点，点E的纵坐标为m．（1）求点A坐标（用m表示）（2）是否存在实数m，使四边形ABCD为正方形，若存在，请求出m的值；若不存在，请说明理由2、如图1，矩形ABCD的边BC在x轴的正半轴上，点E（m，1）是对角线BD的中点，点A、E在反比例函数y=kx的图象上．（1）求AB的长；（2）当矩形ABCD是正方形时，将反比例函数y=kx的图象沿y轴翻折，得到反比例函数y=1kx的图象（如图2），求k1的值；（3）直线y=-x上有一长为2动线段MN，作MH、NP都平行y轴交在条件（2）下，第一象限内的双曲线y=kx于点H、P，问四边形MHPN能否为平行四边形（如图3）？若能，请求出点M的坐标；若不能，请说明理由．【例3】在平面直角坐标系中，已知A(1,0),B(0,1)，矩形OMPN的相邻两边OM，ON分别在x，y轴的正半轴上，O为原点，线段AB与矩形OMPN的两边MP,NP的交点分别为E,F,△AOF∽△BOE（顶点依次对应）（1）求∠FOE；（2）求证：矩形OPMN的顶点P必在某个反比例函数图像上，并写出该函数的解析式。