胡运权排队论习题解

11.1 某建筑工地每月需用水泥800t ，每t 定价2000元，不可缺货。

设每t 每月保管费率为0.2%，每次订购费为300元，求最佳订购批量。

解：每月需求量R=800t/月，每次订购费3003=C 元，货物单价k=2000元/t ，每t 每月的保管费%2.020001⨯=C =4元 则最佳定购量4.34648003002213*=⨯⨯==C R C Q11．2一汽车公司每年使用某种零件150000件，每件每年保管费0.2元，不允许缺货，试比较每次订购费为1000元或100元两种情况下的经济订货批量解: 类型 不允许缺货，补充时间极短根据题意知 R=150000件 1c =0.2 3c =1000或100（1） 当每次订购费为1000元时候的经济订货批量*t =R c c 132=150000*2.01000*2=151=3.65 Q *=R *t =150000*151=38729.83 (2) 当每次订购费为100元时候的经济订货批量*t =R c c 132=150000*2.0100*2=0.0816 Q *=R *t =150000*0.0816=12247.811.12某冬季商品每件进价25元，售价45元。

订购费每次20元，单位缺货费45元，单位存储费5元，期初无存货。

该商品的需求量r 的概率分布见表11-4。

解：25=K 1C =5 2C =45 203=C4.0)100(4.050205452545212====+-=+-r P C C K C该商品在冬季来临前应订购100件。

11.13某厂生产需要某种部件。

该部件外购价值有850元，订购费每次2825元。

若自产，每若选择外购策略时，若发生购物数少于实际需求量的情况，差额部分工厂将自产。

假定期初存货为零。

求工厂的订购策略。

2c =1250,1c =2825,k=850,1c =45N= (2c -k) / (2c + 1c )= (1250-850)/(1250+45)=400/1295=0.30订购90件。

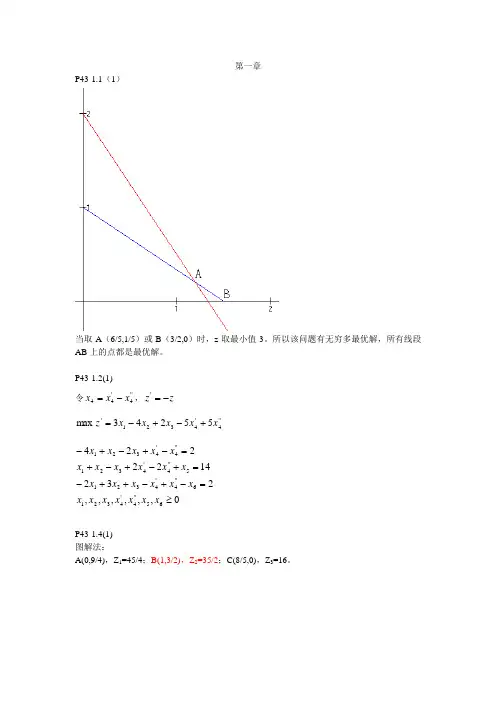
第一章P43-1.1（1）当取A （6/5,1/5）或B （3/2,0）时，z 取最小值3。

所以该问题有无穷多最优解，所有线段AB 上的点都是最优解。

P43-1.2(1)令''4'44x x x -=，z z -='''4'4321'55243max x x x x x z +-+-=,,,,,,232142222465''4'43216''4'43215''4'4321''4'4321≥=-+-++-=+-+-+=-+-+-x x x x x x x x x x x x x x x x x x x x x x x xP43-1.4(1) 图解法：A(0,9/4)，Z 1=45/4；B(1,3/2)，Z 2=35/2；C(8/5,0)，Z 3=16。

单纯形法：10 5 0 0C b X b b x1x2x3x4θ0 x39 3 4 1 0 30 x48 5 2 0 1 8/5δ10 5 0 00 x321/5 0 14/5 1 -3/5 3/210 x18/5 1 2/5 0 1/5 4δ0 1 0 -25 x23/2 0 1 5/14 -3/1410 x1 1 1 0 -1/7 2/7δ0 0 -5/14 -25/14依次相当于：原点；C；B。

P44-1.7(1)2 -1 2 0 0 0 -M -M -MC b X b b x1x2x3x4x5x6x7x8x9θ无界解。

两阶段法：阶段二：P45-1.10证明：CX (0)>=CX*，C*X*>=C*X (0) CX (0)-CX*+C*X*-C*X (0)>=0，即(C*-C)(X*-X (0))>=0。

P45-1.13设饲料i 使用x i （kg ），则543218.03.04.07.02.0m in x x x x x z ++++=s.t. 7001862354321≥++++x x x x x 305.022.05.054321≥++++x x x x x1008.022.05.054321≥++++x x x x x0,,,,54321≥x x x x x第二章P74-2.1(1)321532m ax y y y w ++=22321≤++y y y 243321≤++y y y 4334321=++y y y 无约束321,0,0y y y ≤≥P75-2.4(1),06353322232max 212121212121≥≥≤-≤+≤-≤++=y y y y y y y y y y y y w(2) (8/5,1/5)(3) 无穷多最优解。

胡运权运筹学第五版答案【篇一：运筹学基础及应用第四版胡运权主编课后练习答案】xt>习题一 p46 1.1 (a)412该问题有无穷多最优解，即满足4x1z?3。

6x26且0?x2?的所有?x1,x2?，此时目标函数值(b)用图解法找不到满足所有约束条件的公共范围，所以该问题无可行解。

1.2(a) 约束方程组的系数矩阵12a833106?403000200??0?1t最优解x??0,10,0,7,0,0?。

(b) 约束方程组的系数矩阵1a222314??2??最优解1.3(a)(1) 图解法11??2x??,0,,0?5?5?t。

最优解即为?3x14x295x12x28的解x31,2，最大值z352(2)单纯形法首先在各约束条件上添加松弛变量，将问题转化为标准形式 max z?10x1?5x2?0x3?0x4?3x1?4x2?x3?9s.t. ?5x12x2x48则p3,p4组成一个基。

令x1?x2?0得基可行解x??0,0,9,8?，由此列出初始单纯形表12。

??min?898,53?520，??min?2183,??142?2?新的单纯形表为1,20，表明已找到问题最优解x1?1, x2?32,x3?0 , x4?0。

最大值z*352(b) (1) 图解法6x1?2x2x1?x2?最优解即为?6x12x224x1?x2?5的解x73,22?，最大值z172(2) 单纯形法首先在各约束条件上添加松弛变量，将问题转化为标准形式 max z?2x1?x2?0x3?0x4?0x55x2?x3?15??s.t. ?6x1?2x2?x4?24xxx5125则p3，p4，p5组成一个基。

令x1?x2?0得基可行解x??0,0,15,24,5?，由此列出初始单纯形表12。

??min??,245?,??461?155,24,20，??min?3?32?2新的单纯形表为【篇二：运筹学基础及应用第四版胡运权主编课后练习答案】xt>习题一 p46 1.1 (a)41的所有?x1,x2?，此时目标函数值2该问题有无穷多最优解，即满足4x1?6x2?6且0?x2?z?3。

习题解答（6）1． 证明：序列7、6、5、4、3、2不可能是某个简单图的次的序列。

证明：由定理1有 q v d v v 2)(=∑∈，而在此序列中，∑∈vv v d )(27=为奇数，所以此序列不可能是某个简单图的次的序列。

2． 已知九个人921,,v v v 中1v 和两个人握过手，32,v v 各和四个人握过手，7654,,,v v v v 各 和五个人握过手，98,v v 各和六个人握过手，证明从这九个人中一定可以找出三个人互相握过手。

证明：该问题可以表述为一个9点（代表9个人）的简单图问题，不存在重复边和环，则由题意知，5)()()()(,4)()(,2)(7654321=======v d v d v d v d v d v d v d ， .6)()(98==v d v d 其中],[j i v v 表示i v 和j v 握过手。

对9v 而言，因,6)(9=v d 所以7654,,,v v v v 中至少有两点存在与9v 的连线。

设该两点为4v 和5v ，假设4v 和9v 相联的其它5点之间无边，则,358)(4=-≤v d 这与已知 5)(4=v d 相矛盾。

故假设不成立，即4v 与上述5点间必存在至少两条边，设其中一点为k v ，则k v ， 94,v v 两两相连，即存在三人互相握过手。

3．已知下图表示7个城市间抑修建一条连接各个城市的通信线路，各边的权数表示两个城市之间线路的修建费。

利用“丢边破圈法”，求连接个城市通信线路最小修建费用方案。

F 50 EB 23 C解：在上图中依次去掉GD （6），GC （52），EF （50），AF （48），BG （46）AG （45）各边后，即求得最小生成树T，如下图所示，T中各边权数之和为219。

F E39 42 40A G D37 3823B C。

第一章习题解答1.1 用图解法求解下列线性规划问题。

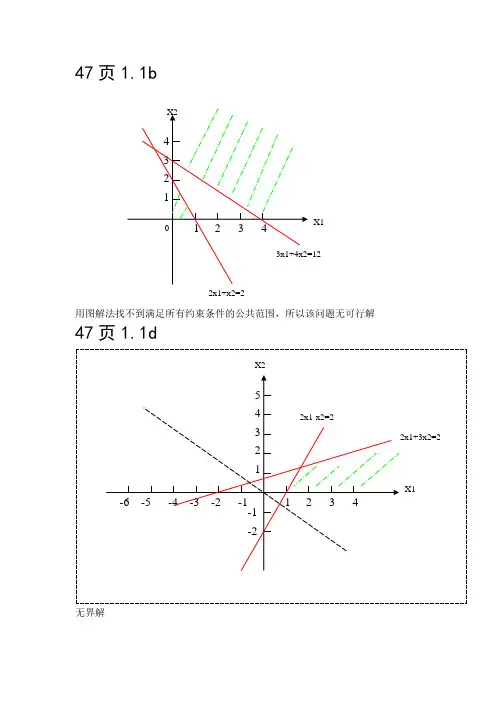
并指出问题具有惟一最优解、无穷多最优解、无界解还是无可行解。

+=32min 21x x Z +=23max 21x x Z ⎪⎩⎪⎨⎧≥≥+≥+0,422664.)1(212121x x x x x x st ⎪⎩⎪⎨⎧≥≥+≤+0,124322.)2(212121x x x x x x st ⎪⎩⎪⎨⎧≤≤≤≤≤++=85105120106.max )3(212121x x x x st x x Z ⎪⎩⎪⎨⎧≥≤+−≥−+=0,23222.65max )4(21212121x x x x x x st x x Z 第一章习题解答无穷多最优解，,422664.32min )1(21212121⎪⎩⎪⎨⎧≥≥+≥++=x x x x x x st x x Z 是一个最优解3,31,121===Z x x 该问题无解⎪⎩⎪⎨⎧≥≥+≤++=0,124322.23max )2(21212121x x x x x x st x x Z 第一章习题解答85105120106.max )3(212121⎪⎩⎪⎨⎧≤≤≤≤≤++=x x x x st x x Z 唯最优解16,6,1021===Z x x 唯一最优解，该问题有无界解⎪⎩⎪⎨⎧≥≤+−≥−+=0,23222.65max )4(21212121x x x x x x st x x Z 第一章习题解答1.2 将下述线性规划问题化成标准形式。

1422245243min )1(432143214321⎪⎪⎧≤+−+−=−+−+−+−=x x x x x x x x x x x x Z .,0,,23243214321⎪⎪⎩⎨≥≥−++−无约束x x x x x x x x st ⎪⎩⎪⎨⎧≥≤≤−+−=++−+−=无约束321321321321,0,0624322min )2(x x x x x x x x x st x x x Z 第一章习题解答.2321422245243min )1(4321432143214321⎪⎪⎪⎨⎧≥−++−≤+−+−=−+−+−+−=x x x x x x x x x x x x st x x x x Z ,0,,4321⎪⎩≥无约束x x x x ⎪⎪⎩⎪⎪⎨⎧≥=−+−++−=+−+−+=−+−+−+−+−=0,,,,,232142222455243max 64241321642413215424132142413214241321x x x x x x x x x x x x x x x x x x x x x x x st x x x x x Z 第一章习题解答⎪⎪⎨⎧≥≤≤−+−=++−+−=无约束321321321321,0,0624322min)2(x x x x x x x x x st x x x Z ⎩⎪⎩⎪⎨⎧≥=++−+=−++−+−+=0,,,,6243322max 43231214323121323121323121x x x x x x x x x x x x x x st x x x x Z第一章习题解答634334max )3(3212121⎪⎪⎧=−+=++=x x x x x st x x Z 517,0,1,59,524,,1,0424321421=====⎪⎪⎩⎨=≥=++Z x x x x j x x x x j 该题是唯一最优解：）（"第一章习题解答⎪⎧≤++−≤++++=151565935121510max 321321x x x x x x x x x Z 该题无可行解。

解：设阶段变量: k=1,2,3状态变量: 第k 个月初的库存量 决策变量: 第k 个月的生产量 状态转移方程: 阶段指标:由于在4月末, 仓库存量为0, 所以对于k=4阶段来说有两种决策：5+4=9 40x4()f x =1 41x对K=3 334()54()f x x f xK=2解得: 第一个月生产500份, 第二个月生产600份, 第三个月生产0份, 第四个月生产0份。

7.4某公司有资金4万元, 可向A, B, C三个项目投资, 已知各项目不同投资额的相应效益值如表7-20所示, 问如何分配资金可使总效益最大。

表7-20解：设阶段变量k, , 每一个项目表示一个阶段;状态变量Sk, 表示可用于第k阶段及其以后阶段的投资金额；决策变量Ｕk, 表示在第k阶段状态为Sk下决定投资的投资额；决策允许集合: 0≤Ｕk≤Sk状态转移方程: Sk+1=Sk-Ｕk;阶段指标函数: V k(SkＵk)；最优指标函数: fk(Sk)=max{ V k(SkＵk)+ fk+1(Sk+1)}终端条件: f4(x4)=0；K=4, f4(x4)=0k=3, 0≤Ｕ3≤S3k=2, 0≤Ｕ2≤S2k=1, 0≤Ｕ1≤S1所以根据以上计算, 可以得到获得总效益最大的资金分配方案为（1, 2, 1）.解: 设第k阶段的状态为Sk；第k阶段决定投入的备件为Xk;Ck(Xk)为第k阶段选择k个零件的费用；Rk(Xk)为第k个阶段选择k个零件的可靠性。

状态转移方程为: Sk+1=Sk- Ck(Xk)递退方程:114431()max{()()}()1()(1)k k K k k k K k K i i k f s R x f s f s C x S C =+=+⎧⎪=⎪⎪=⎨⎪⎪≤-⎪⎩∑所以有上可知当A 1；A 2；A 3；分别为k=1;k=2;k=3时S 1=8; S 2=5,6,7; S 3=1,2,3,4;由上表可知, 最优解的可靠性为0.042；此时X1=1；X2=1；X3=3。

胡运权运筹学第五版答案【篇一：运筹学基础及应用第四版胡运权主编课后练习答案】xt>习题一 p46 1.1 (a)412该问题有无穷多最优解，即满足4x1z?3。

6x26且0?x2?的所有?x1,x2?，此时目标函数值(b)用图解法找不到满足所有约束条件的公共范围，所以该问题无可行解。

1.2(a) 约束方程组的系数矩阵12a833106?403000200??0?1t最优解x??0,10,0,7,0,0?。

(b) 约束方程组的系数矩阵1a222314??2??最优解1.3(a)(1) 图解法11??2x??,0,,0?5?5?t。

最优解即为?3x14x295x12x28的解x31,2，最大值z352(2)单纯形法首先在各约束条件上添加松弛变量，将问题转化为标准形式 max z?10x1?5x2?0x3?0x4?3x1?4x2?x3?9s.t. ?5x12x2x48则p3,p4组成一个基。

令x1?x2?0得基可行解x??0,0,9,8?，由此列出初始单纯形表12。

??min?898,53?520，??min?2183,??142?2?新的单纯形表为1,20，表明已找到问题最优解x1?1, x2?32,x3?0 , x4?0。

最大值z*352(b) (1) 图解法6x1?2x2x1?x2?最优解即为?6x12x224x1?x2?5的解x73,22?，最大值z172(2) 单纯形法首先在各约束条件上添加松弛变量，将问题转化为标准形式 max z?2x1?x2?0x3?0x4?0x55x2?x3?15??s.t. ?6x1?2x2?x4?24xxx5125则p3，p4，p5组成一个基。

令x1?x2?0得基可行解x??0,0,15,24,5?，由此列出初始单纯形表12。

??min??,245?,??461?155,24,20，??min?3?32?2新的单纯形表为【篇二：运筹学基础及应用第四版胡运权主编课后练习答案】xt>习题一 p46 1.1 (a)41的所有?x1,x2?，此时目标函数值2该问题有无穷多最优解，即满足4x1?6x2?6且0?x2?z?3。

胡运权排队论习题解10.1某修理店只有一个修理工人, 来修理的顾客到达次数服从普阿松分布,平均每小时3人,修理时间服从负指数分布,平均需10分钟, 求(1) 修理店空闲时间概率; (2) 店内有4个顾客的概率; (3) 店内至少有一个顾客的概率; (4) 在店内顾客平均数; (5) 等待服务的顾客平均数; (6) 在店内平均逗留时间; (7) 平均等待修理(服务)时间;(8) 必须在店内消耗15分钟以上的概率.04440s q s q 60M /M /1//3 6.1031(1)p 1162111(2)p (1)(1)()223211(3)1p 1223(4)L 1()631312(5)L ()632111(6)()633112(7)()636(8)1-F()W W λμρρρλμλρλμλμλρμλω∞∞====-=-==-=-=-=-====--⋅===--===--===--解：该系统为（）模型，，；；；人；人；小时；小时；1515-(6-3)--(-)6020eee .μλω⨯===11(1)(2)(3)23211(4)(5)2211(6)(7)(8)3615.15-20答：修理店空闲时间概率为；店内有三个顾客的概率为；店内至少有一个顾客的概率为；店内顾客平均数为1人；等待服务顾客平均数为人；在店内平均逗留时间分钟；平均等待修理时间为分钟；必须在店内消耗分钟以上的概率为e10.22015(1)(2)(3)(4) 1.25M /M /1.603(/20λ==设有一单人打字室，顾客的到达为普阿松流，平均到达时间间隔为分钟，打字时间服从指数分布，平均时间为分钟，求顾客来打字不必等待的概率；打字室内顾客的平均数；顾客在打字室内平均逗留时间；若顾客在打字室内的平均逗留时间超过小时，则主人将考虑增加设备及打字员，问顾客的平均到达概率为多少时，主人才会考虑这样做？解：该题属模型人小时0s s s 60)4(/).1531(1)p 11443(2)L 3()4311(3)1()431(4)1.2511.25 3.23.230.2(/).4W W μρλμλμλμλλλ===-=-====--===--=>-≥>-=-，人小时；人；小时；；，，人小时1(1)(2)3(3)41(4)0.2/.答：顾客来打字不必等待的概率为；打字室内顾客平均数为人；顾客在打字室内平均逗留时间为小时；平均到达率为人小时时，店主才会考虑增加设备及打字员 10.3 汽车按平均90辆/h 的poission 流到达高速公路上的一个收费关卡，通过关卡的平均时间为38s 。

P66： 8.某部门有3个生产同类产品的工厂（产地），生产的产品由4个销售点出售，各工厂A 1， A 2，A 3的生产量、各销售点B 1，B 2，B 3，B 4的销售量（假定单位为t ）以及各工厂到销售点的单位运价（元/t ）示于下表中，问如何调运才能使总运费最小？解：一、该运输问题的数学模型为：可以证明：约束矩阵的秩为r (A) = 6. 从而基变量的个数为 6.34333231242322213141141312116115893102114124min x x x x x x x x x x x x x c z i j ij ij +++++++++++==∑∑==⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧==≥=++=++=++=++=+++=+++=+++4,3,2,1;3,2,1,01412148221016342414332313322212312111343332312423222114131211j i x x x x x x x x x x x x x x x x x x x x x x x x x ij 111213142122232431323334x x x x x x x x x x x x 712111111111111111111111111⨯⎛⎫ ⎪⎪⎪ ⎪⎪⎪ ⎪⎪ ⎪⎝⎭二、给出运输问题的初始可行解（初始调运方案）1. 最小元素法思想：优先满足运价（或运距）最小的供销业务。

其余（非基）变量全等于零。

此解满足所有约束条件，且基变量（非零变量）的个数为6（等于m+n-1=3+4-1=6).总运费为（目标函数值） ,1013=x ,821=x ,223=x ,1432=x ,834=x ,614=x ∑∑===3141i j ij ij x c Z 246685143228116410=⨯+⨯+⨯+⨯+⨯+⨯=2. 伏格尔（Vogel)法伏格尔法的基本思想：运输表中各行各列的最小运价与次小运价之差值（罚数）应尽可能地小。