实验一 两个多位十进制数相加的实验

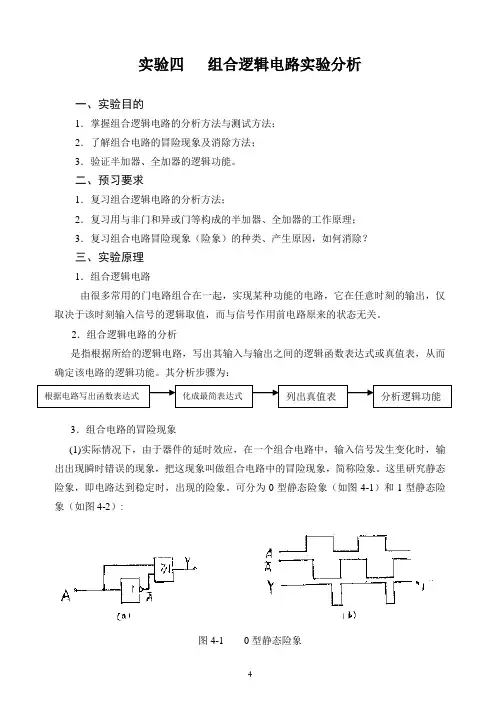
实验四组合逻辑电路实验分析一、实验目的1．掌握组合逻辑电路的分析方法与测试方法；2．了解组合电路的冒险现象及消除方法；3．验证半加器、全加器的逻辑功能。

二、预习要求1．复习组合逻辑电路的分析方法；2．复习用与非门和异或门等构成的半加器、全加器的工作原理；3．复习组合电路冒险现象（险象）的种类、产生原因，如何消除？三、实验原理1．组合逻辑电路由很多常用的门电路组合在一起，实现某种功能的电路，它在任意时刻的输出，仅取决于该时刻输入信号的逻辑取值，而与信号作用前电路原来的状态无关。

2．组合逻辑电路的分析是指根据所给的逻辑电路，写出其输入与输出之间的逻辑函数表达式或真值表，从而确定该电路的逻辑功能。

其分析步骤为：3．组合电路的冒险现象(1)实际情况下，由于器件的延时效应，在一个组合电路中，输入信号发生变化时，输出出现瞬时错误的现象，把这现象叫做组合电路中的冒险现象，简称险象。

这里研究静态险象，即电路达到稳定时，出现的险象。

可分为0型静态险象（如图4-1）和1型静态险象（如图4-2）:图4-1 0型静态险象其输出函数Y=A+A,在电路达到稳定时，即静态时，输出Y总是1。

然而在输入A变化时，输出Y的某些瞬间会出现0，Y出现窄脉冲，存在有静态0型险象。

图4-2 1型静态险象其输出函数Y=A+A,在电路达到稳定时，即静态时，输出Y总是O。

然而在输入A变化时，在输出Y的某些瞬间会出现1，Y出现窄脉冲，存在有静态1型险象。

（2）进一步研究得知，对于任何复杂的组合逻辑电路，只要能成为A+A或A A的形式，必然存在险象。

为了消除险象，通常用增加校正项的方法，如果表达式中出现A+A形式的电路，校正项为被赋值各变量的“乘积项”；表达式中出现A A形式的电路，校正项为被赋值各变量的“和项”。

例如：逻辑电路的表达式为Y=A B+AC；当B=C=1时，Y=A+A，Y正常情况下，稳定后应输出1，但实际中出现了0型静态险象。

这时可以添加校正项BC，则Y A B+AC+ BC=A+A+1=1,从而消除了险象。

多位十进制数加法实验报告实验一两个多位十进制数相加的实验实验一两个多位十进制数相加的实验一、实验目的1、学习数据传送和算术运算指令的用法。

2、熟悉在PC机上建立、汇编、链接、调试和运行8088汇编语言程序的过程。

二、实验内容将两个多位十进制数相加。

要求被加数均以ASCII码形式各自顺序存放在以DATA1和DATA2为首的5个内存单元中（低位在前），结果送回DATA1处。

三、程序框图四、程序清单CRLF MACROMOV DL，0DHMOV AH，02HINT21HMOV DL，0AHMOV AH，02HINT21HENDMDATA SEGMENTDATA1DB 33H，39H，31H，37H，34HDATA2DB 36H，35H，30H，38H，32HDATA ENDSSTACKSEGMENTSTA DB20 DUP(?)TOP EQU LENGTH STASTACKENDSCODE SEGMENTASSUME CS:CODE，DS:DATA，SS:STACK，ES:DATA START：MOV AX，DATAMOV DS，AXMOV AX，STACKMOV SS，AXMOV AX，TOPMOV SP，AXMOV SI，OFFSET DATA2MOV BX，05CALL DISPLCRLFMOV SI，OFFSET DATA1MOV BX，05CALL DISPLCRLFMOV DI，OFFSET DATA2CALL ADDAMOV SI，OFFSET DATA1MOV BX，05CALL DISPLCRLFMOV AX，4C00HINT21HDISPLPROC NEARDS1: MOV AH，02MOV DL，[SI+BX-1]INT21HDEC BXJNZ DS1RETDISPLENDPADDA PROC NEARMOV DX，SIMOV BP，DIMOV BX，05AD1: SUBBYTE PTR [SI+BX-1]，30HSUBBYTE PTR [DI+BX-1]，30HDECBXJNZAD1MOV SI，DXMOV DI，BPMOV CX，05CLCAD2: MOV AL，[SI]MOV BL，[DI]ADC AL，BLAAAMOV [SI]，ALINCSIINCDILOOP AD2MOV SI，DXMOV DI，BPMOV BX，05AD3: ADDBYTE PTR [SI+BX-1]，30H ADDBYTE PTR [DI+BX-1]，30HDECBXJNZ AD3RETADDA ENDPCODE ENDSEND START五、实验要求1．读懂源程序，写出源程序注释。

十进制加法器设计1课程设计的任务与要求 课程设计的任务1、综合应用数字电路知识设计一个十进制加法器。

了解各种元器件的原理及其应用。

2、了解十进制加法器的工作原理。

3、掌握multisim 软件的操作并对设计进行仿真。

4、锻炼自己的动手能力和实际解决问题的能力。

5、通过本设计熟悉中规模集成电路进行时序电路和组合电路设计的方法，掌握十进制加法器的设计方法。

课程设计的要求1、设计一个十进制并运行加法运算的电路。

2、0-9十个字符用于数据输入。

3、要求在数码显示管上显示结果。

2十进制加法器设计方案制定 加法电路设计原理图1加法运算原理框图如图1所示第一步置入两个四位二进制数。

例如（1001）2,（0011）2和（0101）2，（1000），同时在两个七段译码显示器上显示出对应的十进制数9，3和5，8。

2第二步将置入的数运用加法电路进行加法运算。

第三步前面所得结果通过另外两个七段译码器显示。

即：加法运算方式，则（1000）2+（0110）2=（1110）2 十进制8+6=14 并在七段译码显示出14。

运算方案通过开关S1——S8接不同的高低电平来控制输入端所置的两个一位十进制数，译码显示器U8和U9分别显示所置入的两个数。

数A直接置入四位超前进位加法器74LS283的A4——A1端，74LS283的B4——B1端接四个2输入异或门。

四个2输入异或门的一输入端同时接到开关S1上，另一输入端分别接开关S5——S8，通过开关S5——S8控制数B的输入,通过加法器74LS283完成两个数A和B的相加。

由于译码显示器只能显示0——9，所以当A+B>9时不能显示，我们在此用另一片芯片74LS283完成二进制码与8421BCD码的转换，即S>9（1001）2时加上3（0011）2，产生的进位信号送入译码器U10来显示结果的十位，U11显示结果的个位。

3十进制加法器电路设计加法电路的实现用两片4位全加器74LS283和门电路设计一位8421BCD码加法器。

深圳大学实验报告课程名称：微机原理及应用实验实验项目名称：多位十进制数加法器设计学院：物理科学与技术学院专业：应用物理指导教师：报告人：学号：班级：应用物理班实验时间：2015-10-19实验报告提交时间：2015-11-02教务处制五、程序说明（预习）七、实验源程序清单（实验后以电子报告形式存储到指定位置）1．源程序路径及文件名：ADD2.ASM ADD1.ASM2．可执行程序路径及文件名：八、上机调试情况说明EMU8086：一：没有键盘录入1.结果显示如下：2.程序运行时的各段地址：3.两个子程序IP入口：4.改变两个加数数值5.子程序格式及其调用方法和宏汇编区别子程序格式：子程序名称PROC NEAR ; 子程序定义; …子程序内容RET ;子程序返回子程序名称ENDP ;子程序结束调用格式：CALL 子程序名称注意事项：1、子程序不能直接传递参数，需要自行定义变量。

2、注意保护现场和恢复现场。

宏汇编与子程序的区别：1、宏汇编有宏展开，子程序没有2、宏汇编可以传递参数。

二：键盘录入DOS：例如：250+250=500例如：62142+63123=125265九、实验结果与分析结果如下：十、实验总结(必备部分,评分重要依据之一)本次实验实则是对实验二的加强巩固基础上，进行更加友好的人机交互设计；通过本次实验不仅在程序中首先把两个加数固定，在实验二的基础上扩展位数，考虑到最高位进位的情况，并最终得出正确结果；后来又通过键盘录入两个加数，增加了人机交互的设计，如此一来，更加加深了对寄存器的使用，汇编语言宏定义，子程序调用以及DOS功能调用的学习。

同时，通过本次实验的学习，更加熟练了EMU8086工具的使用，也把理论课上学习到的汇编操作指令实际操作，对汇编语言的风格加深认识。

MOV DL,BLINT 21HCRLFJMP BEGINERROR:CRLFMOV AH,09H ;显示输入错误LEA DX,STRING3INT 21HCRLFJMP BEGINEXIT:CRLFMOV AH,09H ;显示成功退出LEA DX,STRING4INT 21HMOV AH,4CHINT 21HCODE ENDSEND START（2）请问你的程序能否处理加数和被加数都介于0~65535范围但计算结果超出该范围的情况？如何改进？可以，如图：主要考虑到最高位是否进位，可以设置一个进位变量加以判断。

实验一、I/O程序设计一．实验内容：I/O程序设计（一）实验内容：1．编程由键盘输入任意一个字符，将该字符的ASCII码值显示在屏幕上。

2．从键盘输入两个1位十进制数，计算二者之和，并将结果显示在屏幕上。

3．编程由键盘输入任意一位数，将该数以二进制数形式显示在屏幕上，例：5=00000101B （二）实验步骤： 1. 画出实验流程图。

2. 运行Tddebug软件，选择Edit菜单编写实验程序 3. 使用Compile菜单中的Compile和Link对实验程序进行汇编、连接，生成执行文件。

4. 使用Rmrun菜单中的Run运行程序，观察运行结果。

5. 使用Rmrun菜单中的Debug调试程序。

单步执行指令，观察各寄存器及数据区的内容。

6. 更改数据区中的数据，考察程序的正确性。

二．分析设计思想。

设计思路：首先将该数以十六进制数形式分解，然后将每一位分别转换为ASCII码送屏幕显示。

其中0H~9H之间的数加30H，即可得0H~9H的ASCII码，而AH~FH的ASCII码，则需再加7H，参见表5-1。

参考程序流程如图2-1所示。

示例程序参见参考程序清单。

三．程序清单及流程DATA SEGMENTMES DB 'Show a as hex:',0AH,0DH,'$'SD DB 'a'DA TA ENDSCODE SEGMENTASSUME CS:CODE,DS:DA TASTART: MOV AX,DATAMOV DS,AXMOV DX,OFFSET MES ；显示提示信息MOV AH,09H INT 21HMOV SI,OFFSET SD 4MOV AL,DS:[SI]AND AL,0F0H ；取高4位MOV CL,4SHR AL,CLCMP AL,0AH ；是否是A以上的数JB C2ADD AL,07HC2: ADD AL,30HMOV DL,AL ；显示字符MOV AH,02HINT 21HMOV AL,DS:[SI]AND AL,0FH ；取低4位CMP AL,0AHJB C3ADD AL,07HC3: ADD AL,30HMOV DL,AL ；显示字符MOV AH,02HINT 21HMOV AH,4CH ；返回DOSINT 21HCODE ENDSEND START四．实验结果。

19+7的解题方式19+7的解题方式有很多种，下面将介绍一种较为常见的解题方式。

一、列竖式加法列竖式是一种常见的数学解题方法，可以将加法运算分步进行，逐位相加。

以19+7为例，按照十位、个位的顺序列竖式如下：1 9+ 7——2 6将19和7的个位数相加得到6，然后将19和7的十位数相加（进位），得到2作为十位数。

最后将十位和个位数相连，得到结果26。

这种解题方式简单直观，适用于小数的加法计算。

二、手算加法法则手算加法法则是一种将加法运算按照规则进行分解的方法，便于计算。

1.利用进位法则，首先将个位相加，如果结果大于等于10，记住进位，将个位数字写下。

9 + 7 = 16，个位数字为6，进位为1。

2.再将十位相加，如果有进位，则将进位加上。

1（进位） + 1（十位） = 2。

3.将十位和个位数字连接起来，得到结果。

2 6。

这种解题方式利用了进位法则，较为灵活，适用于小数和较大数的加法计算。

三、运用十进制加法规则十进制加法规则是一种运用位权法则的数学解题方法，适用于任意数量的位数相加。

1.先将个位数相加，得到个位数字。

9 + 7 = 16，个位数字为6。

2.再将十位数相加，同时将个位数的进位加上。

1（进位） + 1（十位） = 2。

3.将十位和个位数字连接起来，得到结果。

2 6。

这种解题方式利用了位权法则，可以计算任意位数的加法，但需要对每一位的进位注意处理。

四、数形结合法数形结合法是一种将加法运算表示为图形的解题方法，利用图形的具体形状和数量进行计算。

以19+7为例，可以将19视为一组有19个小球的圆柱，将7视为另一组有7个小球的圆柱，然后将两组小球合并。

将两个圆柱上的小球排列在一起，然后数取得总数。

在这种方法中，可以通过对图形进行计数来得到结果。

例如，在数轴上表示两个数，可以找到最大的数，然后在该数点上再数相应的数即可。

这种解题方式利用了空间感和图形感，适用于一些具体物体和空间的加法计算。

五、分组分解法分组分解法是一种将加法运算按照位数进行分解的方法，便于计算。

一位十进制全加器华北电力大学一位十进制全加器课程名称：数字电子技术基础专业班级：电力实1201、电力实1202 指导教师：何玉钧小组成员：朱思丞（1201）潘俊诚（1201）陶冀（1201）曹晟哲（1202）谢力也（1201）吴若冰（1201）一位十进制全加器一、Multisim简介Multisim是一个专门用于电路设计与仿真的工具软件。

它以界面形象直观、操作方便、分析功能强大、易学易用等突出优点，迅速被推广应用。

Multisim仿真软件能将电路原理图的创建、电路的仿真分析及结果输出都集成在一起，并具有绘制电路图所需的元器件及其仿真测试的仪器，可以完成从电路的仿真设计到电路版图生成的全过程，从而为电子系统的设计、电子产品的开发和电子系统工程提供一种全新的手段和便捷的方法。

二、实验目的1.掌握全加器的工作原理。

2.掌握逻辑电路图的设计思路。

3.熟练运用Multisim 软件进行电路的仿真。

4.培养所学理论联系实际，提高分析、解决计算机技术实际问题的独立工作能力。

三、一位十进制全加器设计原理1.输入十个按键8421BCD码编码器原理可以列些十个按键8421BCD码编码器真值表：输入S9 S8 S7 S6 S5 S4 S3 S2 S1 S0 1 1 1 1 1 1 1 1 1 11 1 1 1 1 1 1 1 1 01 1 1 1 1 1 1 1 0 11 1 1 1 1 1 1 0 1 11 1 1 1 1 1 0 1 1 11 1 1 1 1 0 1 1 1 11 1 1 1 0 1 1 1 1 11 1 1 0 1 1 1 1 1 11 1 0 1 1 1 1 1 1 11 0 1 1 1 1 1 1 1 1A 0 0 0 0 0 0 0 0 0 1B 0 0 0 0 0 1 1 1 1 0输出 C 0 0 0 1 1 0 0 1 1 0D GS 0 0 1 0 1 0 1 0 1 00 1 1 1 1 1 1 1 1 1对真值表进行分析可以得知：①该编码器为输入低电平有效；②在按下S0~S9中任意一个键时，即输入信号中有一个为低电平时GS=1，表示有信号输入，而只有S0~S9均为高电平时GS=0，表示无信号输入，此时的输出代码0000为无效代码。

摘要本次课程设计的任务是设计一个具有加减运算功能的简易计算器，并通过合适的方式来显示最后的计算结果。

此次设计电路的完成主要是利用简单的数字电路和电路逻辑运算来进行的。

简易加减计算器电路主要是对数据的输入与显示，数据的加减运算，数据的输出与显示三个主要的方面来设计研究完成的。

在输入电路的部分，我们通过开关的闭合与断开来实现数据的输入，开关闭合接入高电平“1”，断开接入低电平“0”。

而输入的数据将通过显示译码管以十进制的形式显示出来。

由于输入二进制的位数较多，我们采用个位十位分别输入的方式来简化电路。

加减运算电路则主要通过加法器来实现的。

设计电路时，我们将个位和个位、十位和十位分别接入一片加法器。

在进行加法运算时我们所选择的加法器是完全符合要求的，但是在进行减法运算时加法器就不能满足我们的设计要求了。

因此我们将减法转换为加法进行运算，运算时采用补码的形式。

在进行减法时通过异或门将减数的原码全部转换为补码，输入加法器中进行相加。

最后将进位信号加到十位的运算电路上就实现了加减法的运算电路。

在显示电路中，由加法器输出的数据是二进制码。

这些码可能表示超过十的数字，所以显示译码管就不能正确的显示出数字了。

此时要将二进制转化成BCD码，再将BCD 码送到显示译码管中就可以将计算所得的数字显示出来了。

概述1.1设计题目：简易加减计算器1.2设计任务和要求：1）用于两位以下十进制数的加减运算。

2）以合适的方式显示输入数据及计算结果。

1.3设计方案比较：方案一：输入十进制的数字，再通过编码器对十进制的数字进行编码，输出二进制的数据。

运用显示译码器对输入的数字以十进制的形式进行显示。

在进行加减计算的时候将二进制数字运用数模转换，然后再进行相加减。

然后将这些模拟信号再次转换成数字信号转换成数字信号，再将数字信号输入到显示译码管中来显示数剧。

这个方案中要进行数模转换和模数转换所需要的电路器件有些复杂，并且转换的时候需要很长的时间，而且转换以后数值的精度不高。

EAT实验指导书电子_88实验指导书目录第一章系统安装和启动一实验系统工作方式爱迪克实验系统工作在 88串口实验方式用户根据实验要求，进行-88单片机实验时，将-板正面朝上插到实验机的仿真头和实验的四个插座上，板上的两位拨动开关SB1打到88端用实验机配套的串行通讯电缆，将9芯电缆的一端与实验机上的9芯仿真机通讯口插座相连，另一端与PC机的串行口相连打开电源，在PC机上打开88软件，运行实验程序，具体操作参见《_88使用说明》二实验系统工作在88方式下开关初始状态仿真头插座和实验板插座插_板，板上的两位拨动开关SB1打到88端 XB34 : 短路套向上插(端)，第○17模块处于放音功能第○30模块中：短路套全部套向右边，由来控制键盘、显示 SA9：八位开关打到1_88实验指导书目录第二章 88硬件实验实验三实验一实验要求编写程序，以作为输出口控制8个单色灯二实验目的1学习在单板方式下扩展简单I/O接口的方法 2学习编制数据输出程序的设计方法三实验电路及连线PC0～PC7连L0～L7CS连H四实验说明工作于方式0，此时PA、PB、PC均为可独立输入/输出的并行口的各寄存器对应的口地址为：PA口: H PB口: HPC口: H 控制寄存器：H由于各PC机速度不同为达到较好的实验效果，可适当调节亮灭的延时时间2_88实验指导书目录五实验程序框图示例程序见3_88实验指导书目录第三章 88软件实验本指导书提供20个软件实验，可以脱离T实验机运行，调试工具用程序，建议运行环境为纯也可运行88ET集成调试界面，打开要调试的程序，然后进入“工具”菜单下的“方式”，程序即自动加载，这时用户可用的各种命令对程序进行调试实验一两个多位十进制数相减实验一实验要求将两个多位十进制数相减，要求被减数，减数均以码形式按顺序存放在以1和2为首的5个内存单元中，结果送回1处二实验目的1 学习数据传送和算术运算指令的用法2 熟悉在PC机上建立、汇编、链接、调试和运行汇编语言程序的过程三实验程序框图开始显示减数和被减数被减数和减数转换成十六进制数设置计数值清除最低进位位带进位减结果送被减数区调整偏移量N计数值-1=0Y结果转换成码字符串显示结果结束4_88实验指导书目录实验二从键盘输入数据并显示一实验要求编写程序，将键盘接收到的四位十六进制数转换为等值的二进制数，再显示在屏幕上若输入的不是0-F间的数字则显示出错信息并要求重新输入二实验目的掌握接收键盘数据的方法，并了解将键盘数据显示时须转换为码的原理并在程序中设置错误出口三实验程序框图开始初始化。

实验一简单程序编制和上机过程一．实验目的1．掌握计算机常用代码的软件转换技术。

2．熟悉DEBUG软件的使用。

3．掌握简单程序的编程方法。

二．实验内容代码转换是计算机和I/O设备进行信息交换的重要技术之一。

各种I/O设备所提供和接收的数据编码不尽相同。

为了处理这些信息，计算机必须将各种不同编码形式的信息转换成别种适当的数据形式。

例如，键盘输入的数据均为ASC Ⅱ码形式存储在内存中，通常要求将其转换成相应的数据形式。

一般实现代码转换有两种方法：1．软件法利用CPU的算术逻辑运算功能，通过运算或查表实现各种数据代码间的转换。

该方法经济但速度慢。

2．硬件法利用专用代码转换集成电路进行转换。

如74LS74可把BCD码转换为七段代码。

这种方法需要硬件费用，但速度快。

本实验要求掌握软件编码转换技术。

计算机常用的代码有二进制、八进制、十六进制、BCD码、ASCⅡ码、七段码等，它们之间的相互关系如下表所示。

本次试验的内容是ASCⅡ码转换为未组合BCD码设从键盘输入十进制数的ASCⅡ码已存放在起始地址CS ：150H的单元中，把它转换成未组合BCD码后，再分别存入起始地址为CS：15AH的单元中。

若输入的不是十进制数的ASCⅡ码，则相应存放结果单元的内容为“FF”。

提示：1．组合BCD码是一位十进制数字占一个字节，高半字节为0，低半字节为该十进制数字的BCD码。

ASCⅡ码转换为未组合BCD码只需减30H。

2．程序框图如下图所示。

3．程序执行前，需要在CS：150H内存缓冲区写入待转换的ASCⅡ码。

方法如下：方法一：用A命令-ACS：150 DB 35，39，30，41，32CS：155 ∧C方法二：用E 命令-ECS：150，35，39，30，41，32方法三：用F命令-FCS：150 L5 35，39，30，41，321．执行程序后检查执行结果可用D命令：-DCS：15ACS：15A 05，09，00，FF，02ASCⅡ码转换为未组合BCD码的程序流程图参考程序如下：ORG 100HMOV CX，0005HMOV DI，150HBB：MOV BL，0FFHMOV A，[DI]CMP AL，3AHJNB DONESUB AL，30HJB DONEMOV BL，ALDONE：MOV AL，BLMOV [DI+0AH]，ALINC DILOOP BBINT 20HORG 150HDB 35H，39H，30H，41H，32H实验二顺序结构的程序设计一．实验目的1．掌握计算机常用代码的软件转换技术。

组合逻辑电路的仿真1.实验目的➢掌握全加器、译码器、数据选择器电路的特点及设计方法；➢学会应用全加器、译码器及数据选择器设计组合逻辑电路；➢掌握各种组合逻辑电路的仿真。

2.实验器材3.实验内容3.1全加器的EDA仿真a)在Multisim软件中，按照如图1.1所示电路，从TTL库中调74LS00D、74LS86N，从基本库中调VCC、GND、J1、J2、J3，从指示库中调X1、X2等元件，连线构成1位全加器仿真电路，图中J1、J2和J3依次控制两个输入的1位二进制数A、B及低位的二进制数相加向本位的进位C，指示灯X1、X2i分别表示本位输出F和向高位的进位C。

按照功能表分别拨动J1、J2和J3，o即改变输入状态，观察输出的状态变化。

图1.1 一位全加器仿真图b) 按照图1.2及1.3连线进行全加器74LS283及CD4008的功能仿真实验。

图1.2 74LS283功能仿真电路X1X2X3X4X5图1.3 CD4008功能仿真电路c) 利用四位全加器CD4008和四异或门CC4070设计四位无符号数二进制加/减法器，画出仿真图。

解： 分析：二进制加法器可以使用CD4008实现；二进制减法可以转换为补码运算，因为正数补码与原码相同，对负数先求补码，再进行加法运算，最后再对输出求补码，即可得到减法结果。

因为补码=反码+1，反码可以让输入与1异或，+1运算可以通过进位输入端实现。

因此，可以列出真值表如下X1X2X3X4X5上图中，淡黄色为加法运算，橙色为减法运算；绿色为加法结果，其中淡绿色部分与深绿色部分相同；蓝色为加法结果，其中淡蓝色部分与深蓝色部分相同。

因为输入与高电平异或得到负数的反码，与低电平异或得到正数的反码（与原码相同），因此，可以绘制下图所示电路图实现功能：3.2 译码器的EDA 仿真a) 变量译码器变量译码器（又称二进制译码器），用于表示输入变量的状态，如2-4线、3-8线和4-16线译码器。

数学进制的原理及应用教案一、数制的概念及背景1. 数制的定义数制是表示和计算数值的一种方法，它由数字元素和基数两部分组成。

数字元素是由一个或多个特定的符号组成，用来表示数的数位，基数是一个正整数，决定了数位的多少和具体的表示方法。

2. 数制的分类根据基数的不同，数制可以分为多种类型，常见的数制包括十进制、二进制、八进制和十六进制等。

二、十进制的原理及应用1. 十进制的定义十进制是一种基数为10的数制，使用0-9这10个数字元素来表示数位。

每一位上的数值是基数的幂的乘积。

2. 十进制的应用十进制是我们常用的数制，广泛应用于各行各业的计算和表示中。

例如，在数学、物理、经济学等学科中，十进制被用来表示和计算实际数值。

在计算机科学领域，十进制也常用于编程、算法设计等方面。

3. 十进制的计算规则在进行十进制的加减乘除运算时，需要注意以下规则： - 加法：逐位相加，进位处理。

- 减法：逐位相减，借位处理。

- 乘法：按照竖式乘法的方法进行计算。

- 除法：按照长除法的方法进行计算。

三、二进制的原理及应用1. 二进制的定义二进制是一种基数为2的数制，使用0-1这两个数字元素来表示数位。

每一位上的数值是基数的幂的乘积。

2. 二进制的应用二进制在计算机科学领域中起到重要作用，被广泛应用于计算机的存储、传输和计算过程中。

例如，在计算机内部，所有数据都是以二进制形式存储和处理的。

3. 二进制的计算规则在进行二进制的加减乘除运算时，需要注意以下规则： - 加法：逐位相加，进位处理。

- 减法：逐位相减，借位处理。

- 乘法：按照竖式乘法的方法进行计算，结果只能是0或1。

- 除法：按照长除法的方法进行计算，结果只能是0或1。

四、八进制的原理及应用1. 八进制的定义八进制是一种基数为8的数制，使用0-7这八个数字元素来表示数位。

每一位上的数值是基数的幂的乘积。

2. 八进制的应用八进制在计算机科学领域中也有一定的应用，特别是在UNIX系统中，八进制被用来表示文件权限、数据等。

数字电路课程设计一、概述任务：通过解决一两个实际问题，巩固和加深在课程教学中所学到知识和实验技能，基本掌握惯用电子电路普通设计办法，提高电子电路设计和实验能力，为此后从事生产和科研工作打下一定基本。

为毕业设计和此后从事电子技术方面工作打下基本。

设计环节：依照题目拟定性能指标，电路预设计，实验，修改设计。

衡量设计原则：工作稳定可靠，能达到所规定性能指标，并留有恰当裕量；电路简朴、成本低；功耗低；所采用元器件品种少、体积小并且货源充分；便于生产、测试和维修。

二、惯用电子电路普通设计办法惯用电子电路普通设计办法是：选取总体方案，设计单元电路，选取元器件，计算参数，审图，实验（涉及修改测试性能），画出总体电路图。

1．总体方案选取设计电路第一步就是选取总体方案。

所谓总体方案是依照所提出任务、规定和性能指标，用品有一定功能若干单元电路构成一种整体，来实现各项功能，满足设计题目提出规定和技术指标。

由于符合规定总体方案往往不止一种，应当针对任务、规定和条件，查阅关于资料，以广开思路，提出若干不同方案，然后仔细分析每个方案可行性和优缺陷，加以比较，从中取优。

在选取过程中，惯用框图表达各种方案基本原理。

框图普通不必画得太详细，只要阐明基本原理就可以了，但有些核心某些一定要画清晰，必要潮流需画出详细电路来加以分析。

2．单元电路设计在拟定了总体方案、画出详细框图之后，便可进行单元电路设计。

（1）依照设计规定和已选定总体方案原理框图，拟定对各单元电路设计规定，必要时应详细拟定重要单元电路性能指标，应注意各单元电路互相配合，要尽量少用或不用电平转换之类接口电路，以简化电路构造、减少成本。

（2）拟定出单元电Array路规定后，应全面检查以遍，的确无误后方可按一定顺序分别设计各个单元电路。

（3）选取单元电路构造形式。

普通状况下，应查阅关于资料，以丰富知识、开阔眼界，从而找到合用电路。

如果的确找不到性能指标完全满足规定电路时，也可选用与设计规定比较接近电路，然后调节电路参数。

十进制加减法数字电路课程设计报告Company Document number：WTUT-WT88Y-W8BBGB-BWYTT-19998设计名称：设计一个一位十进制加减法器设计内容：1、0-9十个字符和“+”“-”分别对应一个按键，用于数据输入。

2、用一个开关控制加减法器的开关状态。

3、要求在数码显示管上显示结果。

设计目的与要求：1、学习数字逻辑等电路设计方法，熟知加减法器、编码器、译码显示的工作原理及特点；2、培养勤奋认真、分析故障和解决问题的能力。

设计环境或器材、原理与说明：环境：利用多功能虚拟软件Multism8进行电路的制作、调试，并生成文件。

器材：74LS283或者4008， 4个异或门（一片74LS86）（减法）；74LS08，3输入或门（加法） 设计原理:图1分析：如图1所示，第一步置入两个四位二进制数（要求置入的数小于1010），如（1001）2和（0111）2，同时在两个七段译码显示器上显示出对应的十进制数9和7；第二步通过开关选择运算方式加或者减；第三步，若选择加运算方式，所置数送入加法运算电路进行运算，同理若选择减运算方式，则所置数送入减法运算电路运算；第四步，前面所得结果通过另外两个七段译码器显示。

设计过程（步骤）或程序代码：实验电路：1:减法电路的实现：（1）：原理：如图1所示（如下），该电路功能为计算A-B。

若n位二进制原码为N原，则与它相对应的补码为N补=2n-N原，补码与反码的关系式为N 补=N反+1，A-B=A+B补-2n=A+B反+1-2n(2)：因为B○+1= B非，B○+0=B，所以通过异或门74LS86对输入的数B求其反码，并将进位输入端接逻辑1以实现加1，由此求得B的补码。

加法器相加的结果为：A+B反+1，(3)：由于2n=24=(10000)2,相加结果与相2n减只能由加法器进位输出信号完成。

当进位输出信号为1时，它与2n的差为0；当进位输出信号为0时，它与2n差值为1，同时还要发出借位信号。

实验一熟悉C语言程序的运行环境一、实验目的1、了解在该系统上如何编辑、编译、连接和运行一个C 程序；2、通过运行简单的C程序，初步了解C程序的特点。

二、实验预习1、认真阅读简单的C程序介绍，C程序上机步骤部分内容；2、编写好所需要的程序，程序的书写应该清楚整洁，一般检查应该是没有明显的错误。

如果在程序中有疑问的地方，可以标记起来，以便于上机调试时予以注意。

初学者特别忌讳上机前自己不编写程序，到时随便地抄别人的程序。

三、实验指导1、输入并运行一个简单的程序，从而熟悉所用系统的上机方法与步骤。

（1）选择File->New，使编辑窗口变成空白（2）输入下面的程序（例题1.1）#include <stdio.h>void main( ){printf("This is a C program.\n");}（3）按功能键【F9】进行编译和连接，观察屏幕上显示的编译信息。

如果出现“出错信息”，则应找出原因并改正之，再进行编译。

（4）如果编译无错误，按【Ctrl＋F9】键使程序运行，按【Alt＋F5】键，切换到用户屏，观察分析运行结果。

2、输入并运行一个需要在运行时输入数据的程序（1）清空编辑窗口，输入下面的程序（例题1.2）。

#include <stdio.h>void main( ){int a,b,c ;printf("input a & b:");scanf("%d,%d",&a,&b);c=max(a,b);printf("max=%d",c);}int max(int x,int y){int z ;if(x>y)z=x ;else z=y ;return(z);}（2）编译并运行，在运行时从键盘输入整数2 和5，格式为：2, 5（注意：两数据间用逗号分隔开），然后按回车键，按【ALT＋F5】键，观察运行结果。

二进制相加的计算方法二进制加法是计算机基础知识中的重要部分，本文将介绍如何计算两个二进制数的相加。

我们将从最基础的二进制加法开始讲解，并逐步引入进位的概念。

二进制数的表示首先，我们先来了解二进制数的表示方式。

与十进制数不同，二进制数只包含0和1两个数字。

每位上的数称为一个比特（bit），每4个比特可以表示一个十六进制数位。

例如，二进制数1010可以表示为十进制数10，二进制数1101可以表示为十进制数13。

二进制数相加的方法不带进位的二进制相加最简单的情况是两个二进制数没有进位的情况下进行相加。

假设我们要计算二进制数1011和0110的和，可以按照如下步骤进行：1 0 1 1 （1011）+ 0 1 1 0 （0110）----------1 1 1 0 1----------从最低位（最右边）开始，将每一位上的数相加。

当两个数相加的和为0或1时，结果直接写下来。

在这个例子中，最低位相加得到1。

接下来，分别对第2位、第3位和第4位进行相加，得到的结果依次是1、1和0。

最后得到的二进制数为11101，换算为十进制数是29。

带进位的二进制相加当两个二进制数相加的时候，如果某一个位上的数相加为2时，就需要进位。

例如，当相加的位上的数为1和1时，和就是10，其中最低位的0写在当前位，而最高位的1则需要往前进一位。

下面是一个带进位的二进制相加的例子：1 1 0 1 （1101）+ 1 1 1 1 （1111）----------1 1 1 1 0----------在这个例子中，我们首先将最低位上的数相加得到0，并观察到产生了进位。

进位之后，对下一位相加时需要加上进位。

根据规则，1加上进位1等于10。

继续计算第三位、第四位和第五位，得到的结果分别是1、1和1。

最后的进位是0。

因此，最终的二进制和为11110，换算为十进制数是30。

进位的概念在二进制的加法中，进位是一个非常重要的概念。

当两个位上的数相加大于1时，会产生进位。

十进制数的乘法运算在数学中，乘法是一种基本的数学运算，用于计算两个或多个数的积。

对于十进制数的乘法运算，我们可以采用传统的竖式计算方法，也可以利用十进制乘法的特性来进行简便的计算。

首先，我们来回顾一下竖式计算方法。

对于两个十进制数的乘法，我们将其中一个数（被乘数）写在上方，将另一个数（乘数）写在下方。

从乘数的个位数开始，将其与被乘数的每一位数相乘，并写在相应的位置上，然后将每一步的结果相加。

最后得到的结果即为乘法的积。

举例来说，我们来计算234乘以16。

按照上述方法，我们将16写在下方，将234写在上方。

首先，我们用被乘数的个位数4乘以乘数的个位数6，得到24，写在个位上。

然后，我们用4乘以乘数的十位数1，得到4，写在十位上。

接下来，我们用4乘以乘数的百位数0，得到0，写在百位上。

最后，将每一步的结果相加，得到3744，即为乘法的积。

除了竖式计算方法外，我们还可以利用十进制乘法的特性来进行简便的计算。

根据这一特性，我们可以将被乘数和乘数分别拆分为各个位数相乘的部分，并将结果相加得到最终的积。

举例来说，我们继续计算234乘以16。

根据这一特性，我们可以将234拆分为200和30，将16拆分为10和6。

然后，我们将200乘以10得到2000，将200乘以6得到1200，将30乘以10得到300，再将30乘以6得到180。

最后，将这些结果相加，得到2000+1200+300+180=3680，即为乘法的积。

除了上述两种计算方法外，还有一种更加快捷的方法可以用于计算十进制数的乘法，那就是移位相加法。

移位相加法利用了十进制数的位权性质，通过移动乘数的位数来得到每一位乘法的结果，并将结果相加得到最终的积。

举例来说，我们继续计算234乘以16。

首先，我们将乘数16转化为二进制形式，即10000。

然后，我们可以通过移位相加法来得到结果。

首先，我们将被乘数234右移动4位，得到2340000。

然后，我们将得到的结果与原来的被乘数相加，得到2340000+234=2340234。