(完整版)必修4第2章平面向量典型例题及练习

必修4 第二章平面向量检测参考答案一、选择题：1C、2C、3A、4C、5D、6B、7C、8B、9D、10A、11C、12C、二. 填空题6 5 3 5 6 5 3 513 （1，3）．14 28 15 （，）或（，）5 5 5 516 （5，3）17 2 35三. 解答题:18、（1）∵AB ＝（0－1，1－0）＝（－1，1），AC ＝（2－1，5－0）＝（1，5）．∴ 2 AB ＋AC ＝2（－1，1）＋（1，5）＝（－1，7）∴|2 AB ＋AC | ＝ 2 7 2( 1) ＝50 ．（2）∵| AB| ＝( 1)2 12 ＝ 2 ．| AC | ＝12 52 ＝26，AB·AC ＝（－1）×1＋1×5＝4．∴cos ＝AB AC| AB | | AC | ＝42＝2 261313．（3）设所求向量为m ＝（x，y），则x2＋y2＝1．①又BC ＝（2－0，5－1）＝（2，4），由BC⊥m ，得2 x ＋4 y ＝0．②2 5 2 5x x－5 5 由①、②，得或∴（5 55 5y．y．255，－52）或（－555，55）即为所求．19．由题设, 设b= , 则由, 得. ∴,解得sin α=1 或当sin α=1 时，cosα=0；当时，。

故所求的向量或。

2 b ka t b20．解：（1）, 0. [( 3) ] ( ) 0.x y x y 即 a t2 22a b 0,a 4,b 1,4k t(t 3) 0,即k 142t(t 3).（2）由f(t)>0, 得1 2t(t 3) 0,即t(t 3) (t 3)0,则 3 t 0或4t 3.必修4 第二章平面向量检测参考答案一、选择题：1C、2C、3A、4C、5D、6B、7C、8B、9D、10A、11C、12C、二. 填空题6 5 3 5 6 5 3 513 （1，3）．14 28 15 （，）或（，）5 5 5 516 （5，3）17 2 35三. 解答题:18、（1）∵AB ＝（0－1，1－0）＝（－1，1），AC ＝（2－1，5－0）＝（1，5）．∴ 2 AB ＋AC ＝2（－1，1）＋（1，5）＝（－1，7）∴|2 AB ＋AC | ＝ 2 7 2( 1) ＝50 ．（2）∵| AB| ＝( 1)2 12 ＝ 2 ．| AC | ＝12 52 ＝26，AB·AC ＝（－1）×1＋1×5＝4．∴cos ＝AB AC| AB | | AC | ＝42＝2 261313．（3）设所求向量为m ＝（x，y），则x2＋y2＝1．①又BC ＝（2－0，5－1）＝（2，4），由BC⊥m ，得2 x ＋4 y ＝0．②2 5 2 5x x－5 5 由①、②，得或∴（5 55 5y．y．255，－52）或（－555，55）即为所求．19．由题设, 设b= , 则由, 得. ∴,解得sin α=1 或当sin α=1 时，cosα=0；当时，。

必修四第二章--平面向量经典练习题第二章平面向量［基础训练A组］一、选择题1 •化简"AC-BD CD-AB 得( )A • AB B・DAC • BCD • 02. 设為分别是与a,b向的单位向量，则下列结论中正确的是( )A • a^b oB • & a =iC • |a°| |b o 2D ・|a° b o |=23. 已知下列命题中：(1)若k R ,且kb=0 ,则k=0 或 b =0 , ( 2) 若 1 b = 0 , 则a =0或b =0(3 )若不平行的两个非零向量a,b ,满足|a|=|b|,则(a b)宿-b) =0(4)若a与b平行，则；说=曲|b|其中真命题的个数是()A• o i 2 D • 34. 下列命题中正确的是( ) A•若ab= 0,贝V a= 0 或b= 0 若ab =0,贝V a// bC.若a// b,则a在b上的投影为|a| D•若a丄b,贝V ab= (a b)25 •已知平面向量a=(3,1), b=(x,-3)，且b，则x 二( )A • -3B • iC • iD • 3CG•6 •已知向量a =（cos ）s 阮），向量b = （ .3, — 1）则|2a — b|的最大值，最 小值分别是（ ） A • 420B . 4,4.2C • 16,0D • 4,0二、填空题1 •若 OA = （2,8） , OB =（-7,2）,贝12AB= ________32. 平面向量a,b 中，若a=（4,_3）,,=1，且:b=5，则向量b = ___ （3. 若a=3, b=2，且a 与b 的夹角为6°0，则a __________________ 。

4. _______________________________ 把平面上一切单位向量归结到共同的始点，那么这些 向量的终点所构成的图形是 _________________________________ 。

2.3.1 平面向量根本定理A 级 根底稳固一、选择题1．设e 1，e 2是平面内所有向量的一组基底，那么以下四组向量中，不能作为基底的是( )A ．e 1＋e 2和e 1－e 2B ．3e 1－4e 2和6e 1－8e 2C ．e 1＋2e 2和2e 1＋e 2D ．e 1和e 1＋e 2解析：B 中，因为6e 1－8e 2＝2(3e 1－4e 2)， 所以(6e 1－8e 2)∥(3e 1－4e 2)，所以3e 1－4e 2和6e 1－8e 2不能作为基底． 答案：B2．在菱形ABCD 中，∠A ＝π3，那么AB →与AC →的夹角为( )A.π6B.π3C.5π6D.2π3解析：由题意知AC 平分∠BAD ，所以AB →与AC →的夹角为π6.答案：A3．在△ABC 中，点D 在BC 边上，且BD →＝2DC →，设AB →＝a ，AC →＝b ，那么AD →可用基底a ，b 表示为( )A.12(a ＋b ) B.23a ＋13b C.13a ＋23b D.13(a ＋b ) 解析：因为BD →＝2DC →， 所以BD →＝23BC →.所以AD →＝AB →＋BD →＝AB →＋23BC →＝AB →＋23(AC →－AB →)＝13AB →＋23AC →＝13a ＋23b .答案：C4．如图，在△OAB 中，P 为线段AB 上一点，OP →＝xOA →＋yOB →，且BP →＝3PA →，那么( )A ．x ＝23，y ＝13B ．x ＝13，y ＝23C ．x ＝14，y ＝34D ．x ＝34，y ＝14解析：由BP →＝3PA →，得OP →－OB →＝3(OA →－OP →)，整理，得OP →＝34OA →＋14OB →，故x ＝34，y ＝14.答案：D5．(2021·全国卷Ⅰ)在△ABC 中，AD 为BC 边上的中线，E 为AD 的中点，那么EB →＝( ) A.34AB →－14AC → B.14AB →－34AC → C.34AB →＋14AC → D.14AB →＋34AC → 答案：A 二、填空题6．假设OP 1→＝a ，OP 2→＝b ，P 1P →＝λPP 2→(λ≠－1)，那么OP →＝________．解析：因为OP →＝OP 1→＋P 1P →＝OP 1＋λPP 2→＝OP 1→＋λ(OP 2→－OP →)＝OP 1→＋λOP 2→－λOP →， 所以(1＋λ)OP →＝OP 1→＋λOP 2→.所以OP →＝11＋λOP 1→＋λ1＋λOP 2→＝11＋λa ＋λ1＋λb .答案：11＋λa ＋λ1＋λb 7．|a |＝1，|b |＝2，且a －b 与a 垂直，那么a 与b 的夹角为________．解析：如图，作向量OA →＝a ，OB →＝b ，那么BA →＝a －b .由，得OA ＝1，OB ＝2，OA ⊥AB ，所以△OAB 为等腰直角三角形，所以∠AOB ＝45°，所以a 与b 的夹角为45°.答案：45°8．如果3e 1＋4e 2＝a ，2e 1＋3e 2＝b ，其中a ，b 为向量，那么e 1＝________，e 2＝________． 解析：由⎩⎪⎨⎪⎧a ＝3e 1＋4e 2，b ＝2e 1＋3e 2，解得⎩⎪⎨⎪⎧e 1＝3a －4b ，e 2＝3b －2a .答案：3a －4b 3b －2a 三、解答题9．如下图，平面内有三个向量OA →，OB →，OC →，其中OA →与OB →的夹角为120°，OA →与OC →的夹角为30°，且|OA →|＝|OB →|＝1，|OC →|＝23，假设OC →＝λOA →＋μOB →(λ，μ∈R)．求λ＋μ的值．解：如下图，以OA ，OB 所在射线为邻边，OC 为对角线作平行四边形ODCE ，那么OC →＝OD →＋OE →.在直角△OCD 中，因为|OC →|＝23，∠COD ＝30°，∠OCD ＝90°，所以|OD →|＝4，|CD →|＝2，故OD →＝4OA →，OE →＝2OB →，即λ＝4，μ＝2，所以λ＋μ＝6.10．如下图，▱ABCD 中，E ，F 分别是BC ，DC 的中点，G 为DE ，BF 的交点，假设AB →＝a ，AD →＝b ，试以a ，b 为基底表示DE →，BF →，CG →.解：DE →＝AE →－AD →＝AB →＋BE →－AD →＝a ＋12b －b ＝a －12b .BF →＝AF →－AB →＝AD →＋DF →－AB →＝b ＋12a －a ＝b －12a .如下图，连接DB ，延长CG ，交BD 于点O ，点G 是△CBD 的重心，故CG →＝CE →＋EG →＝12CB →＋EG →＝12CB →＋13ED →＝－12b －13⎝ ⎛⎭⎪⎫a －12b ＝－13a －13b .B 级 能力提升1．如果e 1，e 2是平面α内两个不共线的向量，那么以下说法中不正确的选项是( ) ①λe 1＋μe 2(λ，μ∈R)可以表示平面α内的所有向量；②对于平面α内任一向量a ，使a ＝λe 1＋μe 2的实数对(λ，μ)有无穷多个；③假设向量λ1e 1＋μ1e 2与λ2e 1＋μ2e 2共线，那么有且只有一个实数λ，使得λ1e 1＋μ1e 2＝λ(λ2e 1＋μ2e 2)；④假设存在实数λ，μ使得λe 1＋μe 2＝0，那么λ＝μ＝0.A ．①②B ．②③C ．③④D ．②解析：由平面向量根本定理可知，①④是正确的；对于②，由平面向量根本定理可知，一旦一个平面的基底确定，那么任意一个向量在此基底下的实数对是唯一的；对于③，当两向量的系数均为零，即λ1＝λ2＝μ1＝μ2＝0时，这样的λ有无数个．答案：B2．如图，向量BP →＝14BA →，假设OP →＝xOA →＋yOB →，那么x －y ＝________．解析：因为OP →＝OB →＋BP →＝OB →＋14BA →＝OB →＋14(BO →＋OA →)＝14OA →＋34OB →，所以x ＝14，y ＝34.所以x －y ＝－12.答案：－123．设e 1，e 2是不共线的非零向量，且a ＝e 1－2e 2，b ＝e 1＋3e 2. (1)证明：a ，b 可以作为一组基底；(2)以a ，b 为基底，求向量c ＝3e 1－e 2的分解式； (3)假设4e 1－3e 2＝λa ＋μb ，求λ，μ的值．(1)证明：假设a ，b 共线，那么存在λ∈R ，使a ＝λb ， 那么e 1－2e 2＝λ(e 1＋3e 2)．由e 1，e 2不共线得，⎩⎪⎨⎪⎧λ＝1，3λ＝－2，⇒⎩⎪⎨⎪⎧λ＝1，λ＝－23. 所以λ不存在，故a 与b 不共线，可以作为一组基底．(2)解：设c ＝ma ＋nb (m ，n ∈R)，得3e 1－e 2＝m (e 1－2e 2)＋n (e 1＋3e 2)＝(m ＋n )e 1＋(－2m ＋3n )e 2.所以⎩⎪⎨⎪⎧m ＋n ＝3，－2m ＋3n ＝－1，⇒⎩⎪⎨⎪⎧m ＝2，n ＝1.所以c ＝2a ＋b .(3)解：由4e 1－3e 2＝λa ＋μb ，得4e 1－3e 2＝λ(e 1－2e 2)＋μ(e 1＋3e 2)＝(λ＋μ)e 1＋(－2λ＋3μ)e 2.所以⎩⎪⎨⎪⎧λ＋μ＝4，－2λ＋3μ＝－3，⇒⎩⎪⎨⎪⎧λ＝3，μ＝1.故所求λ，μ的值分别为3和1.。

一、选择题1．已知点G 是ABC 的重心，(),AG AB AC R λμλμ=+∈，若120,2,A AB AC ∠=︒⋅=-则AG 的最小值是（ ）A ．3 B ．2 C ．12D ．232．已知O 为坐标原点，点M 的坐标为（2，﹣1），点N 的坐标满足111x y y x x +≥⎧⎪-≤⎨⎪≤⎩,则OM ON ⋅的最大值为（ ）A ．2B ．1C ．0D ．－13．已知函数()sin (0)2f x x a a π⎛⎫=>⎪⎝⎭，点A ，B 分别为()f x 图象在y 轴右侧的第一个最高点和第一个最低点，O 为坐标原点，若OAB 为钝角三角形，则a 的取值范围为（ ）A ．10,(2,)2⎛⎫+∞ ⎪⎝⎭ B ．30,(1,)⎛⎫⋃+∞ ⎪⎝⎭C ．3,1⎛⎫ ⎪ ⎪⎝⎭D ．(1,)+∞4．已知向量()1,2a =，()2,3b =-，若向量c 满足()//c a b +，()c a b ⊥+，则c =（ ） A ．7793⎛⎫ ⎪⎝⎭，B ．7739⎛⎫-- ⎪⎝⎭，C ．7739⎛⎫ ⎪⎝⎭，D ．7793⎛⎫-- ⎪⎝⎭，5．若平面向量与的夹角为，，，则向量的模为（ ） A ．B ．C ．D ．6．在矩形ABCD 中，|AB |＝6，|AD |＝3.若点M 是CD 的中点，点N 是BC 的三等分点，且BN ＝13BC ，则AM ·MN ＝（ ） A ．6B ．4C ．3D ．27．若2a b c ===，且0a b ⋅=，()()0a c b c -⋅-≤，则a b c +-的取值范围是( )A ．[0,222]B ．[0,2]C ．[222,222]-+D ．[222,2]-8．已知向量a ，b 满足||3,||2a b ==，且对任意的实数x ，不等式a xb a b +≥+恒成立，设a ，b 的夹角为θ，则tan θ的值为（ ）A B ．2-C ．D 9．已知向量(cos ,sin )a θθ=，向量(3,1)b =-，则2a b -的最大值，最小值分别是（ ）A ．0B ．4，C ．16，0D ．4，010．在ABC ∆中，060BAC ∠=，5AB =，6AC =，D 是AB 上一点，且5AB CD ⋅=-，则BD 等于（ ）A ．1B ．2C ．3D ．411．在边长为2的菱形ABCD 中，60BAD ∠=︒，点E 是AB 边上的中点，点F 是BC 边上的动点，则DE DF ⋅的取值范围是（ ）A ．⎡⎣B ．2⎣C ．⎤⎦D ．[]0,312．已知平面上的非零．．向量a ，b ，c ，下列说法中正确的是（ ） ①若//a b ，//b c ，则//a c ； ②若2a b =，则2a b =±；③若23x y a b a b +=+，则2x =，3y =； ④若//a b ，则一定存在唯一的实数λ，使得a b λ=. A ．①③B ．①④C ．②③D ．②④二、填空题13．已知平面向量,,a b c 满足()()||2,||2||a c b c a b a b -⋅-=-==.则c 的最大值是________.14．已知向量(12,2)a t =-+，(2,44)b t =-+，(1,)c λ=（其中t ，)R λ∈．若(2)c a b ⊥+，则λ=__．15．向量,a b 满足(1,3),2,()(3)12a b a b a b ==+⋅-=，则a 在b 方向上的投影为__________．16．已知向量2a =，1b =，223a b -=，则向量a ，b 的夹角为_______. 17．如图，正方形ABCD 的边长为2，E 是以CD 为直径的半圆弧上一点，则AD AE ⋅的最大值为______．18．在△ABC 中，BD ＝2DC ，过点D 的直线与直线AB ，AC 分别交于点E ，F ，若AE ＝x AB ，AF ＝y AC （x ＞0，y ＞0），则x +y 的最小值为_____.19．已知O 为ABC 内一点，且满足305OA OB OC =++，延长AO 交BC 于点D .若BD DC λ=，则λ=_____.20．已知平面向量a ，b 满足3a b +=，3a b -=，则向量a 与b 夹角的取值范围是______.三、解答题21．在ABC 中，3AB =，6AC =，23BAC π∠=，D 为边BC 的中点，M 为中线AD 的中点.（1）求中线AD 的长；（2）求BM 与AD 的夹角θ的余弦值. 22．已知()3,0a =，(1,3)b =． （Ⅰ）求a b ⋅和b 的值；（Ⅱ）当()k k ∈R 为何值时，向量a 与k +a b 互相垂直？ 23．已知123PP P 三个顶点的坐标分别为123(cos ,sin ),(cos ,sin ),(cos ,sin )P P P ααββγγ，且1230OP OP OP ++=（O 为坐标原点）．（1）求12POP ∠的大小； （2）试判断123PP P 的形状．24．如图，在正方形ABCD 中，点E 是BC 边上中点，点F 在边CD 上．（1）若点F 是CD 上靠近C 的三等分点，设EF AB AD λμ=+，求λ+μ的值．（2）若AB ＝2，当AE BF ⋅=1时，求DF 的长．25．在ABCD 中，2AB =，23AC =AB 与AD 的夹角为3π． （Ⅰ）求AD ；（Ⅱ）求AC 和BD 夹角的余弦值． 26．已知向量a 、b 的夹角为3π，且||1a =，||3b =. （1）求||a b +的值； （2）求a 与a b +的夹角的余弦.【参考答案】***试卷处理标记，请不要删除一、选择题 1．D 解析：D 【分析】先根据重心得到()13AG AB AC =+，设0,0AB x AC y =>=>，利用数量积计算4xy =，再利用重要不等式求解()2219A AGB AC =+的最小值，即得结果.【详解】点G 是ABC 的重心，设D 为BC 边上的中点，则()2133AG AD AB AC ==+， 因为120,2,A AB AC ∠=︒⋅=-设0,0AB x AC y =>=>，则cos1202xy ︒=-，即4xy =，故()()()222211144249999AG x y x B ACy A =+-≥-=+=，即23AG ≥， 当且仅当2x y ==时等号成立，故AG 的最小值是23. 故选：D. 【点睛】 关键点点睛：本题的解题关键在于通过重心求得向量关系()13AG AB AC =+，利用数量积得到定值，才能利用重要不等式求最值，突破难点，要注意取条件的成立.2．A解析：A【分析】根据题意可得，OM ON ⋅＝2x ﹣y ，令Z ＝2x ﹣y ，做出不等式组所表示的平面区域，做直线l 0：2x ﹣y ＝0，然后把直线l 0向可行域内平移，结合图象可判断取得最大值时的位置． 【详解】根据题意可得，OM ON ⋅＝2x ﹣y ，令Z ＝2x ﹣y做出不等式组所表示的平面区域，如图所示的△ABC 阴影部分：做直线l 0：2x ﹣y ＝0，然后把直线l 0向可行域内平移， 到点A 时Z 最大，而由x+y=11x ⎧⎨=⎩ 可得A （1，0）， 此时Z max ＝2． 故选：A ． 【点睛】本题主要考查了利用线性规划求解最优解及目标函数的最大值，解题的关键是正确作出不等式组所表示的平面区域，并能判断出取得最大值时的最优解的位置．利用线性规划求最值的步骤：(1)在平面直角坐标系内作出可行域．(2)考虑目标函数的几何意义，将目标函数进行变形．常见的类型有截距型（ax by +型）、斜率型（y bx a++型）和距离型（()()22x a y b +++型）．(3)确定最优解：根据目标函数的类型，并结合可行域确定最优解．(4)求最值：将最优解代入目标函数即可求出最大值或最小值。

高中数学平面向量组卷一．选择题〔共18小题〕1．向量与的夹角为θ，定义×为与的“向量积〞，且×是一个向量，它的长度|×|=||||sinθ，假设=〔2，0〕，﹣=〔1，﹣〕，那么|×〔+〕|=〔〕A．4B．C．6D．22．，为单位向量，其夹角为60°，那么〔2﹣〕•=〔〕A．﹣1 B．0C．1D．23．向量=〔1，〕，=〔3，m〕，假设向量，的夹角为，那么实数m=〔〕A．2B．C．0D．﹣4．向量，，且∥，那么=〔〕A．B．C．D．5．如图，在△ABC中，BD=2DC．假设，，那么=〔〕A．B．C．D．6．假设向量=〔2cosα，﹣1〕，=〔，tanα〕，且∥，那么sinα=〔〕A．B．C．D．7．点A〔3，0〕，B〔0，3〕，C〔cosα，sinα〕，O〔0，0〕，假设，那么的夹角为〔〕A．B．C．D．8．设向量=，=不共线，且|+|=1，|﹣|=3，那么△OAB的形状是〔〕A．等边三角形B．直角三角形C．锐角三角形D．钝角三角形9．点G是△ABC的重心，假设A=，•=3，那么||的最小值为〔〕A．B．C．D．210．如图，各棱长都为2的四面体ABCD中，=，=2，那么向量•=〔〕A．﹣B．C．﹣D．11．函数f〔x〕=sin〔2πx+φ〕的局部图象如下图，点B，C是该图象与x轴的交点，过点C的直线与该图象交于D，E两点，那么〔〕•的值为〔〕A．B．C．1D．212．P为三角形ABC部任一点〔不包括边界〕，且满足(﹣〕•〔+﹣2〕=0，那么△ABC的形状一定为〔〕A．等边三角形B．直角三角形C．钝三角形D．等腰三角形13．如下图，设P为△ABC所在平面的一点，并且=+，那么△ABP与△ABC的面积之比等于〔〕A．B．C．D．14．在△ABC中，|AB|=3，|AC|=2，=，那么直线AD通过△ABC的〔〕A．垂心B．外心C．重心D．心15．在△ABC中，∠BAC=60°，AB=2，AC=1，E，F为边BC的三等分点，那么=〔〕A．B．C．D．16．空间向量满足，且的夹角为，O为空间直角坐标系的原点，点A、B满足，，那么△OAB的面积为〔〕A．B．C．D．17．点P为△ABC一点，且++3=，那么△APB，△APC，△BP C的面积之比等于〔〕A．9：4：1 B．1：4：9 C．3：2：1 D．1：2：318．在直角三角形ABC中，点D是斜边AB的中点，点P为线段CD的中点，那么=〔〕A．2B．4C．5D．10二．解答题〔共6小题〕19．如图示，在△ABC中，假设A，B两点坐标分别为〔2，0〕，〔﹣3，4〕点C在AB上，且OC平分∠BOA．〔1〕求∠AOB的余弦值；〔2〕求点C的坐标．20．向量=〔cosθ，sinθ〕和．〔1〕假设∥，求角θ的集合；〔2〕假设，且|﹣|=，求的值．21．如下图，假设D是△ABC的一点，且AB2﹣AC2=DB2﹣DC2．求证：AD⊥BC．22．向量，，其中A、B是△ABC的角，．〔1〕求tanA•tanB的值；〔2〕假设a、b、c分别是角A、B、C的对边，当C最大时，求的值．23．向量且，函数f〔x〕=2〔I〕求函数f〔x〕的最小正周期及单调递增区间；〔II〕假设，分别求tanx及的值．24．，函数f〔x〕=．〔1〕求函数f〔x〕的最小正周期；〔2〕求函数f〔x〕的单调减区间；〔3〕当时，求函数f〔x〕的值域．高中数学平面向量组卷〔2021年09月24日〕参考答案与试题解析一．选择题〔共18小题〕1．向量与的夹角为θ，定义×为与的“向量积〞，且×是一个向量，它的长度|×|=||||sinθ，假设=〔2，0〕，﹣=〔1，﹣〕，那么|×〔+〕|=〔〕A．4B．C．6D．2考点：平面向量数量积的运算．专题：平面向量及应用．分析：利用数量积运算和向量的夹角公式可得=．再利用平方关系可得，利用新定义即可得出．解答：解：由题意，那么，∴=6，==2，=2．∴===．即，得，由定义知，应选：D．点评：此题考察了数量积运算、向量的夹角公式、三角函数的平方关系、新定义，考察了计算能力，属于根底题．2．，为单位向量，其夹角为60°，那么〔2﹣〕•=〔〕A．﹣1 B．0C．1D．2考点：平面向量数量积的运算．专题：平面向量及应用．分析：由条件利用两个向量的数量积的定义，求得、的值，可得〔2﹣〕•的值．解答：解：由题意可得，=1×1×cos60°=，=1，∴〔2﹣〕•=2﹣=0，应选：B．点评：此题主要考察两个向量的数量积的定义，属于根底题．3．向量=〔1，〕，=〔3，m〕，假设向量，的夹角为，那么实数m=〔〕A．2B．C．0D．﹣考点：数量积表示两个向量的夹角．专题：平面向量及应用．分析：由条件利用两个向量的夹角公式、两个向量的数量积公式，求得m的值．解答：解：由题意可得cos===，解得m=，应选：B．点评：此题主要考察两个向量的夹角公式、两个向量的数量积公式的应用，属于根底题．4．向量，，且∥，那么=〔〕A．B．C．D．考点：平行向量与共线向量；同角三角函数间的根本关系；诱导公式的作用．专题：计算题；三角函数的求值．分析：根据向量平行的条件建立关于α的等式，利用同角三角函数的根本关系与诱导公式，化简即可得到的值．解答：解：∵，，且∥，∴，即，得sinα=，由此可得=﹣sinα=．应选：B点评：此题给出向量含有三角函数的坐标式，在向量互相平行的情况下求的值．着重考察了同角三角函数的根本关系、诱导公式和向量平行的条件等知识，属于根底题．5．如图，在△ABC中，BD=2DC．假设，，那么=〔〕A．B．C．D．考点：向量的加法及其几何意义．专题：平面向量及应用．分析：由题意可得=，而，，代入化简可得答案．解答：解：由题意可得=====应选C点评：此题考察平面向量的加法及其几何意义，涉及向量的数乘，属根底题．6．假设向量=〔2cosα，﹣1〕，=〔，tanα〕，且∥，那么sinα=〔〕A．B．C．D．考点：平面向量共线〔平行〕的坐标表示．专题：平面向量及应用．分析：直接由向量共线的坐标表示列式计算．解答：解：∵向量=〔2cosα，﹣1〕，=〔，tanα〕，且∥，那么2cosα•tanα﹣〔﹣1〕×=0，即2sinα=．∴．应选：B．点评：共线问题是一个重要的知识点，在高考题中常常出现，常与向量的模、向量的坐标表示等联系在一起，要特别注意垂直与平行的区别．假设=〔a1，a2〕，=〔b1，b2〕，那么⊥⇔a1a2+b1b2=0，∥⇔a1b2﹣a2b1=0．是根底题．7．点A〔3，0〕，B〔0，3〕，C〔cosα，sinα〕，O〔0，0〕，假设，那么的夹角为〔〕A．B．C．D．考点：平面向量数量积的坐标表示、模、夹角．专题：计算题．分析：根据题意求出的坐标，再由它的模求出角α，进而求出点C的坐标，利用数量积的坐标表示求出和夹角的余弦值，再求出夹角的度数．解答：解：∵A〔3，0〕，C〔cosα，sinα〕，O〔0，0〕，∴=〔3+cosα，sinα〕，∵，∴〔3+cosα〕2+sin2α=13，解得，cosα=，那么α=，即C〔，〕，∴和夹角的余弦值是==，∴和的夹角是．应选：D．点评：此题考察向量线性运算的坐标运算，以及数量积坐标表示的应用，利用向量坐标形式进展运算求出对应向量的模，以及它们的夹角的余弦值，进而结合夹角的围求出夹角的大小．8．设向量=，=不共线，且|+|=1，|﹣|=3，那么△OAB的形状是〔〕A．等边三角形B．直角三角形C．锐角三角形D．钝角三角形考点：平面向量数量积的运算．专题：计算题；平面向量及应用．分析：对|+|=1，|﹣|=3分别平方并作差可得，由其符号可判断∠AOB为钝角，得到答案．解答：解：由|+|=1，得=1，即①，由|﹣|=3，得，即②，①﹣②得，4=﹣8，解得＜0，∴∠AOB为钝角，△OAB为钝角三角形，应选：D．点评：此题考察平面向量数量积运算，属根底题．9．点G是△ABC的重心，假设A=，•=3，那么||的最小值为〔〕A．B．C．D．2考点：平面向量数量积的运算．专题：不等式的解法及应用；平面向量及应用．分析：由A=，•=3，可求得=6，由点G是△ABC的重心，得=，利用不等式那么||2==〔+6〕≥，代入数值可得．解答：解：∵A=，•=3，∴=3，即=6，∵点G是△ABC的重心，∴=，∴||2==〔+6〕≥==2，∴||≥，当且仅当=时取等号，∴||的最小值为，应选B．点评：此题考察平面向量数量积的运算、不等式求最值，注意不等式求最值时适用的条件．10．如图，各棱长都为2的四面体ABCD中，=，=2，那么向量•=〔〕A．﹣B．C．﹣D．考点：平面向量数量积的运算．专题：平面向量及应用．分析：由向量的运算可得=〔〕，=，由数量积的定义可得．解答：解：∵=，=2，∴=〔〕，=，∴=====，∴•=〔〕•〔〕===应选：B点评：此题考察向量数量积的运算，用向量表示未知向量是解决问题的关键，属中档题．11．函数f〔x〕=sin〔2πx+φ〕的局部图象如下图，点B，C是该图象与x轴的交点，过点C的直线与该图象交于D，E两点，那么〔〕•的值为〔〕A．B．C．1D．2考点：平面向量数量积的运算；正弦函数的图象；正弦函数的定义域和值域．专题：平面向量及应用．分析：根据三角函数的图象和性质，求出函数的周期，利用向量的根本运算和向量的数量积定义即可得到结论．解答：解：∵函数f〔x〕=sin〔2πx+φ〕的周期T=，那么BC=，那么C点是一个对称中心，那么根据向量的平行四边形法那么可知：=2•∴〔〕•==2×=．点评：此题主要考察向量的数量积运算，利用三角函数的图象和性质是解决此题的关键．12．P为三角形ABC部任一点〔不包括边界〕，且满足(﹣〕•〔+﹣2〕=0，那么△ABC的形状一定为〔〕A．等边三角形B．直角三角形C．钝三角形D．等腰三角形考点：平面向量数量积的运算．专题：平面向量及应用．分析：利用向量的三角形法那么和平行四边形法那么、向量垂直于数量积的关系即可得出．解答：解：∵，=，〔﹣〕•〔+﹣2〕=0，∴=0．而一定经过边AB的中点，∴垂直平分边AB，即△ABC的形状一定为等腰三角形．点评：此题考察了向量的三角形法那么和平行四边形法那么、向量垂直于数量积的关系、等腰三角形的定义，考察了推理能力，属于难题．13．如下图，设P为△ABC所在平面的一点，并且=+，那么△ABP与△ABC的面积之比等于〔〕A．B．C．D．考点：向量在几何中的应用．专题：计算题；压轴题．分析：此题考察的知识点是向量在几何中的应用，及三角形面积的性质，由△ABP与△ABC为同底不等高的三角形，故高之比即为两个三角面积之间，连接CP并延长后，我们易得到CP与CD长度的关系，进展得到△ABP的面积与△AB C面积之比．解答：解：连接CP并延长交AB于D，∵P、C、D三点共线，∴=λ+μ，且λ+μ=1设=k，结合=+，得=+由平面向量根本定理解之，得λ=，k=3且μ=，∴=+，可得=，∵△ABP的面积与△ABC有一样的底边AB高的比等于||与||之比∴△ABP的面积与△ABC面积之比为，应选：C点评：三角形面积性质：同〔等〕底同〔等〕高的三角形面积相等；同〔等〕底三角形面积这比等于高之比；同〔等〕高三角形面积之比等于底之比．14．在△ABC中，|AB|=3，|AC|=2，=，那么直线AD通过△ABC的〔〕A．垂心B．外心C．重心D．心考点：向量在几何中的应用．专题：综合题；平面向量及应用．分析：首先根据条件可知||=||=，又因为=，设=，=，由向量加法的平行四边形法那么可知四边形AEDF为菱形，从而可确定直线AD通过△ABC的心．解答：解：∵|AB|=3，|AC|=2∴||=||=．设=，=，那么||=||，∴==+．由向量加法的平行四边形法那么可知，四边形AEDF为菱形．∴AD为菱形的对角线，∴AD平分∠EAF．∴直线AD通过△ABC的心．应选：D．点评：此题考察向量加法的平行四边形法那么及其几何意义，属于中档题．15．在△ABC中，∠BAC=60°，AB=2，AC=1，E，F为边BC的三等分点，那么=〔〕A．B．C．D．考点：向量在几何中的应用；平面向量数量积的运算．专题：计算题．分析：先判定三角形形状，然后建立直角坐标系，分别求出，向量的坐标，代入向量数量积的运算公式，即可求出答案．解答：解：∵在△ABC中，∠BAC=60°，AB=2，AC=1，∴根据余弦定理可知BC=由AB=2，AC=1，BC=满足勾股定理可知∠BCA=90°以C为坐标原点，CA、CB方向为x，y轴正方向建立坐标系∵AC=1，BC=，那么C〔0，0〕，A〔1，0〕，B〔0，〕又∵E，F分别是Rt△ABC中BC上的两个三等分点，那么E〔0，〕，F〔0，〕那么=〔﹣1，〕，=〔﹣1，〕∴=1+=应选A．点评：此题考察的知识点是平面向量数量积的运算，其中建立坐标系，将向量数量积的运算坐标化可以简化此题的解答过程．16．空间向量满足，且的夹角为，O为空间直角坐标系的原点，点A、B满足，，那么△OAB的面积为〔〕A．B．C．D．考点：平面向量数量积的运算；三角形的面积公式．专题：平面向量及应用．分析：由向量的运算可得，，以及，代入夹角公式可得cos∠BOA，由平方关系可得sin∠BOA，代入三角形的面积公式S=，计算可得．解答：解：由题意可得====，同理可得====，而=〔〕•〔〕==6×12﹣12=，故cos∠BOA===，可得sin∠BOA==，所以△OAB的面积S===．应选B点评：此题考察平面向量的数量积和三角形面积的求解，熟练掌握公式是解决问题的关键，属中档题．17．点P为△ABC一点，且++3=，那么△APB，△APC，△BPC的面积之比等于〔〕A．9：4：1 B．1：4：9 C．3：2：1 D．1：2：3考点：向量在几何中的应用．专题：计算题；压轴题．分析：先将向量式化为两个向量共线的形式，再利用平行四边形法那么及向量数乘运算的几何意义，三角形面积公式确定面积之比解答：解：∵++3=，∴+=﹣+〕，如图：∵，∴∴F、P、G三点共线，且PF=2PG，GF为三角形ABC的中位线∴====2而S△APB=S△ABC∴△APB，△APC，△BPC的面积之比等于3：2：1应选C点评：此题考察了向量式的化简，向量加法的平行四边形法那么，向量数乘运算的几何意义等向量知识，充分利用向量共线是解决此题的关键18．在直角三角形ABC中，点D是斜边AB的中点，点P为线段CD的中点，那么=〔〕A．2B．4C．5D．10考点：向量在几何中的应用．专题：计算题；综合题．分析：以D为原点，AB所在直线为x轴，建立坐标系，由题意得以AB为直径的圆必定经过C点，因此设AB=2r，∠CDB=α，得到A、B、C和P各点的坐标，运用两点的距离公式求出|PA|2+|PB|2和|PC|2的值，即可求出的值．解答：解：以D为原点，AB所在直线为x轴，建立如图坐标系，∵AB是Rt△ABC的斜边，∴以AB为直径的圆必定经过C点设AB=2r，∠CDB=α，那么A〔﹣r，0〕，B〔r，0〕，C〔rcosα，rsinα〕∵点P为线段CD的中点，∴P〔rcosα，rsinα〕∴|PA|2=+=+r2cosα，|PB|2=+=﹣r2cosα，可得|PA|2+|PB|2=r2又∵点P为线段CD的中点，CD=r∴|PC|2==r2所以：==10应选D点评：此题给出直角三角形ABC斜边AB上中线AD的中点P，求P到A、B距离的平方和与PC平方的比值，着重考察了用解析法解决平面几何问题的知识点，属于中档题．二．解答题〔共6小题〕19．如图示，在△ABC中，假设A，B两点坐标分别为〔2，0〕，〔﹣3，4〕点C在AB上，且OC平分∠BOA．〔1〕求∠AOB的余弦值；〔2〕求点C的坐标．考点：向量在几何中的应用．专题：综合题．分析：〔1〕由题意可得，把代入可求〔2〕设点C〔x，y〕，由OC平分∠BOA可得cos∠AOC=cos∠BOC即=；再由点C在AB即共线，建立关于x，y的关系，可求解答：解：〔1〕由题意可得，，∴==〔2〕设点C〔x，y〕，由OC平分∠BOA可得cos∠AOC=cos∠BOC∵，∴=∴，∴y=2x①又点C在AB即共线，∴4x+5y﹣8=0②由①②解得，∴点C的坐标为点评：此题注意考察了向量的夹角公式的坐标表示的应用，向量共线的坐标表示在三角形中的应用，解题的关键是借助于图象中的条件，灵活的应用向量的根本知识．20．向量=〔cosθ，sinθ〕和．〔1〕假设∥，求角θ的集合；〔2〕假设，且|﹣|=，求的值．考点：平面向量的坐标运算．专题：计算题．分析：〔1〕由题意和共线向量的等价条件，列出关于角θ的方程，求出θ的一个三角函数值，再根据三角函数求出角θ的集合．〔2〕由题意先求出﹣的坐标，根据此向量的长度和向量长度的坐标表示，列出方程求出cos〔θ﹣〕，由余弦的二倍角公式和θ的围求出的值．解答：解：〔1〕由题意知∥，那么cosθ×cosθ﹣sinθ×〔﹣sinθ〕=0，∴sinθ=1，sinθ=，∴角θ的集合={θ|θ=+2kπ或θ=+2kπ，k∈Z}；〔2〕由题意得，﹣=〔cosθ﹣+sinθ，sinθ﹣cosθ〕，∴|﹣|===2=，即cos〔θ﹣〕=，由余弦的二倍角公式得，=①，∵，∴＜＜，∴＜﹣＜，即cos〔﹣〕＜0，∴由①得cos〔﹣〕=﹣．点评：此题考察了共线向量的坐标表示和向量长度的坐标表示，利用两角正弦〔余弦〕和差公式和二倍角公式进展变形求解，注意由条件求出所求角的围，来确定所求三角函数值的符号．21．如下图，假设D是△ABC的一点，且AB2﹣AC2=DB2﹣DC2．求证：AD⊥BC．考点：向量在几何中的应用．专题：计算题；证明题；平面向量及应用．分析：设=，=，=，=，=，将=+、=+代入2﹣2的式子，化简整理2﹣2=2+2•﹣2•﹣2，结合题意2﹣2=2﹣2化简，可得•〔﹣〕=0，再结合向量的加减法法那么得到•=0，由此结合数量积的性质即可得到AD⊥BC．解答：解：设=，=，=，=，=，那么=+，=+．∴2﹣2=〔+〕2﹣〔+〕2=2+2•﹣2•﹣2．∵由AB2﹣AC2=DB2﹣DC2，得2﹣2=2﹣2，∴2+2•﹣2•﹣2=2﹣2，即•〔﹣〕=0．∵=+=﹣，∴•=•〔﹣〕=0，因此，可得⊥，即AD⊥BC．点评：此题给出三角形ABC满足平方关系的点D，求证AD⊥BC．着重考察了平面向量的加减法那么、向量的数量积及其运算性质等知识，属于中档题．22．向量，，其中A、B是△ABC的角，．〔1〕求tanA•tanB的值；〔2〕假设a、b、c分别是角A、B、C的对边，当C最大时，求的值．考点：平面向量的综合题．专题：计算题．分析：〔1〕根据推断出=0，利用向量的数量积运算结合二倍角公式求得tanA•tanB；〔2〕由于tanA•tanB=＞0，利用根本不等式得出当且仅当时，c取得最大值，再利用同角公式求出sinC，sinA，最后由正弦定理求的值．解答：解：〔Ⅰ〕由题意得=0 即，﹣5cos〔A+B〕+4cos〔A﹣B〕=0cosAcosB=9sinAsinB∴tanA•tanB=．〔2〕由于tanA•tanB=＞0，且A、B是△ABC的角，∴tanA＞0，tanB＞0∴=﹣当且仅当取等号．∴c为最大边时，有，tanC=﹣，∴sinC=，sinA=由正弦定理得：=．点评：此题是中档题，考察三角函数的化简与求值，正弦定理的应用，根本不等式的知识，是一道综合题，考察学生分析问题解决问题的能力，公式的熟练程度决定学生的能力的上下．23．向量且，函数f〔x〕=2〔I〕求函数f〔x〕的最小正周期及单调递增区间；〔II〕假设，分别求tanx及的值．考点：平面向量数量积的坐标表示、模、夹角；复合三角函数的单调性．专题：平面向量及应用．分析：〔I〕化简函数f〔x〕=2=2sin〔2x+〕，可得函数的周期，令2kπ﹣≤2x+≤2kπ+，k∈z，求得x的围，即可得到函数的单调递增区间．〔II〕由，求得tanx=，再由==，运算求得结果．解答：〔I〕解：函数f〔x〕=2=2sinxcosx+2cos2x﹣1=sin2x+cos2x=2sin〔2x+〕，故函数的周期为=π，令2kπ﹣≤2x+≤2kπ+，k∈z，求得kπ﹣≤x≤kπ+，故函数的单调递增区间为[kπ﹣，kπ+]，k∈z．〔II〕解：假设，那么sinx=cosx，即tanx=．∴====﹣．点评：此题主要考察两个向量的数量积的定义，三角函数的恒等变换及化简求值，正弦函数的增区间，三角函数的周期性和求法，属于中档题．24．，函数f〔x〕=．〔1〕求函数f〔x〕的最小正周期；〔2〕求函数f〔x〕的单调减区间；〔3〕当时，求函数f〔x〕的值域．考点：平面向量的综合题；三角函数中的恒等变换应用；三角函数的周期性及其求法；复合三角函数的单调性．专题：综合题．分析：〔1〕根据向量的数量积公式，结合二倍角公式、辅助角公式化简函数，利用周期公式，可求函数f〔x〕的最小正周期；〔2〕由2kπ+≤2x+≤2kπ+得kπ+≤x≤kπ+，从而可得f〔x〕的单调减区间；〔3〕由，可得，从而可求函数f〔x〕的值域．解答：解：〔1〕∵，，∴函数f〔x〕==5sinxcosx+sin2x+6cos2x===5sin〔2x+〕+∴f〔x〕的最小正周期；〔2〕由2kπ+≤2x+≤2kπ+得kπ+≤x≤kπ+，k∈Z∴f〔x〕的单调减区间为[kπ+，kπ+]〔k∈Z〕〔3〕∵∴∴∴1≤f〔x〕≤即f〔x〕的值域为[1，]．点评：此题考察向量知识的运用，考察三角函数的化简，考察函数的单调性与值域，化简函数是关键．。

一、选择题1．ABC ∆中，AB AC ⊥，M 是BC 中点，O 是线段AM 上任意一点，且2AB AC ==，则OA OB OA OC +的最小值为（ ）A ．-2B ．2C ．-1D ．12．在ABC ∆中，2AB =，3AC =，5cos 6A =，若O 为ABC ∆的外心（即三角形外接圆的圆心），且AO mAB nAC +=，则2n m -=（ ） A ．199B ．4122-C ．111-D ．17113．在ABC ∆中，5,6AB AC ==，若2B C =，则向量BC 在BA 上的投影是（ ） A ．75-B ．77125-C ．77125D ．754．已知ABC 是边长为2的等边三角形，D ，E 分别是AC 、AB 上的两点，且AE EB =，2AD DC =，与CE 交于点O ，则下列说法正确的是（ ）A ．1AB CD ⋅=- B ．1233BD BC BA =+ C ．3OA OB OC ++=D ．ED 在BC 方向上的投影为765．已知ABC ，若对任意m R ∈，BC mBA CA -≥恒成立，则ABC 为（ ） A ．锐角三角形B ．钝角三角形C ．直角三角形D ．不确定6．在ABC 中，D 为AB 的中点，60A ∠=︒且2AB AC AB CD ⋅=⋅，若ABC 的面积为AC 的长为（ ）A ．BC ．3D ．7．已知两个非零向量a ，b 的夹角为23π，且=2a b -，则·ab 的取值范围是（ ） A ．2,03⎛⎫- ⎪⎝⎭B ．[)2,0-C ．2,03⎡⎫-⎪⎢⎣⎭D ．[)1,0-8．在ABC 中，||:||:||3:4:5AB AC BC =，圆O 是ABC 的内切圆，且与BC 切于D 点，设AB a =，AC b =，则AD =（ ） A ．2355a b + B ．3255a b + C ．2133a b + D ．1233a b +9．如图，已知点D 为ABC 的边BC 上一点，3BD DC =，*()∈n E n N 为AC 边的一列点，满足11(32)4n n n n n E A a E B a E D +=-+，其中实数列{}n a 中，10,1n a a >=，，则{}n a 的通项公式为（ ）A ．1321n -⋅-B ．21n -C ．32n -D ．1231n -⋅-10．在ABC ∆中，060BAC ∠=，5AB =，6AC =，D 是AB 上一点，且5AB CD ⋅=-，则BD 等于（ ）A ．1B ．2C ．3D ．411．已知ABC 中，3AB AC ==，且||||AB AC AB AC +=-，点D ，E 是BC 边的两个三等分点，则AD AE ⋅=（ ） A ．3B ．4C ．5D ．612．如图所示，在ABC 中，点D 在线段BC 上，且3BD DC =，若AD AB AC λμ=+，则λμ=（ ）A ．12B ．13C ．2D ．23二、填空题13．如图，已知四边形ABCD ，AD CD ⊥，AC BC ⊥，E 是AB 的中点，1CE =，若//AD CE ，则AC BD ⋅的最小值为___________.14．如图，已知ABC 为边长为2的等边三角形，动点P 在以BC 为直径的半圆上，若AP AB AC λμ=+，则2λμ+的最小值为_______．15．已知向量2a =，1b =，223a b -=，则向量a ，b 的夹角为_______. 16．如图，设圆M 的半径为2，点C 是圆M 上的定点，A ，B 是圆M 上的两个动点，则CA CB ⋅的最小值是________.17．如图，在等腰三角形ABC 中，已知1AB AC ==，120A ∠=︒，E F 、分别是边AB AC 、上的点，且,AE AB AF AC λμ==,其中(),0,1λμ∈且41λμ+=，若线段EF BC 、的中点分别为M N 、，则MN 的最小值是_____.18．已知平面非零向量,,a b c 两两所成的角相等，1a b c ===，则a b c ++的值为_____．19．已知a →，b →为单位向量，2c a b →→→=-，且,3a b π→→<>=，则,a c →→〈〉=________．20．设λ是正实数，三角形ABC 所在平面上的另三点1A 、1B 、1C 满足：()1AA AB AC λ=+，()1BB BC BA λ=+，()1CC CA CB λ=+，若三角形ABC 与三角形111A B C 的面积相等，则λ的值为_____.三、解答题21．已知ABC 中C ∠是直角，CA CB =，点D 是CB 的中点，E 为AB 上一点．（1）设CA a=，CD b=，当12AE AB=，请用a，b来表示AB，CE.（2）当2AE EB=时，求证：AD CE⊥.22．已知平面直角坐标系中，点O为原点，()()3,1,1,2A B-．(I)求AB的坐标及AB；(Ⅱ)设e为单位向量，且e OB⊥，求e的坐标23．对于任意实数a，b，c，d，表达式ad bc-称为二阶行列式（determinant），记作a bc d，（1）求下列行列式的值：①1001；②1326；③251025--；（2）求证：向量(),p a b=与向量(),q c d=共线的充要条件是0a bc d=；（3）讨论关于x，y的二元一次方程组111222a xb y ca xb y c+=⎧⎨+=⎩（1212a a bb≠）有唯一解的条件，并求出解.（结果用二阶行列式的记号表示）.24．已知()()1,,3,2a m b==-．(1)若()a b b+⊥，求m的值；(2)若·1a b=-，求向量b在向量a方向上的投影．25．如图，在OAB中，P为边AB上的一点2BP PA=，6OA=，2OB=且OA与OB的夹角为60︒.（1）设OP xOA yOB =+，求x ，y 的值； （2）求OP AB ⋅的值. 26．已知(2,0)a =，||1b =． （1）若a 与b 同向，求b ；（2）若a 与b 的夹角为120，求a b +．【参考答案】***试卷处理标记，请不要删除一、选择题 1．C 解析：C 【分析】根据向量求和的平行四边形法则可以得出2OA OB OA OC OA OM ⋅+⋅=⋅，再利用向量的数量积的运算可以得到22OA OM OA OM ⋅=-⋅，因为2OA OM +=求出最小值. 【详解】解：在直角三角形ABC 中，2AB AC ==，则BC =M 为BC 的中点，所以2AM =.设OA x =，(0x ≤≤()2OA OB OA OC OA OB OC OA OM ⋅+⋅=⋅+=⋅ )()2222OA OM xx x =-⋅=-=2212x ⎛=-- ⎝⎭所以当2x =，即22OA =时，原式取得最小值为1-.故选：C. 【点睛】方法点睛：（1）向量求和经常利用平行四边形法则转化为中线的2倍； （2）利用向量三点共线，可以将向量的数量积转化为长度的乘积； （3）根据向量之间模的关系，二元换一元，转化为二次函数求最值即可.2．D解析：D 【分析】设,D E 分别为,AB AC 的中点，连接,OD OE ，则OD AB ⊥，OE AC ⊥，从而得到·0?0OD AB OE AC ==，，坐标化构建m ，n 的方程组，解之即可. 【详解】设,D E 分别为,AB AC 的中点，连接,OD OE ，则OD AB ⊥，OE AC ⊥，又OD AD AO =-，即11222mOD AB mAB nAC AB nAC -=--=-， 同理122nOE AE AO AC mAB -=-=-， 因为212·||?02m OD AB AB nAB AC -=-=， 所以124502m n -⨯-=，又212·||?02nOE AC AC mAB AC -=-=， 所以129502n m -⨯-=，联立方程组124502129502mn n m -⎧⨯-=⎪⎪⎨-⎪⨯-=⎪⎩，解得922811m n ⎧=-⎪⎪⎨⎪=⎪⎩，所以17211n m -=. 故选D 【点睛】本题考查了数量积运算性质、向量垂直与数量积的关系、三角形外心的性质、向量基本定理，考查了推理能力与计算能力，属于中档题．3．B解析：B 【解析】 由正弦定理得，653cos sin sin sin 2sin 5AC AB C B C C C =⇒=⇒=,由余弦定理得，22211cos 25BC AC AB C BC AC BC +-=⇒=⋅,则77cos 125BC θ=- ，故选B. 4．D解析：D 【分析】利用CE AB ⊥，判断出A 错误；由2AD DC =结合平面向量的基本定理，判断出选项B 错误；以E 为原点，EA ，EC 分别为x 轴，y 轴正方向建立平面直角坐标系，写出各点坐标，计算出OA OB OC ++的值，判断出选项C 错误；利用投影的定义计算出D 正确．【详解】由题E 为AB 中点，则CE AB ⊥，0AB CE ⋅=，所以选项A 错误；由平面向量线性运算得2133BD BC BA =+，所以选项B 错误； 以E 为原点，EA ，EC 分别为x 轴，y 轴正方向建立平面直角坐标系，如图所示，()0,0E ，1,0A ，()1,0B -，(3C ，13,33D ⎛ ⎝⎭，设()0,O y ，(3y ∈，()1,BO y =，123,3DO y ⎛=- ⎝⎭， //BO DO ，所以，23133y y -=-，解：32y =， 32OA OB OC OE OE OE ++=+==，所以选项C 错误； 1233ED ⎛= ⎝⎭，(1,3BC =，ED 在BC 方向上的投影为127326BC BCED +⋅==，故选：D ． 【点睛】本题考查平面向量数量积的应用，考查平面向量基本定理，考查投影的定义，考查平面向量的坐标表示，属于中档题．5．C解析：C 【分析】在直线AB 上取一点D ，根据向量减法运算可得到DC CA ≥，由垂线段最短可确定结论. 【详解】在直线AB 上取一点D ，使得mBA BD =，则BC mBA BC BD DC -=-=，DC CA ∴≥.对于任意m R ∈，都有不等式成立，由垂线段最短可知：AC AD ⊥，即AC AB ⊥，ABC ∴为直角三角形.故选：C . 【点睛】本题考查与平面向量结合的三角形形状的判断，关键是能够利用平面向量数乘运算和减法运算的几何意义准确化简不等式.6．B解析：B 【分析】设,,AB c AC b ==先化简2AB AC AB CD ⋅=⋅得3c b =，由ABC 的面积为16bc =，即得AC 的长.【详解】 设,,AB c AC b ==由题得2AB AC AB CD ⋅=⋅，所以2()AB AC AB AD AC AB AD AB AC ⋅=⋅-=⋅-⋅， 所以3,3cos cos 0,332cAB AC AB AD c b c c b π⋅=⋅∴⨯⨯⨯=⨯⨯∴=.因为ABC 的面积为1sin 1623b c bc π⨯⨯⨯=∴=.所以2316,b b =∴=所以AC = 故选：B 【点睛】本题主要考查平面向量的数量积运算，考查三角形的面积的应用，意在考查学生对这些知识的理解掌握水平.7．C解析：C 【分析】对=2a b -两边平方后，结合2·cos 3a b a b π=⋅进行化简可得：224a b b +⋅+=；由基本不等式可得222a b a b +⋅，于是推出403a b<⋅，再结合平面向量数量积即可得解． 【详解】因为2a b -=，所以 2224a a b b -⋅+=，所以2222cos43b baaπ-⋅+=，即224a ab b+⋅+=，由基本不等式的性质可知，222a b a b+⋅，43a b∴<⋅，所以212·cos,0323a b a b a bπ⎡⎫=⋅⋅=-⋅∈-⎪⎢⎣⎭．故选：C．【点睛】本题主要考查平面向量数量积运算，考查利用基本不等式求最值，难度一般.对于平面向量的模长问题，一般采用平方处理，然后结合平面向量数量积的运算公式求解即可．8．B解析：B【分析】由题得三角形是直角三角形，设3,4,5AB AC BC===，设,=,,DB BF x AD AE y EC CF z=====求出,,x y z，再利用平面向量的线性运算求解.【详解】因为||:||:||3:4:5AB AC BC=，所以ABC是直角三角形，设3,4, 5.AB AC BC===如图，设,=,,DB BF x AD AE y EC CF z=====由题得34,2,1,35x yy z x y zx z+=⎧⎪+=∴===⎨⎪+=⎩，所以2232()5555AD AB BD AB BC AB AC AB AB AC=+=+=+-=+3255a b=+.故选：B【点睛】本题主要考查平面向量的线性运算，意在考查学生对这些知识的理解掌握水平.9．D解析：D 【分析】以BA 和BC 为基底，表示n BE ，根据n E ，A ，C 三点共线，可得1193331442+-++=++n n n a a a ，构造等比数列，即可求出通项公式. 【详解】113(32),44+=-+=-=-n n n n n n n n E A a E B a E D E D BD BE BC BE , 113(32)()44n n n n n E A a E B a BC BE +∴=-+- 113(32)(32)44n n n n a a E B a BC +=---+ 又=-n n E A BA BE113(32)(32=)44+∴---+-n n n n n a a E B a BC BA BE113(33)(32)44+-∴++=++n n n n a a BE a BC BA因为n E ，A ，C 三点共线113(33)1(32)44+-++=++∴n n n a a a ，即1=32++n n a a ，即1+1=3(1)++n n a a ，所以数列{1}n a +是等比数列，首项为2，公比为3．1+1=23-∴⋅n n a ，即1=23-1-⋅n n a ， 故选：D ． 【点睛】本题考查了平面向量基本定理和等比数列的通项公式，考查了运算求解能力和逻辑推理能力，属于中档题.10．C解析：C 【解析】在ABC ∆中，060BAC ∠=，5,6AB AC ==，D 是AB 是上一点，且5AB CD ⋅=-， 如图所示，设AD k AB =，所以CD AD AC k AB AC =-=-， 所以21()2556251552AB CD AB k AB AC k AB AB AC k k ⋅=⋅-=-⋅=-⨯⨯=-=-，解得25k =，所以2(1)35BD AB =-=，故选C ．11．B解析：B 【分析】由||||AB AC AB AC +=-知，0AB AC ⋅=，根据平面向量的线性运算可推出2133AD AB AC =+，1233AE AB AC =+，故21123333AD AE AB AC AB AC ⎛⎫⎛⎫⋅=+⋅+ ⎪ ⎪⎝⎭⎝⎭，展开后代入数据进行运算即可.【详解】解：∵||||AB AC AB AC +=-，∴0AB AC ⋅=， ∵点D 是BC 边的三等分点， ∴11()33AD AB BD AB BC AB AC AB =+=+=+-2133AB AC =+.同理可得，1233AE AB AC =+，∴()2221122(3339)3AD AE AB AC AB AC AB AC ⎛⎫⋅=+⋅+=+ ⎪⎝⎭2(99)49=⨯+=.故选：B. 【点睛】本题考查平面向量数量积运算、模的运算、平面向量基本定理，考查转化与化归思想，考查逻辑推理能力、运算求解能力，求解时注意基底的选择.12．B解析：B 【分析】由向量的运算法则，化简得1344AD AB AC =+,再由AD AB AC λμ=+，即可求得,λμ 的值，即可求解. 【详解】由向量的运算法则，可得34=+=+AD AB BD AB BC 313()444AB AC AB AB AC =+-=+,因为AD AB AC λμ=+，所以13,44λμ==，从而求得13λμ=，故选:B ． 【点睛】该题考查的是有关向量的基本定理，在解题的过程中，需要利用向量直角的关系，结合三角形法则，即可求得结果，属于基础题.二、填空题13．【分析】令结合题中已知条件得出通过根据数量积的概念以及二次函数的性质可得结果【详解】令因为所以又因为是的中点所以故可得所以当时取得最小值故答案为：【点睛】关键点点睛：将表示成根据几何关系将所需量用表 解析：1-【分析】令ACD θ∠=，结合题中已知条件得出2CAD πθ∠=-，2CAB πθ∠=-，2sin AC θ=，22sin AD θ=，通过()AC BD AC BA AD ⋅=⋅+，根据数量积的概念以及二次函数的性质可得结果. 【详解】令ACD θ∠=，因为AD CD ⊥，AC BC ⊥，//AD CE ， 所以BCE θ∠=，2ACE CAD πθ∠=∠=-，又因为E 是AB 的中点，1CE =，所以2AB =，1CE =，CBA θ∠=，2CAB πθ∠=-，故可得2sin AC θ=，22sin AD θ=，所以()AC BD AC BA AD AC BA AC AD ⋅=⋅+=⋅+⋅2222sin 2cos 2sin 2sin cos 4sin 4sin 22ππθπθθθθθθ⎛⎫⎛⎫=⨯⨯-++⨯⨯-=- ⎪ ⎪⎝⎭⎝⎭2214sin 12θ⎛⎫=-- ⎪⎝⎭，当21sin 2θ=时，AC BD ⋅取得最小值1-，故答案为：1-. 【点睛】关键点点睛：将BD 表示成BA AD +，根据几何关系将所需量用θ表示，将最后结果表示为关于θ的函数.14．1【分析】如图建系设P 点坐标则可得的坐标根据题意可得的表达式代入所求根据的范围利用三角函数求最值即可得答案【详解】取BC 中点O 以O 为原点OCOA 方向为x 轴y 轴正方向建系如图所示由题意得：所以如图以B解析：1 【分析】如图建系，设P 点坐标(cos ,sin )θθ，则可得,,AP AB AC 的坐标，根据题意，可得,λμ的表达式，代入所求，根据θ的范围，利用三角函数求最值，即可得答案. 【详解】取BC 中点O ，以O 为原点，OC ，OA 方向为x 轴y 轴正方向建系，如图所示由题意得：2sin 603OA =︒=3),(1,0),(1,0)A B C -， 如图以BC 为直径的半圆方程为：221(0)x y y +=≤， 设(cos ,sin )P θθ，因为sin 0θ≤，所以[,2]θππ∈，则(cos ,sin 3)AP θθ=，(1,3),(1,3)AB AC =--=-，因为AP AB AC λμ=+，所以cos sin 333θλμθλμ=-+⎧⎪⎨--⎪⎩，整理可得113cos 22131cos 22μθθλθθ⎧=+⎪⎪⎨⎪=-⎪⎩，所以131113322(cos )cos sin()222226πλμθθθθθ+=-++=-+， 因为[,2]θππ∈，所以713[,]666πππθ+∈， 当1366ππθ+=时，sin()6πθ+取最大值12，所以2λμ+的最小值为31122-=， 故答案为：1 【点睛】解题的关键是在适当位置建系，进而可得点的坐标及向量坐标，利用向量的坐标运算，即可求得2λμ+的表达式，再利用三角函数图像与性质求解，综合性较强，考查分析理解，计算求值的能力，属中档题.15．【分析】已知式平方后求得再由数量积的定义可得夹角【详解】由得∴∴∴故答案为：【点睛】本题考查求向量的夹角解题关键是掌握向量的模与数量积的关系由模求得数量积后可得 解析：23π 【分析】已知式223a b -=平方后求得a b ⋅，再由数量积的定义可得夹角． 【详解】由223a b -=得222(2)4444412a b a a b b a b -=-⋅+=-⋅+=，∴1a b ⋅=-， ∴cos ,2cos ,1a b a b a b <>=<>=-，1cos ,2a b <>=-，∴2,3a b π<>=．故答案为：23π． 【点睛】本题考查求向量的夹角，解题关键是掌握向量的模与数量积的关系，由模求得数量积后可得．16．【分析】延长BC 作圆M 的切线设切点为A1切线与BD 的交点D 结合数量积的几何意义可得点A 运动到A1时在上的投影最小设将结果表示为关于的二次函数求出最值即可【详解】如图延长BC 作圆M 的切线设切点为A1切 解析：2-【分析】延长BC ，作圆M 的切线，设切点为A 1，切线与BD 的交点D ，结合数量积的几何意义可得点A 运动到A 1时，CA 在CB 上的投影最小，设CP x =，将结果表示为关于x 的二次函数，求出最值即可. 【详解】 如图，延长BC ，作圆M 的切线，设切点为A 1，切线与BD 的交点D ，由数量积的几何意义，CA CB ⋅等于CA 在CB 上的投影与CB 之积，当点A 运动到A 1时，CA 在CB 上的投影最小； 设BC 中点P ，连MP ，MA 1，则四边形MPDA 1为矩形； 设CP =x ，则CD =2-x ，CB =2x ，CA CB ⋅=()()222224212x x x x x --⋅=-=--，[]02x ∈，， 所以当1x =时，CA CB ⋅最小，最小值为2-， 故答案为：2-. 【点睛】本题考查平面向量数量积的几何意义，考查了学生的作图能力以及分析问题解决问题的能力，属于中档题.17．【分析】根据条件及向量数量积运算求得连接由三角形中线的性质表示出根据向量的线性运算及数量积公式表示出结合二次函数性质即可求得最小值【详解】根据题意连接如下图所示:在等腰三角形中已知则由向量数量积运算 解析：7【分析】根据条件及向量数量积运算求得AB AC ⋅,连接,AM AN ,由三角形中线的性质表示出,AM AN .根据向量的线性运算及数量积公式表示出2MN ,结合二次函数性质即可求得最小值. 【详解】根据题意,连接,AM AN ,如下图所示:在等腰三角形ABC 中,已知1AB AC ==,120A ∠=︒则由向量数量积运算可知1cos 11cos1202AB AC AB AC A ⋅=⋅=⨯⨯=-线段EF BC 、的中点分别为M N 、则()()1122AM AE AF AB AC λμ=+=+ ()12AN AB AC =+ 由向量减法的线性运算可得11112222MN AN AM AB AC λμ⎛⎫⎛⎫=-=-+- ⎪ ⎪⎝⎭⎝⎭所以2211112222MN AB AC λμ⎡⎤⎛⎫⎛⎫=-+- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦222211111111222222222AB AC AB AC λμλμ⎛⎫⎛⎫⎛⎫⎛⎫=-+-+⨯-⨯-⨯⋅ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭221111111112222222222λμλμ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=-+-+⨯-⨯-⨯- ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭ 因为41λμ+=,代入化简可得22221312111424477MN μμμ⎛⎫=-+=-+ ⎪⎝⎭因为(),0,1λμ∈且41λμ+=10,4μ⎛⎫∴∈ ⎪⎝⎭所以当17μ=时, 2MN 取得最小值17因而minMN==故答案为: 7【点睛】本题考查了平面向量数量积的综合应用,向量的线性运算及模的求法,二次函数最值的应用,属于中档题.18．3或0【分析】由于三个平面向量两两夹角相等可得任意两向量的夹角是或由于三个向量的模已知当两两夹角为时直接算出结果；当两两夹角为时采取平方的方法可求出三个向量的和向量的模【详解】由题意三个平面向量两两解析：3或0 【分析】由于三个平面向量两两夹角相等，可得任意两向量的夹角是0或120︒，由于三个向量的模已知，当,,a b c →→→两两夹角为0时，直接算出结果；当,,a b c →→→两两夹角为120︒时，采取平方的方法可求出三个向量的和向量的模．【详解】由题意三个平面向量两两夹角相等，可得任意两向量的夹角是0或120︒， 当,,a b c →→→两两夹角为0时，,,a b c →→→方向相同，则3a b c →→→++=； 当,,a b c →→→两两夹角为120︒时，由于1a b c ===， 则2222222a b c a b c a b a c b c→→→→→→→→→++=+++⋅+⋅+⋅111211cos120211cos120211cos1200=+++⨯⨯⨯︒+⨯⨯⨯︒+⨯⨯⨯︒=，则20a b c →→→++=，∴0a b c →→→++=. 综上a b c →→→++的值为3或0. 故答案为：3或0. 【点睛】本题考查平面向量的模的求法，涉及向量的夹角和向量的数量积运算，解题的关键是理解向量夹角的定义，考查运算能力.19．【分析】根据向量的夹角公式及数量积的运算计算即可求解【详解】因为又所以故答案为：【点睛】本题主要考查了向量数量积的定义运算法则性质向量的夹角公式属于中档题 解析：6π【分析】根据向量的夹角公式及数量积的运算计算即可求解. 【详解】因为22cos (cos ,|||||2)2|a a ca a c ab a bc π→→→→→→→→→→→→→→-⋅〈〉==--===⋅， 又,0a c π→→〈≤〉≤， 所以,6a c π→→〈〉=，故答案为：6π 【点睛】本题主要考查了向量数量积的定义，运算法则，性质，向量的夹角公式，属于中档题.20．【分析】设的重心为点可知与关于点对称利用重心的向量性质可求得实数的值【详解】设的重心为点则由于和的面积相等则与关于点对称则解得故答案为：【点睛】本题考查了平面向量的数乘运算和线性运算涉及三角形重心向解析：23【分析】设ABC ∆的重心为点G ，可知ABC ∆与111A B C ∆关于点G 对称，利用重心的向量性质可求得实数λ的值. 【详解】设ABC ∆的重心为点G ，则3AB AC AG +=，()13AA AB AC AG λλ∴=+=， 由于ABC ∆和111A B C ∆的面积相等，则ABC ∆与111A B C ∆关于点G 对称， 则12AA AG =，32λ∴=，解得23λ=. 故答案为：23. 【点睛】本题考查了平面向量的数乘运算和线性运算，涉及三角形重心向量性质的应用，考查计算能力，属于中等题.三、解答题21．（1）2AB b a =-，12CE a b =+；（2）证明见解析. 【分析】（1）求出2CB b =，利用AB CB CA =-与12CE CA AB =+化简可得答案； （2）以C 点为坐标原点，以CB ，CA 为x ，y 轴，建立如图所示平面直角坐标系，设()0,A a ， 求出,2a AD a ⎛⎫=- ⎪⎝⎭，2,33a a CE ⎛⎫= ⎪⎝⎭， 可得0AD CE ⋅=，进而可得答案.【详解】（1）∵CA a =，CD b =，点D 是CB 的中点， ∴2CB b =，∴2AB CB CA b a =-=-，∵()1112222CE CA AE a AB a b a a b =+=+=+-=+. （2）以C 点为坐标原点，以CB ，CA 为x ，y 轴，建立如图所示平面直角坐标系，设()0,A a ，∴B 点坐标为(),0a ，另设点E 坐标为(),x y ，∵点D 是CB 的中点， ∴点D 坐标为,02a ⎛⎫⎪⎝⎭，又∵2AE EB =，∴()(),2,x y a a x y -=--，∴23a x =，3a y =， 所以,2a AD a ⎛⎫=-⎪⎝⎭，2,33a a CE ⎛⎫= ⎪⎝⎭， 所以()20233a a aAD CE a ⋅=⨯+-⨯=， ∴AD CE ⊥.【点睛】方法点睛：平面向量数量积的计算问题，往往有两种形式，一是利用数量积的定义式，二是利用数量积的坐标运算公式，涉及几何图形的问题，先建立适当的平面直角坐标系，可起到化繁为简的妙用．22．（1）()4,1=-AB ,17;=AB （2）255,⎛= ⎝⎭e ，或255.⎛=- ⎝⎭e 【详解】试题分析：（I ）利用向量的坐标运算直接求AB 的坐标及AB ； （II ）利用向量的垂直，数量积为0，结合单位向量求解即可． 试题（I ）()()AB 13,214,1=---=-,()22AB 4117;=-+(Ⅱ)设单位向量(),e x y =， 所以221x y +=，即221x y += 又(),1,2⊥=-e OB OB , 所以20x y -+=即2x y =由2221x y x y =⎧⎨+=⎩，解得255x y ⎧=⎪⎪⎨⎪=⎪⎩或者255x y ⎧=⎪⎪⎨⎪=⎪⎩所以25,⎛=⎝⎭e ，或25.⎛=- ⎝⎭e 23．（1）1，0，0；（2）证明见解析；（3）当11220a b a b ≠时，有唯一解，11221122c b c bx a b a b =，11221122a c a c y ab a b =. 【分析】（1）利用行列式的定义可以直接求出行列式的值.（2）若向量(),p a b =与向量(),q c d =共线，由0q ≠和0q =时，分别推导出0a b c d =；反之，若0a bc d=，即0ad bc -=，当c ，d 不全为0时，不妨设0c ≠，则ad b c =，,ab p a c ⎛⎫= ⎪⎝⎭，推导出a p q c =⋅，//p q ，当0c 且0d =时，0q =，(),p a b =与0q =共线，由此能证明向量(),p a b =与向量(),q c d =共线的充要条件是0a bc d=. （3）求出()12211221a b a b x c b c b -=-，()12211221a b a b x a c a c -=-，由此能求出当11220a b a b ≠时，关于x ，y 的二元一次方程组111222a x b y c a x b y c +=⎧⎨+=⎩（12120a a bb ≠）有唯一解，并能求出解. 【详解】解：（1）解：①10101= ②131623026=⨯-⨯=； ③()()2522551001025-=-⨯--⨯=-. （2）证明：若向量(),p a b =与向量(),q c d =共线，则：当0q ≠时，有0ad bc -=，即0a bc d =， 当0q =时，有0c d ==，即0a bad bc c d=-=，∴必要性得证. 反之，若0a bc d=，即0ad bc -=， 当c ，d 不全为0时，即0q ≠时， 不妨设0c ≠，则ad b c =，∴,ab p a c ⎛⎫= ⎪⎝⎭，∵(),q c d =，∴ap q c=⋅，∴//p q ，∴(),p a b =与(),q c d =共线， 当0c且0d =时，0q =，∴(),p a b =与0q =共线，充分性得证.综上，向量(),p a b =与向量(),q c d =共线的充要条件是0a bc d=. （3）用2b 和1b 分别乘上面两个方程的两端，然后两个方程相减，消去y 得：()12211221a b a b x c b c b -=-，①同理，消去x ，得：()12211221a b a b x a c a c -=-，②∴当12210a b a b -≠时，即11220a b a b ≠时，由①②得：1122121221112212c b c b x a b a b a b c b c b a b -==-，1122122111122122a c a c a c a cy a b a b a b a b -==-， ∴当11220a b a b ≠时，关于x ，y 的二元一次方程组111222a x b y c a x b y c +=⎧⎨+=⎩（12120a a bb ≠）有唯一解，且11221122c b c b x a b a b =，11221122a c a c y ab a b =. 【点睛】此题考查行列式求值，考查向量共线的充要条件的证明，考查二元一次方程有解的条件及解的求法，考查运算求解能力，属于中档题 24．（1）8m =（2）5-【分析】（1）先得到()4,2a b m +=-，根据()a b b +⊥可得()0a b b +⋅=,即可求出m ； （2）根据·1a b =-求出m=2,再根据cos ,a b b a b b a b⋅=⋅求b 在向量a 方向上的投影.【详解】()()14,2a b m +=-；()a b b +⊥；()34220m ∴⋅--=；8m ∴=；()2321a b m ⋅=-=-；2m ∴=；()1,2a ∴=；b ∴在向量a 方向上的投影为cos ,5a b b a b b a b⋅=⋅==【点睛】本题主要考查了向量坐标的加法和数量积的运算，向量垂直的充要条件及向量投影的计算公式，属于中档题. 25．（1）23x =，13y =；（2）623-. 【分析】（1）由向量的加减运算，可得()2233=+=+=+-OP OB BP OB BA OB OA OB ，进而可得答案.（2）用OAOB ，表示OP AB ⋅，利用向量数量积公式，即可求得结果. 【详解】（1）因为2BP PA =，所以23BP BA =. ()22213333OP OB BP OB BA OB OA OB OA OB =+=+=+-=+. 又OP xOA xOB =-，又因为OA 、OB 不共线，所以，23x =，13y =（2）结合（1）可得：()2133OP AB OA OB OB OA ⎛⎫⋅=+⋅- ⎪⎝⎭.2222113333=⋅-+-⋅OA OB OA OB OA OB 22121333=⋅-+OA OB OA OB ， 因为6OA =，2OB =，且OA 与OB 的夹角为60︒.所以22112162626232333OP AB ⋅=⨯⨯⨯-⨯+⨯=-. 【点睛】本题考查了向量的加减运算、平面向量基本定理、向量的数量积运算等基本数学知识，考查了运算求解能力和转化的数学思想，属于基础题目.26．（1）(1,0)b =；（2）3(,2a b +=-或33(,2a b +=． 【分析】（1）先设(,)b x y =，再根据向量共线定理即可求解即可； （2）由已知结合向量数量积的定义及数量积的坐标表示即可求解． 【详解】解：（1）设(,)b x y =，由题意可得，存在实数0λ>，使得b a λ=， 即(x ，)(2y λ=，0)(2λ=，0)，所以2x λ=，0y =， 由||1b =可得241λ=，即12λ=或12λ=-（舍)，所以(1,0)b =， （2）设(,)b x y =，所以1·cos12021()12a b a b =︒=⨯⨯-=-， 又因为()()·2,0,2a b x y x =⋅=， 故21x =-即12x =-，因为||1b =，所以221x y +=，故2y =±，当y =，12x =-时，33(,2a b +=，当2y =，12x =-时，3(,)22a b +=-．【点评】本题主要考查了向量共线定理及向量数量积的定义及性质的简单应用，属于中档试题．。

第二章 平面向量 [基础训练A组] 一、选择题 1．化简ACBDCDAB得（ ） A．AB B．DA C．BC D．0 2．设00,ab分别是与,ab向的单位向量，则下列结论中正确的是（ ） A．00ab B．001ab C．00||||2ab D．00||2ab 3．已知下列命题中： （1）若kR，且0kb，则0k或0b， （2）若0ab，则0a或0b （3）若不平行的两个非零向量ba,，满足||||ba，则0)()(baba （4）若a与b平行，则||||abab其中真命题的个数是（ ） A．0 B．1 C．2 D．3 4．下列命题中正确的是（ ） A．若ab＝0，则a＝0或b＝0 B．若ab＝0，则a∥b C．若a∥b，则a在b上的投影为|a| D．若a⊥b，则ab＝(ab)2 5．已知平面向量(3,1)a，(,3)bx，且ab，则x（ ） A．3 B．1 C．1 D．3 6．已知向量)sin,(cosa,向量)1,3(b则|2|ba的最大值，最小值分别是（ ） A．0,24 B．24,4 C．16,0 D．4,0 二、填空题 1．若OA=)8,2(，OB=)2,7(，则31AB=_________ 2．平面向量,ab中，若(4,3)a，b=1，且5ab，则向量b=____。 3．若3a,2b，且a与b的夹角为060，则ab 。 4．把平面上一切单位向量归结到共同的始点，那么这些向量的终点所构成的图形是___________。 5．已知)1,2(a与)2,1(b，要使bta最小，则实数t的值为___________。 三、解答题 1．如图，ABCD中，,EF分别是,BCDC的中点，G为交点，若AB=a，AD=b，试以a，b为基底表示DE、BF、CG．

2．已知向量a与b的夹角为60，||4,(2).(3)72babab,求向量a的模。 3．已知点(2,1)B，且原点O分AB的比为3，又(1,3)b，求b在AB上的投影。 4．已知(1,2)a,)2,3(b,当k为何值时， （1）kab与3ab垂直

一、选择题1．已知点G 是ABC 的重心，(),AG AB AC R λμλμ=+∈，若120,2,A AB AC ∠=︒⋅=-则AG 的最小值是（ ）A ．3 B ．2 C ．12D ．232．已知ABC 为等边三角形，2AB =，ABC 所在平面内的点P 满足1AP AB AC --=，AP 的最小值为（ ）A ．31-B ．221-C ．231-D ．71-3．如图，在ABC 中，AD AB ⊥，2AD =，3DC BD =，则AC AD ⋅的值为（ ）A ．3B ．8C ．12D ．164．已知两个单位向量a ，b ，其中向量a 在向量b 方向上的投影为12．若()()2a b a b λ+⊥-，则实数λ的值为（ ）A ．14-B ．12-C ．0D ．125．在ABC ∆中，5,6AB AC ==，若2B C =，则向量BC 在BA 上的投影是（ ） A ．75-B ．77125-C ．77125D ．756．已知ABC 是边长为2的等边三角形，D ，E 分别是AC 、AB 上的两点，且AE EB =，2AD DC =，与CE 交于点O ，则下列说法正确的是（ ）A ．1AB CD ⋅=-B ．1233BD BC BA =+C ．3OA OB OC ++=D ．ED 在BC 方向上的投影为767．如图，在梯形ABCD 中，//AB CD ，6AB =，3AD CD ==，E 是CD 的中点，14DF DA =，若12AE BF ⋅=-，则梯形ABCD 的高为（ ）A ．1B 6C 5D ．28．在平行四边形ABCD 中，3DE CE =，若AE 交BD 于点M .且AM AB AD λμ=+，则λμ=（ ） A ．23B ．32C ．34D ．439．在ABC 中，||:||:||3:4:5AB AC BC =，圆O 是ABC 的内切圆，且与BC 切于D 点，设AB a =，AC b =，则AD =（ ）A ．2355a b +B ．3255a b + C ．2133a b +D ．1233a b +10．在ABC ∆中，D 为BC 边上一点，且AD BC ⊥，向量AB AC +与向量AD 共线，若10AC =2BC =，0GA GB GC ++=，则AB CG=（ ）A ．3B 5C ．2D 1011．已知向量a 、b 、c 满足0a b c ++=，且a b c <<，则a b ⋅、b c ⋅、a c ⋅中最小的值是（ ） A ．a b ⋅B ．a c ⋅C ．b c ⋅D ．不能确定12．已知ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，向量(,)m a b b c =++，(,)n c b a =-，若//m n ，则C =（ ）A ．56π B ．23π C ．3π D ．6π 二、填空题13．已知平面向量a ，b 不共线，且1a =，1a b ⋅=，记b 与2a b +的夹角是θ，则θ最大时，a b -=_______.14．在梯形ABCD 中，//AB CD ，1CD =，2AB BC ==，120BCD ∠=︒，动点P 和Q 分别在线段BC 和CD 上，且BP BC λ=，14DQ DC λ=，则AP BQ ⋅的最大值为______.15．如图，边长为2的菱形ABCD 的对角线相交于点O ，点P 在线段BD 上运动，若1AB AO ⋅=，则AP PD ⋅的最大值为______.16．已知|a |＝2|b |，|b |≠0，且关于x 的方程x 2+|a |x a b -⋅=0有两相等实根，则向量a 与b 的夹角是_____． 17．已知点()0,1A ，()3,2B，向量()4,3AC =，则向量BC =______.18．已知(2,1)a =-，(1,)b t =，若(2)a b a -⊥，则b =__________19．已知,a b 都是单位向量，且a 与b 的夹角是120，||a b -=_________________. 20．已知向量()()2,3,1,2==-a b ，若ma b +与2a b -平行，则实数m 等于______.三、解答题21．已知平面向量34,55a ⎛⎫= ⎪⎝⎭，2||b =，a与b 夹角为4π.（1）求向量a 在b 方向上的投影； （2）求a b -与a b +夹角的余弦值.22．已知a ，b ，c 是同一平面内的三个向量，其中()1,2a =，()3,b k =-，()2,4c =-.（1）若()//(2)ma c a c +-，求m ； （2）若()a a b ⊥+，c a b λμ=+，求λμ+. 23．已知向量()1,2a =-，()3,1b =-. （1）若()a b a λ+⊥，求实数λ的值；（2）若2c a b =-，2d a b =+，求向量c 与d 的夹角. 24．设向量()3cos ,2sin a θθ=-．（1）当43θπ=时，求a 的值： （2）若()3,1b =-，且//a b，求22cos 124θπθ-⎛⎫+ ⎪⎝⎭的值．25．（1）已知向量()1,3a =，(),2b m =，()3,4c =，且()3a b c -⊥，求实数m 的值；（2）已知(3,2)a =，(2,1)b =-，若a b λ+与a b λ+平行，求实数λ的值 26．已知||1a =，||2b =.（1）若向量a 与向量b 的夹角为135︒，求||a b +及b 在a 方向上的投影； （2）若向量a b -与向量a 垂直，求向量a 与b 的夹角.【参考答案】***试卷处理标记，请不要删除一、选择题 1．D 解析：D 【分析】先根据重心得到()13AG AB AC =+，设0,0AB x AC y =>=>，利用数量积计算4xy =，再利用重要不等式求解()2219A AGB AC =+的最小值，即得结果. 【详解】点G 是ABC 的重心，设D 为BC 边上的中点，则()2133AG AD AB AC ==+， 因为120,2,A AB AC ∠=︒⋅=-设0,0AB x AC y =>=>，则cos1202xy ︒=-，即4xy =，故()()()222211144249999AG x y x B AC y A =+-≥-=+=，即23AG ≥， 当且仅当2x y ==时等号成立，故AG 的最小值是23. 故选：D. 【点睛】 关键点点睛：本题的解题关键在于通过重心求得向量关系()13AG AB AC =+，利用数量积得到定值，才能利用重要不等式求最值，突破难点，要注意取条件的成立.2．C解析：C 【分析】计算出AB AC +的值，利用向量模的三角不等式可求得AP 的最小值. 【详解】2222222cos123AB AC AB AC AB AC AB AC AB AC π+=++⋅=++⋅=，所以，23AB AC += 由平面向量模的三角不等式可得()()231AP AP AB AC AB AC AP AB AC AB AC =--++≥---+=.当且仅当AP AB AC --与AB AC +方向相反时，等号成立.因此，AP 的最小值为1. 故选：C. 【点睛】结论点睛：在求解向量模的最值时，可利用向量模的三角不等式来求解：a b a b a b -≤±≤+. 3．D解析：D 【分析】利用AB 、AD 表示向量AC ，再利用平面向量数量积的运算性质可求得AC AD ⋅的值. 【详解】()3343AC AD DC AD BD AD AD AB AD AB =+=+=+-=-，AD AB ⊥，则0⋅=AD AB ，所以，()224344216AC AD AD AB AD AD ⋅=-⋅==⨯=. 故选：D. 【点睛】方法点睛：求两个向量的数量积有三种方法： （1）利用定义：（2）利用向量的坐标运算； （3）利用数量积的几何意义．具体应用时可根据已知条件的特征来选择，同时要注意数量积运算律的应用．4．C解析：C 【分析】记a 与b 的夹角为θ，则a 在b 上的投影为1cos 2a θ=，然后向量垂直转化为数量积为0可计算λ． 【详解】记a 与b 的夹角为θ，则a 在b 上的投影为cos a θ，则1cos 2a θ=， ∵()()2a b a b λ+⊥-，∴()()()221322221(2)022a b a b a b a b λλλλλλ+⋅-=-+-⋅=-+-⋅==， 故0λ=， 故选：C ． 【点睛】结论点睛：本题考查平面向量的数量积及其几何意义．向量垂直的数量积表示． （1）设,a b 向量的夹角为θ，则a 在b 方向上的投影是cos a b a bθ⋅=；（2）对两个非零向量,a b ，0a b a b ⊥⇔⋅=．5．B解析：B 【解析】 由正弦定理得，653cos sin sin sin 2sin 5AC AB C B C C C =⇒=⇒=,由余弦定理得，22211cos 25BC AC AB C BC AC BC +-=⇒=⋅,则77cos 125BC θ=- ，故选B. 6．D解析：D 【分析】利用CE AB ⊥，判断出A 错误；由2AD DC =结合平面向量的基本定理，判断出选项B 错误；以E 为原点，EA ，EC 分别为x 轴，y 轴正方向建立平面直角坐标系，写出各点坐标，计算出OA OB OC ++的值，判断出选项C 错误；利用投影的定义计算出D 正确． 【详解】由题E 为AB 中点，则CE AB ⊥，0AB CE ⋅=，所以选项A 错误； 由平面向量线性运算得2133BD BC BA =+，所以选项B 错误；以E 为原点，EA ，EC 分别为x 轴，y 轴正方向建立平面直角坐标系，如图所示，()0,0E ，1,0A ，()1,0B -，(3C ，1233D ⎛ ⎝⎭，设()0,O y ，(3y ∈，()1,BO y =，123,33DO y ⎛=-- ⎝⎭，//BO DO ，所以，2313y y =-，解：3y =， 32OA OB OC OE OE OE ++=+==，所以选项C 错误； 123,33ED ⎛⎫= ⎪ ⎪⎝⎭，(1,3BC =，ED 在BC 方向上的投影为127326BC BCED +⋅==，故选：D ． 【点睛】本题考查平面向量数量积的应用，考查平面向量基本定理，考查投影的定义，考查平面向量的坐标表示，属于中档题．7．C解析：C 【分析】以,AD AB 为一组基底，表示向量,AE BF ，然后利用12AE BF ⋅=-，求得2cos 3BAD ∠=，然后由梯形ABCD 的高为sin AD BAD ⋅∠求解. 【详解】因为14AE AD DE AD AB =+=+，34BF AF AB AD AB =-=-， ∴22133113444416AE BF AD AB AD AB AD AB AD AB ⎛⎫⎛⎫⋅=+⋅-=--⋅ ⎪ ⎪⎝⎭⎝⎭， 223113cos 4416AD AB AD AB BAD =--⋅∠，31117936cos 12448BAD =⨯-⨯-∠=-， ∴2cos 3BAD ∠=， ∴25sin 1cos BAD BAD ∠=-∠=， ∴梯形ABCD 的高为sin 5AD BAD ⋅∠=． 故选：C ． 【点睛】本题主要考查平面向量的数量积的运算以及平面向量的基本定理，还考查了数形结合的思想和运算求解的能力，属于中档题.8．B解析：B 【分析】根据已知找到相似三角形，用向量AB 、AD 线性 表示向量AM . 【详解】如图，平行四边形ABCD 中，3DE CE =，ABMEDM ，3322DE DC AB ∴==，()22223323555255AM ME AE AD DE AD AB AB AD ⎛⎫===+=+=+ ⎪⎝⎭. 32λμ= 故选：B 【点睛】此题考查平面向量的线性运算，属于中档题.9．B解析：B 【分析】由题得三角形是直角三角形，设3,4,5AB AC BC ===，设,=,,DB BF x AD AE y EC CF z =====求出,,x y z ，再利用平面向量的线性运算求解.【详解】因为||:||:||3:4:5AB AC BC =，所以ABC 是直角三角形，设3,4, 5.AB AC BC ===如图，设,=,,DB BF x AD AE y EC CF z =====由题得34,2,1,35x y y z x y z x z +=⎧⎪+=∴===⎨⎪+=⎩，所以2232()5555AD AB BD AB BC AB AC AB AB AC =+=+=+-=+3255a b =+. 故选：B 【点睛】本题主要考查平面向量的线性运算，意在考查学生对这些知识的理解掌握水平.10．B解析：B 【解析】取BC 的中点E ，则2AB AC AE +=与向量AD 共线，所以A 、D 、E 三点共线，即ABC ∆中BC 边上的中线与高线重合，则10AB AC ==因为0GA GB GC ++=，所以G 为ABC ∆的重心，则2222() 2.32BC GA GE AC ==-=所以22101,112, 5.2AB CE CG CG==+=∴== 本题选择B 选项.11．C解析：C 【分析】由0a b c ++=，可得2222222().2()a b c a b b c a b c =-+=-+、2222()a c b a c =-+，利用||||||a b c <<，即可比较． 【详解】解：由0a b c ++=，可得()c a b =-+，平方可得2222()a b c a b =-+． 同理可得2222()b c a b c =-+、2222()a c b a c =-+，||||||a b c <<，∴222a b c <<则a b 、b c 、a c 中最小的值是b c ． 故选：C ． 【点睛】本题考查了向量的数量积运算，属于中档题．12．B解析：B 【分析】由//m n ，可得()()()0a b a c b b c +⨯--⨯+=.结合余弦定理，可求角C . 【详解】(,),(,)m a b b c n c b a =++=-，且//m n ，()()()0a b a c b b c ∴+⨯--⨯+=，整理得222c a b ab =++. 又22212cos ,cos 2c a b ab C C =+-∴=-.()20,,3C C ππ∈∴=.故选：B. 【点睛】本题考查向量共线的坐标表示和余弦定理，属于基础题.二、填空题13．【分析】把表示为的函数利用函数的性质求出当最大时的值进而可求出的值【详解】设则所以易得当时取得最小值取得最大值此时故答案为：【点睛】本题考查平面向量的有关计算利用函数的思想求最值是一种常见思路属于中【分析】把cos θ表示为|b|的函数，利用函数的性质求出当θ最大时|b|的值，进而可求出a b -的值. 【详解】 设()0b x x =>，则()22·222b a b a b b x +=⋅+=+，222|2+|=448a b a a b b x +⋅+=+，所以()22·2cos 28b a bb a bx xθ+==++，易得cos 0θ>，()()()2222222222211cos 124811411222263x x x x x x θ+===+⎛⎫-++--+⎪+++⎝⎭， 当24x =时，2cos θ取得最小值，θ取得最大值， 此时22||=21243a b a a b b --⋅+=-+=. 故答案为：3. 【点睛】本题考查平面向量的有关计算，利用函数的思想求最值是一种常见思路.属于中档题.14．【分析】由题可知据平面向量的混合运算法则可化简得到；设函数由对勾函数的性质推出在上的单调性求出最大值即可得解【详解】根据题意作出如下所示图形：∵∴又P 和Q 分别在线段和上∴解得设函数由对勾函数的性质可解析：54【分析】 由题可知114CQ DC λ⎛⎫=-⎪⎝⎭，1,14λ⎡⎤∈⎢⎥⎣⎦，据平面向量的混合运算法则可化简得到117524AP BQ λλ⋅=+-；设函数()117524f λλλ=+-，1,14λ⎡⎤∈⎢⎥⎣⎦，由对勾函数的性质推出()fλ在1,14λ⎡⎤∈⎢⎥⎣⎦上的单调性，求出最大值即可得解. 【详解】根据题意，作出如下所示图形：∵BP BC λ=，14DQ DC λ=，∴114CQ DQ DC DC λ⎛⎫=-=-⎪⎝⎭，又P 和Q 分别在线段BC 和CD 上，∴011014λλ≤≤⎧⎪⎨≤≤⎪⎩，解得1,14λ⎡⎤∈⎢⎥⎣⎦. ()()()114AP BQ AB BP BC CQ AB BC BC DC λλ⎡⎤⎛⎫⋅=+⋅+=+⋅+- ⎪⎢⎥⎝⎭⎣⎦2111144AB BC AB DC BC BC DC λλλλ⎛⎫⎛⎫=⋅+-⋅++-⋅ ⎪ ⎪⎝⎭⎝⎭1111722cos120121cos 04121cos12054424λλλλλλ⎛⎫⎛⎫=⨯⨯︒+-⨯⨯⨯︒+⨯+-⨯⨯⨯︒=+-⎪ ⎪⎝⎭⎝⎭.设函数()117524fλλλ=+-，1,14λ⎡⎤∈⎢⎥⎣⎦， 由对勾函数的性质可知，()f λ在1,410⎡⎢⎣⎭上单调递减，在,110⎛⎤⎥ ⎝⎦上单调递增， ∵114f ⎛⎫=- ⎪⎝⎭，()514f =， ∴()()max 514ff λ==，即AP BQ ⋅的最大值为54.故答案为：54. 【点睛】本题考查平面向量的应用，考查数量积的定义，考查函数的单调性与最值，属于中档题．15．【分析】以为原点和分别为和轴建立的平面直角坐标系求得设得到即可求解【详解】以为原点和分别为和轴建立如图所示的平面直角坐标系设则因为可得联立方程组解答所以设则当时取得最大值最大值为故答案为：【点睛】本解析：34【分析】以O 为原点，OC 和OD 分别为x 和y轴建立的平面直角坐标系，求得(1,0),A D -，设(0,),[P t t ∈，得到23(24AP PD t ⋅=--+，即可求解. 【详解】以O 为原点，OC 和OD 分别为x 和y 轴建立如图所示的平面直角坐标系， 设(,0),(0,),0,0A a B b a b -->>，则224a b +=， 因为1AB AO ⋅=，可得2(,)(,0)1a b a a -⋅==，联立方程组，解答1,3a b ==，所以(1,0),(0,3)A D -，设(0,),[3,3]P t t ∈-，则22333(1,)(0,3)3()244AP PD t t t t t ⋅=⋅-=-+=--+≤， 当3t =时，AP PD ⋅取得最大值，最大值为34.故答案为：34.【点睛】本题主要考查了平面向量的数量积的运算及应用，此类问题通常采取建立直角坐标系，利用平面向量的坐标运算求解，着重考查转化思想，以及运算与求解能力，属于基础题.16．【分析】由关于的方程有两相等实根可得解得即可求出与的夹角【详解】∵已知|且关于的方程有两相等实根∴设向量与的夹角为则可解得则向量与的夹角为故答案为：【点睛】本题考查向量的夹角考查方程的解的应用 解析：23π 【分析】由关于x 的方程20x a b a x +-⋅=有两相等实根,可得240a a b ∆=+⋅=,解得1cos 2θ=-,即可求出a 与b 的夹角【详解】∵已知|2a b =,0b ≠,且关于x 的方程20x a b a x +-⋅=有两相等实根,∴240a a b ∆=+⋅=, 设向量a 与b 的夹角为θ, 则()2242cos 0bb b θ∆=+⨯=,可解得1cos 2θ=-0θπ≤≤,则向量a 与b 的夹角θ为23π 故答案为：23π 【点睛】本题考查向量的夹角,考查方程的解的应用17．【分析】根据向量的坐标运算即可求出【详解】因为所以故答案为：【点睛】本题考查了向量的坐标运算向量模的坐标公式属于基础题目【分析】根据向量的坐标运算即可求出． 【详解】 因为()0,1A ，()3,2B，所以()3,1AB =，()()()4,33,11,2BC AC AB =-=-=，21BC ==【点睛】本题考查了向量的坐标运算，向量模的坐标公式，属于基础题目.18．【分析】根据向量垂直得数量积为0从而求得的值利用求模公式求得向量的模【详解】若则即求得故故答案为：【点睛】本题主要考查平面向量数量积的坐标运算及向量的模的求法意在考查学生的数学运算的学科素养属中档题【分析】根据向量垂直得数量积为0，从而求得t 的值，利用求模公式求得向量的模. 【详解】(2,1)a =-，(1,)b t =，2a b -()3,2t =--，若(2)a b a -⊥，则(2)0a b a -⋅=，即()620t ++=，求得8t故 b ==【点睛】本题主要考查平面向量数量积的坐标运算及向量的模的求法，意在考查学生的数学运算的学科素养，属中档题.19．【分析】根据数量积公式得出的值再由得出答案【详解】故答案为：【点睛】本题主要考查了由数量积求模长属于中档题【分析】根据数量积公式得出a b ⋅的值，再由2||()a b a b -=-得出答案. 【详解】111cos1202a b ⋅=⨯⨯︒=-22222||()2||2||111a b a b a a b b a a b b ∴-=-=-⋅+=-⋅+=++=【点睛】本题主要考查了由数量积求模长，属于中档题.20．【分析】由向量坐标的数乘及加减法运算求出与然后利用向量共线的坐标表示列式求解【详解】解：由向量和所以由与平行所以解得故答案为：【点睛】本题考查了平行向量与共线向量考查了平面向量的坐标运算属于基础题解析：12-【分析】由向量坐标的数乘及加减法运算求出ma b +与2a b -，然后利用向量共线的坐标表示列式求解． 【详解】解：由向量(2,3)a =和(1,2)b =-，所以()()()2,31,221,32m m m b m a ++=-=-+，()()()22,321,24,1a b -=--=-，由ma b +与2a b -平行，所以4(32)(21)0m m ++-=． 解得12m =-． 故答案为：12-． 【点睛】本题考查了平行向量与共线向量，考查了平面向量的坐标运算，属于基础题．三、解答题21．(1)2;(2). 【解析】试题分析：(1)由向量数量积的几何意义可求向量a 在b 方向上的投影;(2)由向量夹角公式可求a -b 与a +b 的夹角的余弦值 试题 (1)|a |=|(34,55)|=1 ∴向量a 在b 方向上的投影为a cosθ=a ?b b=22(2)cos<a -b ,a +b>=()()a b a b a b a b-+-+|a -b |2=|a |2+|b |2-2ab =12,|a b -|=22. |a b +|2=|a |2+|b |2+2ab =52,|a b + (a b -)(a b +)=a 2-b 2=12cos<,a b a b -+>=()()a b a b a b a b-+-+=5. 22．（1）2-；（2）225. 【分析】（1）可以求出(2,24)ma c m m +=-+，2(4,0)a c -=，根据()//(2)ma c a c +-即可得出m 的值；（2）可以求出(2,2)a b k +=-+，根据()a a b ⊥+即可求出k 的值，进而可得出(3λμ-，2)(2λμ-=-，4)，从而可得出λ，μ的值．【详解】（1）(2,24)ma c m m +=-+，2(4,0)a c -=，()//(2)ma c a c +-，240m ∴+=，解得2m =-；（2）(2,2)a b k +=-+，且()a a b ⊥+，∴()22(2)0a a b k +=-++=，解得1k =-， ∴(3,2)(2,4)c a b λμλμλμ=+=--=-，∴3224λμλμ-=-⎧⎨-=⎩，解得14585λμ⎧=⎪⎪⎨⎪=⎪⎩，∴225λμ+=． 【点睛】本题考查了向量坐标的加法、减法和数乘运算，向量垂直的充要条件，平行向量的坐标关系，考查了计算能力，属于基础题． 23．（1）1；（2）34π. 【分析】（1）先求得a λb +，然后利用()0a b a λ+⋅=列方程，解方程求得λ的值.（2）求得,c d 的坐标，利用夹角公式计算出c 与d 的夹角的余弦值，由此求得c 与d 的夹角. 【详解】（1）由()1,2a =-，()3,1b =-得()13,2a b λλλ+=-+-， 因为()a b a λ+⊥，所以()0a b a λ+⋅=， 所以()()13220λλ--++-=， 即550λ-+=， 解得1λ=；（2）由()1,2a =-，()3,1b =-得()25,5c a b =-=-，()25,0d a b =+=，所以25c d ⋅=-，52c =，5d =，设向量c 与d 的夹角为θ，则cos2θ==- 又因为[]0,θπ∈，所以34πθ=， 即向量c 与d 的夹角为34π. 【点睛】本小题主要考查向量垂直的坐标表示，考查向量夹角的计算，考查向量线性运算的坐标表示，属于中档题.24．（1）2；（2）23．【分析】（1）直接利用三角运算结合向量模的运算法则计算得到答案. （2）根据向量平行得到1tan 2θ=，再化简利用齐次式计算得到答案. 【详解】（1）43θπ=，所以4433cos ,2sin ,332a ππ⎛⎫⎛=-= ⎪ ⎝⎭⎝，所以2322a ⎛⎫==⎪； （2）//a b ，则3cos 32sin 0θθ-+⨯=，所以1tan 2θ=， 故22cos 1cos 122sin cos tan 134θθπθθθθ-===++⎛⎫+ ⎪⎝⎭．【点睛】本题考查了向量模的运算，向量平行的应用，三角恒等变换，齐次式求值，意在考查学生的计算能力和综合应用能力. 25．（1）1m =-；（2）1λ=±. 【分析】（1）先求()313,3a b m -=--，再根据向量垂直的坐标运算即可求得1m =-； （2）先计算()32,21a b λλλ+=+-，()23,2a b λλλ+=+-+，再根据向量共线的坐标运算求解即可得1λ=±. 【详解】解：（1）根据题意有：()()()31,33,213,3a b m m -=-=--，∵ ()3a b c -⊥，∴ ()()3313120a b c m -⋅=⨯--=，解得1m =-，所以实数m 的值为：1m =-.（2）根据题意：()()()3,22,132,21a b λλλλλ+=+-=+-，()()()3,22,23,2a b λλλλλ+=+-=+-+，∵ a b λ+与a b λ+平行，∴ ()()()()32223210λλλλ+-+-+-=，解得：1λ=±. 【点睛】本题考查向量的坐标运算，向量垂直与平行的坐标表示，考查运算能力，是基础题. 26．（1）1a b +=；-1；（2）45︒. 【分析】（1）根据平面向量数量积的运算律求出||a b +，再根据平面向量的几何意义求出b 在a 方向上的投影；（2）根据向量垂直，则数量积为零，即可得到1a b ⋅=，再根据夹角公式计算可得；【详解】解：（1）由已知得2222()2121(21a b a b a a b b +=+=+⋅+=+⨯+=，∴1a b +=；b 在a 方向上的投影为||cos1352(12b =-=- （2）由已知得()0a b a -⋅=，即20a a b -⋅=∴1a b ⋅=，∴[]2cos ,,0,212a b a b a b a b π⋅===∈⨯，，∴向量a 与b 的夹角为45︒. 【点睛】本题考查平面向量的数量积及夹角的计算，属于中档题.。

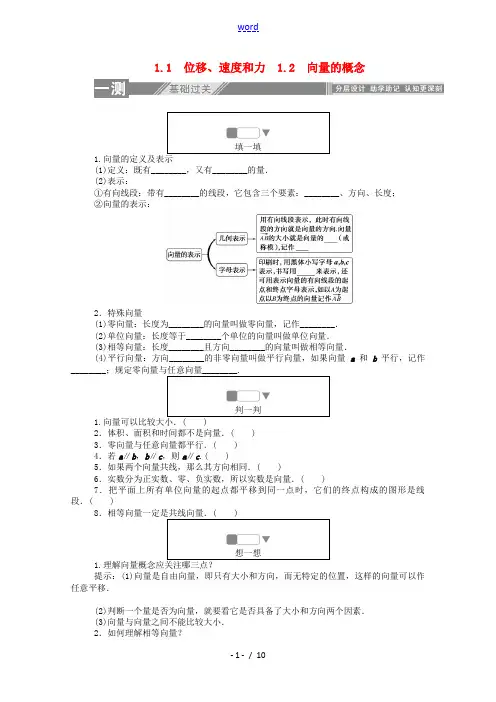
1.1 位移、速度和力 1.2 向量的概念填一填1.向量的定义及表示(1)定义：既有________，又有________的量．(2)表示：①有向线段：带有________的线段，它包含三个要素：________、方向、长度；②向量的表示：2．特殊向量(1)零向量：长度为________的向量叫做零向量，记作________．(2)单位向量：长度等于________个单位的向量叫做单位向量．(3)相等向量：长度________且方向________的向量叫做相等向量．(4)平行向量：方向________的非零向量叫做平行向量，如果向量a和b平行，记作________判一判1.2．体积、面积和时间都不是向量．( )3．零向量与任意向量都平行．( )4．若a∥b，b∥c，则a∥c.( )5．如果两个向量共线，那么其方向相同．( )6．实数分为正实数、零、负实数，所以实数是向量．( )7．把平面上所有单位向量的起点都平移到同一点时，它们的终点构成的图形是线段．( )8想一想1.提示：(1)向量是自由向量，即只有大小和方向，而无特定的位置，这样的向量可以作任意平移．(2)判断一个量是否为向量，就要看它是否具备了大小和方向两个因素．(3)向量与向量之间不能比较大小．2．如何理解相等向量？提示：任意两个相等的非零向量，都可以用同一条有向线段来表示，并且与有向线段的起点无关．在平面上，两个长度相等且指向一致的有向线段表示同一个向量，因为向量完全由它的方向和模确定．3．共线向量与平行向量有无区别？提示：(1)平行向量也称为共线向量，两个概念没有区别． (2)共线向量所在直线可以平行，与平面几何中的共线不同． (3)平行向量可以共线，与平面几何中的直线平行不同． 思考感悟：练一练1.下列物理量：⑦密度；⑧功．其中不是向量的有( )A ．1个B ．2个C ．3个D ．4个2．已知向量a 如图所示，下列说法不正确的是( )A ．也可以用MN →表示 B ．方向是由M 指向N C ．起点是M D ．终点是M3．如图，在矩形ABCD 中，可以用同一条有向线段表示的向量是( ) A.DA →和BC → B.DC →和AB → C.DC →和BC → D.DC →和DA → 4.如图，以1 cm×3 cm 方格纸中的格点为始点和终点的所有向量中，以A 为始点，可以写出________个不同的向量．知识点一 向量的概念1.A ．温度含有零上温度和零下温度，所以温度是向量 B ．单位向量的长度都相等 C ．向量的模是一个非负实数 D ．零向量是长度为0的向量2．给出下列物理量：①密度；②温度；③速度；④质量；⑤功；⑥位移．下列说法正确的是( )A ．①②③是数量，④⑤⑥是向量B ．②④⑥是数量，①③⑤是向量C ．①④是数量，②③⑤⑥是向量D ．①②④⑤是数量，③⑥是向量知识点二向量的表示3.如图，在圆O 中，向量OB →，OC →，AO →是( ) A ．有相同起点的向量 B ．单位向量 C ．模相等的向量 D ．相等的向量4．已知飞机从A 地按北偏东30°的方向飞行2 000 km 到达B 地，再从B 地按南偏东30°的方向飞行2 000 km 到达C 地，再从C 地按西南方向飞行1 000 2 km 到达D 地．(1)作出向量AB →，BC →，CD →，DA →.(2)问D 地在A 地的什么方向？D 地距A 地多远？知识点三 共线向量、相等向量5．如图在等腰梯形ABCD 中．①AB →与CD →是共线向量． ②AB →＝CD →. ③AB →>CD →.以上结论中正确的个数是( ) A ．0 B ．1 C ．2 D ．36．四边形ABCD 为边长为3的正方形，把各边三等分后，共有16个交点，从中选取两个交点作为向量，则与AC →平行且长度为22的向量个数有________个.综合知识 向量的模7.A ，B .点C 为小正方形的顶点，且|AC →|＝ 5.(1)画出所有的向量AC →；(2)求|BC →|的最大值与最小值．基础达标一、选择题1．下列各量中是向量的是( ) A ．时间 B ．加速度 C ．面积 D ．长度2．若a 为任一非零向量，b 的模为1，给出下列各式： ①|a |>|b | ②a ∥b ③|a |>0 ④|b |＝±1. 其中正确的是( ) A ．①④ B．③ C ．①②③ D．②③3．下列说法中正确的个数是( ) ①身高是一个向量②∠AOB 的两条边都是向量③温度含零上和零下温度，所以温度是向量 ④物理学中的加速度是向量 A ．0 B ．1 C ．2 D ．34．设e 1，e 2是两个单位向量，则下列结论中正确的是( ) A ．e 1＝e 2B ．e 1∥e 2C ．|e 1|＝|e 2|D ．以上都不对 5.如图，在正六边形ABCDEF 中，点O 为其中心，则下列判断错误的是( ) A.AB →＝OC → B.AB →∥DE →C ．|AD →|＝|BE →| D.AD →＝FC →6．下列说法中正确的是( ) A ．若|a |>|b |，则a ≤b B ．若|a |＝|b |，则a ＝b C ．若a ＝b ，则a ∥bD ．若a ≠b ，则a 与b 不是共线向量7．已知点O 固定，且|OA →|＝2，则A 点构成的图形是( ) A ．一个点 B ．一条直线 C ．一个圆 D ．不能确定 8.如图所示，四边形ABCD ，CEFG ，CGHD 是全等的菱形，则下列结论中不一定成立的是( )A ．|AB →|＝|EF →| B.AB →与FH →共线 C.BD →与EH →共线 D.CD →＝FG → 二、填空题9．如图，四边形ABCD 是菱形，则在向量AB →，BC →，CD →，DA →，DC →和AD →中，相等的有________对．10．如图，在△ABC 中，∠ACB 的平分线CD 交AB 于点D .若AC →的模为2，BC →的模为3，AD→的模为1，则DB →的模为________．11．给出下列说法： ①零向量是没有方向的； ②零向量的长度为0；③零向量的方向是任意的； ④单位向量的模都相等．其中正确的是________(填上序号)．12．下列说法中，正确的序号是________．①若AB →与C D →是共线向量，则A ，B ，C ，D 四点必在一条直线上； ②零向量都相等；③任一向量与它的平行向量不相等；④若四边形ABCD 是平行四边形，则A B →＝D C →；⑤共线的向量，若始点不同，则终点一定不同． 三、解答题13．如图所示，四边形ABCD 是平行四边形，四边形ABDE 是矩形，找出与向量AB →相等的向量．14．一辆汽车从A 点出发向西行驶了100千米到达B 点，然后又改变方向向北偏西40°行驶了200千米到达C 点，最后又改变方向，向东行驶了100千米到达D 点．(1)作出向量AB →，BC →，CD →；(2)求|AD →|.能力提升 15.如图所示，四边形ABCD 中，AB ＝DC ，N ，M 分别是AD ，BC 上的点，且→＝MA →.求证：DN →＝MB →.16.如图，▱ABCD 中，O 是对角线AC ，BD 的交点，设点集S ＝{A ，B ，C ，D ，O )，向量集合T ＝{MN →|M ，N ∈S ，且M ，N 不重合}．若集合T 中的向量互不相等，试求集合T 中元素的个数．1．1 位移、速度和力 1．2 向量的概念一测 基础过关填一填1．(1)大小 方向(2)方向 起点 长度 |AB →| a →，b →，c →2．(1)0 0 (2)1 (3)相等 相同 (4)相同或相反 a ∥b 平行 判一判1．× 2.√ 3.√ 4.× 5.× 6.× 7.× 8.√ 练一练1．D 2.D 3.B 4.7 二测 考点落实1．解析：选项A 中，温度是数量，因此A 说法错误；选项B 中，单位向量的长度都为1，因此B 说法正确；选项C 中，由于|a |≥0，因此C 说法正确；选项D 说法正确．答案：A2．解析：由物理知识可得：密度、温度、质量、功只有大小，没有方向，因此是数量；而速度、位移既有大小又有方向，因此是向量．答案：D3．解析：∵|OB →|＝|OC →|＝|AO →|＝r (r 为圆O 的半径)，∴C 正确． 答案：C4．解析：(1)由题意，作出向量AB →，BC →，CD →，DA →，如图所示．(2)依题意知，三角形ABC 为正三角形，所以AC ＝2 000 km.又因为∠ACD ＝45°，CD ＝1 0002，所以△ACD 为等腰直角三角形，即AD ＝1 000 2 km ，∠CAD ＝45°，所以D 地在A 地的东南方向，距A 地1 000 2 km.5．解析：①因为AB →与CD →的方向不相同，也不相反，所以AB →与CD →不共线，即①不正确；②由①可知不正确；③因为两个向量不能比较大小，所以③不正确．答案：A 6.解析：如图所示，满足与AC →平行且长度为22的向量有AF →，F A →，EC →，CE →，GH →，HG →，IJ →，JI →共8个．答案：87．解析：(1)画出所有的向量AC →，如图所示．(2)由(1)所画的图知，①当点C 在C 1或C 2时，|BC →|取得最小值12＋22＝5；②当点C在点C 5或C 6时，|BC →|取得最大值42＋52＝41.∴|BC →|的最大值为41，最小值为 5. 三测 学业达标1．解析：加速度是既有大小又有方向的量，是向量．而时间、面积、长度是只有大小的量，是数量．答案：B2．解析：①中，|a |的大小不能确定，故①错误；②中，两个非零向量的方向不确定，故②错误；④中，向量的模是一个非负实数，故④错误；③正确．选B.答案：B3．解析：只有④物理学中的加速度既有大小又有方向是向量，①②③错误．④正确． 答案：B4．解析：单位向量的模都等于1个单位，故C 正确． 答案：C5．解析：由题图可知，|AD →|＝|FC →|，但AD →、FC →不共线，故AD →≠FC →，故选D. 答案：D6．解析：因为向量不能比较大小，所以A 项不正确；即便|a |＝|b |，但是向量的方向不确定，所以B 项不正确；向量相等的条件是方向相同且模相等，所以C 项正确；当向量不相等时，可以共线，故D 项不正确．答案：C7．解析：因为|OA →|＝2，所以点A 在以点O 为圆心、2为半径的圆上，故A 点构成的图形是一个圆．答案：C8．解析：由题意可知AB ＝EF ，AB ∥CD ∥FG ，CD ＝FG ，但是∠DEH 不一定等于∠BDC ，故BD 与EH 不一定平行，所以A ，B ，D 成立，C 不一定成立．答案：C9．解析：AB →＝DC →，BC →＝AD →.其余不相等． 答案：2 10.解析：如图，延长CD ，过点A 作BC 的平行线交CD 的延长线于点E . 因为∠ACD ＝∠BCD ＝∠AED ，所以|AC →|＝|AE →|. 因为△ADE ∽△BDC ，所以|AD →||DB →|＝|AE →||BC →|＝|AC →||BC →|，故|DB →|＝32.答案：3211．解析：由零向量的方向是任意的，知①错误，③正确；由零向量的定义知②正确；由单位向量的模是1，知④正确．答案：②③④12．解析：共线向量即平行向量，只要求方向相同或相反即可，并不要求两个向量AB →，CD →在同一条直线上，所以①错误；因为零向量的长度都为零，且其方向任意，所以零向量相等，所以②正确；因为平行向量的方向可以相同且大小也可以相等，所以任一向量与它的平行向量可能相等，所以③错误；画出图形，可得AB →＝DC →，所以④正确；由共线向量的定义可知：共线的向量，始点不同，终点可能相同，所以⑤不正确．答案：②④13．解析：由四边形ABCD 是平行四边形，四边形ABDE 是矩形，知DC →，E D →与A B →的长度相等且方向相同，所以与向量A B →相等的向量为D C →和E D →.14．解析：(1)向量AB →，BC →，CD →如图所示．(2)连接AD .由题意，易知AB →与CD →方向相反， 故AB →与CD →共线，即AB ∥CD .又|AB →|＝|CD →|，所以四边形ABCD 为平行四边形．所以|AD →|＝|BC →|＝200千米．15．证明：因为AB →＝DC →，所以|AB →|＝|DC →|且AB ∥CD ，所以四边形ABCD 是平行四边形．所以|DA →|＝|CB →|且DA ∥CB .同理可证，四边形AM 是平行四边形，所以|CM →|＝|NA →|，所以|MB →|＝|DN →|，DN ∥MB ，即DN →与MB →的模相等且方向相同，所以DN →＝MB →.16．解析：由题可知，S 中任意两点连成的有向线段共有20个，即AB →、AC →、AD →、AO →；BA →、BC →、BD →、BO →；CA →、CB →、CD →、CO →；DA →、DB →、DC →、DO →；OA →、OB →、OC →、OD →.由平行四边形的性质可知，共有8对向量相等，即AB →＝DC →，AD →＝BC →，DA →＝CB →，BA →＝CD →，AO →＝OC →，OA →＝C O →，D O →＝OB →，OD →＝BO →，又集合T 中向量互不相等，故集合T 中的元素共有12个．。

一、选择题1．已知向量a 、b 满足||||2a b a b ==⋅=，若,,1x y R x y ∈+=，则1|(1)|2x a xb ya y b ⎛⎫-+++- ⎪⎝⎭的最小值为（ ）A ．1B ．3C ．7D ．32．如图，B 是AC 的中点，2BE OB =，P 是平行四边形BCDE 内（含边界）的一点，且(),OP xOA yOB x y R =+∈，则下列结论正确的个数为（ ）①当0x =时，[]2,3y ∈②当P 是线段CE 的中点时，12x =-，52y =③若x y +为定值1，则在平面直角坐标系中，点P 的轨迹是一条线段 ④x y -的最大值为1- A ．1B ．2C ．3D ．43．设平面向量()a=1,2，()b=2,y -，若a b ，则2a b -等于（ ） A ．4B ．5C ．35D ．454．已知ABC 是边长为2的等边三角形，D ，E 分别是AC 、AB 上的两点，且AE EB =，2AD DC =，与CE 交于点O ，则下列说法正确的是（ ）A ．1AB CD ⋅=- B ．1233BD BC BA =+ C ．3OA OB OC ++=D ．ED 在BC 方向上的投影为765．如图，在梯形ABCD 中，//AB CD ，6AB =，3AD CD ==，E 是CD 的中点，14DF DA =，若12AE BF ⋅=-，则梯形ABCD 的高为（ ）A ．1B ．6C 5D ．26．在ABC 中，||:||:||3:4:5AB AC BC =，圆O 是ABC 的内切圆，且与BC 切于D 点，设AB a =，AC b =，则AD =（ ）A ．2355a b +B ．3255a b + C ．2133a b +D ．1233a b +7．若2a b c ===，且0a b ⋅=，()()0a c b c -⋅-≤，则a b c +-的取值范围是( )A ．[0,222]B ．[0,2]C ．[222,222]-+D ．[222,2]-8．已知向量(6,4),(3,),(2,3)a b k c =-==-，若//a b ，则b 与c 的夹角的余弦值为（ ） A ．1213B ．1213-C ．45-D ．459．已知ABC ∆为等边三角形，则cos ,AB BC =( ) A ．3 B ．12-C ．12D ．3210．在边长为2的菱形ABCD 中，60BAD ∠=︒，点E 是AB 边上的中点，点F 是BC 边上的动点，则DE DF ⋅的取值范围是（ ）A ．3⎡⎤⎣⎦B ．33⎣C ．3,3⎤⎦D ．[]0,311．已知ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，向量(,)m a b b c =++，(,)n c b a =-，若//m n ，则C =（ ）A ．56πB ．23π C ．3π D ．6π 12．如图所示，在ABC 中，点D 在线段BC 上，且3BD DC =，若AD AB AC λμ=+，则λμ=（ ）A ．12B ．13C ．2D ．23二、填空题13．已知平面向量,,a b c 满足()()||2,||2||a c b c a b a b -⋅-=-==.则c 的最大值是________.14．已知平面向量a ，b 不共线，且1a =，1a b ⋅=，记b 与2a b +的夹角是θ，则θ最大时，a b -=_______.15．已知平面向量a ，b 夹角为30，若2=a ，则12b a b +-的最小值为______． 16．在ABC 中，90,6C CA CB ∠=︒==，P 为ABC 所在平面内一动点，则()CP AP BP ⋅+的最小值为________．17．在△ABC 中，BD ＝2DC ，过点D 的直线与直线AB ，AC 分别交于点E ，F ，若AE ＝x AB ，AF ＝y AC （x ＞0，y ＞0），则x +y 的最小值为_____.18．如图，在矩形ABCD 中，3AB =，4=AD ，圆M 为BCD △的内切圆，点P 为圆上任意一点， 且AP AB AD λμ=+，则λμ+的最大值为________.19．已知(2,1)a =，(3,4)b =，则a 在b 的方向上的投影为________． 20．若平面向量a ，b 为单位向量，12a b ⋅=，空间向量c 满足||8c =，4a c ⋅=，5b c ⋅=，则对任意的实数12,t t ，12c t a t b --的最小值是___________． 三、解答题21．已知a ，b ，c 是同一平面内的三个向量，其中()1,2a =，()3,b k =-，()2,4c =-.（1）若()//(2)ma c a c +-，求m ； （2）若()a a b ⊥+，c a b λμ=+，求λμ+.22．如图，在正ABC ∆中，2AB =，P ，E 分别是BC 、CA 边上一点，并且3CA EA =，设BP tBC =，AP 与BE 相交于F ．（1）试用AB ，AC 表示AP ； （2）求·AP BE 的取值范围．23．在ABC 中，角,,A B C 所对的边分别为,,a b c 且,b c A =∠的平分线为AD ，若AB AD mAB AC ⋅=⋅.（1）当2m =时，求cos A（2）当23a b ⎛∈ ⎝⎭时，求实数m 的取值范围.24．（1）已知向量()1,3a =，(),2b m =，()3,4c =，且()3a b c -⊥，求实数m 的值；（2）已知(3,2)a =，(2,1)b =-，若a b λ+与a b λ+平行，求实数λ的值 25．已知单位向量1e ，2e 的夹角为60︒，向量12a e e =+，21b e te =-，t R ∈. （1）若//a b ，求t 的值； （2）若2t =，求向量a ，b 的夹角.26．已知向量()1,1,3,(0)2u sin x v sin x cos x ωωωω⎛⎫=-=+> ⎪⎝⎭且函数()f x u v =⋅,若函数f (x )的图象上两个相邻的对称轴距离为2π. (1)求函数f (x )的解析式; (2)将函数y =f (x )的图象向左平移12π个单位后,得到函数y =g (x )的图象,求函数g (x )的表达式并其对称轴;(3)若方程f (x )=m (m >0)在0,2x π⎡⎤∈⎢⎥⎣⎦时,有两个不同实数根x 1,x 2,求实数m 的取值范围,并求出x 1+x 2的值.【参考答案】***试卷处理标记，请不要删除一、选择题 1．C 解析：C 【分析】利用已知条件求出向量a 、b 的夹角，建立直角坐标系把所求问题转化为解析几何问题. 【详解】设a 、b 所成角为θ， 由||||2==a b ，2a b ，则1cos 2θ=，因为0θπ≤≤ 所以3πθ=，记a OA =，b OB =,以OA 所在的直线为x 轴，以过O 点垂直于OA 的直线为y 轴， 建立平面直角坐标系，则()2,0A ，(B ，所以()2,0a OA ==，(1,b OB ==，()(1)2x a xb x -+=-，所以((1)2x a xb x -+=-=，表示点()P x 与点()2,0A 两点间的距离， 由,,1x y R x y ∈+=113,22222ya y b y x ⎛⎫⎛⎛⎫+-=+-=-- ⎪ ⎪ ⎪ ⎝⎭⎝⎭⎝⎭， 所以1322ya y b x ⎛⎫⎛+-=- ⎪ ⎝⎭，表示点()P x 与点32Q ⎛ ⎝⎭两点间的距离，∴1|(1)|2x a xb ya y b ⎛⎫-+++- ⎪⎝⎭的最小值转化为P 到,A Q 两点的距离和最小，(),3P x x 在直线3y x =上，()2,0A 关于直线3y x =的对称点为()1,3R -，PQ PA ∴+的最小值为223313722QR ⎛⎫⎛⎫=++-= ⎪ ⎪ ⎪⎝⎭⎝⎭.故选：C 【点睛】关键点点睛：本题考查了向量模的坐标运算以及模转化为两点之间距离的转化思想，解题的关键是将向量的模转化为点(),3P x x 到()2,0A 、33,22Q ⎛⎫⎪ ⎪⎝⎭两点间的距离，考查了运算求解能力.2．C解析：C 【分析】利用向量共线的充要条件判断出①错，③正确；利用向量的运算法则求出OP ，求出x ，y 判断出②正确,利用三点共线解得④正确 【详解】当0x =时，OP yOB =，则P 在线段BE 上，故13y ≤≤，故①错 当P 是线段CE 的中点时，13()2OP OE EP OB EB BC =+=++ ()11153(2)32222OB OB AB OB OB OB OA OA OB =+-+=-+-=-+，故②对x y +为定值1时，A ，B ，P 三点共线，又P 是平行四边形BCDE 内（含边界）的一点，故P 的轨迹是线段，故③对如图，过P 作//PM AO ，交OE 于M ，作//PN OE ，交AO 的延长线于N ， 则：OP ON OM =+；又OP xOA yOB =+；0x ∴≤，1y ≥；由图形看出，当P 与B 重合时：01OP OA OB =⋅+⋅；此时x 取最大值0，y 取最小值1；所以x y -取最大值1-，故④正确所以选项②③④正确. 故选：C 【点睛】结论点睛：若OC xOA yOB =+，则,,A B C 三点共线1x y ⇔+=.3．D解析：D 【分析】利用向量共线定理即可得出y ，从而计算出2a b -的坐标，利用向量模的公式即可得结果. 【详解】//,220a b y ∴-⨯-=，解得4y =-，()()()221,22,44,8a b ∴-=---=，2224845a b ∴-=+=，故选D.【点睛】本题主要考查平面向量平行的性质以及向量模的坐标表示，属于中档题. 利用向量的位置关系求参数是出题的热点，主要命题方式有两个：（1）两向量平行，利用12210x y x y -=解答；（2）两向量垂直，利用12120x x y y +=解答.4．D解析：D 【分析】利用CE AB ⊥，判断出A 错误；由2AD DC =结合平面向量的基本定理，判断出选项B 错误；以E 为原点，EA ，EC 分别为x 轴，y 轴正方向建立平面直角坐标系，写出各点坐标，计算出OA OB OC ++的值，判断出选项C 错误；利用投影的定义计算出D 正确． 【详解】由题E 为AB 中点，则CE AB ⊥，0AB CE ⋅=，所以选项A 错误；由平面向量线性运算得2133BD BC BA =+，所以选项B 错误； 以E 为原点，EA ，EC 分别为x 轴，y 轴正方向建立平面直角坐标系，如图所示，()0,0E ，1,0A ，()1,0B -，(3C ，13,33D ⎛ ⎝⎭，设()0,O y ，(y ∈，()1,BO y =，1,33DO y ⎛=-- ⎝⎭，//BO DO ，所以，13y y =-，解：y =， 322OA OB OC OE OE OE ++=+==，所以选项C 错误；1,33ED ⎛⎫= ⎪ ⎪⎝⎭，(1,BC =，ED 在BC 方向上的投影为127326BC BCED +⋅==，故选：D ． 【点睛】本题考查平面向量数量积的应用，考查平面向量基本定理，考查投影的定义，考查平面向量的坐标表示，属于中档题．5．C解析：C 【分析】以,AD AB 为一组基底，表示向量,AE BF ，然后利用12AE BF ⋅=-，求得2cos 3BAD ∠=，然后由梯形ABCD 的高为sin AD BAD ⋅∠求解. 【详解】因为14AE AD DE AD AB =+=+，34BF AF AB AD AB =-=-， ∴22133113444416AE BF AD AB AD AB AD AB AD AB ⎛⎫⎛⎫⋅=+⋅-=--⋅ ⎪ ⎪⎝⎭⎝⎭， 223113cos 4416AD AB AD AB BAD =--⋅∠， 31117936cos 12448BAD =⨯-⨯-∠=-， ∴2cos 3BAD ∠=，∴sin BAD ∠==∴梯形ABCD 的高为sin AD BAD ⋅∠=． 故选：C ． 【点睛】本题主要考查平面向量的数量积的运算以及平面向量的基本定理，还考查了数形结合的思想和运算求解的能力，属于中档题.6．B解析：B 【分析】由题得三角形是直角三角形，设3,4,5AB AC BC ===，设,=,,DB BF x AD AE y EC CF z =====求出,,x y z ，再利用平面向量的线性运算求解.【详解】因为||:||:||3:4:5AB AC BC =，所以ABC 是直角三角形，设3,4, 5.AB AC BC ===如图，设,=,,DB BF x AD AE y EC CF z =====由题得34,2,1,35x y y z x y z x z +=⎧⎪+=∴===⎨⎪+=⎩，所以2232()5555AD AB BD AB BC AB AC AB AB AC =+=+=+-=+3255a b =+. 故选：B 【点睛】本题主要考查平面向量的线性运算，意在考查学生对这些知识的理解掌握水平.7．D解析：D 【解析】如图所示：OA a =，OB b =，OC c =，OD a b =+ ∵()()0a c b c -⋅-≤，∴点C 在劣弧AB 上运动，a b c +-表示C 、D 两点间的距离CD ．CD 的最大值是BD ＝２，CD 最小值为OD 2222-=.故选D8．A解析：A 【分析】根据向量平行，由平面向量的坐标运算列方程求出k 的值，再利用平面向量夹角公式求解即可. 【详解】因为(6,4),(3,),a b k =-=且//a b ， 所以61202k k +=⇒=-，(3,2),(2,3)b c =-=-，12cos ,13c b c b c b⋅==， 故选：A. 【点睛】本题主要考查向量平行的性质，考查了平面向量数量积的坐标表示以及向量夹角公式的应用，属于基础题.9．B解析：B 【分析】判断,AB BC 两向量夹角容易出错，是23π，而不是3π 【详解】由图发现,AB BC 的夹角不是B 而是其补角23π，21cos ,cos32AB BC π<>==- 【点睛】本题考查的是两向量夹角的定义，属于易错题，该类型题建议学生多画画图.10．D解析：D 【分析】把DE 用,DA DB 表示，由三点共线把DF 用,DC DB 表示，然后计算数量积，利用函数的知识得取值范围． 【详解】∵菱形ABCD 边长为2，60BAD ∠=︒，2BD =，∴22cos602DA DB DB DC ⋅=⋅=⨯⨯︒=，22cos1202DA DC ⋅=⨯⨯︒=-， ∵E 是AB 边上的中点，∴1()2DE DA DB =+， 点F 是BC 边上，设BF xBC =（01x ≤≤），则()(1)DF DB BF DB xBC DB x DC DB xDC x DB =+=+=+-=+-，DE DF ⋅1()(1)2DA DB xDC x DB ⎡⎤=+⋅+-⎣⎦21(1)(1)2xDA DC x DA DB xDB DC x DB ⎡⎤=⋅+-⋅+⋅+-⎢⎥⎣⎦ []122(1)24(1)3(1)2x x x x x =-+-++-=-， ∵01x ≤≤，∴03(1)3x ≤-≤． 故选：D. 【点睛】本题考查平面向量的数量积，解题关键是对动点F 引入参数x ：BF xBC=（01x ≤≤），这样所求数量积就可表示为x 的函数，从而得到范围．本题考查了向量共线的条件，属于中档题．11．B解析：B 【分析】由//m n ，可得()()()0a b a c b b c +⨯--⨯+=.结合余弦定理，可求角C . 【详解】(,),(,)m a b b c n c b a =++=-，且//m n ，()()()0a b a c b b c ∴+⨯--⨯+=，整理得222c a b ab =++. 又22212cos ,cos 2c a b ab C C =+-∴=-.()20,,3C C ππ∈∴=.故选：B. 【点睛】本题考查向量共线的坐标表示和余弦定理，属于基础题.12．B解析：B 【分析】由向量的运算法则，化简得1344AD AB AC =+,再由AD AB AC λμ=+，即可求得,λμ 的值，即可求解. 【详解】由向量的运算法则，可得34=+=+AD AB BD AB BC 313()444AB AC AB AB AC =+-=+, 因为AD AB AC λμ=+，所以13,44λμ==，从而求得13λμ=，故选:B ． 【点睛】该题考查的是有关向量的基本定理，在解题的过程中，需要利用向量直角的关系，结合三角形法则，即可求得结果，属于基础题.二、填空题13．【分析】设根据得到取中点为D 又由中点坐标得到再由得到的范围然后由求解【详解】设如图所示：因为所以取中点为D 因为所以解得所以所以点C 是以D 为圆心半径为的圆上运动又因为所以当AOB 共线时取等号所以所以【解析：3【分析】设,,OA a OB b OC c ===，根据||2,||2||a b a b -==，得到||2,||2||AB OA OB ==，取AB 中点为D ，又()()2a c b c CA CB -⋅-=⋅=，由中点坐标得到232CB CA CD ⎛⎫+== ⎪⎝⎭，再由2OA OB AB -≤=，得到2||2OA OB OD ⎛⎫+= ⎪⎝⎭的范围，然后由||||||||3c OC OD DC OD =≤+≤+求解. 【详解】设,,OA a OB b OC c ===， 如图所示：因为||2,||2||a b a b -==， 所以||2,||2||AB OA OB ==， 取AB 中点为D ，因为()()2a c b c CA CB -⋅-=⋅=，所以2222||||24AB CB CA CB CA CB CA =-=+-⋅=， 解得228CB CA +=，所以22212322CB CA CD CB CA CB CA ⎛⎫+==++⋅= ⎪⎝⎭所以点C 是以D 3的圆上运动， 又因为2OA OB AB -≤=，所以2OB ≤，当A ，O ，B 共线时，取等号，所以2221||222OA OB OD OB OA OB OA ⎛⎫+==++⋅ ⎪， ()2110432OB ==-≤， 所以||||||||33c OC OD DC OD =≤+≤+≤. 【点睛】关键点点睛：平面向量的中点坐标公式的两次应用：一是CB CD ⎛= ||2,||2||AB OA OB ==求得定值，得到点C 是以D 为圆心的圆上，实现数形结合；二是||2OA OD ⎛= ⎝⎭2OA OB AB -≤=确定范围，然后由||||||c OC OD DC =≤+求解.14．【分析】把表示为的函数利用函数的性质求出当最大时的值进而可求出的值【详解】设则所以易得当时取得最小值取得最大值此时故答案为：【点睛】本题考查平面向量的有关计算利用函数的思想求最值是一种常见思路属于中【分析】把cos θ表示为|b|的函数，利用函数的性质求出当θ最大时|b|的值，进而可求出a b -的值. 【详解】 设()0b x x =>，则()22·222b a b a b b x +=⋅+=+，22|2+|=448a b a a b b +⋅+=+，所以()2·2cos 28b a bb a bx θ+==++易得cos 0θ>，()()()2222222222211cos 124811411222263x x x x x x θ+===+⎛⎫-++--+⎪+++⎝⎭， 当24x =时，2cos θ取得最小值，θ取得最大值，此时22||=21243a b a a b b --⋅+=-+=. 故答案为：3. 【点睛】本题考查平面向量的有关计算，利用函数的思想求最值是一种常见思路.属于中档题.15．【分析】首先设则结合向量夹角为利用对称关系求得其最小值也可以建系利用向量的坐标去求解【详解】解析1：（对称）设则过作于点由于向量夹角为则故所以最小值为到的距离为即的最小值为故答案为：解法2：（建系） 解析：3【分析】首先设a OA =，b OB =，则a b BA -=，结合向量a ，b 夹角为30，利用对称关系，求得其最小值，也可以建系，利用向量的坐标去求解. 【详解】 解析1：（对称）设a OA =，b OB =，则a b BA -=，过B 作BH OA ⊥于点H ． 由于向量a ，b 夹角为30，则12BH OB =，故12b a b BH AB BH A B '+-=+=+， 所以最小值为A '到OA 的距离为3，即12b a b +-的最小值为3．3 解法2：（建系）设()2,0a =，则3,b m ⎛⎫= ⎪⎝⎭，不妨设0m >， 则()222131342442333mb a b m m m m +-=+-+=+-+ 令()234443x f x x x =+-+则()423x f x -'=+()0f x '=，解得1x =，即当1x =时，()min f x = 所以12b a b +-的最小值为【点睛】该题考查的是有关向量的问题，涉及到的知识点有向量模的和的最小值的求解，在解题的过程中，可以利用图形，从对称角度去分析，也可以建系，将其坐标化求解，属于中档题目.16．【分析】建立坐标系利用向量的坐标运算公式将用的坐标表示利用配方法求得最小值【详解】由题意可建立如图所示的直角坐标系易知设则故当且仅当时取得等号∴所求最小值为故答案为：【点睛】本题考查向量的数量积的坐 解析：9-【分析】建立坐标系，利用向量的坐标运算公式将()CP AP BP ⋅+用(),P x y 的坐标表示，利用配方法求得最小值. 【详解】由题意可建立如图所示的直角坐标系，易知()()()6,0,0,6,0,0A B C ，设(),P x y ， 则(,),(6,),(,6)CP x y AP x y BP x y ==-=-，故2233()(26)(26)229922CP AP BP x x y y x y ⎛⎫⎛⎫⋅+=-+-=-+--- ⎪ ⎪⎝⎭⎝⎭．当且仅当32x y ==时取得等号， ∴所求最小值为9-， 故答案为：9-.【点睛】本题考查向量的数量积的坐标运算和配方法求最值，关键在于建立坐标系，用(),P x y 的坐标表达所求的向量的数量积，属中档题.17．【分析】根据向量线性关系的几何应用有令结合已知条件有即可列方程组得到关于k 的表达式表示x+y 最后由基本不等式即可求得最小值【详解】由题意连接可得如下示图∵在△ABC 中＝2即有若令则有又＝x ＝y （x ＞ 解析：2213+【分析】根据向量线性关系的几何应用有1233AD AB AC =+，令DEk DF =结合已知条件有11x kyAD AB AC k k =+++，即可列方程组，得到关于k 的表达式表示x + y ，最后由基本不等式即可求得最小值 【详解】由题意，连接AD 可得如下示图∵在△ABC 中BD ＝2DC ，即有1233AD AB AC =+ 若令DE k DF =，则有111kAD AE AF k k =+++又AE ＝x AB ，AF ＝y AC （x ＞0，y ＞0） ∴11x ky AD AB AC k k =+++ 即113213x k ky k ⎧=⎪⎪+⎨⎪=⎪+⎩有1(1)321(1)3x k y k ⎧=+⎪⎪⎨⎪=+⎪⎩(0)k >∴2111333k x y k +=++≥=+，当且仅当k =min ()13x y +=+故答案为：1+【点睛】本题考查了向量线性关系的几何应用，及利用基本不等式求最值，通过定向量与其它向量的线性关系找到等量关系，进而构建函数并结合基本不等式求最值18．【分析】以点B 为坐标原点建立平面直角坐标系如下图所示由已知条件得出点坐标圆M 的方程设由得出再设（为参数）代入中根据三角函数的值域可求得最大值【详解】以点B 为坐标原点建立平面直角坐标系如下图所示因为在 解析：116【分析】以点B 为坐标原点，建立平面直角坐标系如下图所示，由已知条件得出点坐标，圆M 的方程，设(),P x y ，由AP AB AD λμ=+，得出134y x λμ⎧=-⎪⎪⎨⎪=⎪⎩，再设3cos 1sin x y θθ=+⎧⎨=+⎩（θ为参数），代入λμ+中，根据三角函数的值域，可求得最大值. 【详解】以点B 为坐标原点，建立平面直角坐标系如下图所示，因为在矩形ABCD 中，3AB =，4=AD ，所以圆M 的半径为3+4512r -==， 所以()0,0B ，()0,3A ，()4,0C ，()4,3D，()3,1M ，圆M 的方程为()()22311x y -+-=，设(),P x y ，又AP AB AD λμ=+，所以()()(),30,34,0x y λμ-=-+，解得134y x λμ⎧=-⎪⎪⎨⎪=⎪⎩， 又点P 是圆M 上的点，所以3cos 1sin x y θθ=+⎧⎨=+⎩（θ为参数），所以()1sin 3cos 517sin 1+1+34312124+y x θθβθλμ+=+--+=-=，其中3tan 4β=， 所以，当()sin 1βθ-=时，λμ+取得最大值116，故答案为：116.【点睛】本题考查向量的线性表示，动点的轨迹中的最值问题，属于中档题.19．2【分析】根据向量在的方向上的投影为结合向量的数量积的坐标运算和模的计算公式即可求解【详解】由题意向量可得则在的方向上的投影为故答案为：【点睛】本题主要考查了平面向量数量积的坐标运算和模计算公式的应解析：2 【分析】根据向量a 在b 的方向上的投影为a b b⋅，结合向量的数量积的坐标运算和模的计算公式，即可求解. 【详解】由题意，向量(2,1)a =，(3,4)b =，可得231410a b ⋅=⨯+⨯=，22345b =+=， 则a 在b 的方向上的投影为1025a b b⋅==. 故答案为：2. 【点睛】本题主要考查了平面向量数量积的坐标运算和模计算公式的应用，以及向量的投影的概念与计算，其中解答熟记平面向量的数量积、模及投影的计算公式是解答的关键，着重考查推理与运算能力.20．6【分析】根据题意将其代入并且结合化简整理进而可求得最小值【详解】解：由题得将条件代入可得上式当且仅当取等号故的最小值是故答案为：【点睛】本题主要考查平面向量的数量积及其运算性质以及二次式的最值问题解析：6 【分析】根据题意，221a b ==，将其代入212|()|c t a t b -+，并且结合||8c =，4a c ⋅=，5b c ⋅=，化简整理2222121283|()|(4)363624t c t a t b t t -⎛⎫-+=++-+ ⎪⎝⎭，进而可求得最小值【详解】解：22222212121212()222c t a t b c t a t b t c a t c b t t a b -+=++--+， 由题得221a b ==，||8c =，4a c ⋅=，5b c ⋅=，12a b ⋅=将条件代入可得上式22222212121212()222c t a t b c t a t b t c a t c b t t a b -+=++--+ 22121212164242522t t t t t t =++-⨯-⨯+⨯22222121212128364810(4)363624t t t t t t t t t -⎛⎫=++--+=++-+ ⎪⎝⎭， 当且仅当12t =，24t =取等号， 故12||c t a t b --的最小值是6， 故答案为：6 【点睛】本题主要考查平面向量的数量积及其运算性质以及二次式的最值问题，还考查了运算求解的能力．三、解答题21．（1）2-；（2）225. 【分析】（1）可以求出(2,24)ma c m m +=-+，2(4,0)a c -=，根据()//(2)ma c a c +-即可得出m 的值；（2）可以求出(2,2)a b k +=-+，根据()a a b ⊥+即可求出k 的值，进而可得出(3λμ-，2)(2λμ-=-，4)，从而可得出λ，μ的值．【详解】（1）(2,24)ma c m m +=-+，2(4,0)a c -=，()//(2)ma c a c+-，240m∴+=，解得2m=-；（2）(2,2)a b k+=-+，且()a a b⊥+，∴()22(2)0a ab k+=-++=，解得1k=-，∴(3,2)(2,4)c a bλμλμλμ=+=--=-，∴3224λμλμ-=-⎧⎨-=⎩，解得14585λμ⎧=⎪⎪⎨⎪=⎪⎩，∴225λμ+=．【点睛】本题考查了向量坐标的加法、减法和数乘运算，向量垂直的充要条件，平行向量的坐标关系，考查了计算能力，属于基础题．22．（1）()1AP t AB t AC=-+；（2）10[3-，2]3-．.【分析】（1）由BP tBC=，可推出AP AB tBC=+，而BC AC AB=-，代入化简整理即可得解；（2）由3CA EA=，知13BE AC AB=-，再结合平面向量的数量积可推出12·[(1)]?()(45)33AP BE t AB t AC AC AB t=-+-=-，而[0t∈，1]，从而求得·AP BE 的取值范围．【详解】解：（1）BP tBC=，∴()(1)AP AB BP AB tBC AB t AC AB t AB t AC=+=+=+-=-+．（2）3CA EA=，∴13BE AE AB AC AB=-=-，∴1·[(1)]?()3AP BE t AB t AC AC AB=-+-22141(1)()?333t AB t AB AC t AC=-+-+1414(1)()22cos604333t t t=-+-⨯⨯︒+⨯2(45)3t=-．P是BC边上一点，[0t∴∈，1]，∴210·(45)[33AP BE t =-∈-，2]3-． 【点睛】 本题考查平面向量的线性和数量积运算，熟练掌握平面向量的加法、减法、数乘和数量积的运算法则是解题的关键，考查学生的逻辑推理能力和运算能力，属于中档题． 23．（1）13；（2）322m << 【分析】（1）由题意得,1()2AD AB AC =+；从而可得1()22AB AB AC AB AC ⋅+=⋅；从而可得1cos 3||||AB AC A AB AC ⋅==； （2）222||||cos 2b a AB AC AB AC A -⋅=⋅=,从而可得2211112222AB AD AB m AB AC AB AC a b ⋅==+=+⋅⋅⎛⎫- ⎪⎝⎭；从而求取值范围.. 【详解】解：（1）由题意得,1()2AD AB AC =+； 故1()22AB AB AC AB AC ⋅+=⋅； 故23AB AB AC =⋅；故1cos 3||||AB AC A AB AC ⋅==； （2）||||cos AB AC AB AC A ⋅=⋅2222b a -=； 故21122AB AD AB m AB AC AB AC ⋅==+⋅⋅ 222122b b a =+- 21122a b =+⎛⎫- ⎪⎝⎭；∵1,3a b ⎛∈ ⎝⎭,∴241,3a b ⎛⎫⎛⎫∈ ⎪ ⎪⎝⎭⎝⎭；故213122a b <<⎛⎫- ⎪⎝⎭； 在23112222a b <+<⎛⎫- ⎪⎝⎭. 【点睛】 本题考查了平面向量的应用即解三角形的应用,属于中档题.24．（1）1m =-；（2）1λ=±.【分析】（1）先求()313,3a b m -=--，再根据向量垂直的坐标运算即可求得1m =-；（2）先计算()32,21a b λλλ+=+-，()23,2a b λλλ+=+-+，再根据向量共线的坐标运算求解即可得1λ=±.【详解】解：（1）根据题意有：()()()31,33,213,3a b m m -=-=--，∵ ()3a b c -⊥，∴ ()()3313120a b c m -⋅=⨯--=，解得1m =-， 所以实数m 的值为：1m =-.（2）根据题意：()()()3,22,132,21a b λλλλλ+=+-=+-，()()()3,22,23,2a b λλλλλ+=+-=+-+，∵ a b λ+与a b λ+平行，∴ ()()()()32223210λλλλ+-+-+-=，解得：1λ=±.【点睛】本题考查向量的坐标运算，向量垂直与平行的坐标表示，考查运算能力，是基础题. 25．（1）1t =-；（2）23π. 【分析】（1）根据题意，设a kb =，则有122112()()e e k e te kte ke +=-=-+，分析可得11kt k =-⎧⎨=⎩，解可得t 的值；（2）根据题意，设向量a ，b 的夹角为θ；由数量积的计算公式可得a 、||b 以及a b ， 由cos a b a b θ⋅=计算可得答案．【详解】（1）∵根据题意，向量12a e e =+，21b e te =-，若//a b ，则设a kb =，则有122112()()e e k e te kte ke +=-=-+，则有11kt k =-⎧⎨=⎩，解可得1t =-； （2）根据题意，设向量a ，b 的夹角为θ；若2t =，则212b e e =-，则2221||(2)3b e e =-=，则||3b =，又由12a e e =+，则2212||()3a e e =+=，则||3a =，又由12213()(2)2a b e e e e =+-=-， 则312cos 2||||3a b a b θ-===-⨯，又由0θπ，则23πθ=； 故向量a ，b 的夹角为23π． 【点睛】本题考查向量数量积的计算，涉及向量模的计算公式，属于基础题．26．(1)()26f x sin x π⎛⎫=- ⎪⎝⎭;(2)()2g x sin x =, 对称轴为,42k x k Z ππ=+∈;(3)112m ≤<,,1223x x π+=. 【分析】 (1) 根据向量()1,1,3,(0)2u sin x v sin x cos x ωωωω⎛⎫=-=+> ⎪⎝⎭和函数()f x u v =⋅，利用数量积结合倍角公式和辅助角法得到，()26πω⎛⎫=- ⎪⎝⎭f x sin x ，再根据函数f (x )的图象上两个相邻的对称轴距离为2π求解. (2)依据左加右减，将函数y =f (x )的图象向左平移12π个单位后，得到函数()22126g x sin x sin x ππ⎡⎤⎛⎫=+-= ⎪⎢⎥⎝⎭⎣⎦，令2,2ππ=+∈x k k Z 求其对称轴. (3)作出函数f (x )在0,2π⎡⎤⎢⎥⎣⎦上图象，根据函数y =f (x )与直线y =m 在0,2π⎡⎤⎢⎥⎣⎦上有两个交点求解.再令2,62x k k Z πππ-=+∈，求对称轴.【详解】(1)()()2113322ωωωωωω=+-=+-f x sin x sin x cos x sin x sin xcos x ， 31222226πωωω⎛⎫=-=- ⎪⎝⎭sin x cos x sin x ∵函数f (x )的图象上两个相邻的对称轴距离为2π， ∴22T π=， ∴2(0)2ππωω=>， ∴ω=1， 故函数f (x )的解析式为()sin 26f x x π⎛⎫=-⎪⎝⎭; (2)依题意，()22126g x sin x sin x ππ⎡⎤⎛⎫=+-= ⎪⎢⎥⎝⎭⎣⎦， 令2,2ππ=+∈x k k Z ，则,42ππ=+∈k x k Z ， ∴函数g (x )的对称轴为,42ππ=+∈k x k Z ; (3)∵0,2x π⎡⎤∈⎢⎥⎣⎦， ∴52,666x πππ⎡⎤-∈-⎢⎥⎣⎦， ∴12,162sin x π⎛⎫⎡⎤-∈- ⎪⎢⎥⎝⎭⎣⎦， 函数f (x )在0,2π⎡⎤⎢⎥⎣⎦上的草图如下，依题意，函数y =f (x )与直线y =m 在0,2π⎡⎤⎢⎥⎣⎦上有两个交点，则112m ≤<，令2,62x k k Z πππ-=+∈，则,32k x k Z ππ=+∈， ∴函数f (x )在0,2π⎡⎤⎢⎥⎣⎦上的对称轴为3x π=，则1223x x π+=. 【点睛】 本题主要考查了平面向量和三角函数，三角函数的图象和性质及其应用，还考查了数形结合的思想和运算求解的能力，属于中档题.。