牛顿环法测曲率半径

齿合前轻轻转动测微鼓轮读数有变化，而游标并没有移动。
消除方法：测量时只沿同一方向转动测微鼓轮。
实验方案
23 20 11 中心 11 20 左侧 右侧
左取内切点
右取外切点
D＝右外切点－左内切点
测量方案
干涉条纹数 10 11 12 13 14 15 16 17 18 19 20
左方条纹
第 读数
一 次 测
用牛顿环测透镜的曲率半径
上海师范大学天华学院
实验背景
白光下的肥皂膜
白光入射的牛顿环照片
白光下的水膜
牛顿环装置
单色光的牛顿环照片
实验背景
“牛顿环”是一种分振幅、等厚干涉现象，是光 的波动性的一种表现。 应用极广：测量光波波长、测量微小角度或薄膜 厚度、观测微小长度变化、检测光学表面加工质 量等。利用牛顿环还可以测量液体折射率。 本实验通过牛顿环研究光的干涉现象，测定透镜 的曲率半径，学习读数显微镜的使用等。
就可以测量其折射率n
n dm2 dk2
4(m k)R
实验内容
测量牛顿环直径，计算平凸透镜 曲率半径R。
计算公式：
R
2
Dm
2
Dn
4(m n)
实验装置 读数显微镜
读数标尺
目镜
显微镜筒 调焦旋钮
钠光灯
测微鼓轮
牛顿环
读数显微镜的空程误差
空程误差属系统误差，由螺母与螺杆间的间隙造成；
螺杆
测微鼓轮
(m n) 4(m n)
难点解说
实验中，如果用弦长取代牛顿环直径是否可以？
Dk2m Dk2 4(rk2m rk2 )
4(
l k2 m 4
h2 )
( lk2 4

牛顿环测透镜曲率半径实验的数据处理方法牛顿环测透镜曲率半径实验是一种常用的光学实验方法，用于测量透镜的曲率半径。

本文将介绍牛顿环测量方法以及常用的数据处理方法，帮助读者了解该实验并正确进行数据处理。

一、牛顿环测量方法牛顿环测量方法是通过观察牛顿环的圆心与边缘的环形干涉图案来确定透镜的曲率半径。

具体步骤如下：1. 实验准备首先，我们需要准备一块光滑的透镜和一块玻璃基片。

将透镜和基片放在光源下方，保证光线垂直照射。

2. 形成干涉图案调整透镜和基片的间距，使得玻璃基片上形成一组明暗相间的圆环。

这个圆环就是我们所说的牛顿环。

3. 测量半径使用读数显微镜或目镜放大牛顿环图案。

从内环的直径开始，分别测量每个环的直径。

通常情况下，选取3-5个环作为测量点。

4. 记录数据将每个环的直径数据记录下来。

为了减小误差，需要重复多次测量。

二、数据处理方法牛顿环测量实验会得到一系列环的直径数据，我们需要对这些数据进行处理才能得到透镜的曲率半径。

下面介绍两种常用的数据处理方法。

1. 计算平均值首先，将每次测量得到的环直径求平均值。

这样可以减小由于实验误差导致的数据波动。

2. 曲线拟合通过拟合实验数据的曲线，我们可以得到更精确的透镜曲率半径。

常用的拟合方法有最小二乘法和直线拟合法。

最小二乘法是通过最小化实验数据与拟合曲线之间的距离来确定最优的拟合曲线。

直线拟合法则是将实验数据作为点，通过拟合直线的斜率来得到曲率半径。

三、实验注意事项在进行牛顿环测量实验时，需要注意以下几点。

1. 保持环境稳定实验环境应尽量保持稳定，避免外界震动和温度变化对实验结果的影响。

2. 测量精度使用高精度仪器进行测量，并尽量减小读数误差。

对于每个环的直径测量，应进行多次重复以提高精度。

3. 数据处理准确性在数据处理过程中，需要严格按照公式进行计算，并保留足够的有效数字。

避免舍入误差对最终结果的影响。

四、实验结果的分析与讨论根据实验得到的透镜曲率半径数据，可以进行结果的分析与讨论。

r 2dR (Δ)R
r (k1)R 明环半径
2
2
r kR 暗环半径
牛顿环干涉测定透镜曲率半径
波动光学
结 明环半径 r (k1)R (k1,2,3, )
论
2
暗环半径 r kR (k0,1,2, )
思 1）从反射光中观测，中心点是暗点还是亮点？ 考 从透射光中观测，中心点是暗点还是亮点？
2）属于等厚干涉，条纹间距不等，为什么？
☆干涉条纹的移动演示
每一条 纹对应劈尖 内的一个厚 度，当此厚 度位置改变 时，对应的 条纹随之移 动；当倾斜
角改变条
纹形状改变
波动光学
牛顿环干涉测定透镜曲率半径
【实验目的】
波动光学
1、掌握用牛顿环测定透镜曲率半径的方法； 2、掌握读数显微镜的调节和使用；
3、通过实验加深对等厚干涉原理的理解。
【实验仪器】
2(h d)
牛顿环干涉测定透镜曲率半径
波动光学
总结
1）干涉条纹为光程差相同的点的轨迹，即厚 度相等的点的轨迹
d
b
k1
d
d
2n
b d 2n
牛顿环干涉测定透镜曲率半径
波动光学
2）厚度线性增长条纹等间距，厚度非线性增长 条纹不等间距
3）条纹的动态变化分析（ n,, 变化时）
劈尖角
牛顿环干涉测定透镜曲率半径
5
5 6n 3m 3
牛顿环干涉测定透镜曲率半径
波动光学
例2 如图所示为测量油膜折射率的实验装置 , 在
平面玻璃片G上放一油滴，并展开成圆形油膜，在波
长 60n0m 的单色光垂直入射下，从反射光中可
观察到油膜所形成的干涉条纹 . 已知玻璃的折射率，

牛顿环测透镜曲率半径实验中的误差来源与控制策略牛顿环测透镜曲率半径实验是一种常用的光学实验方法，用于测量透镜的曲率半径。

然而，在实际操作中，由于各种因素的干扰，往往会引入误差，影响测量结果的准确性。

本文将介绍牛顿环测透镜曲率半径实验中可能存在的误差来源，并提出相应的控制策略。

一、误差来源1. 光源的不稳定性：光源的不稳定性是牛顿环测量中常见的误差来源之一。

由于光源的强度和方向不稳定，会导致测量结果的波动和偏差。

2. 边缘环的模糊度：在测量过程中，由于透镜的曲率半径不一致或未完全精磨，会导致边缘环的模糊度增加，从而影响到测量结果的准确性。

3. 透镜与平台接触不均匀：透镜与平台接触不均匀也是造成误差的原因之一。

如果透镜与平台接触面存在微小的空隙或不平整，会导致光线的反射或折射发生变化，从而引入测量误差。

4. 环形干扰：环形干扰是由于光的衍射效应引起的，当光线经过透镜后，出射的光线会受到环形干扰的干扰，从而导致牛顿环的形态发生异常，造成测量结果的偏差。

5. 环形光斑的定位误差：由于环形光斑的大小和位置对测量结果有直接影响，因此环形光斑的定位误差也是一种重要的误差来源。

二、控制策略1. 光源的稳定化：为了减小光源的波动对测量结果的影响，可以采取稳定化措施，如使用稳定性较好的光源、加装滤光片、调节光源电流等，以确保光源的稳定性。

2. 透镜的精磨与检查：为了减小透镜边缘环的模糊度，需要对透镜进行精磨和检查。

在精磨过程中，应注意透镜的曲率半径和平整度，保证透镜的曲率半径均匀一致。

3. 平台调整：为了确保透镜与平台接触均匀，应仔细调整平台的位置和方向，以避免透镜与平台接触时存在空隙或不平整的情况。

4. 环形干扰的补偿：为了减小环形干扰对测量结果的影响，可以采用干涉滤光片、干涉仪等设备对环形干扰进行补偿和消除，以确保测量结果的准确性。

5. 环形光斑的准确定位：为了避免环形光斑的定位误差对测量结果的影响，可以通过调整透镜与光源之间的距离、改变光源的入射角度等方式，确保环形光斑的大小和位置符合要求。

实验 用牛顿环干涉测透镜曲率半径（一）目的：1、掌握用牛顿环测定透镜曲率半径的方法。

2、通过实验加深对等厚干涉原理的理解。

（二）仪器和用具：移测显微镜（JCD 3型）、钠灯牛顿环仪是由待测平凸透镜（凸面曲率半径约为200～300c ｍ〕Ｌ和磨光的平玻璃板Ｐ叠合装在金属框架Ｆ中构成。

框架边上有三个螺旋Ｈ，用以调节Ｌ和Ｐ之间的接触，以改变干涉环纹的形状和位置。

调节Ｈ时，螺旋不可旋得过紧，以免接触压力过大引起透镜弹性形变，甚至损坏透镜。

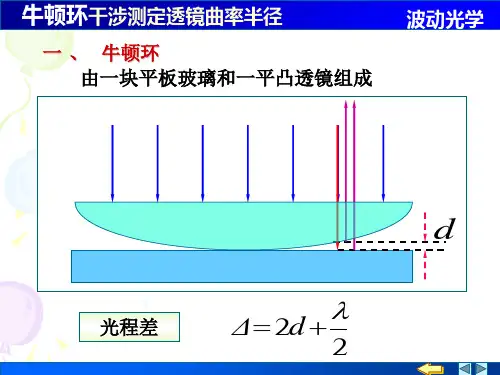
（三）原理：当一曲率半径很大的平凸透镜的凸面与一磨光平玻璃板相接触时，在透镜的凸面与平玻璃板之间将形成一空气薄膜，离接触点等距离的地方，厚度相同。

如图9-2所示，若以波长为的单色平行光投射到这种装置上，则由空气膜上下表面反射的光波将互相干涉，形成的干涉条纹为膜的等厚各点的轨迹，这种干涉是一种等厚干涉。

在反射方向观察时，将看到一组以接触点为中心的亮暗相间的圆环形干涉条纹，而且中心是一暗斑（图a ）；如果在透射方向观察，则看到的干涉环纹与反射光的干涉环纹的光强分布恰成互补，中心是亮斑，原来的亮环处变为暗环，暗环处变为亮环（图ｂ），这种干涉现象最早为牛顿所发现，故称为牛顿环。

设透镜Ｌ的曲率半径为R ，形成的m 级干涉暗条纹的半径为r ｍ，m 级干涉亮条纹的半径为r ｍ’，不难证明r ｍ =λmRr ｍ’=2)12(λ⋅−R m 以上两式表明，当已知时，只要测出D 第m 级暗环（或亮环）的半径，即可算出透镜的曲率半径R ；相反，当R 已知时，即可算出λ。

但由于两接触镜面之间难免附着尘埃，并且在接触时难免发生弹性形变，因而接触处不可能是一个几何点，而是一个圆面，所以近圆心处环纹比较模糊和粗阔，以致难以确切判定环纹的干涉级数m ，即干涉环纹的级数和序数不一定一致。

这样，如果只测量一个环纹的半径，计算结果必然有较大的误差。

为了减少误差，提高测最精度，必须测量距中心较远的、比较清晰的两个环纹的半径，例如测量出第m 1个和第m 2个暗环（或亮环）的半径（这里m 1，m 2均为环序数，不一定是干涉级数），因而（9－1）式应修正为r ｍ2 =（m+j ）R λ式中m 为环序数，（m ＋j ）为干涉级数（j 为干涉级修正值），于是λλR m m R j m j m r r m m )()]()[(12122212−=+−+=− 上式表明，任意两环的半径平方差和干涉级以及环序数无关，而只与两个环的序数之差（m 2-m 1）有关。

实验十用牛顿环测透镜的曲率半径利用透明薄膜上下表面对入射光的依次反射，入射光的振幅将分解成有一定光程差的几部分。

若两束反射光在相遇时的光程差取决于产生反射光的薄膜厚度，则同一干涉条纹所对应的薄膜厚度相同。

这就是所谓的等厚干涉。

牛顿为了研究薄膜颜色，曾经用凸透镜放在平面玻璃上的方法做实验。

他仔细观察了白光在空气薄层上干涉时所产生的彩色条纹，从而首次认识了颜色和空气层厚度之间的关系。

1675年，他在给皇家学会的论文里记述了这个被后人称为牛顿环的实验，但是牛顿在用光是微粒流的理论解释牛顿环时却遇到困难。

19世纪初，托马斯.杨用光的干涉原理解释了牛顿环。

一、实验目的1、观察牛顿环产生的等厚干涉现象，加深对等厚干涉原理的理解。

2、掌握用牛顿环测量透镜曲率半径的方法。

二、实验仪器牛顿环，钠光灯，测微目镜。

三、实验原理1、牛顿环“牛顿环”是一种用分振幅方法实现的等厚干涉现象，最早为牛顿所发现。

为了研究薄膜的颜色，牛顿曾经仔细研究过凸透镜和平面玻璃组成的实验装置。

他的最有价值的成果是发现通过测量同心圆的半径就可算出凸透镜和平面玻璃板之间对应位置空气层的厚度；对应于亮环的空气层厚度与1、3、5…成比例，对应于暗环的空气层厚度与0、2、4…成比例。

但由于他主张光的微粒说（光的干涉是光的波动性的一种表现）而未能对它作出正确的解释。

直到十九世纪初，托马斯．杨才用光的干涉原理解释了牛顿环现象，并参考牛顿的测量结果计算了不同颜色的光波对应的波长和频率。

牛顿环装置是由一块曲率半径较大的平凸玻璃透镜，将其凸面放在一块光学平板玻璃（平晶）上构成的，如图10.1所示。

平凸透镜的凸面与玻璃平板之间形成一层空气薄膜，其厚度从中心接触点到边缘逐渐增加。

若以平行单色光垂直照射到牛顿环上，则经空气层上、下表面反射的二光束存在光程差，它们在平凸透镜的凸面相遇后，将发生干涉。

其干涉图样是以玻璃接触点为中心的一系列明暗相间的同心圆环（如图10.3所示），称为牛顿环。

3. 暗环直径表达式:
r = (2 R hm ) hm ≈ 2 Rhm
2 m
r = mRλ → D = 4mRλ
2 m 2 m
2. 两光相消条件: m = (2m + 1) λ / 2 = 2hm + λ /2
(m = 0,1,2, …… 称干涉级数)
则暗条纹出现在下列位置处:
hm = m
四,技能 1. 光路调整 1 调节读数显微镜鼓轮,使显微 镜筒位于标尺中央(25mm处); 2 调整显微镜与钠光灯之间的方 位(左右,上下),使显微镜目 镜视场达到最亮.
2. 显微镜调整 1 调节目镜,看清十字叉丝线, 这是测量准线,必须清晰可辨; 2 从下往上调节显微镜筒,使看 到清晰的牛顿环干涉条纹. 3. 中心对准 移动牛顿环装置,使干涉环中心 与十字叉丝线交点一致.
4. 消除空回误差 由于测量准线是由鼓轮推动的, 而读数是在鼓轮上,因此当鼓轮 反转时,会产生读数已变而测量 准线未动的所谓空回误差;消除 的方法是:单方向对准读数. 建议:从左边40环单向地测到右 边40环,一可消除空回误差,二 是便于检查测量数据是否有误.
5. 数据实时检查 1 级数越高,级之间的距离是否 越小; 2 各级间左,右间距是否基本对 称.
λ
2
上一页
4. 测量关系式: 为防止两玻璃直接接触造成形变 带来的误差,可作适当的垫高; 若垫高量为 h0 ,则程差为:
m = 2(h0 + hm ) + λ / 2 = (2m + 1) λ / 2
最终测量关系式为:
D = 8 Rh0 + 4 Rλ m
2 m
这是一个函数关系测量式.
三,直测量及测量仪器 1. 直测量: 测量对应于 m 级干涉条纹的直 径 Dm ;每隔 5 环测一个点,共 测 8 个直径,D5,D10,……,D40. 2. 测量仪器: 测量用读数显微镜,它应是一把 通过环中心的尺子,可以测量干 涉环的直径.

用牛顿环测平凸透镜的曲率半径实验报告实验名称：用牛顿环测平凸透镜的曲率半径实验目的：利用牛顿环的成像特性，测量平凸透镜的曲率半径，并掌握测量方法及误差分析。

实验原理：牛顿环实验是一种利用干涉现象来测量曲率半径的方法。

在实验中，光线经过一个平凸透镜后会在光斑处形成一组彩虹环，称为牛顿环。

当凸透镜与玻璃板接触时，光波的反射和折射都会产生相位差，因此彩虹环会发生移动。

根据牛顿环移动的程度，就可以计算出凸透镜的曲率半径。

牛顿环的半径r和平板厚度d之间的关系式为：r = (m-1)λd/m其中m为第m级暗纹，λ为光的波长。

实验步骤：1. 用蘸有甲醇的棉签擦拭干净透镜并与平板紧密相接。

2. 打开白光源，将凹透镜放在光源上方，调整高度，使之位于平板上方10-12厘米，使白光垂直入射，形成明暗相间的彩虹环。

3. 用显微镜对牛顿环进行观察，找到第一级暗圆环的位置，记下光程差d1，并记录m的值。

4. 令平板转过n个角度，找到第m级暗圆环的位置，记下光程差dn，并计算m个不同角度时的光程差d1,d2,…,dm。

5. 根据公式计算出曲率半径r的值。

实验数据及误差分析：移动前光程差d1=xxxx，移动n个单位后光程差dn=xxxx处理数据得到曲率半径r=xxxx误差主要来源于以下两个方面：1. 手动转动平板时，可能会出现误差，导致找到的暗纹位置有偏差。

2. 牛顿环受外界环境影响较大，如温度、湿度等，也会对测量结果产生影响。

实验总结：通过本次实验，我们掌握了利用牛顿环进行测量的方法，并对测量结果进行了误差分析。

同时，我们也发现，在实验中应尽量减少人为因素对实验结果的影响，提高实验精度。

1．实验十四用牛顿环测透镜曲率半径牛顿环是牛顿在1675年所做的著名实验。

牛顿环是等厚干涉的一种，它在光学计量、基本物理量测量等方面有广泛的应用：用牛顿环测定光波的波长、透镜曲率半径，用牛顿环来检验磨制透镜的质量等。

实验目的1、加深对光的干涉原理的理解；2、观察和研究光的等厚干涉现象及其特点；3、掌握用牛顿环测定透镜曲率半径的方法。

实验仪器牛顿环仪、读数显微镜、单色光源(钠灯)。

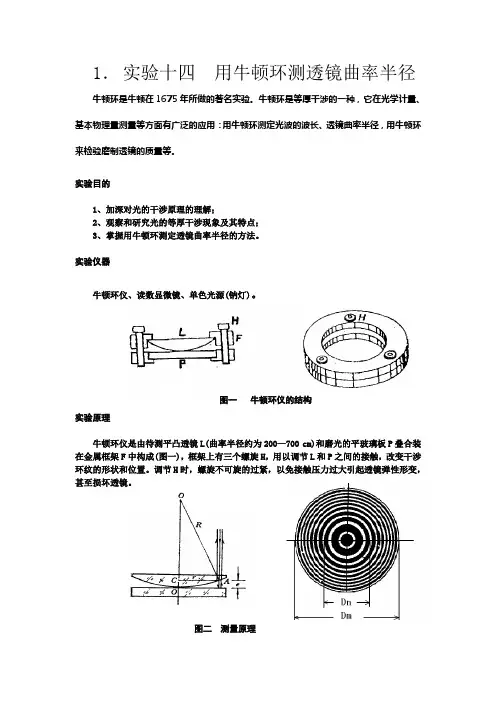
图一牛顿环仪的结构实验原理牛顿环仪是由待测平凸透镜L(曲率半径约为200—700 cm)和磨光的平玻璃板P叠合装在金属框架F中构成(图一)，框架上有三个螺旋H，用以调节L和P之间的接触，改变干涉环纹的形状和位置。

调节H时，螺旋不可旋的过紧，以免接触压力过大引起透镜弹性形变，甚至损坏透镜。

图二测量原理如图二所示．将曲率半径很大的平凸透镜的凸面放在一光学平面玻璃上，在透镜和平面之间形成空气膜，以平行单色光垂直照射时，经空气膜层上、下两表面反射的两束光发生干涉，在空气膜上表面出现一组干涉条纹。

干涉条纹是以接触点O 为圆心的一系列同心圆环，称为牛顿环。

在图中，设r 为牛顿环某环的半径，e 为与该环对应的空气膜层的厚度。

考虑到光在空气膜下表面反射的光，是从光疏介质(空气)入射到光密介质(玻璃)，有半波损失，而在空气膜上表面反射的光，是从光密介质入射到光疏介质，无半波损失。

所以在空气膜上、下表面反射的两束反射光的光程差为22λ+=∆e (1)在直角三角形AOC 中，有：222)(r e R R +-=从而得： eR r e -=22考虑到e<<R, e 跟R 相比可以略去，即Rr e 22= (2)代入(1）式，可得到：22λ+=∆R r根据干涉相长和干涉相消的条件：可得明环半径为：2)12(λR k r -= ),2,1( =k(3)暗纹半径为：λkR r= ),2,1,0( =k(4)必须指出，由于干涉条纹有一定宽度，上式中的r 是第K 级牛顿环的条纹中心到圆环中心的距离。

实验二用牛顿环测平凸透镜的曲率半径实验目的实验原理1.牛顿环现象的产生原理在平行光照射下，将一与光学轴垂直的光学平面玻璃片和一凸透镜组合在一起，二者的光学中心重合，则在它们的接触面之间形成一个光程不同的薄透明带状区域，即牛顿环。

在这个区域内，光波经过两次反射，一次透射后再反射，产生干涉，形成明暗相间的环纹。

光程差相等的光线干涉相干，会加强，光强变大；反之，光线干涉破坏，光强变小。

通过观察牛顿环的位置和直径可以测量得到参考表面的曲率半径。

2.测量曲率半径的方法将透镜放在平行光源下，用放大镜观察透镜正面的牛顿环，调节透镜的位置使透镜与平面玻璃片最近接触，记下此时各级圆环直径，用公式:R = r^2/2t其中，R为曲率半径，r为环的半径，t为玻璃片和透镜间的距离。

实验器材1.牛顿环装置2.凸透镜一只3.平面玻璃片两片4.放大镜实验步骤1.调节牛顿环装置，使其平稳，调整气泡使其位于中央。

2.在透镜正面涂上一层抛光膏，在平面玻璃片上涂上一层胶水。

3.将平面玻璃片和透镜尽可能地平行安装在涂有抛光膏的透镜正面之上，轻轻压下，然后轻轻地移动平面玻璃片，直到找到最小牛顿环。

4.在平面玻璃片周围绕一圈，将牛顿环划分成等分。

5.用放大镜观察牛顿环的位置，记录最小牛顿环的半径。

6. 单独安装透镜在牛顿环装置上，并调节透镜与平面玻璃片之间的距离，用游标卡尺测量该距离。

7. 根据公式R=r^2/2t计算出透镜的曲率半径。

实验注意事项1.实验过程中要轻轻移动平面玻璃片，以免破坏牛顿环的对称性。

2.在调节透镜的位置时，应防止透镜在接触平面玻璃片时产生畸变。

实验结果1.记录不同牛顿环的半径，计算曲率半径R的值。

2.将不同R的值绘制成图像，观察曲线的特点，并说明其意义。

通过实验，测量了平凸透镜的曲率半径，并了解了牛顿环的原理和应用。

通过绘制曲线可以发现，在透镜的中心处，曲率半径最小，在边缘处则最大，而且在两边的变化趋势大致相同，但是变化的速度不一样。

牛顿环曲率半径的测定一、实验目的１. 通过实验加深对等厚干涉现象的理解。

２. 掌握用牛顿环测定透镜曲率半径的方法。

３. 通过实验熟悉读数显微镜的使用方法。

二、实验仪器读数显微镜1、调节显微目镜，使分划板（叉丝）成像清晰。

2、调节显微镜境管的升降和水平位置，使物镜对准物体的待测部分，并使境管上的水平标尺与叉丝、底座平行。

3、调节物镜的升降，使物体的成像清晰。

钠光灯通电一段时间发光稳定后，钠光灯发出589.3nm 的单色光。

三、实验原理当一束单色光入射到透明薄膜上时，通过薄膜上下表面依次反射而产生两束相干光。

如果这两束反射光相遇时的光程差仅取决于薄膜厚度，则同一级干涉条纹对应的薄膜厚度相等，这就是所谓的等厚干涉。

本实验研究牛顿环和劈尖所产生的等厚干涉。

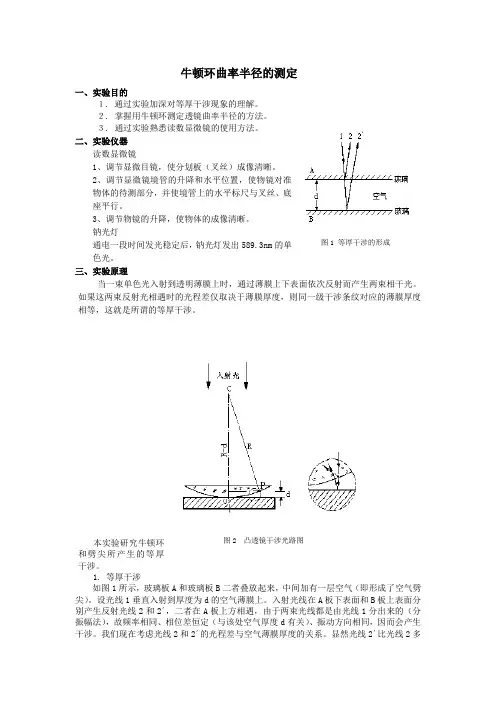
1. 等厚干涉如图1所示，玻璃板A 和玻璃板B 二者叠放起来，中间加有一层空气（即形成了空气劈尖）。

设光线1垂直入射到厚度为d 的空气薄膜上。

入射光线在A 板下表面和B 板上表面分别产生反射光线2和2´，二者在A 板上方相遇，由于两束光线都是由光线1分出来的（分振幅法），故频率相同、相位差恒定（与该处空气厚度d 有关）、振动方向相同，因而会产生干涉。

我们现在考虑光线2和2´的光程差与空气薄膜厚度的关系。

显然光线2´比光线2多传播了一段距离2d 。

此外，由于反射光线2´是由光密媒质（玻璃）向光疏媒质（空气）反射，会产生半波损失。

故总的光程差还应加上半个波长2/λ，即2/2λ+=∆d 。

根据干涉条件，当光程差为波长的整数倍时相互加强，出现亮纹；为半波长的奇数倍时互相减弱，出现暗纹。

因此有：=+=∆22λd ⎪⎩⎪⎨⎧⋅+⋅2)12(22λλK K 出现暗纹，，，出现亮纹 210,3,2,1==K K 光程差∆取决于产生反射光的薄膜厚度。

同一条干涉条纹所对应的空气厚度相同，故称为等厚干涉。

2. 牛顿环当一块曲率半径很大的平凸透镜的凸面放在一块光学平板玻璃上，在透镜的凸面和平板玻璃间形成一个上表面是球面，下表面是平面的空气薄层，其厚度从中心接触点到边缘逐渐增加。

牛顿环测透镜曲率半径实验的误差分析与减小方法引言：牛顿环测透镜的曲率半径是实验物理学中常见的一个实验，通过测量透镜与平板玻璃之间产生的干涉环的半径，可以计算出透镜的曲率半径。

然而，由于实验中存在各种误差影响，测量结果往往会产生偏差。

因此，本文将对牛顿环测透镜曲率半径实验的误差进行分析，并提出减小误差的方法。

一、误差分析1. 初始对准误差在实验前期，透镜与平板玻璃的对准极其重要。

如果对准不精确，会导致干涉环形状不清晰，进而影响测量结果的准确性。

2. 读数误差由于人眼的视觉限制和测量仪器本身的误差，读数误差是不可避免的。

尤其是在对干涉环进行测量时，需要准确地判断出环的边缘位置，这对操作者的眼睛要求较高。

3. 环的形状误差实验中产生的牛顿环并非完美的圆形，形状略微偏离圆形也会导致测量结果的误差。

这可能是由于透镜本身存在微小缺陷或测量装置的精度问题所致。

4. 环的密度分布误差牛顿环的密度分布应当是均匀的，然而实际上可能存在一些干涉环密度不均匀的情况，导致测量结果的偏差。

5. 噪声干扰实验环境中的震动、电磁干扰等因素都可能对测量结果产生影响，引入噪声干扰。

这些干扰可能会使得环的边缘位置产生模糊或发生变化，从而影响测量结果的准确性。

二、减小误差的方法1. 对准优化在实验前期，需要仔细调整透镜与平板玻璃的位置，确保它们之间的距离和倾斜角度符合实验要求。

可以通过放大干涉环或借助光源的角度调节来确保对准的准确性。

2. 使用精确的测量仪器为了减小读数误差，可以使用显微镜等精密仪器进行测量。

这些仪器可以放大干涉环，并提供更清晰的图像，使操作者更加准确地读取环的边缘位置。

3. 平均多次测量结果为了减小环的形状误差和密度分布误差带来的影响，可以进行多次测量，并对测量结果进行平均。

这样可以有效减小随机误差的影响，得到更准确的测量结果。

4. 增加环的密度通过增加环的密度，可以增强环的对比度，使得边缘位置更加清晰。

这可以通过增加光源的亮度或通过选择合适的滤光片来实现。

用牛顿环测曲率半径光学元件的球面曲率半径可以用各种方法和仪器来测定。

常用的有机械法（如用球径仪测量）和光学法。

采用什么方法和仪器，主要取决于所测曲率半径的大小和精度。

本试验介绍的牛顿环法是光学法的一种，这种方法适用于测定大的曲率半径，球面可以是凸面也可以是凹面。

【实验目的】1 学习用牛顿环测量球面曲率半径的原理和方法；2 学会使用测量显微镜和钠光灯。

【实验原理】 1 等厚干涉如图4.5.1，有面广源S 上某一原子发出的某种波长为λ的光线1和2投射到bb 面上（bb 面两边介质的折射率分别为N 和n ）。

其中一条（光线1）经aa 表面反射后和另一条（光线2）相遇于bb 表面附近的C 点，因而在C 点产生干涉。

在C 点处就可以观察到干涉条纹。

如果aa 和bb 表面之间是很薄的空气夹层（折射率n=1），而且夹角很小，光线又近乎垂直地入射到bb 表面上，光线11’和22’的光程差是2/2h δλ=+光程差只与厚度h 有关。

式中λ/2是因为光线由光疏介质射到光密介质且在aa 界面反射时有一相位突变引起的附加光程差。

产生第m 级（m 为一整数）暗条纹的条件是2(21),0,1,2,22h m m λλ+=+=… 即12h m λ=产生第m 级亮条纹的条件是22,0,1,2,22h m m λλ+==… 即1()22h m λ=-因此，在空气层厚度相同处产生同一级干涉条纹，厚度不同处产生不同的干涉条纹，如果上下两个表面的平面性很好，则产生规则的干涉条纹；如果两个表面的平面性很差，则会产生了很不规则的干涉花样。

这些都叫做等厚干涉条纹。

2 用牛顿环测一球面的曲率半径（1）将待测凸透镜的球面AOB 放在平面CD 的上面，如图所示，则形成一个从中心O 向四周逐渐增厚的空气层。

如果单色光源上某一点发出的光线近乎垂直地入射，则其中一部分光线经AOB 表面反射，另一部分经CD 表面反射，形成两束相干光。

这两束光中的两条反射光线将在AOB 表面上某一T 点相遇，从而在T 点产生干涉。

等厚干涉应用
科学研究和工程技术上广泛应用等厚干涉现象。 如，测量光的波长，微小长度变化，检验工件表面光 洁度等。
本实验应用牛顿环干涉测量平凸透镜的曲率半径。
实验目的
1.观察光的等厚干涉现象，加深对 光的干涉原理的理解； 2.学习利用干涉现象测量某些物理 量的方法。
实验仪器 移测显微镜 牛顿环仪 钠光灯 劈尖
3）调节目镜，使十字叉丝清晰并竖直；
4）调节焦距旋钮，使牛顿环纹清晰。
3、测量
1）移动刻度轮，使主尺上的刻度指在25mm处。 2）移动牛顿环，使十字叉丝处于牛顿环中心处。 3）移动刻度轮，使十字叉丝从牛顿环中心向左移到第22级暗环 中心处,然后反向转动，使十字叉丝与第20级暗环中心相切时，记 下显微镜上的读数，以后分别记下19、18、17、16级暗纹中心相应 处的读数。继续向右移动，再分别记录第10、9、8、7、6级暗纹中 心处的显微镜读数。继续右移，经过牛顿环中心后，依次测记右侧 第6、7、8、9、10和16、17、18、19、20级暗纹中心的读数。
由几何关系知：
r
2
R

2
( R h )
h
h
2
0
h
r
带入暗纹条件：
h k
2
2
R
r
r d
2
2R
kR
r
h
透镜曲率半径：
R

k

4k
有逐差法可知，当测得的第m级和第k级的暗环直径dm和dk时，得到曲 率半径的测量公式为：
R d
4、计算 用逐差法测透镜曲率半径，计算平均值。
干涉圆环直径的测量方法
Dm 左xm 右xm
m 级

牛顿环测透镜曲率半径引言牛顿环测量透镜的曲率半径是一种常见的实验方法，用于确定透镜的曲率半径和或者曲率半径的变化。

牛顿环测量法是通过观察透镜与平面玻璃片之间形成的干涉图案来确定透镜的曲率。

本文将介绍牛顿环测量透镜曲率半径的原理、实验装置和步骤，并讨论测量结果的分析和可能的误差来源。

一、牛顿环测量原理牛顿环测量透镜曲率半径的原理基于干涉现象。

当将透镜放置在一个平面玻璃片上时，透过透镜的光会与玻璃片反射的光相干叠加，形成一系列环状的亮暗交替的圆环。

这些圆环就是牛顿环。

干涉图案的特点是中心亮、向外逐渐暗。

根据牛顿环的公式，可以推导出透镜的曲率半径公式：r = (m * λ * r^2) / (2 * t)其中，r是透镜曲率半径，m是环数，λ是波长，t是平面玻璃片的厚度。

由于λ和t都是已知量，所以通过测量环数m，就可以计算出透镜的曲率半径r。

二、实验装置进行牛顿环测量透镜曲率半径实验所需的装置包括：1. 光源：需要稳定、单色和平行的光源，常用的有汞灯、钠灯等。

2. 凸透镜：透镜的曲率半径需要测量的透镜。

3. 平面玻璃片：透镜放置在平面玻璃片上。

4. 显微镜：用于观察干涉图案。

5. 支架和调节装置：用于固定透镜和平面玻璃片，使其位置可以调整。

三、实验步骤以下是进行牛顿环测量透镜曲率半径的一般步骤：1. 将透镜放置在平面玻璃片上，确保两者贴合得非常密切。

2. 将光源对准透镜的中心，并调整光源的位置，使得透过透镜的光束是平行的。

3. 在透镜的一侧放置显微镜，调节显微镜的焦距，使得透镜形成清晰的牛顿环干涉图案。

4. 使用显微镜观察干涉图案，记录环数m的值。

此时，可以将显微镜的目镜固定在一个位置上，然后移动物镜，观察环的变化，直到找到相对清晰的环。

5. 重复实验多次，得到多组数据。

6. 根据实验测得的环数m，代入牛顿环公式，计算透镜的曲率半径r。

四、测量结果与误差分析根据测量结果，可以计算出透镜的曲率半径。

然而，实际测量中可能会存在一些误差，导致测量结果的偏差。

牛顿环测透镜曲率半径实验中的数据处理方法与分析在光学实验中，牛顿环测透镜曲率半径是一种常用的方法。

通过测量透镜与平面玻璃片接触时形成的干涉环的半径，可以得到透镜的曲率半径，从而推导出透镜的光学性质。

本文将介绍牛顿环测透镜曲率半径实验中常用的数据处理方法及分析。

一、实验设备与原理在进行牛顿环测透镜曲率半径实验时，我们需要准备以下设备：1. 透镜：实验中使用的透镜应为高质量光学元件，表面光洁度要求较高。

2. 光源：实验中常用的光源有白炽灯、激光器等，需要注意保证光源的稳定性和单色性。

3. 平面玻璃片：用于与透镜接触形成干涉环。

4. 干涉仪：实验中使用的干涉仪可以是迈克尔逊干涉仪、杨氏干涉仪等，用于观察干涉环。

实验原理如下：当透镜与平面玻璃片接触时，透镜的一端会形成一系列圆形干涉环，这就是牛顿环。

根据干涉环的半径与透镜的曲率半径之间的关系，可以推导出透镜的曲率半径。

二、数据处理方法1. 数据采集：使用干涉仪观察牛顿环，并通过目镜等测量工具测量出不同环的半径。

需要注意的是，要保证测量环境的稳定与干净，避免误差的产生。

2. 数据记录：将不同环的半径数据记录下来，建立一个数据表格。

数据表格中应包括环数、半径值等信息。

3. 数据处理：根据数据表格中的半径值，可以进行以下数据处理。

a. 平均值计算：计算出所有环的半径值的平均数，作为样本的平均半径。

b. 误差计算：根据样本的平均半径和每个环的半径值计算出每个环的相对偏差，以便后续的误差分析。

c. 绘制图表：可以根据实验数据绘制出环数与半径值之间的关系图表，以直观地展示实验结果。

三、数据分析1. 曲率半径计算：根据实验数据和经过处理的结果，可以计算出透镜的曲率半径。

根据牛顿环的干涉公式，曲率半径与环数之间存在着一定的函数关系，可以通过曲线拟合等方法计算出透镜的曲率半径。

这将有助于进一步了解透镜的性质和应用。

2. 误差分析：通过计算出的偏差值，可以进行误差分析，了解实验中可能存在的误差来源和误差范围。

牛顿环测透镜曲率半径实验的数据分析与结果验证近视眼镜、放大镜等光学器件在我们日常生活中扮演着重要的角色。

而准确测定这些光学器件的物理特性对于制造高质量的镜片至关重要。

其中，牛顿环测透镜曲率半径实验是一种常用的方法，本文将对该实验的数据分析与结果验证进行讨论。

1. 实验原理牛顿环测透镜曲率半径实验是通过观察光源经过透镜后在透镜表面上形成的牛顿环，从而推导出透镜的曲率半径。

当透镜与平行光垂直时，透镜表面的牛顿环由一系列明暗相间的圆环组成。

通过测量牛顿环的半径和透镜与平行光的夹角，可以利用几何光学的原理得出透镜曲率半径的数值。

2. 数据分析在进行牛顿环测透镜曲率半径实验时，我们需要测量透镜与平行光的夹角以及不同环的半径。

首先，我们需要使用一束平行光照射到透镜上。

通过倾斜透镜，我们可以观察到圆环，并且测量圆环的半径。

在测量过程中，我们可以采用尺子进行估计，或者使用显微镜等仪器进行精确测量。

此外，为提高测量结果的准确性，我们需要重复进行多次测量，然后取均值。

3. 结果验证在实验过程中，需要验证所得数据是否符合理论预期。

以正透镜为例，根据牛顿环实验原理，透镜与平行光的夹角越小，牛顿环的半径越大；透镜的曲率半径也越小。

因此，我们可以通过绘制透镜与平行光夹角的函数关系图和透镜半径的函数关系图，来验证所得数据与理论值的一致性。

4. 实验误差与改进在进行牛顿环测透镜曲率半径实验时，可能会存在一些误差，例如由于仪器读数不准确、环的边缘模糊等。

为减小误差，我们可以采用以下措施：4.1 使用高精度仪器进行测量，避免人为因素对测量结果的影响。

4.2 重复测量多次，取均值，提高测量结果的准确性。

4.3 注意保持实验环境的稳定，避免因环境变化而产生误差。

5. 实验应用牛顿环测透镜曲率半径实验广泛应用于光学仪器的制造和调整中。

通过该实验，可以准确测定透镜的曲率半径，从而制造出具有预定功能的光学器件，如微型摄像头、高倍显微镜等。

此外，该实验还可用于研究透镜的性质，如折射率、光焦度等，为光学实验与理论的研究提供有价值的数据支撑。