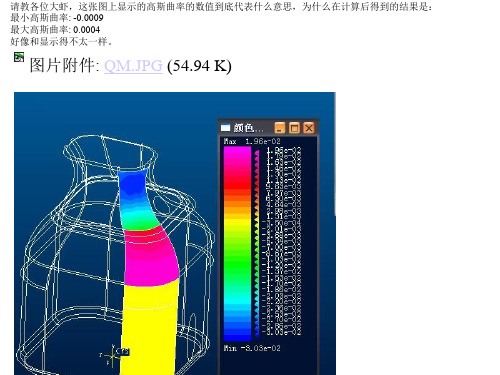
1-2曲率影响

全站仪测量误差分析随着新仪器新设备的不断出现，测量技术的不断提高，同时对工程质量的要求也是愈来愈高，这就对精度的要求加强了许多，随着全站仪在施工放样中的广泛应用，为了使全站仪在实际生产中更好地运用,现结合工程测量理论,对全站仪在测量放样中的误差及其注意事项进行分析。

在我们建筑施工测量中，全站仪主要是用于测量坐标点位的控制和高程的控制，在以下几个方面对全站仪放样的误差作简要概述。

1、全站仪在施工放样中坐标点的误差分析全站仪极坐标法放样点点位中误差MP由测距边边长S(m)、测距中误差ms(m)、水平角中误差mβ(″)和常数ρ=206265″共同构成,其精度估算公式为：而水平角中误差mβ(″)包含了仪器整平对中误差、目标偏心误差、照准误差、仪器本身的测角精度以及外界的影响等。

式(3)表明,对固定的仪器设备,采用相同的方法放样时,误差相等的点分布在一个圆周上,圆心为测站O。

因此对每一个放样控制点O,可以根据点位放样精度m计算圆半径S,在半径范围内的放样点都可由此控制点放样。

由式(1)可看出,放样点位误差中,测距误差较小,主要是测角误差。

因此,操作中应时时注意提高测角精度。

2、全站仪在控制三角高程上的误差分析一般情况下，在测量高程时方法为:设A,B为地面上高度不同的两点。

已知A点高程HA,只要知道A点对B点的高差HAB即可由HB=HA±HAB得到B点的高程HB。

当A、B两点距离较短时，用上述方法较为合适。

在较长距离测量时要考虑地球曲率和大气折光对高差的影响。

设仪器高为i,棱镜高度为l,测得两点间的斜距为S,竖直角α,则AB两点的高差为:一般情况下，当两点距离大于400m时须考虑地球曲率及大气折光的影响，在高差计算时需加两差改正。

式中R为地球曲率半径,取6371km, k为大气折光差系数，k=1-2RC (C为球气差，C=0.43D2/R，D：两点间水平距离)。

从上式中可以看出，当距离较远时，影响高差精度的主要因素就是地球曲率及大气折光，如果高程传递次数较多，累计误差就会加大，在测量时，最好是一次传递高程，若有需要，往返测高程，取其平均值以减小误差。

运算操作数（SUMM，OSUM，DIFF，PROD，DIVI，SQRT）连同参数操作数（CVGT，CVLT，CTGT，CTLT通而又复杂的优化操作数，如在“复合操作数的定义”一节中论述的一样，这些将在本章后面部分可以见到。

因为参数之间差别是空间的，如有效焦距（几十个毫米或者更多）和RMS 斑点尺寸（微米），所以对于一些以镜头长度单位测量的量加上一个为1 的权重通常是足够的。

然而，带有这个权重的有效焦距的残留值不可能为零。

提高权重可以使得到的系统的焦距更接近于要求的有效焦距。

在定义ETGT（边缘厚度大于）操作数时，这种影响是显而易见的。

通常，一个目标值为零的ETGT 将产生一个刚好略小于零的值。

与提高权重相比，规定一个值为.1 或者一些类似数字的目标值更加简单有效。

在改变操作数列表之后，可以通过选择工具，更新来更新每个操作数的当前值。

这对于通过核对来了解每个操作数的值是多少，哪个操作数对评价函数有最大的贡献，是十分有用的。

贡献值的百分数定义如下：这里下标j 表明所有操作数的总和。

这个评价函数将被自动和镜头文件一起被保存。

边界操作数的理解边界操作数，如MNCT、CTGT、DIMX 和其他一些，运行起来与特殊目标值的操作数，如TRAR 和TEAY，稍微有些不一样。

当你给一个参数规定一个边界时，你将指定一个目标值作为边界的定义。

例如，要保持表面5 的最小中心厚度为10mm，你可以使用一个普通的命令，如CTGT 5 10（这里5 在Int1 栏中，10 在目标值栏中）。

如果你更新评价函数，然后观察那个操作数的“数值”栏，这个数值会有两种可能情况：1) 如果违反了边界条件，那是指中心厚度小于10，那么这个厚度的实际值将被显示；2) 如果没违反边界条件，那是指中心厚度大于10，那么数值10 将被显示。

这个规则十分简单：如果违反了边界条件，则显示实际值；如果没违反边界条件，其数值将被设成目标值，因此被优化法则略过。

G0-位置连续，G1-切线连续，G2-曲率连续，G3-曲率变化率连续，G4-曲率变化率的变化率连续: j: C) e: h) c: m. t这些术语用来描述曲面的连续性。

曲面连续性可以理解为相互连接的曲面之间过渡的光滑程度。

提高连续性级别可以使表面看起来更加光滑、流畅。

G0-位置连续! W7 ~6 E! { O8 k5 p图中所示的两组线都是位置连续，他们只是端点重合，而连接处的切线方向和曲率均不一致。

这种连续性的表面看起来会有一个很尖锐的接缝，属于连续性中级别最低的一种。

$ [+ V5 q# X6 m O( J( S+ x8 {2 HG1-切线连续[2 B# O; e& R( B( R( s |1 G- j图中所示的两组曲线属于切线连续，他们不仅在连接处端点重合，而且切线方向一致(可以看到相连的两条线段梳子图的刺在接触点位置是在一条直线上的)。

用过其他PC插图软件的用户，比如CorelDraw，实际上通常得到的都是这种连续性的曲线。

* m" b' d! Q* G这种连续性的表面不会有尖锐的连接接缝，但是由于两种表面在连接处曲率突变，所以在视觉效果上仍然会有很明显的差异。

会有一种表面中断的感觉。

0 O" \9 o3 Y; u1 G" N8 W! p通常用倒角工具生成的过渡面都属于这种连续级别。

因为这些工具通常使用圆周与两个表面切点间的一部分作为倒角面的轮廓线，圆的曲率是固定的，所以结果会产生一个G1连续的表面。

如果想生成更高质量的过渡面，还是要自己动手。

$ r9 [* h) V. nG2-曲率连续图中的两组曲线属于曲率线续。

顾名思义，他们不但符和上述两种连续性的特征，而且在接点处的曲率也是相同的。

如图中所示，两条曲线相交处的梳子图的刺常度和方向都是一致的（可以为0）。

) b* D# C1 F# E0 x这种连续性的曲面没有尖锐接缝，也没有曲率的突变，视觉效果光滑流畅，没有突然中断的感觉（可以用斑马线测试）。

第四章 曲面的第二基本形式与曲面上的曲率§5 曲面上的曲率概念利用上一节所作的准备，围绕曲面弯曲状况的刻画，本节将引入曲面上的基本的和重要的曲率概念，并简要讨论相关的几何体．一．主曲率定义1 曲面 S 上的点 P 处的法曲率关于切方向的两个最值，分别称为曲面 S 在点 P 处的主曲率；使得法曲率达到最值的两个切方向，分别称为曲面 S 在点 P 处的主方向．注记1 ① Weingarten 变换的特征值和特征方向，分别是曲面的主曲率和主方向．② 当两个主曲率 1(P ) 2(P ) 时，曲面在点 P 处有且仅有正交的两组主方向，每一组的单位化向量分别就是Weingarten 变换的单位正交特征向量．而当两个主曲率 1(P ) 2(P ) 时，曲面在点 P 处的任何非零切向都是主方向，Weingarten 矩阵 (P ) 1(P )I 2 ，即 (P )1(P )g (P ) ．主曲率和主方向的计算，自然归结为Weingarten 变换的特征值和特征方向的计算，也就是Weingarten 矩阵的特征值和特征方向的计算．即：① 对于主曲率的算法，当易知Weingarten 矩阵 之时，方程为 (4.3) 式，或直接写为(5.1)I 2 0 ； 等价地，当易知系数矩阵 和 g 之时，其方程可变形为(5.2) g 0 ． ② 对于主方向的算法，各种等价算式为a a i r i 0 为主方向，即非零切方向 a 1:a 2 为主方向, (a 1, a 2) (a 1, a 2) , (a 1, a 2) (0, 0), (a 1, a 2) (a 1, a 2)g , (a 1, a 2) (0, 0) det. ⎝⎛⎭⎫(a 1, a 2) (a 1, a 2)g 0(a2)2a1a2 (a1)2g11g12g22Ω11 12 220 ．主方向所对应的微分方程通常写为(5.3)(d u2)2d u1d u2 (d u1)2g11g12g22Ω11 12 220 ．定义2若曲面S在点P处的两个主曲率相等，则称点P为曲面S上的一个脐点．若曲面S处处为脐点，则称曲面S为全脐曲面．若脐点处的主曲率为零，则称之为平点；若脐点处的主曲率不为零，则称之为圆点．注记2全脐曲面S的法曲率只与点有关而不依赖于切向选取，故只有平面和球面两类；平面上各点为平点，球面上各点为圆点．全脐曲面主方向所对应的微分方程是蜕化的恒等式．二．Gauss曲率和平均曲率定义3对于正则曲面S，其在点P处的两个主曲率的乘积 ，称为其在点P处的Gauss曲率或总曲率；其在点P处的两个主曲率的算术平均值H，称为其在点P处的平均曲率．注记3①注意到(4.4)-(4.5) 式，Gauss曲率和平均曲率分别具有用Weingarten矩阵或两个基本形式系数的表达式，分别列为(5.4) |Ω||g|LN-M2EG-F2,(5.5) H tr.2LG- 2MF NE2(EG-F2)．②主曲率方程 (4.3) 式现可改写为(5.6) 2 2H 0 ；其中H 2 ( 1 2)24≥0 ．③Gauss曲率在容许参数变换下不变；平均曲率在保向参数变换下不变，在反向参数变换下变号．④当曲面三阶连续可微时，Gauss曲率和平均曲率分别是连续可微函数；此时，两个主曲率函数(5.7) i H H2 , i 1, 2处处连续，并且在非脐点处连续可微．⑤ 平均曲率等于法曲率按切方向的积分平均值（留作习题）．⑥ 平均曲率不是等距不变量．反例如圆柱面和平面．例1 证明可展曲面的Gauss 曲率 0 ．证明 对可展曲面 S 的直纹面参数化 r (u , v ) a (u )v l (u ) ，由可展定义得知 n v 0 ，故其第二基本形式系数满足M r u n v 0 , N r v n v 0 ,于是LN - M 2 EG - F 20 ． □ 在上例中，若取准线使 a l 0 且 l 1 ，则可展曲面 S 的第一和第二基本形式系数矩阵同时对角化，Weingarten 矩阵则为特征值对角阵，而且(5.8) 1 L E, 2 0 ． 三．Gauss 映射和第三基本形式Gauss 在考察曲面的弯曲程度刻画时，注意到曲面的单位法向在单位球面上的行为对于曲面弯曲状况的反映，并进一步明确了两者的依赖程度，进而在曲面论中做出了卓有成效的工作．观察熟知的一些曲面，比如平面、圆柱面、圆锥面、椭球面、双叶双曲面、双曲抛物面等等，可以直观感受到单位法向不同的行为和曲面不同的弯曲状况之间有着密切联系．定义4 对于 C 3 正则曲面 S : r (u 1, u 2) 及其单位法向量场 n (u 1, u 2) ，曲面 S 到以原点为心的单位球面 S 2(1) 上的映射(5.9) G : S S 2(1) r (u 1, u 2) G (r (u 1, u 2)) n (u 1, u 2)称为曲面 S 的Gauss 映射．二次微分形式图4-5(5.10) Ⅲ d n d n称为曲面S的第三基本形式．性质①n1 n2 r1 r2．② (P) limU收缩至P A(G(U))A(U)，其中P U S , U为单连通区域，A(G(U)) 是G(U)⊂S2(1) 的面积，A(U) 是U S的面积．③Ⅲ 2HⅡ Ⅰ 0 ．证明①由Weingarten公式得n1 n2 [( 11r1 12r2)] [( 21r1 22r2)]r1 r2 r1 r2．②A(U)r1(U)| r1 r2| d u1d u2 ,A(G(U))r1(U) | n1 n2| d u1d u2r1(U)|K|| r1 r2|d u1d u2．而由积分中值定理，P* U使r1(U) |K||r1 r2|d u1d u2 |K (P*)|r1(U)|r1 r2|d u1d u2．故而lim U收缩至P A(G(U))A(U)limP* P|K (P*)| |K (P)|．③结论用系数矩阵等价表示为( g1)g( g1)T 2H g 0g1 2H g 0g1 g1 2H g1 I2 0(tr. ) I2 0 ．而最后的等式对于二阶方阵总成立（用特征值理论则知是显然的），用元素计算可直接验证为i k k j (tr. ) i j i ji1 1j i2 2j ( 11 22) i j ( 11 22 12 21) i j 0 ．□习题⒈对于螺面r= (u cos v , u sin v , u v) ，试求：①主曲率 1和 2；②Gauss曲率和平均曲率．⒉试求球面的Gauss曲率和平均曲率与球面半径的关系．⒊试证：平均曲率等于法曲率按切方向的积分平均值，即 2 H(P) 2πκ(P, ) d ．⒋试证：直纹面的Gauss曲率处处非正．⒌设正则曲面S: r(u1, u2) 当常数 足够小时 1 2 H 2 0 ．按参数相同作对应曲面S*: r*(u1, u2) r(u1, u2) n(u1, u2) ，其中n为曲面S的单位法向量场．试证：①S和S* 在对应点具有相同的单位法向和法线；②S和S* 在对应点的Weingarten矩阵具有关系式 * (I2 )1；③S和S* 在对应点的Gauss曲率和平均曲率具有关系式*1 2 H 2，H*H1 2 H 2；④S的曲率线对应于S* 的曲率线．⒍已知曲面S在一点处沿着一组等分周角的m个切方向的法曲率分别为 n(1), …,n (m)，m 2 ．试证：S在该点的平均曲率Hn(1)… n(m)m．⒎试证：曲面S的第三基本形式恒为零的充要条件为S是平面．工作总结-财务处长个人工作总结[工作总结-财务处长个人工作总结]工作总结-财务处长个人工作总结（范文）工作总结-财务处长个人工作总结2009-07-06 11：52财务处长个人工作总结光阴似箭、岁月如梭，转眼之间一年过去了，新的一年已经开始，工作总结-财务处长个人工作总结。

半导体晶片近边缘几何形态评价第1部分：高度径向二阶导数法1范围本文件描述了近边缘曲率高度z的径向二阶导数（ZDD）法。

本文件规定了适用于硅片或其他半导体材料晶片近边缘几何形态的评价方法之一：近边缘曲率。

2规范性引用文件下列文件中的内容通过文中的规范性引用而构成本文件必不可少的条款。

其中，注日期的引用文件，仅该日期对应的版本适用于本文件；不注日期的引用文件，其最新版本（包括所有的修改单）适用于本文件。

GB/T 14264 半导体材料术语GB/T 25915.1-2010 洁净室及相关受控环境第1部分：气洁净度等级3术语和定义GB/T 14264界定的术语和定义适用于本文件。

3.1近边缘曲率 near-edge curvature；ZDD（radial double derivative of z（height））使用晶片高度的阵列数据获得垂直于硅片中位面一系列Z坐标的径向二阶导数所描述的参数。

3.2边缘去除 edge exclusion nominal；EE从合格质量区边界到晶片物理周边的距离。

4方法原理将晶片按照不同的半径和圆心角划分为若干扇形区域，选取每个扇形区域中高度数据阵列，逐一计算沿半径方向的二阶导数，从而定量评价半导体晶片的近边缘形态。

5干扰因素5.1 测试过程中，机械装置的精度会影响测试位置，从而影响采样点的空间位置，会导致测试结果偏差。

5.2空间分辨率不够、错位或噪声等数据缺陷，会导致测试结果偏差。

5.3高度数据阵列的间距、曲率上扇形分区的个数和曲率微分方法会影响ZDD计算的噪声。

5.4 晶片边缘的卷曲特性（的太小，则ZDD　Edge-Roll-Off）导致ZDD随着半径增加而快速变化，如果边缘去除设置的输出不稳定从而干扰评价的客观性，因此需要建立满足实际应用需求的边缘去除。

5.5晶片直径、切口尺寸等形状误差会影响测试采样点的空间位置，从而导致测试结果偏差。

5.6晶片洁净度可能会对扫描结果产生噪声干扰，从而导致测试结果偏差。

曲率曲率是数学中一个重要而深奥的概念，它被广泛应用于多个学科领域，包括物理学、几何学和工程学等。

本文将对曲率的定义、性质和应用进行探讨，帮助读者更好地理解这一概念。

曲率是描述曲线和曲面弯曲程度的一个数值指标。

一般来说，曲线的曲率是指曲线在某一点上几何形状的变化程度。

曲面的曲率则是指曲面在某一点上的沿不同方向的几何形状的变化程度。

对于平面上的曲线来说，曲率可以用曲率半径来表示。

曲率半径是一个与曲线曲率成反比的数值，如果曲线越弯曲，曲率半径就越小。

通过计算曲率半径，我们可以对曲线的弯曲程度进行定量分析。

当曲率半径为无穷大时，曲线是直线；反之，当曲率半径为零时，曲线上的任意一点是奇点。

曲率半径可以在物理学、几何学和工程学等领域中得到广泛应用。

对于曲面来说，曲率的计算稍微复杂一些。

曲面上的曲率可以通过计算曲面上的两个主曲率和平均曲率来获得。

主曲率是在点上切平面内的两个正交方向上的曲率，平均曲率是两个主曲率的平均值。

曲面上的曲率可以帮助我们确定曲面上的凸凹部分，从而在工程设计中提供重要的参考信息。

曲率在物理学中有着广泛的应用。

在牛顿力学中，弯曲轨道上的物体会受到曲率半径的影响，从而产生向心力。

在相对论中，曲率可以描述时空的弯曲，是爱因斯坦场方程中的核心概念之一。

曲率在光学中也有着重要的应用，它可以帮助我们理解光线在光学元件中的传播路径。

除了物理学外，曲率在几何学和工程学中也扮演着重要角色。

在几何学中，曲率是研究曲线和曲面性质的基本工具，它可以帮助我们理解和刻画抽象的几何对象。

在工程学中，曲率可以用来描述和分析工程结构的变形情况，从而为工程设计提供依据。

总之，曲率是一个重要的数学概念，它在多个学科领域中有着广泛的应用。

通过对曲率的理解和研究，我们可以更好地揭示自然界和人工构造物的性质，为科学研究和工程实践提供有力支持。

希望通过本文的介绍，读者能对曲率有一个初步的认识，并进一步探索曲率在各个学科领域中的应用。