地图投影判别

现代地图学教程 第3章 地图投影及其判别与变换
§3 常用地图投影
3.1 世界地图常用的地图投影
3.1.3 正轴等角圆柱投影（墨卡托投影） 3、等角航线
在该投影图上，不仅保持了方向和相对位置的正确，而且能使等角航线表 示为直线，因此对航海、航空具有重要的实际应用价值。只要在图上将航 行的两点间连一直线，并量好该直线与经线的夹角，一直保持这个角度即 可到达终点。
现代地图学教程 第3章 地图投影及其判别与变换
§3 常用地图投影
3.1 世界地图常用的地图投影
3.1.1 等差分纬线多圆锥投影
2、变形特点
• 该投影是属于面积变形不大的任意投影，从 整体构图上有较好的球形感； • 陆地部分变形分布比较均匀，其轮廓形状比 较接近真实，并配置在较为适中的位置，完整 地表现了太平洋及沿岸国家，突出了我国与太 平洋各国之间的联系； • 中央经线和±44纬线的交点处没有角度变形 ，我国境内绝大部分地区的角度变形在10以 内，只有少数地区可达13左右 ； • 面积比等于1的等变形线自西向东贯穿我国中 部，我国境内绝大部分地区的面积变形在10% 以内 。
现代地图学教程 第3章 地图投影及其判别与变换
§4 地图投影的选择、判别与变换
4.1 地图投影选择的依据
3. 地图的内容 主题和内容不同，对投影的要求也不同。
• 要求方向正确，应选择等角投影 • 要求面积对比正确，应选择等积投影 • 教学或一般参考图，要求各方面变形都不大，则 应选择任意投影
现代地图学教程 第3章 地图投影及其判别与变换
现代地图学教程 第3章 地图投影及其判别与变换
§4 地图投影的选择、判别与变换
4.1 地图投影选择的依据
2.制图比例尺 不同比例尺地图对精度要求不同，投影亦不同。 大比例尺地形图，对精度要求高，宜采用变形小的投影

地图学 实验教材李永青 主编资源与环境学院土地资源教研室目录实验一：地图投影的判别 (2)实验二：用等比数列法进行河流的概括、选取 (4)实验三：利用点状符号设计分区统计图表 (5)实验一 地图投影的判别一、目的辨认各类地图投影是为了了解地图投影的变形性质和分布特点，以便于正确使用地图。

通过实习学会判别地图投影的方法。

二、用具地图集、两脚规、直尺、钱币、透明纸。

三、要求从地图集中选择一些常见的地图投影加以辨认，具体包括世界图、东西半球、南北半球、大洲图和一些分国图。

要求将辨认的结果填入记录表格内。

四、实习内容地图投影是地图的数学基础，它直接影响地图的使用，地图是地理工作者不可缺少的工具，有很多地理知识是从地图上获得的，如果在使用地图时不了解投影的特性往往会得出错误的结论。

例如：在小比例尺等角或等积投影图上式算距离，在等角投影图上对比不同地区的面积以及在等积投影图上观察各地区的形状特征等都会得出错误结论。

目前国内外出版的地图，大部分都注明投影的名称。

有的还附有有关投影的资料，这对于使用地图当然是很方便的。

但是也有一些地图没注明投影的名称和有关说明。

因此，需要我们运用有关地图投影的知识来判别投影。

地图投影的辨认，主要是对小比例尺地图而言，大比例持往往是属于国家地形图系列，投影资料一般易于查知。

另外由于大比例尺地图包括的地区范围小，不管采用什么投影，变形都是很小的，使用时可忽略不计。

地图投影的辨认是一项比较复杂的工作，有时比计算一个具体投影还要困难，同时，也不是所有的投影都能采用辨别的方法。

但辨认一般的常用投影并不是很困难的通常按下列步骤进行辨认。

1.根据地图上经纬线的形状确定投影类型。

首先对地图经纬线网作一般观察，应用所学过的各类投影的特点确定其投影是属于哪一类型，如方位、圆柱、圆锥还是伪圆锥、伪圆柱投影等。

判别经纬线形状的方法如下：直线只要用直尺比量便可确认，判断曲线是否为圆弧可将透明纸覆盖在曲线之上，在透明纸上沿曲线按一定间隔定出三个以上的点，然后沿曲线移动透明纸，使这些点位于曲线的不同位置，如这些点处处都与曲线吻合，则证明曲线是圆弧，否则就是其他曲线。

ds ' m ds
Vm m 1
= 0 不变 > 0 变大 < 0 变小
2)面积变形 面积比和面积变形： 投影平面上微小面积（变形 椭圆面积）dF′与球面上相应的微小面积（微小圆面 积）dF之比。
P 表示面积比 Vpቤተ መጻሕፍቲ ባይዱ表示面积变形
dF’
πa * r * b * r
P=
dF
=
π r2
= a*b
其中，等距投影是在特定方向上没有长度变形的任 意投影（m=1）。
§3
一.
地图投影的选择
地图投影的选择依据
1.制图区域的地理位置、形状和范围
2.制图比例尺
3.地图的内容
4.出版方式
1.制图区域的地理位置、形状和范围
2.制图比例尺
不同比例尺地图对精度要求不同，投影亦不同。 大比例尺地形图，对精度要求高，宜采用变形 小的投影。
测量学与地图学
电子教案
第七章、地图投影
第七章、地图投影
§1 、地图投影及其变形
§2 、地图投影的分类
§3 、地图投影的选择
§4 、地图投影的判别
§1 、地图投影及其变形
一 、地图投影
按照一定的数学法则，将地球椭球面上的经纬网转换 到平面上，使地面点位的地理坐标 （λ、φ） 与地图上相 对应点位的平面直角坐标（x,y） 或极坐标 (δ,ρ)间，建立 起一一对应的函数关系：
③等距割圆锥投影
条件：m = 1 ;
原苏联出版的苏联全图，采用(j1 = 47 ° ； j2 = 62 °)的该投影。
3. 伪圆锥投影
由法国彭纳（R. Bonne）在圆锥投影的基础上，根据某些 条件改变经线形状设计而成，故又称彭纳投影(等积投影)。

地图投影的判别与选择第五节地图投影的判别与选择⼀、地图投影的判别地图投影是地图的数学基础，它直接影响地图的使⽤。

地图是地理⼯作者不可缺少的⼯具，有很多地理知识是从图上获得的。

如果在使⽤地图时，不了解投影的特性，往往会得出错误的结论。

例如在⼩⽐例尺等⾓或等积投影图上量算距离，在等⾓投影图上对⽐不同地区的⾯积，以及在等积投影图上观察各地区的形状特征等。

⽬前，国内外出版的地图上⼤多数都注明地图投影名称，这对于使⽤地图，当然是很⽅便的。

但是，也有⼀些地图不注明投影名称和有关说明，因此，我们必须运⽤地图投影的知识，根据不同投影的特征——经纬线形状，结合制图区域所在的地理位置、轮廓形状及地图的内容和⽤途等，综合进⾏分析、判断和进⾏必要的量算来判别它们。

地图投影的判别，主要是对⼩⽐例尺地图⽽⾔。

⼤⽐例尺地图往往是属于国家地形图系列，投影资料⼀般易于查知。

另外由于⼤⽐例尺地图包括的地区范围⼩，不管采⽤什么投影，变形都是很⼩的，在使⽤时可以忽略不计。

判别地图投影⼀般是先根据经纬线⽹形状确定投影种类，如⽅位、圆柱、圆锥等，其次是判定投影的变形性质，如等⾓、等积或任意投影。

（⼀）确定投影种类对于常见的地图投影，⼀般还是⽐较容易确定它的种类的，表2-16列出⼀些常见投影，供判别时参考。

判别经纬线形状的⽅法如下：直线只要⽤直尺量度，便可确定。

判断曲线是否为圆弧，可以将透明纸覆盖在曲线之上，在透明纸上沿曲线按⼀定间隔定出三个以上的点，然后沿曲线移动透明纸，使这些点位于曲线的不同位置，如这些点处处都与曲线吻合，则证明曲线是圆弧，否则就是其他曲线。

判别同⼼圆弧与同轴圆弧，则可以量测相邻圆弧间的垂线距离，若处处相等则为同⼼圆弧，否则是同轴圆弧。

（⼆）确定投影的变形性质当已确定投影的种类后，对有些投影的变形性质是⽐较容易判定的。

例如已确定为圆锥投影，那么只须量任⼀条经线上纬线间隔从投影中⼼向南、北⽅向的变化就可以判别变形性质：如果相等，则为等距投影；逐渐扩⼤，为等⾓投影；逐渐缩⼩，为等积投影。

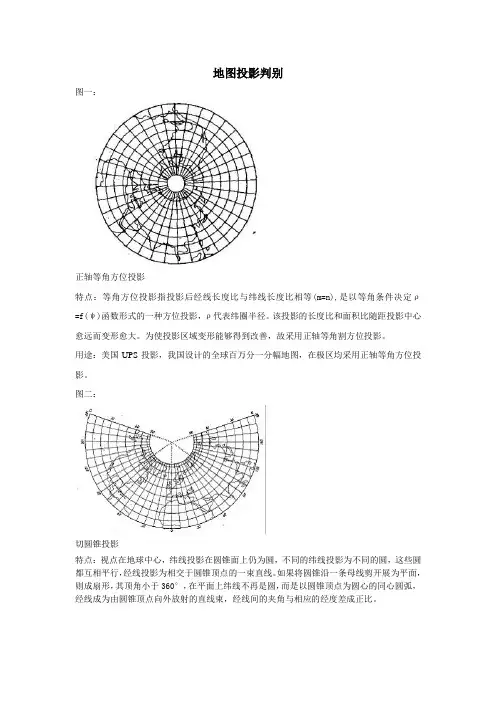
地图投影判别图一：正轴等角方位投影特点：等角方位投影指投影后经线长度比与纬线长度比相等(m=n),是以等角条件决定ρ=f(ψ)函数形式的一种方位投影，ρ代表纬圈半径。

该投影的长度比和面积比随距投影中心愈远而变形愈大。

为使投影区域变形能够得到改善，故采用正轴等角割方位投影。

用途：美国UPS投影，我国设计的全球百万分一分幅地图，在极区均采用正轴等角方位投影。

图二：切圆锥投影特点：视点在地球中心，纬线投影在圆锥面上仍为圆，不同的纬线投影为不同的圆，这些圆都互相平行，经线投影为相交于圆锥顶点的一束直线。

如果将圆锥沿一条母线剪开展为平面，则成扇形，其顶角小于360°，在平面上纬线不再是圆，而是以圆锥顶点为圆心的同心圆弧，经线成为由圆锥顶点向外放射的直线束，经线间的夹角与相应的经度差成正比。

用途：由于圆锥投影具有上述的变形分布规律，因此该投影适于编制处于中纬地区沿纬线方向东西延伸地域的地图，同时，圆锥投影的经纬网又比较简单，所以在中纬度的国家广泛应用。

图三：等距圆锥投影特点：等距圆锥投影上虽然具有长度、面积和角度变形，但变形值却比较小，它的角度变形小于等积圆锥投影，面积变形小于等角圆锥投影。

用途：例如苏联出版的苏联全图。

说明：图二与图三都属于圆锥投影。

圆锥投影的各种变形都是纬度ψ的函数，随纬度变化而变化，而与经度λ无关。

圆锥面与球面相切的切线，或圆锥表面与球面相割的两条割线，即标准纬线。

距标准纬线愈远，其变形愈大。

标准纬线外的变形分布规律均为正变形，而标准纬线之间呈负变形。

图四：正轴等积切圆柱投影特点：正轴等面积切圆柱投影又称“兰勃特等积圆柱投影”。

设将圆柱投影面与球面上赤道相切，按等面积条件，用数学方法将经纬线网投影到圆柱面上。

经线为等距平行直线，纬线为垂直经线的平行直线，纬线间隔随纬度增加而缩小。

角度与长度变形在高纬度地带很显著。

用途：适用于赤道附近地区的地图。

图五：等角圆柱墨卡托投影特点：在等角圆柱投影中，球面上微分圆投影后的图形保持圆形，即一点上的长度比向任何方向均相等。

墨卡托投影多被航海图所采用，因为： 等角航线被投影为直线，便于航迹绘算。 等角性质投影，保持图上方位与实地一致。 经纬线形状简单，便于绘制。
我国海图上多采用割圆柱投影。
不同的海域，选用不同的标准纬线。
1∶5万成套海图的标准纬线
地 区 纬 度 标准纬线
3930 38 28 24 不含台湾
几 何 投 影

按投影条件分为：——非几何投影
伪方位投影、伪圆柱投影、伪圆锥投影、多圆锥投影
4 地图投影的分类、判别和选择
4.1 地图投影的分类

根据几何投影的几个特性组合命名
例：横轴等积方位投影、正轴等角割圆锥投影、正
轴等角切圆柱投影（墨卡托Mercator投影）
N N N
S
S
S
正轴 切圆柱投影
4 地图投影的分类、判别和选择
4.1 地图投影的分类 以正轴为例

圆锥投影
经线:为放射直线 纬线:为同心圆弧。 等距：纬距相等。 等积：纬距从图幅中央向南北 逐渐缩小。 等角：纬距从图幅中央向南北 逐渐扩大。

4 地图投影的分类、判别和选择
4.1 地图投影的分类

圆锥投影
标准线：切线或割线无变形。 等变形线：以投影中心为圆心呈同心圆分布。正轴时等 变形线平行于纬线。
在两条标准纬线之间为负向变形，两条标准纬线以外是正向变形。
标准纬线以北的变形增长快于南边。
等角割圆锥投影能减小制图区域长度变形，有效改善变形分布。所以，在 制图实践中，常用等角割圆锥投影。
正轴等积圆锥投影
亚尔勃斯投影，Albers’

Projection
全国性自然地图中的各种分布图、类型图、区划图以及全国性 社会经济地图中的行政区划图、人口密度图、土地利用图

地图投影判别主要确定下列几个问题： （1）投影的种类——属方位、圆柱、圆锥 ）投影的种类——属方位、圆柱、圆锥 或其他投影； （2）变形性质——属等角、等积、等距或 ）变形性质—— ——属等角、等积、等距或 任意投影； （3）投影方式——相切、相割，标准点、 ）投影方式——相切、相割，标准点、 线的位置。
1、投影种类的确定
主要根据经纬网的形状来确定。 要求熟悉各种投影经纬网的形状。 主要注意： （1）直线与曲线（用直尺量比） （2）圆弧与曲线（用点迹法） （3）同心圆弧与同轴圆弧（比较两弧间距） （4）正轴方位投影与正轴圆锥投影（经线夹 角与对应的经度差）
2、确定投影变形性质
概略方法：通过经线上相同纬度差两纬线的间 距变化来确定，前提是找到标准线，分清切投 影或割投影。 精确方法：通过量算图上经线长度和按比例地 球上对应经线的长度，得到经线上的长度比M 球上对应经线的长度，得到经线上的长度比M， 再量算图上纬线的长度和按比例地球上的对应 纬线长度，得出纬线的长度比N 再看M 纬线长度，得出纬线的长度比N。再看M、N之 间的关系，判断投影变形 的性质。
二、投影的选择
投影的选择受很多因素的影响，主要有： 1、地图内容和用途 2、制图区域的大小 3、制图区域形状和地理位置 4、地图的出版方式 5、地图内容转绘和图面配置
一、地图投影的Βιβλιοθήκη 别目前国内外出版的地图大都注明了地图 投影的名称，有利于地图的使用。但也有 部分地图不注明投影，这就要运用地图投 影知识进行判别。 大比例尺地图往往属于国家地形图系列， 投影是固定的、明确的，资料也易于查找。 有些大比例地图区域小，无论何种投影， 变形均小，可以忽略不计，无需判别。 所以，地图投影的判别主要是针对小比 例尺地图，即小于1:100万的地图。 例尺地图，即小于1:100万的地图。

进阶练习题
2. 如何判断地图投影的类型？
答案：判断地图投影的类型可以通过观察地图上的经纬线形状和分布特点。例如，如果经纬线呈现为直线或近似直线，并且 没有明显的角度或面积变形，则可能是方位投影或圆柱投影；如果经纬线呈现为曲线或折线，并且有明显的角度或面积变形 ，则可能是圆锥投影或多圆锥投影。
进阶练习题
研发更精确的投影算法
随着地理信息系统（GIS）和遥感技术的发展，对地图投 影的精度要求越来越高，需要研发更精确的投影算法以满 足实际需求。
探索新型投影方式
目前常见的投影方式有等角投影、等面积投影和任意投影 等，未来可以探索更多新型的投影方式，以满足不同应用 场景的需求。
考虑地球模型的影响
地球是一个近似于椭球的球体，不同的地球模型对地图投 影的结果会产生影响，未来需要深入研究地球模型对地图 投影的影响，以提高投影精度。
1. 什么是地图投影？
答案：地图投影是将地球表面上的经纬网按照一定的数学法则转绘到平 面上的过程。
2. 地图投影有哪些基本类型？
基础练习题
答案
地图投影的基本类型包括方位投影、圆柱投影、圆锥投影和多圆锥投影等。
答案
等角投影是指保持角度不变的投影方式，其特点是变形小，但面积和长度变形 较大；等面积投影是指保持面积不变的投影方式，其特点是面积不变，但角度 和长度变形较大。
3. 如何纠正地图投影变形？
答案：纠正地图投影变形的方法包括多项式映射、共形映射和物理映射等。具体方法是根据地图的具 体情况和需求，选择合适的纠正方法，对原始地图进行投影变换，以减小或消除投影变形。
进阶练习题
4. 如何应用地图投影于实际工作？
答案：地图投影在实际工作中的应用非常广泛，例如在地理 信息系统、导航、气象预报、军事指挥等领域中都需要用到 地图投影。通过选择合适的地图投影，可以更好地满足实际 工作的需求，提高地图的精度和使用价值。

距 离 最 短
1)何谓墨卡托投影?
∗2
2
墨卡托投影－正轴等角圆柱投影
• 即设想与地轴方向一致的圆柱与地球 相切或相割，将球面上的经纬网按等 角的条件投影到圆柱面上,然后把圆柱 面沿着一条母线剪开并展成平面。
2)经纬网形状及经纬距变化规律
2 3
• 经线和纬线是两组相互垂直的平行直线 • 经线间隔相等 • 纬线间隔由赤道向两极逐渐扩大
• 广义的多圆锥投影
•即指纬线为同轴圆弧的投影。
（1）普通多圆锥投影
4
8 • 投影条件：m0=1，n=1 • 经纬网特征： • 变形情况： • 属于任意投影，中央经线是一条没有变 形的线，离开中央经线愈远变形愈大。
• 用途：地球仪
（2）等差分纬线多圆锥投影
4
9 • 这是中国地图出版社于1963年设计的一种任意 性质的，不等分纬线的多圆锥投影。
– 中央经线为直线，其余的经线为椭圆曲线。 – 纬线是间隔不等的平行直线，其间隔从赤道向两极逐
渐减小。同一纬线上的经线间隔相等。 – 等积投影。
（3） 伪圆柱投影——摩尔威特投影
4
4 • 用途：世界地图、东西半球图、大洋图
（4） 伪圆柱投影——古德投影
4 5
• 设计思想：对摩尔维特等积伪圆柱投影进行“分瓣投
4 6
• 特点：海/陆完整（尽量
减少投影变形，而不惜
图面的连续性）
• 用途：世界地图
2. 多圆锥投影
4 7
• 狭义的多圆锥投影
•是指用多个不同锥顶角的圆锥与地 球相切，并获得若干以各标准纬线 为中心的投影带，然后将这些投影 带沿着某一经线连接起来。由于圆 锥顶点不是一个，所以纬线投影为 同轴圆弧。

– 椭圆与圆的半径不等，且在 某一点附近随方向的改变而 变化，长度变形； – 椭圆面积与圆面积为不等面 积的变形； – A′与A位置不同，角度产生 了变形；由圆变为椭圆，形 状发生改变.
24
• （2）等变形线
• 等变形线 投影面上变形值相等的点的连线。用来 显示地图投影变形的大小和分布状况。不同投影 有不同形状的等变形线
s i n ( ' ) a b t a n 将两式相除，得： c o s c o s ' a
sin( ') ab sin( ') ab
显然当（ + ′ ）= 90°时，右 a b s i n ( ' ) s i n ( ' )端取最大值，则最大方向变形： a b
11
极值长度比和主方向
– 极值长度比 投影后,保持正 交的一对直径即构成变形椭 圆的长短轴。称为极大和极 小长度比。 – 通常用ａ和ｂ表示，是个变 量，在不同点上其值不等； 在同一点上也随方向不同而 变化。
12
– 经纬线为正交，经线长度比（ｍ）和纬 线长度比（ｎ）即为极大和极小长度比。 – 经纬线投影后不正交，其交角为θ，则 ｍ、ｎ和ａ、ｂ之间具有下列关系： m2＋n2＝ａ2＋ｂ2 mnsinθ＝ａｂ （ａ＋ｂ）2＝m2＋n2＋2mnsinθ （ａ－ｂ）2＝m2＋n2－2 mnsinθ
• P102 常用投影的等变形线分布
d F' π a b P 2 ab d F π l
Vp p 1
= 0 不变 > 0 变大 < 0 变小
P = a· b = m ·n P = m ·n ·sinq
(q = 90) (q ≠ 90)
面积比是变量，随位置的不同而变化。

22
• 投影前以O为圆心，OM为半径微分 圆的方程式为：
ｘ2＋ｙ2＝ｒ2
投影后得到以O′为中心，θ为交角的
两共轭直径为斜坐标轴的椭圆方程
式
x'2 a2
y'2 b2
1
23
• 比较变形椭圆与微分圆，
– 椭圆与圆的半径不等，且在 某一点附近随方向的改变而 变化，长度变形；
– 椭圆面积与圆面积为不等面 积的变形；
长度比是变量，随位置和方向的变化而变化。
11
极值长度比和主方向
– 极值长度比 投影后,保持正 交的一对直径即构成变形椭 圆的长短轴。称为极大和极 小长度比。
– 通常用ａ和ｂ表示，是个变 量，在不同点上其值不等； 在同一点上也随方向不同而 变化。
12
– 经纬线为正交，经线长度比（ｍ）和纬 线长度比（ｎ）即为极大和极小长度比。
面积比是变量，随位置的不同而变化。
16
（3） 角度变形 ：
• 投影面上过一点的任意两方向线的夹角α′与地面上相
应两方向线的夹角α之差值，以α′－α表示。设ω/2代
表α－α′
最大角度变形:
sin ab
或
2 ab
si n
2
m2n22msniqn m2n22msniqn
– 角度变形是形状变形的具体标志。
第三章 地图投影及其判别与变换
第一节 地图投影基本概念
• 一、地图投影的基本概念 • 1.地图投影的科学内涵 • 地图是纸质平面图，而地球椭球面是个曲
面。 • 将曲面展开，使其成为没有破裂和重叠的
平面。
2
3
2.定义
• 地图投影：在球面与平面之间建立点与点 之间对应函数关系的数学方法。

为坐标轴，推导其投影变形。
（3）角度变形
（3）角度变形
（3）角度变形
' (180 2 ') (180 2 )
X A
2( ')
即： ( ')
Y
2
将上式代入（2-14）式得：
sin sin（ '）= a b
2
ab
若已知经线长度比m，纬线长度比n，以及经
纬线夹角q，则角度最大变形公式可写成：
❖ 因此，通过对地图与地球仪上经纬网的比较， 可以发现，地图投影变形表现在长度、面积和 角度三方面。
地球仪与地图上经纬网比较
a
b
纬线长度a 经线长度b、c 同一纬线上，经差相同的纬线弧长c
c 同一经线上，纬差相同的经线弧长 同纬度带，同经差构成球形梯面b、 c 经纬线正交否b、c
1.变形概念
❖ 地图投影变形是球面转化成平面的必然结果， 没有变形的投影是不存在的。
若投影后，经纬线不正交，则：
P = a·b= m ·n ·sinq (q ≠ 90)
面积比和面积变形因位置不同而异
（3）角度变形
❖ 地面上任意两条方向线的夹角а，与经过投影后的相应 两方向线夹角а′之差值，称为角度变形
❖ 投影面上经纬线夹角变形ε为： ε＝θ′-90°
❖ 过地面上一点可以引无数的方向线，由两条方向线组 成的角度有无数个。
❖ 利用变形椭圆的图解和理论，我们就能更为科 学和准确地阐述地图投影的概念、变形的性质 及变形大小
微分圆何以投影后为椭圆
❖ 经线CD和纬线AB为直角坐标系X、Y，圆心 0为直角坐标系原点
x' x
m 为经线长度比；
y' y
n

一、高斯投影
（1）基本概念：
如下图所示，假想有一个椭圆柱面横套在地球椭球体外面，并与某一 条子午线（此子午线称为中央子午线或轴子午线）相切，椭圆柱的中 心轴通过椭球体中心，然后用一定投影方法，将中央子午线两侧各一 定经差范围内的地区投影到椭圆柱面上，再将此柱面展开即成为投影 面，此投影为高斯投影。高斯投影是正形投影的一种。
（2）分带投影
高斯投影 6 带：自0 子午线起每隔经差 6 自西向东分带，依次编号
1,2,3,…。我国6 带中央子午线的经度，由75 起每隔 6 而至135, 共计 11带（13～23带），带号用 n 表示，中央子午线的经度用L0 表示，它 们的关系是L0 6n 3 ,如下图所示。
高斯投影3带：它的中央子午线一部分同 6 带中央子午线重合，一部 分同6 带的分界子午线重合，如用 n表示3 带的带号，L 表示 3带中
（4）高斯平面投影的特点：
（5） 椭球面三角系化算到高斯投影面
将椭球面三角系归算到高斯投影面的主要内容是：
➢将起始点的大地坐标归算为高斯平面直角坐标；为了检核还 应进行反算，亦即根据反算。
➢通过计算该点的子午线收敛角及方向改正，将椭球面上起算 边大地方位角归算到高斯平面上相应边的坐标方位角。
➢通过计算各方向的曲率改正和方向改正，将椭球面上各三角 形内角归算到高斯平面上的由相应直线组成的三角形内角。
➢通过计算距离改正，将椭球面上起算边的长度归算到高斯平 面上的直线长度。
➢当控制网跨越两个相邻投影带，需要进行平面坐标的邻带换 算。
正形投影的一般条件
高斯投影首先必须满足正形投影的一般条件。图a为椭球面，图b为它 在和p2平，面其上坐的标投均影已。注在在椭图球面上上，d有S为无大限地接线近的的微两分点弧和长，p2 ，其投方影位后角为为AP。1 在投影面上，建立如图b所示的坐标系，dS 的投影弧长为 ds 。

关于地图学中几种投影的总结类型一、方位投影方位投影是以平面作为投影面，使平面与地球表面相切或相割，并将球面上的经纬线投影到平面上所得到的图形。

方位投影可分为透视方位投影类和非透视方位投影两。

根据投影面和地球球面相切位置的不同，透视投影可分为三种①当投影面切于地球极点时，称为正轴方位投影。

②当投影面切于赤道时，称为横轴方位投影。

③当投影面切于既不在极点也不在赤道时，称为斜轴方位投影。

一、正轴方位投影投影中心为极点，纬线为同心圆，经线为同心圆的半径，两条经线间的夹角与实地相等。

等变形线都是以投影中心为圆心的同心圆。

包括等角、等距变形性质，主要用于制作两极地区图。

1.正轴等角方位投影平射正轴方位投影又叫等角方位投影或球面投影。

投影条件：视点位于球面上，投影面切于极点。

特点：①纬线投影为以极点为圆心的同心圆，纬线方向上的长度比大于1。

赤道上的长度变形比原来扩大1倍。

②经线投影为以极点为圆心的放射性直线束，经线夹角等于相应的经差，沿经线方向上的长度比大于1，赤道上各点沿经线方向上的长度变形比原来扩大1倍。

③这种投影的误差分布规律是，由投影中心向外逐渐增大。

④经纬线投影后，仍保持正交，所以经纬线方向就是主方向，又因为m = n，即主方向长度比相等，⑤没有角度变形，但面积变形较大，在投影边缘面积变形是中心的四倍。

2.正轴等距方位投影等距方位投影属于任意投影，它既不等积也不等角。

投影后经线保持正长，经线上纬距保持相等。

角度、面积等变形线为以投影中心为圆心的同心圆。

在此投影中，球面上的微圆投影为椭圆，且误差椭圆的长半径和纬线方向一致，短半径与经线方向一致，并且等于微圆半径r 又由于自投影中心，纬线扩大的程度越来越大，所以变形椭圆的长半径也越来越长，椭圆就越来越扁了。

等距正轴方位投影常用来做两极的投影。

二．横轴方位投影平面与球面相切，其切点位于赤道上的任意点。

特点：通过投影中心的中央经线和赤道投影为直线，其他经纬线投影后都是对称于中央经线和赤道的曲线1.横轴等距方位投影其特点是在中央经线上从中心向南向北，纬线间隔相等；在赤道上，自投影中心向西，向东，经线间隔是逐渐扩大的。

3)已知彭纳投影内应有一条纬线和所有的经线相垂 直，所以只有这条纬线能满足m = n =1的条件， 经观察与各经线交角最接近于直角的是在南纬20º 处。通过进一步的量算，得知在1、2和3点处的 沿经线长度比m也接近1，由于它满足了m = n =1 的条件，从而证实了南纬20º处的纬线与各经线均 呈正交。其次，中央经线上各纬线所截取的线段 相等，故mc=1，这样就完全符合彭纳投影的特点。 通过如上反复分析验证，始可确认为彭纳投影， 其标准纬线位于南纬20º处。
1．首先确定投影系统，如属方位、圆柱或圆锥；或为多圆锥、伪方位 投影等；
2．其次了解投影的变形性质，如属等角、等面积或任意、等距离投影 等；
3．还需确定投影形式：诸如投影常数、标准纬线和无变形点的地理位 置，投影面和地球表面相切或相割的位置以及投影中心的经纬度等。
一、 确定地图投影系统
假如某一地图投影的经纬线形状已被认定，其投影系统便 不难判别。我们已了解到经纬线形状不外乎是直线、二次 曲线、正弦曲线及其它曲线等，现分别简述于下： 1．经纬线形状为直线时，还应区分成等距离平行直线、 非等距平行直线或交于一点的直线束； 2．经纬线形状为二次曲线时，应区分出是圆、椭圆、双 曲线或抛物线。如肯定无疑是圆，还要进一步识别是属于 同心圆还是同轴圆。我们可以采用几何的或图解的方法来 识别各类曲线。 3．正弦曲线也是通过图解的方法予以判别的，其它在伪 投影中的各类曲线一般较难识别，需作特殊方法的验证。
第二节 地图投影的选择
• 制作地图过程中选择地图投影是一个重要的问题，投 影的性质与经纬网形状不仅对于编制地图的过程有影 响，而且对以后使用地图也有很大的影响。
• 现代制作地图的方法和过程日益完善，用于编图资料 的地图质量愈好，对所编图的要求也愈高。因此对于 地图数学基础，其中主要的一个要求——地图投影的 要求也愈高。

地图投影的判别不同类型的投影通常具有不同的经纬线特点，因此投影类型可以通过判别经纬线网的形状来确定。

在确定投影类型时，准确区分经纬线是直线与曲线、同心圆弧与同轴圆弧，是非常重要的。

不同的投影具有不同的变形特点。

判别投影的类型和变形性质，是正确使用地图的基础。

由于大比例尺地图通常属于国家基本比例尺地形图，投影简单，易于查知，且包含的制图区域小，无论采用何种投影，变形都很小。

因此，地图投影的判别主要是针对小比例尺地图而言。

判别地图投影，一般先是根据经纬线网的形状确定投影的类型，如方位投影、圆柱投影、圆锥投影等；然后是判定投影的变形性质，如等角、等积或任意投影。

1、确定投影类型不同类型的投影通常具有不同的经纬线特点，因此投影类型可以通过判别经纬线网的形状来确定。

在确定投影类型时，准确区分经纬线是直线与曲线、同心圆弧与同轴圆弧，是非常重要的。

直线只要用直尺比量，便可确定。

判断曲线是否为圆弧，可用点迹法，即将透明纸覆盖在曲线上，在透明纸上沿曲线按一定间距定出3至6个点，然后沿曲线徐徐向一端移动透明纸，若这些点始终都不偏离此曲线，则证明此曲线是圆弧，否则就是其它曲线。

判别纬线是同心圆弧还是同轴圆弧，可量算相邻圆弧间的纬线间隔（即经线长），若处处相等，则证明这些圆弧为同心圆弧，否则便是同轴圆弧。

此外，由于正轴圆锥投影与正轴方位投影的经纬线形状有时可能完全相同，因此，在判别时，可以通过以下两种方法来区分：一是量算相邻两条经线的夹角是否与实地经差相等。

若相等则为方位投影，否则就是圆锥投影；二是分析制图区域所处的地理位置。

若制图区域在极地一带，则为正轴方位投影，若在中纬度地带，则为圆锥投影。

2、确定投影变形性质在确定了投影的类型之后，可以进一步根据经纬线网的图形特征，确定投影的变形性质。

通常，中央经线上纬线间距的变化规律是确定投影变形性质的重要标志。

如已确定某投影为圆锥投影，那么中央经线上的纬线间距如果相等，则为等距投影；如从中部向上下两端逐渐扩大，为等角投影；如从中部向上下两端逐渐缩小，为等积投影。

19世纪，地图投影主要保证大比例尺地图 的数学基础，以适应军事制图发展和地形测量 扩大的需要。19世纪还出现了高斯投影，它是 德国高斯设计提出的横轴等角椭圆柱投影，这 种投影法经德国克吕格尔加以补充，成为高斯 -克吕格尔投影。19世纪末期以后俄国一些学 者对投影作了较深入地研究，对圆锥投影常数 的确定提出了新见解，又提出了根据已知变形 分布推求新投影和利用数值法求出投影坐标的 新方法。20世纪50年代以来中国提出了双重方 位投影、双标准经线等角圆柱投影等新方法。 20世纪60年代以来，美国学者对地图投影的研 究结果，提出空间投影、变比例尺地图投影和 多交点地图投影，为人造地球卫星等提供了所 需的投影。
GIS中地图投影的重要性
• 地图投影定义：就是指建立地球表面（或 其他星球表面或天球面）上的点与投影平 面（即地图平面）上点之间的一一对应关 系的方法。即建立之间的数学转换公式。 它将作为一个不可展平的曲面即地球表面 投影到一个平面的基本方法，保证了空间 信息在区域上的联系与完整。这个投影过 程将产生投影变形，而且不同的投影方法 具有不同性质和大小的投影变形。
3、根据投影面与地球表面的相关位置分类： ①正轴投影②斜轴投影③横轴投影 4、几何投影中根据投影面与地球表面的关系： ①切投影②割投影
常见种类 有墨卡托投影、高斯-克吕格投影、斜轴等面
积方位投影、双标准纬线等角圆锥投影、等 差分纬线多圆锥投影、正轴方位投影等。
地图投影的变换
• 1、反解变换法 • 2、正解变换法 • 3、综合变换法 • 4、数值变换法 • 5、数值-解析变换法
重要性： 1、目前的地图数据仍是GIS的主要信息源，空间
分析通常也是地图分析为主体的。各种地图根 据其各方面不同而选择不同，因此，人们从地 图上获取GIS空间信息时，必须考虑其所使用的 投影及其坐标系。 2、地理坐标为球面坐标，不方便进行距离、方 位、面积等参数的量算，通过具有严密数学基 础的地图投影转换，变换成异域操作分析的平 面直角坐标系或极地坐标系。 3、GIS中的地图尽管属于数字地图，其信息源也 可能不是平面地图，但最终信息将以它显示或 输出，然而地球椭球体为不可展平面，这是需 地图投影