液液传热实验讲义

适量喝酒会有六大养生好处我们知道喝酒会增加肾的负担，还会有安全风险，那么，你是否知道喝酒也是有养生好处的呢？保健专家发现，适量喝酒会有六大养生好处，让你的体质得到更好保健，还可以防治疾病。

究竟，适量喝酒会有哪些养生好处？接下来，专家就从饮食健康的角度考虑，详细介绍了适量喝酒的好处。

1、降低有害胆固醇营养学家和医学家都曾对“法国悖论”迷惑不解：法国人明明吃那么多高饱和脂肪的食物，但他们患冠心病的概率却那么低。

这到底是为什么呢？后来，研究人员发现，“法国悖论”的产生主要归功于红葡萄酒。

红葡萄酒是法国人日常饮食中不可缺少的角色，它可以减少有害胆固醇，预防血栓，从而降低冠心病的患病率。

为了达到这样的效果，女人每天应该喝一杯葡萄酒（100-150毫升），而男人可以喝两杯（200-250毫升左右）。

2、激发大脑智能葡萄酒可以提高人体有益胆固醇的含量，从而让血液更通畅地流向大脑。

研究人员相信，适量饮酒或许可以扩大大脑的血管，提高血流量，抗击与痴呆症相关的有毒蛋白质。

另外，酒精可以让脑细胞产生可控性压力，从而帮助它们更好地处理可能导致痴呆症的强大压力。

3、控制体重实践已经证明，长期适量饮酒（男人每天2杯，女人1杯）之后，人体可以有效地代谢酒精，不会引起体重增加。

如果每周喝5-7杯酒，可以有效帮助减少吃零食和宵夜的次数，防止进食过量。

比如，一杯淡味啤酒就可以让你的肠胃产生饱足感，控制食欲，但又不会带来过高的卡路里。

4、预防胆结石胆结石的主要构成成分之一就是胆固醇。

葡萄酒中的抗氧化物可以提高人体（包括胆囊）里的有益胆固醇含量，减少有害胆固醇，从而预防胆结石的产生。

5、预防肿瘤红葡萄酒中的白藜芦醇具有强大的健康功效，可以预防脂肪积累，降低胰岛素抗性，预防糖尿病。

一些研究人员相信，白藜芦醇可以通过抑制肿瘤血管的生长来达到预防和治疗肿瘤的效果。

它甚至还可以通过阻隔雌性激素的生长效应来抑制乳腺癌细胞的生长。

6、预防糖尿病医学家希望人们记住，适量饮用的酒精饮料可以像其他食物那样给人体带来一定的健康效应。

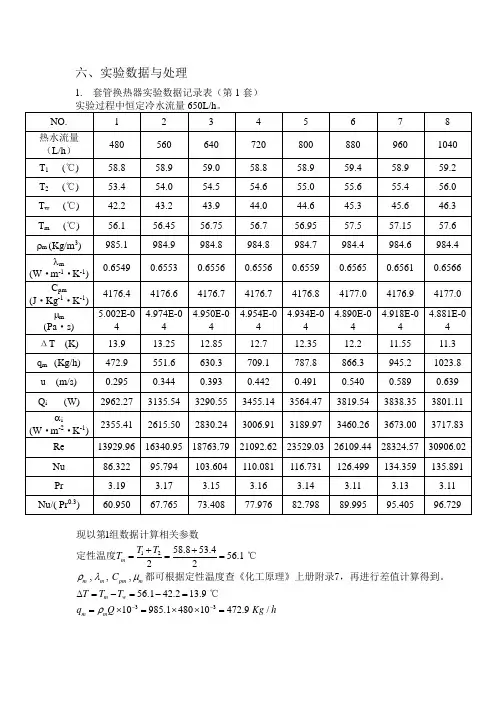
六、实验数据与处理1. 套管换热器实验数据记录表（第1套）1233158.853.456.122,,,56.142.213.910985.148010472.9/m m m pm m m w m m T T T C T T T q Q Kg hρλμρ--++===∆=-=-==⨯=⨯⨯=现以第组数据计算相关参数定性温度℃都可根据定性温度查《化工原理》上册附录7，再进行差值计算得到。

℃()()()32223124144480100.295/2410472.9()4176.458.853.42962.2736002962.272355.410.024 1.213.9985.10.2950.024R ··13929.96e 5.0021023i i m pm i i i i m m i m i Q Q u m s A d Q q C T T WQ W m K N A T u d u d ππαπρμαλ-----⨯⨯====⨯=-=⨯⨯-====∆⨯⨯⨯⨯⨯=====⨯0.340.355.410.0245.00286.3220.65494176.4Pr 3.190.654986.322/Pr 6100.9503.19pm m m C Nu λμ-=⨯=====⨯⨯210028003500αiRe2.列管换热器实验数据记录表（第1套）m，m m pm m m 不重复计算。

()()()()()()12521211221211124360.9756.924.245.01105320 1.572/2183693164174.3856.945.19.6=28.956.924.2ln ln 4503.019.660240i i m pm m WT t T t t Q Q u m sA d Q T t q C T t t t P T T t T ππ-------∆==-⎛⎫⎛⎫- ⎪⨯⨯====⨯ ⎪-⎝⎭-⎝⎭-==-⨯⨯-=-==逆现以第组数据计算有关参℃数12210.219.60.1256.919.656.945.02.5924.219.6987.6 1.5720.006Re 17194.10.0005417ln 1=0.98894i T T R t t ud R Q K d ρμϕπ-=---===--⨯⨯===-==单壳程双管程换热器的温差校正系数可用下面的经验公式计算204360.971264.99/()40.008 1.228.6m W m K L t π==∆⨯⨯⨯KRe3. 求出关联式0.3Re Pr m Nu C C m =中常数、的值。

一、实验目的1. 了解液体中热传递的基本原理和规律；2. 通过实验观察液体中热传递的现象，验证热传递的规律；3. 掌握液体中热传递实验的基本操作和数据处理方法。

二、实验原理热传递是热量从高温物体传递到低温物体的过程，其方式有三种：传导、对流和辐射。

本实验主要研究液体中的热传递，即通过传导和对流的方式。

传导：热量通过物质内部微观粒子的碰撞和振动传递，主要发生在固体和液体中。

本实验中，热量通过液体内部的微观粒子传递，使液体温度发生变化。

对流：热量通过流体（气体或液体）的流动传递，主要发生在流体中。

本实验中，热量通过液体流动传递，使液体温度发生变化。

三、实验仪器与材料1. 实验仪器：温度计、秒表、加热器、试管、烧杯、搅拌器、热源（如酒精灯）；2. 实验材料：水、盐水、食用油。

四、实验步骤1. 准备实验器材，将水、盐水、食用油分别倒入试管、烧杯中，记录初始温度；2. 使用加热器加热水、盐水、食用油，同时使用搅拌器搅拌，观察温度变化；3. 记录不同时间点的温度，计算温度变化速率；4. 比较水、盐水、食用油在相同加热条件下温度变化速率的差异；5. 分析实验结果，得出结论。

五、实验结果与分析1. 实验结果（1）水在加热过程中，温度逐渐升高，且温度变化速率较快；（2）盐水在加热过程中，温度逐渐升高，但温度变化速率较水慢；（3）食用油在加热过程中，温度逐渐升高，但温度变化速率较水慢。

2. 分析（1）水、盐水、食用油在加热过程中，温度变化速率的差异主要与热传导和对流有关。

水的热传导和对流性能较好，故温度变化速率较快；盐水的热传导和对流性能较水差，故温度变化速率较慢；食用油的热传导和对流性能较差，故温度变化速率较慢。

（2）在相同加热条件下，盐水的温度变化速率较水慢，说明盐水的热传导和对流性能较水差。

这是因为盐水中溶解了盐，导致其密度增加，热传导和对流性能降低。

六、实验结论1. 液体中的热传递主要通过传导和对流的方式实现；2. 液体的热传导和对流性能与液体种类、密度、温度等因素有关；3. 实验结果表明，水、盐水、食用油在相同加热条件下，温度变化速率存在差异，且盐水温度变化速率较水慢。

第一章 导热理论基础本章重点：准确理解温度场、温度梯度、导热系数等基本概念，准确掌握导热基本定律及导热问题的基本分析方法。

物质内部导热机理的物理模型：（1）分子热运动；（2）晶格（分子在无限大空间里排列成周期性点阵）振动形成的声子运动；（3）自由电子运动。

物质内部的导热过程依赖于上述三种机理中的部分项，这几种机理在不同形态的物质中所起的作用是不同的。

导热理论从宏观研究问题，采用连续介质模型。

第一节 基本概念及傅里叶定律1-1 导热基本概念一、温度场(temperature field)（一）定义：在某一时刻，物体内各点温度分布的总称，称为即为温度场（标量场）。

它是空间坐标和时间坐标的函数。

在直角坐标系下，温度场可表示为：),,,(τz y x f t = （1-1）（二）分类：1．从时间坐标分：① 稳态温度场：不随时间变化的温度场，温度分布与时间无关，0=∂∂τt ，此时，),,(z y x f t =。

（如设备正常运行工况） 稳态导热：发生于稳态温度场中的导热。

② 非稳态温度场：随时间而变化的温度场，温度分布与时间有关，),,,(τz y x f t =。

（设备启动和停车过程）非稳态导热：在非稳态温度场中发生的导热。

2．从空间坐标分： ① 三维温度场：温度与三个坐标有关的温度场，⎩⎨⎧==稳态非稳态),,(),,,(z y x f t z y x f t τ ② 二维温度场：温度与二个坐标有关的温度场，⎩⎨⎧==稳态非稳态),(),,(y x f t y x f t τ∆tt-∆tgrad t③ 一维温度场：温度只与一个坐标有关的温度场，⎩⎨⎧==稳态非稳态，)()(x f t x f t τ 二、等温面与等温线1．等温面(isothermal surface)：在同一时刻，物体内温度相同的点连成的面即为等温面。

2．等温线(isotherms)：用一个平面与等温面相截，所得的交线称为等温线。

为了直观地表示出物体内部的温度分布，可采用图示法，标绘出物体中的等温面（线）。

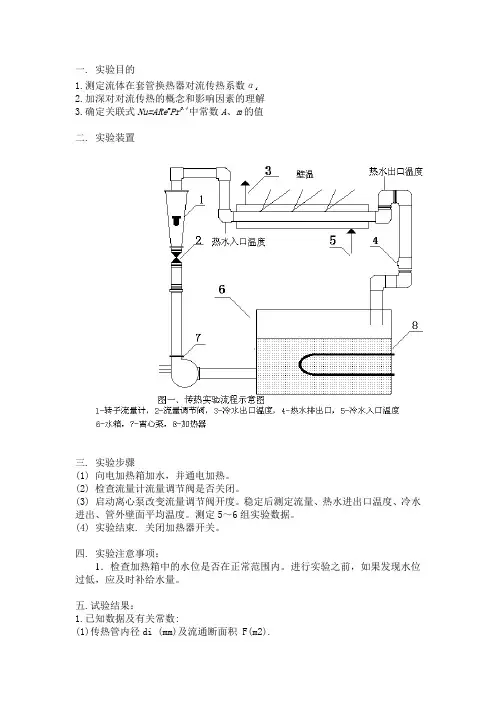
一. 实验目的1.测定流体在套管换热器对流传热系数αi2.加深对对流传热的概念和影响因素的理解3.确定关联式Nu=ARe m Pr0.4中常数A、m的值二. 实验装置三. 实验步骤(1) 向电加热箱加水，并通电加热。

(2) 检查流量计流量调节阀是否关闭。

(3) 启动离心泵改变流量调节阀开度。

稳定后测定流量、热水进出口温度、冷水进出、管外壁面平均温度。

测定5～6组实验数据。

(4) 实验结束. 关闭加热器开关。

四. 实验注意事项：1．检查加热箱中的水位是否在正常范围内。

进行实验之前，如果发现水位过低，应及时补给水量。

五.试验结果：1.已知数据及有关常数:(1)传热管内径di (mm)及流通断面积 F(m2).di ＝18.00(ｍｍ),＝0.018 (ｍ);F ＝π(di2)／4＝3.142×(0.018) 2／4＝0.0002545（m2）. (2)传热管有效长度 L(ｍ)及传热面积si(m2). L ＝1.00ｍ) Si ＝πL di ＝3.142×1.00×0.0180＝0.05656(m2). (3)定性温度at(℃)取t 值为空气进口温度T1(℃)及出口温度T2 (℃)的平均值, 即at=（T1+T2）/2(4)水在定性温度下的性质计算方法，取水在50℃和60℃的物性作以温度T 为变量的一次函数，然后将定性温度代入而求得，参考公式： 密度： ρ= -0.5t + 1013.1 导热系数：λ = 0.11t + 59.3 黏度： μ = -7.95t + 946.9(5)热量衡算式：Q=（V*Cp*ρ*dT ）/3600式中：V —冷流体在套管内的平均体积流量，m 3 / h ； 对流传热系数: ()i m i i s t Q ⨯∆=/α （W/m 2·℃） 式中：i α—管内流体对流传热系数，W/(m 2·℃)； Q i —管内传热速率，W ； S i —管内换热面积，m 2； mi t ∆—传热膜温差，℃。

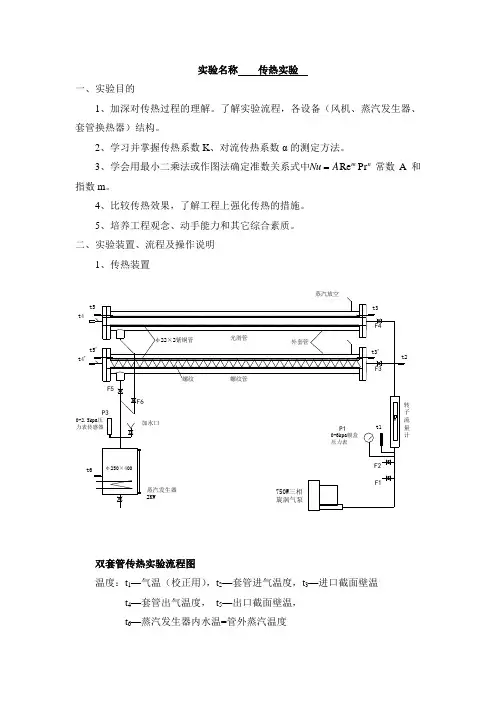
123 t4—套管出气温度，t5—出口截面壁温，t6—蒸汽发生器内水温=管外蒸汽温度说明：因为蒸汽与大气相通，蒸汽发生器内为接近常压，因此t6也可看作管外饱和蒸汽温度。

压力：进气压力膜盒压力表（校正流量用），蒸汽发生器压力传感器（控制蒸气量用）阀门：F1、F2—放空阀，F3、F4—冷空气进口阀，F5、F6—蒸汽进口阀、F2是开启状态，F3或F4有一个是全开，说明：在风机启动时，必须保证F1一个全关闭。

在启动加热电源时，必须保证F5或F6一个全开，一个全关。

2、流程说明：本装置主体套管换热器内由一根紫铜管，外套管由抛光不锈钢制作。

两端法兰连接，在外套管上为方便观察管内蒸汽冷凝情况，设置有两对视盅，后视盅有源照明。

管内铜管测点间有效长度1000（毫米）。

下套管换热器内有弹簧螺纹，作为管内强化传热与上光滑管内无强化传热进行比较。

空气由风机送来，经转子流量计后进入被加热铜管进行加热升温，自另一端排出放空。

在进出口两个截面上，在铜管管壁内和管内空气中心分别装有2支热电阻，可分别测出两个截面上的壁温和管中心的气温；一个热电阻t1可将转子流量计前进口的气温测出，一个热电阻可将蒸汽温度t6测出，其分别用1、2、3、4、5、6来表示，如图示。

蒸汽来源蒸汽发生器，内装有一组2kw加热源，由调压器控制加热电压以便控制加热蒸汽量。

蒸汽进入套管换热器的铜管外套，冷凝释放潜热，为防止蒸汽内有不凝气体设置有放空口，以排出少部分蒸汽为代价，而冷凝液则回流到蒸汽发生器内再利用。

3.有关设备仪表参数：旋涡气泵：风压14kPa，风量72m3/h ，750w套管换热器：内加热紫铜管：φ22×2，有效加热长1000 mm外抛光不锈钢套管：φ100×2蒸汽发生器：容积10 升，可调电加热：2 kw操作压力：常压（配0—2500Pa膜盒压力表）转子流量计：LZB-40，4—40m3/h调压器：2kw固态模块调压电阻传感器：Pt100温度数显仪表：温度巡检仪表，显示精度0.1℃ 压力传感器：0—2500Pa 膜盒压力表：0—6000Pa本实验消耗和自备设施： 蒸馏水： 电负荷：2.75 kw 三、实验原理1、管内Nu 、α的测定计算⑴、管内空气质量流量的计算G [kg/s]空气转子流量计的标定条件：P 0=101325 Pa T 0 =273+20 K ρ0=1.205 kg/m 3 空气转子流量计的实际条件：P 1=P 0+ΔP Pa ΔP—为进气压力表读数T 1 =273+t 1 K t 1—为进气温度10011ρρT p T p ⋅⋅=kg/m 3则实际风量为：1001ρρV V =管内空气的质量流量为：G=V 1*ρ1 [kg/s] ⑵、管内雷诺数Re 的计算因为空气在管内流动时，其温度、密度、风速均发生变化，而质量流量却为定值，因此，其雷诺数计算按下式进行：μπμρd G du Re ⋅==4上式中的物性数据μ可按管内定性温度t 定=(t 2+t 4)/2求出。

实验四 液—液热交换总传热系数及膜系数的测定一、实验目的在工业生产和实验研究中，常遇到两种液体进行热交换，来达到加热或者冷却 之目的。

为了强化热量传递过程，往往需要将流体进行强制流动。

对于在强制对流下进行的液一液热交换，曾有不少学者进行过研究，并取得了不少求算流体传热膜系数的关联式。

每一个关联式都是在特定的条件下，由大量实验数据归纳而成。

对于新的物系或者新的设备，仍需要通过实验来取得传热系数的数据及其计算式 。

本实验利用套管热器实验装置，测定液—液热交换的总传热系数，以及流体在圆管内作强制湍流时的传热膜系数。

希望通过本实验，对这种传热过程的实验研究方法有所了解，在实验技能上受到一定的训练，并加深对流体传热基本原理的理解。

二、实验原理1、总传热系数K 的测定冷热流体通过固体间壁所进行的热交换过程由给热—导热—给热三部分组成。

单位时间内热流体向冷流体传递热量，可由总的传热速率方程式及热量衡算方程表示：)/()()(12,,21,,s J t t c q T T c q t A K c p c m h p h m m -=-=∆⋅⋅=Φ （4—1）或 )/(22s J t A K m ∆⋅⋅=Φ （4—2）式中：Φ——传热速率，J/s ；A ——固体壁面积，即热交换面积，m 2； A ——管的外表面积，m 2； K ——传热系数，W·m -2·K -1；K 2——基于管外表面的传热系数，W·m -2·K -1；m t ∆——两种流体的平均温度差，K 。

c m h m q q ,,,——分别为热流体和冷流体的质量流量，kg·s -1；c p ，h ，c p ，c ——分别为热流体和冷流体的定性温度时的比热容，J·kg -1·K -1；T 1，T 2——分别为热流体进口温度、出口温度，K ； t 1，t 2——分别为冷流体出口温度、进口温度，K ；2121ln t t t t t m ∆∆∆-∆=∆ （4—3） 21,t t ∆∆——分别为热交换器两端冷热流体的温度差，K 。

第二章 传热操作技术1、 有一∅108mm ⨯4mm 的管道，内通以200KPa 的饱和蒸气。

已知其外壁温度为110℃。

内壁温度以蒸气温度计。

求每米管长的导热量。

解：已知：2254 5.410r mm m-==⨯2221 5.410410 5.010r m---=⨯-⨯=⨯1L m = 2110t ω=℃ 查表得145m λω-=⋅⋅℃ 1120t ω=℃()22212 3.14112011045236720.375.4105.01036720.37n n l t Q W r l l r W πλ--⨯⨯⨯-⨯===⨯⨯∴每米管长的导热量为2、 水在一圆形直管内呈强制湍流时，若流量及物性均不变，现将管内径减半，则管内对流传热系数为原来的多少倍？解：已知：12λλ=2112d d =21P P C C = 21μμ= 21ρρ=21qV qV =22224qV u d π=0.822222222222240.023nP qV d d C d d ρπλμμλ⎛⎫ ⎪⎪⎛⎫⎪∴= ⎪ ⎪⎝⎭⎪ ⎪⎝⎭0.8122222111210.811240.023222 3.48nP d qV d C d ρπλμμλαα⎛⎫⎪ ⎪⎛⎫⎪= ⎪ ⎪⎝⎭⎪ ⎪⎝⎭=⨯=3、用一列管式换热器来加热某某溶液，加热剂为热水。

拟定水走管程，溶液走壳程，已知溶液的平均比热容为13.05KJ Kg -℃，进出口温度分别为35℃和60℃，其流量为1600Kg h -；水的进出口温度分别为90℃和70℃。

若不考虑热损失，试求热水的消耗量和该换热器的热负荷。

解：已知： 190n t =℃ 270n t =℃ 135c t =℃ 260c t =℃33.0510P CC J Kg ⋅=⨯℃ 111600600/36006mc q kg h kg s --===由题意可知：()21313.051025612708.3C mc pc c c C Q q C t t Q W=-=⨯⨯⨯=代入数据又不考虑热损失，则在单位时间内热流体放出的热量等于冷流体吸收的热量()()()121212C hh mh Ph n n C Cmh P h n n Ph n n Q Q Q q C t t Q Q q C t t C t t ∴==-∴==--查表可得80℃时，314.19510Ph C J kg -=⨯℃1312708.30.154.1951020mh q kg s-∴==⨯⨯∴热水的消耗量为10.15kg s -，该换热器的热负荷为12708.3w 。

换热器的操作及传热系数的测定一、实验目的1•了解换热器的结构；2•掌握换热器主要性能指标的标定方法; 3•学会换热器的操作方法。

二、实验原理在工业生产中换热器是一种经常使用的换热设备。

它是由许多个传热元 件(如列管换热器的管束)组成。

冷、热流体借助于换热器中的传热元件进 行热量交换而达到加热或冷却任务。

由于传热元件的结构形式繁多，由此构 成的各种换热器之性能差异颇大。

为了合理的选用或设计换热器对它们的性 能应该要充分的了解。

除了文献资料外，实验测定换热器的性能是重要途径 之一。

换热器是一种节能设备，它既能回收热能，又需消耗机械能。

因此，度 量一个换热器性能好坏的标准是换热器的传热系数 K 和流体通过换热器的 阻力损失△ p 。

前者反映了回收热量的能力，后者是消耗机械能的标志。

因 此•在组织换热器的性能测定时，需要安排上述两方面的内容。

1 •传热系数K速率方程式为：Q 二K 」t m ，式中:In而 Q = q v p Cp A t = q v p Cp ( t 2 - t i )换热系数K 是冷流体侧的传热面为基准的传热系数。

即：K 二f(G c ,G h )丄二丄 Ac. - AcK 二：h 乓'A m 符号说明：K 传热系数，W/m 2K ; a 流体的给热系数，W/m 2.K ;实验七 传热实验 1 /5A 换热器的传热面积，m 2;Qv 流体的体积流量，m 3/s ；"t m 逆 （「-上2）- （T 2 - 切Cp 流体的恒压热容。

j/kg.K ;T 热流体温度，C; t 冷流体温度，C ;△t 传热温度差，K o5 传热平均温差的修正系数，全逆流时£.严1，对于单壳程双管程或二管程以上的沁值可从录附计算方法中求得。

入固体壁导热系数，W/m.K ;S 固体壁厚度，m。

由传热速率方程式可知：影响传热量的参数有传热面积A，传热系数K和过程的平均温度△ t m三要素。

第六章 单相流体对流换热及准则关联式第一节 管内受迫对流换热本章重点：准确掌握准则方程式的适用条件和定性温度、定型尺寸的确定。

1-1 一般分析),,,,,,,,(l c t t u f h p f w μαρλ=流体受迫在管内对流换热时，还应考虑以下因素的影响：① 进口段与充分发展段，② 平均流速与平均温度，③ 物性场的不均匀性，④ 管子的几何特征。

一、进口段与充分发展段1．流体在管内流动的主要特征是，流动存在着两个明显的流动区段，即流动进口（或发展）段和流动充分发展段，如图所示。

（1）从管子进口到边界层汇合处的这段管长内的流动称为管内流动进口段。

（2）进入定型流动的区域称为流动充分发展段。

在流动充分发展段，流体的径向速度分量v 为零，且轴向速度u 不再沿轴向变化，即：0=∂∂xu， 0=v 2．管内的流态（1）如果边界层在管中心处汇合时流体流动仍然保持层流，那么进入充分发展区后也就继续保持层流流动状态，从而构成流体管内层流流动过程。

2300Re <用νdu m =Re 判断流态, 式中 m u 为管内流体的截面平均流速， d 为管子的内直径，ν为流体的运动黏度。

（2）如果边界层在管中心处汇合时流体已经从层流流动完全转变为紊流流动，那么进入充分发展区后就会维持紊流流动状态，从而构成流体管内紊流流动过程。

410Re >（3）如果边界层汇合时正处于流动从层流向紊流过渡的区域，那么其后的流动就会是过渡性的不稳定的流动，称为流体管内过渡流动过程。

410Re 2300<<3．热进口段和热充分发展段当流体温度和管壁温度不同时，在管子的进口区域同时也有热边界层在发展，随着流体向管内深入，热边界层最后也会在管中心汇合，从而进入热充分发展的流动换热区域，在热边界层汇合之前也就必然存在热进口区段。

随着流动从层流变为紊流， 热边界层亦有层流和紊流热边界层之分。

热充分发展段的特征对常物性流体，在常热流和常壁温边界条件下，热充分发展段的特征是：)(1x f t f =及)(2x f t w =与管内任意点的温度),(r x f t =组成的无量纲温度⎪⎪⎭⎫⎝⎛--x f x w w t t t t ,,x ,随管长保持不变，即： 0,,x ,=⎪⎪⎭⎫ ⎝⎛--∂∂x f x w w t t t t x 式中，t —管内任意点的温度，),(r x f t = ⇒xf x w w t t tt ,,x ,--仅是r 的函数。