数学史与数学方法论.doc
- 格式:doc
- 大小:385.93 KB
- 文档页数:7

小学数学老师应该读的书作为一名小学数学老师,在教学工作中除了掌握扎实的数学知识外,还应该具备广泛的专业知识和教育理论。
只有通过不断的学习,才能不断提高自己的专业水平,更好地为学生的数学学习提供支持。
下面是一些小学数学老师应该读的书,帮助他们更好地进行教学和教育。
一、数学教育理论类书籍1.《数学教育解剖》:本书通过对数学教育的历史、理论、实践的深入分析,帮助数学教师了解数学教育的本质和方法,提高他们的教学效果。
2.《数学教育学》:该书详细介绍了数学教育的基本理论、原则和方法,旨在帮助数学教师理解儿童数学思维的特点,掌握有效的教学策略。
3.《数学教学设计与组织》:本书以小学数学教学为背景,介绍了数学教学设计的原则和方法,帮助教师合理组织教学内容,提高学生的学习兴趣和学习效果。
二、数学教材与资源类书籍1.《小学数学教学与评价》:本书主要介绍了小学数学教学的基本要求和评价方法,对教师进行了实用的指导,帮助他们更好地选用教材,设计教学活动,并进行学生的评价。
2.《数学教学用书研究》:该书聚焦于小学数学教学用书的选取与使用,通过深入分析不同教材的优缺点,为教师提供了选择合适教材的方法和技巧。
3.《数学学习资源开发与利用》:本书介绍了各类数学学习资源的开发和利用方法,包括教学演示软件、互联网资源、课堂教具等,帮助教师在课堂中更好地利用这些资源,提高学生的学习效果。
三、数学思维与解题类书籍1.《小学数学思维导图法》:本书通过介绍思维导图在数学教学中的应用,帮助教师培养学生的数学思维能力,提高他们解决数学问题的能力。
2.《小学数学解题方法论》:该书详细介绍了小学数学解题的方法和技巧,包括举一反三、透视法、等价转化等,帮助教师和学生更好地面对各类数学问题。
3.《小学数学奥林匹克解题技巧》:本书以小学数学奥林匹克竞赛为背景,介绍了一些解题技巧和思维方法,帮助教师培养学生的数学思维和解题能力。
四、数学史与数学文化类书籍1.《数学之美》:本书以娓娓道来的方式讲述了数学的发展历程和数学家的故事,帮助教师了解数学的魅力和价值,激发学生对数学的兴趣。

华罗庚的数学思想和方法论华罗庚的数学思想和方法论————————————华罗庚(1871-1959),清末民初著名的数学家,也是中国近代数学的奠基者。
他的数学思想和方法论,在中国乃至世界数学史上都有重要的影响力。
一、华罗庚的数学思想1. 重视实践华罗庚提出“实践出真知”的观点,他认为,只有将数学从理论上运用到实际中,才能有助于深入了解数学本质。
他曾经说过:“数学是一个可以用来推理实际问题的工具,其本质就在于实践中。
”华罗庚在《数学史》一书中重点提出了“以实践为导向”的发展历程。
2. 强调实用性华罗庚强调将数学从理论上运用到实际中,而不是仅仅在理论上研究和推理。
他认为,数学必须有实际意义,而不是仅仅是为了表明一个抽象的概念而已。
例如,他在《中国数学史》一书中强调:“数学的发展不是为了改变人们的思想,而是为了使其在实际生活中有用。
”3. 追求创新华罗庚注重实践,但他也强调要创新。
他认为,理论研究不能固步自封,必须要不断改进和发展。
他曾说过:“创新是数学的生命。
要想使数学发展,就必须要有新的理论,新的方法和新的思想。
”二、华罗庚的方法论1. 坚持实用原则华罗庚认为,在实际应用中,要遵循“实用原则”。
他说:“数学的发展不是为了表明一个抽象的概念而已,而是要找到更快更准确的方法来解决实际问题。
”这就是华罗庚对实用原则的重要思想。
2. 坚持理论服务实际华罗庚强调要将理论服务于实际,而不能将实际服务于理论。
他说:“数学不能因为它本身的复杂性而忽略实际问题;要想发展数学,就必须要根据实际来创造理论。
”3. 坚持学科交叉华罗庚强调要建立各学科之间的关系,将各学科内容相互补充。
他说:“要想发展数学,就必须要将数学与其他学科相互结合,并从多方面深入地进行研究。
”这也是华罗庚对学科交叉的重要思想。
总之,华罗庚在中国乃至世界数学史上都留下了重要的影响力。
他重视实践、强调实用性、追求创新、坚持实用原则、坚持理论服务实际、坚持学科交叉等理念都对中国近代数学的发展具有重要的意义。

数学方法论1研究数学方法论的意义和目的什么叫方法论?方法论(methodology)就是把某种共同的发展规律和研究方法作为对象的一门学问。
如所知,各门科学都有方法论,数学当然也有它自已的方法论。
数学方法论主要是研究和讨论数学的发展、数学的思想方法以及数学中的发现、发明与创新等法则的一门学问。
数这是一门工具性很强的科学,它和别的科学比较起业还具有较高的抽象性特征,为了有效地发展它、改进它、应用它或者把它很好地传授给学生们,就需要对这门科学的发展规律、研究方法、发现与发明等法则有所掌握。
因此,数学研究工作者、数学业教师、科技工作者,以及高年级大学生、研究生等都需要知道一些数学方法论。
由于数学领域的许多概念与理论题材都是通过人脑的抽象思维形式表现出来的,这里不仅包含有思维对象(数学本体)的辩证法,而且还有着思维运动过程(认识与反映过程)的辩证法,所以数学方法论还给哲学家、自然辩证法研究工作者以及心理学家们提供了值得分析研究的素材。
凡是看过恩格斯《自然辩证法》的读者都知道,即使在初等数学里也充满着辨证法。
我们又知道,数学方法论中的许多方法和原理是从数学发展史中总结归纳出来的,所以数学工作者还必须学习一点数学史。
从近代数发展史中,我们看到有许多杰出的数学家曾转绕着数学基础问题展开了一系列争论,以致形成了各个著名的流派,如逻辑主义派、直觉主义派、形式主义派与柏拉图主义派等。
直到现今,这些流派的观点主张对数学体系的内在发展,还产生着不同程度的影响。
各个数学流派对数学基础问题的研究,各有其方法论主张。
事实上,他们各有所偏,各有所见。
只有运用科学的反映论,才能从他们的观点主张中分析总结出较为正确的数学方法论观点。
因此,对于今日的数学工作者来说,无论为了掌握、运用或者去发展数学方法论,都必须自觉地采取科学的反映观点(即辩证法的反映观点)去考察问题和分析问题。
2宏观方法论与微观的方法论数学科学的发展规律可以从数学发展史的丰富材料中归纳分析出来。

第一章数学的萌芽 1古埃及的数学 公元前2900年以后,埃及人建造了许多金字塔,作为法老的坟墓。
从金字塔的结构,可知当时埃及人已懂得不少天文和几何的知识。
例如基底直角的误差与底面正方形两边同正北的偏差都非常小。
现今对古埃及数学的认识,主要根据两卷用僧侣文写成的纸草书;一卷藏在伦敦,叫做兰德纸草书,一卷藏在莫斯科。
2埃及最古老的文字是象形文字,后来演变成一种较简单的书写体,通常叫僧侣文。
除了这两卷纸草书外,还有一些写在羊皮上或用象形文字刻在石碑上和木头上的史料,藏于世界各地。
两卷纸草书的年代在公元前1850~前1650年之间,相当于中国的夏代。
3古埃及的计数制 埃及很早就用十进记数法,古埃及人的计数系统是叠加制,但却不知道位值制,每一个较高的单位是用特殊的符号来表示的。
例如111,象形文字写成三个不同的字符,而不是将 1重复三次。
埃及算术主要是加法,而乘法是加法的重复。
他们能解决一些一元一次方程的问题,并有等差、等比数列的初步知识。
占特别重要地位的是分数算法,即把所有分数都化成单位分数(即分子是1的分数)的和。
兰德纸草书用很大的篇幅来记载2/N(N 从5到101)型的分数分解成单位分数的结果。
为什么要这样分解以及用什么方法去分解,到现在还是一个谜。
这种繁杂的分数算法实际上阻碍了算术的进一步发展。
纸草书还给出圆面积的计算方法:将直径减去它的1/9之后再平方。
计算的结果相当于用 3.1605作为圆周率,不过他们并没有圆周率这个概念。
根据莫斯科纸草书,推测他们也许知道正四棱台体积的计算方法。
总之,古代埃及人积累了一定的实践经验,但还没有上升为系统的理论。
4埃及几何的突出成就:古埃及人在建筑规模宏大的教堂、金字塔等都需要测量,尼罗河水泛滥后冲刷了许多边界标记,为他们认识基本几何形状和形成几何概念提供了实际背景。
因此古埃及人的几何学知识较为丰富,在两种纸草书中,有26个十几何问题,许多与金字塔有关,如:在莫斯科纸草书中有:一个截顶金,字塔的垂直高度为6,底边为4,顶边为2求体积。

数学史研究数学概念、数学方法和数学思想的起源与发展,及其与社会政治、经济和一般文化的联系。
3.什么是数学数学是量的科学。
(希腊哲学家亚里士多德,BC 4世纪)数学是研究现实世界的空间形式与数量关系的科学。
(恩格斯,19世纪)数学这个领域已被称为模式的科学,其目的是要揭示人们从自然界和数学本身的抽象世界中所观察到的结构和对称性。
(数学的新定义)数学史的分期---------简答题(必背)Ⅰ数学的起源与早期发展(公元前6世纪前)Ⅱ初等数学时期(公元前6世纪~16世纪)①古代希腊数学(公元前6世纪~6世纪)②中世纪东方数学(3世纪~15世纪)③欧洲文艺复兴时期(15世纪~16世纪)Ⅲ近代数学时期(17世纪~18世纪)Ⅳ现代数学时期(1820 ’~现在)①现代数学酝酿时期(1820 ’~1870)②现代数学形成时期(1870 ~1940 ’)③现代数学繁荣时期(1950 ~现在)埃及与美索不达米亚数学美索不达米亚(巴比伦)数学的主要贡献是:60进制记数系统;三项二次,三次代数方程;初等代数变换思想;几何学。
古埃及数学形成在公元前3100年~公元前332年之间,其主要的贡献是:十进制的概念;加法运算;单位分数;几何学的萌芽;代数学的萌芽第二章古代数学古希腊数学横跨公元前600年至公元600年。
古希腊数学分两个阶段:古典时期(早期)的希腊数学(公元前600年至公元300年);亚历山大时期及后期的希腊数学(公元300年至公元600年)。
古希腊数学的代表人物有:⑴最早的希腊数学家---泰勒斯(公元前625年至公元前547年)泰勒斯是历史上有记载的第一位数学家和论证几何学的鼻祖主要贡献:圆的直径将圆分为两个相等的部分、等腰三角形两底角相等、两相交直线形成的对顶角相等。
泰勒斯定理:半圆上的圆周角是直角。
⑵毕达哥拉斯(公元前580年至公元前500年)主要贡献:成立了著名的毕达哥拉斯学派,致力于哲学和数学的研究;发现和证明了毕达哥拉斯定理(勾股定理);⑶柏拉图(公元前427年至公元前347年)主要贡献:柏拉图的具体数学成就不多,但对数学方法的研究贡献很大。

《数学方法论》教学大纲数学方法论是关于数学研究的基本方法,是数学研究的基本策略。
数学思想方法是数学教育的重要依据。
通过中学数学思想方法概论的学习,让学生理解观察、实验、类比、归纳、联想、分析、综合、抽象、概括等基本的研究方法,把握数学的逻辑方法、思维方法、模型方法等。
通过这些内容的学习无疑有益于学生数学教育素养的提高。
一、课时总数: 108学时,其中自学52学时,面授56学时。
二、课程内容:第一章数学的起源与发展第一节数学发展各个时期简析第二节中国数学的起源与发展第三节数学发展的动力本章内容要求学生了解数学史的分期,初步掌握数学发展的规律,把握中国数学发展的线索,通过了解九章算术认识中国数学的历史,正确认识数学与世界的关系,正确认识数学。
把握数学发展的动力。
P.60练习题1—15第二章数学概观第一节数学的对象和特征第二节数学的地位第三节辩证唯物主义数学观第四节数学基础论及其简要评价通过本章学习,要求学生了解关于数学的特征的主要观点,把握数学的三大特征,认识数学在科学、自然科学、人类文化中的地位和作用。
形成辩证唯物主义的数学观,能运用辩证唯物观去把握数学、理解数学,了解数学悖论形成的原因,了解逻辑主义、直觉主义、形成主义等数学三大学派的主要观点,并能指出其不足。
P.108 练习题1~11,13,14,15,17第三章数学研究的一般方法第一节观察与实验第二节划分与比较第三节分析与综合第四节抽象与概括第五节特殊与一般通过本章学习,认识观察与实验、划分与比较、分析与综合、抽象与概括、特殊与一般在数学研究中的重要作用,要求学生掌握观察与实验的一般规律,了解概念划分的原则,理解划分的标准,掌握划分的方法;能灵活运用分析与综合方法去解决各种问题,理解抽象与概括的涵义,学会抽象与概括数学概念、原理等;掌握特殊化与一般化解决问题的策略。
P.144 练习题 3~5,6~8, 9,10第四章数学中的逻辑方法第一节逻辑思维的基本形式第二节形式逻辑方法与辩证逻辑方法第三节逻辑推理规则第四节常用的逻辑推理方法第五节数学证明与逻辑推理错误剖析通过本章学习,让学生理解概念、判断和推理是逻辑思维的基本形式,理解概念的内涵与外延的涵义以及概念间的各种关系;认识判断与推理的各种形式,了解形式逻辑与辩证逻辑的关系;掌握命题基本形式以及逻辑等价的涵义,灵活运用逻辑推理规则,掌握正确的逻辑推理方法,理解数学证明的意义,避免逻辑推理中的错误。

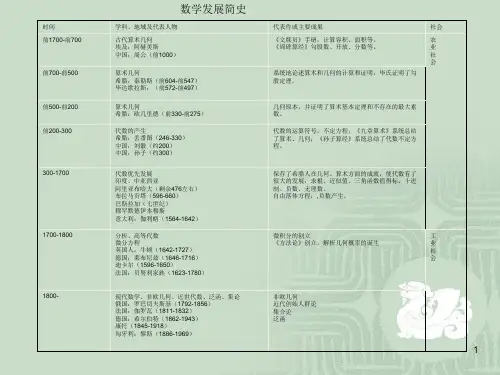
数学发展简史数学是人类最古老的科学知识之一.就人类对数的认识和运用来看,一般讲从公元前3000年左右的埃及象形文字就已开始,迄今已有5000年的历史.那么到底什么是数学呢?实际上数学是一门历史性很强的科学或者说累积性很强,它的内涵随着时代的变化而变化,给数学下一个一劳永逸的定义是不可能的。
从公元前4世纪的希腊哲学家亚里士多德到17世纪的笛卡儿、19世纪的恩格斯、20世纪的罗素等很多数学家都曾给数学下过定义。
用的较多也较容易理解的是恩格斯的定义。
他说,数学,是研究数量关系与空间形式的一门科学。
20世纪80年代的一批美国学者将数学定义为:数学这个领域已被称作模式的科学,其目的是要揭示人们从自然界和数学本身的抽象世界中所观察到的结构和对称性。
这一定义以其高度的概括性,已日益引起关注并获得大多数数学家的认同与接受。
第一阶段:数学的萌芽阶段(公元前3000年—公元前600年)这一阶段,我们称之为数学的萌芽阶段,或者说准学科阶段。
在这一阶段里,数学还没有发展成为一门有明确结构的独立的理性的学科,还不具备抽象,还没有方法论,还没有论证和推理。
数学文化在这一阶段的杰出代表是古巴比伦数学、中国数学、埃及数学、印度数学等。
这一阶段的世界数学文化呈一种多元发展态势。
第二阶段:数学的形成阶段(公元前5世纪—公元16世纪)这一阶段,通常称之为数学科学的形成时期,它的开始是以希腊人的出场为典型标志,结束于公元16世纪,也就是在变量数学产生之前,人们常称此阶段为常量数学阶段,也就是数学学科完成了以常量为主要内容的框架体系。
这一时期,希腊数学家取得辉煌成绩,他们引入了证明,提出了抽象,发现了自然数,发现了无理数(注:这是数学史上第一次危机。
《原本》第五卷中将比例理论由可公度量推广到不可公度量,使它能适用与更广泛的几何命题证明,从而巧妙的回避了无理量引起的麻烦。
但问题的根本解决要到19世纪借助极限过程对无理数做出严格定义之后).最大的光荣是欧几里得写的《原本》和阿波罗尼奥斯的《圆锥曲线论》。

数学历史:方法论的线索数学是一门古老的学科,它伴随着人类文明的产生而产生,至少有四、五千年的历史。
数学的最初的概念和原理在远古时代就萌芽了,经过四千多年世界许多民族的共同努力,才发展到今天这样内容丰富、分支众多、应用广泛的庞大系统。
了解数学的发展历史有助于培养学生对学习数学的兴趣,下面的内容希望对他们能有所帮助!定理证明和数值计算是数学中两项最主要的活动形式。
证明主要是用演绎法,以公理化思想为主;计算若是按一定程序,即按一种机械的过程进行就叫做机械化思想的算法。
贯穿在整个数学发展历史过程中,有两个中心思想,一个是公理化思想,另一个是机械化思想。
公理化思想源于古希腊,欧几里得的《几何原本》是公理化思想的代表。
机械化思想则贯穿于整个中国古代数学,《九章算术》为其代表。
作为数学两种主流的公理化思想和机械化思想都对数学的发展起过巨大的作用。
现在我们从思想力法论的角度,即从数学发展中以公理化思想为主的演绎倾向和以机械化思想为主的算法倾向交替取得主导地位的线索来描述整个数学发展史。
古代巴比伦和埃及的原始算法最早占主导地位,后来被希腊式的演绎几何所接替。
到中世纪,希腊数学衰落下去,算法倾向在中国、印度和阿拉伯地区繁荣起来。
17、18世纪是欧洲人寻求无穷小算法的`英雄年代,而从19世纪初,罗巴切夫斯基非欧几何出现以后,特别是70年代起,几何演绎倾向又重新在比古希腊几何高得多的水准上占优势。
近代数学时期的演绎倾向是从19世纪20至30年代开始,在70年代以后进入全盛时期。
这个新的演绎时代与古希腊―个显著的不同是演绎方法的运用远远超出了几何而扩展到其他领域,首先是数学分析。
探讨微积分运算的严格的逻辑基础,导致了从柯西极限论到外尔斯特拉斯的极限算术化和康托尔集合论贯穿了整个19世纪的分析严格化运动。
自外尔斯特拉斯以后,现代分析几乎完全改变了牛顿、莱布尼兹,乃至欧拉、拉格朗日时代的风貌而成为抽象的演绎科学,如果说,17世纪将代数算法运用于几何而发展出解析几何,19世纪则反过来,将几何演绎运用于代数而产生抽象代数。

第一章一、数学的起源:古埃及人在建造神奇的金字塔、狮身人面像以及神庙的同时,也创立了相当发达的数学,保存至今有关数学的纸草书有两种:一是陈列于英国伦敦大不列颠博物馆东方展室中的兰德纸草书;二是收藏于俄国莫斯科美术博物馆,被称为莫斯科纸草书。
二、1、古埃及人的计数制:使用的是十进制,并且有数字的专门符号,当一个数出现某个数码的若干倍时,就将它的符号重复若干次,这说明,技术系统是叠加制而不是位值制。
以有分数概念。
2、古埃及代数:纸草书中出现“计算若干”的问题,实际上相当于方程问题,他们解决这类问题的方法是试位法。
有关数列问题记载。
3古埃及几何:古埃及人通过具体问题说明了正四棱台的体积公式(如:)著名数学史家贝尔形象地将这一古埃及数学杰作称为“最伟大的埃及金字塔”。
三4、古埃及的几何学:古埃及人用具体问题说明了正四棱台的体积公式(三、1、古巴比伦的计数制:他们用的是楔形文字,计数系统是60进制。
2、古巴比伦的代数:已经知道某些类型的一元二次方程的求根公式,他们还讨论了某些三次方程和双二次方程的解法。
还发现了级数问题,勾股数表。
3古巴比伦的几何:实际中的几何问题都可以转化为代数问题,他们的面积和体积计算是按照一些固定的法则和公式给出的。
4、古巴比伦的天文学;公元前5000年到公元前4000年,古巴比伦人就已开始使用年、月、日的天文历法,他们年历是从春分开始的,一年有12个月,每月有30天,每6年加上第13个月作为闰月,一星期有7天。
第二章1、希腊数学初创期主要数学发现和发展:公元前6世纪—公元前3世纪期间出现许多数学学派(1)享有“希腊科学之父”盛誉的泰勒斯创立了古希腊历史上的第一个数学学派——爱奥尼亚学派。
内接于半圆的角必为直角这一定理被人们称为“泰勒斯定理”。
泰勒斯将逻辑学中演绎推理引入数学,奠定了演绎数学的基础,这使他获得第一位数学家和论证几何学鼻祖的美誉。
曾经利用相似直角三角形通过测量手杖和金字塔的影子长求出金字塔的高度,又用全等三角形的知识计算出海船到海岸的距离,被西方称为“测量学的鼻祖”。
引言概述:教资数学史是教育考试中的一个重要考点,了解数学史的发展对于理解数学思想、方法和理论具有重要意义。
本文将重点介绍教资数学史的相关内容,包括数学的起源、数学在古代的发展、数学在中世纪的发展、数学在近代的发展以及数学在现代的发展。
通过对这五个大点的详细阐述,希望能够帮助读者更好地掌握教资数学史的核心知识,并为教育考试做好准备。
正文内容:一、数学的起源1.数学的定义和作用2.数学在古代的起源3.古代数学的发展特点4.古希腊数学的贡献5.古代数学在中国和印度的发展二、数学在古代的发展1.古代数学的主要内容2.古代数学家的代表人物和贡献3.古代数学思想的特点4.古代数学在天文学和地理学中的应用5.古代数学的传承与影响三、数学在中世纪的发展1.中世纪数学的特点与背景2.中世纪数学家的代表人物和贡献3.中世纪数学的研究内容和方法4.中世纪数学中的重要定理和方程式5.中世纪数学对科学方法的影响四、数学在近代的发展1.近代数学的背景和特点2.近代数学的主要研究领域和方向3.近代数学的发展与科学技术的关系4.近代数学家的代表人物和贡献5.近代数学的重大突破和发展趋势五、数学在现代的发展1.现代数学的定义和特点2.现代数学的研究领域和学科体系3.现代数学的理论与应用4.现代数学的发展与社会进步的关系5.现代数学家的代表人物和贡献总结:通过对教资数学史的重点内容进行介绍和阐述,我们可以看到数学的发展历程中涌现了无数杰出的数学家和重要的数学成果。
从古代到现代,数学经历了从实用到抽象的转变,从个别问题到整体理论的发展,给人类社会的科学技术进步作出了重要贡献。
因此,我们应该重视教资数学史的学习和研究,加深对数学本质的理解,提高数学教育水平。
同时,我们也要关注数学史的现代应用,与其他学科进行交叉融合,不断创新和发展数学的理论与方法,为解决实际问题和促进社会进步做出更大的贡献。
数学方法论稿范文
一般来说,数学方法论的基础是数学模型。
通常,建立数学模型是为
了解决具有复杂性的问题,可以使用模型来检验现实世界的情况,并用来
做出有益的改变和改善。
数学模型分为几种类型:概率模型、运筹学模型、社会计算模型等等。
数学方法论的另一个基础是数学方法。
它们可以用于研究和解决各种
复杂的问题。
举例来说,可以使用数学分析、统计学、优化方法、积分和
微分方程等。
这些数学方法可以帮助用户建模并验证现实世界中的情况,
改进和优化模型。
此外,数学方法可以帮助用户推断出结论并建立有用的
预测。
最后,数学方法论还涉及到计算技术。
举例来说,为了更好地解决现
实问题,需要使用计算机代码,可以使用计算机和相关技术来支持建模、
优化和模拟。
此外,计算机软件可以帮助用户完成大量重复性的计算,从
而提高工作效率。
总的来说,数学方法论是一种应用于复杂问题分析、解决和预测的学
术研究方法。
最新数学史与方法论自学考试知识点及答案(十多套资料)1. 简述数学史的定义及数学史课程的内容。
答:数学史研究数学概念、数学方法和数学思想的起源与发展及其与社会政治经济和一般文化的联系。
数学史课程的功能可以概括成以下四部分:(1)掌握历史知识:通过学习关于数学的专门知识,更好的从整体上把握数学。
(2)复习已有知识:按学科讲述学过的数学知识,系统的提高对该学科的理解。
(3)了解新的知识:通过学习数学各学科的发展,了解没有学过的学科的内容。
(4)受到思想教育:通过了解数学家为数学而奋斗的高尚品质,陶冶数学情操。
2. 简述数学内涵的历史发展。
答:数学的内涵随时代的变化而变化,一般可分为四个阶段。
A 数学是量的科学:公元前4世纪。
B 数学是研究现实世界空间形式与数量关系的科学;19世纪。
C 数学研究各种量之间的关系与联系:20世纪50年代。
D 数学是作为模式的科学:20世纪80年代。
1. 简述河谷文明及其数学。
答:历史学家往往把四大文明古国的文明称之为“河谷文明”,因为这些国家是在河流的入海口建立的。
尼罗河孕育了埃及文明;底格里斯河、幼发拉底河孕育了巴比伦文明;黄河和长江孕育了中国文明;印度河和恒河孕育了印度文明。
埃及、美索不达米亚的数学产生较早,纪元前已经衰微,而印度、中国的数学崛起较晚,却延续至中世纪。
2. 简述纸草书与泥板文书中的数学。
答:古埃及人在一种纸莎草压制成的叶片上书写,幸存至今,被称为纸草书。
莱茵德纸草书(现存于伦敦大英博物馆)中有84个数学题目;莫斯科纸草书(现存于俄国普希金精细艺术博物馆)中有25个数学题目;还有其他纸草书。
纸草书中的数学知识包括:(1)算术,包括加法运算、单位分数、十进制计数、位置法;(2)几何,包括面积、体积计算和四棱台体积公式。
美索不达米亚人用尖芦管在湿泥板上写字,然后将湿泥板晒干或烘干,幸存至今,被称之为泥板文书。
出土50万块其中数学文献300块。
泥板文书中的数学包括:(1)记数,包括偰形文、60制、位值原理;(2)程序化算法,包括û1.414213;(3)数表;(4)x²–px–q=0 ,x³=a,X³+X²=a (5)几何,测量、面积、体积公式、相似形、勾股数值。
《数学史》读书报告——以李文林著《数学史概论》为例本学期我选修了陈静安教授的“数学史与数学方法论”,一共选读了李文林著《数学史概论》与钱佩玲《中学数学思想方法》两本书,以下对李文林著《数学史概论》作一个读后的总结。
一、《数学史概论》简介及其特点《数学史概论(第2版)》以重大数学思想的发展为主线,阐述了从远古到现代数学的历史。
书中对古代希腊和东方数学有精炼的介绍和恰当的分析;同时充分论述了文艺复兴以来近现代数学的演进与变革,尤其是20世纪数学的概观,内容新颖。
《数学史概论(第2版)》中西合炉,将中国数学放在世界数学的背景中述说,更具客观性与启发性。
《数学史概论(第2版)》脉络分明,重点突出,并注意引用生动的史实和丰富的图片。
本书共分十五章,其中第一章“数学的起源与早期发展”介绍了人类在蒙昧时期由于生产生活的需要,逐渐形成了数与形的概念,从最早的手指计数到石头计数,再到结绳计数直到距今大约五千多年前,出现了书写计数以及相应的计数系统。
在灿烂的“河谷文明”中,重点介绍了埃及数学和美索不达米亚数学。
第二章“古代希腊数学”,介绍了雅典时期和亚历山大时期的数学,其中重点对数学家泰勒斯、毕达哥拉斯、欧几里得、阿基米德及阿波罗尼奥斯及其成就作了详尽的介绍。
第三章“中世纪的中国数学”,从古代著作《世本》中提到的黄帝使“隶首作算数”,殷商甲骨文中使用的完整的十进制计数,到两汉时期、魏晋南北朝时期以及宋元时期达到了发展的高潮。
介绍的著作主要有《周髀算经》,《九章算术》,《算经十书》,介绍了刘徽的“割圆术”和他在面积、体积公式推证的成就,祖冲之父子推算“圆周率”,在推导几何图形体积公式时提出了“出入相补”及“祖氏原理”;第四章“印度与阿拉伯的数学”;第五章“近代数学的兴起”,讲述了中世纪的欧洲,从代数学、三角学、透视学、射影几何等方面的发展向近代数学的过渡,以至解析几何的诞生;第六章“微积分的创立”,分别介绍了牛顿和莱布尼茨从不同的角度提出的微积分原理;第七章“分析时代”;第八章至第十章,分别以代数、几何、分析这三大领域的变革为主要线索,介绍了19世纪数学的发展;第十一章至十三章是“20世纪数学概观”,分别介绍了纯粹数学的主要趋势、空前发展的应用数学、现代数学成果十例;第十四章“数学与社会”,第十五章“中国现代数学的开拓”。
数学命题预测试卷(二)
(理工类)
(考试时间120分钟)
一、选择题(本大题共15小题,每小题5分,共75分。
在每小题给出的四个选
项中,只有一项是符合题目要求的)
1.已知集合{}0,a M =,{
}2,1=N ,且{}1=N M I ,那么N M Y 等于( ) A .{}2,1,0,a B .{
}2,1,0,1 C .{}2,1,0 D .不能确定 2.已知c b a c b a 23,32=-=+,a 与b 的关系是( )
A .b a =
B .b a 2=
C .b a -=
D .b a 2-=
3.已知︒=︒=35,10βα,那么)tan 1)(tan 1(βα++的值等于( )
A .3
B .2
C .21+
D .31+
4.函数x x y 44sin 2cos 2-=的最小正周期是( )
A .π
B .π2
C .
2π D .π4 5.函数x x y -⎪⎭⎫ ⎝⎛=221的定义域为( )
A .R x ∈
B .2,≠∈x R x 且
C .0,≠∈x R x 且
D .20<<x
6.以方程0622=--x x 的两根的倒数为根的一元二次方程为( )
A .0262=-+x x
B .01862=--x x
C .032
32=--x x D .019182=++x x 7.顶点在点A (2,-1),准线为x 轴的抛物线方程是( )
A .)1(2)2(2+=-y x
B .)1(4)2(2+-=-y x
C .)1(2)2(2-=+y x
D .)1(4)2(2-=+y x
8.设0<m ,那么实数m 的三角形式是( )
A .)0sin 0(cos i m +
B .)sin (cos ππi m +
C .⎪⎭
⎫ ⎝⎛+-23cos 23sin ππi m D .)sin (cos ππi m +- 9.“0,0=≠=B C A ”是“二元二次方程022=+++++F Ey Dx Cy Bxy Ax 表示
圆”的( )
A .充分非必要条件
B .必要非充分条件
C .充分且必要条件
D .既非充分又非必要条件
10.已知)0(1)1(2>++=x x x x
f ,则)(x f =( ) A .x x 112+- B .x
x 112-+ C .x x 112-- D .x
x 112++ 11.设定义域在R 上的函数x x x f =)(,则)(x f 是( )
A .奇函数,增函数
B .偶函数,增函数
C .奇函数,减函数
D .偶函数,减函数
12.6)22(x
x + 的展开式中常数项是( ) A .30 B .20 C .15 D .10
13.若直线b ax y +=过第一、二、四象限,则圆⎩⎨⎧+=+=θ
θsin cos r b y r a x (θ为参数)的
圆心在( )
A .第一象限
B .第二象限
C .第三象限
D .第四象限
14.)2
1arccos(-的值为( ) A .6π- B .3π- C .3π D .3
2π 15.由1,2,3,4组成的无重复数字的四位数,按从小到大的顺序排成一个数
列{}n a ,则18a 等于( )
A .1243
B .3421
C .4123
D .3412
二、填空题(本大题共4题,每小题4分,共16分。
把答案填在题中横线上)
16.已知m
m x x +-=+33cos 3sin ,那么m 的取值范围是 . 17.函数16123+-=x x y 在[]3,3-上的最小值是 .
18.已知圆的方程为088222=+-++y x y x ,过)0,2(P 作该圆的一条切线,切
线的长为 .
19.五人站成一排,其中某人恰好站在中间的概率是 .
三、解答题(本大题共5小题,共59分。
解答应写出推理、演算步骤)
20.(本小题满分11分)
已知)10( 1cot <<-=a a a θ,求θ
θθθcos sin cos sin 22++-a a 的值.
21.(本小题满分12分)
首项为25的等差数列,其前9项的和等于前17项的和,问这个数列前多少
项的和最大?
22.(本小题满分12分)
已知函数⎪⎪⎭⎫ ⎝⎛-=-2222
2log )1(x x x f . (1)求)(x f 的解析式及)(x f 的定义域.
(2)判定)(x f 的单调性.
23.(本小题满分12分)
如右图所示,在正三棱柱C B A ABC '''-中,B B B A '='3.
(1)求证:C B B A '⊥' ;
(2)求二面角C C B A -'-的大小.
24.(本小题满分12分) 设P ,Q 是抛物线x y =2上满足OQ OP ⊥的任意两点,其中O 为坐标原点,
P ,Q 都不是抛物线的顶点.
(1)求证:PQ 所在直线与x 轴交于定点.
(2)求OPQ ∆面积的最小值.
参考答案
一、选择题
1.C 2.A 3.B 4.A 5.C 6.A 7.B 8.D
9.B 10.D 11.A 12.A 13.B 14.D 15.B
二、填空题
16.1-≥m 或9-≤m 17.0 18.4 19.5
1 三、解答题
20.解 )cos cos (cos sin cos sin cos sin 22222θθθ
θθθθθ-++-=++-a a a a a
θ
θθθ22222cos )cos (sin sin 2-+=a a θ
θθ22222cos )1(sin sin 2-+=a a a θ
222cot )1(2-+=a a a 2
1)1(222-=-⋅-+=
a
a a a a 21.解 设此数列公差为d ,由已知得
d d S 362252
)19(92599+=-⋅+
⋅= d d S 1364252)117(17251717+=-⋅+⋅= Θ 179S S =
故 d d 136********+=+ 得2-=d
∴ 169)13()2()1(2
1252+--=-⋅-+⨯=n n n n S n 故当13=n 时,n S 有最大值169,即这三个数数前13项和最大.
22.解 (1)Θ )1(1)1(1log 2log )1(2222222
x x x x x f ---+=⎪⎪⎭⎫ ⎝⎛-=- ∴ x
x x f -+=11log )(2 要使)(x f 有意义,必须
011>-+x x 即0)1)(1(<-+x x 11<<-x
故)(x f 的定义域为)1,1(-∈x .
(2)设1121<<<-x x ,则 2221122111log 11log )()(x x x x x f x f -+--+=- )
1)(1()1)(1(log 21212x x x x +--+=
由于1121<<<-x x ∴ 0)1)(1(21>-+x x ,0)1)(1(21>+-x x 而0)(2)1)(1()1)(1(212121<-=+---+x x x x x x 故1)1)(1()1)(1(02121<+--+<x x x x ,0)1)(1()1)(1(log 21212<+--+x x x x 故)()(21x f x f <
故)(x f 为增函数.
23.解(1)取BC 中点D ,连AD ,连D B ',C B '交于O 设1='B B ,则3='B A ,22,2===BD BC AB ∴ 2tan ,2tan ='∠=''∠DB B C B B ∴ DB B C B B '∠=''∠ ∴ DB B ~BO B '∆'∆ ∴ ︒='∠90OB B ,即D B C B '⊥' 又 易证AD C B ⊥' ∴ C B B A '⊥'
(2)Θ D B C B AD C B '⊥'⊥', ∴ AOD ∠为二面角C C B A -'-的平面角 Θ 2
6='D B ∴ 66=
DO ∴ 36
6
2
2
3tan =⋅=∠AOD ∴ 3arctan =∠AOD
24.解(1)设OP 的方程:)0(>=k kx y ,则OQ 的方程:x k
y 1-=
联立方程组⎩⎨⎧==x
y kx y 2,得交点)1,1(2k k P 联立方程组⎪⎩
⎪⎨⎧=-=x y x k y 21,得交点),(2k k Q -
故PQ 所在直线方程为)(11
222k x k k k k k y ---
-=+ 令0=y ,得1=x
又1=k 时,PQ 的方程为1=x
从而PQ 所在直线过一定点R (1,0).
(2))( 2
1Q P QOR POR POQ y y OR S S S -=
+=∆∆∆ 1)1(21)1(121≥+=+⋅⋅=k k k k 故1=k 时,POQ ∆的面积最小值为1.。