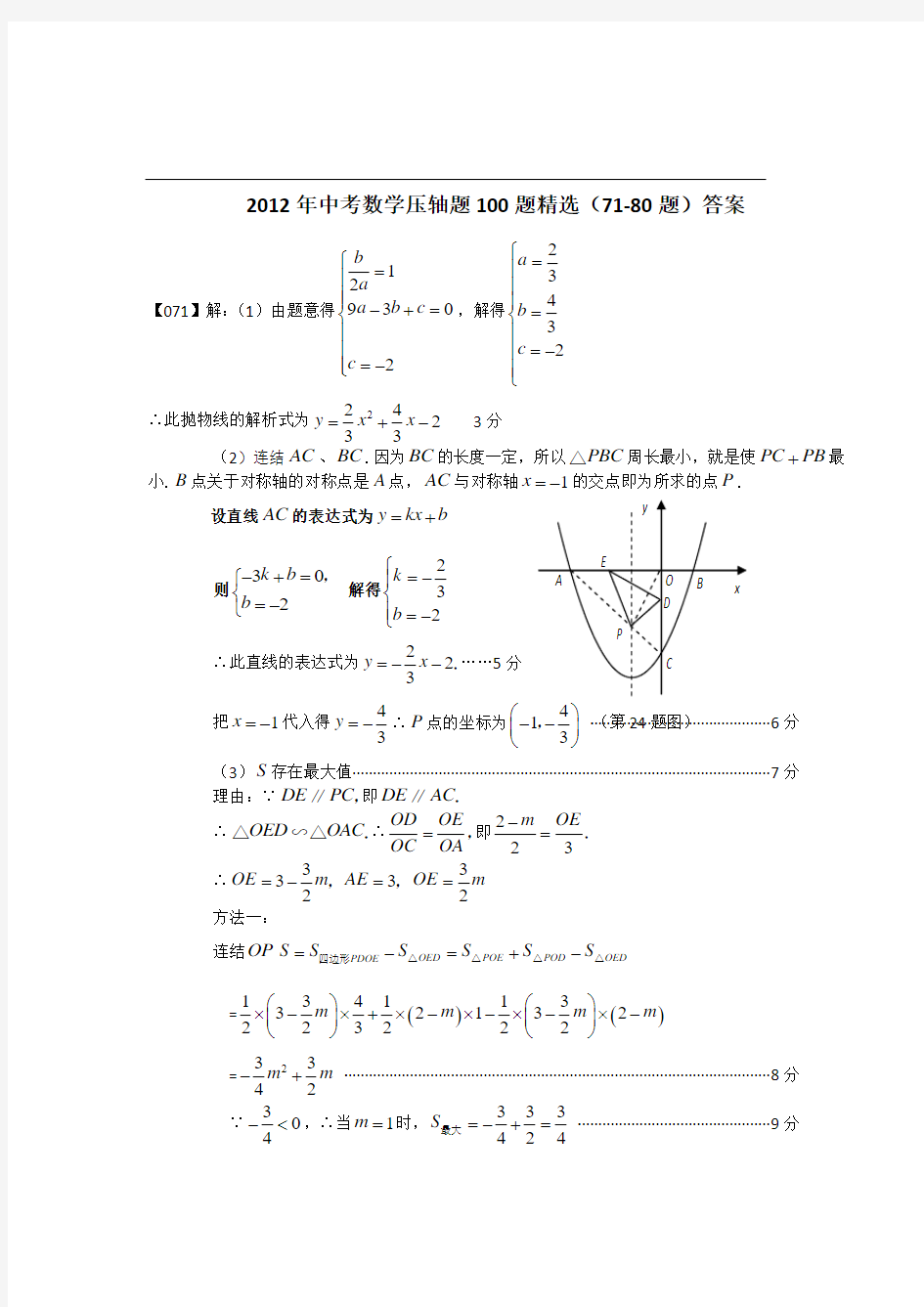
② ⊙Q 是△OAB 的内切圆 ,可设⊙Q 的半径为r ∵
862
1
)1086(21??=++=
?r S OAB ,解得r=2.………………………………………8分 设⊙Q 与OB 、AB 、OA 分别切于点F 、G 、H
可知,OF =2∴BF =BG =OB -OF =6-2=4,设直线PD 与⊙Q 交于点 I 、J ,过Q 作Q M ⊥IJ 于点M ,连结IQ 、QG , ∵QI =2,2.12
1
==IJ IM ∴ 6.122=-=
IM QI QM ∴ 在矩形GQMD 中,GD =QM =1.6
∴BD =BG+GD =4+1.6=5.6,由108cos ===
∠BA BC BP BD CBA ,得74
5
==BD BP ∴点P 的坐标为(7,6)…………………………………………………………………11分
当PE 在圆心Q 的另一侧时,同理可求点P 的坐标为(3,6)………………………12分 综上,P 点的坐标为(7,6)或(3,6).………………………………………………13分。 【078】(1)1y x =- ················································································································· 2分 (2)∵OP t =,∴Q 点的横坐标为1
2
t , ①当1012t <
<,即02t <<时,112
QM t =-, ∴11122OPQ S t t ??
=
- ???
△. ·········································································································· 3分 ②当2t ≥时,11
1122
QM t t =-
=-,
∴11122OPQ
S t t ??
=- ???△.∴1110222111 2.
22
t t t S t t t ???
-<< ?????=????- ?????,
,,≥······················································ 4分 当1
012
t <
<,即02t <<时,211111(1)2244S t t t ??=-=--+ ???,
∴当1t =时,S 有最大值
1
4
. ·································································································· 6分 (3)由1O A O B ==,所以OAB △是等腰直角三角形,若在1L 上存在点C ,使得CPQ △是以Q 为直角顶点的等腰直角三角形,则PQ QC =,所以OQ QC =,又1L x ∥轴,则C ,O 两点关于直线L 对称,所以1AC OA ==,得(11)C ,. ······································································· 7 分 下证90PQC ∠=°.连CB ,则四边形OACB 是正方形.
法一:(i )当点P 在线段OB 上,Q 在线段AB 上 (Q 与B C 、不重合)时,如图–1.
由对称性,得BCQ QOP QPO QOP ∠=∠∠=∠,, ∴ 180QPB QCB QPB QPO ∠+∠=∠+∠=°,
∴ 360()90PQC QPB QCB PBC ∠=-∠+∠+∠=°°. ··················································· 8分 (ii )当点P 在线段OB 的延长线上,Q 在线段AB 上时,如图–2,如图–3
∵12QPB QCB ∠=∠∠=∠,, ∴90PQC PBC ∠=∠=°. ···························· 9分 (iii )当点Q 与点B 重合时,显然90PQC ∠=°. 综合(i )(ii )(iii ),90PQC ∠=°.
∴在1L 上存在点(11)C ,,使得CPQ △是以Q 为直角顶点的等腰直角三角形. ············· 11 分
L 1
法二:由1OA OB ==,所以OAB △是等腰直角三角形,若在1L 上存在点C ,使得CPQ △是以Q 为直角顶点的等腰直角三角形,则PQ QC =,所以OQ QC =,又1L x ∥轴, 则C ,O 两点关于直线L 对称,所以1AC OA ==,得(11)C ,. ································································· 7 分 延长MQ 与1L 交于点N .
(i )如图–4,当点Q 在线段AB 上(Q 与A B 、不重合)时, ∵四边形OACB 是正方形,
∴四边形OMNA 和四边形MNCB 都是矩形,AQN △和QBM △都是等腰直角三角形. ∴90NC MB MQ NQ AN OM QNC QMB ====∠=∠=,,°. 又∵OM MP =, ∴MP QN =, ∴QNC QMP △≌△, ∴MPQ NQC ∠=∠, 又∵90MQP MPQ ∠+∠=°, ∴90MQP NQC ∠+∠=°.
∴90CQP ∠=°. ················································································································· 8分 (ii )当点Q 与点B 重合时,显然90PQC ∠=°. ················································ 9分 (iii )Q 在线段AB 的延长线上时,如图–5, ∵BCQ MPQ ∠=∠,∠1=∠2 ∴90CQP CBM ∠=∠=°
L 1
综合(i )(ii )(iii ),90PQC ∠=°.
∴在1L 上存在点(11)C ,,使得CPQ △是以Q 为直角顶点的等腰直角三角形. ········ 11分
法三:由1OA OB ==,所以OAB △是等腰直角三角形,若在1L 上存在点C ,使得CPQ △是以Q 为直角顶点的等腰直角三角形,则PQ QC =,所以OQ QC =,又1L x ∥轴,
则C ,O 两点关于直线L 对称,所以1AC OA ==,得(11)C ,. ·························· 9分 连PC ,∵|1|PB t =-,1
2
OM t =
,12t MQ =-,
∴2
2
2
2
2
(1)122PC PB BC t t t =+=-+=-+,
2
2
2
22222
11222t t t OQ OP CQ OM MQ t ????===+=+-=-+ ? ?????
.
∴222
PC OP QC =+,∴90CQP ∠=°. ·········································································· 10分 ∴在1L 上存在点(11)C ,,使得CPQ △是以Q 为直角顶点的等腰直角三角形. ·
··········· 11分 【079】解:(1)解2
7120x x -+=得1243x x ==,
OA OB >,43OA OB ∴==, ·
························································································ 1分 在Rt AOB △
中,由勾股定理有5AB ==,4
sin 5
OA ABC AB ∴∠=
= (2)∵点E 在x 轴上,163AOE S =△,11623AO OE ∴?=,8
3
OE ∴=
880033E E ????
∴- ? ?????
,或, ······························································································· 1分
L 1
23题图-5
由已知可知D (6,4),设DE y kx b =+,当803E ?? ???
,
时有 46803k b k b =+???=+??解得65
165k b ?=????=-??
∴61655DE y x =-,同理803E ??- ???,时,6161313DE
y x =+ ··· 1分 在AOE △中,8
9043
AOE OA OE ∠===
°,, 在AOD △中,9046OAD OA OD ∠===°,,,
OE OA
OA OD
=,AOE DAO ∴△∽△
(3)满足条件的点有四个,123475224244(38)(30)1472525F F F F ????
----- ? ?????
,;
,;,;, ··· 4分 说明:本卷中所有题目,若由其它方法得出正确结论,可参照本评 【080】(1)过点C 作CD AB ⊥,垂足为D .则2AD =, 当MN 运动到被CD 垂直平分时,四边形MNQP
是矩形, 即3
2
AM =
时,四边形MNQP 是矩形, 3
2
t ∴=
秒时,四边形MNQP 是矩形. tan 60PM AM =°=MNQP S ∴=四边形
(2)1°当01t <<时, 1()2MNQP
S PM QN MN =+四边形·12=2°当12t ≤≤时
1
()2
MNQP S PM QN MN =+四边形·
1)12t ?=-?·=3°当23t <<时,
1
()2
MNQP S PM QN MN =+四边形·
1))2
t t ?=--?
C
P
Q
B
A M D N
=+····························································· 10分
2020年中考数学挑战压轴题(含答案)
2020 挑战压轴题中考数学 精讲解读篇 因动点产生的相似三角形问题 1.如图,在平面直角坐标系xOy中,将抛物线y=x2的对称轴绕着点P(0,2)顺时针旋转45°后与该抛物线交于A、B两点,点Q是该抛物线上一点. (1)求直线AB的函数表达式; (2)如图①,若点Q在直线AB的下方,求点Q到直线AB的距离的最大值;(3)如图②,若点Q在y轴左侧,且点T(0,t)(t<2)是射线PO上一点,当以P、B、Q为顶点的三角形与△PAT相似时,求所有满足条件的t的值. 2.如图,已知BC是半圆O的直径,BC=8,过线段BO上一动点D,作AD⊥BC 交半圆O于点A,联结AO,过点B作BH⊥AO,垂足为点H,BH的延长线交半圆O于点F. (1)求证:AH=BD; (2)设BD=x,BE?BF=y,求y关于x的函数关系式; (3)如图2,若联结FA并延长交CB的延长线于点G,当△FAE与△FBG相似时,求BD的长度.
3.如图,在平面直角坐标系xOy中,直线AB过点A(3,0)、B(0,m)(m>0),tan∠BAO=2. (1)求直线AB的表达式; (2)反比例函数y=的图象与直线AB交于第一象限内的C、D两点(BD<BC),当AD=2DB时,求k1的值; (3)设线段AB的中点为E,过点E作x轴的垂线,垂足为点M,交反比例函数y=的图象于点F,分别联结OE、OF,当△OEF∽△OBE时,请直接写出满足条件的所有k2的值. 4.如图,在Rt△ABC中,∠ACB=90°,AC=1,BC=7,点D是边CA延长线的一点,AE⊥BD,垂足为点E,AE的延长线交CA的平行线BF于点F,连结CE交AB于点G. (1)当点E是BD的中点时,求tan∠AFB的值; (2)CE?AF的值是否随线段AD长度的改变而变化?如果不变,求出CE?AF的值;如果变化,请说明理由; (3)当△BGE和△BAF相似时,求线段AF的长.
中考数学压轴题100题精选【含答案】
中考数学压轴题100题精选【含答案】 【001 】如图,已知抛物线 2 (1)y a x =-+a ≠0)经过点(2)A -,0,抛物线的顶点为D ,过O 作射线OM AD ∥.过顶点D 平行于x 轴的直线交射线OM 于点C ,B 在x 轴正半轴上,连结BC . (1)求该抛物线的解析式; (2)若动点P 从点O 出发,以每秒1个长度单位的速度沿射线OM 运动,设点P 运动的时间为 ()t s .问当t 为何值时,四边形DAOP 分别为平行四边形?直角梯形?等腰梯形? (3)若O C O B =,动点P 和动点Q 分别从点O 和点B 同时出发,分别以每秒1个长度单位和2个长度单位的速度沿OC 和BO 运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为t ()s ,连接PQ ,当t 为何值时,四边形BCPQ 的面积最小?并求出最小值及此时PQ 的长. 【002】如图16,在Rt △ABC 中,∠C=90°,AC = 3,AB = 5.点P 从点C 出发沿CA 以每秒1 个单位长的速度向点A 匀速运动,到达点A 后立刻以原来的速度沿AC 返回;点Q 从点A 出发沿AB 以每秒1个单位长的速度向点B 匀速运动.伴随着P 、Q 的运动,DE 保持垂直平分PQ ,且交PQ 于点D ,交折线QB-BC-CP 于点E .点P 、Q 同时出发,当点Q 到达点B 时停止运动,点P 也随之停止.设点P 、Q 运动的时间是t 秒(t >0). (1)当t = 2时,AP = ,点Q 到AC 的距离是 ; (2)在点P 从C 向A 运动的过程中,求△APQ 的面积S 与 t 的函数关系式;(不必写出t 的取值范围) (3)在点E 从B 向C 运动的过程中,四边形QBED 能否成 为直角梯形?若能,求t 的值.若不能,请说明理由;
2016年中考数学压轴题精选及详解
2020年中考数学压轴题精选解析 中考压轴题分类专题三——抛物线中的等腰三角形 基本题型:已知AB ,抛物线()02≠++=a c bx ax y ,点P 在抛物线上(或坐标轴上,或 抛物线的对称轴上),若ABP ?为等腰三角形,求点P 坐标。 分两大类进行讨论: (1)AB 为底时(即PA PB =):点P 在AB 的垂直平分线上。 利用中点公式求出AB 的中点M ; 利用两点的斜率公式求出AB k ,因为两直线垂直斜率乘积为1-,进而求出AB 的垂直平分线的斜率k ; 利用中点M 与斜率k 求出AB 的垂直平分线的解析式; 将AB 的垂直平分线的解析式与抛物线(或坐标轴,或抛物线的对称轴)的解析式联立即可求出点P 坐标。 (2)AB 为腰时,分两类讨论: ①以A ∠为顶角时(即AP AB =):点P 在以A 为圆心以AB 为半径的圆上。 ②以B ∠为顶角时(即BP BA =):点P 在以B 为圆心以 AB 为半径的圆上。 利用圆的一般方程列出A e (或B e )的方程,与抛物线(或坐标轴,或抛物线的对称轴)的解析式联立即可求出点P 坐标。 中考压轴题分类专题四——抛物线中的直角三角形 基本题型:已知AB ,抛物线()02≠++=a c bx ax y ,点P 在抛物线上(或坐标轴上,或 抛物线的对称轴上),若ABP ?为直角三角形,求点P 坐标。 分两大类进行讨论: (1)AB 为斜边时(即PA PB ⊥):点P 在以AB 为直径的圆周上。 利用中点公式求出AB 的中点M ; 利用圆的一般方程列出M e 的方程,与抛物线(或坐标轴,或抛物线的对称轴)的解析式联立即可求出点P 坐标。 (2)AB 为直角边时,分两类讨论: ①以A ∠为直角时(即AP AB ⊥): ②以B ∠为直角时(即BP BA ⊥): 利用两点的斜率公式求出AB k ,因为两直线垂直斜率乘积为1-,进而求出PA (或PB )的斜率 k ;进而求出PA (或PB )的解析式; 将PA (或PB )的解析式与抛物线(或坐标轴,或抛物线的对称轴)的解析式联立即可求出点P 坐标。 所需知识点: 一、 两点之间距离公式: 已知两点()()2211y ,x Q ,y ,x P , 则由勾股定理可得:()()2 21221y y x x PQ -+-= 。 二、 圆的方程: 点()y ,x P 在⊙M 上,⊙M 中的圆心M 为()b ,a ,半径为R 。 则()()R b y a x PM =-+-= 22,得到方程☆:()()22 2 R b y a x =-+-。 ∴P 在☆的图象上,即☆为⊙M 的方程。 三、 中点公式: 四、 已知两点()()2211y ,x Q ,y ,x P ,则线段PQ 的中点M 为??? ??++22 2121y y ,x x 。 五、 任意两点的斜率公式: 已知两点()()2211y ,x Q ,y ,x P ,则直线PQ 的斜率: 2 12 1x x y y k PQ --= 。 中考压轴题分类专题五——抛物线中的四边形 基本题型:一、已知AB ,抛物线()02≠++=a c bx ax y ,点P 在抛物线上(或坐标轴上, 或抛物线的对称轴上),若四边形ABPQ 为平行四边形,求点P 坐标。 分两大类进行讨论: (1)AB 为边时 (2)AB 为对角线时 二、已知AB ,抛物线()02 ≠++=a c bx ax y ,点P 在抛物线上(或坐标轴上,或抛物线的对 称轴上),若四边形ABPQ 为距形,求点P 坐标。 在四边形ABPQ 为平行四边形的基础上,运用以下两种方法进行讨论: (1)邻边互相垂直 (2)对角线相等 三、已知AB ,抛物线()02 ≠++=a c bx ax y ,点P 在抛物线上(或坐标轴上,或抛物线的对 称轴上),若四边形ABPQ 为菱形,求点P 坐标。 在四边形ABPQ 为平行四边形的基础上,运用以下两种方法进行讨论: (1)邻边相等 (2)对角线互相垂直
2020年版挑战中考数学压轴题详解(115页)
目录 第一部分函数图象中点的存在性问题 1.1 因动点产生的相似三角形问题 例1 上海市中考第24题 例2 苏州市中考第29题 例3 黄冈市中考第25题 例4 义乌市中考第24题 例5 临沂市中考第26题 例6 苏州市中考第29题 1.2 因动点产生的等腰三角形问题 例1 上海市虹口区中考模拟第25题 例2 扬州市中考第27题 例3 临沂市中考第26题 例4 湖州市中考第24题 例5 盐城市中考第28题 例6 南通市中考第27题 例7 江西省中考第25题 1.3 因动点产生的直角三角形问题 例1 山西省中考第26题 例2 广州市中考第24题 例3 杭州市中考第22题 例4 浙江省中考第23题 例5 北京市中考第24题 例6 嘉兴市中考第24题 例7 河南省中考第23题 1.4 因动点产生的平行四边形问题 例1 上海市松江区中考模拟第24题 例2 福州市中考第21题 例3 烟台市中考第26题 例4 上海市中考第24题 例5 江西省中考第24题 例6 山西省中考第26题 例7 江西省中考第24题 1.5 因动点产生的梯形问题 例1 上海市松江中考模拟第24题 例2 衢州市中考第24题 例4 义乌市中考第24题
例5 杭州市中考第24题 例7 广州市中考第25题 1.6 因动点产生的面积问题 例1 苏州市中考第29题 例2 菏泽市中考第21题 例3 河南省中考第23题 例4 南通市中考第28题 例5 广州市中考第25题 例6 扬州市中考第28题 例7 兰州市中考第29题 1.7 因动点产生的相切问题 例1 上海市杨浦区中考模拟第25题 例2 河北省中考第25题 例3 无锡市中考第28题 1.8 因动点产生的线段和差问题 例1 天津市中考第25题 例2 滨州市中考第24题 例3 山西省中考第26题 第二部分图形运动中的函数关系问题 2.1 由比例线段产生的函数关系问题 例1 宁波市中考第26题 例2 上海市徐汇区中考模拟第25题 例3 连云港市中考第26题 例4 上海市中考第25题 2.2 由面积公式产生的函数关系问题 例1 菏泽市中考第21题 例2 广东省中考第22题 例3 河北省中考第26题 例4 淮安市中考第28题 例5 山西省中考第26题 例6 重庆市中考第26题 第三部分图形运动中的计算说理问题 3.1 代数计算及通过代数计算进行说理问题 例1 南京市中考第26题 例2 南昌市中考第25题 3.2几何证明及通过几何计算进行说理问题 例1 上海市黄浦区中考模拟第24题 例2 江西省中考第24题
2020中考数学压轴题100题精选(附答案解析)
2020中考数学压轴题100题精选 (附答案解析) 【001 】如图,已知抛物线2(1)y a x =-+(a ≠0)经过点 (2)A -,0,抛物线的顶点为D ,过O 作射线OM AD ∥.过顶点D 平行于x 轴的直线交射线OM 于点C ,B 在x 轴正半轴上,连结 BC . (1)求该抛物线的解析式; (2)若动点P 从点O 出发,以每秒1个长度单位的速度沿射线OM 运动,设点P 运动的时间为()t s .问当t 为何值时,四边形DAOP 分别为平行四边形?直角梯形?等腰梯形? (3)若OC OB =,动点P 和动点Q 分别从点O 和点B 同时出发,分别以每秒1个长度单位和2个长度单位的速度沿OC 和BO 运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为t ()s ,连接PQ ,当t 为何值时,四边形BCPQ 的面积最小?并求出最小值及此时PQ 的长.
【002】如图16,在Rt△ABC中,∠C=90°,AC = 3,AB = 5.点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动,到达点A后立刻以原来的速度沿AC返回;点Q从点A 出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB-BC-CP于点E.点P、Q同时出发,当点Q到达点B 时停止运动,点P也随之停止.设点P、Q运动的时间是t 秒(t>0). (1)当t = 2时,AP = ,点Q到AC的距离是; (2)在点P从C向A运动的过程中,求△APQ的面积S 与 t的函数关系式;(不必写出t的取值范围)(3)在点E从B向C 成 为直角梯形?若能,求t (4)当DE经过点C 时,请直接 图16 【003】如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0)、C(8,0)、D(8,8).抛物线y=ax2+bx过A、C两点. (1)直接写出点A的坐标,并求出抛物线的解析式;
中考数学压轴题解题方法大全及技巧
专业资料整理分享 中考数学压轴题解题技巧 湖北竹溪城关中学明道银 解中考数学压轴题秘诀(一) 数学综合题关键是第24题和25题,我们不妨把它分为函数型综合题和几何型综合题。 (一)函数型综合题:是先给定直角坐标系和几何图形,求(已知)函数的解析式(即在求解前已知函数的类型),然后进行图形的研究,求点的坐标或研究图形的某些性质。初中已知函数有:①一次函数(包括正比例函数)和常值函数,它们所对应的图像是直线;②反比例函数,它所对应的图像是双曲线; ③二次函数,它所对应的图像是抛物线。求已知函数的解析式主要方法是待定系数法,关键是求点的坐标,而求点的坐标基本方法是几何法(图形法)和代数法(解析法)。此类题基本在第24题,满分12分,基本分2-3小题来呈现。 (二)几何型综合题:是先给定几何图形,根据已知条件进行计算,然后有动点(或动线段)运动,对应产生线段、面积等的变化,求对应的(未知)函数的解析式(即在没有求出之前不知道函数解析式的形式是什么)和求函数的定义域,最后根据所求的函数关系进行探索研究,一般有:在什么条件下图形是等腰三角形、直角三角形、四边形是菱形、梯形等或探索两个三角形满足什么条件相似等或探究线段之间的位置关系等或探索面积之间满足一定关系求x的值等和直线(圆)与圆的相切时求自变量的值等。求未知函数解析式的关键是
列出包含自变量和因变量之间的等量关系(即列出含有x、y的方程),变形写成y=f(x)的形式。一般有直接法(直接列出含有x和y的方程)和复合法(列出含有x和y和第三个变量的方程,然后求出第三个变量和x之间的函数关系式,代入消去第三个变量,得到y=f(x)的形式),当然还有参数法,这个已超出初中数学教学要求。找等量关系的途径在初中主要有利用勾股定理、平行线截得比例线段、三角形相似、面积相等方法。求定义域主要是寻找图形的特殊位置(极限位置)和根据解析式求解。而最后的探索问题千变万化,但少不了对图形的分析和研究,用几何和代数的方法求出x的值。几何型综合题基本在第25题做为压轴题出现,满分14分,一般分三小题呈现。 在解数学综合题时我们要做到:数形结合记心头,大题小作来转化,潜在条件不能忘,化动为静多画图,分类讨论要严密,方程函数是工具,计算推理要严谨,创新品质得提高。 解中考数学压轴题秘诀(二) 具有选拔功能的中考压轴题是为考察考生综合运用知识的能力而设计的题目,其特点是知识点多,覆盖面广,条件隐蔽,关系复杂,思路难觅,解法灵活。解数学压轴题,一要树立必胜的信心,二要具备扎实的基础知识和熟练的基本技能,三要掌握常用的解题策略。现介绍几种常用的解题策略,供初三同学参考。 1、以坐标系为桥梁,运用数形结合思想:
最新全国各地中考数学解答题压轴题解析2
全国各地中考数学解答题压轴题解析2
2011年全国各地中考数学解答题压轴题解析(2) 1.(湖南长沙10分)如图,在平面直角坐标系中,已知 点A(0,2),点P是x轴上一动点,以线段AP为一边, 在其一侧作等边三角线APQ。当点P运动到原点O处时, 记Q得位置为B。 (1)求点B的坐标; (2)求证:当点P在x轴上运动(P不与Q重合)时,∠ABQ为定值; (3)是否存在点P,使得以A、O、Q、B为顶点的四边形是梯形?若存在,请求出P点的坐标;若不存在,请说明理由。 【答案】解:(1)过点B作BC⊥y轴于点C, ∵A(0,2),△AOB为等边三角形, ∴AB=OB=2,∠BAO=60°, ∴BC=3,OC=AC=1。即B( 3 1,)。 (2)不失一般性,当点P在x轴上运动(P不与O重合)时, ∵∠PAQ==∠OAB=60°,∴∠PAO=∠QAB, 在△APO和△AQB中,∵AP=AQ,∠PAO=∠QAB,AO=AB,∴△APO≌△AQB总成立。 ∴∠ABQ=∠AOP=90°总成立。 ∴当点P在x轴上运动(P不与Q重合)时,∠ABQ为定值90°。 (3)由(2)可知,点Q总在过点B且与AB垂直的直线上, ∴AO与BQ不平行。
①当点P 在x 轴负半轴上时,点Q 在点B 的下方, 此时,若AB∥OQ ,四边形AOQB 即是梯形, 当AB∥OQ 时,∠BQO=90°,∠BOQ=∠ABO=60°。 又OB=OA=2,可求得BQ=3。 由(2)可知,△APO≌△AQB ,∴OP=BQ=3, ∴此时P 的坐标为(3 0-, )。 ②当点P 在x 轴正半轴上时,点Q 在点B 的上方, 此时,若AQ∥OB ,四边形AOQB 即是梯形, 当AQ∥OB 时,∠ABQ=90°,∠QAB=∠ABO=60°。 又AB= 2,可求得BQ=23, 由(2)可知,△APO≌△AQB ,∴OP=BQ=23, ∴此时P 的坐标为(23 0, )。 综上所述,P 的坐标为(3 0-, )或(23 0,)。 【考点】等边三角形的性质,坐标与图形性质;全等三角形的判定和性质,勾股定理,梯形的判定。 【分析】(1)根据题意作辅助线过点B 作BC⊥y 轴于点C ,根据等边三角形的性质即可求出点B 的坐标。 (2)根据∠PAQ═∠OAB=60°,可知∠PAO=∠QAB ,得出△APO≌△AQB 总成立,得出当点P 在x 轴上运动(P 不与Q 重合)时,∠ABQ 为定值90°。 (3)根据点P 在x 的正半轴还是负半轴两种情况讨论,再根据全等三角形的性质即可得出结果。 2.(湖南永州10分)探究问题:
中考数学《压轴题》专题训练含答案解析
压轴题 1、已知,在平行四边形O ABC 中,O A=5,AB =4,∠OCA=90°,动点P 从O 点出发沿射线OA 方向以每秒2个单位的速度移动,同时动点Q从A 点出发沿射线AB 方向以每秒1个单位的速度移动.设移动的时间为t秒. (1)求直线AC 的解析式; (2)试求出当t 为何值时,△O AC 与△PAQ 相似; (3)若⊙P 的半径为 58,⊙Q 的半径为2 3 ;当⊙P 与对角线AC 相切时,判断⊙Q 与直线AC 、B C的位置关系,并求出Q 点坐标。 解:(1)42033 y x =- + (2)①当0≤t≤2.5时,P在O A上,若∠OAQ =90°时, 故此时△OA C与△PAQ 不可能相似. 当t>2.5时,①若∠APQ=90°,则△A PQ ∽△OCA , ∵t>2.5,∴ 符合条件. ②若∠A QP=90°,则△APQ ∽△∠OA C, ∵t>2.5,∴ 符合条件.
综上可知,当 时,△O AC 与△APQ 相似. (3)⊙Q 与直线AC、B C均相切,Q 点坐标为( 10 9 ,5 31) 。 2、如图,以矩形OABC 的顶点O 为原点,OA 所在的直线为x轴,OC 所在的直线为y轴,建立平面直角坐标系.已知OA =3,OC =2,点E 是AB 的中点,在OA 上取一点D ,将△BD A沿BD 翻折,使点A 落在BC 边上的点F 处. (1)直接写出点E 、F 的坐标; (2)设顶点为F 的抛物线交y 轴正半轴...于点P ,且以点E 、F 、P 为顶点的三角形是等腰三角形,求该抛物线的解析式; (3)在x 轴、y轴上是否分别存在点M 、N ,使得四边形MNF E的周长最小?如果存在,求出周长的最小值;如果不存在,请说明理由. 解:(1)(31)E ,;(12)F ,.(2)在Rt EBF △中,90B ∠=, 2222125EF EB BF ∴=+=+=. 设点P 的坐标为(0)n ,,其中0n >, 顶点(1 2)F ,, ∴设抛物线解析式为2 (1)2(0)y a x a =-+≠. ①如图①,当EF PF =时,22 EF PF =,2 2 1(2)5n ∴+-=. 解得10n =(舍去);24n =.(04)P ∴,.24(01)2a ∴=-+.解得2a =. ∴抛物线的解析式为22(1)2y x =-+ (第2题)
2018挑战中考数学压轴题((全套)含答案与解析)
第一部分函数图象中点的存在性问题 §1.1因动点产生的相似三角形问题 例1 2014 年衡阳市中考第 28 题 例2 2014 年益阳市中考第 21 题 例3 2015 年湘西州中考第 26 题 例4 2015 年张家界市中考第 25 题 例5 2016 年常德市中考第 26 题 例6 2016 年岳阳市中考第 24 题 例 72016年上海市崇明县中考模拟第25 题 例 82016年上海市黄浦区中考模拟第26 题 §1.2因动点产生的等腰三角形问题 例9 2014 年长沙市中考第 26 题 例10 2014 年张家界市第 25 题 例11 2014 年邵阳市中考第 26 题 例12 2014 年娄底市中考第 27 题 例13 2015 年怀化市中考第 22 题 例14 2015 年长沙市中考第 26 题 例15 2016 年娄底市中考第 26 题 例 162016年上海市长宁区金山区中考模拟第25 题例 172016年河南省中考第 23 题
§1.3因动点产生的直角三角形问题 例19 2015 年益阳市中考第 21 题 例20 2015 年湘潭市中考第 26 题 例21 2016 年郴州市中考第 26 题 例22 2016 年上海市松江区中考模拟第 25 题 例23 2016 年义乌市绍兴市中考第 24 题 §1.4因动点产生的平行四边形问题 例24 2014 年岳阳市中考第 24 题 例25 2014 年益阳市中考第 20 题 例26 2014 年邵阳市中考第 25 题 例27 2015 年郴州市中考第 25 题 例28 2015 年黄冈市中考第 24 题 例29 2016 年衡阳市中考第 26 题 例 302016年上海市嘉定区宝山区中考模拟中考第24 题例 312016年上海市徐汇区中考模拟第 24 题 §1.5因动点产生的面积问题 例32 2014 年常德市中考第 25 题 例33 2014 年永州市中考第 25 题
中考数学压轴题精选含详细答案
目 录 2.1 由比例线段产生的函数关系问题 例1 2012年上海市徐汇区中考模拟第25题 例2 2012年连云港市中考第26题 例3 2010年上海市中考第25题 例1 2012年上海市徐汇区中考模拟第25题 在Rt △ABC 中,∠C =90°,AC =6,53sin B ,⊙B 的半径长为1,⊙B 交边CB 于点P ,点O 是边AB 上的动点. (1)如图1,将⊙B 绕点P 旋转180°得到⊙M ,请判断⊙M 与直线AB 的位置关系; (2)如图2,在(1)的条件下,当△OMP 是等腰三角形时,求OA 的长; (3)如图3,点N 是边BC 上的动点,如果以NB 为半径的⊙N 和以OA 为半径的⊙O 外切,设NB =y ,OA =x ,求y 关于x 的函数关系式及定义域. 图1 图2 图3 动感体验 请打开几何画板文件名“12徐汇25”,拖动点O 在AB 上运动,观察△OMP 的三个顶点与对边的垂直平分线的位置关系,可以体验到,点O 和点P 可以落在对边的垂直平分线上,点M 不能. 请打开超级画板文件名“12徐汇25”, 分别点击“等腰”按钮的左部和中部,观察三个角度的大小,可得两种等腰的情形.点击“相切”按钮,可得y 关于x 的函数关系. 思路点拨 1.∠B 的三角比反复用到,注意对应关系,防止错乱. 2.分三种情况探究等腰△OMP ,各种情况都有各自特殊的位置关系,用几何说理的方法比较简单. 3.探求y 关于x 的函数关系式,作△OBN 的边OB 上的高,把△OBN 分割为两个具有公共直角边的直角三角形. 满分解答
(1) 在Rt △ABC 中,AC =6,53sin =B , 所以AB =10,BC =8. 过点M 作MD ⊥AB ,垂足为D . 在Rt △BMD 中,BM =2,3sin 5MD B BM ==,所以65 MD =. 因此MD >MP ,⊙M 与直线AB 相离. 图4 (2)①如图4,MO ≥MD >MP ,因此不存在MO =MP 的情况. ②如图5,当PM =PO 时,又因为PB =PO ,因此△BOM 是直角三角形. 在Rt △BOM 中,BM =2,4cos 5BO B BM ==,所以85BO =.此时425 OA =. ③如图6,当OM =OP 时,设底边MP 对应的高为OE . 在Rt △BOE 中,BE =32,4cos 5BE B BO ==,所以158BO =.此时658 OA =. 图5 图6 (3)如图7,过点N 作NF ⊥AB ,垂足为F .联结ON . 当两圆外切时,半径和等于圆心距,所以ON =x +y . 在Rt △BNF 中,BN =y ,3sin 5B =,4cos 5B =,所以35NF y =,45 BF y =. 在Rt △ONF 中,4105 OF AB AO BF x y =--=--,由勾股定理得ON 2=OF 2+NF 2. 于是得到22243()(10)()55 x y x y y +=--+. 整理,得2505040 x y x -=+.定义域为0<x <5. 图7 图8 考点伸展 第(2)题也可以这样思考: 如图8,在Rt △BMF 中,BM =2,65MF =,85 BF =.
数学中考数学压轴题(讲义及答案)附解析
一、中考数学压轴题 1.如图,在长方形ABCD 中,AB =4cm ,BE =5cm ,点E 是AD 边上的一点,AE 、DE 分别长acm .bcm ,满足(a -3)2+|2a +b -9|=0.动点P 从B 点出发,以2cm/s 的速度沿B→C→D 运动,最终到达点D ,设运动时间为t s . (1)a =______cm ,b =______cm ; (2)t 为何值时,EP 把四边形BCDE 的周长平分? (3)另有一点Q 从点E 出发,按照E→D→C 的路径运动,且速度为1cm/s ,若P 、Q 两点同时出发,当其中一点到达终点时,另一点随之停止运动.求t 为何值时,△BPQ 的面积等于6cm 2. 2.在平面直角坐标系中,抛物线2 4y mx mx n =-+(m >0)与x 轴交于A ,B 两点,点B 在点A 的右侧,顶点为C ,抛物线与y 轴交于点D ,直线CA 交y 轴于E ,且 :3:4??=ABC BCE S S . (1)求点A ,点B 的坐标; (2)将△BCO 绕点C 逆时针旋转一定角度后,点B 与点A 重合,点O 恰好落在y 轴上, ①求直线CE 的解析式; ②求抛物线的解析式. 3.如图1,抛物线2 (0)y ax bx c a =++≠的顶点为C (1,4),交x 轴于A 、B 两点,交y 轴于点D ,其中点B 的坐标为(3,0). (1)求抛物线的解析式; (2)如图2,点E 是BD 上方抛物线上的一点,连接AE 交DB 于点F ,若AF=2EF ,求出点E 的坐标. (3)如图3,点M 的坐标为( 3 2 ,0),点P 是对称轴左侧抛物线上的一点,连接MP ,将MP 沿MD 折叠,若点P 恰好落在抛物线的对称轴CE 上,请求出点P 的横坐标.
中考数学压轴题解题技巧及训练完整版
中考数学压轴题解题技巧及训练完整版 Pleasure Group Office【T985AB-B866SYT-B182C-BS682T-STT18】
中考数学压轴题解题技巧 (完整版) 数学综压轴题是为考察考生综合运用知识的能力而设计的,集中体现知识的综合性和方法的综合性,多数为函数型综合题和几何型综合题。 函数型综合题:是给定直角坐标系和几何图形,先求函数的解析式,再进行图形的研究,求点的坐标或研究图形的某些性质。求已知函数的解析式主要方法是待定系数法,关键是求点的坐标,而求点的坐标基本方法是几何法(图形法)和代数法(解析法)。 几何型综合题:是先给定几何图形,根据已知条件进行计算,然后有动点(或动线段)运动,对应产生线段、面积等的变化,求对应的(未知)函数的解析式,求函数的自变量的取值范围,最后根据所求的函数关系进行探索研究。一般有:在什么条件下图形是等腰三角形、直角三角形,四边形是平行四边形、菱形、梯形等,或探索两个三角形满足什么条件相似等,或探究线段之间的数量、位置关系等,或探索面积之间满足一定关系时求x的值等,或直线(圆)与圆的相切时求自变量的值等。求未知函数解析式的关键是列出包含自变量和因变量之间的等量关系(即列出含有x、y的方程),变形写成y=f(x)的形式。找等量关系的途径在初中主要有利用勾股定理、平行线截得比例线段、三角形相似、面积相等方法。求函数的自变量的取值范围主要是寻找图形的特殊位置(极端位置)和根据解析式求解。而最后的探索问题千变万化,但少不了对图形的分析和研究,用几何和代数的方法求出x 的值。 解中考压轴题技能:中考压轴题大多是以坐标系为桥梁,运用数形结合思想,通过建立点与数即坐标之间的对应关系,一方面可用代数方法研究几何图形的性质,另一方面又可借助几何直观,得到某些代数问题的解答。关键是掌握几种常用的数学思想方法。 一是运用函数与方程思想。以直线或抛物线知识为载体,列(解)方程或方程组求其解析式、研究其性质。 二是运用分类讨论的思想。对问题的条件或结论的多变性进行考察和探究。 三是运用转化的数学的思想。由已知向未知,由复杂向简单的转换。中考压轴题它是对考生综合能力的一个全面考察,所涉及的知识面广,所使用的数学思想方法也较全面。因此,可把压轴题分离为相对独立而又单一的知识或方法组块去思考和探究。 解中考压轴题技能技巧: 一是对自身数学学习状况做一个完整的全面的认识。根据自己的情况考试的时候重心定位准确,防止“捡芝麻丢西瓜”。所以,在心中一定要给压轴题或几个“难点”一个时间上的限制,如果超过你设置的上限,必须要停
中考数学压轴题精选及答案(整理版)
20XX 年全国各地中考数学压轴题精选 1、(黄石市20XX 年)(本小题满分9分)已知⊙1O 与⊙2O 相交于A 、B 两点,点1 O 在⊙2O 上,C 为⊙2O 上一点(不与A ,B ,1O 重合) ,直线CB 与⊙1O 交于另一点D 。 (1)如图(8),若 AC 是⊙2O 的直径,求证:AC CD =; (2)如图(9),若C 是⊙1O 外一点,求证:1O C AD ⊥; (3)如图(10),若C 是⊙1O 内一点,判断(2)中的结论是否成立。 2、(黄石市20XX 年)(本小题满分10分)已知二次函数 2248y x mx m =-+- (1)当2x ≤时,函数值 y 随x 的增大而减小,求m 的取值范围。 (2)以抛物线 2248y x mx m =-+-的顶点A 为一个顶点作该抛物线的内接 正三角形 AMN (M ,N 两点在抛物线上) ,请问:△AMN 的面积是与m 无关的定值吗?若是,请求出这个定值;若不是,请说明理由。 (3)若抛物线 2248y x mx m =-+-与x 轴交点的横坐标均为整数,求整数m 的值。
3、(20XX 年广东茂名市)如图,⊙P 与y 轴相切于坐标原点O (0,0) ,与x 轴相交于点A (5,0),过点A 的直线AB 与 y 轴的正半轴交于点B ,与⊙P 交于点C . (1)已知AC=3,求点B的坐标; (4分) (2)若AC=a , D 是O B的中点.问:点O 、P 、C 、D 四点是否在同一圆上?请说明 理由.如果这四点在同一圆上,记这个圆的圆心为1O ,函数 x k y = 的图象经过点1O ,求k 的值(用含a 的代数式表示). 4、庆市潼南县20XX 年)如图,在平面直角坐标系中,△ABC 是直角三角形,∠ ACB =90,AC =BC ,OA =1,OC =4,抛物线2y x bx c =++经过A ,B 两点,抛物 线的顶点为D . (1)求b ,c 的值; (2)点E 是直角三角形ABC 斜边AB 上一动点(点A 、B 除外),过点E 作x 轴的 垂线 交抛物线于点F ,当线段EF 的长度最大时,求点E 的坐标; (3)在(2)的条件下:①求以点E、B、F、D为顶点的四边形的面积;②在抛 物线上是否存在一点P ,使△EFP 是以EF 为直角边的直角三角形? 若存在,求出所有点P 的坐标;若不存在,说明理由. 第3题图 χ y
中考数学二轮复习中考数学压轴题知识点及练习题附解析(1)
一、中考数学压轴题 1.(1)如图1,A 是⊙O 上一动点,P 是⊙O 外一点,在图中作出PA 最小时的点A . (2)如图2,Rt △ABC 中,∠C =90°,AC =8,BC =6,以点C 为圆心的⊙C 的半径是3.6,Q 是⊙C 上一动点,在线段AB 上确定点P 的位置,使PQ 的长最小,并求出其最小值. (3)如图3,矩形ABCD 中,AB =6,BC =9,以D 为圆心,3为半径作⊙D ,E 为⊙D 上一动点,连接AE ,以AE 为直角边作Rt △AEF ,∠EAF =90°,tan ∠AEF = 1 3 ,试探究四边形ADCF 的面积是否有最大或最小值,如果有,请求出最大或最小值,否则,请说明理由. 2.如图,已知抛物线y =2ax bx c ++与x 轴交于A 3,0-(),B 33,0()两点,与y 轴交于点C 0,3(). (1)求抛物线的解析式及顶点M 坐标; (2)在抛物线的对称轴上找到点P ,使得PAC 的周长最小,并求出点P 的坐标; (3)在(2)的条件下,若点D 是线段OC 上的一个动点(不与点O 、C 重合).过点 D 作D E //PC 交x 轴于点E .设CD 的长为m ,问当m 取何值时, PDE ABMC 1 S S 9 =四边形. 3.如图1,在平面直角坐标系中,抛物线239 334 y x x = --x 轴交于A B 、两点(点A 在点B 的左侧),与y 轴交于点 C . (1)过点C 的直线5 334 y x = -x 轴于点H ,若点P 是第四象限内抛物线上的一个动
点,且在对称轴的右侧,过点P 作//PQ y 轴交直线CH 于点Q ,作//PN x 轴交对称轴于点N ,以PQ PN 、为邻边作矩形PQMN ,当矩形PQMN 的周长最大时,在y 轴上有一动点K ,x 轴上有一动点T ,一动点G 从线段CP 的中点R 出发以每秒1个单位的速度沿R K T →→的路径运动到点T ,再沿线段TB 以每秒2个单位的速度运动到B 点处停止运动,求动点G 运动时间的最小值: (2)如图2, 将ABC ?绕点B 顺时针旋转至A BC ''?的位置, 点A C 、的对应点分别为A C ''、,且点C '恰好落在抛物线的对称轴上,连接AC '.点E 是y 轴上的一个动点,连 接AE C E '、, 将AC E ?'沿直线C E '翻折为A C E ?'', 是否存在点E , 使得BAA ?'为等腰三角形?若存在,请求出点E 的坐标;若不存在,请说明理由. 4.如图1,正方形CEFG 绕正方形ABCD 的顶点C 旋转,连接AF ,点M 是AF 中点. (1)当点G 在BC 上时,如图2,连接BM 、MG ,求证:BM =MG ; (2)在旋转过程中,当点B 、G 、F 三点在同一直线上,若AB =5,CE =3,则MF = ; (3)在旋转过程中,当点G 在对角线AC 上时,连接DG 、MG ,请你画出图形,探究DG 、MG 的数量关系,并说明理由. 5.“阅读素养的培养是构建核心素养的重要基础,重庆十一中学校以‘大阅读’特色课程实施为突破口,着力提升学生的核心素养.”全校师生积极响应和配合,开展各种活动丰富其课余生活.在数学兴趣小组中,同学们从书上认识了很多有趣的数.其中有一个“和平数”引起了同学们的兴趣.描述如下:一个四位数,记千位上和百位上的数字之和为x ,十位上和个位上的数字之和为y ,如果x y =,那么称这个四位数为“和平数”. 例如:1423,14x =+,23y =+,因为x y =,所以1423是“和平数”. (1)直接写出:最小的“和平数”是________,最大的“和平数”是__________; (2)求同时满足下列条件的所有“和平数”:
中考数学压轴题的解题攻略
中考数学压轴题的解题攻略 具有选拔功能的中考压轴题是为考察考生综合运用知识的能力而设计的题目,其特点是知识点多,覆盖面广,条件隐蔽,关系复杂,思路难觅,解法灵活。解数学压轴题,一要树立必胜的信心,二要具备扎实的基础知识和熟练的基本技能,三要掌握常用的解题策略。现介绍几种常用的解题策略,供初三同学参考。 1、以坐标系为桥梁,运用数形结合思想 纵观最近几年各地的中考压轴题,绝大部分都是与坐标系有关的,其特点是通过建立点与数即坐标之间的对应关系,一方面可用代数方法研究几何图形的性质,另一方面又可借助几何直观,得到某些代数问题的解答。 2、以直线或抛物线知识为载体,运用函数与方程思想 直线与抛物线是初中数学中的两类重要函数,即一次函数与二次函数所表示的图形。因此,无论是求其解析式还是研究其性质,都离不开函数与方程的思想。例如函数解析式的确定,往往需要根据已知条件列方程或方程组并解之而得。3、利用条件或结论的多变性,运用分类讨论的思想 分类讨论思想可用来检测学生思维的准确性与严密性,常常通过条件的多变性或结论的不确定性来进行考察,有些问题,如果不注意对各种情况分类讨论,就有可能造成错解或漏解,纵观近几年的中考压轴题分类讨论思想解题已成为新
的热点。 4、综合多个知识点,运用等价转换思想 任何一个数学问题的解决都离不开转换的思想,初中数学中的转换大体包括由已知向未知,由复杂向简单的转换,而作为中考压轴题,更注意不同知识之间的联系与转换,一道中考压轴题一般是融代数、几何、三角于一体的综合试题,转换的思路更要得到充分的应用。中考压轴题所考察的并非孤立的知识点,也并非个别的思想方法,它是对考生综合能力的一个全面考察,所涉及的知识面广,所使用的数学思想方法也较全面。因此有的考生对压轴题有一种恐惧感,认为自己的水平一般,做不了,甚至连看也没看就放弃了,当然也就得不到应得的分数,为了提高压轴题的得分率,考试中还需要有一种分题、分段的得分策略。 5、分题得分:中考压轴题一般在大题下都有两至三个小题,难易程度是第(1)小题较易,第(2)小题中等,第(3)小题偏难,在解答时要把第(1)小题的分数一定拿到,第(2)小题的分数要力争拿到,第(3)小题的分数要争取得到,这样就大大提高了获得中考数学高分的可能性。 其实,任何一门学科都离不开死记硬背,关键是记忆有技 巧,“死记”之后会“活用”。不记住那些基础知识,怎么会向高层次进军?尤其是语文学科涉猎的范围很广,要真正提高学生的写作水平,单靠分析文章的写作技巧是远远不够的,必须从基
2019年中考数学压轴题精选例题及答案解析
一.解答题(共30小题) 1.(顺义区)如图,直线l 1:y=kx+b平行于直线y=x﹣1,且与直线l 2 : 相交于点P(﹣1,0). (1)求直线l 1、l 2 的解析式; (2)直线l 1 与y轴交于点A.一动点C从点A出发,先沿平行于x轴的方向运 动,到达直线l 2上的点B 1 处后,改为垂直于x轴的方向运动,到达直线l 1 上的 点A 1处后,再沿平行于x轴的方向运动,到达直线l 2 上的点B 2 处后,又改为垂 直于x轴的方向运动,到达直线l 1上的点A 2 处后,仍沿平行于x轴的方向运动,… 照此规律运动,动点C依次经过点B 1,A 1 ,B 2 ,A 2 ,B 3 ,A 3 ,…,B n ,A n ,… ①求点B 1,B 2 ,A 1 ,A 2 的坐标; ②请你通过归纳得出点A n 、B n 的坐标;并求当动点C到达A n 处时,运动的总路径 的长? 2.(莆田)如图1,在平面直角坐标系xOy中,矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=1,OC=2,点D在边OC上且OD=. (1)求直线AC的解析式; (2)在y轴上是否存在点P,直线PD与矩形对角线AC交于点M,使得△DMC为等腰三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由. (3)抛物线y=﹣x2经过怎样平移,才能使得平移后的抛物线过点D和点E(点E在y轴的正半轴上),且△ODE沿DE折叠后点O落在边AB上O′处.
3.(资阳)已知Z 市某种生活必需品的年需求量y 1(万件)、供应量y 2(万件)与价格x (元/件)在一定范围内分别近似满足下列函数关系式:y 1=﹣4x+190,y 2=5x ﹣170.当y 1=y 2时,称该商品的价格为稳定价格,需求量为稳定需求量;当y 1<y 2时,称该商品的供求关系为供过于求;当y 1>y 2时,称该商品的供求关系为供不应求. (1)求该商品的稳定价格和稳定需求量; (2)当价格为45(元/件)时,该商品的供求关系如何?为什么? 4.(哈尔滨)如图1,在平面直角坐标系中,点O 是坐标原点,四边形ABCO 是菱形,点A 的坐标为(﹣3,4),点C 在x 轴的正半轴上,直线AC 交y 轴于点M ,AB 边交y 轴于点H . (1)求直线AC 的解析式; (2)连接BM ,如图2,动点P 从点A 出发,沿折线ABC 方向以2个单位/秒的速度向终点C 匀速运动,设△PMB 的面积为S (S≠0),点P 的运动时间为t 秒,求S 与t 之间的函数关系式(要求写出自变量t 的取值范围); (3)在(2)的条件下,当t 为何值时,∠MPB 与∠BCO 互为余角,并求此时直线OP 与直线AC 所夹锐角的正切值. 5.(桂林)如图已知直线L :y=x+3,它与x 轴、y 轴的交点分别为A 、B 两点. (1)求点A 、点B 的坐标. (2)设F 为x 轴上一动点,用尺规作图作出⊙P,使⊙P 经过点B 且与x 轴相切于点F (不写作法,保留作图痕迹). (3)设(2)中所作的⊙P 的圆心坐标为P (x ,y ),求y 关于x 的函数关系式. (4)是否存在这样的⊙P,既与x 轴相切又与直线L 相切于点B ?若存在,求出圆心P 的坐标;若不存在,请说明理由.
2017挑战中考数学压轴题(第七版精选)
k 第一部分 函数图象中点的存在性问题 1.1 因动点产生的相似三角形问题 1.如图1,在平面直角坐标系xOy 中,顶点为M 的抛物线y =ax 2+bx (a >0)经过点A 和x 轴正半轴上的点B ,AO =BO =2,∠AOB =120°. (1)求这条抛物线的表达式; (2)连结OM ,求∠AOM 的大小; (3)如果点C 在x 轴上,且△ABC 与△AOM 相似,求点C 的坐标. 图1 2.如图1,已知抛物线211(1)444 b y x b x = -++(b 是实数且b >2)与x 轴的正半轴分别交于点A 、B (点A 位于点B 是左侧),与y 轴的正半轴交于点C . (1)点B 的坐标为______,点C 的坐标为__________(用含b 的代数式表示); (2)请你探索在第一象限内是否存在点P ,使得四边形PCOB 的面积等于2b ,且△PBC 是以点P 为直角顶点的等腰直角三角形?如果存在,求出点P 的坐标;如果不存在,请说 明理由; (3)请你进一步探索在第一象限内是否存在点Q ,使得△QCO 、△QOA 和△QAB 中的任 意两个三角形均相似(全等可看作相似的特殊情况)?如果存在,求出点Q 的坐标;如果不存在,请说明理由. 图1
3.如图1,已知抛物线的方程C1: 1 (2)() y x x m m =-+-(m>0)与x轴交于点B、C,与y 轴交于点E,且点B在点C的左侧. (1)若抛物线C1过点M(2, 2),求实数m的值; (2)在(1)的条件下,求△BCE的面积; (3)在(1)的条件下,在抛物线的对称轴上找一点H,使得BH+EH最小,求出点H的坐标; (4)在第四象限内,抛物线C1上是否存在点F,使得以点B、C、F为顶点的三角形与△BCE相似?若存在,求m的值;若不存在,请说明理由. 图1 4.如图1,已知梯形OABC,抛物线分别过点O(0,0)、A(2,0)、B(6,3). (1)直接写出抛物线的对称轴、解析式及顶点M的坐标; (2)将图1中梯形OABC的上下底边所在的直线OA、CB以相同的速度同时向上平移,分别交抛物线于点O1、A1、C1、B1,得到如图2的梯形O1A1B1C1.设梯形O1A1B1C1的面积为S,A1、B1的坐标分别为(x1,y1)、(x2,y2).用含S的代数式表示x2-x1,并求出当S=36时点A1的坐标; (3)在图1中,设点D的坐标为(1,3),动点P从点B出发,以每秒1个单位长度的速度沿着线段BC运动,动点Q从点D出发,以与点P相同的速度沿着线段DM运动.P、Q两点同时出发,当点Q到达点M时,P、Q两点同时停止运动.设P、Q两点的运动时间为t,是否存在某一时刻t,使得直线PQ、直线AB、x轴围成的三角形与直线PQ、直线AB、抛物线的对称轴围成的三角形相似?若存在,请求出t的值;若不存在,请说明理由. 图1 图2