最近邻分类方法例题

k紧邻分类的距离计算方法k-近邻分类（k-nearest neighbors classification）是一种常用的机器学习算法，它通过计算样本之间的距离来进行分类。

本文将介绍k-近邻分类的距离计算方法，并探讨其在实际应用中的优缺点。

一、距离计算方法在k-近邻分类中，计算样本之间的距离是非常重要的一步。

常用的距离计算方法有欧氏距离、曼哈顿距离、闵可夫斯基距离等。

下面分别介绍这些距离计算方法的原理和特点。

1. 欧氏距离（Euclidean Distance）欧氏距离是最常用的距离计算方法之一，它用于计算两个样本之间的直线距离。

假设有两个样本点A(x1, y1)和B(x2, y2)，则它们之间的欧氏距离可以表示为：d(A, B) = sqrt((x2 - x1)^2 + (y2 - y1)^2)欧氏距离的优点是计算简单，直观易懂。

然而，它对异常值比较敏感，可能会导致错误的分类结果。

2. 曼哈顿距离（Manhattan Distance）曼哈顿距离是另一种常用的距离计算方法，它用于计算两个样本之间的城市街区距离。

假设有两个样本点A(x1, y1)和B(x2, y2)，则它们之间的曼哈顿距离可以表示为：d(A, B) = |x2 - x1| + |y2 - y1|曼哈顿距离的优点是不受异常值的影响，对于离群点具有较好的鲁棒性。

然而，它没有考虑样本之间的斜率差异，可能导致分类结果不准确。

3. 闵可夫斯基距离（Minkowski Distance）闵可夫斯基距离是欧氏距离和曼哈顿距离的一种推广，它通过一个参数p来调节距离的计算方式。

当p=2时，闵可夫斯基距离等同于欧氏距离；当p=1时，闵可夫斯基距离等同于曼哈顿距离。

d(A, B) = (|x2 - x1|^p + |y2 - y1|^p)^(1/p)闵可夫斯基距离的优点是可以根据具体问题选择合适的p值，从而权衡欧氏距离和曼哈顿距离的影响。

然而，它的计算复杂度较高，需要考虑到p的选择和样本特征的归一化问题。

K近邻分类算法范文K近邻（K Nearest Neighbors，KNN）分类算法是一种基本的机器学习算法，用于解决分类问题。

它是一种非参数算法，可以用于处理离散和连续型特征的数据集。

本文将详细介绍KNN算法的原理、步骤和算法的优缺点。

一、KNN算法原理1.计算距离：对于新样本，需要与训练集中每个样本计算距离。

常用的距离度量方法有欧式距离、曼哈顿距离和闵可夫斯基距离等。

2.选择K个最近邻居：根据距离选择K个最近邻居。

K的选择是一个重要参数，通常通过交叉验证来确定。

4.输出分类结果：将新样本标记为投票结果的类别。

二、KNN算法步骤KNN算法的步骤如下：1.数据预处理：对训练集进行数据预处理，包括特征标准化、缺失值处理和离散特征转换等。

2.特征选择：通过统计分析、特征重要性评估等方法选择合适的特征。

3.计算距离：对于新样本，计算它与训练集中每个样本的距离。

4.选择最近邻：根据距离选择K个最近邻居。

6.进行预测：将新样本标记为投票结果的类别。

7.模型评估：使用评估指标（如准确率、召回率和F1分数等）评估模型性能。

三、KNN算法的优缺点KNN算法具有以下优点：1.简单易理解：KNN算法的原理直观简单，易于理解和实现。

2.无假设：KNN算法不需要对数据做任何假设，适用于多种类型的数据。

3.非参数模型：KNN算法是一种非参数学习算法，不对数据分布做任何假设，适用于复杂的数据集。

KNN算法也有以下缺点：1.计算复杂度高：KNN算法需要计算新样本与训练集中所有样本的距离，计算复杂度较高，尤其是在大数据集上。

2.内存开销大：KNN算法需要保存整个训练集，占用内存较大。

3.对数据特征缩放敏感：KNN算法对特征缩放敏感，如果特征尺度不同，可能会导致距离计算不准确。

四、总结KNN算法是一种简单而有效的分类算法，适用于多种类型的数据。

通过计算新样本与训练集中所有样本的距离，并选择最近的K个邻居进行投票决策，可以得到新样本的分类结果。

三、 近邻聚类算法1、实验目的掌握最近邻法和k -近邻法的基本原理和程序流程。

2、实验原理(1) 最近邻法设有c 个类别的模式识别问题，每类有标明类别的样本N i 个，i =1, 2, …, c 。

规定ωi 类的判别函数为：()min ,1,2,,i i k i kg k N =-= x x x(1.1)式中，ik x 表示ωi 类样本集中第k 个样本。

最近邻决策规则可以写为：若()()min ,1,2,,j i ig g i c == x x ，则决策x ∈ωj(2) k -近邻法在N 个已知样本中，找出x 的k 个近邻。

若k 1, …, k c 分别是k 个近邻中属于ω1, …, ωc 类的样本数，则判别函数定义为：()1,2,,i i g k i c == x(1.2)k -近邻法决策规则为：若()max ,1,2,,j i ig k i c == x ，则决策x ∈ωj3、 实验步骤理解并编写最近邻法和k -近邻法法，并用下表的样本集对程序进行验证。

x 1x 2x 3x 1x 2x 3x 1x 2 x 3 -5.01 -8.12 -3.68 -0.91 -0.18 -0.05 5.35 2.268.13-5.43 -3.48 -3.54 1.30 -2.06 -3.53 5.123.22 -2.661.08 -5.52 1.66 -7.75 4.54 -0.95 -1.34 -5.31 -9.87 0.86 -3.78 -4.11 -5.47 0.50 3.92 4.483.42 5.19 -2.67 0.63 7.39 6.14 5.72 -4.85 7.11 2.399.214.943.292.083.601.264.36 7.174.33 -0.98-2.51 2.09 -2.59 5.37 -4.63 -3.65 5.75 3.97 6.65-2.25 -2.13 -6.94 7.18 1.46 -6.66 0.77 0.27 2.415.56 2.86 -2.26 -7.39 1.176.30 0.90 -0.43 -8.711.03 -3.33 4.33 -7.50 -6.32 -0.31 3.52 -0.36 6.434、实验报告分析实验结果；总结本实验的心得体会，对不足之处提出改进意见；试分析最近邻法和k-近邻法的异同和优劣。

四、近邻分类法
对“data3.m”数据，采用剪辑法、压缩法生成参考集，近似描绘其决策面，并用所有数据测试其分类效果。
1.近邻法算法：
近邻法NN(nearest neighborhood)的基本思想是：以全部训练样本作为代表点，计算测试样本与这些代表点的距离，即所有样本的距离，并以最近邻者的类别作为决策。最初的近邻法是由Cover和Hart与1968年提出的。
步骤3：结束过程。若Grabbag中所有样本在执行步骤2时没有发生转入Store的现象，或Grabbag已称空集，则算法终止，否则转入步骤2.
2.近邻法参考核心程序：
3.近邻法分类实验结果：
两分剪辑近邻法：
步骤1将原始样本随机分为两个集合：预测集T和参考集R，分别含有 和 个样本，设两个集合所含样本数量之比为 。来自预测集T合参考集R的样本分别完成考试和参考任务，相互独立。
步骤2对预测及T中的任一个样本 ，利用参考集R采用近邻对其进行分类决策，判定 所属类别为 ，而样本 自身实际所属类别为 ，如 和 不相同，则将不相容样本 从预测集T中删除，预测及T样本数量 减1。对预测集中所有样本依次进行判定，直至删除所有的不相容样本的，得到经过剪辑的考试样本集TE。
步骤1：初始化。Store是空集，原样本集存入Grabbag；从Grabbag中任意选择一样本放入Store中作为新样本集得第一个样本。样本集生成，在Grabbag中取出第i各样本用Store中的当前样本集按最近邻法。
步骤2：分类。若分类错误，则将该样本从Grabbag转入Store中，若分类正确，则将该样本放回Grabbag中。
步骤3利用经过剪辑的考试样本集TE，采用最近邻法对测试样本X做出分类决策。
重复剪辑近邻法：当采用两分剪辑近邻法，预测集T和参考集R所含的样本是由总样本随机产生的，剪辑只针对预测集T中的样本，而参考集R中的样本则经过剪辑。为进一步提高近邻法的分类性能，在样本数量足够多的情况下，可以针对所有样本重复地执行剪辑程序。

B
x
22
近邻法的改进
树搜索算法
1. 置B＝∞，L＝0，p＝0（L是当前水平，p是当前结点） 2. 将当前结点的所有直接后继结点放入一个目录表中，并对 这些结点计算D(x, Mp) 3. 对步骤2中的每个结点p，根据规则1，如果有
D(x, Mp)> B+ rp ，
则从目录表中去掉p
第五章 近邻法 郝红卫 23
距离，并决策x与离它最近的样本同类。
第五章 近邻法 郝红卫
9
最近邻法
最近邻法的错误率
令P为最近邻法的错误率，P*为贝叶斯错误率，c为类别数。
可以证明，存在下述关系
c P* P P *(2 P*) c 1
或近似为 P* ≤ P ≤ 2P*
第五章 近邻法 郝红卫
10
k- 近 邻 法
对最近邻法的推广
第五章近邻法郝红卫1第五章近邻法?51引言?52距离度量?53最近邻法?54k近邻法?55近邻法的改进?56可作拒绝决策的近邻法第五章近邻法郝红卫2引言?最小距离法中用均值作为每一类的代表点?很多情况下均值不一定能很好地代表各类?代表点的选择很关键?将全部样本都作为代表点近邻法第五章近邻法郝红卫3引言?除代表点外另一个要素是距离?到目前为止我们主要使用了欧式距离?实际上距离的概念要广泛得多?先来讨论距离度量的性质第五章近邻法郝红卫4距离度量度量d本质上是一个函数该函数给出了两个模式之间的标量距离的大小
i 1
d
也被称为Manhattan距离或街区距离、绝对距离 显然，欧式距离和绝对距离是明氏距离的两个特例 手工运算时，为简便起见，通常采用绝对距离
第五章 近邻法 郝红卫 7
最近邻法
最近邻决策规则
假定有c个类别1 , 2 , … , c的分类问题，每类有标明类别的样本Ni个，

- 1 -
最近邻点法
最近邻点法是一种常用的数据挖掘技术，它可以用来分类、回归、
聚类等任务。简单来说，最近邻点法就是通过找出与待分类数据最接
近的已知数据点，来决定待分类数据的类别。通常情况下，会选择欧
氏距离或曼哈顿距离等度量方法来计算距离。最近邻点法的优点在于
简单易懂、易于实现，而缺点则在于容易受到噪声数据和特征选择的
影响。为了解决这个问题，人们常常会采用加权最近邻点法或者局部
加权最近邻点法等改进方法。

knn分类器例题
KNN（K-Nearest Neighbors）分类器是一种基于实例的学习，或者说是非泛化学习。

它的基本思想是：在特征空间中，如果一个实例的大部分近邻都属于某个类别，则该实例也属于这个类别。

以下是一个简单的KNN分类器的例子：
假设我们有一个数据集，其中包含两个特征（例如：颜色和形状）和对应的类别标签（例如：水果的种类）。

我们的任务是根据给定的特征值预测一个实例的类别。

首先，我们需要计算待分类实例与数据集中每个实例的距离。

这可以通过欧几里得距离、曼哈顿距离等度量方式来完成。

然后，我们选择距离最近的k个实例。

通常，k是一个用户定义的常数，通常取一个较小的整数，如3或5。

最后，我们查看k个最近邻实例的类别标签，并选择最常见的类别作为待分类实例的预测类别。

以下是一个简单的Python代码示例：
例如，如果我们有以下训练数据和标签：
4], [5, 6], [7, 8]]
train_labels = ['A', 'B', 'B', 'A']
```一个新实例的类别：
这个例子中，我们使用了欧几里得距离作为度量方式，
但也可以使用其他距离度量方式，如曼哈顿距离。

此外，我们还可以使用其他方法来选择k个最近邻实例，例如基于密度的最近邻方法。

机器学习实例---1.1、k-近邻算法（简单k-nn）机器学习实例---1.1、k-近邻算法（简单k-nn）⼀、总结⼀句话总结：> 【取最邻近的分类标签】：算法提取样本最相似数据(最近邻)的分类标签> 【k的出处】：⼀般来说，我们只选择样本数据集中前k个最相似的数据，这就是k-近邻算法中k的出处> 【k-近邻算法实例】：⽐如，现在我这个k值取3，那么在电影例⼦中，按距离依次排序的三个点分别是动作⽚(108,5)、动作⽚(115,8)、爱情⽚(5,89)。

【在这三个点中，动作⽚出现的频率为三分之⼆，爱情⽚出现的频率为三分之⼀】，所以该红⾊圆点标记的电影为动作⽚。

这个判别过程就是k-近邻算法。

1、k-近邻算法距离度量？> ⽤欧⽒距离就好：$$| A B | = \sqrt { ( x _ { 1 } - x _ { 2 } ) ^ { 2 } + ( y _ { 1 } - y _ { 2 } ) ^ { 2 } }$$> 例如：(101,20)->动作⽚(108,5)的距离约为16.552、简单的k-近邻算法步骤？> 1、【计算距离】：计算已知类别数据集中的点与当前点之间的距离；> 2、【距离排序】：按照距离递增次序排序；> 3、【选k个点】：选取与当前点【距离最⼩】的k个点；> 4、【确定k个点的类别】：确定前k个点所在类别的出现频率；返回前k个点所出现频率最⾼的类别作为当前点的预测分类。

3、k-邻近算法不具有显式的学习过程？> 【没进⾏数据训练】：k-近邻算法没有进⾏数据的训练，【直接使⽤未知的数据与已知的数据进⾏⽐较，得到结果】。

因此，可以说k-邻近算法不具有显式的学习过程。

4、完整的k-近邻算法流程？> 1、【收集与准备数据】：可以使⽤爬⾍进⾏数据的收集，也可以使⽤第三⽅提供的免费或收费的数据。

⼀般来讲，数据放在txt⽂本⽂件中，按照⼀定的格式进⾏存储，便于解析及处理。

knn算法解决实际问题的例子(一)KNN算法解决实际问题K最近邻（K-Nearest Neighbor, KNN）算法是一种常见的机器学习算法，可以用于解决多种实际问题。

下面是一些KNN算法在实际问题中的应用示例：1. 电影分类•问题描述：为了帮助用户选择适合的电影，我们需要根据用户的历史观看记录和评分，将电影进行分类，比如喜剧、动作、爱情等分类。

•解决思路：使用KNN算法，将用户的历史观看记录和评分作为特征向量，根据特征向量的相似度度量，找到K个和当前电影最相似的电影，将它们的分类作为当前电影的分类。

2. 图像识别•问题描述：给定一张未知分类的图像，我们需要将它分为不同的类别，比如动物、植物、建筑等。

•解决思路：使用KNN算法，将已知类别的图像转换成特征向量，比如使用图像的像素值作为特征，然后根据特征向量的相似度度量，找到K个和未知图像最相似的图像，将它们的类别作为未知图像的类别。

3. 推荐系统•问题描述：根据用户的历史行为和兴趣，向用户推荐适合的商品、音乐或文章等。

•解决思路：使用KNN算法，将用户的历史行为和兴趣转换成特征向量，比如使用用户的点击记录和评分作为特征，然后根据特征向量的相似度度量，找到K个和用户兴趣最接近的商品、音乐或文章，将它们推荐给用户。

4. 病症诊断•问题描述：根据病人的症状，判断可能的疾病并给出诊断结果。

•解决思路：使用KNN算法，将病人的症状转换成特征向量，比如使用病人的体温、心率、血压等作为特征，然后根据特征向量的相似度度量，找到K个和病人症状最相似的病例，将它们的疾病作为当前病人的诊断结果。

5. 文本分类•问题描述：对给定的文本进行分类，比如新闻分类、情感分析等。

•解决思路：使用KNN算法，将文本转换成特征向量，比如使用词袋模型或tf-idf作为特征，然后根据特征向量的相似度度量，找到K个和当前文本最相似的文本，将它们的类别作为当前文本的分类。

以上是一些KNN算法在实际问题中的应用示例，KNN的优点在于简单易理解、无需训练等，但也有一些缺点，比如计算复杂度较高、对噪声数据敏感等。

KNN邻近分类算法K邻近（k-Nearest Neighbor，KNN）分类算法是最简单的机器学习算法了。

它采⽤测量不同特征值之间的距离⽅法进⾏分类。

它的思想很简单：计算⼀个点A与其他所有点之间的距离，取出与该点最近的k个点，然后统计这k个点⾥⾯所属分类⽐例最⼤的，则点A属于该分类。

下⾯⽤⼀个例⼦来说明⼀下：电影名称打⽃次数接吻次数电影类型California Man3104RomanceHe’s Not Really into Dudes2100RomanceBeautiful Woman181RomanceKevin Longblade10110ActionRobo Slayer 3000995ActionAmped II982Action简单说⼀下这个数据的意思：这⾥⽤打⽃次数和接吻次数来界定电影类型，如上，接吻多的是Romance类型的，⽽打⽃多的是动作电影。

还有⼀部名字未知（这⾥名字未知是为了防⽌能从名字中猜出电影类型），打⽃次数为18次，接吻次数为90次的电影，它到底属于哪种类型的电影呢？KNN算法要做的，就是先⽤打⽃次数和接吻次数作为电影的坐标，然后计算其他六部电影与未知电影之间的距离，取得前K个距离最近的电影，然后统计这k个距离最近的电影⾥，属于哪种类型的电影最多，⽐如Action最多，则说明未知的这部电影属于动作⽚类型。

在实际使⽤中，有⼏个问题是值得注意的：K值的选取，选多⼤合适呢？计算两者间距离，⽤哪种距离会更好呢？计算量太⼤怎么办？假设样本中，类型分布⾮常不均，⽐如Action的电影有200部，但是Romance的电影只有20部，这样计算起来，即使不是Action的电影，也会因为Action的样本太多，导致k个最近邻居⾥有不少Action的电影，这样该怎么办呢？没有万能的算法，只有在⼀定使⽤环境中最优的算法。

1.1 算法指导思想kNN算法的指导思想是“近朱者⾚，近墨者⿊”，由你的邻居来推断出你的类别。

KNN算法及其示例一、KNN算法概述KNN可以说是最简单的分类算法之一，同时，它也是最常用的分类算法之一，注意KNN算法是有监督学习中的分类算法，它看起来和另一个机器学习算法Kmeans有点像（Kmeans是无监督学习算法），但却是有本质区别的。

那么什么是KNN算法呢，接下来我们就来介绍介绍吧。

二、KNN算法介绍KNN的全称是K Nearest Neighbors，意思是K个最近的邻居，从这个名字我们就能看出一些KNN算法的蛛丝马迹了。

K个最近邻居，毫无疑问，K的取值肯定是至关重要的。

那么最近的邻居又是怎么回事呢？其实啊，KNN的原理就是当预测一个新的值x 的时候，根据它距离最近的K个点是什么类别来判断x属于哪个类别。

听起来有点绕，还是看看图吧。

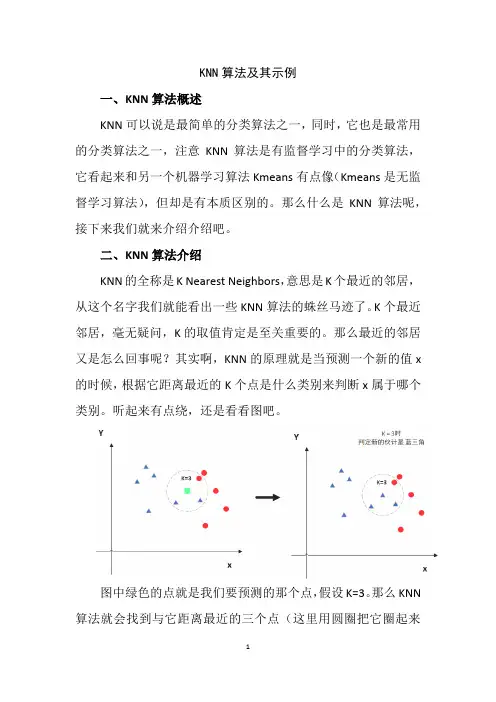
图中绿色的点就是我们要预测的那个点，假设K=3。

那么KNN 算法就会找到与它距离最近的三个点（这里用圆圈把它圈起来了），看看哪种类别多一些，比如这个例子中是蓝色三角形多一些，新来的绿色点就归类到蓝三角了。

但是，当K=5的时候，判定就变成不一样了。

这次变成红圆多一些，所以新来的绿点被归类成红圆。

从这个例子中，我们就能看得出K的取值是很重要的。

明白了大概原理后，我们就来说一说细节的东西吧，主要有两个，K值的选取和点距离的计算。

2.1距离计算要度量空间中点距离的话，有好几种度量方式，比如常见的曼哈顿距离计算，欧式距离计算等等。

不过通常KNN算法中使用的是欧式距离，这里只是简单说一下，拿二维平面为例，，二维空间两个点的欧式距离计算公式如下：ρ=√(x2−x1)2+(y2−y1)2这个高中应该就有接触到的了，其实就是计算（x1,y1）和（x2,y2）的距离。

拓展到多维空间，则公式变成这样：d(x,y)=√(x112222n n2这样我们就明白了如何计算距离，KNN算法最简单粗暴的就是将预测点与所有点距离进行计算，然后保存并排序，选出前面K个值看看哪些类别比较多。

但其实也可以通过一些数据结构来辅助，比如最大堆，这里就不多做介绍，有兴趣可以百度最大堆相关数据结构的知识。

24
压缩近邻算法
数据经MultiEdit算法剪辑后再使用 Condensing压缩近邻算法的结果
25
5.4 小结



近邻法是典型的非参数法 在原理上最直观，方法上也十分简单， 明显的缺点就是计算量大，存储量大; 近邻法
26
习题
1.
设在一个二维空间，A类有三个训练样本，图 中用红点表示，B类四个样本，图中用蓝点表 示。试问：
规则2： 如果满足：D(x, M p ) B D(xi , M p ) 则xi不是x的最近邻
14

树搜索算法
1. 2.
3. 4.
5.
6.
置B=∞，L=0，p=0 将当前结点的所有直接后继结点放入一个目录表中， 并对这些结点计算D(x,Mp) 根据规则1从目录表中去掉step2中的某些结点 如果目录表已无结点则置L=L-1，如果L=0则停止， 否则转Step3。如果目录表有一个以上的结点，则转 step5 在目录表中选出最近结点p’为当前执行结点。如果当 前的水平L是最终水平，则转Step6，否则置L=L+1， 转Step2 对当前执行结点p’中的每个xi，根据规则2决定是否 计算D(x, xi)。若D(x, xi)<B，则置NN=i和B= D(x, xi)， 处理完当前执行结点中的每个xi后转Step3
P* P 0

当各类后验概率分布为均匀分布时：
1 P(i | x) C
C 1 P* P C
7
5.2 k-近邻法

k-近邻法: 最近邻法的扩展，其基本规 则是，在所有N个样本中找到与测试样本 的k个最近邻者，其中各类别所占个数表 示成ki, i＝1，…，c。定义判别函数为： gi(x)=ki, i=1, 2,…,c。

最近邻法和k-近邻法一.基本概念：最近邻法：对于未知样本x，比较x与N个已知类别的样本之间的欧式距离，并决策x 与距离它最近的样本同类。

K近邻法：取未知样本x的k个近邻，看这k个近邻中多数属于哪一类，就把x归为哪一类。

K取奇数，为了是避免k1=k2的情况。

二.问题分析：要判别x属于哪一类，关键要求得与x最近的k个样本（当k=1时，即是最近邻法），然后判别这k个样本的多数属于哪一类。

可采用欧式距离公式求得两个样本间的距离s=sqrt（（x1-x2）^2+(y1-y2)^2）三.算法分析：该算法中任取每类样本的一半作为训练样本，其余作为测试样本。

例如iris中取每类样本的25组作为训练样本，剩余25组作为测试样本，依次求得与一测试样本x距离最近的k 个样本，并判断k个样本多数属于哪一类，则x就属于哪类。

测试10次，取10次分类正确率的平均值来检验算法的性能。

四.MATLAB代码：最近邻算实现对Iris分类clc;totalsum=0;for ii=1:10data=load('iris.txt');data1=data(1:50,1:4);%任取Iris-setosa数据的25组rbow1=randperm(50);trainsample1=data1(rbow1(:,1:25),1:4);rbow1(:,26:50)=sort(rbow1(:,26:50));%剩余的25组按行下标大小顺序排列testsample1=data1(rbow1(:,26:50),1:4);data2=data(51:100,1:4);%任取Iris-versicolor数据的25组 rbow2=randperm(50); trainsample2=data2(rbow2(:,1:25),1:4);rbow2(:,26:50)=sort(rbow2(:,26:50));testsample2=data2(rbow2(:,26:50),1:4);data3=data(101:150,1:4);%任取Iris-virginica数据的25组rbow3=randperm(50);trainsample3=data3(rbow3(:,1:25),1:4);rbow3(:,26:50)=sort(rbow3(:,26:50));testsample3=data3(rbow3(:,26:50),1:4);trainsample=cat(1,trainsample1,trainsample2,trainsample3);%包含75组数据的样本集testsample=cat(1,testsample1,testsample2,testsample3);newchar=zeros(1,75);sum=0;[i,j]=size(trainsample);%i=60,j=4[u,v]=size(testsample);%u=90,v=4for x=1:ufor y=1:iresult=sqrt((testsample(x,1)-trainsample(y,1))^2+(testsample(x,2)-trainsample(y,2))^2+(testsampl e(x,3)-trainsample(y,3))^2+(testsample(x,4)-trainsample(y,4))^2); %欧式距离newchar(1,y)=result;end;[new,Ind]=sort(newchar);class1=0;class2=0;class3=0;if Ind(1,1)<=25class1=class1+1;elseif Ind(1,1)>25&&Ind(1,1)<=50class2=class2+1;elseclass3=class3+1;endif class1>class2&&class1>class3m=1;ty='Iris-setosa';elseif class2>class1&&class2>class3m=2;ty='Iris-versicolor';elseif class3>class1&&class3>class2m=3;ty='Iris-virginica';elsem=0;ty='none';endif x<=25&&m>0disp(sprintf('第%d组数据分类后为%s类',rbow1(:,x+25),ty));elseif x<=25&&m==0disp(sprintf('第%d组数据分类后为%s类',rbow1(:,x+25),'none'));endif x>25&&x<=50&&m>0disp(sprintf('第%d组数据分类后为%s类',50+rbow2(:,x),ty));elseif x>25&&x<=50&&m==0disp(sprintf('第%d组数据分类后为%s类',50+rbow2(:,x),'none'));endif x>50&&x<=75&&m>0disp(sprintf('第%d组数据分类后为%s类',100+rbow3(:,x-25),ty));elseif x>50&&x<=75&&m==0disp(sprintf('第%d组数据分类后为%s类',100+rbow3(:,x-25),'none'));endif (x<=25&&m==1)||(x>25&&x<=50&&m==2)||(x>50&&x<=75&&m==3)sum=sum+1;endenddisp(sprintf('第%d次分类识别率为%4.2f',ii,sum/75)); totalsum=totalsum+(sum/75);enddisp(sprintf('10次分类平均识别率为%4.2f',totalsum/10));测试结果：第3组数据分类后为Iris-setosa类第5组数据分类后为Iris-setosa类第6组数据分类后为Iris-setosa类第7组数据分类后为Iris-setosa类第10组数据分类后为Iris-setosa类第11组数据分类后为Iris-setosa类第12组数据分类后为Iris-setosa类第14组数据分类后为Iris-setosa类第16组数据分类后为Iris-setosa类第18组数据分类后为Iris-setosa类第19组数据分类后为Iris-setosa类第20组数据分类后为Iris-setosa类第23组数据分类后为Iris-setosa类第24组数据分类后为Iris-setosa类第26组数据分类后为Iris-setosa类第28组数据分类后为Iris-setosa类第30组数据分类后为Iris-setosa类第31组数据分类后为Iris-setosa类第34组数据分类后为Iris-setosa类第37组数据分类后为Iris-setosa类第39组数据分类后为Iris-setosa类第41组数据分类后为Iris-setosa类第44组数据分类后为Iris-setosa类第45组数据分类后为Iris-setosa类第49组数据分类后为Iris-setosa类第51组数据分类后为Iris-versicolor类第53组数据分类后为Iris-versicolor类第54组数据分类后为Iris-versicolor类第55组数据分类后为Iris-versicolor类第57组数据分类后为Iris-versicolor类第58组数据分类后为Iris-versicolor类第59组数据分类后为Iris-versicolor类第60组数据分类后为Iris-versicolor类第61组数据分类后为Iris-versicolor类第62组数据分类后为Iris-versicolor类第68组数据分类后为Iris-versicolor类第70组数据分类后为Iris-versicolor类第71组数据分类后为Iris-virginica类第74组数据分类后为Iris-versicolor类第75组数据分类后为Iris-versicolor类第77组数据分类后为Iris-versicolor类第79组数据分类后为Iris-versicolor类第80组数据分类后为Iris-versicolor类第84组数据分类后为Iris-virginica类第85组数据分类后为Iris-versicolor类第92组数据分类后为Iris-versicolor类第95组数据分类后为Iris-versicolor类第97组数据分类后为Iris-versicolor类第98组数据分类后为Iris-versicolor类第99组数据分类后为Iris-versicolor类第102组数据分类后为Iris-virginica类第103组数据分类后为Iris-virginica类第105组数据分类后为Iris-virginica类第106组数据分类后为Iris-virginica类第107组数据分类后为Iris-versicolor类第108组数据分类后为Iris-virginica类第114组数据分类后为Iris-virginica类第118组数据分类后为Iris-virginica类第119组数据分类后为Iris-virginica类第124组数据分类后为Iris-virginica类第125组数据分类后为Iris-virginica类第126组数据分类后为Iris-virginica类第127组数据分类后为Iris-virginica类第128组数据分类后为Iris-virginica类第129组数据分类后为Iris-virginica类第130组数据分类后为Iris-virginica类第133组数据分类后为Iris-virginica类第135组数据分类后为Iris-virginica类第137组数据分类后为Iris-virginica类第138组数据分类后为Iris-virginica类第142组数据分类后为Iris-virginica类第144组数据分类后为Iris-virginica类第148组数据分类后为Iris-virginica类第149组数据分类后为Iris-virginica类第150组数据分类后为Iris-virginica类k近邻法对wine分类：clc;otalsum=0;for ii=1:10 %循环测试10次data=load('wine.txt');%导入wine数据data1=data(1:59,1:13);%任取第一类数据的30组rbow1=randperm(59);trainsample1=data1(sort(rbow1(:,1:30)),1:13);rbow1(:,31:59)=sort(rbow1(:,31:59)); %剩余的29组按行下标大小顺序排列testsample1=data1(rbow1(:,31:59),1:13);data2=data(60:130,1:13);%任取第二类数据的35组rbow2=randperm(71);trainsample2=data2(sort(rbow2(:,1:35)),1:13);rbow2(:,36:71)=sort(rbow2(:,36:71));testsample2=data2(rbow2(:,36:71),1:13);data3=data(131:178,1:13);%任取第三类数据的24组rbow3=randperm(48);trainsample3=data3(sort(rbow3(:,1:24)),1:13);rbow3(:,25:48)=sort(rbow3(:,25:48));testsample3=data3(rbow3(:,25:48),1:13);train_sample=cat(1,trainsample1,trainsample2,trainsample3);%包含89组数据的样本集test_sample=cat(1,testsample1,testsample2,testsample3); k=19;%19近邻法newchar=zeros(1,89);sum=0;[i,j]=size(train_sample);%i=89,j=13[u,v]=size(test_sample);%u=89,v=13for x=1:ufor y=1:iresult=sqrt((test_sample(x,1)-train_sample(y,1))^2+(test_sample(x,2)-train_sample(y,2))^2+(test_ sample(x,3)-train_sample(y,3))^2+(test_sample(x,4)-train_sample(y,4))^2+(test_sample(x,5)-train _sample(y,5))^2+(test_sample(x,6)-train_sample(y,6))^2+(test_sample(x,7)-train_sample(y,7))^2+ (test_sample(x,8)-train_sample(y,8))^2+(test_sample(x,9)-train_sample(y,9))^2+(test_sample(x,10)-train_sample(y,10))^2+(test_sample(x,11)-train_sample(y,11))^2+(test_sample(x,12)-train_sa mple(y,12))^2+(test_sample(x,13)-train_sample(y,13))^2); %欧式距离newchar(1,y)=result;end;[new,Ind]=sort(newchar); class1=0; class 2=0; class 3=0;for n=1:kif Ind(1,n)<=30class 1= class 1+1;elseif Ind(1,n)>30&&Ind(1,n)<=65class 2= class 2+1;elseclass 3= class3+1;endendif class 1>= class 2&& class1>= class3m=1;elseif class2>= class1&& class2>= class3m=2;elseif class3>= class1&& class3>= class2m=3;endif x<=29disp(sprintf('第%d组数据分类后为第%d类',rbow1(:,30+x),m));elseif x>29&&x<=65disp(sprintf('第%d组数据分类后为第%d类',59+rbow2(:,x+6),m));elseif x>65&&x<=89disp(sprintf('第%d组数据分类后为第%d类',130+rbow3(:,x-41),m));endif (x<=29&&m==1)||(x>29&&x<=65&&m==2)||(x>65&&x<=89&&m==3)sum=sum+1;endenddisp(sprintf('第%d次分类识别率为%4.2f',ii,sum/89));totalsum=totalsum+(sum/89);enddisp(sprintf('10次分类平均识别率为%4.2f',totalsum/10));第2组数据分类后为第1类第4组数据分类后为第1类第5组数据分类后为第3类第6组数据分类后为第1类第8组数据分类后为第1类第10组数据分类后为第1类第11组数据分类后为第1类第14组数据分类后为第1类第19组数据分类后为第1类第20组数据分类后为第3类第21组数据分类后为第3类第22组数据分类后为第3类第26组数据分类后为第3类第27组数据分类后为第1类第28组数据分类后为第1类第30组数据分类后为第1类第33组数据分类后为第1类第36组数据分类后为第1类第37组数据分类后为第1类第43组数据分类后为第1类第44组数据分类后为第3类第45组数据分类后为第1类第46组数据分类后为第1类第49组数据分类后为第1类第52组数据分类后为第1类第54组数据分类后为第1类第56组数据分类后为第1类第57组数据分类后为第1类第60组数据分类后为第2类第61组数据分类后为第3类第63组数据分类后为第3类第65组数据分类后为第2类第66组数据分类后为第3类第67组数据分类后为第2类第71组数据分类后为第1类第72组数据分类后为第2类第74组数据分类后为第1类第76组数据分类后为第2类第77组数据分类后为第2类第79组数据分类后为第3类第81组数据分类后为第2类第82组数据分类后为第3类第83组数据分类后为第3类第84组数据分类后为第2类第86组数据分类后为第2类第87组数据分类后为第2类第88组数据分类后为第2类第93组数据分类后为第2类第96组数据分类后为第1类第98组数据分类后为第2类第99组数据分类后为第3类第104组数据分类后为第2类第105组数据分类后为第3类第106组数据分类后为第2类第110组数据分类后为第3类第113组数据分类后为第3类第114组数据分类后为第2类第115组数据分类后为第2类第116组数据分类后为第2类第118组数据分类后为第2类第122组数据分类后为第2类第123组数据分类后为第2类第124组数据分类后为第2类第133组数据分类后为第3类第134组数据分类后为第3类第135组数据分类后为第2类第136组数据分类后为第3类第139组数据分类后为第3类第140组数据分类后为第3类第142组数据分类后为第3类第144组数据分类后为第2类第145组数据分类后为第1类第146组数据分类后为第3类第148组数据分类后为第3类第149组数据分类后为第2类第152组数据分类后为第2类第157组数据分类后为第2类第159组数据分类后为第3类第161组数据分类后为第2类第162组数据分类后为第3类第163组数据分类后为第3类第164组数据分类后为第3类第165组数据分类后为第3类第167组数据分类后为第3类第168组数据分类后为第3类第173组数据分类后为第3类第174组数据分类后为第3类五：问题和收获：该算法的优缺点总结为：优点：算法简单且识别率较高；缺点：算法需要计算未知样本x与周围每个样本的距离，然后排序选择最近的k个近邻，计算量和时间复杂度高。