西电计算方法上机作业-02101284

计算方法上机作业

姓名： 班级：021014 学号：02101284

第一章

例1：对n=0,1,2，…，40计算定积分?01

5

x x n

+dx

解：利用递推公式：1-n y =

n 51-5

1

n y n=40，39，…1 注意到：2461=61?0140x dx ≤?015x x 40+dx ≤?0

140x dx=2051

取： 40y ≈

21（2461+205

1

）≈0.0044715 Matlab 程序如下：

y0=(1/205+1/246)/2; n=40;

fprintf('y[%d]=%f\n',n,y0); while (1)

y1=1/(5*n)-y0/5;

fprintf('y[%d]=%f\n',n-1,y1); if (n<=1)break ; end y0=y1; n=n-1; end

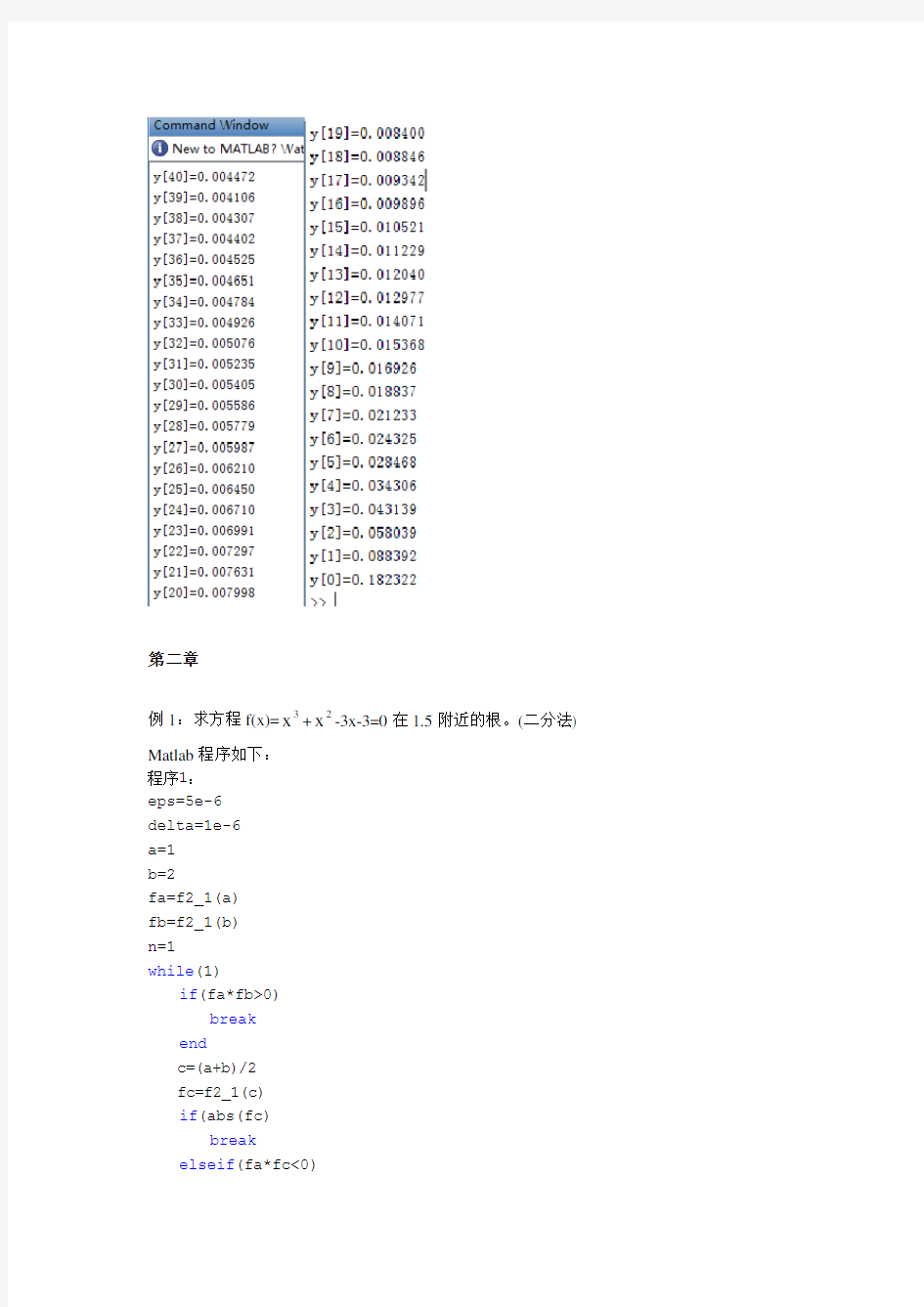
输出结果（截图）：

第二章

例1：求方程f(x)=3x+2x-3x-3=0在1.5附近的根。(二分法)

Matlab程序如下：

程序1：

eps=5e-6

delta=1e-6

a=1

b=2

fa=f2_1(a)

fb=f2_1(b)

n=1

while(1)

if(fa*fb>0)

break

end

c=(a+b)/2

fc=f2_1(c)

if(abs(fc)

break

elseif(fa*fc<0)

b=c

fb=fc

else

a=c

fa=fc

end

if(b-a

break

end

n=n+1

n;c;fc;

end

程序2：

function output=f2_1(x) output=x*x*x+x*x-3*x-3 end

输出结果（截图）

故原方程的根为1.732052

例2：求方程f(x)=3x+2x-3x-3=0在1.5附近的根。（牛顿迭代法）

Matlab程序如下：

程序1：

esp=5e-6

delta=1e-6

N=100

k=0

x0=1.0

while(1)

x1=x0-func2_2(x0)/func2_2_1(x0)

k=k+1

if(k>N|abs(x1)

disp('Newton method failed')

break

end

if abs(x1)<1

d=x1-x0

else

d=(x1-x0)/x1

end

x0=x1

if(abs(d)

end

end

fprintf('%f',x0)

程序2：

function y=func2_2_1(x)

y=3*x*x+2*x-3

end

程序3：

function y=func2_2(x)

y=x*x*x+x*x-3*x-3

end

输出结果（截图）

原方程的根为x=1.732051

第三章

例1 解方程组??

?

??=++-=++-=++035

.3643.5072.1835.2137.2623.4712.3347.1183.1555.3304.2101.0321321321x x x x x x x x x

Matlab 程序如下：

function GEpiv(A,b)

A=[0.101 2.304 3.555;-1.347 3.712 4.623;-2.835 1.072 5.643]; b=[1.183;2.137;3.035]; [m,n]=size(A); nb=n+1; Ab=[A b]; for i=1:m-1

[pivot,p]=max(abs(Ab(i:n,i))); ip=p+i-1; if ip~=i

Ab([i ip],:)=Ab([ip i],:); end

pivot=Ab(i,i);

for k=i+1:m

Ab(k,i:nb)=Ab(k,i:nb)-(Ab(k,i)/pivot)*Ab(i,i:nb); end end

x=zeros(n,1);

x(n)=Ab(n,nb)/Ab(n,n); for i=n-1:-1:1

x(i)=(Ab(i,nb)-Ab(i,i+1:n)*x(i+1:n,1))/Ab(i,i); end for k=1:n

fprintf('x[%d]=%f\n',k,x(k)); end

输出结果（截图）

例3 求解方程组b Αx =

?

?

???

????

???-----=381265973274581221

A ，????????????=4911427b Matlab 程序如下：

function LUpiv(A,b) [m,n]=size(A); nb=n+1; Ab=[A b];

Ab(2:m,1)=Ab(2:m,1)/Ab(1,1); for k=2:m for j=k:nb

Ab(k,j)=Ab(k,j)-Ab(k,1:k-1)*Ab(1:k-1,j); end

for i=k+1:m

Ab(i,k)=(Ab(i,k)-Ab(i,1:k-1)*Ab(1:k-1,k))/Ab(k,k); end

end

x=zeros(n,1);

x(n)=Ab(n,nb)/Ab(n,n); for k=n-1:-1:1

x(k)=(Ab(k,nb)-Ab(k,k+1:n)*x(k+1:n,1))/Ab(k,k); end for k=1:n

fprintf('x[%d]=%f\n',k,x(k)); end

输出结果（截图）

例4 用雅可比迭代法解方程组

???

??=--=-+=++1

6321382825321

321321x x x x x x x x x Matlab 程序如下：

function Jacobi(A,b,max,eps) A=[5 2 1;2 8 -3;1 -3 -6]; b=[8;21;1]; max=50; eps=10e-7; n=length(A); x=zeros(n,1); xl=zeros(n,1); k=0; while 1

xl(1)=(b(1)-A(1,2:n)*x(2:n,1))/A(1,1); for i=2:n-1

xl(i)=(b(i)-A(i,1:i-1)*x(1:i-1,1)-A(i,i+1:n)*x(i+1:n,1))/A(i,i); end

xl(n)=(b(n)-A(n,1:n-1)*x(1:n-1,1))/A(n,n); k=k+1;

if sum(abs(xl-x))

fprintf('number=%d\n',k); break ; end if k>=max

fprintf('The Method is disconvergent\n'); break ; end x=xl; end if k

fprintf('x[%d]=%f\n',i,xl(i)); end end end

输出结果（截图）

例5 用高斯-赛德尔迭代解方程组

???

??=++=-+=+-36

12363311420238321

321321x x x x x x x x x

Matlab 程序如下：

function GauseSeidel(A,b,max,eps) A=[8 -3 2;4 11 -1;6 3 12]; b=[20;33;36] eps=10e-7; max=20; n=length(A); x=zeros(n,1); xl=zeros(n,1); k=0; while 1

xl(1)=(b(1)-A(1,2:n)*x(2:n,1))/A(1,1); for i=2:n-1

xl(i)=(b(i)-A(i,1:i-1)*xl(1:i-1,1)-A(i,i+1:n)*x(i+1:n,1))/A(i,i);

end

xl(n)=(b(n)-A(n,1:n-1)*xl(1:n-1,1))/A(n,n);

k=k+1;

if sum(abs(xl-x))

fprintf('number=%d\n',k);

break;

end

if k>=max

fprintf('The Method is disconvergent\n');

break;

end

x=xl;

end

if k

for i=1:n

fprintf('x[%d]=%f\n',i,xl(i));

end

end

end

输出结果（截图）

第四章

例1 已知函数表

用三次拉格朗日插值多项式求x=0.5635时的函数近似值。

Matlab程序如下：

function lagrint(x,y,xi)

xi=[0.5635]

x=[0.56160;0.56280;0.56401;0.56521]

y=[0.82741;0.82659;0.82577;0.82495]

dxi=xi-x;

n=length(x);

L=zeros(size(y));

L(1)=prod(dxi(2:n))/prod(x(1)-x(2:n)); L(n)=prod(dxi(1:n-1))/prod(x(n)-x(1:n-1)); for j=2:n-1

num=prod(dxi(1:j-1))*prod(dxi(j+1:n)); den=prod(x(j)-x(1:j-1))*prod(x(j)-x(j+1:n)); L(j)=num/den; end

yi=sum(y.*L);

fprintf('x=%f,y=%f\n',xi,yi); end

输出结果（截图）

用牛顿插值多项式求)596.0(n N 和)895.0(n N 。 Matlab 程序如下：

function newtint(x,y,xhat) x=[0.4; 0.55; 0.65 ;0.8 ;0.9]

y=[0.41075; 0.57815 ;0.69675 ;0.88811 ;1.02652] xhat=[0.596 ;0.895] n=length(y); c=y(:); for j=2:n for i=n:-1:j

c(i)=(c(i)-c(i-1))/(x(i)-x(i-j+1)); end end yhat=c(n); for i=n-1:-1:1

yhat=yhat.*(xhat-x(i))+c(i);

end

fprintf('N(%f)=%f\n',xhat,yhat); end

输出结果（截图）

第六章

例1 用复化辛卜生法计算积分dx x I ?+=1

0211

。

Matlab 程序如下：

function Simpson(a,b) a=0; b=1; n=2; for i=1:3

x=a:(b-a)/(2*n):b; m=2*n+1; h=(b-a)/n;

s=(h/6)*(f(a)+2*sum(f(x(3:2:m-2)))+4*sum(f(x(2:2:m-1)))+f(b)); fprintf('s(%d)=%f\n',n,s); n=n*2; end end

输出结果（截图）

例3 用变步长梯形法计算积分dx x I ?+=1

0211

。

Matlab 程序如下：

function adaptTrap(a,b,eps) a=0; b=1; eps=10e-7; h=b-a; T1=0;

T2=(b-a)/2*(f(a)+f(b)); n=1;

while abs(T1-T2)>eps T1=T2; m=2*n+1;

x=a:(b-a)/(2*n):b; s=sum(f(x(2:2:m-1))); T2=1/2*(T1+h*s); n=n*2; h=h/2; end

fprintf('T(%d)=%f\n',n,T2); end

输出结果（截图）

例5 用龙贝格方法计算积分dx x I ?+=1

0211

。

Matlab 程序如下：

function Romberg(a,b,eps) a=0; b=1; eps=10e-7; A=zeros(4,4);

A(1,1)=(b-a)/2*(f(a)+f(b));

i=1;

n=1;

while 1

i=i+1;

m=2*n+1;

x=a:(b-a)/(2*n):b;

A(i,1)=1/2*(A(i-1,1)+(b-a)/n*sum(f(x(2:2:m-1))));

if i>4

k=4;

else

k=i;

end

for j=2:k

A(i,j)=A(i,j-1)+1/(4^(j-1)-1)*(A(i,j-1)-A(i-1,j-1));

end

if abs(A(i,4)-A(i-1,4))

break;

end

n=n*2;

end

fprintf('R=%f\n',A(i,4));

end

输出结果（截图）

计算方法_习题第一、二章答案..

第一章 误差 1 问3.142，3.141，7 22分别作为π的近似值各具有几位有效数字？ 分析 利用有效数字的概念可直接得出。 解 π=3.141 592 65… 记x 1=3.142，x 2=3.141，x 3=7 22. 由π- x 1=3.141 59…-3.142=-0.000 40…知 34111 10||1022 x π--?<-≤? 因而x 1具有4位有效数字。 由π- x 2=3.141 59…-3.141=-0.000 59…知 223102 1||1021--?≤-

数值分析上机作业

数值分析上机实验报告 选题：曲线拟合的最小二乘法 指导老师： 专业： 学号： 姓名：

课题八曲线拟合的最小二乘法 一、问题提出 从随机的数据中找出其规律性，给出其近似表达式的问题，在生产实践和科学实验中大量存在，通常利用数据的最小二乘法求得拟合曲线。 在某冶炼过程中，根据统计数据的含碳量与时间关系，试求含碳量y 与时间t 的拟合曲线。 二、要求 1、用最小二乘法进行曲线拟合； 2、近似解析表达式为()33221t a t a t a t ++=?； 3、打印出拟合函数()t ?，并打印出()j t ?与()j t y 的误差，12,,2,1 =j ； 4、另外选取一个近似表达式，尝试拟合效果的比较； 5、*绘制出曲线拟合图*。 三、目的和意义 1、掌握曲线拟合的最小二乘法； 2、最小二乘法亦可用于解超定线代数方程组； 3、探索拟合函数的选择与拟合精度间的关系。 四、计算公式 对于给定的测量数据(x i ,f i )(i=1,2,…，n )，设函数分布为 ∑==m j j j x a x y 0)()(? 特别的，取)(x j ?为多项式 j j x x =)(? (j=0, 1,…，m )

则根据最小二乘法原理，可以构造泛函 ∑∑==-=n i m j i j j i m x a f a a a H 1 10))((),,,(? 令 0=??k a H (k=0, 1,…，m ) 则可以得到法方程 ???? ??????? ?=????????????????????????),(),(),(),(),(),(),(),(),(),(),(),(1010101111000100m m m m m m m m f f f a a a ????????????????????? 求该解方程组，则可以得到解m a a a ,,,10 ，因此可得到数据的最小二乘解 ∑=≈m j j j x a x f 0)()(? 曲线拟合：实际工作中，变量间未必都有线性关系，如服药后血药浓度与时间的关系；疾病疗效与疗程长短的关系；毒物剂量与致死率的关系等常呈曲线关系。曲线拟合是指选择适当的曲线类型来拟合观测数据，并用拟合的曲线方程分析两变量间的关系。 五、结构程序设计 在程序结构方面主要是按照顺序结构进行设计，在进行曲线的拟合时，为了进行比较，在程序设计中，直接调用了最小二乘法的拟合函数polyfit ，并且依次调用了plot 、figure 、hold on 函数进行图象的绘制，最后调用了一个绝对值函数abs 用于计算拟合函数与原有数据的误差，进行拟合效果的比较。

计算方法上机作业

计算方法上机报告 姓名： 学号： 班级： 上课班级：

说明： 本次上机实验使用的编程语言是Matlab 语言，编译环境为MATLAB 7.11.0，运行平台为Windows 7。 1. 对以下和式计算： ∑ ∞ ? ?? ??+-+-+-+=0681581482184161n n n n S n ，要求： ① 若只需保留11个有效数字，该如何进行计算； ② 若要保留30个有效数字，则又将如何进行计算； （1） 算法思想 1、根据精度要求估计所加的项数，可以使用后验误差估计，通项为： 1421114 16818485861681 n n n a n n n n n ε??= ---<< ?+++++??； 2、为了保证计算结果的准确性，写程序时，从后向前计算； 3、使用Matlab 时，可以使用以下函数控制位数： digits(位数)或vpa(变量，精度为数) （2）算法结构 1. ;0=s ?? ? ??+-+-+-+= 681581482184161n n n n t n ； 2. for 0,1,2,,n i =??? if 10m t -≤ end; 3. for ,1,2,,0n i i i =--??? ;s s t =+

（3）Matlab源程序 clear; %清除工作空间变量 clc; %清除命令窗口命令 m=input('请输入有效数字的位数m='); %输入有效数字的位数 s=0; for n=0:50 t=(1/16^n)*(4/(8*n+1)-2/(8*n+4)-1/(8*n+5)-1/(8*n+6)); if t<=10^(-m) %判断通项与精度的关系break; end end; fprintf('需要将n值加到n=%d\n',n-1); %需要将n值加到的数值 for i=n-1:-1:0 t=(1/16^i)*(4/(8*i+1)-2/(8*i+4)-1/(8*i+5)-1/(8*i+6)); s=s+t; %求和运算 end s=vpa(s,m) %控制s的精度 （4）结果与分析 当保留11位有效数字时，需要将n值加到n=7， s =3.1415926536； 当保留30位有效数字时，需要将n值加到n=22, s =3.14159265358979323846264338328。 通过上面的实验结果可以看出，通过从后往前计算，这种算法很好的保证了计算结果要求保留的准确数字位数的要求。

计算方法上机题答案

2.用下列方法求方程e^x+10x-2=0的近似根，要求误差不超过5*10的负4次方，并比较计算量 （1）二分法 （局部，大图不太看得清，故后面两小题都用局部截图） （2）迭代法

（3）牛顿法 顺序消元法 #include #include #include int main() { int N=4,i,j,p,q,k; double m; double a[4][5]; double x1,x2,x3,x4; for (i=0;i

for(k=p+1;kmax1 max1=abs(A(i,k));r=i; end end

数值分析上机作业

昆明理工大学工科研究生《数值分析》上机实验 学院：材料科学与工程学院 专业：材料物理与化学 学号：2011230024 姓名: 郑录 任课教师：胡杰

P277-E1 1.已知矩阵A= 10787 7565 86109 75910 ?? ?? ?? ?? ?? ??,B= 23456 44567 03678 00289 00010 ?? ?? ?? ?? ?? ?? ?? ?? ,错误！未找到引用源。 = 11/21/31/41/51/6 1/21/31/41/51/61/7 1/31/41/51/61/71/8 1/41/51/61/71/81/9 1/51/61/71/81/91/10 1/61/71/81/91/101/11?????????????????? （1）用MA TLAB函数“eig”求矩阵全部特征值。 （2）用基本QR算法求全部特征值（可用MA TLAB函数“qr”实现矩阵的QR分解）。解：MA TLAB程序如下： 求矩阵A的特征值： clear; A=[10 7 8 7;7 5 6 5;8 6 10 9;7 5 9 10]; E=eig(A) 输出结果： 求矩阵B的特征值： clear; B=[2 3 4 5 6;4 4 5 6 7;0 3 6 7 8;0 0 2 8 9;0 0 0 1 0]; E=eig(B) 输出结果：

求矩阵错误！未找到引用源。的特征值： clear; 错误！未找到引用源。=[1 1/2 1/3 1/4 1/5 1/6; 1/2 1/3 1/4 1/5 1/6 1/7; 1/3 1/4 1/5 1/6 1/7 1/8; 1/4 1/5 1/6 1/7 1/8 1/9;1/5 1/6 1/7 1/8 1/9 1/10; 1/6 1/7 1/8 1/9 1/10 1/11]; E=eig(错误！未找到引用源。) 输出结果： （2）A= 10 7877565861097 5 9 10 第一步：A0=hess(A);[Q0,R0]=qr(A0);A1=R0*Q0 返回得到： 第二部：[Q1,R1]=qr(A1);A2=R1*Q1

《数值计算方法》上机实验报告

《数值计算方法》上机实验报告华北电力大学 实验名称数值il?算方法》上机实验课程名称数值计算方法专业班级：电力实08学生姓名：李超然学号:200801001008 成绩: 指导教师:郝育黔老师实验日期：2010年04月华北电力大学实验报告数值计算方法上机实验报吿一. 各算法的算法原理及计算机程序框图1、牛顿法求解非线性方程 *对于非线性方程，若已知根的一个近似值，将在处展开成一阶 xxfx ()0, fx ()xkk 泰勒公式 "f 0 / 2 八八,fxfxfxxxxx 0 0 0 0 0 kkkk2! 忽略高次项，有 ，fxfxfxxx 0 ()()()，，, kkk 右端是直线方程，用这个直线方程来近似非线性方程。将非线性方程的 **根代入，即fx ()0, X ，* fxfxxx 0 0 0 0, ,, kkk fx 0 fx 0 0,

解出 fX 0 *k XX,, k' fx 0 k 水将右端取为，则是比更接近于的近似值，即xxxxk, Ik, Ik fx ()k 八XX, Ikk* fx()k 这就是牛顿迭代公式。 ,2,计算机程序框图:，见, ,3,输入变量、输出变量说明: X输入变量:迭代初值，迭代精度，迭代最大次数，\0 输出变量:当前迭代次数，当前迭代值xkl ,4,具体算例及求解结果: 2/16 华北电力大学实验报吿 开始 读入 l>k /fx()0?,0 fx 0 Oxx，，01* fx ()0 XX,,，?10 kk, ,1，kN, ?xx, 10 输出迭代输出X输出奇异标志1失败标志

,3,输入变量、输出变量说明: 结束 例：导出计算的牛顿迭代公式，并il ?算。（课本P39例2-16） 115cc （0）, 求解结果: 10. 750000 10.723837 10. 723805 10. 723805 2、列主元素消去法求解线性方程组，1,算法原理: 高斯消去法是利用现行方程组初等变换中的一种变换，即用一个不为零的数乘 -个 方程后加只另一个方程，使方程组变成同解的上三角方程组，然后再自下而上 对上三角 3/16 华北电力大学实验报告方程组求解。 列选主元是当高斯消元到第步时，从列的以下（包括）的各元素中选出绝 aakkkkkk 对值最大的，然后通过行交换将其交换到的位置上。交换系数矩阵中的 两行（包括常ekk 数项），只相当于两个方程的位置交换了，因此，列选主元不影响求解的结 ,2,计算机程序框图:，见下页, 输入变量:系数矩阵元素，常向量元素baiji 输出变量:解向量元素bbb,,12n

计算方法上机作业

计算方法第四次上机报告 2.用欧拉方法解初值 y’=10x(1-y) 0<=x<=1 Y(0)=0 取步长h=0.1,保留5位有效数字，并与准确解相比较 分析：该题目考察欧拉方法解初值问题 程序如下： function Heun(a,b,y0,n) h=(b-a)/n;x=a:h:b; y=y0*ones(1,n+1); for j=2:n+1 yp=y(j-1)+h*f(x(j-1),y(j-1)); yc=y(j-1)+h*f(x(j),yp); y(j)=1/2*(yp+yc); end for k=1:n+1 fprintf('x[%d]=%f\ty[%d]=%f\n',k-1,x(k),k-1,y(k)); end function z=f(xx,yy) z=10*xx*(1-yy); 运行结果： >> Heun(0,1,0,10) x[0]=0.000000 y[0]=0.000000 x[1]=0.100000 y[1]=0.050000 x[2]=0.200000 y[2]=0.183000

x[3]=0.300000 y[3]=0.362740 x[4]=0.400000 y[4]=0.547545 x[5]=0.500000 y[5]=0.705905 x[6]=0.600000 y[6]=0.823543 x[7]=0.700000 y[7]=0.901184 x[8]=0.800000 y[8]=0.947627 x[9]=0.900000 y[9]=0.973290 x[10]=1.000000 y[10]=0.986645 >> 分析： 该结果与准确结果相比比较接近，但是有一定的误差。 6.用四阶龙格—库塔公式解第三题中的初值问题，取步长h=0.2，保留五位有效数字。 题目目的分析： 该题考查四阶龙格-库塔方法和改进欧拉方法求解精确度问题。 程序： 改进欧拉法： function Heun(a,b,y0,n) h=(b-a)/n;x=a:h:b; y=y0*ones(1,n+1); for j=2:n+1 yp=y(j-1)+h*f(x(j-1),y(j-1)); yc=y(j-1)+h*f(x(j),yp); y(j)=1/2*(yp+yc); end for k=1:n+1 fprintf('x[%d]=%f\ty[%d]=%f\n',k-1,x(k),k-1,y(k)); end

计算方法试题库讲解

计算方法 一、填空题 1.假定x ≤1，用泰勒多项式?+??+++=! !212n x x x e n x ,计算e x 的值，若要求截断误差不超过0.005，则n=_5___ 2. 解 方 程 03432 3=-+x －　 x x 的牛顿迭代公式 )463/()343(121121311+--+--=------k k k k k k k x x x x x x x 3.一阶常微分方程初值问题 ?????= ='y x y y x f y 0 0)() ,(,其改进的欧拉方法格式为)],(),([21 1 1 y x y x y y i i i i i i f f h +++++= 4.解三对角线方程组的计算方法称为追赶法或回代法 5. 数值求解初值问题的四阶龙格——库塔公式的局部截断误差为o(h 5 ) 6.在ALGOL 中，简单算术表达式y x 3 + 的写法为x+y ↑3 7.循环语句分为离散型循环,步长型循环,当型循环. 8.函数)(x f 在[a,b]上的一次（线性）插值函数= )(x l )()(b f a b a x a f b a b x --+-- 9.在实际进行插值时插值时，将插值范围分为若干段，然后在每个分段上使用低阶插值————如线性插值和抛物插值，这就是所谓分段插值法 10、数值计算中，误差主要来源于模型误差、观测误差、截断误差和舍入误差。 11、电子计算机的结构大体上可分为输入设备 、 存储器、运算器、控制器、 输出设备 五个主要部分。 12、算式2 cos sin 2x x x +在ALGOL 中写为))2cos()(sin(2↑+↑x x x 。 13、ALGOL 算法语言的基本符号分为 字母 、 数字 、 逻辑值、 定义符四大

东南大学数值分析上机作业汇总

东南大学数值分析上机作业 汇总 -标准化文件发布号：（9456-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII

数值分析上机报告 院系： 学号： 姓名：

目录 作业1、舍入误差与有效数 (1) 1、函数文件cxdd.m (1) 2、函数文件cddx.m (1) 3、两种方法有效位数对比 (1) 4、心得 (2) 作业2、Newton迭代法 (2) 1、通用程序函数文件 (3) 2、局部收敛性 (4) （1）最大δ值文件 (4) （2）验证局部收敛性 (4) 3、心得 (6) 作业3、列主元素Gauss消去法 (7) 1、列主元Gauss消去法的通用程序 (7) 2、解题中线性方程组 (7) 3、心得 (9) 作业4、三次样条插值函数 (10) 1、第一型三次样条插值函数通用程序： (10) 2、数据输入及计算结果 (12)

作业1、舍入误差与有效数 设∑ =-=N j N j S 2 2 11 ，其精确值为?? ? ??---1112321N N . （1）编制按从小到大的顺序1 1 131121222-? ??+-+-=N S N ，计算N S 的通用程序； （2）编制按从大到小的顺序()1 21 11111222-???+--+-=N N S N ，计算N S 的通用程序； （3）按两种顺序分别计算642101010,,S S S ,并指出有效位数； （4）通过本上机你明白了什么？ 程序： 1、函数文件cxdd.m function S=cxdd(N) S=0; i=2.0; while (i<=N) S=S+1.0/(i*i-1); i=i+1; end script 运行结果（省略>>）： S=cxdd(80) S= 0.737577 2、函数文件cddx.m function S=cddx (N) S=0; for i=N:-1:2 S=S+1/(i*i-1); end script 运行结果（省略>>）： S=cddx(80) S= 0.737577 3、两种方法有效位数对比

计算方法上机实习题大作业(实验报告).

计算方法实验报告 班级： 学号： 姓名： 成绩： 1 舍入误差及稳定性 一、实验目的 （1）通过上机编程，复习巩固以前所学程序设计语言及上机操作指令； （2）通过上机计算，了解舍入误差所引起的数值不稳定性 二、实验内容 1、用两种不同的顺序计算10000 21n n -=∑，分析其误差的变化 2、已知连分数() 1 01223//(.../)n n a f b b a b a a b =+ +++，利用下面的算法计算f ： 1 1 ,i n n i i i a d b d b d ++==+ (1,2,...,0 i n n =-- 0f d = 写一程序，读入011,,,...,,,...,,n n n b b b a a 计算并打印f 3、给出一个有效的算法和一个无效的算法计算积分 1 041 n n x y dx x =+? (0,1,...,1 n = 4、设2 2 11N N j S j == -∑ ，已知其精确值为1311221N N ?? -- ?+?? （1）编制按从大到小的顺序计算N S 的程序 （2）编制按从小到大的顺序计算N S 的程序 （3）按两种顺序分别计算10001000030000,,,S S S 并指出有效位数 三、实验步骤、程序设计、实验结果及分析 1、用两种不同的顺序计算10000 2 1n n -=∑，分析其误差的变化 （1）实验步骤： 分别从1~10000和从10000~1两种顺序进行计算，应包含的头文件有stdio.h 和math.h （2）程序设计： a.顺序计算

#include #include void main() { double sum=0; int n=1; while(1) { sum=sum+(1/pow(n,2)); if(n%1000==0)printf("sun[%d]=%-30f",n,sum); if(n>=10000)break; n++; } printf("sum[%d]=%f\n",n,sum); } b.逆序计算 #include #include void main() { double sum=0; int n=10000; while(1) { sum=sum+(1/pow(n,2)); if(n%1000==0) printf("sum[%d]=%-30f",n,sum); if(n<=1)break; n--; } printf("sum[%d]=%f\n",n,sum); } （3）实验结果及分析： 程序运行结果： a.顺序计算

(完整版)数值计算方法上机实习题答案

1． 设?+=1 05dx x x I n n ， （1） 由递推公式n I I n n 1 51+-=-，从0I 的几个近似值出发，计算20I ； 解：易得：0I =ln6-ln5=0.1823, 程序为： I=0.182; for n=1:20 I=(-5)*I+1/n; end I 输出结果为：20I = -3.0666e+010 （2） 粗糙估计20I ，用n I I n n 51 5111+- =--，计算0I ； 因为 0095.05 6 0079.01020 201 020 ≈<<≈??dx x I dx x 所以取0087.0)0095.00079.0(2 1 20=+= I 程序为：I=0.0087; for n=1:20 I=(-1/5)*I+1/(5*n); end I 0I = 0.0083 （3） 分析结果的可靠性及产生此现象的原因(重点分析原因)。 首先分析两种递推式的误差；设第一递推式中开始时的误差为000I I E '-=，递推过程的舍入误差不计。并记n n n I I E '-=，则有01)5(5E E E n n n -==-=-Λ。因为=20E 20020)5(I E >>-，所此递推式不可靠。而在第二种递推式中n n E E E )5 1(5110-==-=Λ，误差在缩小， 所以此递推式是可靠的。出现以上运行结果的主要原因是在构造递推式过程中，考虑误差是否得到控制， 即算法是否数值稳定。 2． 求方程0210=-+x e x 的近似根，要求4 1105-+?<-k k x x ，并比较计算量。 （1） 在[0，1]上用二分法； 程序：a=0;b=1.0; while abs(b-a)>5*1e-4 c=(b+a)/2;

(完整word版)计算方法习题集及答案.doc

习题一 1. 什么叫数值方法？数值方法的基本思想及其优劣的评价标准如何？ 数值方法是利用计算机求解数学问题近似解的方法 x max x i , x ( x 1 , x 2 , x n ) T R n 及 A n R n n . 2. 试证明 max a ij , A ( a ij ) 1 i n 1 i n 1 j 证明： （ 1）令 x r max x i 1 i n n p 1/ p n x i p 1/ p n x r p 1/ p 1/ p x lim( x i lim x r [ ( ] lim x r [ lim x r ) ) ( ) ] x r n p i 1 p i 1 x r p i 1 x r p 即 x x r n p 1/ p n p 1/ p 又 lim( lim( x r x i ) x r ) p i 1 p i 1 即 x x r x x r ⑵ 设 x (x 1,... x n ) 0 ，不妨设 A 0 ， n n n n 令 max a ij Ax max a ij x j max a ij x j max x i max a ij x 1 i n j 1 1 i n j 1 1 i n j 1 1 i n 1 i n j 1 即对任意非零 x R n ，有 Ax x 下面证明存在向量 x 0 0 ，使得 Ax 0 ， x 0 n ( x 1,... x n )T 。其中 x j 设 j a i 0 j ，取向量 x 0 sign(a i 0 j )( j 1,2,..., n) 。 1 n n 显然 x 0 1 且 Ax 0 任意分量为 a i 0 j x j a i 0 j ， i 1 i 1 n n 故有 Ax 0 max a ij x j a i 0 j 即证。 i i 1 j 1 3. 古代数学家祖冲之曾以 355 作为圆周率的近似值，问此近似值具有多少位有效数字？ 113 解： x 325 &0.314159292 101 133 x x 355 0.266 10 6 0.5 101 7 该近似值具有 7 为有效数字。

东南大学-数值分析上机题作业-MATLAB版

2015.1.9 上机作业题报告 JONMMX 2000

1.Chapter 1 1.1题目 设S N =∑1j 2?1 N j=2 ，其精确值为 )1 1 123(21+--N N 。 （1）编制按从大到小的顺序1 1 131121222-+ ??+-+-=N S N ，计算S N 的通用程序。 （2）编制按从小到大的顺序1 21 1)1(111222-+ ??+--+-= N N S N ，计算S N 的通用程序。 （3）按两种顺序分别计算64210,10,10S S S ,并指出有效位数。（编制程序时用单精度） （4）通过本次上机题，你明白了什么？ 1.2程序 1.3运行结果

1.4结果分析 按从大到小的顺序，有效位数分别为：6，4，3。 按从小到大的顺序，有效位数分别为：5，6，6。 可以看出，不同的算法造成的误差限是不同的，好的算法可以让结果更加精确。当采用从大到小的顺序累加的算法时，误差限随着N 的增大而增大，可见在累加的过程中，误差在放大，造成结果的误差较大。因此，采取从小到大的顺序累加得到的结果更加精确。 2.Chapter 2 2.1题目 （1）给定初值0x 及容许误差ε，编制牛顿法解方程f(x)=0的通用程序。 （2）给定方程03 )(3 =-=x x x f ,易知其有三个根3,0,3321= *=*-=*x x x ○1由牛顿方法的局部收敛性可知存在,0>δ当),(0δδ+-∈x 时，Newton 迭代序列收敛于根x2*。试确定尽可能大的δ。 ○2试取若干初始值，观察当),1(),1,(),,(),,1(),1,(0+∞+-----∞∈δδδδx 时Newton 序列的收敛性以及收敛于哪一个根。 （3）通过本上机题，你明白了什么？ 2.2程序

计算方法上机作业集合

第一次&第二次上机作业 上机作业： 1.在Matlab上执行：>> 5.1-5-0.1和>> 1.5-1-0.5 给出执行结果，并简要分析一下产生现象的原因。 解：执行结果如下： 在Matlab中，小数值很难用二进制进行描述。由于计算精度的影响，相近两数相减会出现误差。 2.（课本181页第一题） 解：（1）n=0时，积分得I0=ln6-ln5，编写如下图代码

从以上代码显示的结果可以看出，I 20的近似值为0.7465 （2）I I =∫I I 5+I 10dx,可得∫I I 610dx ≤∫I I 5+I 10dx ≤∫I I 510dx,得 16(I +1)≤I I ≤15(I +1),则有1126≤I 20≤1105, 取I 20=1 105 ,以此逆序估算I 0。代码段及结果如下图所示

（3）从I20估计的过程更为可靠。首先根据积分得表达式是可知，被积函数随着n的增大，其所围面积应当是逐步减小的，即积分值应是随着n的递增二单调减小的，（1）中输出的值不满足这一条件，（2）满足。设I I表示I I的近似值，I I-I I=(?5)I(I0?I0)(根据递推公式可以导出此式),可以看出，随着n的增大，误差也在增大，所以顺序估计时，算法不稳定性逐渐增大，逆序估计情况则刚好相反，误差不断减小，算法逐渐趋于稳定。 2.（课本181页第二题）

（1）上机代码如图所示 求得近似根为0.09058 （2）上机代码如图所示 得近似根为0.09064；

（3）牛顿法上机代码如下 计算所得近似解为0.09091 第三次上机作业上机作业181页第四题 线性方程组为 [1.13483.8326 0.53011.7875 1.16513.4017 2.53301.5435 3.4129 4.9317 1.23714.9998 8.76431.3142 10.67210.0147 ][ I1 I2 I3 I4 ]=[ 9.5342 6.3941 18.4231 16.9237 ] （1）顺序消元法 A=[1.1348,3.8326,1.1651,3.4017;0.5301,1.7875,2.5330,1.5435; 3.4129, 4.9317,8.7643,1.3142;1.2371,4.9998,10.6721,0.0147]; b=[9.5342;6.3941;18.4231;16.9237]; 上机代码（函数部分）如下 function [b] = gaus( A,b )%用b返回方程组的解 B=[A,b]; n=length(b); RA=rank(A); RB=rank(B);

数值分析上机作业1-1

数值计算方法上机题目1 1、实验1. 病态问题 实验目的： 算法有“优”与“劣”之分，问题也有“好”和“坏”之别。所谓坏问题就是问题本身的解对数据变化的比较敏感，反之属于好问题。希望读者通过本实验对此有一个初步的体会。 数值分析的大部分研究课题中，如线性代数方程组、矩阵特征值问题、非线性方程及方程组等都存在病态的问题。病态问题要通过研究和构造特殊的算法来解决，当然一般要付出一些代价（如耗用更多的机器时间、占用更多的存储空间等）。 问题提出： 考虑一个高次的代数多项式 ∏=-= ---=20 1)()20)...(2)(1()(k k x x x x x p （E1-1） 显然该多项式的全部根为l ，2，…，20，共计20个，且每个根都是单重的（也称为简 单的）。现考虑该多项式方程的一个扰动 0)(19 =+x x p ε (E1-2) 其中ε是一个非常小的数。这相当于是对（E1-1）中19 x 的系数作一个小的扰动。我们希望比较（E1-1）和（E1-2）根的差别，从而分析方程（E1-1）的解对扰动的敏感性。 实验内容： 为了实现方便，我们先介绍两个 Matlab 函数：“roots ”和“poly ”，输入函数 u ＝roots （a ） 其中若变量a 存储1+n 维的向量，则该函数的输出u 为一个n 维的向量。设a 的元素依次为121,...,,+n a a a ，则输出u 的各分量是多项式方程 0...1121=++++-n n n n a x a x a x a 的全部根，而函数 b=poly(v) 的输出b 是一个n ＋1维变量，它是以n 维变量v 的各分量为根的多项式的系数。可见“roots ”和“Poly ”是两个互逆的运算函数. ve=zeros(1,21); ve(2)=ess; roots(poly(1:20))+ve) 上述简单的Matlab 程序便得到（E1-2）的全部根，程序中的“ess ”即是（E1-2）中的ε。 实验要求： （1）选择充分小的ess ，反复进行上述实验，记录结果的变化并分析它们。如果扰动项的系数ε很小，我们自然感觉（E1-1）和(E1-2)的解应当相差很小。计算中你有什么出乎意料的发现？表明有些解关于如此的扰动敏感性如何？ （2）将方程（E1-2）中的扰动项改成18 x ε或其他形式，实验中又有怎样的现象出现？

西交计算方法A上机大作业

计算方法A 上机大作业 1. 共轭梯度法求解线性方程组 算法原理：由定理3.4.1可知系数矩阵A 是对称正定矩阵的线性方程组Ax=b 的解与求解二次函数1()2 T T f x x Ax b x =-极小点具有等价性，所以可以利用共轭梯度法求解1()2 T T f x x Ax b x = -的极小点来达到求解Ax=b 的目的。 共轭梯度法在形式上具有迭代法的特征，在给定初始值情况下，根据迭代公式： (1)()()k k k k x x d α+=+ 产生的迭代序列(1)(2)(3)x x x ，，，... 在无舍入误差假定下，最多经过n 次迭代，就可求得()f x 的最小值，也就是方程Ax=b 的解。 首先导出最佳步长k α的计算式。 假设迭代点()k x 和搜索方向()k d 已经给定，便可以通过()()()() k k f x d φαα=+的极小化 ()()min ()()k k f x d φαα=+ 来求得，根据多元复合函数的求导法则得: ()()()'()()k k T k f x d d φαα=?+ 令'()0φα=，得到: ()() ()()k T k k k T k r d d Ad α=，其中()()k k r b Ax =- 然后确定搜索方向()k d 。给定初始向量(0)x 后，由于负梯度方向是函数下降最快的方向，故第一次迭代取搜索方向(0) (0)(0)(0)()d r f x b Ax ==-?=-。令 (1)(0)00x x d α=+ 其中(0)(0)0(0)(0) T T r d d Ad α=。第二次迭代时，从(1) x 出发的搜索方向不再取(1)r ，而是选取(1) (1)(0)0d r d β=+，使得(1)d 与(0)d 是关于矩阵A 的共轭向量，由此可 求得参数0β:

计算方法作业参考答案(不断更新)

: 第一次作业 1.下列各数都是经过四舍五入得到的近似数，指出他们有几位有效数字，并写出绝对误差限。 9800107480.566.385031.01021.1*65*5*4*3*2*1=?=====x x x x x x 解： 1* 11011021.01021.1?==x ，有5位有效数字，绝对误差限为4-5-1105.0105.0?=?； 1-* 2 1031.0031.0?==x ，有2位有效数字，绝对误差限为3-2-1-105.0105.0?=?； 3* 3103856.06.385?==x ；有4位有效数字，绝对误差限为-14-3105.0105.0?=?； 2* 41056480.0480.56?==x ；有5位有效数字，绝对误差限为3-5-2105.0105.0?=?； ; 65* 5 107.0107?=?=x ；有1位有效数字，绝对误差限为51-6105.0105.0?=?； 4* 6 109800.09800?==x ；有4位有效数字，绝对误差限为5.0105.04-4=?。 2.要使20的近似值的相对误差限小于%1.0，要取几位有效数字 解：由于110447213595.047213595.420??=?=，设要取n 位有效数字，则根据 定理，有()()%1.01081 1021111

计算方法作业2

《计算方法》上机指导书

实验1 MATLAB 基本命令 1．掌握MATLAB 的程序设计 实验内容：对以下问题，编写M 文件。 (1) 生成一个5×5矩阵，编程求其最大值及其所处的位置。 (2) 编程求∑=20 1!n n 。 (3) 一球从100米高度自由落下，每次落地后反跳回原高度的一半，再落下。求它在 第10次落地时，共经过多少米？第10次反弹有多高？ 2．掌握MATLAB 的绘图命令 实验内容：对于自变量x 的取值属于[0，3π]，在同一图形窗口画出如下图形。 （1）1sin()cos()y x x =?； （2）21 2sin()cos()3 y x x =-；

实验2 插值方法与数值积分 1. 研究人口数据的插值与预测 实验内容：下表给出了从1940年到1990年的美国人口，用插值方法推测1930年、1965年、2010年人口的近似值。 美国人口数据 1930年美国的人口大约是123,203千人，你认为你得到的1965年和2010年的人口数字精确度如何？ 2．最小二乘法拟合经验公式 实验内容：某类疾病发病率为y ‰和年龄段x (每五年为一段，例如0~5岁为第一段，6~10岁为第二段……)之间有形如bx ae y =的经验关系，观测得到的数据表如下 （1）用最小二乘法确定模型bx ae y =中的参数a 和b 。 （2）利用MATLAB 画出离散数据及拟合函数bx ae y =图形。 3.复化求积公式 实验内容：对于定积分? +=1 02 4dx x x I 。 （1）分别取利用复化梯形公式计算，并与真值比较。再画出计算误差与n 之间的曲线。 （2）取[0，1]上的9个点，分别用复化梯形公式和复化辛普森公式计算，并比较精度。

计算方法练习题与答案

练习题与答案 练习题一 练习题二 练习题三 练习题四 练习题五 练习题六 练习题七 练习题八 练习题答案 练习题一 一、是非题 1.*x=–1 2.0326作为x的近似值一定具有6位有效数字，且其误差限 ≤ 4 10 2 1 - ? 。() 2.对两个不同数的近似数，误差越小，有效数位越多。( ) 3.一个近似数的有效数位愈多，其相对误差限愈小。( ) 4.用 2 1 2 x - 近似表示cos x产生舍入误差。( )

5. 3.14和 3.142作为π的近似值有效数字位数相同。 ( ) 二、填空题 1. 为了使计算 ()()2334912111y x x x =+ -+ ---的乘除法次数尽量少，应将该 表达式改写为 ； 2. * x =–0.003457是x 舍入得到的近似值，它有 位有效数字，误差限 为 ，相对误差限为 ； 3. 误差的来源是 ； 4. 截断误差为 ； 5. 设计算法应遵循的原则是 。 三、选择题 1．* x =–0.026900作为x 的近似值，它的有效数字位数为( ) 。 (A) 7； (B) 3； (C) 不能确定 (D) 5. 2．舍入误差是( )产生的误差。 (A) 只取有限位数 (B) 模型准确值与用数值方法求得的准确值 (C) 观察与测量 (D) 数学模型准确值与实际值 3．用 1+x 近似表示e x 所产生的误差是( )误差。 (A). 模型 (B). 观测 (C). 截断 (D). 舍入 4．用s *=21 g t 2表示自由落体运动距离与时间的关系式 (g 为重力加速度)，s t 是在 时间t 内的实际距离，则s t - s *是（ ）误差。 (A). 舍入 (B). 观测 (C). 模型 (D). 截断 5．1.41300作为2的近似值，有( )位有效数字。 (A) 3； (B) 4； (C) 5； (D) 6。 四、计算题

计算方法练习题与答案

练习题与答案练习题一 练习题二 练习题三 练习题四 练习题五 练习题六 练习题七 练习题八 练习题答案 练习题一 一、是非题 1.*x=–作为x的近似值一定具有6位有效数字，且其误差限 4 10 2 1 - ? 。 () 2.对两个不同数的近似数，误差越小，有效数位越多。 ( ) 3.一个近似数的有效数位愈多，其相对误差限愈小。 ( ) 4.用 2 1 2 x - 近似表示cos x产生舍入误差。 ( )

和作为π的近似值有效数字位数相同。 ( ) 二、填空题 1.为了使计算 ()()23 34912111y x x x =+ -+ ---的乘除法次数尽量少，应将该表 达式改写为 ； 2.* x =–是x 舍入得到的近似值，它有 位有效数字，误差限 为 ，相对误差限为 ； 3.误差的来源是 ； 4.截断误差为 ； 5.设计算法应遵循的原则 是 。 三、选择题 1．* x =–作为x 的近似值，它的有效数字位数为( ) 。 (A) 7； (B) 3； (C) 不能确定 (D) 5. 2．舍入误差是( )产生的误差。 (A) 只取有限位数 (B) 模型准确值与用数值方法求得的准确值 (C) 观察与测量 (D) 数学模型准确值与实际值 3．用 1+x 近似表示e x 所产生的误差是( )误差。 (A). 模型 (B). 观测 (C). 截断 (D). 舍入 4．用s *=21 g t 2表示自由落体运动距离与时间的关系式 (g 为重力加速度)，s t 是 在时间t 内的实际距离，则s t s *是（ ）误差。 (A). 舍入 (B). 观测 (C). 模型 (D). 截断 5．作为2的近似值，有( )位有效数字。 (A) 3； (B) 4； (C) 5； (D) 6。