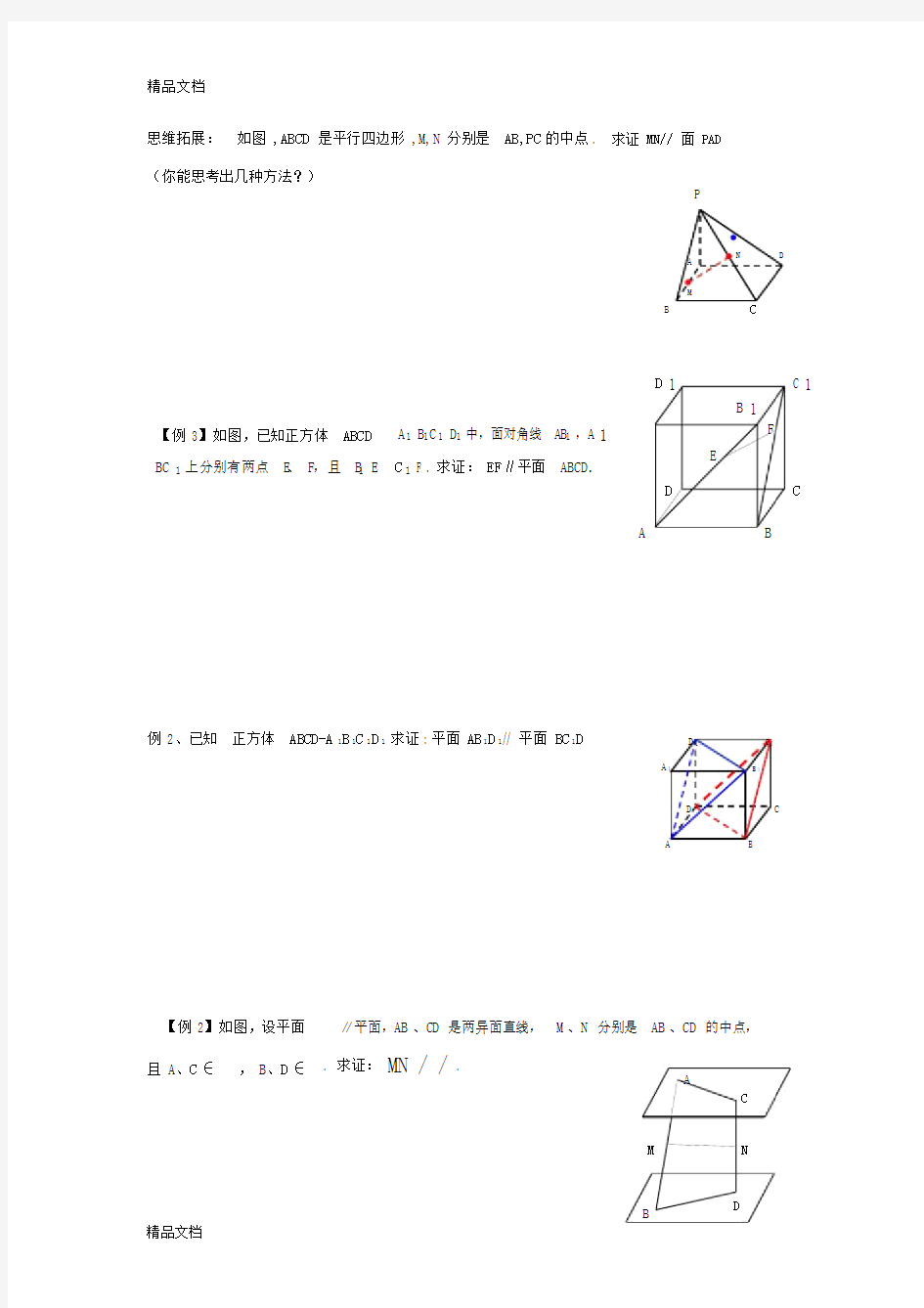
思维拓展:如图 ,ABCD是平行四边形,M,N 分别是 AB,PC的中点 .求证MN//面PAD
(你能思考出几种方法?)
P
A
M
N D
B C
D 1 C 1
B 1
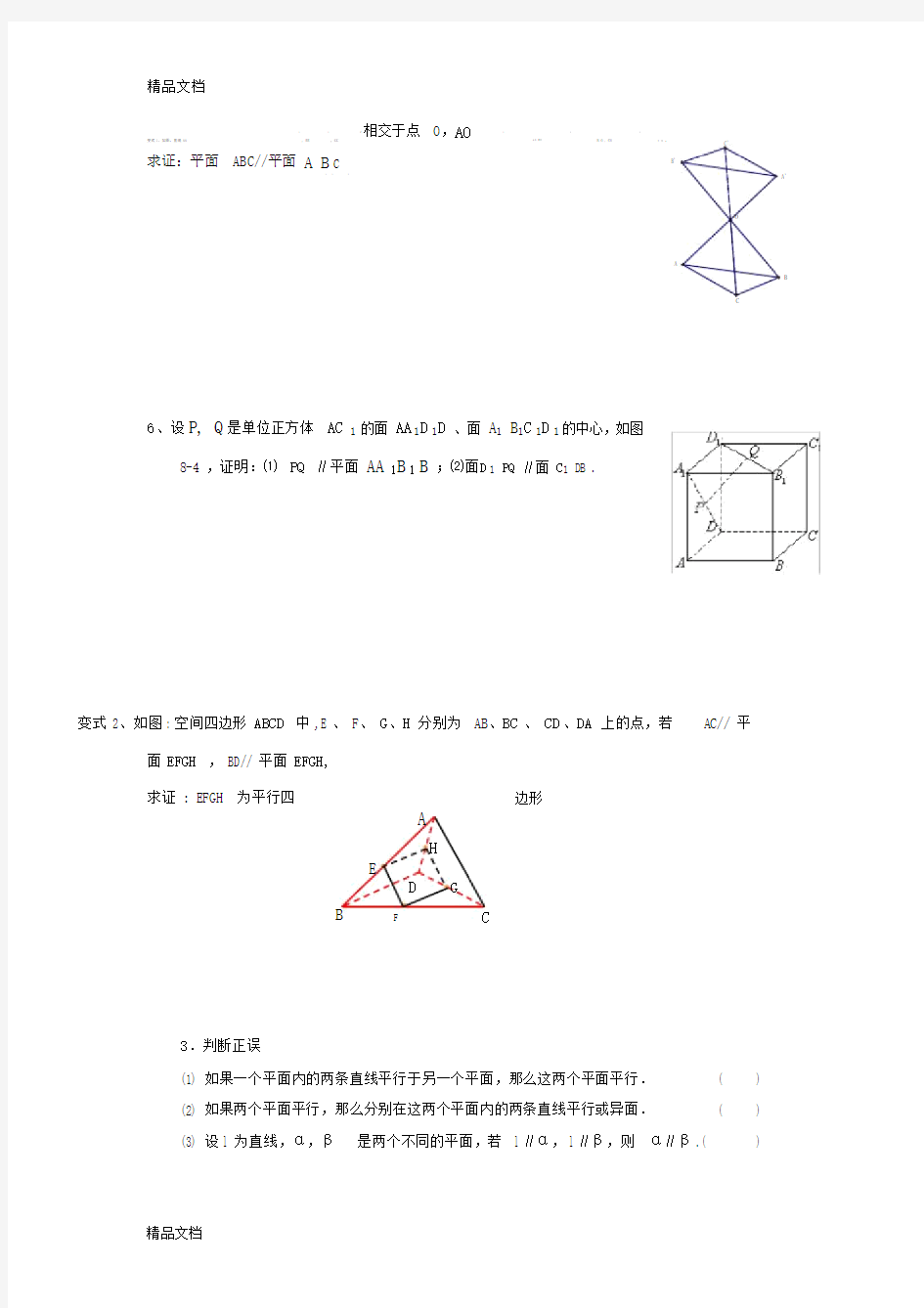
【例 3】如图,已知正方体 ABCD A1 B1C1 D1中,面对角线 AB1,A 1 F
BC1上分别有两点 E、 F,且 B1 E C1 F . 求证: EF∥平面 ABCD.
E
D C
A B
例 2、已知正方体 ABCD-A1B1C1D1求证 : 平面 AB1D1// 平面 BC1D D1 C
1
A1B1
D C
A B
【例 2】如图,设平面∥平面,AB、CD是两异面直线,M、N分别是AB、CD的中点,
且 A、C∈, B、D∈. 求证:MN / / .
A
C
M N
'
'
'
相交于点 O ,AO
'
'
'
变式 1、如图,直线 AA
, BB , CC A O, BO
B O , CO
C O ,
C'
求证:平面 ABC// 平面 A B C
B'
'
A'
' '
O
A
B
C
6、设 P, Q 是单位正方体 AC 1 的面 AA 1D 1D 、面 A 1 B 1C 1D 1的中心,如图
8-4 ,证明:⑴ PQ ∥平面 AA 1B 1 B ;⑵面 D 1 PQ ∥面 C 1 DB .
变式 2、如图 : 空间四边形 ABCD 中 ,E 、 F 、 G 、H 分别为 AB 、BC 、 CD 、DA 上的点,若
AC// 平
面 EFGH , BD// 平面 EFGH,
求证 : EFGH 为平行四 边形
A
H
E
B
D G
F
C
3.判断正误
(1) 如果一个平面内的两条直线平行于另一个平面,那么这两个平面平行. ( ) (2) 如果两个平面平行,那么分别在这两个平面内的两条直线平行或异面.
(
) (3) 设 l 为直线,α,β 是两个不同的平面,若 l ∥α, l ∥β,则 α∥β .(
)
4.下列条件中,能判断两个平面平行的是() A.一个平面内的一条直线平行于另一个平面
B.一个平面内的两条直线平行于另一个平面
C.一个平面内有无数条直线平行于另一个平面
D.一个平面内任何一条直线都平行于另一个平面
5.已知平面α∥β,直线a? α,有下列说法:
①a与β 内的所有直线平行;
②a与β 内无数条直线平行;
③a与β 内的任意一条直线都不垂直.
其中真命题的序号是________.
【例 1】如图,在几何体ABCDE中,四边形 ABCD 是矩形, AB⊥平面 BEC,BE⊥EC,AB= BE=EC= 2,G,F 分别是线段BE, DC的中点.
求证: GF∥平面ADE.
如图所示,斜三棱柱ABC- A1B1C1中,点 D,D1分别为AC, A1C1上的中点. (1) 证明: AD1∥平面 BDC1;
(2)证明: BD∥平面 AB1D1.
【例 2】如图,四棱锥P-ABCD的底面是边长为8 的正方形,四条侧棱长均为 2 17.
点G, E, F, H 分别是棱 PB, AB, CD, PC上共面
的四点,平面 GEFH⊥平面 ABCD,BC∥平面 GEFH.
(1)证明: GH∥EF; (2) 若 EB=2,求四边形 GEFH的
面积.
【例 3】如图所示,已知 ABCD-A1B1C1D1是棱长为 3 的正方
体,点 E 在 AA1上,点 F 在 CC1上, G 在 BB1上,且 AE=
FC1=B1G=1,H 是B1C1的中点.(1) 求证:E、B、F、D1
四点共面; (2) 求证:平面 A1GH∥平面 BED1F.
4 如图,在三棱柱ABC- A1B1C1中, E, F, G, H 分别是AB ,AC, A1B1, A1C1的中点,求证:(1)B ,C, H, G四点共面;
(2) 平面 EFA1∥平面 BCHG.
D B A 1 A F 立体几何——平行的证明 【例1】如图,四棱锥P -ABCD 的底面是平行四边形,点E 、F 分 别为棱AB 、 PD 的中点.求证:AF ∥平面PCE ; 分析:取PC 的中点G ,连EG.,FG ,则易证AEGF 是平行四边形 【例2】如图,已知直角梯形ABCD 中,AB∥CD,AB⊥BC,AB =1,BC =2,CD =1+3,过A 作AE⊥CD,垂足为E ,G 、F 分别为AD 、CE 的中点,现将△ADE 沿AE 折叠,使得DE⊥EC。 (Ⅰ)求证:BC⊥面CDE ; (Ⅱ)求证:FG∥面BCD ; 分析:取DB 的中点H ,连GH,HC 则易证FGHC 是平行四边形 【例3】已知直三棱柱ABC -A 1B 1C 1中,D, E, F 分别为AA 1, CC 1, AB 的中点, M 为BE 的中点, AC⊥BE . 求证: (Ⅰ)C 1D⊥BC; (Ⅱ)C 1D∥平面B 1FM. 分 析 : 连 EA , 易 证 C 1EAD 是 平 行 四 是 (第1题图)
P E D C B A MF -,,AD CD AD BA ⊥⊥//EB PAD 平面E F G M AD CD BD BC AM EFG 求证: AB 1 ABEF ⊥ABCD ABEF ABCD 090,BAD FAB BC ∠=∠=//= 1 2 AD BE //= 12 AF ,G H ,FA FD BCHG ,,,C D F E ) 利用平行 四边形的性质 【例9】正方体ABCD —A 1B 1C 1D 1中O 为正方形ABCD 的中心,M 为BB 1的中点, 求证: D 1O 2 1 中点为PD E 求证:AE ∥平面PBC ; 分析:取PC 的中点F ,连EF 则易证ABFE 是平行四边形 【例11】在如图所示的几何体中,四边形ABCD 为平行四边形,∠ ACB=90?,EA⊥平面ABCD,EF ∥AB,FG∥BC,EG∥AC.AB=2EF。若M是线段AD的中点,求证:GM∥平面ABFE; (I )证法一: 因为 EF 90ACB ∠=? 90,EGF ABC ∠=??. EFG ?BC FG 2 1= ABCD BC AM 2 1=FA ?GM ? A B C D E F G M
第四章立体几何--平行及位置关系 一.课标要求: 1.平面的基本性质与推论 借助长方体模型,在直观认识和理解空间点、线、面的位置关系的基础上,抽象出空间线、面位置关系的定义,并了解如下可以作为推理依据的公理和定理: ◆公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内; ◆公理2:过不在一条直线上的三点,有且只有一个平面; ◆公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线; ◆公理4:平行于同一条直线的两条直线平行; ◆定理:空间中如果两个角的两条边分别对应平行,那么这两个角相等或互补。 2.空间中的平行关系 以立体几何的上述定义、公理和定理为出发点,通过直观感知、操作确认、思辨论证,认识和理解空间中线面平行、垂直的有关性质与判定。通过直观感知、操作确认,归纳出以下判定定理: ◆平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行; ◆一个平面内的两条相交直线与另一个平面平行,则这两个平面平行; 通过直观感知、操作确认,归纳出以下性质定理,并加以证明: ◆一条直线与一个平面平行,则过该直线的任一个平面与此平面的交线与该直线平 行; ◆两个平面平行,则任意一个平面与这两个平面相交所得的交线相互平行; ◆垂直于同一个平面的两条直线平行 能运用已获得的结论证明一些空间位置关系的简单命题。 二.命题走向 立体几何在高考中占据重要的地位,通过近几年的高考情况分析,考察的重点及难点稳定,高考始终把直线与直线、直线与平面、平面与平面平行的性质和判定作为考察重点。在难度上也始终以中等偏难为主,在新课标教材中将立体几何要求进行了降低,重点在对图形及几何体的认识上,实现平面到空间的转化,示知识深化和拓展的重点,因而在这部分知识
高三文科数学专题复习:立体几何平行、垂直问题 【基础知识点】 一、平行问题 1.直线与平面平行的判定与性质 定义判定定理性质性质定理 图形 条件a∥α 结论a∥αb∥αa∩α=a∥b 2. 面面平行的判定与性质 判定 性质 定义定理 图形 条件α∥β,a?β 结论α∥βα∥βa∥b a∥α 平行问题的转化关系: 二、垂直问题 一、直线与平面垂直 1.直线和平面垂直的定义:直线l与平面α内的都垂直,就说直线l与平面α互相垂直.2.直线与平面垂直的判定定理及推论 文字语言图形语言符号语言 判定定理 一条直线与一个平面内的两条相交直线都垂直,则该直线与此平 面垂直 推论 如果在两条平行直线中,有一条垂直于平面,那么另一条直线也垂直这个平面
文字语言 图形语言 符号语言 性质定理 垂直于同一个平面的 两条直线平行 4.直线和平面垂直的常用性质 ①直线垂直于平面,则垂直于平面内任意直线. ②垂直于同一个平面的两条直线平行. ③垂直于同一条直线的两平面平行. 二、平面与平面垂直 1.平面与平面垂直的判定定理 文字语言 图形语言 符号语言 判定定理 一个平面过另一个平 面的垂线,则这两个平 面垂直 2.平面与平面垂直的性质定理 文字语言 图形语言 符号语言 性质定理 两个平面垂直,则一个 平面内垂直于交线的直线垂直于另一个平 面 类型一、平行与垂直 例1、如图,已知三棱锥A BPC -中,,,AP PC AC BC ⊥⊥M 为AB 中点,D 为PB 中点, 且△PMB 为正三角形。(Ⅰ)求证:DM ∥平面APC ; (Ⅱ)求证:平面ABC ⊥平面APC ; (Ⅲ)若BC 4=,20AB =,求三棱锥D BCM -的体积。 M D A P B C
高三复习——立体几何平行问题专题(学生版) ——李洪波一、基础过关 1. 定理性质梳理 2.平行关系的总结 面面平行 线面平行线线平行
二、概念理解——判断下列命题真假 (1)若直线l 与平面α平行,则l 与平面α内的任意一条直线都平行;( ) (2)如果两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行;( ) (3)若直线l 与平面α平行,则l 与平面α内的任意一条直线都没有公共点;( ) (4)平行于同一平面的两条直线互相平行;( ) (5)αα//,//a b b a ??; ( ) (6)b a b a ////,//?αα; ( ) (7)αα////,//a b b a ?; ( ) (8)b a b a //,//??αα; ( ) (9)已知平面 α,β 和直线 m ,若,//,m m αβ?,则 α
练习:如图13,正方形ABCD与正方形ABEF所在平面相交于AB,在AE、BD上各有一 .求证:PQ∥平面BCE. 点P、Q,且AP DQ
解法二:(简要过程) A B C D F E P Q 解法三:(简要过程) A B C D F E P Q 四、举一反三 1.(17文科1)如图,在下列四个正方体中,A ,B 为正方体的两个顶点,M ,N ,Q 为所在棱的中点,则在这四个正方体中,直接AB 与平面MNQ 不平行的是( ) 2.(17文科2)如图,四棱锥P-ABCD 中,侧面PAD 为等边三角形且垂直于底面ABCD ,AB =BC = 1 2 AD ,
∠BAD =∠ABC =90°.证明:直线BC∥平面PAD ; 3.(16文科3)如图,四棱锥中,平面,AD BC ,AB , 4PA BC ==,M 为线段AD 上一点,2AM MD =,N 为PC 的中点.证明MN 平面PAB .
高考中常见的立体几何题型和解题方法 黔江中学高三数学教师:付 超 高考立体几何试题一般共有2——3道(选择、填空题1——2道, 解答题1道), 共计总分18——23分左右,考查的知识点在20个以内. 选择填空题考核立几中的 逻辑推理型问题, 而解答题着重考查立几中的计算型问题, 当然, 二者均应以正 确的空间想象为前提. 随着新的课程改革的进一步实施,立体几何考题正朝着“多 一点思考,少一点计算”的方向发展.从历年的考题变化看, 以简单几何体为载体 的线面位置关系的论证,角与距离的探求是常考常新的热门话题. 一、知识整合 1.有关平行与垂直(线线、线面及面面)的问题,是在解决立体几何问题的过 程中,大量的、反复遇到的,而且是以各种各样的问题(包括论证、计算角、与 距离等)中不可缺少的内容,因此在主体几何的总复习中,首先应从解决“平行 与垂直”的有关问题着手,通过较为基本问题,熟悉公理、定理的内容和功能, 通过对问题的分析与概括,掌握立体几何中解决问题的规律——充分利用线线平 行(垂直)、线面平行(垂直)、面面平行(垂直)相互转化的思想,以提高逻辑思维能 力和空间想象能力. 2. 判定两个平面平行的方法: (1)根据定义——证明两平面没有公共点; (2)判定定理——证明一个平面内的两条相交直线都平行于另一个平面; (3)证明两平面同垂直于一条直线。 3.两个平面平行的主要性质: ⑴由定义知:“两平行平面没有公共点”。 ⑵由定义推得:“两个平面平行,其中一个平面内的直线必平行于另一个平 面。 ⑶两个平面平行的性质定理:“如果两个平行平面同时和第三个平面相交, 那 么它们的交线平行”。 ⑷一条直线垂直于两个平行平面中的一个平面,它也垂直于另一个平面。 ⑸夹在两个平行平面间的平行线段相等。 ⑹经过平面外一点只有一个平面和已知平面平行。 以上性质⑵、⑷、⑸、⑹在课文中虽未直接列为“性质定理”,但在解题过 程中均可直接作为性质定理引用。 4.空间角和距离是空间图形中最基本的数量关系,空间角主要研究射影以 及与射影有关的定理、空间两直线所成的角、直线和平面所成的角、以及二面角 和二面角的平面角等.解这类问题的基本思路是把空间问题转化为平面问题去解 决. 空间角,是对由点、直线、平面所组成的空间图形中各种元素间的位置关系 进行定量分析的一个重要概念,由它们的定义,可得其取值范围,如两异面直线 所成的角θ∈(0,2π],直线与平面所成的角θ∈0,2π?????? ,二面角的大小,可用它们的平面角来度量,其平面角θ∈[0,π].对于空间角的计算,总是通过一定 的手段将其转化为一个平面内的角,并把 它置于一个平面图形,而且是一个三
课时作业7 平行关系的性质 |基础巩固|(25分钟,60分) 一、选择题(每小题5分,共25分) 1. 如图所示,长方体ABCD-A1B1C1D1中,E、F分别是棱AA1和BB1的中点,过EF的平面EFGH分别交BC和AD于G、H,则HG与AB的位置关系是() A.平行 B.相交 C.异面 D.平行和异面 解析:∵E、F分别是AA1、BB1的中点,∴EF∥AB.又AB?平面EFGH,EF?平面EFGH,∴AB∥平面EFGH.又AB?平面ABCD,平面ABCD∩平面EFGH=GH, ∴AB∥GH. 答案:A 2.已知a,b表示两条不同的直线,α,β表示两个不重合的平面,给出下列四个命题: ①若α∥β,a?α,b?β,则a∥b;②若a∥b,a∥α,b∥β,则α∥β;③若α∥β,a?α,则a∥β;④若a∥α,a∥β,则α∥β. 其中正确的个数为() A.1B.2 C.3 D.4 解析:对于①,a∥b或a与b是异面直线,故①错;对于②,也可能是α与β相交,故②错;对于④,同样α与β也可能相交,故④错.只有③对. 答案:A 3.在空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,当BD∥平面EFGH时,下列结论正确的是() A.E,F,G,H一定是各边的中点 B.G,H一定是CD,DA的中点 C.BE:EA=BF:FC,且DH:HA=DG:GC D.AE:EB=AH:HD,且BF:FC=DG:GC 解析:由BD∥平面EFGH,得BD∥EH,BD∥FG,则AE:EB=AH:HD,且BF:FC =DG:GC. 答案:D 4.若平面α∥平面β,直线a∥平面α,点B在平面β内,则在平面β内且过点B的所有直线中() A.不一定存在与a平行的直线 B.只有两条与a平行的直线 C.存在无数条与a平行的直线 D.存在唯一与a平行的直线
立体几何---空间平行关系 【基础知识梳理】 1、平行关系知识框图 【基础知识检测】 一、选择题 1、平行于同一个平面的两条直线的位置关系是( ) A.一定平行 B.平行或相交 C.一定相交 D.平行或相交或异面 2、过直线l 外两点,作与直线l 平行的平面,这样的平面的个数是( ) A.有无 数个 B.不能作出 C.只能作出一个 D.以上都有可能 3、已知m ,n 为两条不同的直线,α,β为两个不同的平面,则下列命题中正确的是( ) A .,,//,////m n m n ααββαβ??? B . //,,//m n m n αβαβ??? C .,//m m n n αα⊥⊥? 4、下列命题正确的为 ( ) A.0 B.1 C.2 D.3 (1)平行于同一直线的两平面平行 (2)垂直于同一直线的两平面平行. (3)若α ∥β, 则平面α 内任一直线 a ,a ∥β. (4)若n ?α ,m ? α,n ∥β,m ∥β,则α∥β. 二、填空题 5、点A 是平面α 外的一点,过A 和平面α 平行的直线有 条. 6、点A 是直线l 外一点,过点A 和直线l 平行的平面有 个. 7、过两条平行线中的一条和另一条直线平行的平面有 个.
8、过两条异面直线中的一条和另一条直线平行的平面有 个. 9、如果21//l l ,1l 平行于平面α,则2l 与平面α 10、如果两直线b a ,相交,a 平行于平面α,则b 与平面α的位置关系是—— 三、解答题 11、如图,已知Q P 、是正方体1111-D C B A ABCD 的面ABCD 和面1111D C B A 的中心, 求证:PQ //平面11A ADD 立体几何---空间平行关系答案 1-3D4C 5-7无数个8、一个9、平行或在平面内
D E B 1 A 1 C 1 C A B M 高中立体几何证明线面平行问题(数学作业十七) (1) 通过“平移”再利用平行四边形的性质 1.如图,四棱锥P -ABCD 的底面是平行四边形,点E 、F 分别为棱AB 、 PD 的中点.求证: AF ∥平面PCE ; 2、已知直三棱柱ABC -A 1B 1C 1中,D, E, F 分别为AA 1, CC 1, AB 的中点, M 为BE 的中点, AC ⊥BE. 求证: (Ⅰ)C 1D ⊥BC ; (Ⅱ)C 1D ∥平面B 1FM. 3、如图所示, 四棱锥P ABCD 底面是直角梯形, E F B A C D P (第
,,AD CD AD BA ⊥⊥CD=2AB, E 为PC 的中点, 证明: //EB PAD 平面; (2) 利用三角形中位线的性质 4、如图,已知E 、F 、G 、M 分别是四面体的棱AD 、CD 、BD 、BC 的中点,求证:AM ∥平面EFG 。 5、如图,ABCD 是正方形,O 是正方形的中心,E 是PC 的中点。 求证: PA ∥平面BDE 6.如图,三棱柱ABC —A 1B 1C 1中, D 为AC A B C D E F G M
P E D C B A 的中点. 求证:AB 12 1中点为PD E 求证:AE ∥平面PBC ; (4)利用对应线段成比例 9、如图:S 是平行四边形ABCD 平面外一点,M 、N 分别是SA 、 BD 上的点,且SM AM =ND BN , 求证:MN ∥平面SDC (5)利用面面平行 10、如图,三棱锥ABC P -中,PB ⊥底面,90BCA ∠=o ,PB=BC=CA , 为的中点,为的中点,点在上,且2AF FP =. (1)求证:BE ⊥平面; (2)求证://CM 平面;
高中数学-立体几何位置关系-平行与垂直证明方法汇总 (一)立体几何中平行问题 证明直线和平面平行的方法有: ①利用定义采用反证法; ②平行判定定理; ③利用面面平行,证线面平行。 主要方法是②、③两法 在使用判定定理时关键是确定出面内的 与面外直线平行的直线. 常用具体方法:中位线和相似 例1、P是平行四边形ABCD所在平面外一点,Q是PA的中点. 求证:PC∥面BDQ. 证明:如图,连结AC交BD于点O. ∵ABCD是平行四边形, ∴A O=O C.连结O Q,则O Q在平面BDQ内, 且O Q是△APC的中位线, ∴PC∥O Q. ∵PC在平面BDQ外, ∴PC∥平面BDQ. 例2、在棱长为a的正方体ABCD-A1B1C1D1中,设M、N、E、F分别是棱A1B1、A1D1、C1D1、B1C1的中点.求证: (1)E、F、B、D四点共面; (2)面AMN∥面EFBD.
证明:(1)分别连结B 1D 1、ED 、FB ,如图, 则由正方体性质得 B 1D 1∥BD. ∵E 、F 分别是D 1C 1和B 1C 1的中点, ∴EF ∥ 21B 1D 1.∴EF ∥2 1 BD. ∴E 、F 、B 、D 对共面. (2)连结A 1C 1交MN 于P 点,交EF 于点Q ,连结AC 交BD 于点O ,分别连结PA 、Q O . ∵M 、N 为A 1B 1、A 1D 1的中点, ∴MN ∥EF ,EF ?面EFBD. ∴MN ∥面EFBD. ∵PQ ∥A O , ∴四边形PA O Q 为平行四边形. ∴PA ∥O Q. 而O Q ?平面EFBD , ∴PA ∥面EFBD.且PA ∩MN=P ,PA 、MN ?面AMN , ∴平面AMN ∥平面EFBD. 例3如图(1),在直角梯形P 1DCB 中,P 1D//BC ,CD ⊥P 1D ,且P 1D=8,BC=4,DC=4 6, A 是P 1D 的中点,沿A B 把平面P 1AB 折起到平面PAB 的位置(如图(2)),使二面角P —CD —B 成45°,设E 、F 分别是线段AB 、PD 的中点. 求证:AF//平面PE C ; 证明:如图,设PC 中点为G ,连结FG ,
c c ∥∥b a b a ∥?本文档系统总结归纳了立体几何中平行与垂直证明方法,特别适合于高三总复习时对学生构建知识网络、探求解题思路、归纳梳理解题方法。是一份不可多得的好资料。 一、“平行关系”常见证明方法 (一)直线与直线平行的证明 1) 利用某些平面图形的特性:如平行四边形的对边互相平行 2) 利用三角形中位线性质 3) 利用空间平行线的传递性(即公理4): 平行于同一条直线的两条直线互相平行。 4) 利用直线与平面平行的性质定理: 如果一条直线与一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。 5) 利用平面与平面平行的性质定理: 如果两个平行平面同时和第三个平面相交,那么它们的交线平行. 6) 利用直线与平面垂直的性质定理: 垂直于同一个平面的两条直线互相平行。 a b α β b a a =??βαβ α∥b a ∥? b a b a ////??? ? ?? ==γβγαβαI I β α ⊥⊥b a b a ∥?α a b
7) 利用平面内直线与直线垂直的性质: 在同一个平面内,垂直于同一条直线的两条直线互相平行。 8) 利用定义:在同一个平面内且两条直线没有公共点 (二)直线与平面平行的证明 1) 利用直线与平面平行的判定定理: 平面外的一条直线与此平面内的一条直线平行,则该直线与此平面平行。 2) 利用平面与平面平行的性质推论: 两个平面互相平行,则其中一个平面内的任一直线平行于另一个平面。 3) 利用定义:直线在平面外,且直线与平面没有公共点 (三)平面与平面平行的证明 常见证明方法: 1) 利用平面与平面平行的判定定理: 一个平面内的两条相交直线与另一个平面平行,则这两个平面平行。 α b a β α a β αα∥?a β ∥a ?α αββ////∩??b a P b a b a =α β//?α β b a P b ∥a b a αα??α ∥a ?
2015-2017立体几何高考真题 1、(2015年1卷6题)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺。问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放斛的米约有( ) (A )14斛 (B )22斛 (C )36斛 (D )66斛 【答案】B 【分析】设圆锥底面半径为r ,则 12384r ??==16 3 r =,所以米堆的体积为211163()5433????=3209,故堆放的米约为 320 9 ÷1.62≈22,故选B. 考点:圆锥的性质和圆锥的体积公式 2、(2015年1卷11题)圆柱被一个平面截去一部分后和半球(半径为r )组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16 + 20π,则r=( ) (A )1 (B )2 (C )4 (D )8 【答案】B 【分析】由正视图和俯视图知,该几何体是半球和半个圆柱的组合体,圆柱的半径和球的半径都为r ,圆柱的高为2r ,其表面积为221 42222 r r r r r r πππ?+?++?=2254r r π+=16 + 20π,解得r=2,故选B. 考点:简单几何体的三视图;球的表面积公式、圆柱的测面积公式 3、(2015年1卷18题)如图,四边形ABCD 为菱形,∠ABC=120°,E ,F 是平面ABCD 同一侧的两点,BE ⊥平面ABCD ,DF ⊥平面ABCD ,BE=2DF ,AE ⊥EC.
高中立体几何证明平行的专题训练 深圳市龙岗区东升学校一一罗虎胜 立体几何中证明线面平行或面面平行都可转化为 线线平行,而证明线线平行一般有以下的一些方法: (1)通过“平移”。 (2)利用三角形中位线的性质。 (3)利用平行四边形的性质。 (4)利用对应线段成比例。 (5)利用面面平行,等等。 ⑴通过“平移”再利用平行四边形的性质 1. 如图,四棱锥P—ABCD的底面是平行四边形,点E、F 分另为棱AB、PD的中点.求证:AF //平面PCE; P 分析:取PC的中点G,连EG.,FG,则易证AEGF是平行四边形 F E A (第1题 图) 2、如图,已知直角梯形ABCD 中,AB // CD,AB 丄BC,AB = 1,BC = 2,CD = 1 + -?. 3,过A作AE丄CD,垂足为E,G、F分别为AD、CE的中点,现将△ ADE沿AE折叠,使得DE 丄EC. (I)求证:BC 丄面CDE ; (H)求证:FG //面BCD ; 分析:取DB的中点H,连GH,HC贝惕证FGHC是平行四边形
的中点,证明:EB//平面PAD ; 分析::取PD 的中点F ,连EF,AF 则易证 ABEF 是 平行四边形 (2)利用三角形中位线的性质 5、如图,已知E 、F 、G 、M 分别是四面体的棱 AD AM //平面 EFG 。 3、已知直三棱柱 ABC — A 1B 1C 1中,D, E, F 分别为 AA 1, CC 1, AB 的中点, M 为BE 的中点,AC 丄BE.求证: (i) C 1D 丄BC ; (n) C 1D //平面 B i FM. 分析:连EA ,易证C 1EAD 是平行四边形,于是 MF//EA D A A 1 4、如图所示,四棱锥P ABCD 底面是直角梯形, BA AD, CD AD ,CD=2AB, E 为 PC 分析:连 MD 交GF 于H ,易证EH 是厶AMD 的中位线 6、如图,ABCD 是正方形,0是正方形的中心, E 是PC C
高一数学 必修二 空间中平行与垂直关系 强化练习 1.空间中,垂直于同一直线的两条直线 A. 平行 B .相交 C .异面 A.若 m//l, n//l ,则 m//n B .若 m 〃 ,n 〃 ,则 m//n C.若m ,m ,则 D .若m , ,则m 〃 或m 3. 下列说法正确的是() A. 如果一条直线与一个平面内的无数条直线平行,则这条直线与这个平面平行 B. 两个平面相交于唯一的公共点 C. 如果一条直线与一个平面有两个不同的公共点,则它们必有无数个公共点 D. 平面外的一条直线必与该平面内无数条直线平行 4. 如图,ABCD- A i BiGD 为正方体, A. BD// 平面 CBD B. AG 丄B i C C. AC 丄平面CBD D. 直线CC 与平面CBD 所成的角为45° 5. 如图,四棱锥 V ABCD 中,底面ABCD 是边长为2的正方形,其他四个侧面都是侧 棱长为.5的等腰三角形,则二面角 V AB C 的大小 ( ) A. 30 B . 45 C . 60 D . 120 6. 下列四个结论: ⑴两条直线都和同一个平面平行,则这两条直线平行。 ⑵两条直线没有公共点,则这两条直线平行。 ⑶两条直线都和第三条直线垂直,则这两条直线平行。 ⑷一条直线和一个平面内无数条直线没有公共点,则这条直线和这个平面平行。 其中正确的个数为( ) A. 0 B . 1 C . 2 D . 3 7.在四面体ABCD 中,已知棱AC 的长为.2,其余各棱长都为1,则二面角 A CD B 的 余弦值为( ) A. 1 B .1 C .-D 2 3 3 .3 2.已知互不相同的直线l,m,n 与平面 ,则下列叙述错误的是( () D .以上均有可能
1 思维拓展: 如图,ABCD 是平行四边形,M,N 分别是AB,PC 的中点. 求证MN//面PAD (你能思考出几种方法?) 【例3】如图,已知正方体 中,面对角线,上分别有两点E 、F ,且.求证:EF ∥平面ABCD . 例2、已知 正方体ABCD-A 1B 1C 1D 1求证:平面AB 1D 1//平面BC 1D 【例2】如图,设平面∥平面,AB 、CD 是两异面直线,M 、N 分别是AB 、CD 的中点,且A 、C∈,B 、D∈. 求证:. 1111 A B C D A B C D -1A B 1 B C 11B E C F =αβαβ//M N αA B C D F E C 1 B 1A 1 D 1 D 1 B 1 A 1 D C B A C 1α β A B C D M N P C
2 变式1、如图,直线相交于点O ,,, 求证:平面ABC //平面 6、设是单位正方体的面、面的中心,如图 8-4,证明:⑴∥平面;⑵面 ∥面. 变式2、如图:空间四边形ABCD 中,E 、F 、 G 、H 分别为AB 、BC 、CD 、DA 上的点,若AC//平面EFGH ,BD//平面EFGH, 求证: EFGH 为平行四 边形 3.判断正误 (1)如果一个平面内的两条直线平行于另一个平面,那么这两个平面平行.( ) (2)如果两个平面平行,那么分别在这两个平面内的两条直线平行或异面.( ) (3)设l 为直线,α,β是两个不同的平面,若l∥α,l∥β,则α∥β.( ) ' '' ,,CC BB AA ,'O A AO =O B BO ' =O C CO ' =' ' ' C B A ,P Q 1A C 11A A D D 1111A B C D P Q 11A A B B 1D P Q 1C D B
立体几何(平行关系的证明) 线面平行的证明 利用中位线 1.在四棱锥ABCD P -中,底面ABCD 是正方形,侧棱⊥PD 底面ABCD ,DC PD =,E 是PC 的中点,作PB EF ⊥交PB 于点F 。证明 :∥PA 平面EDB 。 2.如图,矩形ABCD 中,ABE AD 平面⊥,2===BC EB AE ,F 为CE 上的点,且 ACE BF 平面⊥.求证;BFD AE 平面//; 3.如图,四边形ABCD 与''ABB A 都是边长为a 的正方形,点E 是A A '的中点, 'A A ⊥平面ABCD 。求证:C A '//平面BDE 。 B C
N M A B D C O A B C E F P 1 A 1 C 1 B 利用平行四边形 4.如图,在四棱锥O ABCD -中,底面ABCD 四边长为1的菱形, 4 ABC π ∠= , OA ABCD ⊥底面, 2OA =,M 为OA 的中点, N 为BC 的中点。证明:直线MN OCD 平面‖ 5.在直三棱柱111C B A ABC -中, AC=4,CB=2,AA 1=2 ο60=∠ACB ,E 、F 分别是BC C A ,11的中点。 证明://1F C 平面ABE 。 6.如图,PA 垂直于矩形ABCD 所在的平面,AD PA 2==,CD 22=,E 、F 分别 是AB 、PD 的中点。求证:AF//平面PCE ;
利用比例 7.如下图,设P 为长方形ABCD 所在平面外一点,M ,N 分别为AB ,PD 上的点,且MB AM =NP DN ,求证:直线MN ∥平面PBC. 8.如图,正方形ABCD 的边长为13,平面ABCD 外一点P 到正方形各顶点的距离都是13, M ,N 分别是PA ,DB 上的点,且58PM MA BN ND ==∶∶∶.求证:直线MN //平面PBC 。 9 正方形ABCD 交正方形ABEF 于AB (如图所示)M 、N 在对角线AC 、FB 上且AM= FN 。求证:MN //平面BCE A B C E N D M P D A B C F E M N
F G G A B C D E C A B D E F D E B 1A 1C 1C A B F M 高中立体几何证明平行 的专题(基本方法) 立体几何中证明线面平行或面面平行都可 转化为 线线平行,而证明线线平行一般有以下的一些方法: (1)通过“平移”。(2)利用三角形中位线的性质。(3)利用平行四边形的性质。 (4)利用对应线段成比例。(5)利用面面平行,等等。 (1) 通过“平移”再利用平行四边形的性质 1.如图,四棱锥P -ABCD 的底面是平行四边形,点E 、F 分 别 为棱AB 、 PD 的中点.求证:AF ∥平面PCE ; 分析:取PC 的中点G ,连EG.,FG ,则易证AEGF 是平行四 边形 2、如图,已知直角梯形ABCD 中,AB ∥CD ,AB ⊥BC ,AB =1, BC =2,CD =1+3, 过A 作AE ⊥CD ,垂足为E ,G 、F 分别为AD 、CE 的中点,现将 △ADE 沿AE 折叠,使得DE ⊥EC. (Ⅰ)求证:BC ⊥面CDE ; (Ⅱ)求证:FG ∥面BCD ; 分析:取DB 的中点H ,连GH,HC 则易证FGHC 是平行四边形 3、已知直三棱柱ABC -A 1B 1C 1中,D, E, F 分别为AA 1, CC 1, AB 的中点, M 为BE 的中点, AC ⊥BE. 求证: (Ⅰ)C 1D ⊥BC ; (Ⅱ)C 1D ∥平面B 1FM. 分析:连EA ,易证C 1EAD 是平行四边形,于是MF//EA 4、如图所示, 四棱锥P -ABCD 底面是直角梯形, ,,AD CD AD BA ⊥ ⊥CD=2AB, E 为PC 的中点, 证明: //EB PAD 平面; 分析::取PD 的中点F ,连EF,AF 则易证ABEF 是平行四边形 (2) 利用三角形中位线的性质 5、如图,已知E 、F 、G 、M 分别是四面体的棱AD 、CD 、BD 、BC 的中点,求证:AM ∥平面EFG 。 分析:连MD 交GF 于H ,易证EH 是△AMD 的中位线 6、如图,ABCD 是正方形,O 是正方形的中心,E 是PC 的中点。 求证: PA ∥平面BDE 7.如图,三棱柱ABC —A 1B 1C 1中, D 为AC 的中点. 求证:AB 1//面BDC 1; 分析:连B 1C 交BC 1于点E ,易证ED 是 E F B A C D P (第1题图) A B C D E F G M
立体几何中的平行问题 (1)线面平行思考途径 I.转化为直线与平面无公共点;II.转化为线线平行;III.转化为面面平行 支持定理 ①////a b b a a ααα???????? ; ②////a a αββα?????; 配图助记 (2)线线平行:思考途径 I.转化为判定共面二直线无交点; II.转化为二直线同与第三条直线平行; III.转化为线面平行; IV.转化为线面垂直; V.转化为面面平行. 支持定理 ①////a a a b b αβαβ??????=?;②//a a b b αα⊥???⊥?;③////a a b b αβαγβγ??=???=? ;④//////a b c b a c ???? 配图助记 (3)面面平行:思考途径 I.转化为判定二平面无公共点; II.转化为线面平行; III.转化为线面垂直. 支持定理 ①,////,//a b a b o a b αααβββ????=???? ;②//a a ααββ⊥???⊥?;③//////αβαγγβ???? 配图助记 αb βa a b α b γβ α a a β α b O β a α β α γ α β a a α b β α a
一、线面平行 1、如图,在底面为平行四边形的四棱锥立体中,AB AC ⊥,PA ⊥平面ABCD ,且PA AB =,点E 是PD 的中点.(Ⅱ)求证://PB 平面AEC ; 2、在四棱锥P ABCD -中,AB //CD ,AB AD ⊥, 4,2AB AD CD ===,PA ⊥平面ABCD ,4PA =. (Ⅰ)设平面PAB 平面PCD m =,求证:CD //m ; 3、如图,直三棱柱-'''ABC A B C ,=90BAC ∠?,=='AB AC AA λ,点,M N 分别为'A B 和''B C 的中点 (1)证明://''MN AACC 平面; P D C B A
1 D B A 1 A F 立体几何——平行的证明 【例1】如图,四棱锥P -ABCD 的底面是平行四边形,点E 、F 分 别为棱AB 、 PD 的中点.求证:AF ∥平面PCE ; 分析:取PC 的中点G ,连EG .,FG ,则易证AEGF 是平行四边形 【例2】如图,已知直角梯形ABCD 中,AB ∥CD ,AB ⊥BC ,AB =1,BC =2,CD =1+3,过A 作AE ⊥CD ,垂足为E ,G 、F 分别为AD 、CE 的中点,现将△ADE 沿AE 折叠,使得DE ⊥EC 。 (Ⅰ)求证:BC ⊥面CDE ; (Ⅱ)求证:FG ∥面BCD ; 分析:取DB 的中点H ,连GH,HC 则易证FGHC 是平行四边形 【例3】已知直三棱柱ABC -A 1B 1C 1中,D, E, F 分别为AA 1, CC 1, AB 的中点, M 为BE 的中点, AC ⊥BE. 求证: (Ⅰ)C 1D ⊥BC ; (Ⅱ)C 1D ∥平面B 1FM. 分析:连EA ,易证C 1EAD 是平行四边形,于是MF//EA (第1题图)
2 【例4】如图所示, 四棱锥P -ABCD 底面是直角梯形, ,,AD CD AD BA ⊥⊥CD=2AB, E 为PC 的中点, 证明: //EB PAD 平面; 分析::取PD 的中点F ,连EF,AF 则易证ABEF 是平行四边形 (2) 利用三角形中位线的性质 【例5】如图,已知E 、F 、G 、M 分别是四面体的棱AD 、CD 、BD 、BC 的中点,求证:AM ∥平面EFG 。 分析:连MD 交GF 于H ,易证EH 是△AMD 的中位线 【例6】如图,ABCD 是正方形,O 是正方形的中心,E 是PC 的中点。 求证: PA ∥平面BDE 【例7】如图,三棱柱ABC —A 1B 1C 1中, D 为AC 的中点. 求证:AB 1//面BDC 1; 分析:连B 1C 交BC 1于点E ,易证ED 是 △B 1AC 的中位线 A B C D E F G M
专题:平行问题 主要考点:线面平行 面面平行 线面平行的判定定理:如果一个平面内的一条直线和另平面内的一条直线平行,那么这条直线和这个平面 平行。定理模式:,,////a b a b a ααα??? 面面平行的判定定理:如果一个平面内有两条相交直线都平行于一个平面,那么这两个平面平行。 定理的模式://////a b a b P a b ββαβαα?? ? ??? =??? ??? 1、如右图所示,已知P 、Q 是正方体的面11A B BA 和面ABCD 的中心. 证明:PQ ∥平面11C B BC 2、如图,在底面为平行四边形的四棱锥P ABCD -中,点E 是PD 的中点.求证://PB 平面AEC . 3、如图,在直四棱柱ABCD-A 1B 1C 1D 1中,底面ABCD 为等腰梯形,AB//CD ,AB=4, BC=CD=2, AA 1=2, E 、E 1、 F 分别是棱AD 、AA 1、AB 的中点。 证明:直线EE 1//平面FCC 1; 4、两个全等的正方形ABCD 和ABEF 所在平面相交于AB ,M ∈AC ,N ∈FB ,且AM =FN ,求证:MN ∥平面BCE 。 E A B C F E 1 A 1 B 1 C 1 D 1 D _ P
5、已知在四棱锥P-ABCD 中,ABCD 为平行四边形,E 为PC 的中点,O 为BD 的中点. 求证:OE //平面ADP 6、在四棱锥P-ABCD 中,底面四边形ABCD 是平行四边形,E,F 分别是AB ,PD 的中点. 求证://AF 平面PCE 3、如图所示,ABC ?为正三角形,EC ⊥平面ABC ,//BD CE ,且2C E C A B D ==,F 、M 是CE 、EA 的中点。求证: (1)//DM 平面ABC ; (2)面//FDM 面ABC . 10.P 是△ABC 所在平面外一点,A ′、B ′、C ′分别是△PBC 、△PCA 、△PAB 的重心。 (1)求证:平面A ′B ′C ′∥平面ABC ; (2)S △A′B′C′∶S △ABC 的值。 P A B C D E O P B C D A E F B C A M D F E
高中数学总复习- 第七章立体几何-空间中的平行和垂直关系 【知识结构图】 第3课空间中的平行关系 【考点导读】 1 ?掌握直线和平面平行、两个平面平行的判定定理和性质定理。 2 ?明确定义与定理的不同,定义是可逆的,既是判定也是性质,而判定定理与性质定理多是不可逆的。 3. 要能灵活的对“线线平行”、“线面平行”和“面面平行”进行转化。 【基础练习】 1. 若a、b为异面直线,直线c // a,则c与b的位置关系是异面或相交
2 ?给出下列四个命题①垂直于同一直线的两条直线互相平行?②垂直于同一平面的两个平面互相平 行. ③若直线1(2与同一平面所成的角相等,则1」2互相平行. ④若直线1(2是异面直线,则与1(2都相交的两条直线是异面直线. 其中假命题的个数是_4 _______ 个。 3?对于任意的直线I与平面a,在平面a内必有直线m使m与I 垂直。: 4. 已知a、b、c是三条不重合的直线, a、B、r是三个不重合的平面,下面 六个命题: ①a// c, b// c a// b;②a // r, b II r a // b;③a// c, B // c a// B ; ④a// r, B // r a// B ;⑤a// c,a// c a//a;⑥a // r ,a// r a //a. 其中正确的命题是①④________ 【范例导析】例1.如图,在四面体ABCD中,截面EFGH是平行四边形. 求证:AB//平面EFG 证明:?面EFGH是截面. ???点E, F, G, H分别在BC, BD, DA AC上. ??? EH 面ABC GF 面ABD 由已知,EH// GF. ? EH// 面ABD 又T EH,—面BAC 面AB6面ABD=AB ?EH// AB. ?AB// 面EFG 例2. 如图,在正方体ABC—A1B1C1D中,点N在BD上,点M在BC上,并且CM=DN. D C
立体几何中的平行与垂直问题作业 1.如图所示,在三棱柱ABC—A1B1C1中,四边形AA1B1B为矩形,平面AA1B1B⊥平面ABC,点E,F分别是侧面AA1B1B,BB1C1C对角线的交点. (1)求证:EF∥平面ABC; (2)求证:BB1⊥AC. 2.(2019·苏锡一模)如图29-7,正三棱柱ABCA1B1C1的高为6,其底面边长为2.已知点M,N分别是棱A1C1,AC的中点,点D 是棱CC1上靠近C的三等分点. 求证:(1)B1M∥平面A1BN; (2)AD⊥平面A1BN.
立体几何中的平行与垂直问题作业答案 1.如图所示,在三棱柱ABC—A1B1C1中,四边形AA1B1B为矩形,平面AA1B1B⊥平面ABC,点E,F分别是侧面AA1B1B,BB1C1C对角线的交点. (1)求证:EF∥平面ABC; (2)求证:BB1⊥AC. (1)证明:因为在三棱柱ABC-A1B1C1中, 所以四边形AA1B1B,四边形BB1C1C均为平行 四边形, 又因为E,F分别是侧面AA1B1B,BB1C1C对 角线的交点, 所以E,F分别是AB1,CB1的中点, 所以EF∥AC,又因为EF?平面ABC,AC?平面ABC, 所以EF∥平面ABC; (2)证明:因为四边形AA1B1B为矩形, 所以BB1⊥AB, 又因为平面AA1B1B⊥平面ABC,BB1?平面AA1B1B,平面AA1B1B
∩平面ABC=AB, 所以BB1⊥平面ABC, 因为AC?平面ABC所以BB1⊥AC. 2.(2019·苏锡一模)如图29-7,正三棱柱ABC-A1B1C1的高为6,其底面边长为2.已知点M,N分别是棱A1C1, AC的中点,点D是棱CC1上靠近C的三等分点. 求证:(1) B1M∥平面A1BN; (2)AD⊥平面A1BN. (1)证明:连接MN,正三棱柱ABC-A1B1C1 中,四边形AA1C1C是平行四边形,AA1∥CC1 且AA1=CC1,因为点M,N分别是棱A1C1, AC的中点,所以MN∥AA1且MN=AA1, 又正三棱柱ABC-A1B1C1中AA1∥BB1且AA1=BB1, 所以MN∥BB1且MN=BB1,所以四边形MNBB1是平行四边形,所以B1M∥BN,又B1M 平面A1BN,BN?平面A1BN,所以B1M∥平面A1BN. (2)证明:正三棱柱ABC-A1B1C1中,AA1⊥平面ABC,BN?平面ABC,所以BN⊥AA1, 在正△ABC中,N是AC的中点,所以BN⊥AC,又AA1,AC?平面AA1C1C,AA1∩AC=A, 所以BN⊥平面AA1C1C,又AD?平面AA1C1C,所以AD⊥BN, 由题意得,AA1=6,AC=2,AN=1,CD= 6 3 ,所以 AA1 AC= AN CD = 3 2 , 又∠A1AN=∠ACD= π 2 ,所以△A1AN∽△ACD,则∠AA1N=∠CAD,