各种谱函数

2.频谱Spectrum

对时域信号作傅立叶变换，得到的直接结果即为频谱Spectrum。它是复数，因此有幅值和相位信息。同时显示同一频谱的幅值和相位的图形称为波德图(bode)，如下图所示。

频谱图中的0Hz表示时域信号的平均值或称为直流偏量。频谱只有线性形式，不像自谱有线性形式和平方形式。由于频谱是复数形式，包含相位信息，当信号中包含不相关的噪声成分时，由于噪声成分的相位是杂乱无序的，那么多次线性平均之后，可以将不相关的噪声平均掉。另外，即使是相关的频率成分，如单频信号进行线性平均时，线性平均次数越多，幅值也越趋向于0（关于这一点后续有文章推出）。

如两个单频信号幅值和频率相同，但相位相反，那么，当对这两个信号进行平均时，那么，它们的幅值将为0。在汽车排气系统中，有一种主动消音机制，就是先接收声音，然后将声音反相回放回去，从而达到消音的目的，利用的就是这个原理。

相对而言，频谱是计算其他谱函数的基础，像计算自谱、互谱和频响函数等，都需要用到频谱。

在频谱的基础上，衍生出了相位参考谱。故名思义，在计算相位参考谱时，需要选择一个信号作为参考信号，那么与此信号相关的成分将不会被平均掉，而与此信号不相关的成分将会被平均掉。像在做发动机TPA 时，经常在发动机上表面安装一个单向的加速度传感器，这个单向加速度传感器信号作用之一就是用来做相位参考的。

另外，由于频谱还包含相位信息，因此，可用于ODS计算。

3.自谱AutoPower

自谱或称为自功率谱本质是由频谱计算得到的，它是复数频谱乘以它的共轭（不要问我什么是共轭哟）。因此，自谱是实数，没有相位信息。由于它是实数，因此可以进行线性平均。

由于它是复数频谱与它的共轭的乘积，因此自谱有平方形式，平方形式的自谱称为自功率谱Power。对平方形式的自谱再求平方根，对应为线性形式，称为线性自功率谱AutoPower Linear。

线性自功率谱是最常用的，它是很多软件默认的谱函数形式，它告诉我们信号中含有哪些频率成分，某信号的线性自功率谱如下图所示。

4.功率谱密度PSD

功率谱密度PSD表征的是单位频率上的能量分布。它等于自功率谱除以频率分辨率，因此，它的单位为（信号单位^2/Hz）。由于自谱是实数，因此，功率谱也是实数，可进行线性平均。它只有RMS格式。

不同的试验人员试验时可能会采用不同的频率分辨率，因此，谱函数的幅值可能会有差异，不方便进行对比。而PSD剔除了频率分辨率的影响，因而，可比性更强。在各类国标中，通常用的都是PSD。

如果信号是随机信号，当用线性自功率谱时，不同的频率分辨率下，线性自功率谱幅值明显不同，如下图所示。

而当用PSD表示时，即使采用不同的频率分辨率，PSD都相同，如下图所示。

因此，对于随机信号，通常应用PSD来表征。应用在路谱采集，随机激励采集等情况。

5.能量谱ESD

能量谱ESD通常用于瞬态信号。因为对于瞬态信号而言，研究它的总能量比研究它在采样总时间内的平均功率更有意义。它也只有RMS格式。实际运算是将PSD的值倍乘以测量周期T的值。因此，一般很少用ESD，某信号的ESD如下图所示。

6.互谱CrossPower

互谱也是通过频谱计算得到的，但是是一个信号的频谱乘以另一个信号的频谱的共轭得到，它的结果为复数形式，有幅值和相位信号，任一频率下的相位为两个信号的相位差。因此，计算互谱时，一定是两个信号。

如果对互谱进行线性平均，那么两个信号不相关的成分将会被弱化。

互功率谱蕴涵有两个信号之间在幅值和相位上的相互关系信息。它在任意频率处的相位值，表示两个信号在该频率的相对相位（相位差），因此，可用它研究两个信号的相位关系。

另一方面，相位移动，表示的是时间移动（相移对应时移），因此，可利用互谱检测和确定信号传递的延迟。

在声强估计时，通过声强探头上两个麦克风，计算它们的互谱，进行声强估计。

在OMA分析时，用到的也是互谱。计算传递率（这个传递率不同于之前的评价隔振装置隔振效果用的传递率）时，也是互谱与自谱之比。只不过此时是两个响应信号之比。

互谱另一个重要的应用是计算频响函数FRF和相干。如进行H1估计时，用的是响应与激励的互谱除以激励的自谱，而H2估计刚好相反，用的是响应的自谱除以响应和激励的互谱。

7.频响函数FRF

频响函数是响应与激励之比，表征的是结构的固有属性。可类比弹簧的静刚度来理解，当弹簧制作好之后，它的刚度也就确定了，拉力大一点，弹簧的伸长量也大一点。类似，频响函数也有这样的特点，激励大一点，结构的响应也会大一点。与弹簧静刚度不同的是，它是随频率变化的，是结构的动态特性，是固有属性，与外界激励没有关系。

我们都知道锤击法或激振器法进行模态测试都测量频响函数。频响函数是模态分析所必需的数据。在这就不对频响函数作过多说明了。

8.相干函数

相干反映多分量组成的输出信号中最大能量与输出信号中总能量的比值。相干可用于检测由别的通道信号功率引起的一测量通道的功率。据此用于评估频响函数的测量质量。另外，它不仅用于评估输入输出关系，还可用来评估多个激振器给出的激振力之间的相干关系。

相干函数是个平均函数，如锤击法测试时，当力锤锤击第一次，相干杂乱无章（LMS软件）或者完全为1（有的软件设置为1），这是因为第一次，起不到平均的作用。要体现出相干函数的作用，至少要锤击两次或两次以上。

相干函数的取值范围在0和1之间。高值（接近于1）表明输出几乎完全由输入引起，你可以充分相信频响函数的测量结果。低值（接近于0）表明有其它的输入信号没有被测量出，或存在严重的噪声，泄漏，或系统有明显的非线性或时延等诸类问题。

下图为某一测点的频响函数和相干曲线，从相干曲线上可以看出，在反共振峰处，相干系数往下掉，如图中728Hz处，相干只有0.28。这是因为，在反共振峰处，结构没有响应或响应很微弱，因此，激励与响应之间没有因果关系。而在共振峰处，刚好相反，结构很容易被激励起来，相干系数接近1。

9.Overall Level

Overall Level，也称为总量级，表征的是信号的总有效值随时间或转速（或其他信号）的变化曲线。我们知道有效值表征的是信号的能量，因此，overall level表明的是信号能量的变化趋势。所以，通常在做FFT计算时，同时计算overall level。

Overall Level的计算过程如下：对一帧长度的时域信号作FFT，得到瞬时频谱S，计算该瞬时频谱整个带宽内的总有效值A，然后根据FFT计算的参数设置（重叠或步长参数），重复上一步的计算过程，直到计算完所有的时域信号。将各瞬时频谱得到的总有效值，按时间或转速大小关系连成曲线，就是所谓的Overall Level。大致过程所下图所示。

对于旋转机械而言，所有的阶次切片的总和就是Overall Level。

综上所述，频谱是各种谱函数的计算基础，一般很少用它，除非在TPA或ODS中才可能用到。AutoPower Linear(线性自功率谱)是最常用的，也是大多数软件作FFT计算时的默认设置。而AutoPower(自功率谱)也很少用，计算AutoPower Linear，PSD时都要用到它。PSD也很常用，比方模态分析，路谱测试，随机信号采集等。ESD一般用来表征瞬态信号。互谱是个中间量，经常用它来计算FRF、相干、估计声强或OMA分析等。FRF/相干，大家都知道，模态分析必需的数据类型，或者一些连接点的灵敏度分析也是用它。Overall Level

表征的是信号能量的变化趋势，因此，这个也经常用来表示信号能量的变化趋势，特别是对旋转机械。各种谱函数的Peak，RMS和Peak-Peak格式不关键，因为可以相互转换，默认可能是Peak。

怎样理解分布函数

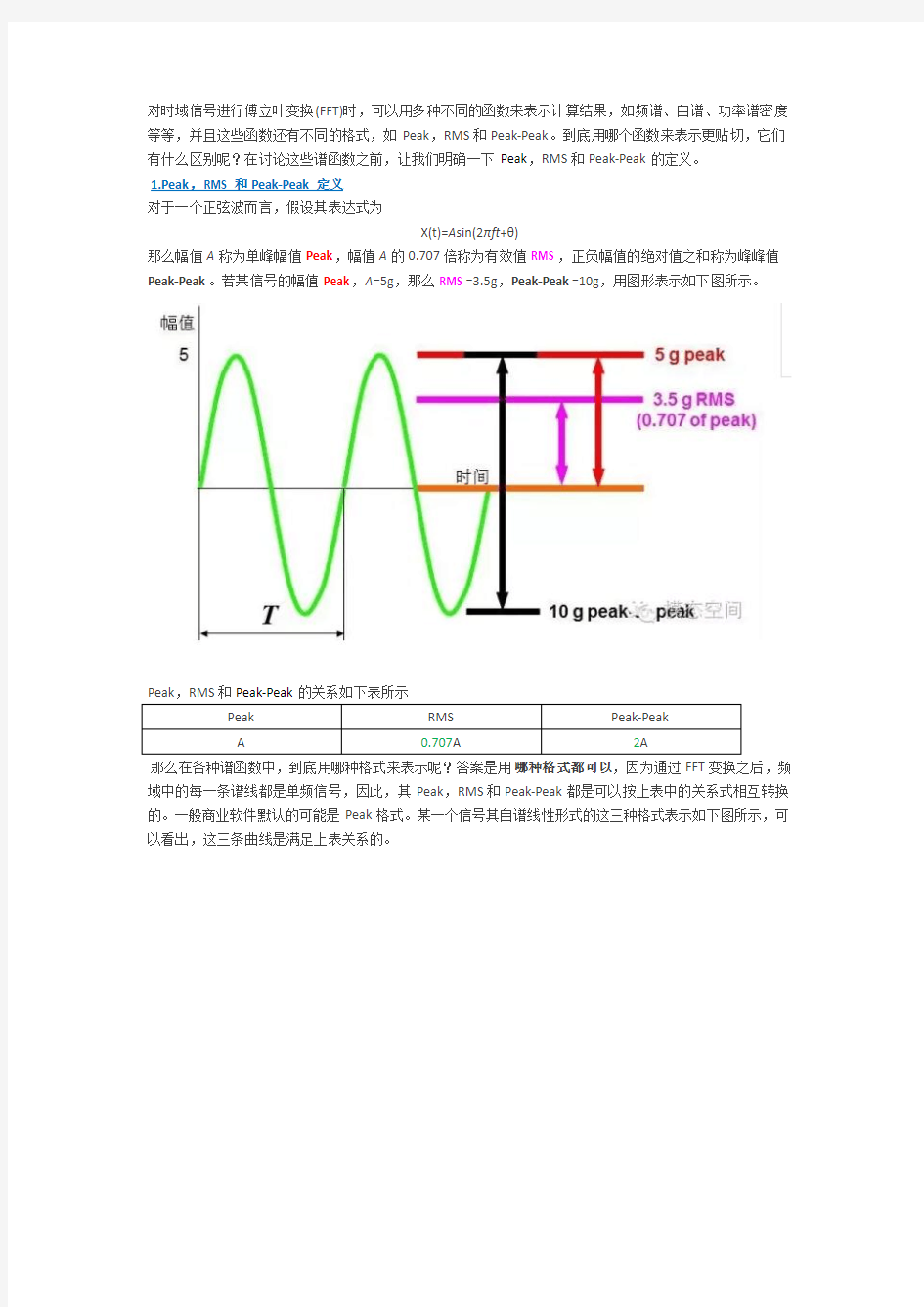
怎样理解分布函数 概率论中一个非常重要的函数就是分布函数,知道了随机变量的 分布函数,就知道了它的概率分布,也就可以计算概率了。 一、理解好分布函数的定义: F(x)=P(X≤x), 所以分布函数在任意一点x的值,表示随机变量落在x点左边(X≤x)的概率。它的定义域是(-∞,+∞),值域是[0,1]. 二、掌握好分布函数的性质: (1)0≤F(x)≤1; (2)F(+∞)=1,F(-∞)=0; 可以利用这条性质确定分布函数中的参数,例如: 设随机变量X的分布函数为:F(x)=A+Barctanx,求常数A与B. 就应利用本性质计算出A=1/2,B=1/π. (3)单调不减; (4)右连续性。 三、会利用分布函数求概率 在利用分布函数求概率时,以下公式经常利用。

(1)P(a

经验分布函数及其应用

经验分布函数及其应用 经验分布函数定义 定义：设12n x x x ?，，，是总体(离散型、或连续型，分布函数F(x)未知)的n 个独立观测值，按大小顺序可排成12***n x x x ≤≤?≤。若1**k k x x x +＜＜，则不超过x 的观测值的频率为函数，就等于在n 次重复独立试验中事件{}x ξ≤的频率。 ()110,=,,1,2,,1 1,k k n n x x k x x x k n n x x x F * **+*?≤??<≤=-??>? *?…… 我们称此函数()n F x 为总体的经验分布函数或样本分布函数。 简单性质： 1.对于每一组观测值1,2,i i x i ξ*=*=，……,n ，()n F x *单调，非降，左连 续且在1,2,i x x i =*=，……,n 点有间断点，在每个点的跳跃值都是1 n 。 2.显然 ()01n F x ≤≤，具有分布函数的其他性质。 3.()n F x *为样本1 2n x x x ?，，，的函数，是一统计量，即为一随机变量，由于1 2n x x x ?，，，相互独立且有相同的分布函数()F x ，

因而它等价于n 次独立重复试验的伯努利概型中事件{}x ξ≤发生k 次其余n k -次不发生的额概率，即有： {}{}()()1()k n k k k n n k P F x C F x F x n -??==-??? ? 4.格列汶科定理 设总体ξ的分布函数为()F x ，经验分布函数为 ()n F x *，对于任何实数 x ，记 ()()sup n x n F x F x D -∞<<*+∞=- 则有lim 01n n P D →∞????==?????? 其中n D 也为一统计量用来衡量()n F x *与()F x 之间在所有的x 的值上 的最大差异程度，格列汶科定理证明了统计量n D 以概率为1地收敛于0，也就是如下所要说的经验分布函数的收敛性问题。 经验分布函数的收敛性 经验分布函数在统计中有着非常重要的作用, 是理论分布函数与实际数据间的桥梁, 本科教材中已经指出, 当样本容量足够大时, 经验分布函数依概率收敛于总体分布函数,所以, 统计推断才得以以样本为依据, 而得到合理的结果。而事实上, 经验分布函数与总体分布函数还有更进一步的收敛关系, 下简单介绍之

功率谱密度

第九章 功率谱密度 张华，031120517 介绍 ● 确定信号的光谱分析：自相关——窗口式傅立叶变换 ● 平稳随机信号的光谱分析:方差——信号模型 ● 附加白噪声的正弦估计：消除干扰——eigen 分析 9.1基于DFT 的光谱分析 能量谱及相关特性：维纳-辛钦理论∑∞ -∞ =-= m fm j xx xx e m r m P π2)()( ● 离散傅立叶变换：理论的使用范围和频域取样； 窗口技术——转化结果的泄露和丢失 ● 时间/频率转换：不确定原则N Fs NT T f ==?= ?11 ● 零填充和有用的窗函数 维纳-辛钦理论 )] ()([)()()()()()(2* 2 2k m x m x E m r e m r f X f X e m x f X xx m mf j xx m mf j +== == ∑∑∞ -∞ =-∞ -∞=-ππ 9.1.1自相关估计 ● 平稳随机信号的光谱估计:1 ,1,0,)()(1)(1 -=+-=∑--=∧ N m m k x k x m N m r m N k xx ● Down_weight 估计: ∑--=∧+= ??? ??-≤-=1 ) ()(1 011)(m N k xx m k x k x N m r N m N m m w ）（其他 )(m r xx ∧ 的均值和方差: 均值:)()1()]()([1 )]([1 m r N m m k x k x E N m r E xx m N k xx -=+= ∑--=∧ 方差:∑∞-∞ =∧ +-+=k xx xx xx xx m k r m k r k r N m r Var )]()()([1)]([2 9.1.2周期图法: 无参数的PSD 估计 周期图:

实验五 经验分布函数图形的绘制与演示

实验六 经验分布函数图形的绘制与演示 6.1 实验原理 设()F x 是总体X 的分布函数，12,,,n X X X "是来自总体X 的简单随机样本．对任意一个实数x ，定义函数 #()(),i n X x F x x n ≤=?∞<<∞. (6.1) 其中#()i X x ≤表示样本分量12,,,n X X X "中小于或等于x 的个数，或者说，()n F x 是事件“X x ≤”发生的频率．易见)(x F n 满足分布函数的性质（单增、有界、右连续等），故)(x F n 为一分布函数，称)(x F n 为总体X 的经验分布函数．由格列汶科定理知 lim sup ()()0 1.n n x P F x F x →∞?∞<<∞???==???? 该定理说明)(x F n 在整个实数轴上以概率1均匀收敛于()F x ．当样本容量n 充分大时，经验分布函数)(x F n 可以作为总体分布函数()F x 的一个良好的近似，这是数理统计学中以样本推断总体的理论依据． 当给定样本值1212(,,,)(,,,)n n X X X x x x =""时，若将12,,,n x x x "从小到大排序：(1)(2)()n x x x ≤≤≤"，得到有序样本)()2()1(,,,n x x x "，由定义(6.1)知，)(x F n 的形式为 (1)()(1)()0,,(),,1,2,,1,1,. n k k n x x k F x x x x k n n x x +??" (6.2) 这就是根据样本观测值得到的经验分布函数的具体形式． 6.2 实验目的及要求 理解经验分布函数的构成，经验分布函数是样本的函数，随着样本观测值的变化而变化，通过实验学习经验分布函数图形的绘制方法和动态演示过程．具体要求为 1. 任意产生一组随机样本，对该样本从小到大排序； 2. 利用排序后的样本作经验分布函数图形； 3. 让样本动态变化，观察相应的经验分布函数图形的变化，写出实验体会．

功率谱和功率谱密度的区别

谱让人联想到的Fourier变换，是一个时间平均（time average）概念，对能量就是能量谱，对功率就是功率谱。 功率谱的概念是针对功率有限信号的，所表现的是单位频带内信号功率随频率的变化情况。保留了频谱的幅度信息，但是丢掉了相位信息，所以频谱不同的信号其功率谱是可能相同的。 有两点需要注意： 1. 功率谱是随机过程的统计平均概念，平稳随机过程的功率谱是一个确定函数；而频谱是随机过程样本的Fourier变换，对于一个随机过程而言，频谱也是一个“随机过程”。（随机的频域序列） 2. 功率概念和幅度概念的差别。此外，只能对宽平稳的各态历经的二阶矩过程谈功率谱，其存在性取决于二阶矩是否存在并且二阶矩的Fourier变换收敛；而频谱的存在性仅仅取决于该随机过程的该样本的Fourier变换是否收敛。 频谱分析： 对动态信号在频率域内进行分析，分析的结果是以频率为坐标的各种物理量的谱线和曲线，可得到各种幅值以频率为变量的频谱函数F(ω)。频谱分析中可求得幅值谱、相位谱、功率谱和各种谱密度等等。频谱分析过程较为复杂，它是以傅里叶级数和傅里叶积分为基础的。 功率谱密度： 功率谱密度（PSD），它定义了信号或者时间序列的功率如何随频率分布。这里功率可能是实际物理上的功率，或者更经常便于表示抽象的信号被定义为信号数值的平方，也就是当信号的负载为1欧姆(ohm)时的实际功率。

由于平均值不为零的信号不是平方可积的，所以在这种情况下就没有傅里叶变换。维纳-辛钦定理（Wiener-Khinchin theorem）提供了一个简单的替换方法，如果信号可以看作是平稳随机过程，那么功率谱密度就是信号自相关函数的傅里叶变换。 信号的功率谱密度当且仅当信号是广义的平稳过程的时候才存在。如果信号不是平稳过程，那么自相关函数一定是两个变量的函数，这样就不存在功率谱密度，但是可以使用类似的技术估计时变谱密度。 随机信号是时域无限信号，不具备可积分条件，因此不能直接进行傅氏变换。一般用具有统计特性的功率谱来作为谱分析的依据。 功率谱与自相关函数是一个傅氏变换对。 功率谱具有单位频率的平均功率量纲。所以标准叫法是功率谱密度。从名字分解来看就是说，观察对象是功率，观察域是谱域。 通过功率谱密度函数，可以看出随机信号的能量随着频率的分布情况。像白噪声就是平行于一条直线。 一般我们讲的功率谱密度都是针对平稳随机过程的，由于平稳随机过程的样本函数一般不是绝对可积的，因此不能直接对它进行傅立叶分析。可以有三种办法来重新定义谱密度，来克服上述困难。 1. 用相关函数的傅立叶变换来定义谱密度； 2. 用随机过程的有限时间傅立叶变换来定义谱密度； 3. 用平稳随机过程的谱分解来定义谱密度。 三种定义方式对应于不同的用处，首先第一种方式前提是平稳随机过程不包含周

功率谱密度

t=0:0.0001:0.1; %时间间隔为0.0001，说明采样频率为10000Hz x=square(2*pi*1000*t); %产生基频为1000Hz的方波信号 n=randn(size(t)); %白噪声 f=x+n; %在信号中加入白噪声 figure(1); subplot(2,1,1); plot(f); %画出原始信号的波形图 ylabel('幅值(V)'); xlabel('时间(s)'); title('原始信号'); y=fft(f,1000); %对原始信号进行离散傅里叶变换，参加DFT采样点的个数为1000 subplot(2,1,2); m=abs(y); f1=(0:length(y)/2-1)'*10000/length(y);%计算变换后不同点对应的幅值plot(f1,m(1:length(y)/2)); ylabel('幅值的模'); xlabel('时间(s)'); title('原始信号傅里叶变换'); %用周期图法估计功率谱密度 p=y.*conj(y)/1000; %计算功率谱密度 ff=10000*(0:499)/1000; %计算变换后不同点对应的频率值 figure(2); plot(ff,p(1:500)); ylabel('幅值'); xlabel('频率(Hz)'); title('功率谱密度（周期图法）'); 功率谱估计在现代信号处理中是一个很重要的课题，涉及的问题很多。在这里，结合matlab，我做一个粗略介绍。功率谱估计可以分为经典谱估计方法与现代谱估计方法。经典谱估计中最简单的就是周期图法，又分为直接法与间接法。直接法先取N点数据的傅里叶变换（即频谱），然后取频谱与其共轭的乘积，就得到功率谱的估计；间接法先计

分布函数

分布函数 分布函数（Cumulative Distribution Function, CDF）是概率统计中重要的函数，正是通过它，可用数学分析的方法来研究随机变量。 1.伯努利分布 伯努利分布(Bernoulli distribution)又叫做两点分布或者0-1分布，是一个离散型概率分布，若伯努利实验成功，则伯努利随机变量取值为1，如果失败，则伯努利随机变量取值为0。并记成功的概率为p，那么失败的概率就是1p -，则数学期望为p，方差为(1) p p -，概率密度函数为 2.二项分布 二项分布即重复n次独立的伯努利试验。在每次试验中只有两种可能的结果，而且两种结果发生与否互相对立，并且相互独立，与其它各次试验结果无关，事件发生与否的概率在每一次独立试验中都保持不变，则这一系列试验总称为n重伯努利实验，当试验次数为1时，二项分布服从0-1分布。假设每次试验的成功概率为p，则二项分布的密度函数为： 二项分布函数的数学期望为np，方差为(1) np p -，记为~(,) X B n p。概率密度分布图如下所示。 3.正态分布 正态分布（Normal distribution）又名高斯分布（Gaussian distribution），若随机变量X服从一个数学期望为μ、标准方差为σ2的高斯分布，记为：X~N(μ,σ2),则其概率密度函数为 正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。通常所说的标准正态分布是μ = 0,σ = 1的正态分布。 分布曲线特征： 图形特征 集中性：正态曲线的高峰位于正中央，即均数所在的位置。 对称性：正态曲线以均数为中心，左右对称，曲线两端永远不与横轴相交。 均匀变动性：正态曲线由均数所在处开始，分别向左右两侧逐渐均匀下降。 曲线与横轴间的面积总等于1，相当于概率密度函数的函数从正无穷到负无穷积分的概率为1。即频率的总和为100%。

功率谱密度

功率谱密度谱是一种概率统计方法，是对随机变量均方值的量度。一般用于随机振动分析，连续瞬态响应只能通过概率分布函数进行描述，即出现某水平响应所对应的概率。 功率谱密度是结构在随机动态载荷激励下响应的统计结果，是一条功率谱密度值—频率值的关系曲线，其中功率谱密度可以是位移功率谱密度、速度功率谱密度、加速度功率谱密度、力功率谱密度等形式。数学上，功率谱密度值—频率值的关系曲线下的面积就是方差，即响应标准偏差的平方值。 谱是个很不严格的东西，常常指信号的Fourier变换，是一个时间平均（time average）概念功率谱的概念是针对功率有限信号的(能量有限信号可用能量谱分析)，所表现的是单位频带内信号功率随频率的变换情况。保留频谱的幅度信息，但是丢掉了相位信息，所以频谱不同的信号其功率谱是可能相同的。有两个重要区别：1。功率谱是随机过程的统计平均概念，平稳随机过程的功率谱是一个确定函数；而频谱是随机过程样本的Fourier变换，对于一个随机过程而言，频谱也是一个“随机过程”。（随机的频域序列）2。功率概念和幅度概念的差别。此外，只能对宽平稳的各态历经的二阶矩过程谈功率谱，其存在性取决于二阶局是否存在并且二阶矩的Fourier变换收敛；而频谱的存在性仅仅取决于该随机过程的该样本的Fourier变换是否收敛。热心网友回答提问者对于答案的评价：谢谢解答。 频谱分析（也称频率分析），是对动态信号在频率域内进行分析，分析的 结果是以频率为坐标的各种物理量的谱线和曲线，可得到各种幅值以频率为变 量的频谱函数F(ω)。频谱分析中可求得幅值谱、相位谱、功率谱和各种谱密 度等等。频谱分析过程较为复杂，它是以傅里叶级数和傅里叶积分为基础的。 功率谱是个什么概念？它有单位吗? 随机信号是时域无限信号，不具备可积分条件，因此不能直接进行傅氏变换。一般用具有统计特性的功率谱来作为谱分析的依据。功率谱与自相关函数是一个傅氏变换对。功率谱具有单位频率的平均功率量纲。所以标准叫法是功率谱密度。通过功率谱密度函数，可以看出随机信号的能量随着频率的分布情况。像白噪声就是平行于w轴，在w轴上方的一条直线。 功率谱密度，从名字分解来看就是说，观察对象是功率，观察域是谱域，通常指频域，密度，就是指观察对象在观察域上的分布情况。一般我们讲的功率谱密度都是针对平稳随机过程的，由于平稳随机过程的样本函数一般不是绝对可积的，因此不能直接对它进行傅立叶分析。可以有三种办法来重新定义谱密度，来克服上述困难。 一是用相关函数的傅立叶变换来定义谱密度；二是用随机过程的有限时间傅立叶变换来定义谱密度；三是用平稳随机过程的谱分解来定义谱密度。三种定义方式对应于不同的用处，首先第一种方式前提是平稳随机过程不包含周期分量并且均值为零，这样才能保证相关函数在时差趋向于无穷时衰减，所以lonelystar说的不全对，光靠相关函数解决不了许多问题，要求太严格了；对于第二种方式，虽然一个平稳随机过程在无限时间上不能进行傅立叶变换，但是对于有限区间，傅立叶变换总是存在的，可以先架构有限时间区间上的变换，在对时间区间取极限，这个定义方式就是当前快速傅立叶变换（FFT）估计谱密度的依据；第三种方式是根据维纳的广义谐和分析理论：Generalized harmonic analysis, Acta Math, 55(1930),117-258,利用傅立叶-斯蒂吉斯积分，对均方连续的零均值平稳随机过程进行重构，在依靠正交性来建立的。 另外，对于非平稳随机过程，也有三种谱密度建立方法，由于字数限制，功率谱密度的单位

功率谱密度机器实现

1.基本方法 周期图法是直接将信号的采样数据x(n)进行Fourier变换求取功率谱密度估计的方法。假定有限长随机信号序列为x(n)。它的Fourier变换和功率谱密度估计存在下面的关系： 式中，N为随机信号序列x(n)的长度。在离散的频率点f=kΔf,有： 其中，FFT[x(n)]为对序列x(n)的Fourier变换，由于FFT[x(n)]的周期为N，求得的功率谱估计以N为周期，因此这种方法称为周期图法。下面用例子说明如何采用这种方法进行功率谱 用有限长样本序列的Fourier变换来表示随机序列的功率谱，只是一种估计或近似，不可避免存在误差。为了减少误差，使功率谱估计更加平滑，可采用分段平均周期图法（Bartlett法）、加窗平均周期图法（Welch法）等方法加以改进。 2. 分段平均周期图法（Bartlett法） 将信号序列x(n)，n=0,1,…,N-1，分成互不重叠的P个小段，每小段由m个采样值，则 P*m=N。对每个小段信号序列进行功率谱估计，然后再取平均作为整个序列x(n)的功率谱估计。 平均周期图法还可以对信号x(n)进行重叠分段，如按2:1重叠分段，即前一段信号和后一段信号有一半是重叠的。对每一小段信号序列进行功率谱估计，然后再取平均值作为整个序列x(n)的功率谱估计。这两种方法都称为平均周期图法，一般后者比前者好。程序运行结果为图9-5，上图采用不重叠分段法的功率谱估计，下图为2:1重叠分段的功率谱估计，可见后者估计曲线较为平滑。与上例比较，平均周期图法功率谱估计具有明显效果（涨落曲线靠近0dB）。 3.加窗平均周期图法 加窗平均周期图法是对分段平均周期图法的改进。在信号序列x(n)分段后，用非矩形窗口对每一小段信号序列进行预处理，再采用前述分段平均周期图法进行整个信号序列x(n)的功率谱估计。由窗函数的基本知识（第7章）可知，采用合适的非矩形窗口对信号进行处理可减小“频谱泄露”，同时可增加频峰的宽度，从而提高频谱分辨率。 其中上图采用无重叠数据分段的加窗平均周期图法进行功率谱估计，而下图采用重叠数据分段的加窗平均周期图法进行功率谱估计，显然后者是更佳的，信号谱峰加宽，而噪声谱均在0dB附近，更为平坦（注意采用无重叠数据分段噪声的最大的下降分贝数大于5dB，而重叠数据分段周期图法噪声的最大下降分贝数小于5dB）。 4. Welch法估计及其MATLAB函数 Welch功率谱密度就是用改进的平均周期图法来求取随机信号的功率谱密度估计的。Welch 法采用信号重叠分段、加窗函数和FFT算法等计算一个信号序列的自功率谱估计(PSD如上例中的下半部分的求法)和两个信号序列的互功率谱估计（CSD）。 MATLAB信号处理工具箱函数提供了专门的函数PSD和CSD自动实现Welch法估计，而不需要自己编程。 （1）函数psd利用Welch法估计一个信号自功率谱密度，函数调用格式为： [Pxx[,f]]=psd(x[,Nfft,Fs,window,Noverlap,’dflag’])

(完整word版)功率谱密度估计方法的MATLAB实现

功率谱密度估计方法的MATLAB实现 在应用数学和物理学中，谱密度、功率谱密度和能量谱密度是一个用于信号的通用概念，它表示每赫兹的功率、每赫兹的能量这样的物理量纲。在物理学中，信号通常是波的形式，例如电磁波、随机振动或者声波。当波的频谱密度乘以一个适当的系数后将得到每单位频率波携带的功率，这被称为信号的功率谱密度（power spectral density, PSD）或者谱功率分布（spectral power distribution, SPD）。功率谱密度的单位通常用每赫兹的瓦特数（W/Hz）表示，或者使用波长而不是频率，即每纳米的瓦特数（W/nm）来表示。信号的功率谱密度当且仅当信号是广义的平稳过程的时候才存在。如果信号不是平稳过程，那么自相关函数一定是两个变量的函数，这样就不存在功率谱密度，但是可以使用类似的技术估计时变谱密度。信号功率谱的概念和应用是电子工程的基础，尤其是在电子通信系统中，例如无线电和微波通信、雷达以及相关系统。因此学习如何进行功率谱密度估计十分重要，借助于Matlab工具可以实现各种谱估计方法的模拟仿真并输出结果。下面对周期图法、修正周期图法、最大熵法、Levinson递推法和Burg法的功率谱密度估计方法进行程序设计及仿真并给出仿真结果。 以下程序运行平台：Matlab R2015a（8.5.0.197613） 一、周期图法谱估计程序 1、源程序 Fs=100000; %采样频率100kHz N=1024; %数据长度N=1024 n=0:N-1; t=n/Fs; xn=sin(2000*2*pi*t); %正弦波,f=2000Hz Y=awgn(xn,10); %加入信噪比为10db的高斯白噪声 subplot(2,1,1); plot(n,Y) title('信号') xlabel('时间');ylabel('幅度');

经验分布函数图绘制与演示

经验分布函数图绘制与演示

————————————————————————————————作者：————————————————————————————————日期：

实验二经验分布函数图形的绘制与演示 实验序号：2日期：2014 年 5 月 29 日班级数学学院2012级 F 班学号124080545 姓名王信 实验名称经验分布函数图形的绘制与演示 问题的背景和目的： 设X1,X2,…,X n是取自总体X的随机样本，F n(x)是总体X的经验分布函数，当n→∞时由格列汶科定理知 该定理说明F n(x)在整个实数轴上一概率1均匀收敛于F(x)。当样本容量n充分大时，经验分布函数F n(x)可以作为总体分布函数F(x)的一个良好的近似，这是数理 统计学中以样本推断总体的理论依据。 实验内容： 1、理解经验分布函数的构成,经验分布函数是样本的函数,随着样本观测值的变 化而变化。通过实验学习经验分布函数图形的绘制方法和动态演示过程 2、任意产生一组随机样本，对该样本从小到大排序；然后利用排序后的样本作 经验分布函数图形；让样本动态发生变化，观察相应的经验分布函数的数值和图形的 变化。 实验所用软件及版本：Excel 2003 实验过程： 1、经验分布函数的作图n=4。 ①在Excel中产生一个服从均匀分布U(1,6)的样本容量n=4的随机样本。在单元格A2中 输入产生均匀分布U(1,6)的随机数命令“=1+5*RAND()”，再将其拖放填充至A5,就可在 单元格区域A2:A5中产生4个样本观测值x1,x2,x3,x4,每按一次F9键，这些随机数就会 发生变化，这为我们进行动态显示带来方便。接着我们把样本观测值x1,x2,x3,x4从小到 大排序，在单元格B2：B5中分别使用命令“=SMALL($A$2:$A$5,1)”(k=1,2,3,4)得到顺 序样本观测值。 ②在单元格C2内输入起始值0，单击【编辑】/【填充】/【系列】，在出现的对话框输入 相应选项（如图1所示），就可在单元格区域C2：C702中顺序产生0,0.01,0.02,…,7 共703个自变量x的取值序列。 图1 ③在D2单元格内输入公式

谱密度,功率谱密度,能量谱密度

谱密度, 功率谱密度, 能量谱密度 在应用数学和物理学中，谱密度、功率谱密度和能量谱密度是一个用于信号的通用概念，它表示每赫兹的功率、每赫兹的能量这样的物理量纲。 解释 在物理学中，信号通常是波的形式，例如电磁波、随机振动或者声波。当波的频谱密度乘以一个适当的系数后将得到每单位频率波携带的功率，这被称为信号的功率谱密度（power spectral density, PSD）或者谱功率分布（spectral power distribution, SPD）。功率谱密度的单位通常用每赫兹的瓦特数（W/Hz）表示，或者使用波长而不是频率，即每纳米的瓦特数（W/nm）来表示。 尽管并非一定要为信号或者它的变量赋予一定的物理量纲，下面的讨论中假设信号在时域内变化。 定义 能量谱密度 能量谱密度描述的是信号或者时间序列的能量或者变化如何随着频率分布。如 果是一个有限能量信号，即平方可积，那么信号的谱密度就是信号连续傅里叶变换幅度的平方。 其中是角频率（循环频率的倍），是的连续傅里叶变换。是的共轭函数。 如果信号是离散的，经过有限的元素之后，仍然得到能量谱密度： 其中是的离散时间傅里叶变换。如果所定义的数值个数是有限 的，这个序列可以看作是周期性的，使用离散傅里叶变换得到离散频谱，或者用零值进行扩充从而可以作为无限序列的情况计算谱密度。

乘数因子经常不是绝对的，它随着不同傅里叶变换定义的归一化 常数的不同而不同。 功率谱密度 上面能量谱密度的定义要求信号的傅里叶变换必须存在，也就是说信号平方可积或者平方可加。一个经常更加有用的替换表示是功率谱密度（PSD），它定义了信号或者时间序列的功率如何随频率分布。这里功率可能是实际物理上的功率，或者更经常便于表示抽象的信号被定义为信号数值的平方，也就是当信号的负载为1欧姆(ohm)时的实际功率。此瞬时功率（平均功率的中间值）可表示 为： 由于平均值不为零的信号不是平方可积的，所以在这种情况下就没有傅里叶变换。幸运的是维纳-辛钦定理（Wiener-Khinchin theorem）提供了一个简单的替换方法，如果信号可以看作是平稳随机过程，那么功率谱密度就是信号自相关函数的傅里叶变换。 信号的功率谱密度当且仅当信号是广义的平稳过程的时候才存在。如果信号不是平稳过程，那么自相关函数一定是两个变量的函数，这样就不存在功率谱密度，但是可以使用类似的技术估计时变谱密度。 属性 ? 的谱密度和 的自相关组成一个傅里叶变换对（对于功率谱密度和能量谱密度来说，使用着不同的自相关函数定义）。 ?通常使用傅里叶变换技术估计谱密度，但是也可以使用如Welch法（Welch's method）和最大熵这样的技术。 ?傅里叶分析的结果之一就是Parseval定理（Parseval's theorem），这个定理表明能量谱密度曲线下的面积等于信号幅度平方下的面积，总的能量是： ：上面的定理在离散情况下也是成立的。另外的一个结论是功率谱密度下总的功率与对应的总的平均信号功率相等，它是逐渐趋近于零的自相关函数。 相关概念 ?大多数“频率”图实际上仅仅表示了谱密度。有时完整的频率要用两部分来表示，一部分是对应于频率的“幅度”（它就是谱密度），另外一部分是

功率谱密度机器实现

1. 基本方法 周期图法是直接将信号的采样数据x(n)进行Fourier变换求取功率谱密度估计的方法。假定有限长随机信号序列为x(n)。它的Fourier变换和功率谱密度估计存在下面的关系： 式中，N为随机信号序列x(n)的长度。在离散的频率点f=kΔf,有： 其中，FFT[x(n)]为对序列x(n)的Fourier变换，由于FFT[x(n)]的周期为N，求得的功率谱估计以N为周期，因此这种方法称为周期图法。下面用例子说明如何采用这种方法进行功率谱 用有限长样本序列的Fourier变换来表示随机序列的功率谱，只是一种估计或近似，不可避免存在误差。为了减少误差，使功率谱估计更加平滑，可采用分段平均周期图法（Bartlett法）、加窗平均周期图法（Welch 法）等方法加以改进。 2. 分段平均周期图法（Bartlett法） 将信号序列x(n)，n=0,1,…,N-1，分成互不重叠的P个小段，每小段由m个采样值，则P*m=N。对每个小段信号序列进行功率谱估计，然后再取平均作为整个序列x(n)的功率谱估计。 平均周期图法还可以对信号x(n)进行重叠分段，如按2:1重叠分段，即前一段信号和后一段信号有一半是重叠的。对每一小段信号序列进行功率谱估计，然后再取平均值作为整个序列x(n)的功率谱估计。这两种方法都称为平均周期图法，一般后者比前者好。程序运行结果为图9-5，上图采用不重叠分段法的功率谱估计，下图为2:1重叠分段的功率谱估计，可见后者估计曲线较为平滑。与上例比较，平均周期图法功率谱估计具有明显效果（涨落曲线靠近0dB）。 3.加窗平均周期图法 加窗平均周期图法是对分段平均周期图法的改进。在信号序列x(n)分段后，用非矩形窗口对每一小段信号序列进行预处理，再采用前述分段平均周期图法进行整个信号序列x(n)的功率谱估计。由窗函数的基本知识（第7章）可知，采用合适的非矩形窗口对信号进行处理可减小“频谱泄露”，同时可增加频峰的宽度，从而提高频谱分辨率。 其中上图采用无重叠数据分段的加窗平均周期图法进行功率谱估计，而下图采用重叠数据分段的加窗平均周期图法进行功率谱估计，显然后者是更佳的，信号谱峰加宽，而噪声谱均在0dB附近，更为平坦（注意采用无重叠数据分段噪声的最大的下降分贝数大于5dB，而重叠数据分段周期图法噪声的最大下降分贝数小于5dB）。 4. Welch法估计及其MATLAB函数 Welch功率谱密度就是用改进的平均周期图法来求取随机信号的功率谱密度估计的。Welch 法采用信号重叠分段、加窗函数和FFT算法等计算一个信号序列的自功率谱估计(PSD如上例中的下半部分的求法)和两个信号序列的互功率谱估计（CSD）。 MATLAB信号处理工具箱函数提供了专门的函数PSD和CSD自动实现Welch法估计，而不需要自己编程。 （1）函数psd利用Welch法估计一个信号自功率谱密度，函数调用格式为： [Pxx[,f]]=psd(x[,Nfft,Fs,window,Noverlap,’dflag’]) 式中，x为信号序列；Nfft为采用的FFT长度。这一值决定了功率谱估计速度，当Nfft采用2的幂时，程序采用快速算法；Fs为采样频率；Window定义窗函数和x分段序列的长度。窗函数长度必须小于或等于Nfft，否则会给出错误信息；Noverlap为分段序列重叠的采样

常见的分布函数

6数理统计的基本概念 6.1 基本要求 1 理解总体、样本(品)、样本容量、简单随机样本的概念。能在总体分布给定情况下，正确无误地写出样本的联合分布，这是本章的难点。 2*了解样本的频率分布、经验分布函数的定义，了解频率直方图的作法。 3 了解χ2分布、t分布和F分布的概念及性质，了解临界值的概念并会查表计算。 4 理解样本均值、样本方差及样本矩的概念。了解样本矩的性质，能借助计算器快速完成样本均值、样本方差观察值的计算。了解正态总体的某些常用抽样分布。 6.2 内容提要 6.2.1 总体和样本 1 总体和个体研究对象的某项特征指标值的全体称为总体(或母体)，组成总体的每个元素称为个体。总体是一个随机变量，常用X，Y等来表示。 2 样本从总体中随机抽出n个个体称为容量为n的样本，其中每个个体称为样品，它们都是随机变量。 3 简单随机样本设X1，X2，…，X n是来自总体X的容量为n 的样本，如果这n个随机变量X1，X2，…，X n相互独立且每个样品X i与总体X具有相同的分布，则称X1，X2，…，X n为总体X的简单随机样本。 4 样本的联合分布 *该部分内容考研不作要求。 149

150 若总体X 具有分布函数F (x )，则样本(X 1，X 2，…，X n )的联合分布函数为 ∏== n i i n x F x x x F 1 21) (),,,( 若总体X 为连续型随机变量，其概率密度函数为f (x )，则样本的联合概率密度为 ∏ == n i i n x f x x x f 1 21) (),,,( (6.1) 若总体X 为离散型随机变量，其分布律为P {X =a i }=p i (i =1，2，…n)，则样本的联合分布为 ∏=== ===n i i i n n x X P x X x X x X P 1 22 11} {},,,{ (6.2) 其中),,,(21n x x x 为),,,(21n X X X 的任一组可能的观察值。 6.2.2 样本分布 1 频率分布 设样本值(x 1，x 2，…，x n )中不同的数值是x 1*，x 2*，…，x l *，记相应的频数分别为n 1，n 2，…，n l ，其中x 1*< x 2*<…< x l * 且n n l i i =∑=1 。 则样本的频数分布及频率分布可由表6-1给出。

第49讲 直方图和经验分布函数

§6.2直方图和箱线图

在数理统计中，我们常常用图形来直观地显示观察到的数据，以便对总体X的分布有一个 直观、粗略的了解。 四川大学徐小湛本节讲以下图形： 直方图 箱线图（自学） 经验分布函数及其图形

直方图（频率直方图）Histogram

百度传课 我们通过一个例子来说明直方图的作法。 25 19 39 72 49 58 65 75 68 66 61 78 51 60 45 74 73 77 29 16 90 12 64 61 40 57 40 46 81 51 52 58 73 70 87 33 49 61 83 41 52 46 38 77 63 75 61 45 51 62 51 59 66 68 97 53 54 70 54 54 38 50 83 50 最低分和最高分分别是 12 和 97 例1 设有64个学生的考试成绩如下： 四川大学 徐小湛

25 19 39 72 49 58 65 75 68 66 61 78 51 60 45百74度73传7课7 显得杂乱无章 29 16 90 12 64 61 40 57 40 46 81 51 52 58 73 70 87 33 49 61 83 41 52 46 38 77 63 75 61 45 51 62 51 59 66 68 97 53 54 70 54 54 38 50 83 50 四川大学 徐小湛 用Excel 作出数据的条形图(柱形图)(Bar Chart)

四川大学 用Excel将成绩排序：121619252933383839404041454546 464949505051515151525253545454 575858596061616161626364656666 686870707273737475757777788183 83 87 90 97

功率谱和功率谱密度的区别

谱让人联想到的Fourier变换, 是一个时间平均（time aｖeｒａｇｅ)概念，对能量就是能量谱,对功率就是功率谱。 功率谱的概念是针对功率有限信号的,所表现的是单位频带内信号功率随频率的变化情况。保留了频谱的幅度信息,但是丢掉了相位信息，所以频谱不同的信号其功率谱是可能相同的。 有两点需要注意:?1. 功率谱是随机过程的统计平均概念，平稳随机过程的功率谱是一个确定函数;而频谱是随机过程样本的Fouriｅr变换，对于一个随机过程而言，频谱也是一个“随机过程”。（随机的频域序列)?2. 功率概念和幅度概念的差别。此外，只能对宽平稳的各态历经的二阶矩过程谈功率谱，其存在性取决于二阶矩是否存在并且二阶矩的Fｏuｒieｒ变换收敛;而频谱的存在性仅仅取决于该随机过程的该样本的Fｏuｒiｅｒ变换是否收敛。 频谱分析： 对动态信号在频率域内进行分析，分析的结果是以频率为坐标的各种物理量的谱线和曲线，可得到各种幅值以频率为变量的频谱函数Ｆ(ω)。频谱分析中可求得幅值谱、相位谱、功率谱和各种谱密度等等。频谱分析过程较为复杂，它是以傅里叶级数和傅里叶积分为基础的。 功率谱密度: 功率谱密度(PSＤ),它定义了信号或者时间序列的功率如何随频率分布。这里功率可能是实际物理上的功率，或者更经常便于表示抽象的信号被定义为信号数值的平方,也就是当信号的负载为1欧姆（ohm）时的实际功率。 由于平均值不为零的信号不是平方可积的，所以在这种情况下就没有傅里叶变换。维纳－辛钦定理（Wｉener－Khinchin ｔｈeｏｒｅｍ)提供了一个简单的替换方法,如果信号可以看作是平稳随机过程,那么功率谱密度就是信号自相关函数的傅里叶变换。 信号的功率谱密度当且仅当信号是广义的平稳过程的时候才存在。如果信号不是平稳过程,那么自相关函数一定是两个变量的函数,这样就不存在功率谱密度，但是可以使用类似的技术估计时变谱密度。 随机信号是时域无限信号，不具备可积分条件，因此不能直接进行傅氏变换。一般用具有统计特性的功率谱来作为谱分析的依据。?功率谱与自相关函数是一个傅氏变换对。?功率谱具有单位频率的平均功率量纲。所以标准叫法是功率谱密度。从名字分解来看就是说,观察对象是功率，观察域是谱域。 通过功率谱密度函数,可以看出随机信号的能量随着频率的分布情况。像白噪声就是平行于一条直线。 一般我们讲的功率谱密度都是针对平稳随机过程的，由于平稳随机过程的样本函数一般不是绝对可积的，因此不能直接对它进行傅立叶分析。可以有三种办法来重新定义谱密度，来克服上述困难。?1. 用相关函数的傅立叶变换来定义谱密度；?２．用随机过程的有限时间傅立叶变换来定义谱密度；?3. 用平稳随机过程的谱分解来定义谱密度。?三种定义方式对应于不同的用处,首先第一种方

功率谱密度

功率谱密度 [编辑本段] 简介 在物理学中，信号通常是波的形式，例如电磁波、随机振动或者声波。当波的频谱密度乘以一个适当的系数后将得到每单位频率波携带的功率，这被称为信号的功率谱密度（power spectral density, PSD）或者谱功率分布（spectral power distribu tion, SPD）。功率谱密度的单位通常用每赫兹的瓦特数（W/Hz）表示，或者使用波长而不是频率，即每纳米的瓦特数（W/nm）来表示。 [编辑本段] 详细说明 尽管并非一定要为信号或者它的变量赋予一定的物理量纲，下面的讨论中假设信号在时域内变化。 上面能量谱密度的定义要求信号的傅里叶变换必须存在，也就是说信号平方可积或者平方可加。一个经常更加有用的替换表示是功率谱密度（PSD），它定义了信号或者时间序列的功率如何随频率分布。这里功率可能是实际物理上的功率，或者更经常便于表示抽象的信号被定义为信号数值的平方，也就是当信号的负载为1欧姆(oh m)时的实际功率。此瞬时功率（平均功率的中间值）可表示为： 由于平均值不为零的信号不是平方可积的，所以在这种情况下就没有傅里叶变换。幸运的是维纳-辛钦定理（Wiener-Khinchin theorem）提供了一个简单的替换方法，如果信号可以看作是平稳随机过程，那么功率谱密度就是信号自相关函数的傅里叶变换。 信号的功率谱密度当且仅当信号是广义的平稳过程的时候才存在。如果信号不是平稳过程，那么自相关函数一定是两个变量的函数，这样就不存在功率谱密度，但是可以使用类似的技术估计时变谱密度。 f(t) 的谱密度和f(t) 的自相关组成一个傅里叶变换对（对于功率谱密度和能量谱密度来说，使用着不同的自相关函数定义）。 通常使用傅里叶变换技术估计谱密度，但是也可以使用如Welch法（Welch's method）和最大熵这样的技术。 傅里叶分析的结果之一就是Parseval定理（Parseval's theorem），这个定理表明能量谱密度曲线下的面积等于信号幅度平方下的面积，总的能量是：：上面的定理在离散情况下也是成立的。另外的一个结论是功率谱密度下总的功率与对应的总的平均信号功率相等，它是逐渐趋近于零的自相关函数。 功率谱密度谱是一种概率统计方法，是对随机变量均方值的量度。一般用于随机振动分析，连续瞬态响应只能通过概率分布函数进行描述，即出现某水平响应所对应的概率。 功率谱密度的定义是单位频带内的“功率”（均方值）