
圆锥曲线的谢国芳定理
——继帕斯卡定理和布列安桑定理之后又一朵射影几何的奇葩
谢国芳(Roy Xie ) Email: roixie@https://www.doczj.com/doc/f413955763.html,
摘要: 本文在帕斯卡定理和布列安桑定理的基础上得到了关于圆锥曲线的一个美妙深刻的新定理,作为推论证明了双心六边形的三条对角线和三条对边切点的连线六线共点。
关键词: 帕斯卡定理 布列安桑定理 极线 配极原理 双心六边形
Abstract : In this article we derive an elegant and deep new theorem concerning conic sections based on Pascal ’s theorem and Brianchon ’s theorem, and prove that the three diagonals and the three lines connecting two tangent points on each pair of opposite sides of a bicentric hexagon are concurrent as a corollary .
Key words : Pascal ’s theorem, Brianchon ’s theorem, polar line, polar reciprocation, bicentric hexagon
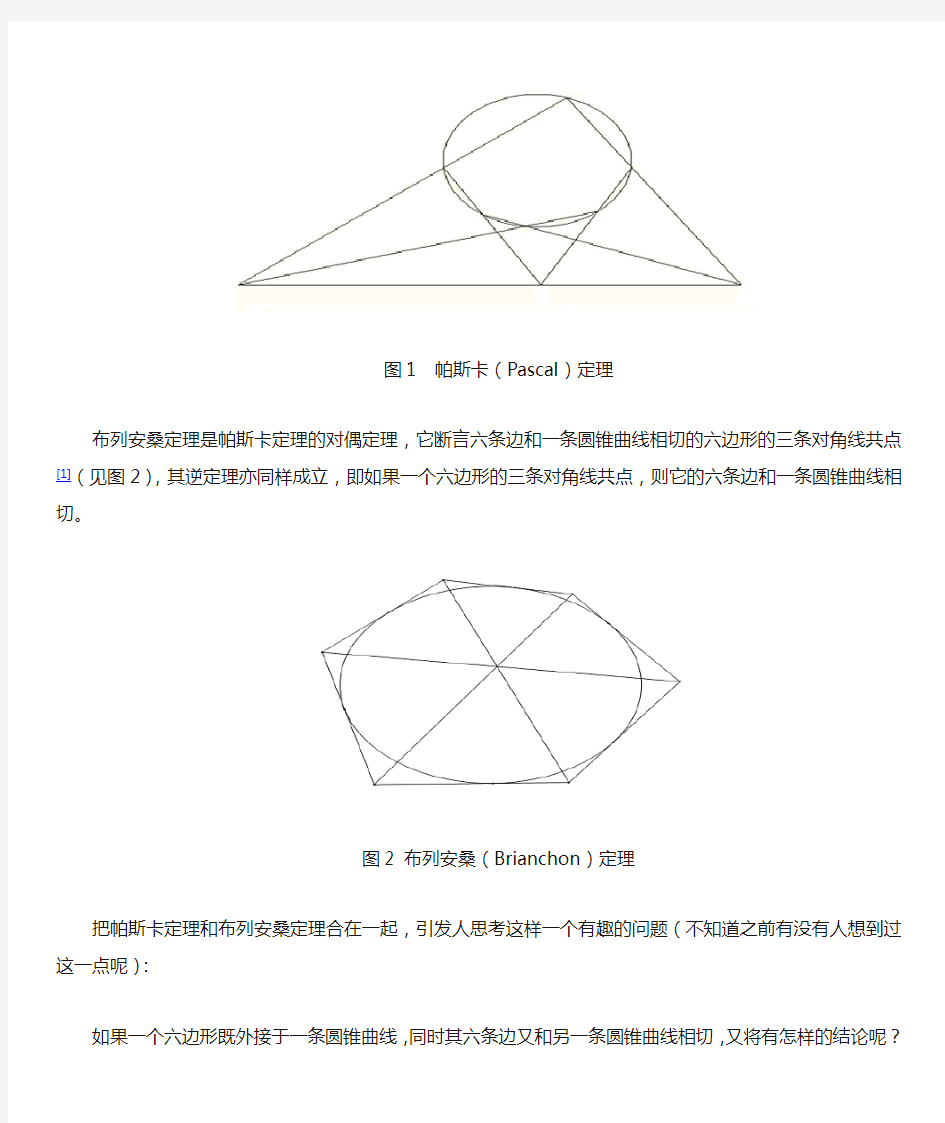
帕斯卡(Pascal )定理和布列安桑(Brianchon )定理是关于圆锥曲线的两个基本定理,帕斯卡定理断言,圆锥曲线内接六边形的三组对边的交点共线(见图1),其逆定理也同样成立,即如果一个六边形的三组对边的交点共线,则它的六个顶点在一条圆锥曲线上。
图1 帕斯卡(Pascal )定理
布列安桑定理是帕斯卡定理的对偶定理,它断言六条边和一条圆锥曲线相切的六边形的三条对角线共点[1]
(见图2),其逆定理亦同样成立,即如果一个六边形的三条对角线共点,则它的六条边和一条圆锥曲线相切。
图2 布列安桑(Brianchon)定理
把帕斯卡定理和布列安桑定理合在一起,引发人思考这样一个有趣的问题(不知道之前有没有人想到过这一点呢):
如果一个六边形既外接于一条圆锥曲线,同时其六条边又和另一条圆锥曲线相切,又将有怎样的结论呢?
请读者务必先独立思考这个问题,一定要动手用几何画板或其他几何作图软件画几个图,做一些探索性的实验之后才看下面一页(倘若你不会画圆锥曲线,没关系,可以全部用圆代替),只有这样你才能切身感受到几何的巨大魅力和下面这个定理的神奇绝妙,匪夷所思:
定理1圆锥曲线的谢国芳定理
若一个六边形的六个顶点在一条圆锥曲线上,六条边和另一条圆锥曲线相切,则它的三条对角线和三条对边切点的连线六线共点(见图3和图4)。
图3
图4
实际上,定理1中所描述的六边形可以称为“彭赛列六边形”,因为它正是满足著名的彭赛列闭合定理(Poncelet's Closure Theorem or Poncelet's porism)的六边形。法国人把该定理称为“le grand théorème de Poncelet”,译成中文即“伟大的彭赛列定理”或“彭赛列大定理”,可见其重要,实际上,它堪称是整个几何中最深刻伟大的定理,这并不是我个人的私见,像Richard Schwartz 等大数学家就是这么认为的,参见Dynamiser la géométrie élémentaire- introduction à des travaux de Richard Schwartz一文(百度文库https://www.doczj.com/doc/f413955763.html,/view/e39d9e09f78a6529647d536c.html),可惜国内对这个伟大的定理介绍极少。
关于彭赛列闭合定理的一个中文介绍参见
《伟大的彭赛列闭合定理的一个绝妙证明—An Ingenious Proof of Poncelet's Closure Theorem》
网址:https://www.doczj.com/doc/f413955763.html,/Maths/GeometryTheorems/Poncelet_porism.htm
英文介绍参见https://www.doczj.com/doc/f413955763.html,/PonceletsPorism.html
我们于是也可以把定理1等价地表述为:
一个彭赛列六边形的三条对角线和三条对边切点的连线六线共点。
作为定理1的特例,我们有下面这个优美的平面几何定理:[2]
谢国芳双心六边形定理
一个双心六边形即既有外接圆又有内切圆(或旁切圆)的六边形的三条对角线和三条对边切点的连线六线共点(见下图)。
为了证明定理1,我们需要下面这个关键的引理。
引理1谢国芳四边形引理
若一个四边形的四条边和一条圆锥曲线相切[3],则两条对边切点的连线和两条对角线四线共点(见下图)。
B
A
该引理揭示了圆锥曲线的另一个重要的基本性质,可以找到很多应用,下面将它归结为布列安桑定理的极限情形加以证明。
证明: 如图7,设四边形ABCD 的四条边A B , BC , CD , D A 分别和圆锥曲线Γ相切于点
, , , P Q R S ,在Γ上点P 的邻近取两点12,P P , 设过1P 的切线和过2P 的切线交于点'P , 1'P P 交A D 于点'A ,2'P P 交BC 于点'B ;同样在Γ上点R 的邻近取两点12,R R , 设过1R 的切线和过2R 的切线交于点'R , 1'R R 交BC 于点'C , 2'R R 交A D 于点'D 。
应用布列安桑定理于六边形''''''A P B C R D ,可知其三条对角线''A C , ''B D , ''P R 共点,当点1P 和
2P 无限趋近于点P , 点1R 和2R 无限趋近于点R 时,点', ', ', 'A B C D 分别无限趋近于点, , , A B C D ,点'
P 和'R 分别无限趋近于四边形ABCD 的对边A B 和CD 上的切点P 和R ,直线''P R , ''A C , ''B D 分别无限趋近于直线P R , AC , B D , 由''A C , ''B D , ''P R 三线共点可推知P R , AC , B D 三线共点。
同理可证SQ , AC , B D 三线共点,设I 为AC 和B D 的交点,则AC , B D , P R ,SQ 四线共点于
I 。证毕。
图7
有了引理1,我们就可以完成对定理1的证明了。
定理1(圆锥曲线的谢国芳定理)的证明:
如图8,设六边形的六个顶点1A , 2A ,3A , 4A , 5A , 6A 在圆锥曲线∑上,边
122334455661,,,,,A A A A A A A A A A A A 和另一条圆锥曲线Γ相切,切点依次为123456,,,,,B B B B B B ,由帕斯卡
定理可知直线12A A 和45A A 的交点P 、23A A 和56A A 的交点Q 、 34A A 和61A A 的交点R 三点共线[4]
,注意到直线14B B , 25B B , 36B B 正好分别是点, , P Q R 关于Γ的极线,根据配极原理可知14B B , 25B B , 36B B 三线共点,设该点为I ,在由直线12A A , 23A A , 45A A , 56A A 围成的四边形中应用引理1,可知25A A 亦通过点I ,同理可证14A A 和36A A 也通过点I 。证毕。
图8
完全类似地,应用配极原理和帕斯卡定理的逆定理,可以证明定理1的“逆”:
圆锥曲线的谢国芳定理之逆定理
若一个六边形的六条边和一条圆锥曲线相切,其三条对边切点的连线三线共点,则该六边形的六个顶点必在另一条圆锥曲线上。
[注1] 本文中的对角线都指主对角线,若六边形的六个顶点记作1A , 2A ,3A , 4A , 5A , 6A ,则三条(主)对角线为14A A , 25A A , 36A A 。
[注2] 从表面上看这完全是一个平面几何问题,但笔者觉得用传统的平面几何方法或者解析几何方法是极难甚至几乎是不可能证明的,尽管如此,仍很希望看到这方面的尝试,若有人取得成功,务请发函至roixie@https://www.doczj.com/doc/f413955763.html, 告知,不胜感谢。
[注3] 和五条直线相切的圆锥曲线唯一,和四条直线相切的圆锥曲线有无穷多个,构成带一个参数的曲线族。
[注4] 这三个交点中的一个或三个都可能为无穷远点(若两个为无穷远点,通过这两个无穷远点的直线就是无穷远直线l ,帕斯卡定理保证了第三个交点也在无穷远直线上,即也是一个无穷远点)。
作者简介: 谢国芳,浙江绍兴人,独立语言学者和数学研究者,著有《解密英语——学外语从零点到绝顶的最速路经》、《日语汉字读音规律揭秘》、《破解韩国语单词的奥秘》等,建有以传播外语和数学知识与文化为宗旨的网站“语数之光”。已发表的数学和物理论文有:
4. 《一般三次方程的简明新求根公式和根的判别法则》 (2012年第21期《数学学习与研究》)
1、勾股定理(毕达哥拉斯定理) 2、射影定理(欧几里得定理) 3、三角形的三条中线交于一点,并且,各中线被这个点分成2:1的两部分 4、四边形两边中心的连线的两条对角线中心的连线交于一点 5、间隔的连接六边形的边的中心所作出的两个三角形的重心是重合的。 6、三角形各边的垂直一平分线交于一点。 7、三角形的三条高线交于一点 8、设三角形ABC的外心为O,垂心为H,从O向BC边引垂线,设垂足为L,则AH=2OL 9、三角形的外心,垂心,重心在同一条直线(欧拉线)上。 10、(九点圆或欧拉圆或费尔巴赫圆)三角形中,三边中心、从各顶点向其对边所引垂线的垂足,以及垂心与各顶点连线的中点,这九个点在同一个圆上, 11、欧拉定理:三角形的外心、重心、九点圆圆心、垂心依次位于同一直线(欧拉线)上 12、库立奇*大上定理:(圆内接四边形的九点圆) 圆周上有四点,过其中任三点作三角形,这四个三角形的九点圆圆心都在同一圆周上,我们把过这四个九点圆圆心的圆叫做圆内接四边形的九点圆。 13、(内心)三角形的三条内角平分线交于一点,内切圆的半径公式:r=(s-a)(s-b)(s-c)s,s为三角形周长的一半 14、(旁心)三角形的一个内角平分线和另外两个顶点处的外角平分线交于一点 15、中线定理:(巴布斯定理)设三角形ABC的边BC的中点为P,则有AB2+AC2=2(AP2+BP2) 16、斯图尔特定理:P将三角形ABC的边BC内分成m:n,则有n×AB2+m×AC2=(m+n)AP2+mnm+nBC2 17、波罗摩及多定理:圆内接四边形ABCD的对角线互相垂直时,连接AB中点M和对角线交点E的直线垂直于CD 18、阿波罗尼斯定理:到两定点A、B的距离之比为定比m:n(值不为1)的点P,位于将线段AB分成m:n的内分点C和外分点D为直径两端点的定圆周上 19、托勒密定理:设四边形ABCD内接于圆,则有AB×CD+AD×BC=AC×BD 20、以任意三角形ABC的边BC、CA、AB为底边,分别向外作底角都是30度的等腰△BDC、△CEA、△AFB,则△DEF是正三角形,
专题平面几何的四个重 要定理 SANY标准化小组 #QS8QHH-HHGX8Q8-GNHHJ8-HHMHGN#
竞赛专题讲座06 -平面几何四个重要定理 四个重要定理: 梅涅劳斯(Menelaus)定理(梅氏线) △ABC的三边BC、CA、AB或其延长线上有点P、Q、R,则P、 Q、R共线的充要条件是。 塞瓦(Ceva)定理(塞瓦点) △ABC的三边BC、CA、AB上有点P、Q、R,则AP、BQ、CR共点 的充要条件是。 托勒密(Ptolemy)定理 四边形的两对边乘积之和等于其对角线乘积的充要条件是该 四边形内接于一圆。 西姆松(Simson)定理(西姆松线) 从一点向三角形的三边所引垂线的垂足共线的充要条件是 该点落在三角形的外接圆上。 例题: 1.设AD是△ABC的边BC上的中线,直线CF交AD于F。求 证:。
【分析】CEF截△ABD→(梅氏定理) 【评注】也可以添加辅助线证明:过A、B、D之一作CF的平行线。 2.过△ABC的重心G的直线分别交AB、AC于E、F, 交CB于D。 求证:。 【分析】连结并延长AG交BC于M,则M为BC的 中点。 DEG截△ABM→(梅氏定理) DGF截△ACM→(梅氏定理) ∴===1 【评注】梅氏定理 3. D、E、F分别在△ABC的BC、CA、AB边上, ,AD、BE、CF交成△LMN。 求S△LMN。 【分析】 【评注】梅氏定理 4.以△ABC各边为底边向外作相似的 等腰△BCE、△CAF、△ABG。求证:AE、 BF、CG相交于一点。
【分析】 【评注】塞瓦定理 5.已知△ABC中,∠B=2∠C。求证:AC2=AB2+AB·BC。 【分析】过A作BC的平行线交△ABC的外接圆于D,连结BD。则 CD=DA=AB,AC=BD。 由托勒密定理, AC·BD=AD·BC+CD·AB。 【评注】托勒密定理 6.已知正七边形A 1A2A3A4A5A6A7。 求证:。(第21届全苏数学竞赛) 【分析】 【评注】托勒密定理 7.△ABC的BC边上的高AD的延长线交 外接圆于P,作PE⊥AB于E,延长ED交 AC延长线于F。 求证:BC·EF=BF·CE+BE·CF。 【分析】 【评注】西姆松定理(西姆松线) 8.正六边形ABCDEF的对角线AC、CE分别被内分点M、N分成的 比为AM:AC=CN:CE=k,且B、M、N共 线。求k。(23-IMO-5) 【分析】 【评注】面积法 9. O为△ABC内一点,分别以d a、d b、d c表示O到BC、CA、AB的距离,以R a、 R b、R c表示O到A、B、C的距离。
第十九讲平面几何中的几个著名定理 几何学起源于土地测量,几千年来,人们对几何学进行了深入的研究,现已发展成为一门具有严密的逻辑体系的数学分支.人们从少量的公理出发,经过演绎推理得到不少结论,这些结论一般就称为定理.平面几何中有不少定理,除了教科书中所阐述的一些定理外,还有许多著名的定理,以这些定理为基础,可以推出不少几何事实,得到完美的结论,以至巧妙而简捷地解决不少问题.而这些定理的证明本身,给我们许多有价值的数学思想方法,对开阔眼界、活跃思维都颇为有益.有些定理的证明方法及其引伸出的结论体现了数学的美,使人们感到对这些定理的理解也可以看作是一种享受.下面我们来介绍一些著名的定理. 1.梅内劳斯定理 亚历山大里亚的梅内劳斯(Menelaus,约公元100年,他和斯巴达的Menelaus是两个人)曾著《球面论》,着重讨论球面三角形的几何性质.以他的名子命名的“梅内劳斯定理”现载在初等几何和射影几何的书中,是证明点共线的重要定理. 定理一直线与△ABC的三边AB,BC,CA或延长线分别相交于X,Y,Z,则 证过A,B,C分别作直线XZY的垂线,设垂足分别为Q,P,S,见图3-98.由△AXQ∽△BXP得
同理 将这三式相乘,得 说明(1)如果直线与△ABC的边都不相交,而相交在延长线上,同样可证得上述结论,但一定要有交点,且交点不在顶点上,否则定理的结论中的分母出现零,分子也出现零,这时定理的结论应改为 AX×BY×CZ=XB×YC×ZA, 仍然成立. (2)梅内劳斯定理的逆定理也成立,即“在△ABC 的边AB和AC上分别取点X,Z,在BC的延长线上取点Y,如果 那么X,Y,Z共线”.梅内劳斯定理的逆定理常被用来证明三点共线. 例1 已知△ABC的内角∠B和∠C的平分线分别为BE和CF,∠A的外角平分线与BC的延长线相交于D,求证:D,E,F共线. 证如图3-99有 相乘后得
液压千斤顶帕斯卡原理 液压千斤顶又称油压千斤顶,是一种采用柱塞或液压缸作为刚性顶举件的千斤顶。简单起重设备一般只备有起升机构,用以起升重物。构造简单、重量轻、便于携带,移动方便。常用的简单起重设备有液压千斤顶、滑车和卷扬机等。 千斤顶是一种起重高度小的最简单的起重设备。它有机械式和液压式两种。机械式千斤顶又有齿条式与螺旋式两种,由于起重量小,操作费力,一般只用于机械维修工作,在修桥过程中不适用。液压工程千斤顶结构紧凑,工作平稳,有自锁作用。 通用液压千斤顶适用于起重高度不大的各种起重作业。它由油室1、油泵2、储油腔3、活塞4、摇把5、油阀6等主要部分组成。 专用液压千斤顶使专用的张拉机具,在制作预应力混凝土构件时,对预应力钢筋施加张力。专用液压千斤顶多为双作用式。常用的有穿心式和锥锚式两种。 其工作原理。张拉时,打开前后油嘴,从后油嘴向张拉工作油室内供油,张拉缸缸体向后移动。由于缸索锚固在千斤顶层部的工具锚上,因此千斤顶通过工具将钢索拉长。 当钢索张拉到需要的长度时,关闭后油嘴,从前油嘴进油至顶压缸内,使顶压缸活塞向前伸移而顶住锚塞,并将锚塞压入锚圈中,从而使钢索锚固。打开后油嘴并继续从前油嘴进油,这时张拉缸向前移动,缸内油液回流。最后打开前油嘴,使顶压缸内的油液回流,顶压活塞由于复位弹簧的作用而复还原位。超薄液压千斤顶. 小千斤顶有外壳、大活塞、小活塞、扳手、油箱等部件组成。工作原理是扳手往上走带动小活塞向上,油箱里的油通过油管和单向阀门被吸进小活塞下部,扳手往下压时带动小活塞向下,油箱与小活塞下部油路被单向阀门堵上。 小活塞下部的油通过内部油路和单向阀门被压进大活塞下部,因杠杆作用小活塞下部压力增大数十倍,大活塞面积又是小活塞面积的数十倍,有手动产生的油压被挤进大活塞,有帕斯卡原理知大小活塞面积比与压力比相同。 这样一来,手上的力通过扳手到小活塞上增大了十多倍(暂按15倍),小活塞到大活塞力有增大十多倍(暂按15倍),到大活塞(顶车时伸出的活动部分)力量=15X15=225倍的力量了,假若手上用每20公斤力,就可以产生20X225=4500公斤(4.5吨)的力量。工作原理就是如此。当用完后,有一个平时关闭的阀门手动打开,油就靠汽车重量将油挤回油箱。 注意事项: 1:液压千斤顶在顶升作业时,要选择合适吨位的液压千斤顶:承载能力不可超负荷,选择液压千斤顶的承载能力需大于重物重力的1.2倍;液压千斤顶最低高度合适,为了便于取出,
帕斯卡原理及其应用 ?帕斯卡原理: 加在密闭液体上的压强,能够大小不变地被液体向各个方向传递,这个规律被称为帕斯卡原理。帕斯卡原理揭示了液体压强的传递规律,是许多液压系统和液压机工作的基础。如用于维修汽车的液压千斤顶(如图),汽车的液压刹车系统,铲车等部用了液压技术。 液压机的工作原理如图所示,两个活塞,与同一容器的液体相接触。施加于小活塞的压强被液体传递给大活塞,大活塞便可以产生一个与其表面面积成正比的力。 ?帕斯卡: 帕斯卡发现了液体传递压强的基本规律,这就是著名的帕斯卡定律.所有的液压机械都是根据帕斯卡定律设计的,所以帕斯卡被称为“液压机之父”. 通过观察,帕斯卡设计了“帕斯卡球”实验,帕斯卡球是一个壁上有许多小孔的空心球,球上连接一个圆筒,筒里有可以移动的活塞.把水灌进球和筒里,向里压活塞,水便从各个小孔里喷射出来了,成了一支“多孔水枪”帕斯卡球的实验证明,液体能够把它所受到的压强向各个方向.通过观察发现每个孔喷出去水的距离差不多,这说明,每个孔所受到的压强都相同。 在初中阶段,液体压强原理可表述为:“液体内部向各个方向都有压强,压强随液体深度的增加而增大,同种液体在同一深度的各处,各个方向的压强大小相等; 不同的液体,在同一深度产生的压强大小与液体的密度有关,密度越大,液体的压强越大。” 特点:加在封闭液体上的压强能够大小不变地被液体向各个方向传递。同种液体在同一深度液体向各个方向的压强都相等。 裂桶实验: 帕斯卡在1648年表演了用一个著名的实验:他用一个密闭的装满水的桶,在桶盖上插入一根细长的管子,从楼房的阳台上向细管子里灌水。结果只到了几杯水,
桶就裂了,桶里的水就从裂缝中流了出来。原来由于细管子的容积较小,几杯水灌进去,其深度h很大。一个容器里的液体,对容器底部(或侧壁)产生的压力远大于液体自身所受的重力。
【认识平面几何的61个著名定理,自行画出图形来学习,★部分要求证明出来】 ★1、勾股定理(毕达哥拉斯定理) ★2、射影定理(欧几里得定理) ★3、三角形的三条中线交于一点,并且,各中线被这个点分成2:1的两部分 4、四边形两边中心的连线和两条对角线中心的连线交于一点 5、间隔的连接六边形的边的中心所作出的两个三角形的重心是重合的。 ★6、三角形各边的垂直平分线交于一点。 ★7、从三角形的各顶点向其对边所作的三条垂线交于一点 8、设三角形ABC 的外心为O ,垂心为H ,从O 向BC 边引垂线,设垂足不L ,则AH=2OL 9、三角形的外心,垂心,重心在同一条直线上。 10、(九点圆或欧拉圆或费尔巴赫圆)三角形中,三边中心、从各顶点向其对边所引垂线的垂足,以及垂心与各顶点连线的中点,这九个点在同一个圆上, 11、欧拉定理:三角形的外心、重心、九点圆圆心、垂心依次位于同一直线(欧拉线)上 12、库立奇大上定理:(圆内接四边形的九点圆) 圆周上有四点,过其中任三点作三角形,这四个三角形的九点圆圆心都在同一圆周上,我们把过这四个九点圆圆心的圆叫做圆内接四边形的九点圆。 ★13、(内心)三角形的三条内角平分线交于一点,内切圆的半径公式: ()()()s c s b s a s r ---=,s 为三角形周长的一半 ★14、(旁心)三角形的一个内角平分线和另外两个顶点处的外角平分线交于一点 15、中线定理:(巴布斯定理)设三角形ABC 的边BC 的中点为P ,则有AB 2+AC 2=2(AP 2+BP 2) 16、斯图尔特定理:P 将三角形ABC 的边BC 分成m 和n 两段,则有n×AB 2+m×AC 2=BC×(AP 2+mn ) 17、波罗摩及多定理:圆内接四边形ABCD 的对角线互相垂直时,连接AB 中点M 和对角线交点E 的直线垂直于CD 18、阿波罗尼斯定理:到两定点A 、B 的距离之比为定比m:n (值不为1)的点P ,位于将线段AB 分成m:n 的内分点C 和外分点D 为直径两端点的定圆周上 ★19、托勒密定理:设四边形ABCD 内接于圆,则有AB×CD+AD×BC=AC×BD
平面几何四大定理 平面几何四个重要定理 四个重要定理: 梅涅劳斯(Me nelau s)定理(梅氏线) △ABC 的三边BC 、CA 、AB 或其延长线上有点P 、Q 、R,则P、Q 、R共线的充要条件是 1RB AR QA CQ PC BP =??。 塞瓦(Ceva)定理(塞瓦点) △ABC 的三边BC 、CA 、AB 上有点P 、Q 、R ,则AP 、BQ 、CR 共点的充要条件是 1RB AR QA CQ PC BP =??。 托勒密(Pto lemy)定理 四边形的两对边乘积之和等于其对角线乘积的充要条件是该四边形内接于一圆。 西姆松(S imso n)定理(西姆松线) 该点落在三角形的外接圆上。 例题: 1. 设AD 是△A BC的边BC 上的中线,直线CF 交AD 于F 。求 证:FB AF 2ED AE = 。 【分析】CEF 截△ABD → 1FA BF CB DC ED AE =??(梅氏定理) 【评注】也可以添加辅助线证明:过A 、B、D 之一作CF 的平行 线。 2. 过△ABC 的重心G 的直线分别交AB 、AC 于E 、F,交CB 于
平面几何四大定理 D 。 求证: 1FA CF EA BE =+。 【分析】连结并延长AG 交BC 于M,则M为BC 的中点。 DEG 截△AB M→1DB MD GM AG EA BE =??(梅氏定理) D GF 截△AC M→1DC MD GM AG FA CF =??(梅氏定理) ∴FA CF EA BE + =MD AG )DC DB (GM ?+?=MD GM 2MD 2GM ??=1 【评注】梅氏定理 3. D 、E 、F 分别在△ABC 的BC 、C A、AB 边上, λ===EA CE FB AF DC BD ,A D、BE 、CF 交成△LMN 。 求S △LMN 。 【分析】 【评注】梅氏定理 4. 以△ABC 各边为底边向外作相似的等腰△B CE 、△CAF 、 △ABG 。求证:AE 、BF 、CG 相交于一点。 【分析】 【评注】塞瓦定理 5. 已知△ABC 中,∠B=2∠C。求证:AC 2=AB 2+AB ·B C。
定义 帕斯卡定律:加在密闭液体任一部分的压强,必然按其原来的大小,由液体向各个方向传递。 原理的发现 发现定理1651~1654年,帕斯卡研究了液体静力学和空气的重力的各种效应。经过数年的观察、实验和思考,综合成《论液体的平衡和空气的重力》一书。提出了著名的帕斯卡定律(或称帕斯卡原理),即;加在密闭液体任何一部分上的压强,必然按照其原来的大小由液体向各个方向传递。 原理的意义 著名科学史家沃尔夫称,帕斯卡的这一发现是17世纪力学发展的一个重要里程碑。帕斯卡在此书中详细讨论了液体压强问题。在第一章中,帕斯卡叙述了几种实验,它们的结果表明,任何水柱,不论直立或倾斜,也不论其截面积的大小,只要竖直高度相同,则施加于水柱底部的某一已知面积的活塞上的力也相同。这一个力实际上是液体所受的重力。书中详细叙述了密封容器中的流体能传递压强,讨论了连通器的原理。帕斯卡利用一个充水的容器,它有两个圆筒形的出口,除此之外,其他部分都封闭。两个出口的截面积相差100倍,在每一个出口的圆筒中放入一个大小刚好适合的活塞,则小活塞上一个人施加的推力等于大活塞上100人所施加的推力,因而可以胜过大活塞上99个人施加的推力,不管这两个出口大小的比例如何,只要施加于两个活塞上的力和两个出口的大小成比例,则水的平衡就可以实现。帕斯卡在书中一一叙述了密闭液体、压强不变、向各方传递等帕斯卡定律的基本点。 定律的发现 此书是帕斯卡于1653年写成的,但直到他逝世后的第二年----1663年才首次面世。帕斯卡是在大量观察、实验的基础上,又用虚功原理加以;证明才发现了帕斯卡定律的。在帕斯卡做过的大量实验中,最著名的一个是这样的:他用一个木酒桶,顶端开一个孔,孔中插接一根很长的铁管子,将接插口密封好。实验的时候,酒桶中先权满水,然后慢慢地往铁管子里注几杯水,当管子中的水柱高达几米的时候,就见木桶突然破裂,水从裂缝中向四面八方喷出。帕斯卡定律的发现,为流体静力学的建立奠定了基础。 发展 帕斯卡还在这一定律的基础上提出了连通器的原理和后来得到广泛应用的水压机的最初设想。他又指出器壁上所受的、由于液体重力而产生的压强,仅仅与深度有关;他用实验,并从理论上解释了与此有关的液体静力学佯谬现象。他在一周之内就突击读完了欧几里得《几何原本》的前六本,并还能把它应用于力学。1653年,他进入牛津大学里奥尔学院做工读生。他没有取得学士学位,而是在1663年获得文学硕士学位。 应用 帕斯卡定律是流体(气体或液体)力学中,指封闭容器中的静止流体的某一部分发生的压强变化,将毫无损失地传递至流体的各个部分和容器壁。帕斯卡首先阐述了此定律。压强等于作用力除以作用面积。根据帕斯卡原理,在水力系统中的一个活塞上施加一定的压强,必将在另一个活塞上产生相同的压强增量。如果第二个活塞的面积是第一个活塞的面积的10倍,那么作用于第二个活塞上的力将增大为第一个活塞的10倍,而两个活塞上的压强仍然相等。水压机就是帕斯卡原理的实例。它具有多种用途,如液压制动等。帕斯卡还发现:静止流体中任一点的压强各向相等,即该点在通过它的所有平面上的压强都相等。这一事实也称作帕斯卡原理(定律)。
. . 平面几何四个重要定理 四个重要定理: 梅涅劳斯(Menelaus)定理(梅氏线) △ABC 的三边BC 、CA 、AB 或其延长线上有点P 、Q 、R , 则P 、Q 、R 共线的充要条件是 1RB AR QA CQ PC BP =??。 塞瓦(Ceva)定理(塞瓦点) △ABC 的三边BC 、CA 、AB 上有点P 、Q 、R ,则AP 、BQ 、CR 共点的充要条件是 1RB AR QA CQ PC BP =??。 托勒密(Ptolemy)定理 四边形的两对边乘积之和等于其对角线乘积的充要条件是该四边形内接于一圆。 西姆松(Simson)定理(西姆松线) 该点落在三角形的外接圆上。 例题: 1. 设AD 是△ABC 的边BC 上的中线,直线CF 交AD 于F 。 求证:FB AF 2ED AE = 。 【分析】CEF 截△ABD → 1FA BF CB DC ED AE =??(梅氏定理) 【评注】也可以添加辅助线证明:过A 、B 、D 之一作CF 的平 行线。 2. 过△ABC 的重心G 的直线分别交AB 、AC 于E 、F ,交CB
DEG 截△ABM →1DB MD GM AG EA BE =??(梅氏定理) DGF 截△ACM →1DC MD GM AG FA CF =??(梅氏定理) ∴FA CF EA BE +=MD AG )DC DB (GM ?+?=MD GM 2MD 2GM ??=1 【评注】梅氏定理 3. D 、E 、F 分别在△ABC 的BC 、CA 、AB 边上, λ===EA CE FB AF DC BD ,AD 、BE 、CF 交成△LMN 。 求S △LMN 。 【分析】 【评注】梅氏定理 4. 以△ABC 各边为底边向外作相似的等腰△BCE 、△CAF 、 △ABG 。求证:AE 、BF 、CG 相交于一点。 【分析】 B
用面积法证明Pascal 定理的方法与技巧 [帕斯卡定理] 如图,用一条6-闭折线依次连接圆上的六个点A B C D E F 、、、、、,其中 AB DE G BC EF H CD FA I ,,,则G H I 、、三点共线。 E F [证1]首先,连接GI ,设'GI BC H GI EF H ,;
E F 图(1)
E F 图(2) 顺次连接圆上的6个相邻点,得到圆的接凸六边形AEBDFC;
F
E F 连接G I 、与圆周上的六点A B C D E F 、、、、、,设 ' ' 'GH GH HI H I ,,则 'GBC GEF IBC IEF S S GH HI S S ,,从而'' ' GBC IEF IBC GEF S S GH H I HI GH S S 。 GBC IEF GBC IEF IFC GBE IFC GBE IBC GEF IFC GBE IBC GEF GEF IBC S S S S S S S S BG BC FI FE S S S S S S FI FC BG BE S S BG BC FI FE CI CF EG EB BG FI FC BG BE EG EF CI CB BC FI FC FI FE BG BE CI CF EG EF EG EB CI CB 1, 可知, 1',即得 '1'GH H I HI GH ,即' 'GH GH HI H I 。 由于'H H 、都是线段GI 上的点,可知'H H 、同向分线段GI 的比相等, 故'H H 、为同一点(重合),从而证明了G H I 、、三点共线。
1 平面几何中几个重要定理及其证明 一、塞瓦定理 1.塞瓦定理及其证明 定理:在?ABC 内一点P ,该点与?ABC 的三个顶点相连所在的三条直线分别交?ABC 三边AB 、BC 、CA 于点D 、E 、F ,且D 、E 、F 三点均不是?ABC 的顶点,则有 1AD BE CF DB EC FA ??=. 证明:运用面积比可得 ADC ADP BDP BDC S S AD DB S S ????==. 根据等比定理有 ADC ADC ADP APC ADP BDP BDC BDC BDP BPC S S S S S S S S S S ??????????-=== -, 所以 APC BPC S AD DB S ??=.同理可得 APB APC S BE EC S ??=, BPC APB S CF FA S ??=. 三式相乘得 1AD BE CF DB EC FA ??=. 注:在运用三角形的面积比时,要把握住两个三角形是“等高”还是“等底”,这样就可以产生出“边之比”. 2.塞瓦定理的逆定理及其证明 定理:在?ABC 三边AB 、BC 、CA 上各有一点D 、E 、F ,且D 、E 、F 均不是?ABC 的顶点,若 1AD BE CF DB EC FA ??=,那么直线CD 、AE 、BF 三线共点. 证明:设直线AE 与直线BF 交于点P ,直线CP 交AB 于点D /,则据塞瓦定理有 // 1AD BE CF D B EC FA ??=. 因为 1AD BE CF DB EC FA ??=,所以有 A B C D F P A B C D E F P D /
平面几何定理及公式 1 过两点有且只有一条直线 2 两点之间线段最短 3 同角或等角的补角相等 4 同角或等角的余角相等 5 过一点有且只有一条直线和已知直线垂直 6 直线外一点与直线上各点连接的所有线段中,垂线段最短 7 平行公理经过直线外一点,有且只有一条直线与这条直线平行 8 如果两条直线都和第三条直线平行,这两条直线也互相平行 9 同位角相等,两直线平行 10 内错角相等,两直线平行 11 同旁内角互补,两直线平行 12两直线平行,同位角相等 13 两直线平行,内错角相等 14 两直线平行,同旁内角互补 15 定理三角形两边的和大于第三边 16 推论三角形两边的差小于第三边 17 三角形内角和定理三角形三个内角的和等于180° 18 推论1 直角三角形的两个锐角互余 19 推论2 三角形的一个外角等于和它不相邻的两个内角的和 20 推论3 三角形的一个外角大于任何一个和它不相邻的内角 21 全等三角形的对应边、对应角相等 22边角边公理(SAS) 有两边和它们的夹角对应相等的两个三角形全等 23 角边角公理( ASA)有两角和它们的夹边对应相等的两个三角形全等 24 推论(AAS) 有两角和其中一角的对边对应相等的两个三角形全等 25 边边边公理(SSS) 有三边对应相等的两个三角形全等
26 斜边、直角边公理(HL) 有斜边和一条直角边对应相等的两个直角三角形全等 27 定理1 在角的平分线上的点到这个角的两边的距离相等 28 定理2 到一个角的两边的距离相同的点,在这个角的平分线上 29 角的平分线是到角的两边距离相等的所有点的集合 30 等腰三角形的性质定理等腰三角形的两个底角相等(即等边对等角) 31 推论1 等腰三角形顶角的平分线平分底边并且垂直于底边 32 等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合 33 推论3 等边三角形的各角都相等,并且每一个角都等于60° 34 等腰三角形的判定定理如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边) 35 推论1 三个角都相等的三角形是等边三角形 36 推论2 有一个角等于60°的等腰三角形是等边三角形 37 在直角三角形中,如果一个锐角等于30°那么它所对的直角边等于斜边的一半 38 直角三角形斜边上的中线等于斜边上的一半 39 定理线段垂直平分线上的点和这条线段两个端点的距离相等 40 逆定理和一条线段两个端点距离相等的点,在这条线段的垂直平分线上 41 线段的垂直平分线可看作和线段两端点距离相等的所有点的集合 42 定理1 关于某条直线对称的两个图形是全等形 43 定理2 如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线 44定理3 两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上 45逆定理如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称 46勾股定理直角三角形两直角边a、b的平方和、等于斜边c的平方,即a^2+b^2=c^2 47勾股定理的逆定理如果三角形的三边长a、b、c有关系a^2+b^2=c^2 ,那么这个三角形是直角三角形 48定理四边形的内角和等于360° 49四边形的外角和等于360° 50多边形内角和定理n边形的内角的和等于(n-2)×180° 51推论任意多边的外角和等于360°
(高中)平面几何基础知识(基本定理、基本性质) 1. 勾股定理(毕达哥拉斯定理)(广义勾股定理)(1)锐角对边的平方,等于其他两边之平方和,减去 这两边中的一边和另一边在这边上的射影乘积的两倍. (2)钝角对边的平方等于其他两边的平方和,加上这两边中的一边与另一边在这边上的射影乘积的两倍. 2. 射影定理(欧几里得定理) 3. 中线定理(巴布斯定理)设△ABC 的边BC 的中点为P ,则有)(22222BP AP AC AB +=+; 中线长:2 222 2 2 a c b m a -+= . 4. 垂线定理:2222BD BC AD AC CD AB -=-?⊥. 高线长:C b B c A a bc c p b p a p p a h a sin sin sin ))()((2=== ---= . 5. 角平分线定理:三角形一个角的平分线分对边所成的两条线段与这个角的两边对应成比例. 如△ABC 中,AD 平分∠BAC ,则AC AB DC BD =;(外角平分线定理). 角平分线长:2 cos 2)(2A c b b c a p bcp c b t a += -+=(其中p 为周长一半). 6. 正弦定理: R C c B b A a 2sin sin sin === ,(其中R 为三角形外接圆半径). 7. 余弦定理:C ab b a c cos 2222-+=. 8. 张角定理:AB DAC AC BAD AD BAC ∠+ ∠=∠sin sin sin . 9. 斯特瓦尔特(Stewart )定理:设已知△ABC 及其底边上B 、C 两点间的一点D ,则有AB 2·DC +AC 2·BD -AD 2·BC =BC ·DC ·BD . 10. 圆周角定理:同弧所对的圆周角相等,等于圆心角的一半.(圆外角如何转化?) 11. 弦切角定理:弦切角等于夹弧所对的圆周角. 12. 圆幂定理:(相交弦定理:垂径定理:切割线定理(割线定理):切线长定理:) 13. 布拉美古塔(Brahmagupta )定理: 在圆内接四边形ABCD 中,AC ⊥BD ,自对角线的交点P 向 一边作垂线,其延长线必平分对边. 14. 点到圆的幂:设P 为⊙O 所在平面上任意一点,PO =d ,⊙O 的半径为r ,则d 2-r 2 就是点P 对 于⊙O 的幂.过P 任作一直线与⊙O 交于点A 、B ,则PA ·PB = |d 2 -r 2 |.“到两圆等幂的点的轨迹是与此二圆的连心线垂直的一条直线,如果此二圆相交,则该轨迹是此二圆的公共弦所在直线”这个结论.这条直线称为两圆的“根轴”.三个圆两两的根轴如果不互相平行,则它们交于一点,这一 点称为三圆的“根心”.三个圆的根心对于三个圆等幂.当三个圆两两相交时,三条公共弦(就是两两的根轴)所在直线交于一点. 15. 托勒密(Ptolemy )定理:圆内接四边形对角线之积等于两组对边乘积之和,即 AC ·BD =AB ·CD +AD ·BC ,(逆命题成立) .(广义托勒密定理)AB ·CD +AD ·BC ≥AC ·BD . 16. 蝴蝶定理:AB 是⊙O 的弦,M 是其中点,弦CD 、EF 经过点M ,CF 、DE 交AB 于P 、Q ,求证:MP =QM . 17. 费马点:定理1等边三角形外接圆上一点,到该三角形较近两顶点距离之和等于到另一顶点的 距离;不在等边三角形外接圆上的点,到该三角形两顶点距离之和大于到另一点的距离.定理2 三 角形每一内角都小于120°时,在三角形内必存在一点,它对三条边所张的角都是120°,该点到三顶点距离和达到最小,称为“费马点”,当三角形有一内角不小于120°时,此角的顶点即为费马
第2课时液体压强的应用、帕斯卡定律 【教学目标】 一、知识与技能 1.认识连通器,了解连通器的原理和在生产、生活中的应用. 2.了解帕斯卡定律及其应用. 3.通过本课时的学习,进一步巩固液体压强的综合运用. 二、过程与方法 1.能联系生活实际,感知连通器在生活中的应用. 2.通过实例帮助学生理解液体的压力和流体的重力之间的关系,液体压强和液体传递压强的区别. 三、情感、态度与价值观 通过对三峡船闸的认识,培养学生的民族自信心和自豪感. 【教学重点】 连通器的概念和应用. 【教学难点】 液体的压力和流体的重力之间的关系. 【教具准备】 多媒体课件、连通器、注射器三只、墨水、三通管、乳胶管、砝码. 【教学课时】 1课时 【巩固复习】 教师引导学生复习上一节内容,并讲解学生所做的课后作业(教师可针对性地挑选部分难题讲解),加强学生对知识的巩固. 【新课引入】 教师出示茶壶、水位计和乳牛自动喂水器的图片,引导学生思考它们在结构上有什么相同点?
学生观察后积极发言:茶壶、水位计和乳牛自动喂水器,它们各自的底部都互相连通. 师像这样上端开口,下端连通的容器叫做连通器,下面我们就一起来学习它. 【课堂导学】 【指导预习】 阅读课本P152-P154页的文字内容和插图,在基本概念、定义、规定及规律上,用红笔做上记号,并完成学案中“课前预习”部分.各小组交流讨论,提出预习疑问. 【交流展示】 1.小组代表举手发言,报告“课前预习”答案,教师评价订正. 2.学生质疑,教师指导释疑. 【拓展探究】 知识点1连通器 师1.演示课本图8-22连通器的实验,引导学生观察,并回答连通器的原理是什么? 生:1.当连通器中装有同种液体且液体不流动时,各容器中液面保持相平. 师2.课本图8-23中左管盛水,右管盛煤油,两管液面是否一样平?为什么? 生:2.两管液面不一样平,平衡时F 左=F 右 ,p 左 =p 右 ,由于ρ 水 >ρ 油 ,由p =ρgh可知h 水 高中平面几何定理汇总及证明 1.共边比例定理 有公共边AB的两个三角形的顶点分别是P、Q,AB与PQ的连线交于点M,则有以下比例式成立:△ PAB的面积:△ QAB的面积=PM:QM. 证明:分如下四种情况,分别作三角形高,由相似三角形可证 S△PAB=(S△PAM-S△PMB) =(S△PAM/S△PMB-1)×S△PMB =(AM/BM-1)×S△PMB(等高底共线,面积比=底长比) 同理,S△QAB=(AM/BM-1)×S△QMB 所以,S△PAB/S△QAB=S△PMB/S△QMB=PM/QM(等高底共线,面积比=底长比) 定理得证! 特殊情况:当PB∥AQ时,易知△PAB与△QAB的高相等,从而S△PAB=S△QAB,反之,S△PAB=S△QAB,则PB∥AQ。 2.正弦定理 在任意一个平面三角形中,各边和它所对角的正弦值的比相等且等于外接圆半径的2倍”,即a/sinA = b/sinB =c/sinC = 2r=R(r为外接圆半径,R为直径) 证明: 现将△ABC,做其外接圆,设圆心为O。我们考虑∠C及其对边 AB。设AB长度为c。 若∠C为直角,则AB就是⊙O的直径,即c= 2r。 ∵(特殊角正弦函数值) ∴ 若∠C为锐角或钝角,过B作直径BC`交⊙O于C`,连接C'A, 显然BC'= 2r=R。 若∠C为锐角,则C'与C落于AB的同侧, 此时∠C'=∠C(同弧所对的圆周角相等) ∴在Rt△ABC'中有 若∠C为钝角,则C'与C落于AB的异侧,BC的对边为a,此时∠C'=∠A,亦可推出。 考虑同一个三角形内的三个角及三条边,同理,分别列式可得 。 在△ABC中,D是边BC上异于B,C或其延长线上的一点,连结AD, 则有BD/CD=(sin∠BAD/sin∠CAD)*(AB/AC)。 证明: S△ABD/S△ACD=BD/CD………… (1.1) S△ABD/S△ACD=[(1/2)×AB×AD×sin∠BAD]/[(1/2) ×AC×AD×sin∠CAD] = (sin∠BAD/sin∠CAD) ×(AB/AC) …………(1.2) 由1.1式和1.2式得 BD/CD=(sin∠BAD/sin∠CAD) ×(AB/AC) 4.张角定理 在△ABC中,D是BC上的一点,连结AD。那么∠∠∠。 证明: 设∠1=∠BAD,∠2=∠CAD 由分角定理, S△ABD/S△ABC=BD/BC=(AD/AC)*(sin∠1/sin∠BAC) → (BD/BC)*(sin∠BAC/AD)=sin∠1/AC (1.1) S△ACD/S△ABC=CD/BC=(AD/AB)*(sin∠2/sin∠BAC) → (CD/BC)*(sin∠BAC/AD)=sin∠2/AB (1.2) (1.1)式+(1.2)式即得sin∠1/AC+sin∠2/AB=sin∠BAC/AD 5.帕普斯定理 直线l1上依次有点A,B,C,直线l2上依次有点D,E,F,设AE,BD交于G,AF,DC交于I,BF,EC交于H,则G,I,H共线。 实用标准文案 平面几何四个重要定理 四个重要定理 梅涅劳斯(Menelaus)定理(梅氏线) △ABC的三边BC、CA、AB或其延长线上有点P、Q、 BP CQ AR 则P、Q、R共线的充要条件是竺竺竺1。 PC QA RB 塞瓦(Ceva)定理(塞瓦点) △ABC的三边BC、CA、AB上有点P、 CR共点的充要条件是聖C2竺1。 PC QA RB 托勒密(Ptolemy)定理 四边形的两对边乘积之和等于其对角线乘积的充要条件是 该四边形内接于一圆。 西姆松(Simson)定理(西姆松线) 从一点向三角形的三边所引垂线的垂足共线的充要条件是 P 该点落在三角形的外接圆上。 例题: 1 . 设AD 是△ABC 的边BC 上的中线,直线CF 交AD 于F 。求 AE 2AF 证: ED FB AE DC BF 【分析】CEF 截△ABD T 1 (梅氏定理) ED CB FA 行线。 【评注】也可以添加辅助线证明:过 A 、B 、D 之一作CF 的平 △ 2 .过MBC的重心G的直线分别交 交CB于D。 求证: BE EA CF FA 【分析】连结并延长AG交BC于M,贝U M为BC的中点。 DEG 截AABM T BE EA AG GM MD DB DGF 截AACM T竺 FA GM DC 1 (梅氏定理)1 (梅氏定理) BE CF GM (DB DC) = GM 2MD EA FA = AG MD = 2GM MD 【评注】梅氏定理 3 . D 、E 、F 分别在△ ABC 的 BC 、CA 、AB 边上, 求 S/LMN 。 【分析】 BD AF CE DC FB EA ,AD 、BE 、CF 交成△ LMN 。 【评注】梅氏定理 4 .以△ABC 各边为底边向外作相似的等腰厶 ABG 。求证:AE 、BF 、CG 相交于一点。 【分析】 A F E M N D C BCE 、MAF 、△ 帕斯卡定律 [教学目标] 1.知识和技能 (1)知道液体(或气体)能够传递压强。 (2)理解帕斯卡定律。 2.过程和方法 (1)通过注射器的实验感受液体对压强的传递。 (2)通过帕斯卡球和实验3研究液体传递压强的规律。 3.情感、态度和价值观 (1)通过液体传递压强规律的过程,培养学生的观察和分析能力。 (2)通过对实验的分析,培养学生能用简洁、正确的语言表述结论。 (3)通过对帕斯卡的事迹介绍,培养学生树立正确的科学观。 [教学重点] 帕斯卡定律 [教学准备] 注射器、帕斯卡球、烧杯、玻璃管、水、橡皮球。 [教学设计思路] 本节课的主要内容是:研究密闭液体传递压强的规律——帕斯卡定律。 本节课的基本思路是:以实验为基础,通过分析,揭示密闭液体(或气体)传递压强的规律,即帕斯卡定律。 本节课要突出的重点是帕斯卡定律。首先通过实验1,让学生认识液体能够传递压强;通过实验2和3,揭示密闭液体能够向各个方向传递压强并且压强大小不变,进而建立帕斯卡定律。通过例题巩固帕斯卡定律的内容。 [教学流程] [教学过程设计] 一、准备知识 1、压力:垂直作用在物体表面上的力叫做压力。 2、压强:单位面积上所受的压力叫压强,压强是用来反映压力作用效果的物理量。 3、如右图,重为G,侧面积为S的正方体木块,在压力 F的作用下静止在竖直墙面上,求墙面受到的压力和压强? F 解:F’= F;P = F’/ S = F / S 二、新课 1、帕斯卡定律 实验1: 在注射器内灌一些水,当一手指按压注射器活塞时,堵着出口端的另一手指能感受到水的压力吗? 结论1: 水(或其他液体)能够传递压强。 实验2: 帕斯卡球实验。在球内注满水,给球内的水施加一个压强,要求学生观察实验现象,并思考球内的水,能把受到的压强向什么方向传递。 结论2: 球内的水能将它在某一处受到的压强向各个方向传递。这是液体具有流动性的缘故。 实验3 : 在一玻璃瓶中倒入适量的水,用三根玻璃管穿过软木塞深入水中,另用一根玻璃管穿过软木塞插入瓶内空气中,它的一端连接一个能压气的橡皮球。用石蜡封住瓶口,使瓶内的水密闭。 实验时,用手压橡皮球,给瓶内充气,使水面产生一个压强。要求学生观察三根玻璃管中液面的变化情况,并分析原因。 结论3: 加在密闭液体上的压强,能被液体向各个方向传递,且被传递的压强大小相等。 这是法国科学家帕斯卡通过反复的研究,发现的规律,所以叫帕斯卡定律。帕斯卡定律内容: 平面几何四个重要定理 四个重要定理: 梅涅劳斯(Menelaus)定理(梅氏线) △ABC 的三边BC 、CA 、AB 或其延长线上有点P 、Q 、R ,则P 、Q 、R 共线的充要条件是 1RB AR QA CQ PC BP =??。 塞瓦(Ceva)定理(塞瓦点) △ABC 的三边BC 、CA 、AB 上有点P 、Q 、R ,则AP 、BQ 、CR 共点的充要条件是 1RB AR QA CQ PC BP =??。 托勒密(Ptolemy)定理 四边形的两对边乘积之和等于其对角线乘积的充要条件是该四边形内接于一圆。 西姆松(Simson)定理(西姆松线) 该点落在三角形的外接圆上。 例题: 1. 设AD 是△ABC 的边BC 上的中线,直线CF 交AD 于F 。求证: FB AF 2ED AE = 。 【分析】CEF 截△ABD → 1FA BF CB DC ED AE =??(梅氏定理) 【评注】也可以添加辅助线证明:过A 、B 、D 之一作CF 的平行 线。 2. 过△ABC 的重心G 的直线分别交AB 、AC 于E 、F ,交 CB 于D 。 求证:1FA CF EA BE =+。 【分析】连结并延长AG 交BC 于M ,则M 为BC 的中点。 DEG 截△ABM → 1DB MD GM AG EA BE =??(梅氏定理) DGF 截△ACM →1DC MD GM AG FA CF =??(梅氏定理) ∴FA CF EA BE +=MD AG )DC DB (GM ?+?=MD GM 2MD 2GM ??=1 【评注】梅氏定理 3. D 、E 、F 分别在△ABC 的BC 、CA 、AB 边上, λ===EA CE FB AF DC BD ,AD 、BE 、CF 交成△LMN 。 求S △LMN 。 【分析】 【评注】梅氏定理十大高中平面几何几何定理汇总及证明
平面几何四大神奇定理
帕斯卡定律
平面几何四大神奇定理