
机器分配
总公司拥有高效生产设备M台,准备分给下属的N个公司。各分公司若获得这些设备,可以为国家提供一定的盈利。问:如何分配这M台设备才能使国家得到的盈利最大?求出最大盈利值。其中M<=15,N<=10。分配原则:每个公司有权获得任意数目的设备,但总台数不得超过总设备数M。
数据文件格式为:第一行保存两个数,第一个数是设备台数M,第二个数是分公司数N。接下来是一个M*N 的矩阵,表明了第I个公司分配J台机器的盈利。
用机器数来做状态,数组F[I,J]表示前I个公司分配J台机器的最大盈利。则状态转移方程为:
F[I,J]=Max{F[I-1,K] + V alue[I,J-K]} (1<=I<=N,1<=J<=M,0<=K<=J )
初始值: F(0,0)=0
时间复杂度O(N*M2)
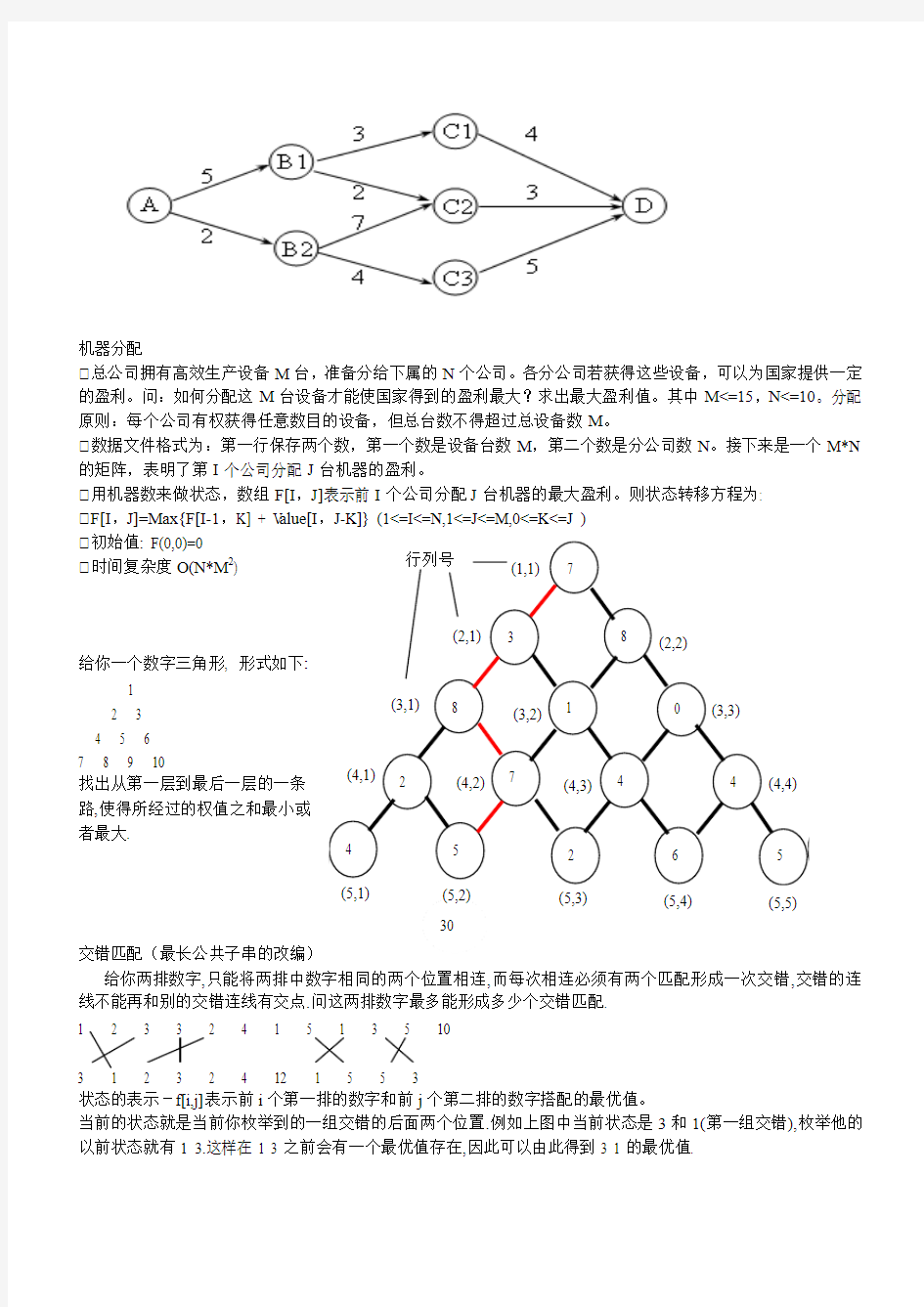
给你一个数字三角形, 形式如下:
1
2 3
4 5 6
7 8 9 10
找出从第一层到最后一层的一条
路,使得所经过的权值之和最小或
者最大.
(5,2) (5,3) (5,4) (5,5)
30
交错匹配(最长公共子串的改编)
给你两排数字,只能将两排中数字相同的两个位置相连,而每次相连必须有两个匹配形成一次交错,交错的连线不能再和别的交错连线有交点.问这两排数字最多能形成多少个交错匹配.
1 2 3 3 2 4 1 5 1 3 5 10
3 1 2 3 2
4 12 1
5 5 3
状态的表示-f[i,j]表示前i个第一排的数字和前j个第二排的数字搭配的最优值。
当前的状态就是当前你枚举到的一组交错的后面两个位置.例如上图中当前状态是3和1(第一组交错),枚举他的以前状态就有1 3.这样在1 3之前会有一个最优值存在,因此可以由此得到3 1的最优值.
买车票(Ural1031)
Ekaterinburg城到Sverdlovsk城有直线形的铁路线。两城之间还有其他一些停靠站,总站数为N。各站按照离Ekaterinburg城的距离编号。Ekaterinburg城编号为1,Sverdlovsk城编号为N。
某两站之间车票价格由这两站的距离X决定.
当0 当L1 当L2 当两站距离大于L3时没有直达票,所以有时候要买几次票做几次车才行。比如,在上面的例图中,2-6没有直达票,有几种买票方法可以从2-6,其中一种是买C2元的2-3车票,再买C3元的3-6车票。 给定起点站和终点站还有L1,L2,L3,C1,C2,C3,求出要从起点到终点最少要花多少钱. 预处理 很容易想出一个N^2的预处理,但是那样是会超时的.由于尽量要让车站离得远(费用是一样的啊)因此在每种收费情况下,每个车站的以前状态车站一定是递增的序列.这里是只要O(N)的程序: for j:=1 to 3 do begin k:=en-1; for i:=en downto be do begin while (way[i]-way[k]<=l[j])and(k>=be) do dec(k); p[i][j]:=k+1; end; end; 数组P[i][j]表示的是I状态的第j种以前状态. 动态规划的部分 for i:=be+1 to en do {枚举当前状态} begin cost[i]:=maxlongint; for j:=1 to 3 do {枚举以前状态} begin if (p[i][j]<>i) and (cost[i] > cost[p[i][j]] + c[j]) then cost[i]:=cost[p[i][j]]+c[j]; end; end; 文字游戏(fairfox邀请赛1) 句子是abcd 他共有4种完全划分方案: ab/cd a/b/c/d a/b/cd ab/c/d; 当前状态就是单词在句子中向后靠的位置,以前状态就是确定这个单词位置以后,除掉这个单词长度后的一个位置.状态转移方程是:F[i]:=F[i]+F[i-length(word[j])] IOI中有一题《前缀》也是类似的题目. 最佳加法表达式 有一个由1..9组成的数字串.问如果将m个加号插入到这个数字串中.使得所形成的算术表达式的值最小. 用f[i,j],表示的是在前i个字符中插入j个加号能达到的最小值,最后的答案也就是F[length(s),m]. 于是就有一个动规的方程: F[i,j]:=min(f[i,j],f[k,j-1]+num[k+1,i]) num[k+1,i]表示k+1位到i位所形成的数字.这里显然是把加号插入了第k+1个位置上. 巴比伦塔 问题描述: 有很多的不同种类的立方体(长宽高不同),每一类有无限多个.将他们一层层的叠加起来,要求上面的一块立方体的下底面一定要比下面的一块立方体的上底面要小,就是长和宽都要小于.问最多能建成多高的塔. 经过研究可以发现,每一种类的立方体有3种不同的摆放方式,而每种摆放方式最多用1次,所以可以分离出3*N块“不同”的立方体,接下来,或许你仍然不知道如何动规,那么就试试排序.列出所有的石块的所有摆放方式xi,yi,zi.必须全部保证xi 滑雪(上海2002) 题目的大意是给出一个矩阵,如: 对于所给出的矩阵找出一条最长的递减链,满足链中相邻的两个元素间都是在矩阵中相邻的. 对于有给出的数字进行递减排序,然后两重循环就搞定问题.动态转移方程是: F[i]:=max(F[i],F[j]+1); 满足条件是i与j在原矩阵中相邻. 试想,如果你不知道要排序,你能想到这题是用动态规划吗? 硬币问题(经典问题) 就是给出n种硬币的面值,问面值M有多少种不同的表示方法. 动态转移方程是F[i]:=F[i]+F[I-cost[j]].当前状态是i,以前状态是i-cost[j]. 多米诺骨牌(某题的简化) 有N张多米诺骨牌,每张的两端有两个数字,范围在1..6之间.每张骨牌可以正放,也可以反放.求出一种摆放的情况,使得所有的骨牌上端数字之和与下端数字之和的差值最小.求出最小差值. 可以这么考虑这个问题:我们把每一个骨牌的上下差值记下。接下来的任务便是将这些值分成两组,使得他们的和的差值最小。动规过程如下: f[0]:=true; for i:=1 to n do for j:=sum downto a[i] do f[j]:=f[j] or f[j-a[i]]; Sum表示所有差值的和. a[i]表示第i块骨牌的差值. J是当前状态,j-a[i]是以前状态.f[j]表示j这个差值能否通过组合得到。接下来的程序就不用我多说了。 商店购物(IOI) 这一题更是需要开一个五维bool型数组.还需要通过递归求出组合形式.动规的方程我就不写了. 图状动规 城堡 某国聪明美丽的公主要找一位如意郎君,她希望未来的夫君是一个聪明善良,节俭但又不吝啬的人。为了找到理想的人选,她的爸爸—国王,给她修建了一座城堡,这个城堡有很多房间,房间之间有走廊连接,但每进入一个房间必须要花费一定数量的钱币,公主就在某个房间中等待。开始,国王给每个候选人一样多的钱币,候选人从同一个地点出发,直到找到美丽的公主为止,如果这时哪个人找到了公主,并且钱币刚好用完,那么他将会赢得公主的芳心。 既然是问我们能不能到达,所以想想就应该知道,动规的数组是bool型的.一开始时,只有出发的房间记为true. 但是,并不是以每个房间作为状态,因为还存在一个把钱用光的问题.到达同一个房间时,如果剩余的钱不一样,也就会有不同的决策. 所以状态就是在剩余j个钱币的时候能否到达第i个房间.用f[i,j]来表示. 于是动态转移方程也就出来了 树状动规 没有上司的晚会 某公司要举办一次晚会,但是为了使得晚会的气氛更加活跃,每个参加晚会的人都不希望在晚会中见到他的上司,要不然他们会很扫兴。现在已知每个人的活跃指数和上司关系(当然不可能存在环),求邀请哪些人来能使得晚会的总活跃指数最大。 按照要求构建一张关系图,可见这是一棵树。对于这类最值问题,向来是用动态规划求解的。 任何一个点的取舍可以看作一种决策,那么状态就是在某个点取的时候或者不取的时候,以他为跟的子树能有的最大活跃总值。分别可以用f[i,1]和f[i,0]表示。 当这个点取的时候,他的所有儿子都不能取,所以f[i,1]:=sum(f[j,0],j为i的儿子)+i的权值。 不取的时候,他的所有儿子取不取无所谓,不过当然应该取价值最大的一种情况。所以f[i,0]:=sum(max(f[j,1],f[j,0]),j为i的i儿子)。 这就是树状动规的基本形态。 二次动规 在动规的基础上再进行动规,就叫做二次动规。 买票 有一座n层的楼房,某个人要到第n层的任何一个房间买票。每层楼都有m个房间。而如果要到第i层的第j 个房间买票,那么必须先在第i-1层的第j个房间买票或者在第i层的与这个房间相邻的房间买过票才行.而每个房间所要收取的票费是不同的,给定每个房间内买票需要的费用,问要在第n层的任意一间房间内买到票的最小消费是多少. 显然不能写这样的状态转移方程:f[i,j]:=min(f[i-1,j],f[i,j-1],f[i,j+1])+w[j].因为无法有一种处理顺序使得在f[i,j]之前同时求得f[i,j-1]和f[i,j+1]的最优值. 所以动规分两次进行.第一次用状态转移方程f[i,j]:=min(f[i,j-1],f[i-1,j])+w[i]求出一个不一定是最优的解.再用f[i,j]:=min(f[i,j],f[i,j+1],j from m-1 downto 1)+w[i]求出最终的最优解,可以证明这样的能够求出真正的最优解. 要注意的是这两次动规不能分开做,而要在处理每一层的时候都要做,要不然显然无法求得最优值。 网络(Ural1056,求树的中心) 题目大意是:有一棵有N个结点的树,给出每个结点的父亲(即给出这棵树),边的权都是1。每个结点延树的边可以走到树的任意一个结点,令Ai为第i个结点最远能走的距离,求出Ai最小的结点有哪些。如有多个最小的Ai,则都要输出。这里N<=10000 枚举每个点,然后DFS复杂度O(N2),超时是显然的事情。 可以发现其实有很多DFS都重复做了同样的工作,产生了浪费,所以应该选择动态规划解决这个问题。 树上的动规,是否直接可以写出下面的状态转移方城呢? f[i]:=max(f[son],f[father])+1 废话,显然是不行的,son和father的值不可能同时得到。 第一次动规做f[i]:=max(f[son])+1,第二次动规做f[i]:=max(f[i],f[father] + 1) 。 但是存在一个问题就是如果f[father]的值是从i那里得到的,这样计算显然就错了。 不要放弃,在实际操作过程中,f需要记下两个值,一个是最优值,一个是次优值,这两个值必须由不用的子结点得到。这样当最优值发生矛盾的时候,次优值一定不会矛盾。问题就解决了。复杂度O(N)十分的理想。 垃圾陷阱(USACO&TJU1087) 卡门——农夫约翰极其珍视的一条Holsteins奶牛——已经落了到“垃圾井”中。“垃圾井”是农夫们扔垃圾的地方,它的深度为D (2 <= D <= 100)英尺。卡门想把垃圾堆起来,等到堆得与井同样高时,她就能逃出井外了。另外,卡门可以通过吃一些垃圾来维持自己的生命。每个垃圾都可以用来吃或堆放,并且堆放垃圾不用花费卡门的时间。假设卡门预先知道了每个垃圾扔下的时间t(0 < t <= 1000),以及每个垃圾堆放的高度h(1 <= h <= 25)和吃进该垃圾能维持生命的时间f(1 <= f <= 30),要求出卡门最早能逃出井外的时间,假设卡门当前体内有足够持续10小时的能量,如果卡门10小时内没有进食,卡门就将饿死。 字符串距离(TJU1086) 设有字符串X,我们称在X的头尾及中间插入任意多个空格后构成的新字符串为X的扩展串,如字符串X为“abcbcd”,则字符串“abcb□cd”,“□a□bcbcd□”和“abcb□cd□”都是X的扩展串,这里“□”代表空格字符。如果A1是字符串A的扩展串,B1是字符串B的扩展串,A1与B1具有相同的长度,那么我们定义字符串A1与B1的距离为相应位置上的字符的距离总和,而两个非空格字符的距离定义为它们的ASCII码的差的绝对值,而空格字符与其它任意字符之间的距离为已知的定值K,空格字符与空格字符的距离为O。在字符串A、B的所有扩展串中,必定存在两个等长的扩展串A1、B1,使得A1与B1之间的距离达到最小,我们将这一距离定义为字符串A、B的距离。请你写一个程序,求出字符串A、B的距离。 二叉苹果树(Ural1018) 有一棵苹果树,如果树枝有分叉,一定是分2叉(就是说没有只有1个儿子的结点) 这棵树共有N个结点(叶子点或者树枝分叉点),编号为1-N,树根编号一定是1。 我们用一根树枝两端连接的结点的编号来描述一根树枝的位置。下面是一颗有4个树枝的树 2 5 \ / 3 4 \ / 1 现在这颗树枝条太多了,需要剪枝。但是一些树枝上长有苹果。 给定需要保留的树枝数量,求出最多能留住多少苹果。 最长前缀IOI'96&USACO 1.4.3) 在生物学中,一些生物的结构是用包含其要素的大写字母序列来表示的。生物学家对于把长的序列分解成较短的(称之为元素的)序列很感兴趣。如果一个集合P中的元素可以通过串联组成一个序列S ,那么我们认为序列S 可以分解为P中的元素。并不是所有的元素都必须出现。举个例子,序列ABABACABAAB 可以分解为下面集合中的元素:{A, AB, BA, CA, BBC} 序列S 的前面K 个字符称作S 中长度为K 的前缀。设计一个程序,输入一个元素集合以及一个大写字母序列,计算这个序列最长的前缀的长度。 得知Atlantis即将沉没的消息以后,King决定把他的人民送到安全的国外去。但是码头已经废弃很多很多年了。码头前有一个迷宫,国王的骑士只身闯入了这个迷宫……骑士在迷宫的出口遇到了不明生物的袭击!骑士因为是单独作战,所以很快便招架不住了,他的大马被打得奄奄一息(。。。)这个时候,迷宫中的两座石像(一个是猫老大,一个是天使。(!!!!!))里放出了无数锋利的刀片,把不明生物全部杀死,骑士当场晕倒在地。等他醒来,发现马已经死了,手上多了一个戒指,上面写着:“这个戒指会帮助你逃脱。它赋予了神奇的力量。有了它,每次移动如果是只要|x-x1|+|y-y1|<=P(P在输入中给出),且(x1, y1)不是障碍物,你就能实现(x, y) -> (x1, y1)的移动!”(Angel暗自想:还有这么心黑的……)迷宫为n*m的矩阵。骑士从(n, m)到(1, 1)。问:在戒指的帮助下,骑士最少要多少步才能回到入口?在步数最少的前提下,总共有多少种办法到达入口?注意,骑士不会傻到一直停留在原地不动。 2001年普及组第4题--装箱问题 【问题描述】 有一个箱子容量为V(正整数,0≤V≤20000),同时有n个物品(0 【输入格式】 输入文件box.in有若干行。 第一行:一个整数,表示箱子容量V; 第二行:一个整数,表示物品个数n; 接下来n行,分别表示这n个物品的各自体积。 【输出格式】 输出文件box.out只有一行数据,该行只有一个数,表示最小的箱子剩余空间。 【输入样例】【输出样例】 24 0 6 8 3 12 7 9 7 1996年提高组第4题--砝码秤重__数据加强版 【问题描述】 设有n种砝码,第k种砝码有ck个,每个重量均为wk,求:用这些砝码能秤出的不同重量 的个数,但不包括一个砝码也不用的情况。 【输入格式】 输入文件weight.in的第一行只有一个数n,表示不同的砝码的种类数. 第2行至第n+1行,每行有两个整数.第k+1行的两个数分别表示第k种砝码的个数和重量. 【输出格式】 输出文件weight.out中只有一行数据:Total=N。表示用这些砝码能秤出的不同重量数, (不包括一个砝码也不用的情况。) 【输入样例】【输出样例】【样例说明】 2 Total=6 重量1,2,3,4,5,6都能秤得 2 1 对于100%的数据,砝码的种类n满足:1≤n≤100; 对于30%的数据,砝码的总数量C满足:1≤C≤20; 对于100%的数据,砝码的总数量C满足:1≤C≤100; 对于所有的数据,砝码的总重量W满足:1≤W≤400000; 【分析】 以a[I]表示第I种砝码数;w[I]表示第I种砝码重量; for i:=1 to n do for j:=1 to a[i] do begin for k:=v downto w[i] do if s[k-w[i]] then s[k]:=true; end; total:=0; for i:=1 to v do if s[i] then total:=total+1; 石子归并-szgb.pas 【问题描述】 有一堆石头质量分别为W1,W2,…,Wn.(Wi≤10000),将石头合并为两堆,使两堆质量的差最小。 【输入】 输入文件szgb.in的第一行只有一个整数n(1≤n≤50),表示有n堆石子。 接下去的n行,为每堆石子质量。 【输出】 输出文件szgb.out的只有一行,该行只有一个整数,表示最小的质量差. 【样例输入】【样例输出】 5 3 5 8 13 27 14 【分析】 若所有石子总质量为sum,一半为half,则相当于容量为half的装箱问题 勇闯黄金十二宫……白羊宫-同济ACM第1100题_补圣衣 Time Limit:1s Memory Limit:1000k Total Submit:7441 Accepted:1015 下载样例程序(PE) Background 话说星矢、紫龙、冰河、阿瞬为了救活雅典娜,必须勇闯黄金十二宫。 Problem 首先他们来到了白羊宫,身为白羊座黄金圣斗士的穆先生,早就知道假教皇的阴谋,于是他决定 现在已知四人圣衣有几处破损(s1,s2,s3,s4),而且每处破损程度不同,破损程度越厉害,穆先生 就需要更多时间来修好它。破损程度用穆先生需修好它用的时间表示(A1...As1,B1...Bs2,C1...Cs3, D1...Ds4)。不过穆先生能力很强,可以同时修补2处破损。但是这2处破损,只能是同一件圣衣上的。 就是说他只能同时修补一件圣衣,修好了,才能修补下一件。 Input 本题包含多组数据,每组数据5行. 第1行,为s1,s2,s3,s4(1≤s1,s2,s3,s4≤20) 第2行,为A1...As1 共s1个数,表示第一件圣衣上每个破损处的程度,也就是穆先生修好它所用的时间 第3行,为B1...Bs2 共s2个数,表示第二件圣衣上每个破损处的程度,也就是穆先生修好它所用的时间第4行,为C1...Cs3 共s3个数,表示第三件圣衣上每个破损处的程度,也就是穆先生修好它所用的时间第5行,为D1...Ds4 共s4个数,表示第四件圣衣上每个破损处的程度,也就是穆先生修好它所用的时间 (1≤A1...As1,B1...Bs2,C1...Cs3,D1...Ds4≤60) Output 对于每组数据输出一行,为穆先生修好四件圣衣所要的最短时间。 Sample Input Sample Output 1 2 1 3 20 5 4 3 6 2 4 3 【分析】 将每件圣衣中的所有破损,分成两份,使每份总和之差最小,于是,本题变为求四次石子归并问题了 01背包问题 【问题描述】 有n个物品,体积分别为s[1],s[2],…,s[n];重量分别为w[1],w[2],…,w[n]。在这些物品 中任取若干个,装入一个容积为V的背包,求背包中能得到的重量的最大值。 其中V,n,s[1..n],w[1..n]均为正整数,n≤100,V≤20000,s[i]≤20000,w[i]≤1000000。 【输入】 输入数据有若干行: 第1行有2个以空格分隔的数v和n,分别表示背包的容积和物品数。 以下第2行至第n+1行共n行表示n个物品的体积和重量的情况: 第2行有2个以空格分隔的数,表示第1种物品体积s[1]和重量w[1]; 第3行有2个以空格分隔的数,表示第3种物品体积s[3]和重量w[3]; …… …… 第n+1行有2个以空格分隔的数,表示第n种物品体积s[n]和重量w[n]; 【输出】 输出数据只有1行,该行只有一个数,表示背包中能得到的最大重量。 【分析】 以f[i,j]表示:在前i种物品中作适当选择,在容量为j的背包中能得到的最大重量。 即: (1)当I=0时,不使用物品,能得重量当然为0; j=0时,容量0中的背包重量为0。 (2)当j f[i,j]=f[i-1,j] (3)当j>=s[i]时,有两种方案可供选择: ①选择第i个物品,最大重量f[i-1,j-s[i]]+w[i]: ②不选择第i个物品,最大重量f[i-1,j]: f[i,j]为两者的较大者。 挤牛奶-同济ACM第1132题 Time Limit:1s Memory Limit:32768k Total Submit:1445 Accepted:408 下载样例程序(PE) Problem 小卡卡终于帮农夫John找到了走丢的那一头奶牛,John为了感谢小卡卡,不仅告诉了他在Pascal山脉上可能存在Pascal圣地最大的宝藏,还说要请小卡卡喝牛奶。 可是农夫John发现他家里所储藏的牛奶已经喝光了,所以要临时给奶牛挤奶。小卡卡实在是 太好心了,说要帮农夫John一起挤牛奶。John答应了,他把他的n头奶牛中的n/2头(n是个偶数) 分给小卡卡挤,他自己挤剩下的n/2头奶牛。但是每一头奶牛都有不同的产奶量,农夫John为了让 小卡卡减轻负担,他希望他们两个所挤的牛奶的总量之差最小。小卡卡得知了每头奶牛的产奶情况 之后很快就解决了这个问题。 Input 该题含有多组测试数据。 每组测试数据第一行一个整数n,n为偶数且小于100。表示有n头奶牛。 第二行n个整数分别给出每头奶牛的产奶量(产奶量的总和不超过2000)。 Output 输出小卡卡和农夫所挤的牛奶量的最小差值。 Sample Input Sample Output 6 0 7 9 2 6 4 2 【分析】 (一)状态描述 以w[i]表示第i头奶牛的产奶量。 以f[i,j,k]表示在前i头奶牛中选择j头奶牛时,能否得到奶量k. 在前i头奶牛中任意选取j头奶牛,若有某种选择方案,使所有选中奶牛的产奶量和为k,则f[i,j,k]=True; 若在前i头奶牛中无论如何选取j头奶牛,选取的产奶量和均无法达到k,则f[i,j,k]=False。 如果总产奶量为sum,一半为half,求使f[n,n/2,k]为true的最大的k(k<=half),所求为sum-2k 【问题描述】 你现在拿到了许多的礼物,你要把这些礼物放进袋子里。你只有一个最多装下V 体积物品的袋子,你不能全部放进去。你也拿不动那么重的东西。你估计你能拿的最大重量为G。现在你了解了每一 个物品的完美值、重量和体积,你当然想让袋子中装的物品的完美值总和最大,你又得计划一下了。【输入】 第一行:G 和V 表示最大重量和体积。 第二行:N 表示拿到N 件礼物。 第三到N+2行:每行3个数Ti Gi Vi 表示各礼物的完美值、重量和体积 【输出】 输出共一个数,表示可能获得的最大完美值。 【输入输出样例】 输入(pack.in):输出(pack.out): 6 5 50 4 10 2 2 20 3 2 40 4 3 30 3 3 【数据范围】 对于20%的数据N,V,G,Ti,Vi,Gi≤10 对于50%的数据N,V,G,Ti,Vi,Gi≤100 对于80%的数据N,V,G,Ti,Vi,Gi≤300 80%到100%的数据是N,V,G,Ti,Vi,Gi≤380 的离散随机数据。 一般性的最少硬币组成问题coinYB.pas coinYB.exe 从n种币值为a[1..n]的硬币中,任选几个硬币组成价值为V的一堆货币,问最少需要几个硬币? 其中每种硬币的数量没有限制。1<=n<=100,1<=v<=100000,1<=a[i]<=100000 输入文件coinYB.in中有两行:第一行有两个数v和n;第二行有n个以空格分隔的数,表示n个币值. 输出文件coinYB.out中只有一行,该行只有一个数,表示所需的最少硬币数, 如果无论如何选取硬币,均不能得到币值v,则输出0. 【分析】 (一)状态描述 以a[i]表示第i种硬币的面值。 以c[i,j]表示在前i种硬币中作出最优选择,得到面值j所需要的硬币枚数. (二)状态转移方程 c[i,j]=min{c[i-1,j],1+c[i-1,j-a[i]} 硬币问题的动态规划算法: for j:=1 to v do c[j]:=maxlongint; c[0]:=0; for i:=1 to n do for j:=a[i] to v do {硬币可以使用多次,所以是to,而不是downto} if c[j]>1+c[j-a[i]] then c[j]:=1+c[j-a[i]]; if c[v]<>maxlogint then writeln(c[v]) else writeln(0); 2001年浙江省队选拔---积木城堡 castle.pas(castle.exe) XC的儿子小XC最喜欢玩的游戏用积木垒漂亮的城堡。城堡是用一些立方体的积木垒成的,城堡的每一层是一块积木。小XC是一个比他爸爸XC还聪明的孩子,他发现垒城堡的时候,如果下面的积木比上面的积木大,那么城堡便不易倒。所以他在垒城堡的时候总是遵循这样的规则。小XC想把自己垒的城堡送给幼儿园里漂亮的女孩子们,这样可以增加他的好感度。为了公平起见,他决定把送给每个女孩子一样高的城堡,这样可以避免女孩子们为了获得更漂亮的城堡而引起争执。可是他发现自己在垒城堡的时候并没有预先考虑到这一点。所以他现在要改造城堡。由于他没有多余的积木了,他灵机一动,想出了一个巧妙的改造方案。他决定从每一个城堡中挪去一些积木,使得最终每座城堡都一样高。为了使他的城堡更雄伟,他觉得应该使最后的城堡都尽可能的高。 任务: 请你帮助小XC编一个程序,根据他垒的所有城堡的信息,决定应该移去哪些积木才能获得最佳的效果。输入文件castle.in 第一行是一个整数N(N<=100),表示一共有几座城堡。 以下N行每行是一系列非负整数,用一个空格分隔,按从下往上的顺序依次给出一座城堡中所有积木的棱长。用-1结束。一座城堡中的积木不超过100块,每块积木的棱长不超过100。 输出文件castle.out 一个整数,表示最后城堡的最大可能的高度。如果找不到合适的方案,则输出0。 输入样例输出样例 2 3 2 1 –1 测试数据: 3 2 1 –1 ftp://10.10.0.78 登录名:olpk 【分析】 1。求得所有城堡中高度和最小值v; 2. 对所有城堡,作体积和为v的装箱问题 3. for j←v downto 0 do 4. if 高度和j对所有的城堡都可得到then 5. 输出j;break;{退出j循环} 生物基元问题 一个生物体的结构可以用“基元”的序列表示,一个“基元"用一些英文字符串表示。对于一个基元集合P,可以将字符串S看作由n个基元P1,P2,…,Pn依次连接而成的。问题是给定一个字符串S和一个基元集 合P,使S的前缀可由P中的基元组成。求这个前缀的最大长度。基元的长度最大为20,字符中的长度最大为500000.例如基元集合为{A,AB,BBC,CA,BA},字符串为ABABACABAABCB,则最大长度为11,其具体 组成如下图所示: ABABACABAABCB 【分析】 一.状态描述 以s[1..v]表示字符串; 以p[1..n]表示n个基元; 以can[k]表示考虑当前基元时,以s[1..k]能否由基元组成,true时s[1..k]可由基元组成,否则不能; 二.状态转移方程 can[k]=can[k] or (can[k-w] and s[k-w+1..k]=p[i]) 2. for j←1 to v do can[k]←false 3. for j←1 to v do {遍历串s} 4. for i←1 to n do {遍历n个基元,第i个基元的长度为Wi} 5. if (j>=Wi) and can[j-Wi] and (s[j-Wi+1..j]=p[i][1..Wi]) then 6. Can[j]←true 7. for j←v downto 0 do 8. if can[j] then 9. 输出j; break; 2001年9月11日,一场突发的灾难将纽约世界贸易中心大厦夷为平地,Mr. F曾亲眼目睹了这次灾难。为了纪念“9?11”事件,Mr. F决定自己用水晶来搭建一座双塔。Mr. F有N块水晶,每块水晶有一个高度,他想用这N块水晶搭建两座有同样高度的塔,使他们成为一座双塔,Mr. F可以从这N块水晶中任取M (1≤M≤N)块来搭建。但是他不知道能否使两座塔有同样的高度,也不知道如果能搭建成一座双塔,这座 双塔的最大高度是多少。所以他来请你帮忙。 给定水晶的数量N(1≤N≤100)和每块水晶的高度Hi(N块水晶高度的总和不超过2000),你的任务是判断Mr. F能否用这些水晶搭建成一座双塔(两座塔有同样的高度),如果能,则输出所能搭建的双塔的最 大高度,否则输出“Impossible”。 输入格式Input Format 输入的第一行为一个数N,表示水晶的数量。第二行为N个数,第i个数表示第i个水晶的高度。 5 1 3 4 5 2 输出格式Output Format 输出仅包含一行,如果能搭成一座双塔,则输出双塔的最大高度,否则输出一个字符串“Impossible”。 7 1996年提高组第3题--挖地雷 【问题描述】 在一个地图上有N个地窖(N<=20),每个地窖中埋有一定数量的地雷。同时,给出地窖之间的连接路径。当地窖及其连接的数据给出之后,某人可以从任一处开始挖地雷,然后可以沿着指出的连接往下挖(仅能选择一条路径),当无连接时挖地雷工作结束。例如下图表示: 有4 V1→V3→V4→V5;V1→V4→V5; 设计一个挖地雷的方案,使某人能挖到最多的地雷。 【输入格式】 输入文件wdl.in有若干行。 第1行只有一个数字,表示地窖的个数N。 第2行有N个数,分别表示每个地窖中的地雷个数。 第3行至第N+1行表示地窖之间的连接情况: 第3行有n-1个数(0或1),表示第一个地窖至第2个、第3个、…、第n个地窖有否路径连接。 V1 V2 V3 V4 V5 第4行有n-2个数,表示第二个地窖至第3个、第4个、…、第n个地窖有否路径连接。 … … 第n+1行有1个数,表示第n-1个地窖至第n个地窖有否路径连接.(0表示没有路径,1表示有路径)。 【输出格式】 输出文件wdl.out有两行数据。 第一行表示挖得最多地雷时的挖地雷的顺序,各地窖序号间以一个空格分隔,不得有多余的空格。如有多种方案,则输出任意一种即可。(不唯一) 第二行只有一个数,表示能挖到的最多地雷数。 【输入样例】 10 8 4 7 6 1 1 1 0 0 0 0 1 1 1 【输出样例】 1 3 4 5 27 1999提高组第1题-拦截导弹 【问题描述】 某国为了防御敌国的导弹袭击,发展出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷:虽然它的第一发炮弹能够到达任意的高度,但是以后每一发炮弹都不能高于前一发的高度。某天,雷达捕捉到敌国的导弹来袭。由于该系统还在试用阶段,所以只有一套系统,因此有可能不能拦截所有的导弹。输入导弹依次飞来的高度(雷达给出的高度数据是不大于30000的正整数):计算这套系统最多能拦截多少导弹; 【输入格式】 输入文件missile.in只有一行数据,包括若干以空格分隔的正整数,表示来袭的导弹的高度. 【输出格式】 输出文件missile.out只有一个正整数,表示最多能拦截的导弹数; 【输入样例】 389 207 155 300 299 170 158 65 【输出样例】 6 【分析】 以数组元素a[i]表示第i发炮弹的高度。 以数组元素count[i]表示:使用这套拦截系统,拦截第i枚来袭导弹后,在第i枚至最后一枚导弹(第n枚)中,最多能拦截的导弹数。则显然有:count[n]=1;拦截的第n枚导弹是最后一枚,当然在第n枚至第n枚中,只能拦截这一枚导弹。求的为count[1],count[2],…,count[n]中的最大者。 2004年提高组第3题-合唱队形 【问题描述】 N位同学站成一排,音乐老师要请其中的(N-K)位同学出列,使得剩下的K位同学排成合唱队形。合唱队形是指这样的一种队形:设K位同学从左到右依次编号为1,2…,K,他们的身高分别为T1,T2,…,TK,则他们的身高满足T1<... 【输入格式】 输入文件chorus.in有2行数据。 第一行是一个整数n(2<=n<=100),表示同学的总数。 第二行有n个整数,用空格分隔,第i个整数Ti(130<=Ti<=230)是第i位同学的身高(厘米)。 【输出格式】 输出文件chorus.out包括一行,这一行只包含一个整数,就是最少需要几位同学出列。 【输入样例】 8 186 186 150 200 160 130 197 220 【输出样例】 4 【数据规模】 对于50%的数据,保证有n<=20; 对于全部的数据,保证有n<=100。 勇闯黄金十二宫……射手宫-同济ACM第1108题 Time Limit:1s Memory Limit:1500k Background 话说星矢、紫龙、冰河、阿瞬为了救活雅典娜,必须勇闯黄金十二宫。 Problem 第九个他们来到射手宫,身为射手座黄金圣斗士的艾尔里斯是狮子座圣斗士艾尔里亚的哥哥,他早在13年前就发现了撒加杀了真教皇,并且自己做了假教皇。然而他却被撒加迫害致死。现在星矢四人已经来到了射手宫。艾尔里斯的灵魂想考验一下这些圣斗士们的水平,墙上留下了一道题目。“已知艾尔里斯和弟弟艾尔里亚的基因基本相同, 由于基因表达起来不方便,所以就用n个数字来表示。(因为至今共发现100000种基因, 所以每个数字都<=100000)兄弟之间的基因个数是相同的,就是说他们都有n个数字。 且对于每个人,这n个数字互不相同。现在要求兄弟之间基因的最长公共部分。可以不连续。” 如果,他们解决不了这题,就通不过射手宫了。不过还好,他们顺利地通过了! Input 本题包含多组数据. 第1行,为n(1<=n<=100000) 下面2行,每行n个数字, 表示了一个人的所以基因。 Output 对于每组数据输出一行,为他们两人基因的最长公共部分的长度。 Sample Input 7 1 2 3 4 5 6 7 7 6 5 4 1 2 3 【分析】 一.状态描述 以a[1..n]和b[1..n]表示兄弟俩的基因。 以f[i,j]表示a[1..i]和b[1..j]中最长公共部分的长度。所求为f[n,n]. Time Limit:1s Memory Limit:32768k Total Submit:1996 Accepted:384 Problem Tom是一个非常有创业精神的人,由于大学学的是汽车制造专业,所以毕业后他用有限的资金开了一家汽车零件加工厂专门为汽车制造商制造零件。由于资金有限他只能先购买一台加工机器。现在他却遇到了麻烦,多家汽车制造商需要他加工一些不同零件(由于厂家和零件不同,所以给的加工费也不同),而且不同厂家对于不同零件的加工时间要求不同(有些加工时间要求甚至是冲突的,但开始和结束时间相同不算冲突)。 Tom当然希望能把所有的零件都加工完,以得到更多的加工费,但当一些零件的加工时间要求有冲突时,在某个时间内他只能选择某种零件加工(因为他只有一台机器),为了赚得尽量多的加工费,Tom不知如何进行取舍。现在请你帮Tom设计一个程序,合理选择部分(或全部)零件进行加工,使得得到最大的加工费。 Input 第一行是一个整数m,表示测试数据的个数。 每组测试数据的第一行是一个整数n(n<=30000),表示共有n个零件须加工。 接下来的n行中,每行有3个整数,分别表示每个零件加工的时间要求。 第一个表示开始时间,第二个表示该零件加工的结束时间,第三个表示加工该零件可以得到的加工费。 注:数据中的每个数值不会超过100000. Output 对每组测试数据,输出一个整数,表示Tom可以得到的最大加工费。 Sample Input Sample Output 1 30 3 1 3 10 4 6 20 2 5 25 勇闯黄金十二宫……双鱼宫-同济ACM第1111题 Time Limit:1s Memory Limit:1000k Background 话说星矢、紫龙、冰河、阿瞬为了救活雅典娜,必须勇闯黄金十二宫。 Problem 最后一个他们来到双鱼宫,身为双鱼座黄金圣斗士的阿布罗狄被人称为最美丽、最漂亮的圣斗士,他的武器就是一些毒玫瑰花。然而紫龙和冰河在前面两个宫的战斗中已经牺牲了,而阿瞬为了要让星矢能快点到达教庭,他一个人留下来和阿布罗狄单挑。于阿布罗狄的毒玫瑰花粉可以扩散,阿瞬的锁链旋转星云阵就防不住了。于是他脱下圣衣,要使出他的绝强招术:星云旋风。不过阿瞬发星云旋风只能发一段时间,但是可以发很多次。已知现在阿瞬可以发n次星云旋风,每次攻击有一个起始时间Si和一个结束时间Fi(Si<=Fi),但是一旦选中一次攻击就必须全部攻击完,中途不能停止,而且必须从起始时间开始。因为每次的攻击效果相同,所以当然是次数越多越好,问阿瞬最多可以攻击多少次。 最后阿瞬打败了阿布罗狄,但是他也被阿布罗狄的玫瑰花吸干了血。(后来又被雅典娜救活了,那是后话。)星矢也成功地到达教庭,救活了雅典娜,并且打败了假教皇,双子座的撒加。 Input 本题包含多组数据. 第1行,为n(1<=n<=500)若数据加强为1<=n<=1万,用什么算法? 下面n行,每行2个数字,为Si,Fi,0<=Si<=Fi<=32767,表示第i次攻击的起始时间和结束时间。 Sample Input Sample Output 3 2 0 2 0 1 1 3 Pascal山脉-同济ACM第1134题 Time Limit:1s Memory Limit:32768k Problem 小卡卡顺着老者所指的方向,来到了Pascal神峰的顶峰。老者告诉小卡卡,Pascal山脉有很多座山,都排在一条直线上,每座山都有不同的高度。Pascal山的山顶有一个神奇的洞穴,进入这个洞穴后,你将会到达这座山前方的另一座山,更加神奇的是,你到达的山一定比他所在的山高度要小。而Pascal圣地最大的宝藏就藏在某一座Pascal 山上的洞穴中,这个洞穴的特点是它有一道石门封闭着。小卡卡很想知道进入每座山的洞穴后,他所到达的不同的山会有多少种可能。 Input 该题含有多组测试数据。 第一行一个整数n,表示山的个数.(1<=n<=20000) 第二行以后n行从前到后给出每座山的高度。另外两座山可以有相同的高度. (1<=每座山的高度<=maxlongint) Output 共n行,每行一个整数.第i行的整数表示他进入第i号山的洞穴后能够到达的不同的山的个数. Sample Input Sample Output 5 0 1 1 2 2 3 3 4 4 5 光荣的梦想-同济ACM第1176题 Time Limit:1s Memory Limit:32768k Total Submit:294 Accepted:127 Problem Prince对他在这片大陆上维护的秩序感到满意,于是决定启程离开艾泽拉斯。在他动身之前,Prince决定赋予King_Bette最强大的能量以守护世界、保卫这里的平衡与和谐。在那个时代,平衡是个梦想。因为有很多奇异的物种拥有各种不稳定的能量,平衡瞬间即被打破。KB决定求助于你,帮助他完成这个梦想。一串数列即表示一个世界的状态。平衡是指这串数列以升序排列。而从一串无序数列到有序数列需要通过交换数列中的元素来实现。 KB的能量只能交换相邻两个数字。他想知道他最少需要交换几次就能使数列有序。 Input 本题有多组数据。第一行为数据的组数N。对于每组数据,第一行为数列中数的个数n,第二行为n <= 10000 对于每组数据,输出一个整数,表示最少需要交换几次能达到平衡状态。 Sample Input Sample Output 2 0 4 2 1 2 3 4 4 2 1 4 3 象形文字{限时2秒,空间16MB hie.pas/hie.exe} 【题目描述】 光光回到家,完成了双休日的作业,就开始看书,光光对历史非常感兴趣,于是光光就开始看一本古印度的书。书上面印了很多的象形文字,为了叙述简便,我们把每一种形状的象形文字抽象成为一个1到70的数字,比如有这么一串文字:1 27 50 27 29,光光好像看出了什么,觉得如果添加上若干个文字之后,就能够成为一个回文的一句话。比如上面一句话最少需要添加两个字才能变为回文的一句话。添加方法分别为: (1)方法1:1 29 27 50 27 29 1,或 (2)方法2:29 1 27 50 27 1 29 我们可以知道,给定一句话,通过添加若干个字符是可以成为一个回文句子的。因此,光光需要知道,他最少需要添加多少个文字,才能使这句话变成回文的? 【输入格式】 输入文件hie.in包含以下内容: 第一行:一个数字n,代表原句有n个字符。 第二行:n个数字,代表这句话的内容。 【输出格式】 输出文件hie.out包含一行,代表了最少添加文字的个数。 【样例输入】【样例输出】 5 2 1 27 50 27 29 【数据规模】 30%的数据中,n<=200; 100%的数据中,n<=5000; 【分析】 本题的实质是求总的逆序对数。因此可采用与“光荣的梦想”相似的算法解决本题。 1 27 29 50 27 27 50 29 27 1 假定原始的n个数字为a[1..n],将其倒置得b[1..n];使用“同济ACM第1108题”的方法,求得a数组与b 数组的最长公共子串长度max;此时a数组与b数组中共有max个相同,在a数组中加上b中与a不同的n-max 个,在b数组中加上n-max个与a中与b不同的n-max个,得到a与b完全相同。此时,a与b均为回文数了。 【算法复杂性】 (1)时间:O(n2)的时间,因为n<=5000,限时2秒时,O(n2)的算法也能过;当然本题存在O(nlog2n)的算法,详见pascal简介.xls文件。 因为f[i,j]只与f[i-1,j-1],f[i,j-1],f[i-1,j]有关。 2003年提高组第3题--加分二叉树 【问题描述】 设一个n个节点的二叉树tree的中序遍历为(l,2,3,…,n),其中数字1,2,3,…,n为节点编号。 每个节点都有一个分数(均为正整数),记第j个节点的分数为di,tree及它的每个子树都有一个加分,任一棵子树subtree(也包含tree本身)的加分计算方法如下: subtree的左子树的加分×subtree的右子树的加分+subtree的根的分数 若某个子树为空,规定其加分为1,叶子的加分就是叶节点本身的分数。不考虑它的空子树。试求一棵符合中序遍历为(1,2,3,…,n)且加分最高的二叉树tree。要求输出; (1)tree的最高加分 (2)tree的前序遍历 【输入格式】文件binary.in 第1行:一个整数n(n<30),为节点个数。 第2行:n个用空格隔开的整数,为每个节点的分数(分数<100)。 【输出格式】文件binary.out 第1行:一个整数,为最高加分(结果不会超过4,000,000,000)。 第2行:n个用空格隔开的整数,为该树的前序遍历。 【输入样例】【输出样例】 5 145 5 7 1 2 10 3 1 2 4 5 【分析】 一.状态描述 以f[i,j]表示第i个结点至第j个结点间能得到的最大加分; 得到最大加分时,第i个结点至第j个结点以结点r[i,j]为根; 二.状态转移方程 f[i,j]=MAX{f[i,p-1]*f[p+1,j]+f[p,p]},其中p∈[i,j] 三.初值f[i,i]=结点i的本身分数;r[i,i]=i; 2000年普及组第3题--乘积最大 问题描述 今年是国际数学联盟确定的“2000——世界数学年”,又恰逢我国著名数学家华罗庚先生诞辰90周年。在华罗庚先生的家乡江苏金坛,组织了一场别开生面的数学智力竞赛的活动,你的一个好朋友XZ也有幸得以参加。活动中,主持人给所有参加活动的选手出了这样一道题目:设有一个长度为N的数字串,要求选手使用K个乘号将它分成K+1个部分,找出一种分法,使得这K+1个部分的乘积能够为最大。同时,为了帮助选手能够正确理解题意,主持人还举了如下的一个例子: 有一个数字串:312,当N=3,K=1时会有以下两种分法: 1) 3*12=36 2) 31*2=62 这时,符合题目要求的结果是:31*2=62 第一行共有2个自然数N ,K (6≤N ≤40,1≤K ≤6) 第二行是一个长度为N 的数字串。 输出(至文件maxmu.out 中)相对于输入,应输出所求得的最大乘积(一个自然数)。 样例输入 样例输出 4 2 62 1231 【分析】 一.状态描述 以f[i,j]表示前i 个数字中插入j 个乘号能得到的最大值; 以a[1..n]表示n 个原始数字; 所求为f[n,k]; 二.状态转移方程 f[i,j]=MAX{f[j,j-1]*a[j+1..i],f[j+1,j-1]*a[j+2..i],…,f[i -1,j-1]*a[i]} 三.初值 插入0个乘号时的值:f[i,0]=a[1..i];{即原数字串的前i 个数字} NOIP2003年普及组第2题--数字游戏(p2003_2.pas) 【问题描述】 丁丁最近沉迷于一个数字游戏之中。这个游戏看似简单,但丁丁在研究了许多天 之后却发觉原来在简单的规则下想要赢得这个游戏并不那么容易。游戏是这样的,在 你面前有一圈整数(一共n 个),你要按顺序将其分为m 个部分,各部分内的数字相加, 相加所得的m 个结果对10取模后再相乘,最终得到一个数k 。游戏的要求是使你所得 的k 最大或者最小。例如,对于下面这圈数字(n=4,m=2): 当要求最小值时,((2-1) mod 10)×((4+3) mod 10)=1×7=7,要求最大值 时,为((2+4+3) mod 10)×(-1 mod 10)=9×9=81。 特别值得注意的是,无论是负数还是正数,对10取模的结果均为非负值。 丁丁请你编写程序帮他赢得这个游戏。 【输入格式】 输入文件GAME.in 第一行有两个整数,n (1≤n ≤50)和m (1≤m ≤9)。 以下n 行每行有个整数,其绝对值不大于104,按顺序给出圈中的数字,首尾相接。 【输出格式】 输出文件GAME.out 有两行,各包含一个非负整数。 第一行是你程序得到的最小值,第二行是最大值。 【输入样例】 【输出样例】 4 2 7 4 81 3 -1 2 3 -1 动态规划是用空间换时间的一种方法的抽象。其关键是发现子问题和记录其结果。然后利用这些结果减轻运算量。 比如01背包问题。 因为背包最大容量M未知。所以,我们的程序要从1到M一个一个的试。比如,开始任选N件物品的一个。看对应M的背包,能不能放进去,如果能放进去,并且还有多的空间,则,多出来的空间里能放N-1物品中的最大价值。怎么能保证总选择是最大价值呢?看下表。 测试数据: 10,3 3,4 4,5 5,6 c[i][j]数组保存了1,2,3号物品依次选择后的最大价值. 这个最大价值是怎么得来的呢?从背包容量为0开始,1号物品先试,0,1,2,的容量都不能放.所以置0,背包容量为3则里面放4.这样,这一排背包容量为 4,5,6,....10的时候,最佳方案都是放4.假如1号物品放入背包.则再看2号物品.当背包容量为3的时候,最佳方案还是上一排的最价方案c为4.而背包容量为5的时候,则最佳方案为自己的重量5.背包容量为7的时候,很显然是5加上一个值了。加谁??很显然是7-4=3的时候.上一排c3的最佳方案是4.所以。 总的最佳方案是5+4为9.这样.一排一排推下去。最右下放的数据就是最大的价值了。(注意第3排的背包容量为7的时候,最佳方案不是本身的6.而是上一排的9.说明这时候3号物品没有被选.选的是1,2号物品.所以得9.) 从以上最大价值的构造过程中可以看出。 f(n,m)=max{f(n-1,m), f(n-1,m-w[n])+P(n,m)}这就是书本上写的动态规划方程.这回清楚了吗? 下面是实际程序: #include [1]POJ动态规划题目列表 容易: 1018, 1050, 1083, 1088, 1125, 1143, 1157, 1163, 1178, 1179, 1189, 1208, 1276, 1322, 1414, 1456, 1458, 1609, 1644, 1664, 1690, 1699, 1740(博弈), 1742, 1887, 1926(马尔科夫矩阵,求平衡), 1936,1952, 1953, 1958, 1959, 1962, 1975, 1989, 2018, 2029,2039, 2063, 2081, 2082,2181, 2184, 2192, 2231, 2279, 2329, 2336, 2346, 2353,2355, 2356, 2385, 2392, 2424, 不易: 1019,1037, 1080, 1112, 1141, 1170, 1192, 1239, 1655, 1695, 1707,1733(区间减法加并查集), 1737, 1837, 1850, 1920(加强版汉罗塔), 1934(全部最长公共子序列), 1937(计算几何), 1964(最大矩形面积,O(n)算法), 2138, 2151, 2161(烦,没写), 2178, 推荐: 1015, 1635, 1636(挺好的), 1671, 1682, 1692(优化), 1704, 1717, 1722, 1726, 1732, 1770, 1821, 1853, 1949, 2019, 2127, 2176, 2228, 2287, 2342, 2374, 2378, 2384, 2411 状态 DP 树 DP 构造最优解四边形不等式单调队列 1015 Jury Compromise 1029 False coin 1036 Gangsters 1037 A decorative fence 1038 Bugs Integrated, Inc. 1042 Gone Fishing 1050 To the Max 1062 昂贵的聘礼 1074 Parallel Expectations 1080 Human Gene Functions 1088 滑雪 1093 Formatting Text 1112 Team Them Up! 1141 Brackets Sequence 1143 Number Game 01背包问题,是用来介绍动态规划算法最经典的例子,网上关于01背包问题的讲解也很多,我写这篇文章力争做到用最简单的方式,最少的公式把01背包问题讲解透彻。 01背包的状态转换方程f[i,j] = Max{ f[i-1,j-Wi]+Pi( j >= Wi ), f[i-1,j] } f[i,j]表示在前i件物品中选择若干件放在承重为j 的背包中,可以取得的最大价值。 Pi表示第i件物品的价值。 决策:为了背包中物品总价值最大化,第i件物品应该放入背包中吗? 题目描述: 有编号分别为a,b,c,d,e的五件物品,它们的重量分别是2,2,6,5,4,它们的价值分别是6,3,5,4,6,现在给你个承重为10的背包,如何让背包里装入的物品具有最 首先要明确这张表是从右到左,至底向上生成的。 为了叙述方便,用e10单元格表示e行10列的单元格,这个单元格的意义是用来表示只有物品e时,有个承重为10的背包,那么这个背包的最大价值是6,因为e物品的重量是4,背包装的了,把e装进去后价值为6。然后是e9单元格表示背包承重9,只有物品e, e装进去后,背包价值为6,接着是e8, e7单元格,一直到e3单元格表示背包承重3,但物品e承重4,装不了,所以e3=0, 对于d10单元格,表示只有物品e,d时,承重为10的背包,所能装入的最大价值,是10,因为物品e,d这个背包都能装进去。对于承重为9的背包,d9=10,是怎么得出的呢? 根据01背包的状态转换方程,需要考察两个值, 一个是f[i-1,j],对于这个例子来说就是e9的值6,另一个是f[i-1,j-Wi]+Pi; 在这里, f[i-1,j]表示我有一个承重为9的背包,当只有物品e可选时,这个背包能装入的最大价值 f[i-1,j-Wi]表示我有一个承重为4的背包(等于当前背包承重减去物品d的重量),当只有物品e可选时,这个背包能装入的最大价值 f[i-1,j-Wi]就是指单元格e4值为6,Pi指的是d物品的价值,即4 由于f[i-1,j-Wi]+Pi = 6 + 4 = 10 大于f[i-1,j] = 6,所以物品d应该放入承重为9的背包,所以d9=10. 动态规划法、回溯法解0-1背包问题 2012级计科庞佳奇 一、问题描述与分析 1.动态规划算法通常用于求解具有某种最优性质的问题。在这类问题中,可能会 有许多可行解。每一个解都对应于一个值,我们希望找到具有最优值的解。动态规划算法与分治法类似,其基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。与分治法不同的是,适合于用动态规划求解的问题,经分解得到子问题往往不是互相独立的。若用分治法来解这类问题,则分解得到的子问题数目太多,有些子问题被重复计算了很多次。如果我们能够保存已解决的子问题的答案,而在需要时再找出已求得的答案,这样就可以避免大量的重复计算,节省时间。我们可以用一个表来记录所有已解的子问题的答案。 不管该子问题以后是否被用到,只要它被计算过,就将其结果填入表中。这就是动态规划法的基本思路。具体的动态规划算法多种多样,但它们具有相同的填表格式。 多阶段决策问题中,各个阶段采取的决策,一般来说是与时间有关的,决策依赖于当前状态,又随即引起状态的转移,一个决策序列就是在变化的状态中产生出来的,故有“动态”的含义,称这种解决多阶段决策最优化问题的方法为动态规划方法。任何思想方法都有一定的局限性,超出了特定条件,它就失去了作用。同样,动态规划也并不是万能的。适用动态规划的问题必须满足最优化原理和无后效性。1.最优化原理(最优子结构性质)最优化原理可这样阐述:一个最优化策略具有这样的性质,不论过去状态和决策如何,对前面的决策所形成的状态而言,余下的诸决策必须构成最优策略。简而言之,一个最优化策略的子策略总是最优的。一个问题满足最优化原理又称其具有最优子结构性质。2.无后效性将各阶段按照一定的次序排列好之后,对于某个给定的阶段状态,它以前各阶段的状态无法直接影响它未来的决策,而只能通过当前的这个状态。换句话说,每个状态都是过去历史的一个完整总结。这就是无后向性,又称为无后效性。3.子问题的重叠性动态规划将原来具有指数级时间复杂度的搜索算法改进成了具有多项式时间复杂度的算法。其中的关键在于解决冗余,这是动态规划算法的根本目的。动态规划实质上是一种以空间换时间的技术,它在实现的过程中,不得不存储产生过程中的各种状态,所以它的空间复杂度要大于其它的算法。 01背包是在M件物品取出若干件放在空间为W的背包里,每件物品的体积为W1,W2……Wn,与之相对应的价值为P1,P2……Pn。求出获得最大价值的方案。 2.回溯法(探索与回溯法)是一种选优搜索法,按选优条件向前搜索,以达到目 标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为“回溯点”。 在包含问题的所有解的解空间树中,按照深度优先搜索的策略,从根结点出发深度探索解空间树。当探索到某一结点时,要先判断该结点是否包含问题的解,如果包含,就从该结点出发继续探索下去,如果该结点不包含问题的解,则逐层向其祖先结点回溯。(其实回溯法就是对隐式图的深度优先搜索算法)。若用回溯法求问题的所有解时,要回溯到根,且根结点的所有可行的子树都要已被搜索遍才结束。 关于求解0/1背包问题的动态规划算法 摘要:本文通过研究动态规划原理,提出了根据该原理解决0/1背包问题的方法与算法实现, 并对算法的正确性作了验证.观察程序运行结果,发现基于动态规划的算法能够得到正确的决策方案且比穷举法有效. 关键字:动态规划;0/1背包;约束条件;序偶;决策序列;支配规则 1、引 言 科学研究与工程实践中,常常会遇到许多优化问题,而有这么一类问题,它们的活动过程可以分为若干个阶段,但整个过程受到某一条件的限制。这若干个阶段的不同决策的组合就构成一个完整的决策。0/1背包问题就是一个典型的在资源有限的条件下,追求总的收益最大的资源有效分配的优化问题。 对于0/1背包问题,我们可以这样描述:设有一确定容量为C 的包及两个向量C ’=(S 1,S 2,……,S n )和P=(P 1,P 2,……,P N ),再设X 为一整数集合,即X=1,2,3,……,N ,X 为SI 、PI 的下标集,T 为X 的子集,那么问题就是找出满足约束条件∑S i 〈=C ,使∑PI 获得最大的子集T 。在实际运用中,S 的元素可以是N 个经营项目各自所消耗的资源,C 可以是所能提供的资源总量,P 的元素可是人们从各项项目中得到的利润。 0/1背包问题是工程问题的典型概括,怎么样高效求出最优决策,是人们关心的问题。 2、求解问题的动态规划原理与算法 2.1动态规划原理的描述 求解问题的动态规划有向前处理法向后处理法两种,这里使用向前处理法求解0/1背包问题。对于0/1背包问题,可以通过作出变量X 1,X 2,……,X N 的一个决策序列来得到它的解。而对于变量X 的决策就是决定它是取0值还是取1值。假定决策这些X 的次序为X n ,X N-1,……,X 0。在对X 0做出决策之后,问题处于下列两种状态之一:包的剩余容量是M ,没任何效益;剩余容量是M-w ,效益值增长了P 。显然,之后对X n-1,Xn-2,……,X 1的决策相对于决策X 所产生的问题状态应该是最优的,否则X n ,……,X 1就不可能是最优决策序列。如果设F j (X )是KNAP (1,j ,X )最优解的值,那么F n (M )就可表示为 F N (M )=max(f n (M),f n-1(M-w n )+p n )} (1) 对于任意的f i (X),这里i>0,则有 f i (X)=max{f i-1(X),f i-1(X-w i )+p i } (2) 为了能由前向后推而最后求解出F N (M ),需从F 0(X )开始。对于所有的X>=0,有F 0(X )=0,当X<0时,有F 0(X )等于负无穷。根据(2),可求出0〈X 〈W 1和X 〉=W 1情况下F 1(X )的值。接着由(2)不断求出F 2,F 3,……,F N 在X 相应取值范围内的值。 2.2 0/1背包问题算法的抽象描述 (1)初始化各个元素的重量W[i]、效益值P[i]、包的最大容量M ; (2)初始化S0; (3)生成S i ; 动态规划练习题 [题1] 多米诺骨牌(DOMINO) 问题描述:有一种多米诺骨牌是平面的,其正面被分成上下两部分,每一部分的表面或者为空,或者被标上1至6个点。现有一行排列在桌面上:顶行骨牌的点数之和为6+1+1+1=9;底行骨牌点数之和为1+5+3+2=11。顶行和底行的差值是2。这个差值是两行点数之和的差的绝对值。每个多米诺骨牌都可以上下倒置转换,即上部变为下部,下部变为上部。 现在的任务是,以最少的翻转次数,使得顶行和底行之间的差值最小。对于上面这个例子,我们只需翻转最后一个骨牌,就可以使得顶行和底行的差值为0,所以例子的答案为1。 输入格式: 文件的第一行是一个整数n(1〈=n〈=1000〉,表示有n个多米诺骨牌在桌面上排成一行。接下来共有n行,每行包含两个整数a、b(0〈=a、b〈=6,中间用空格分开〉。第I+1行的a、b分别表示第I个多米诺骨牌的上部与下部的点数(0表示空)。 输出格式: 只有一个整数在文件的第一行。这个整数表示翻动骨牌的最少次数,从而使得顶行和底行的差值最小。 [题2] Perform巡回演出 题目描述: Flute市的Phlharmoniker乐团2000年准备到Harp市做一次大型演出,本着普及古典音乐的目的,乐团指挥L.Y.M准备在到达Harp市之前先在周围一些小城市作一段时间的巡回演出,此后的几天里,音乐家们将每天搭乘一个航班从一个城市飞到另一个城市,最后才到达目的地Harp市(乐团可多次在同一城市演出). 由于航线的费用和班次每天都在变,城市和城市之间都有一份循环的航班表,每一时间,每一方向,航班表循环的周期都可能不同.现要求寻找一张花费费用最小的演出表. 输入: 输入文件包括若干个场景.每个场景的描述由一对整数n(2<=n<=10)和k(1<=k<=1000)开始,音乐家们要在这n个城市作巡回演出,城市用1..n标号,其中1是起点Flute市,n是终点Harp市,接下来有n*(n-1)份航班表,一份航班表一行,描述每对城市之间的航线和价格,第一组n-1份航班表对应从城市1到其他城市(2,3,...n)的航班,接下的n-1行是从城市2到其他城市(1,3,4...n)的航班,如此下去. 每份航班又一个整数d(1<=d<=30)开始,表示航班表循环的周期,接下来的d个非负整数表示1,2...d天对应的两个城市的航班的价格,价格为零表示那天两个城市之间没有航班.例如"3 75 0 80"表示第一天机票价格是75KOI,第二天没有航班,第三天的机票是80KOI,然后循环:第四天又是75KOI,第五天没有航班,如此循环.输入文件由n=k=0的场景结束. 输出: 对每个场景如果乐团可能从城市1出发,每天都要飞往另一个城市,最后(经过k天)抵达城市n,则输出这k个航班价格之和的最小值.如果不可能存在这样的巡回演出路线,输出0. 样例输入: 样例输出: 0/1背包问题动态规划详解及C++代码 1. 问题描述 给定一个载重量为C的背包 有n个物品 其重量为wi 价值为vi 1<=i<=n 要求:把物品装入背包 并使包内物品价值最大2. 问题分析 在0/1背包问题中 物体或者被装入背包 或者不被装入背包 只有两种选择。循环变量i j意义 前i个物品能够装入载重量为j的背包中 数组c意义 c[i][j]表示前i个物品能装入载重量为j的背包中物品的最大价值 若w[i]>j 第i个物品不装入背包 否则 若w[i]<=j且第i个物品装入背包后的价值>c[i-1][j] 则记录当前最大价值 替换为第i个物品装入背包后的价值 其c++代码如下 #include 0/1 背包问题动态规划详解及C代码 动态规划是用空间换时间的一种方法的抽象。其关键是发现子问题和记录其结果。然后利用这些结果减轻运算量。 问题描述: 给定N中物品和一个背包。物品i的重量是W i,其价值位V i,背包的容量为C。问应该如何选择装入背包的物品,使得转入背包的物品的总价值为最大?? 在选择物品的时候,对每种物品i只有两种选择,即装入背包或不装入背包。不能讲物品i 装入多次,也不能只装入物品的一部分。因此,该问题被称为0-1背包问题。 问题分析:令V(i,j)表示在前i(1<=i<=n)个物品中能够装入容量为就j(1<=j<=C)的背包中的物品的最大价值,则可以得到如下的动态规划函数: (1) V(i,0)=V(0,j)=0 (2) V(i,j)=V(i-1,j) j 顺序对齐 源程序名ALIGN.??? (PAS,C,CPP) 可执行文件名ALIGN.EXE 输入文件名ALIGN.IN 输出文件名 ALIGN.OUT 考虑两个字符串右对齐的最佳解法。例如,有一个右对齐方案中字符串是AADDEFGGHC 和ADCDEGH。 AAD_DEFGGHC ADCDE__GH_ 每一个数值匹配的位置值2分,一段连续的空格值-1分。所以总分是匹配点的2倍减去连续空格的段数,在上述给定的例子中,6个位置(A,D,D,E,G,H)匹配,三段空格,所以得分2*6+(-1)*3=9,注意,我们并不处罚左边的不匹配位置。若匹配的位置是两个不同的字符,则既不得分也不失分。 请你写个程序找出最佳右对齐方案。 输入 输入文件包含两行,每行一个字符串,最长50个字符。字符全部是大字字母。 输出 一行,为最佳对齐的得分。 样例 ALIGN.IN AADDEFGGHC ADCDEGH ALIGN.OUT 9 _______________________________________________________________________________ 任务安排 源程序名BATCH.??? (PAS,C,CPP) 可执行文件名BATCH.EXE 输入文件名BATCH.IN 输出文件名 BATCH.OUT N个任务排成一个序列在一台机器上等待完成(顺序不得改变),这N个任务被分成若干批,每批包含相邻的若干任务。从时刻0开始,这些任务被分批加工,第i个任务单独完成所需的时间是T i。在每批任务开始前,机器需要启动时间S,而完成这批任务所需的时间是各个任务需要时间的总和(同一批任务将在同一时刻完成)。每个任务的费用是它的完成时刻乘以一个费用系数F i。请确定一个分组方案,使得总费用最小。 0/1背包问题动态规划详解及C代码 动态规划是用空间换时间的一种方法的抽象。其关键是发现子问题和记录其结果。然后利用这些结果减轻运算量。 比如01背包问题。 /*一个旅行者有一个最多能用M公斤的背包,现在有N件物品, 它们的重量分别是W1,W2,...,Wn, 它们的价值分别为P1,P2,...,Pn. 若每种物品只有一件求旅行者能获得最大总价值。 输入格式: M,N W1,P1 W2,P2 ...... 输出格式: X*/ 因为背包最大容量M未知。所以,我们的程序要从1到M一个的试。比如,开始任选N件物品的一个。看对应M的背包,能不能放进去,如果能放进去,并且还有多的空间,则,多出来的空间里能放N-1物品中的最大价值。怎么能保证总选择是最大价值呢?看下表。 测试数据: 10,3 3,4 4,5 5,6 c[i][j]数组保存了1,2,3号物品依次选择后的最大价值. 这个最大价值是怎么得来的呢?从背包容量为0开始,1号物品先试,0,1,2,的容量都不能放.所以置0,背包容量为3则里面放 4."这样,这一排背包容量为4,5,6,....10的时候,最佳方案都是放 4."假如1号物品放入背包.则再看2号物品.当背包容量为3的时候,最佳方案还是上一排的最价方案c为 4."而背包容量为5的时候,则最佳方案为自己的重量 5."背包容量为7的时候,很显然是5加上一个值了。加谁??很显然是7-4=3的时候.上一排c3的最佳方案是 4."所以。总的最佳方案是5+4为 9."这样.一排推下去。最右下放的数据就是最大的价值了。(注意第3排的背包容量为7的时候,最佳方案不是本身的 6."而是上一排的 9."说明这时候3号物品没有被选.选的是1,2号物品.所以得 9.") 从以上最大价值的构造过程中可以看出。 f(n,m)=max{f(n-1,m), f(n-1,m-w[n])+P(n,m)}这就是书本上写的动态规划方程.这回清楚了吗? 下面是实际程序(在VC 6."0环境下通过): #include 动态规划之-0-1背包问题及改进 有N件物品和一个容量为V的背包。第i件物品的重量是w[i],价值是v[i]。求解将哪些物品装入背包可使这些物品的重量总和不超过背包容量,且价值总和最大。在选择装入背包的物品时,对于每种物品i,只能选择装包或不装包,不能装入多次,也不能部分装入,因此成为0-1背包问题。 形式化描述为:给定n个物品,背包容量C >0,重量第i件物品的重量w[i]>0, 价值v[i] >0 , 1≤i≤n.要求找一n元向量(X1,X2,…,X n,), X i∈{0,1}, 使得∑(w[i] * Xi)≤C,且∑ v[i] * Xi达最大.即一个特殊的整数规划问题。 数学描述为: 求解最优值: 设最优值m(i,j)为背包容量为j、可选择物品为i,i+1,……,n时的最优值(装入包的最大价值)。所以原问题的解为m(1,C) 将原问题分解为其子结构来求解。要求原问题的解m(1,C),可从m(n,C),m(n-1,C),m(n-2,C).....来依次求解,即可装包物品分别为(物品n)、(物品n-1,n)、(物品n-2,n-1,n)、……、(物品1,物品2,……物品n-1,物品n)。最后求出的值即为最优值m(1,C)。 若求m(i,j),此时已经求出m(i+1,j),即第i+1个物品放入和不放入时这二者的最大值。 对于此时背包剩余容量j=0,1,2,3……C,分两种情况: (1)当w[i] > j,即第i个物品重量大于背包容量j时,m(i,j)=m(i+1,j) (2)当w[i] <= j,即第i个物品重量不大于背包容量j时,这时要判断物品i放入和不放入对m的影响。 若不放入物品i,则此时m(i,j)=m(i+1,j) 若放入物品i,此时背包 动态规划 一·动态规划法的发展及其研究内容 动态规划是运筹学的一个分支,是求解决策过程最优化的数学方法。20世纪50年代初美国数学家R.E.BELLMAN等人在研究多阶段决策过程的优化问题时,提出了著名的最优化原理,把多阶段问题转化为一系列的单阶段问题,逐个求解创立了解决这类过程优化问题的新方法——动态规划。1957年出版的他的名著《Dynamic Proggramming》,这是该领域的第一本著作。 动态规划问世以来,在经济管理·生产调度·工程技术和最优控制等方面得到了广泛的应用。例如最短路线·库存管理·资源分配·设备更新·组合·排序·装载等问题,采用动态规划法求解比用其他方法更为简便。 二·动态规划法基本概念 一个多阶段决策过程最优化问题的动态规划模型通常包括以下几个要素: 1.阶段 阶段(stage)是对整个过程的自然划分。通常根据时间顺序或是空间特征来划分阶段,对于与时间,空间无关的“静态”优化问题,可以根据其自然特征,人为的赋予“时段”概念,将静态问题动态化,以便按阶段的顺序解优化问题。阶段变量一般用k=1.2….n.表示。 1.状态 状态(state)是我们所研究的问题(也叫系统)在过个阶段的初始状态或客观条件。它应能描述过程的特征并且具有无后效性,即当某阶段的状态给定时,这个阶段以后的过程的演变与该阶段以前各阶段的状态无关。通常还要求状态是可以直接或者是间接可以观测的。描述状态的变量称为状态变量(State Virable)用s 表示,状态变量的取值集合称为状态集合,用S表示。变量允许取值的范围称为允许状态集合(set of admissble states).用x(k)表示第k阶段的状态变量,它可以是一个数或者是一个向量。用X(k)表示第k阶段的允许状态集合。 n 个阶段的决策过程有n+1个状态变量,x(n+1)是x(n)的演变的结果。 根据演变过程的具体情况,状态变量可以是离散的或是连续的。为了计算方便有时将连续变量离散化,为了分析的方便有时又将离散的变量视为连续的。 2.决策 当一个阶段的状态确定后,可以做出各种选择从而演变到下一阶段的某个状态,这种选择手段称为决策(decision),在最优控制问题中也称为控制(control)描述决策的变量称为决策变量(decision virable)。变量允许取值的范围称为允许决策集合(set of admissble 动态规划 装箱问题(01背包): 有一个箱子容量为VV(正整数,0≤V≤20000),同时有n个物品(0 完全背包的模板题面是这样的:设有n种物品,每种物品有一个重量及一个价值。但每种物品的数量是无限的,同时有一个背包,最大载重量为M,今从n种物品中选取若干件(同一种物品可以无限选取),使其重量的和小于等于M,而价值的和为最大。 完全背包 [无限量]的采摘药输入: 70 3 71 100 69 1 1 2 输出:140 每个数组在满足条件,可以遍历多次 01背包 实现代码:采药-传送门 输入: 70 3 71 100 69 1 1 2 输出:3 每个数组遍历一遍 题目描述 金明今天很开心,家里购置的新房就要领钥匙了,新房里有一间他自己专用的很宽敞的房间。更让他高兴的是,妈妈昨天对他说:“你的房间需要购买哪些物品,怎么布置,你说了算,只要不超过N元钱就行”。今天一早金明就开始做预算,但是他想买的东西太多了,肯定会超过妈妈限定的N元。于是,他把每件物品规定了一个重要度,分为5等:用整数1-5表示,第5等最重要。他还从因特网上查到了每件物品的价格(都是整数元)。他希望在不超过N元(可以等于N 元)的前提下,使每件物品的价格与重要度的乘积的总和最大。 设第jj件物品的价格为v_[j],重要度为w_[j],共选中了k件物品,编号依次为j_1,j_2,…,j_k,则所求的总和为: w_[j_k]v[j1]×w[j1]+v[j2]×w[j2]+…+v[jk]×w[jk]。 第七章动态规划 规划问题的最终目的就是确定各决策变量的取值,以使目标函数达到极大或极小。在线性规划和非线性规划中,决策变量都是以集合的形式被一次性处理的;然而,有时我们也会面对决策变量需分期、分批处理的多阶段决策问题。所谓多阶段决策问题是指这样一类活动过程:它可以分解为若干个互相联系的阶段,在每一阶段分别对应着一组可供选取的决策集合;即构成过程的每个阶段都需要进行一次决策的决策问题。将各个阶段的决策综合起来构成一个决策序列,称为一个策略。显然,由于各个阶段选取的决策不同,对应整个过程可以有一系列不同的策略。当过程采取某个具体策略时,相应可以得到一个确定的效果,采取不同的策略,就会得到不同的效果。多阶段的决策问题,就是要在所有可能采取的策略中选取一个最优的策略,以便得到最佳的效果。动态规划(dynamic programming)同前面介绍过的各种优化方法不同,它不是一种算法,而是考察问题的一种途径。动态规划是一种求解多阶段决策问题的系统技术,可以说它横跨整个规划领域(线性规划和非线性规划)。当然,由于动态规划不是一种特定的算法,因而它不象线性规划那样有一个标准的数学表达式和明确定义的一组规则,动态规划必须对具体问题进行具体的分析处理。在多阶段决策问题中,有些问题对阶段的划分具有明显的时序性,动态规划的“动态”二字也由此而得名。动态规划的主要创始人是美国数学家贝尔曼(Bellman)。20世纪40年代末50年代初,当时在兰德公司(Rand Corporation)从事研究工作的贝尔曼首先提出了动态规划的概念。1957年贝尔曼发表了数篇研究论文,并出版了他的第一部著作《动态规划》。该著作成为了当时唯一的进一步研究和应用动态规划的理论源泉。1961年贝尔曼出版了他的第二部著作,并于1962年同杜瑞佛思(Dreyfus)合作出版了第三部著作。在贝尔曼及其助手们致力于发展和推广这一技术的同时,其他一些学者也对动态规划的发展做出了重大的贡献,其中最值得一提的是爱尔思(Aris)和梅特顿(Mitten)。爱尔思先后于1961年和1964年出版了两部关于动态规划的著作,并于1964年同尼母霍思尔(Nemhauser)、威尔德(Wild)一道创建了处理分枝、循环性多阶段决策系统的一般性理论。梅特顿提出了许多对动态规划后来发展有着重要意义的基础性观点,并且对明晰动态规划路径的数学性质做出了巨大的贡献。 动态规划在工程技术、经济管理等社会各个领域都有着广泛的应用,并且获得了显著的效果。在经济管理方面,动态规划可以用来解决最优路径问题、资源分配问题、生产调度问题、库存管理问题、排序问题、设备更新问题以及生产过程最优控制问题等,是经济管理中一种重要的决策技术。许多规划问题用动态规划的方法来处理,常比线性规划或非线性规划更有效。特别是对于离散的问题,由于解析数学无法发挥作用,动态规划便成为了一种非常有用的工具。 动态规划可以按照决策过程的演变是否确定分为确定性动态规划和随机性动态规划;也可以按照决策变量的取值是否连续分为连续性动态规划和离散性动态规划。本教材主要介绍动态规划的基本概念、理论和方法,并通过典型的案例说明这些理论和方法的应用。 §7.1 动态规划的基本理论 1.1多阶段决策过程的数学描述 有这样一类活动过程,其整个过程可分为若干相互联系的阶段,每一阶段都要作出相应的决策,以使整个过程达到最佳的活动效果。任何一个阶段(stage,即决策点)都是由输入(input)、决策(decision)、状态转移律(transformation function)和输出(output)构成的,如图7-1(a)所示。其中输入和输出也称为状态(state),输入称为输入状态,输出称为输出状态。 u v a动态规划题列表 SANY GROUP system office room 【SANYUA16H-SANYHUASANYUA8Q8- 103 Stacking Boxes 108 Maximum Sum maximum 111 History Grading 116 Unidirectional TSP 147 Dollars 164 String Computer 166 Making Change 231 Testing the Catcher 348 Optimal Array Multiplication Sequence 357 Let Me Count The Ways 437 The Tower of Babylon 473 Raucous Rockers 481 What Goes Up 497 Strategic Defense Initiative 507 Jill Rides Again 531 Compromise 562 Dividing Coins 590 Always on the Run 607 Scheduling Lectures 620 Cellular Structure 624 CD 674 Coin Change 702 The Vindictive Coach 709 Formatting Text 711 Dividing up 714 Copying Books 787 Maximum Sub-sequence Product 825 Walking on the Safe Side 836 Largest Submatrix 882 The Mailbox Manufacturers Problem 907 Winterim Backpacking Trip 909 The BitPack Data Compression Problem 910 TV game 926 Walking Around Wisely 944 Happy Numbers 986 How Many? 988 Many paths, one destination 990 Diving For Gold 991 Safe Salutations 10003 Cutting Sticks 10029 Edit Step Ladders XXXX大学计算机学院实验报告计算机学院2017级软件工程专业 5 班指导教师 学号姓名2019年10 月21 日成绩 实验内容、上机调试程序、程序运行结果 System.out.println("选中的物品是第"); for(int i=1;i<=n;i++){ for(int j=1;j<=maxweight;j++){ //当前最大价值等于放前一件的最大价值 maxvalue[i][j] = maxvalue[i-1][j]; //如果当前物品的重量小于总重量,可以放进去或者拿出别的东西再放进去 if(weight[i-1] <= j){ //比较(不放这个物品的价值)和(这个物品的价值放进去加上当前能放的总重量减去当前物品重量时取i-1个物品是的对应重量时候的最高价值) if(maxvalue[i-1][j-weight[i-1]] + value[i - 1] > maxvalue[i-1][j]){ maxvalue[i][j] = maxvalue[i-1][j-weight[i-1]] + value[i - 1]; } } } } return maxvalue[n][maxweight]; } public static void main(String[] args) { int weight[] = {2,3,4,5}; int value[] = {3,4,5,7}; int maxweight = 8; System.out.println(knapsack(weight,value,maxweight)); } } 完成效果: 动态规划题目及其代码By LYLtim 1、数塔问题(tower.pas) 设有一个三角形的数塔,如下图所示。顶点结点称为根结点,每个结点有一个整数数值。从顶点出发,在每一结点可以选择向左走或是向右走,一起走到底层,要求找出一条路径,使路径上的值最大。 【样例输入】tower.in 5 {数塔层数} 13 11 8 12 7 26 6 14 15 8 12 7 13 24 11 【样例输出】tower.out max=86 【参考程序】 uses math; var n,i,j:byte; a:array[1..10,1..10]of word; f:array[1..10,1..10]of word; begin assign(input,'tower.in');reset(input); assign(output,'tower.out');rewrite(output); readln(n); for i:=1 to n do begin for j:=1 to i do read(a[i,j]); readln; end; fillchar(f,sizeof(f),0); for i:=1 to n do f[n,i]:=a[n,i]; for i:=n-1 downto 1 do for j:=1 to i do f[i,j]:=max(f[i+1,j],f[i+1,j+1])+a[i,j]; writeln('max=',f[1,1]); close(input);close(output); end. 2、拦截导弹(missile.pas) 某国为了防御敌国的导弹袭击,发展出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷:虽然它的第一发炮弹能够到达任意的高度,但是以后每一发炮弹都不能高于前一发的高度。某天,雷达捕捉到敌国的导弹来袭。由于该系统还在试用阶段,所以只有一套系统,因此有可能不能拦截所有的导弹。 输入导弹依次飞来的高度(雷达给出的高度数据是不大于30000的正整数), 动态规划习题 Document serial number【NL89WT-NY98YT-NC8CB-NNUUT-NUT108】 动态规划专题分类视图数轴动规题: 题1.2001年普及组第4题--装箱问题 【问题描述】有一个箱子容量为V(正整数,0≤V≤20000),同时有n个物品(0 对于100%的数据,砝码的种类n满足:1≤n≤100; 对于30%的数据,砝码的总数量C满足:1≤C≤20; 对于100%的数据,砝码的总数量C满足:1≤C≤100; 对于所有的数据,砝码的总重量W满足:1≤W≤400000; 题3.石子归并-szgb.pas 【问题描述】有一堆石头质量分别为W1,W2,…,Wn.(Wi≤10000),将石头合并为两堆,使两堆质量的差最小。 【输入】输入文件szgb.in的第一行只有一个整数n(1≤n≤50),表示有n堆石子。接下去的n行,为每堆石子质量。 【输出】输出文件szgb.out的只有一行,该行只有一个整数,表示最小的质量差. 【样例输入】 5 5 8 13 27 14 【样例输出】 3 题4.补圣衣 【问题描述】有四个人,每人身上的衣服分别有s1,s2,s3和s4处破损,而且每处破损程度不同,破损程度用需修好它用的时间表示 (A1...As1,B1...Bs2,C1...Cs3,D1...Ds4)。不过你可以同时修补2处破损。但是这2处破损,只能是同一件衣服上的。就是说你只能同时修补一件衣服,修好了,才能修补下一件。 【输入】本题包含5行数据:第1行,为s1,s2,s3,s4(1≤s1,s2,s3,s4≤20) 第2行,为A1...As1共s1个数,表示第一件衣服上每个破损修好它所需的时间 第3行,为B1...Bs2共s2个数,表示第二件衣服上每个破损修好它所需的时间 第4行,为C1...Cs3共s3个数,表示第三件衣服上每个破损修好它所需的时间 第5行,为D1...Ds4共s4个数,表示第四件衣服上每个破损修好它所需的时间 (1≤A1...As1,B1...Bs2,C1...Cs3,D1...Ds4≤60) 【输出】输出一行,为修好四件衣服所要的最短时间。 【样例输入】 1213 5 43 6 243 【样例输出】 20 题5.光光的作业homework.pas/homework.exe 【问题描述】光光上了高中,科目增多了。在长假里,光光的老师们都非常严厉,都给他布置了一定量的作业。假期里,光光一共有的时间是k小时。在长假前,老师们一共给光光布置了n份作业,第i份作业需要的时间是ti小时。但是由于老师们互相不01背包问题动态规划详解
POJ 动态规划题目列表
动态规划之01背包问题(最易理解的讲解)
算法分析与程序设计动态规划及回溯法解背包问题
解0-1背包问题的动态规划算法
动态规划练习试题和解答
01背包问题动态规划详解及C++代码
0-1背包问题动态规划详解及代码
动态规划题库
0-1背包问题动态规划详解及代码
动态规划之-0-1背包问题及改进
动态规划法求解生产与存储问题
动态规划试题
动态规划习题
uva动态规划题列表
实验报告:动态规划---0-1背包问题)
动态规划题目和代码
动态规划习题完整版