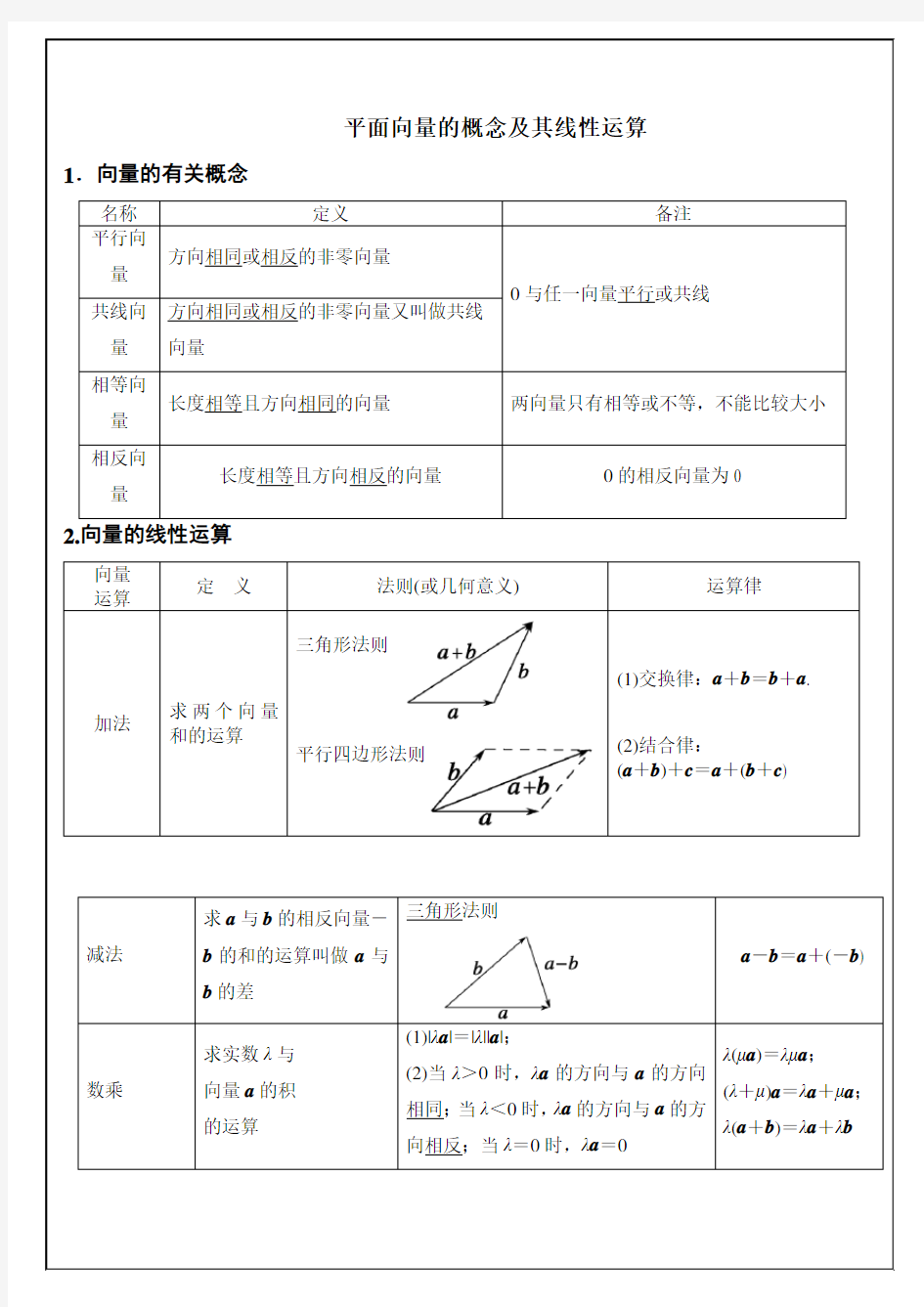

平面向量的概念及其线性运算1.向量的有关概念
名称定义备注
平行向
量方向相同或相反的非零向量
0与任一向量平行或共线
共线向
量方向相同或相反的非零向量又叫做共线向量
相等向
量
长度相等且方向相同的向量两向量只有相等或不等,不能比较大小相反向
量
长度相等且方向相反的向量0的相反向量为0
2.向量的线性运算
向量
运算
定义法则(或几何意义)运算律
加法求两个向量
和的运算
三角形法则
平行四边形法则
(1)交换律:a+b=b+a.
(2)结合律:
(a+b)+c=a+(b+c)
减法求a与b的相反向量-
b的和的运算叫做a与
b的差
三角形法则
a-b=a+(-b)
数乘求实数λ与
向量a的积
的运算
(1)|λa|=|λ||a|;
(2)当λ>0时,λa的方向与a的方向
相同;当λ<0时,λa的方向与a的方
向相反;当λ=0时,λa=0
λ(μa)=λμa;
(λ+μ)a=λa+μa;
λ(a+b)=λa+λb
P
C
A
B
Q 【例4】若点O 是△ABC 所在平面内的一点,且满足|OB →-OC →|=|OB →+OC →-2OA →
|,则△ABC 的形 状为________.
【例5】在△ABC 中,E ,F 分别为AC ,AB 的中点,BE 与CF 相交于G 点,设AB →=a ,AC →
=b , 试用a ,b 表示AG →
.
【课堂巩固】
1. 如图,设P 、Q 为△ABC 内的两点,且2155AP AB AC =+u u u r u u u r u u u r , AQ uuu r =23AB u u u r +14
AC u u u
r ,则△ABP 的面积与△ABQ
的面积之比为( )
A .1
5 B .
45 C . 14 D .13
3.如图,在△ABC 中,已知2AB =,3BC =,60ABC ∠=?,AH BC ⊥于H ,M 为AH 的中点,若
AM AB BC λμ=+u u u u r u u u r u u u r
,则λμ+= .
3、向量a ,b ,c 在正方形网格中的位置如图所示.若c =λa +μb (λ,μ∈R),则
λ
μ
=_________.
3、ABC ?的外接圆的圆心为O ,两条边上的高的交点为H ,)(OC OB OA m OH ++=,则实数m 的值是多少?
A
B
C
H
?M
b
c
a
4、在△ABC 中,过中线AD 的中点E 任作一条直线分别交AB ,AC 于M ,N 两点,若AM →=xAB →, AN →=yAC →
, 求y x +4的最小值。
5、如图,已知2,1,4,OA OB OC OA OB ===u u u r u u u r u u u r u u u r u u u r 与的夹角为1200,OA OC u u u r u u u r 与的夹角为300
,用,OA OB OC u u u r u u u r u u u r 表示.
6、在平面上,12AB AB ⊥u u u r u u u u r ,121OB OB ==u u u r u u u u r ,12AP AB AB =+u u u r u u u r u u u u r .若1
2OP
A .50,2??
? ?? B .57,22?? ? ?? C .5,22?? ? ?? D .7,22?? ? ??
7.已知直角梯形ABCD 中,AD //BC ,0
90ADC ∠=,2,1AD BC ==,P 是腰DC 上的动点,则3PA PB +u u u r u u u r
的最小值为____________
8.O 是平面上一定点,,,A B C 是平面上不共线的三个点,动点P 满足(),[0,),||||
AB AC OP OA AB AC λλ=++∈+∞u u u r u u u r
u u u r u u u r u u u r u u u r
则P 的轨迹一定通过△ABC 的 A .外心
B .内心
C .重心
D .垂心
B
C
A
O
G
C
O
B
A
9.如右图,平面内的两条相交直线OP 1和OP 2将该平面分割成四个部分Ⅰ,Ⅱ,Ⅲ,Ⅳ(不包含边 界).设OP →=mOP 1→+nOP 2→
,且点P 落在第Ⅲ部分,则实数m ,n 满足( ) A .m >0,n >0 B .m >0,n <0 C .m <0,n >0 D .m <0,n <0
8.如图, O 是△ABC 外任一点,若1()
3OG OA OB OC =++u u u r u u u r u u u r u u u r ,求证:G 是△ABC 重心
9.已知:如图,点L 、M 、N 分别为△ABC 的边BC 、CA 、AB 上的点,且BL BC =l ,CM CA =m ,AN
AB =n , 若AL
→+BM →+CN →=0.求证:l =m =n .
10、在平行四边形ABCD 中,E 和F 分别是边CD 和BC 的点.且
1BF a FC a =-,1DE b
EC b
=
-,若 AC AE AF λμ=+u u u r u u u r u u u r
,其中λ,μ∈R ,则λμ+= .
F
E
D
C
B
A
11、如图所示,OM AB ∥,点P 在由射线OM 、线段OB 及AB 的延长线围成的阴影区域内(不含边界)运动,且OP xOA yOB =+u u u r
u u u r
u u u r
,则x 的取值范围是 ;当1
2
x =-时,y 的取值范围是 .
O
B
M
A
P
12、如图,两块斜边长相等的直角三角板拼在一起.若AD xAB y AC =+u u u r
u u u r
u u u r
, 则x = , y = .
13.已知点P 在△ABC 所在的平面内,若2PA u u u r +3PB u u u r +4PC u u u r =3AB u u u r
,则△P AB 与△PBC 的面积的
比值为________.
14.如图,在△ABC 中,∠A =60°,∠A 的平分线交BC 于D ,若AB =4,且AD u u u r =14AC u u u r +λAB u u u r
(λ∈
R ),则AD 的长为________.
15.在△ABC 中,a ,b ,c 分别是角A ,B ,C 所对的边,且3a BC u u u r +4b CA u u u r +5c AB u u u r
=0,则a ∶b ∶c
=________.
16、如图,在边长为1的正三角形ABC 中,E ,F 分别是边AB ,AC 上的点,若AE u u u r =m AB u u u r ,AF u u u r
= n AC u u u r
,其中m ,n ∈(0,1).设EF 的中点为M ,BC 的中点为N .
(1)若A ,M ,N 三点共线,求证:m =n ;
(2)若m +n =1,求|MN u u u u r
|的最小值.
60?
45?
E
D
B
C
A
【课后思考】
1.如图,正六边形ABCDEF 中,P 是△CDE 内(包括边界)的动点.设AP u u u r =αAB u u u r +βAF u u u r
(α,β∈R ),
则α+β的取值范围是________.
2.设G 为△ABO 的重心,过G 的直线与边OA 和OB 分别交于P 和Q ,已知,
△OAB 与△OPQ 的面积分别为S 和T ,
(1)求y=f(x)的解析式及定义域; (2)求的取值范围。
+9.5共线向量与共面向量 一、知识点 1、空间向量的定义 2、空间向量的加减与数乘运算 3、平行六面体的定义和性质 4、共线向量的定义或平行向量的概念、向量与平面平行(共面)意义及它们的表示 法 5、共线向量定理及推论、空间直线的向量参数方程和线段中点的向量公式 6、共面向量及推论、空间平面的向量参数方程(即点在平面内的充要条件) 7、空间向量基本定理及其推论 8、空间向量夹角和模的概念和表示方法 9、两个向量数量积的概念、性质和计算方法及运算律 10、两个向量的数量积的主要用途,用它解决立体几何中的一些简单问题。 二、课时安排5课时 第一课时:空间向量及其加减与数乘运算 教学目标: 1、理解空间向量的概念,掌握空间向量的几何表示法和字母表示法; 2、会用图形说明空间向量的加法、减法和数乘向量及它们的运算律; 3、了解平行六面体的定义和性质; 4、能运用空间向量的运算意义及运算律解决简单的立体几何中的问题。 教学重点: 空间向量的加法、减法和数乘运算及运算律 教学难点: 应用向量解决立体几何问题 教学过程: 复习回顾 在第五章《平面向量》中,我们学习了有关平面向量的一些知识,什么叫做向量?向量是怎样表示的呢? 既有大小又有方向的量叫向量.向量的表示方法有: ①用有向线段表示; ②用字母a、b等表示; ③用有向线段的起点与终点字母:AB. 数学上所说的向量是自由向量,也就是说在保持向量的方向、大小的前提下可以将向
量进行平移,由此我们可以得出向量相等的概念,请同学们回忆一下. 长度相等且方向相同的向量叫相等向量. 学习了向量的有关概念以后,我们学习了向量的加减以及数乘向量运算: ⒈向量的加法: ⒉向量的减法: ⒊实数与向量的积: 实数λ与向量a的积是一个向量,记作λa,其长度和方向规定如下: (1)|λa|=|λ||a| (2)当λ>0时,λa与a同向; 当λ<0时,λa与a反向; 当λ=0时,λa=0. 关于向量的以上几种运算,请同学们回忆一下,有哪些运算律呢? 向量加法和数乘向量满足以下运算律 加法交换律:a+b=b+a 加法结合律:(a+b)+c=a+(b+c) 数乘分配律:λ(a+b)=λa+λb 今天我们将在第五章平面向量的基础上,类比地引入空间向量的概念、表示方法、相同或向等关系、空间向量的加法、减法、数乘以及这三种运算的运算率,并进行一些简单的应用.请同学们阅读课本P26~P27. 探索研究 1、空间向量的概念 ⑴定义:在空间,我们把具有大小和方向的量叫做向量。 注:①“空间的一个平移就是一个向量”,即“将图形上的所有点沿相同方向移动相同的长度”。 ②向量不能比较大小。 ⑵向量的表示: ①几何表示:用有向线段表示 ②字母表示:用黑体小写英文字母表示
培优点8 向量共线定理的应用 【方法总结】 向量共线定理可以解决一些向量共线,点共线问题,也可由共线求参数;对于线段的定比分点问题,用向量共线定理求解则更加简洁. 【典例】1 (1)若点M 是△ABC 所在平面内一点,且满足|3AM →-A B →-AC →|=0,则△ABM 与△ ABC 的面积之比等于( ) A.34 B.14 C.13 D.12 【答案】 C 【解析】 ∵|3AM →-AB →-AC →|=0,∴3AM →-AB →-AC →=0,∴AB →+AC →=3AM →. 设BC 的中点为G ,则AB →+AC →=2AG →, ∴3AM →=2AG →,即AM →=23 AG →, ∴点M 在线段AG 上,且|A M →||A G →| =23. ∴S △ABM S △ABG =|AM →||AG →|=23,易得S △ABG S △ABC =|BG →||BC →| =12, ∴ S △ABM S △ABC =S △ABM S △ABG ·S △ABG S △ABC =23×12=13, 即△ABM 与△ABC 的面积之比等于13 . (2)在△ABC 中,AN →=12AC →,P 是BN 上的一点,若AP →=mAB →+38 AC →,则实数m 的值为________. 【答案】 14
【解析】 方法一 ∵B ,P ,N 三点共线, ∴BP →∥PN →,∴存在实数λ,使得BP →=λPN →(λ>0), ∴AP →-AB →=λ(AN →-AP →), ∵λ>0,∴AP →=11+λ AB →+λ1+λ AN →. ∵AN →=12AC →,AP →=mAB →+38 AC →, ∴AP →=mAB →+34 AN →, ∴????? 11+λ=m , λ1+λ=34,解得????? λ=3,m =14. 方法二 ∵AN →=12AC →,AP →=mAB →+38 AC →, ∴AP →=mAB →+34 AN →. ∵B ,P ,N 三点共线,∴m +34=1,∴m =14 . 【典例】2 (1)(2020·河北省石家庄一中质检)在△ABC 中,D 为线段AC 的中点,点E 在边 BC 上,且BE =12 EC ,AE 与BD 交于点O ,则AO →等于( ) A.12AB →+14 AC → B.14AB →+14AC → C.14AB →+12 AC → D.12AB →+12 AC → 【答案】 A 【解析】 如图,设AO →=λAE →(λ>0),
平面向量中“三点共线向量定理”探究 三点共线定理在教材中没有作为定理使用,但在各级考试中却应用广泛,笔者尝试通过 聚焦结论,优化思路,多维度揭示定理的价值所在. () 0.a b b a b a b λλ≠=r r r r r r r r 向量共线定理:对平面内的任意两个向量 、 , // 的充要条件是:存在唯一的 实数 ,使由该定理可以得到平面内三点共线定理: ()121212+= OA OB OP OP OA OB R λλλλλλ=+∈u u u r u u u r u u u r u u u r u u u r u u u r 三点共线定理:已知平面内一组基底 , 及任一向量 ,, , 则A ,B ,P 三点共线,当且仅当 1. ()() ()1122121,,1,=1,,+= A B P AP AB OP OA OB OA OP OA O OP OA O B B λλλλλλλλλλλλλ=?-=-?=-+-=+=u u u r u u u r u u u r u u u r u u u r u u u u u u r u u u r u u u r u u u r u u u r u u u r r 证明:如图 , 三点共线,当且仅当有唯一一个实数 , ,且使令则 1. ()()()()()() 1212112212=1,1;2+= OA OP OP OA OB OP OA OB OA AP AB OB OP OA OB λλλλλλλλλλλλλλ?-===-+?-=-?=+u u u r u u u r u u u r u u u r u u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u u u u r r u ur 的系数之和等于1 即为向量,的变化而变化的定理特.如图, 且1征:向量, 的系数点P 的位置是随着令 , 当点P 在线段AB 内()() ()() ()() 12121212121,1,,=10,10,1=1,01,0=10,,0=0=110 =1=10 1. λλλλλλλλλλλλλλλλλλλλλλλλλ-∈=∈-∈-∞=∈+∞<-<<>∈+∞=∈-∞-===-===此时 此时,0,当点P 在线段AB 的延长线上时, ,点P 在线段AB 反向延长线上时, ,当点P 与点A , ,当点P 与点B 重合时, 时此时此时此时,, ,重合时, 111AP PB OP OA OB λλλλ ?==+++u u u r u u u r u u u r u u u r u u u r 推论:在OAB 中,P 为直线AB 上的一点,且则 O 1()
05—平面向量的概念、运算及平面向量基本定理 突破点(一)平面向量的有关概念 知识点:向量、零向量、单位向量、平行向量、相等向量、相反向量 考点 平面向量的有关概念 [典例]⑴设a , b 都是非零向量,下列四个条件中,使 向=而成立的充分条件是( ) A . a =- b B . a // b C . a = 2b D . a // b 且 |a|= |b| ⑵设a o 为单位向量,下列命题中:①若 a 为平面内的某个向量,贝U a = |a| a o ;②若a 与a o 平行,则 a = |a|a o ;③若a 与a o 平行且|a|= 1,则a = a o .假命题的个数是( ) A . o B . 1 C . 2 D . 3 [解析]⑴因为向量合的方向与向量a 相同,向量£的方向与向量b 相同,且£,所以向量a 与 |a| |b| |a| |b| 向量b 方向相同,故可排除选项 A , B , D.当a = 2b 时,a =警=b ,故a = 2b 是耳=g 成立的充分条件. |a| |2b| |b| |a| |b| (2)向量是既有大小又有方向的量, a 与|a|a o 的模相同,但方向不一定相同,故①是假命题;若 a 与a o 平行,则a 与a o 的方向有两种情况:一是同向,二是反向,反向时 a =- |a|a o ,故②③也是假命题.综上 所述,假命题的个数是 3. [答案](1)C (2)D _ _[易错提醒」_____________ _____________ 厂7i)两个向量不能比较大小,只可以判断它们是否相等,但它们的模可以比较大小 […(2)大小与方向是向量的两个要素?j 分别是向量的代数特征与几何特征; (3)向量可以自由平移,任意一组平行向量都可以移到同一直线上. 突破点(二)平面向量的线性运算 1. 向量的线性运算: 加法、减法、数乘 2. 平面向量共线定理: 向量b 与a(a ^ o )共线的充 要条件是有且只有一个实数 人使得b = 1 [答案](1)D ⑵1 —…_[方法技巧丄—――――_—_ _―_—_ _―_……_ _―_…_ _―_…_ _―_…_ _―_…「 i 1.平面向量的线性运算技巧: ⑴不含图形的情况:可直接运用相应运算法则求解. ⑵含图形的情况:将它们转化到 ] 三角形或平行四边形中,充分利用相等向量、相反向量、三角形的中位线等性质,把未知向量用已知向量表示岀来求解. 2?利用平面向量的线性运算求参数的一般思路: (1)没有图形的准确作出图形,确定每一个点的位置. (2)利用平行四 边形法则或三角形法贝U 进行转化丄转化为要求的向量形式._ _ (3) 比较,观察可知所求.__________ 考点二 平面向量共线定理的应用 [例2Lu 设两个非零向J a 和b 不共鈿 平面向量的线性运算 …uuur …"uLu r 考点一 ~~uuur ----- u uur [例 1] (1)在厶 ABC 中,AB = c , AC = b.若点 D 满足 BD = 2 DC 12 5 2 A.3b + 3C B.gC — 3b 2 1 2 1 C.gb — 3c D.gb + 3C uuuu 1 uuur ⑵在△ ABC 中,N 是AC 边上一点且 AN = NC , P 是BN 上一点, 数m 的值是 ______________ . uuur umr [解析](1)由题可知BC = AC - uuur + BD = c + 2 1 —c)= 3b + §c,故选 D. uuuu 1 uuur (2)如图,因为AN = 2 NC ,所以 uuur 2 uuuu m AB + 3 AN ?因为B ,P ,N 三点共线, ―uuur ,贝U AD =( ) UULT uuur 2 uuur 若 AP = m AB + 9 AC ,则实 2 uuir 2 uuir uur uuur uuur uuur UULT AB = b — c , '^BD = 2 DC ,「.BD = 3 BC = 3(b — c),则 AD = AB uuuu 1 uuur AN = 3 AC ,所以 2 所以m +3= 1,则 UULT uuur 2 uuur AP = m AB + 9 AC = 1 m = 3.
向量共线定理及其扩展应用 例题1 设两个非零向量a与b不共线。 (1)若AB=a+b,=2a+8b,=3(a-b), 求证:A,B,D三点共线; (2)试确定实数k,使k a+b和a+k b共线。 (1)证明:∵AB=a+b,=2a+8b,=3(a-b),∴BD=+=2a+8b+3(a-b) =2a+8b+3a-3b=5(a+b)=5AB, ∴AB,BD共线。
又∵它们有公共点B ,∴A ,B ,D 三点共线。 (2)假设k a +b 与a +k b 共线, 则存在实数λ,使k a +b =λ(a +k b ), 即(k -λ)a =(λk -1)b 。 又a ,b 是两个不共线的非零向量, ∴k -λ=λk -1=0。 消去λ,得k 2-1=0,∴k =±1。 总结提升: (1)证明三点共线,通常转化为证明由这三点为起点、终点的两个向量共线,向量共线定理是解决向量共线问题的依据。 (2)注意向量共线与三点共线的区别与联系,当两向量共线且有公共点时,才能得出三点共线。 (3)向量a ,b 共线是指存在不全为零的实数λ1,λ2,使λ1a +λ2b =0成立;若λ1a +λ2b =0,当且仅当λ1=λ2=0时成立,则向量a ,b 不共线。 【三点共线定理】 已知,PA PB 为平面内两个不共线的向量,设PC xPA yPB =+,则A ,B ,C 三点共线的充要条件为x +y =1。 特别地有:当点P 在线段AB 上时,x>0,y>0; 当点P 在线段AB 之外时,xy<0。 证明:充分性 如图,因为A ,B , C 三点共线,设AC AB λ=,则 ()=(1)PC PA AC PA AB PA PB PA PA PB λλλλ=+=+=+--+, 又由PC xPA yPB =+,所以1x y λ λ=-??=? ,所以x+y=1。 必要性
向量三点共线定理及其扩展应用详解 一、平面向量中三点共线定理的扩展及其应用 一、问题的提出及证明. 1、向量三点共线定理:在平面中A 、B 、C 三点共线的充要条件是: .O A xOB yOC =+(O 为平面内任意一点),其中1x y +=. 那么1x y +<、1x y +>时分别有什么结证?并给予证明. 结论扩展如下:1、如果O 为平面内直线BC 外任意一点,则 当1x y +<时 A 与O 点在直线BC 同侧,1x y +>时, A 与O 点在直线BC 的异侧,证明如下: 设 O A xOB yOC =+ 且 A 与B 、C 不共线,延长OA 与直线BC 交于A 1点 设 1O A O A λ=(λ≠0、λ≠1)A 1与B 、C 共线 则 存在两个不全为零的实数m 、n 1 O A m O B n O C =+ 且1m n += 则 OA mOB nOC λ=+ m n OA OB OC λ λ ?=+ m x λ ∴= 、n y λ = 1 m n x y λ λ ++= = (1)1λ> 则 1x y +< 则 11 1 OA OA OA λ = < ∴A 与O 点在直线BC 的同侧(如图[1]) (2)0λ<,则1 01x y λ +=<<,此时OA 与1OA 反向 A 与O 在直线BC 的同侧(如图[2]) 图[2] B C A 1 O A O A 1 B C A 图[1]
(3)1o λ<<,则1x y +> 此时 111 OA OA OA λ => ∴ A 与O 在直线BC 的异侧(如图[3]) 图[3] 2、如图[4]过O 作直线平行AB , 延长BO 、AO 、将AB 的O 侧区 域划分为6个部分,并设OP xOA yOB =+, 则点P 落在各区域时,x 、y 满足的条件是: (Ⅰ)区:0001x y x y ??<+??>??<+?? ????-<+
平面向量基本定理及坐标表示强化训练 姓名__________ 一、选择题 1.下列向量给中,能作为表示它们所在平面内所有向量的基底的是 ( ) A .e 1=(0,0), e 2 =(1,-2) ; B .e 1=(-1,2),e 2 =(5,7); C .e 1=(3,5),e 2 =(6,10); D .e 1=(2,-3) ,e 2 =)4 3,2 1(- 2. 若AB u u u r =3a, CD u u u r =-5a ,且||||AD BC =u u u r u u u r ,则四边形ABCD 是 ( ) A .平行四边形 B .菱形 C .等腰梯形 D .不等腰梯形 3. 在△ABC 中,已知D 是AB 边上一点,若AD → =2DB →, CD → =13CA →+λCB → ,则λ 等于() A. 23 B. 13 C. 13- D. 2 3- 4.已知向量a 、b ,且AB u u u r =a +2b ,BC u u u r = -5a +6b ,CD u u u r =7a -2b ,则一定共线的三点是 ( ) A .A 、 B 、D B .A 、B 、 C C .B 、C 、 D D .A 、C 、D 5.如果e 1、 e 2是平面α内两个不共线的向量,那么在下列各说法中错误的有 ( )①λe 1+μe 2(λ, μ∈R)可以表示平面α内的所有向量; ②对于平面α中的任一向量a ,使a =λe 1+μe 2的λ, μ有无数多对; ③若向量λ1e 1+μ1e 2与λ2e 1+μ2e 2共线,则有且只有一个实数k ,使λ2e 1+μ2e 2=k (λ1e 1+μ1e 2); ④若实数λ, μ使λe 1+μe 2=0,则λ=μ=0. A .①② B .②③ C .③④ D .仅② 6.过△ABC 的重心任作一直线分别交AB 、AC 于点D 、E ,若AD u u u r =x AB u u u r ,AE u u u r =y AC u u u r ,xy ≠0,则11 x y +的值 为 ( ) A .4 B .3 C .2 D .1 7.若向量a =(1,1),b =(1,-1) ,c =(-2,4) ,则c = ( ) A .-a +3b B .3a -b C .a -3b D .-3a +b 二、填空题 8.作用于原点的两力F 1 =(1,1) ,F 2 =(2,3) ,为使得它们平衡,需加力F 3= ; 9.若A (2,3),B (x , 4),C (3,y ),且AB u u u r =2AC u u u r ,则x = ,y = ; 10.已知A (2,3),B (1,4)且12 AB u u u r =(sin α,cos β), α,β∈(-2π,2 π),则α+β= *11.已知 a =(1,2) , b =(-3,2),若k a +b 与a -3b 平行,则实数k 的值为
平面向量中“三点共线定理”妙用 对平面内任意的两个向量b a b b a //),0(,≠的充要条件是:存在唯一的实数λ,使b a λ= 由该定理可以得到平面内三点共线定理: 三点共线定理:在平面中A 、B 、P 三点共线的充要条件是:对于该平面内任意一点的O ,存在唯一的一对实数x,y 使得:OP xOA yOB =+且1x y +=. 特别地有:当点P 在线段AB 上时,0,0x y >> 当点P 在线段AB 之外时,0xy < 例1已知等差数列{a n }的前n 项和为S n ,若1200OB a OA a OC =+,且A 、B 、C 三点共线,(设 直线不过点O ),则S 200=( ) A .100 B .101 C .200 D .201 解:由平面三点共线的向量式定理可知:a 1+a 200=1,∴1200200200() 1002 a a S += =,故选A. 例2 已知P 是ABC ?的边BC 上的任一点,且满足R y x AC y AB x AP ∈+=.,,则y x 4 1+的最小值是 解:点P 落在ABC 的边BC 上 ∴B ,P,C 三点共线 x>0,y>040,0y x x y ∴ >> 由基本不等式可知:4424y x y x x y x y +≥?=,取等号时4y x x y =224y x ∴=2y x ∴=±0,0x y >> 2y x ∴=1x y +=12 ,33 x y ∴==,符合 所以 y x 4 1+的最小值为9
例3如图,在△ABC中,1 3 AN NC =,点P是BC上的一点,若 2 11 AP mAB AC =+,则实数m的值为() A. 9 11 B. 5 11 C. 3 11 D. 2 11 解:,, B P N三点共线,又228 4 111111 AP mAB AC mAB AN mAB AN =+=+?=+ 8 1 11 m ∴+= 3 11 m ∴=,故选C 例4如图,在△ABC中,点O是BC的中点,过点O的直线分别交直线AB、AC于不同的两点M、N,若AB=m AM,AC=n AN,则m+n的值为. 解:因为O是BC的中点,故连接AO,如图4,由向量加法的平行四边形法则可知: 1 () 2 AO AB AC ∴=+m AB AM =,AC nAN =又,, M O N三点共线, ∴由平面内三点共线定理可得:1 22 m n +=2 m n ∴+= 例5 如图所示:点是△的重心,、分别是边、上的动点,且、、三点共线. 设,,证明:是定值; 证明:因为G是OAB的重心,211 ()() 323 OG OA OB OA OB ∴=?+=+ 又,, P G Q三点共线,111 33 x y ∴+= 11 3 x y ∴+= 11 x y ∴+为定值3 G OAB P Q OA OB P G Q OA x OP=OB y OQ= y x 1 1 +
平面向量基本定理 一.教学目标: 了解平面向量基本定理,理解平面向量的坐标概念,会用坐标形式进行向量的加法、数乘的运算,掌握向量坐标形式的平行的条件; 教学重点: 用向量的坐标表示向量加法、减法、数乘运算和平行. 二.课前预习 1.已知=(x,2),=(1,x),若//,则x 的值为 ( ) A 、2 B 、 2- C 、 2± D 、 2 2.下列各组向量,共线的是 ( ) ()A (2,3),(4,6)a b =-=r r ()B (2,3),(3,2)a b ==r r ()C (1,2),(7,14)a b =-=r r ()D (3,2),(6,4)a b =-=-r r 3.已知点)4,3(),1,3(),4,2(----C B A ,且?=?=2,3,则=MN ____ 4.已知点(1,5)A -和向量=(2,3),若=3,则点B 的坐标为 三.知识归纳 1. 平面向量基本定理:如果12,e e u r u u r 是同一平面内的两个___________向量,那么对于这一平面内的任意向量a r ,有且只有一对实数12,λλ,使1122a e e λλ=+r u r u u r 成立。其中12,e e u r u u r 叫做这一平面的一组____________,即对基底的要求是向量___________________; 2.坐标表示法:在直角坐标系内,分别取与x 轴,y 轴方向相同的两个单位向量i ?,j ? 作基底, 则对任一向量a ?,有且只有一对实数x ,y ,使j y i x a ???+=、就把_________叫做向量a ? 的坐标,记作____________。 3.向量的坐标计算:O (0,0)为坐标原点,点A 的坐标为(x ,y ),则向量的坐标为=___________,点1P 、2P 的坐标分别为(1x ,1y ),2P (2x ,2y ),则向量21P P 的坐标为
平面向量中“三点共线定理”妙用 对平面内任意的两个向量b a b b a //),0(, 的充要条件是:存在唯一的实数 ,使b a 由该定理可以得到平面内三点共线定理: 三点共线定理:在平面中A 、B 、P 三点共线的充要条件是:对于该平面内任意一点 的O ,存在唯一的一对实数x,y 使得:OP xOA yOB u u u v u v u u u v 且1x y 。 特别地有:当点P 在线段AB 上时,0,0x y 当点P 在线段AB 之外时,0xy 笔者在经过多年高三复习教学中发现,运用平面向量中三点 共线定理与它的两个推广形式解决高考题,模拟题往往会使会问题的解决过程变得十分简单!本文将通过研究一些高考真题、模拟题和变式题去探究平面向量中三点共线定理与它的两个推广形式的妙用,供同行交流。 例1(06年江西高考题理科第7题)已知等差数列{a n }的前n 项和为S n ,若 1200OB a OA a OC u u u r u u u r u u u r ,且A 、B 、C 三点共线, (设直线不过点O ),则S 200=( ) A .100 B .101 C .200 D .201 解:由平面三点共线的向量式定理可知:a 1+a 200=1,∴1200200200() 1002 a a S ,故选A 。 点评:本题把平面三点共线问题与等差数列求和问题巧妙地结合在一起,是一道经典的高考题。 例2 已知P 是ABC 的边BC 上的任一点,且满足R y x AC y AB x AP .,,则y x 4 1 的最小值是 解:Q 点P 落在ABC V 的边BC 上 B ,P,C 三点共线 AP xAB yAC u u u r u u u r u u u r Q 1x y 且x>0,y>0 14141444()1()()145y x y x x y x y x y x y x y x y Q x>0,y>040,0y x x y 由基本不等式可知:4424y x y x x y x y ,取等号时
平面向量共线问题的探讨 摘要:平面向量的平行与垂直是高中数学新课程向量部分的重要内容,本文旨在对平面向量平行(即共线)相关定理进行推广,得到两个更加具有一般性的结论,并举例说明它们的应用,使问题的解决更简捷。 关键词:平面向量、共线定理、推广、应用。 平面向量的共线,这部分内容比较重要,在各种考试中也频频出现,教材上就两个向量共线已给出两个定理: (1) 向量()≠与向量共线?存在唯一实数λ,使得a b λ=成 立。 (2) 向量()11,y x a =与向量()22,y x b =,则∥?01221=-y x y x 在此基础之上,笔者对向量共线问题,再做进一步探讨及推广,若有不当之处,请各位老师指正。对于定理(2)给出的结论,向量,b 的基底是单位正交向量:,j ,下面我们给出的结论中,涉及到的基底不一定是单位正交向量:i ,,而是任意一组基底:1e 与2e ,它更具有一般性。 推论1:若1e ,2e 是不共线的两个向量,2111e y e x a +=,2212e y e x +=,与b 共线 ?01221=-y x y x 证明:与b 共线,当且仅当=λ, ?2111e y e x +() 2212e y e x +=λ ?2111e y e x +2212e y e x λλ+= 由平面向量基本定理得:???==2121y y x x λλ ①2y ?-②2x ?消去λ得:01221=-y x y x ① ②
所以,a 与b 共线?01221=-y x y x 。 上述结论还可以进一步推广为: 推论2:对于任意向量1e ,2e ,若2111e y e x +=,2212e y e x +=,那么与共线 ?1e ∥2e 或01221=-y x y x 证明:分两种情况: 1e 与2e 平行和1e 与2e 不平行 (1)1e 与2e 平行时,结论成立。 (2)1e 与2e 不平行时,a 与共线,当且仅当a =b λ, 有:2111e y e x +() 2212e y e x +=λ 即:2111e y e x +2212e y e x λλ+= 由平面向量基本定理得:???==2121y y x x λλ ①2y ?-②2x ?消去λ得:01221=-y x y x 即:当且仅当01221=-y x y x 时,与b 共线 综合(1)(2)知:与b 共线?1e ∥2e 或01221=-y x y x 上述两个结论,尤其第二个,对向量共线的问题阐述得比较完备。 在高考、模拟考、联考等一系列考试中,常出现向量共线的问题,下面是两个结论针对一些考题的应用,所有例题都给出多种解法,其中“另解”应用了上述结论,多种解法进行对比后,我们可以看出应用上述结论可以使问题的解决更简捷,从而节省时间。 例1.(2009重庆卷文)已知向量)1,1(=a ,),2(x b = 若b a +与24-平行,则实数x 的值是 ( ) A .-2 B .0 C .1 D .2 解法1:因为)1,1(=a ,),2(x b = ,所以)1,3(+=+x b a ,① ②
向量法证明三点共线的又一方法及应用 蒋李萍 2011年10月24日 平面向量既具有数量特征,又具有图形特征,学习向量的应用,可以启发同学们从新的视角去分析、解决问题,有益于培养创新能力. 下面就一道习题的应用探究为例进行说明. 原题 已知OB λOA μOC =+,其中1λμ+=. 求证:A 、B 、C 三点共线 思路:通过向量共线(如AB k AC =)得三点共线. 证明:如图,由1λμ+=得1λμ=-,则 (1)OB λOA μOC μOA μOC =+=-+ ∴()OB OA μOC OA -=- ∴AB μAC = ∴A 、B 、C 三点共线. 思考:1. 此题揭示了证明三点共线的又一向量方法,点O 具有灵活性; 2. 反之也成立(证明略):若A 、B 、C 三点共线,则存在唯一实数对λ、μ,满 足OB λOA μOC =+,且1λμ+=.揭示了三点共线的又一个性质; 3. 特别地,12λμ== 时,1 ()2 OB OA OC =+,点B 为AC 的中点,揭示了OAC 中线OB 的一个向量公式,应用广泛. 应用举例: 例1 如图,平行四边形ABCD 中,点M 是AB 的中点,点N 在BD 上,且1 3 BN BD =. 利用向量法证明:M 、N 、C 三点共线. 思路分析:选择点B ,只须证明BN λBM μBC =+,且1λμ+=. 证明:由已知BD BA BC =+,又点N 在BD 上,且1 3 BN BD = ,得 1111()3333BN BD BA BC BA BC ==+=+ 又点M 是AB 的中点, 1 2BM BA ∴=,即2BA BM = 21 33BN BM BC ∴=+ 而21133 += ∴M 、N 、C 三点共线. D A B C M N
2.3.1平面向量基本定理 学习目标: 1. 了解基底的含义,理解平面向量基本定理,会用基底表示平面内任一向量. 2. 掌握两个向量夹角的定义以及两向量垂直的定义. 3. 两个向量的夹角与两条直线所成的角. 学习重点:平面向量基本定理 学习难点:两个向量的夹角与两条直线所成的角. 课上导学: [基础初探] 教材整理1平面向量基本定理 阅读教材P93至P94第六行以上内容,完成下列问题. 1. ____________ 定理:如果e i, e是同一平面内的两个向量,那么对于这一平面内的____________ 向量a, ______________ 实数入,入2,使a= _________________________ 2. ____________ 基底:___________________________ 的向量e1, e2叫做表示这一平面内______________________________ 向量的一
组基底. 判断(正确的打“,错误的打“X” ) (1) 一个平面内只有一对不共线的向量可作为表示该平面内所 有向量的基底.() (2) 若e i, e是同一平面内两个不共线向量,则入& + 说 k, 入2为实数)可以表示该平面内所有向量.() (3) 若ae i + be2=ce i + de2(a, b, c, d€ R),则a = c, b = d.( ) 教材整理2两向量的夹角与垂直 阅读教材P94第六行以下至例1内容,完成下列问题. 1. __________________ 夹角:已知两个_________________ a 和b,作OA= a, OB= b,则__ = B叫做向量a与b的夹角.
平面向量基本定理 [学习目标] 1.理解平面向量基本定理的内容,了解向量一组基底的含义.2.在平面内,当一组基底选定后,会用这组基底来表示其他向量.3.会应用平面向量基本定理解决有关平面向量的综合问题. 知识点一 平面向量基本定理 (1)定理:如果e 1,e 2是同一平面内的两个不共线向量,那么对于这一平面内的任意向量a ,有且只有一对实数λ1,λ2,使a =λ1e 1+λ2e 2. (2)基底:把不共线的向量e 1,e 2叫做表示这一平面内所有向量的一组基底. 思考 如图所示,e 1,e 2是两个不共线的向量,试用e 1,e 2表示向量AB →,CD →,EF →,GH →,HG → , a . 答案 通过观察,可得: AB →=2e 1+3e 2,CD →=-e 1+4e 2,EF → =4e 1-4e 2, GH → =-2e 1+5e 2,HG → =2e 1-5e 2,a =-2e 1. 知识点二 两向量的夹角与垂直 (1)夹角:已知两个非零向量a 和b ,如图,作OA →=a ,OB → =b ,则∠AOB =θ (0°≤θ≤180°),叫做向量a 与b 的夹角. ①范围:向量a 与b 的夹角的范围是[0°,180°]. ②当θ=0°时,a 与b 同向. ③当θ=180°时,a 与b 反向. (2)垂直:如果a 与b 的夹角是90°,则称a 与b 垂直,记作a⊥b .
思考 在等边三角形ABC 中,试写出下面向量的夹角. ①AB →、AC →;②AB →、CA →;③BA →、CA →;④AB →、BA →. 答案 ①AB →与AC → 的夹角为60°; ②AB →与CA → 的夹角为120°; ③BA →与CA → 的夹角为60°; ④AB →与BA → 的夹角为180°. 题型一 对向量的基底认识 例1 如果e 1,e 2是平面α内两个不共线的向量,那么下列说法中不正确的是________. ①λe 1+μe 2(λ、μ∈R )可以表示平面α内的所有向量; ②对于平面α内任一向量a ,使a =λe 1+μe 2的实数对(λ,μ)有无穷多个; ③若向量λ1e 1+μ1e 2与λ2e 1+μ2e 2共线,则有且只有一个实数λ,使得λ1e 1+μ1e 2= λ(λ2e 1+μ2e 2); ④若存在实数λ,μ使得λe 1+μe 2=0,则λ=μ=0. 答案 ②③ 解析 由平面向量基本定理可知,①④是正确的. 对于②,由平面向量基本定理可知,一旦一个平面的基底确定,那么任意一个向量在此基底下的实数对是惟一的. 对于③,当两向量的系数均为零,即λ1=λ2=μ1=μ2=0时,这样的λ有无数个. 跟踪训练1 设e 1、e 2是不共线的两个向量,给出下列四组向量:①e 1与e 1+e 2;②e 1-2e 2与e 2-2e 1;③e 1-2e 2与4e 2-2e 1;④e 1+e 2与e 1-e 2.其中能作为平面内所有向量的一组基底的序号是______.(写出所有满足条件的序号)
平面向量三点共线定理的推论及空间推广 南昌外国语学校 梁懿涛 邮编:330025 地址:江西省南昌市桃苑西路126号南昌外国语学校 电话: 电子信箱: 一.问题的来源 平面向量三点共线定理:对于共面向量,,OA OB OC u u u r u u u r u u u r ,OC xOA yOB =+u u u r u u u r u u u r ,则A 、B 、C 三点共线的充要条件是1x y +=. 二.问题的提出 问题1.在上述定理中,如果1x y +<、1x y +>时,分别有什么结论 问题2.x 、y 有什么特定的意义吗 问题3.上述问题可以推广到空间吗 三.问题的解决 推论1. 对于不共线向量,OA OB u u u r u u u r ,若OC xOA yOB =+u u u r u u u r u u u r ,则 (1)点C 在直线AB 外侧(不含点O 一侧)的充要条件是1x y +>. (2)点C 在直线AB 内侧(含点O 一侧)的充要条件是1x y +<. 证明:(1)必要性:如图1-1,连OC 交AB 于点C ',则存在实数λ,使得(1)OC OC λλ'=>u u u r u u u u r ,(1)OC x OA y OB x y '''''=++=u u u u r u u u r u u u r ,OC x OA y OB λλ''∴=+u u u r u u u r u u u r ,,x x y y λλ''==, ()1x y x y λ''∴+=+>. 充分性:1x y +>Q ,∴存在1λ>,使得,x x y y λλ''==且1x y ''+=. ()OC x OA y OB OC λλ'''∴=+=u u u r u u u r u u u r u u u u r ,C 'Q 在直线AB 上,C ∴在直线AB 外侧. 同理可证(2). 进一步分析,得: 推论1'. 对于不共线向量,OA OB u u u r u u u r ,若OC xOA yOB =+u u u r u u u r u u u r ,则 (1)连接AB 得直线1l ,过点O 作平行于1l 的直线2l ,则1l 、2l 将平面OAB 分成三个区域,如图1-2点C 落在各区域时,x 、y 满足的条件是: (Ⅰ)区:1x y +>;(Ⅱ)区:01x y <+<;(Ⅲ)区:0x y +<.特别地,当点C 落在1l 上时,1x y +=;当点C 落在2l 上时,0x y +=. (2)直线OA 、OB 将平面OAB 分成四个区域,如图1-3,则点C 落在各区域时,x 、y 满足的条件是: (Ⅰ)区:00x y >??>?;(Ⅱ)区:00x y ?;(Ⅲ)区:00x y ??>,则点C 在线段AB 上;当0,0x y ><,则点C 在线段BA 的延长线上;当0,0x y <>,则点C 在线段AB 的延长线 上. 证明:OC xOA yOB =+u u u r u u u r u u u r Q 且1x y +=,OC xOC yOC xOA yOB ∴=+=+u u u r u u u r u u u r u u u r u u u r ,xCA yBC =u u u r u u u r , ||||||||AC y BC x ∴=。当0,0x y >>时,CA u u u r 与BC uuu r 同向,如图2-1所示,则点C 在线段AB 上;当0,0x y ><时,CA u u u r 与BC uuu r 反向,且||||AC BC <,如图2-2所示,则点C 在线段BA 的延长线上;当0,0x y <>时,CA u u u r 与BC uuu r 反向,且||||AC BC >,如图2-3所示,则点C 在线段AB 的延长线上.
平面向量补充讲义----三点共线定理 班级:__________姓名:___________ 三点共线定理:若平面内,向量12,OP OP 不共线,向量12OP OP OP λμ=+, 则12,,P P P 三点共线的等价条件是1λμ+=.(如图,共线时λ满足:221P P P P λ=) 说明1:若12,,P P P 三点共线,设221P P P P λ=,则11OP OP PP =+,则 例1.如图,在△ABC 中,13 AN NC =,点P 是BN 上的一点,若211 AP mAB AC =+,则实数m 的值为( ) A .911 B. 511 C. 311 D. 211 练习 例2.,点在边上,,设,则( ) 例3.如图,点是△的重心,、分别是边、上的动点, 且、、三点共线.设,,求: 的值 推论:如图,若平面内,向量12,OP OP 不共线,点P 为直线12P P 的 平行线上任意一点,且向量 12OP OP OP λμ=+,则λμ+为定值. (这条平行线称为等和线) 例4 .已知点G 为ABC ?重心,P 为GBC ?内动点(不包括边界),且AP AB AC λμ=+,则λμ+的取 值范围是__________________;2λμ+的取值范围是_______________________. OAB ?P AB 3AB AP =,OA a OB b ==OP =12.33A a b +21.33 B a b +. C 1233a b -. D 2133a b -G OAB P Q OA OB P G Q x =y =y x 11+2 12P 1