
信号与系统第5章习题
一、选择题
1.某理想低通滤波器的频率特性为,则其时域特性为()
A. B. C. D.
1、已知某连续时间LTI系统的频率响应如下图所示,若系统输入信号,,则系统的稳态响应为()
A.
B.
C.
D.
2、波形如下图的信号通过一截止频率为50πrad/s,通带内传输幅值为1,相移为0的理想低通滤波器,则输出的频率分量为()
A.
B.
C.
D.
3. 系统的幅频特性和相频特性如图下所示,则下列信号通过系统时不产生失真的是()
A. B.
C. D.
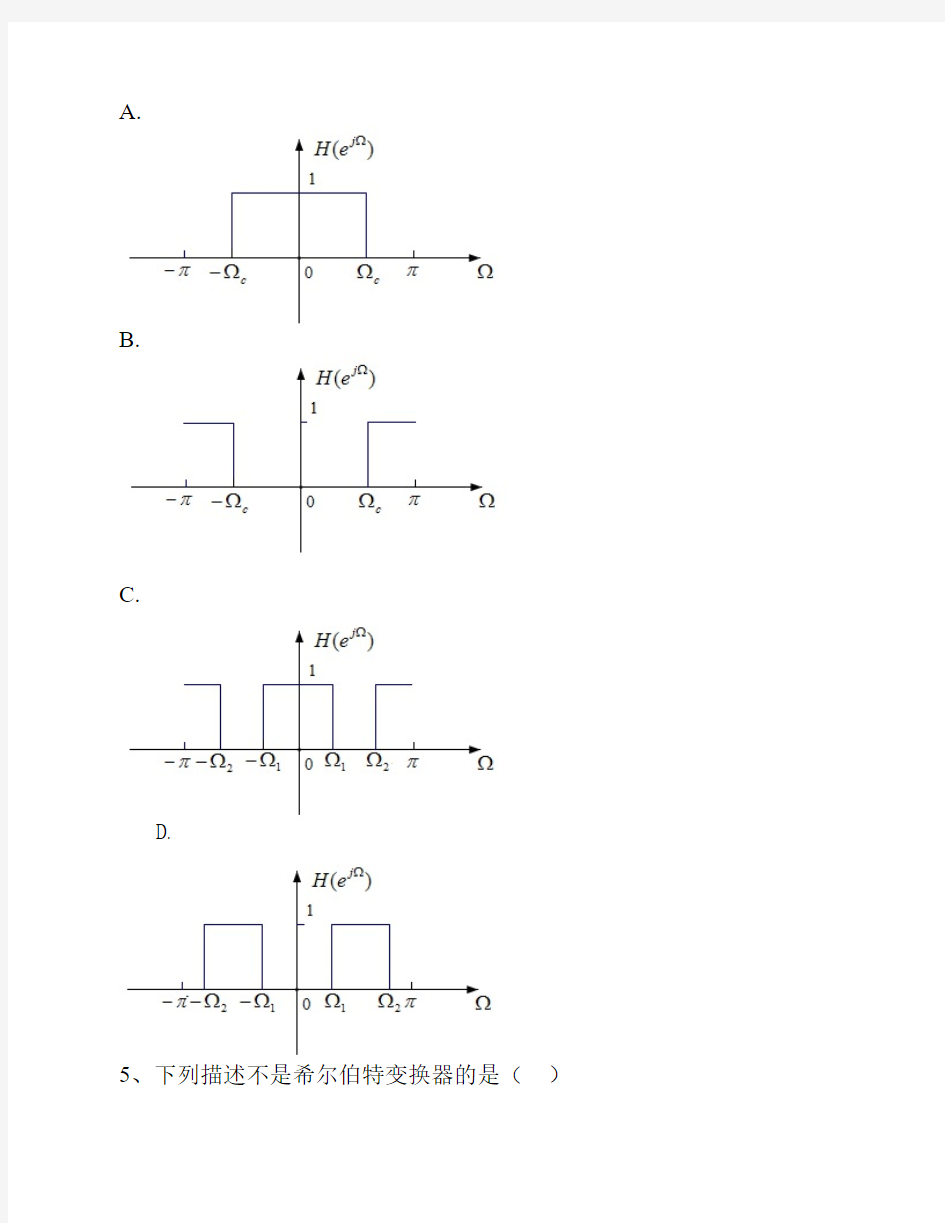
4、如下图所示的理想数字滤波器,其中为带阻滤波器的是()
A.
B.
C.
D.
5、下列描述不是希尔伯特变换器的是()
A.;
B.;
C.,其中为输入,为输出;
D. 。
二、判断题
1、系统的时域求解也都可以通过傅里叶变换方式求解()
2、频率响应的系统是无失真传输系统()
3、线性失真不包括新的频率成分生成的失真()
4、理想低通滤波器在物理上不能实现的原因是系统过于复杂()
5、矩形脉冲信号通过系统后的上升时间与系统的带宽成正比()
6、在通信系统中,信号需要通过调制以提高传输质量()
7、在通信系统中,传输效率和传输质量始终存在相互制约()
三、简答题
1、连续系统频率响应的物理含义及工程概念是什么?
2、无失真传输系统物理上可否实现?有何理论意义?
3、如何理解信号与系统的频率匹配?
4、单边带调制、频分复用有何实际意义?
四、计算题
教材P251习题:5-9、5-11、5-16、5-21
第5章 连续时间信号的抽样与量化 5.1 试证明时域抽样定理。 证明: 设抽样脉冲序列是一个周期性冲激序列,它可以表示为 ∑∞ -∞ =-= n s T nT t t )()(δδ 由频域卷积定理得到抽样信号的频谱为: [])()(21 )(ωδωπ ωT s F F *= ()[]∑∞ -∞ =-= n s s n F T ωω1 式中)(ωF 为原信号)(t f 的频谱,)(ωδT 为单位冲激序列)(t T δ的频谱。可知抽样后信号的频谱)(ωs F 由)(ωF 以 s ω为周期进行周期延拓后再与s T 1相乘而得到,这意味着如果 m s ωω2≥,抽样后的信号)(t f s 就包含了信号)(t f 的全部信息。如果m s ωω2<,即抽样 间隔m s f T 21 > ,则抽样后信号的频谱在相邻的周期内发生混叠,此时不可能无失真地重建原信号。 因此必须要求满足m s f T 21 ≤ ,)(t f 才能由)(t f s 完全恢复,这就证明了抽样定理。 5.2 确定下列信号的最低抽样频率和奈奎斯特间隔: (1))50(t Sa (2))100(2 t Sa (3) )100()50(t Sa t Sa + (4))60()100(2 t Sa t Sa + 解:抽样的最大间隔m s f T 21=称为奈奎斯特间隔,最低抽样速率m s f f 2=称为奈奎斯特速率,最低采样频率m s ωω2=称为奈奎斯特频率。 (1))]50()50([50 )50(--+? ωωπ u u t Sa ,由此知s rad m /50=ω,则π 25 = m f , 由抽样定理得:最低抽样频率π 50 2= =m s f f ,奈奎斯特间隔50 1π == s s f T 。 (2))200 1(100 )100(2 ω π - ? t Sa 脉宽为400,由此可得s rad m /200=ω,则π 100 = m f ,由抽样定理得最低抽样频率
5.23 解: (a ) (b )设如图示。 为实偶序列,为实偶信号。或。 而:, 或 (c ), (d ) (e ), 根据实偶虚实关系,可得:,而 (f )(i ), (ii ), , 2.18解:方程两边取FT ,得 6 ][][)(0 0== = ∑∑+∞ ?∞ ==+∞ ?∞ =?n n n j j n x e n x e X ωω][1n x ) (1111)()(][ω ω ωj e X j j j FT e e X e X n x ∠=?→←0123-1 -2-3-6 6 -1 2 1 [] n Q ][1n x ∴)(1ωj e X ∴0)(1=∠ω j e X πω=∠)(1j e X ]2[][1?=n x n x ∴ ) (] 2)([1)2(1)()()()(1ω ω ωωωωωωj j e X j j e X j j j j j e e X e e X e e X e X ∠?∠?==?=∴ωω 2)(?=∠j e X ω πω 2)(?=∠j e X Q ∫? = π πωω ω π d e e X n x n j j )(21 ][∴ π πωπ πω 4]0[2)(=?=∫?x d e X j 2 ][) 1(][)(=?= = ∑∑+∞ ?∞ ==+∞ ?∞ =?n n n n j j n x e n x e X π ωωπQ )}(Im{)}(Re{)(][][][][ω ωωj j j FT o e e X j e X e X n x n x n x n x +=?→←+==?)}(Re{][ω j FT e e X n x ?→←2 ][][][n x n x n x e ?+=-3 -1 2 1 x[n] 1 2 3 -1 -2 -4 6 n 4 5 7 -7 -1 2 1 x[-n] -4-3-2-1-5-6 -8 2 n 1 3 64 5 7 -7 -4 -3-2-1 -5 -6 -8 2 n 1 3 -1/2 2 1/2 [] 1 Q ∫∑? +∞ ?∞ ==π π ωω πd e X n x j n 2 2 )(21 ][π πωπ π ω28] [2)(2 2 =? =∑∫+∞ ?∞ =? n j n x d e X Q ∑+∞ ?∞ =?= n n j j e n x e X ωω][)(∑+∞ ?∞ =???= n n j j e n x jn d e dX ωωω ][)() (∴ ∫∑? ∞ +?∞ == ?π π ω ωωπ d d e dX n x jn j n 2 2 )(21] [)(ππωωπ πω 316][2)(2 2 ==∑∫∞ +?∞ =?n j n nx d d e dX