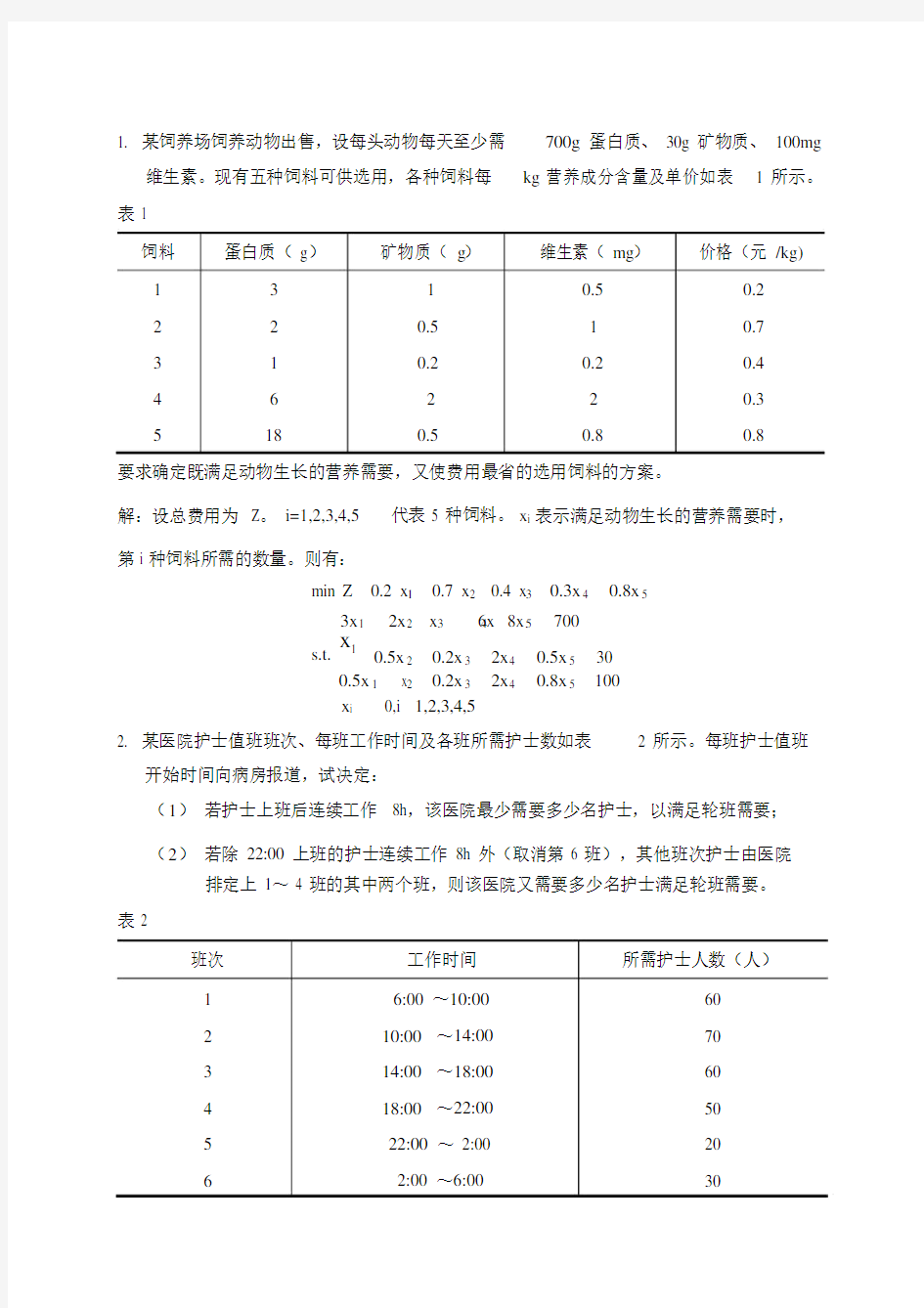

1. 某饲养场饲养动物出售,设每头动物每天至少需
700g 蛋白质、 30g 矿物质、 100mg 维生素。现有五种饲料可供选用,各种饲料每 kg 营养成分含量及单价如表 1 所示。
表 1
饲料 蛋白质( g )
矿物质( g )
维生素( mg )
价格(元 /kg)
1 3 1 0.5 0.
2 2 2 0.5 1 0.7
3 1 0.2 0.2 0.
4 4 6 2 2 0.3 5
18
0.5
0.8
0.8
要求确定既满足动物生长的营养需要,又使费用最省的选用饲料的方案。
解:设总费用为 Z 。 i=1,2,3,4,5 代表 5 种饲料。 x i 表示满足动物生长的营养需要时,
第 i 种饲料所需的数量。则有:
min Z 0.2 x 1 0.7 x 2 0.4 x 3 0.3x 4 0.8x 5
3x 1
2x 2 x 3 6x 4 8x 5 700
s.t.
x 1
0.5x 2 0.2x 3 2x 4 0.5x 5 30
0.5x 1 x 2 0.2x 3 2x 4 0.8x 5 100 x i 0,i 1,2,3,4,5
2. 某医院护士值班班次、每班工作时间及各班所需护士数如表
2 所示。每班护士值班
开始时间向病房报道,试决定:
( 1) 若护士上班后连续工作 8h ,该医院最少需要多少名护士,以满足轮班需要;
( 2) 若除 22:00 上班的护士连续工作 8h 外(取消第 6 班),其他班次护士由医院
排定上 1~ 4 班的其中两个班,则该医院又需要多少名护士满足轮班需要。
表 2
班次 工作时间 所需护士人数(人)
1 6:00 ~10:00 60
2 10:00 ~14:00 70
3 14:00 ~18:00 60
4 18:00 ~22:00 50
5 22:00 ~ 2:00 20 6
2:00 ~6:00
30
解:(1)设 x i 第 i 班开始上班的人数, i=1,2,3,4,5,6
min Z
x 1 x 2 x 3 x 4 x 5 x 6
x 1 x 6 60 x 1 x 2 70
x 2 x 3 60
s.t. x 3
x 4 50 x 4 x 5 20 x 5 x 6
30
x i
0, i 1,2,3,4,5,6且为整数
解:(2)在题设情况下,可知第五班一定要 30 个人才能满足轮班需要。则设设 x i 第 i 班开始上班的人数, i=1,2,3,4 。
min Z
x 1 x 2 x 3 x 4 30
y 11 x 1 y 21 x 2 y 31 x 3 y 41 x 4 60,第一班约束 y 11 1, y 11 y 12
y 13 y 14 2 y 12 x 1 y 22 x 2 y 32 x 3 y 42 x 4 70,第二班约束 y 22 1, y 21 y 22 y 23 y 24 2
s.t. y 13 x 1 y 23 x 2 y 33 x 3 y 43 x 4 60,第三班约束
y 33 1, y 31 y 32 y 33 y 34 2 y 14 x 1
y 24
x 2
y 34
x 3
y 44
x
4
50,第四班约束 y 44 1, y 41 y 42 y 43 y 44
2
x i 0, y ij 是 0 — 1变量, i , j 1,2,3,4
3. 要在长度为 l 的一根圆钢上截取不同长度的零件毛坯,毛坯长度有 n 种,分别为 a j
( j =1,2 , n )。问每种毛坯应当截取多少根,才能使圆钢残料最少,试建立本问题的数学模型。
解:设 x i 表示各种毛坯的数量, i=1,2,
n 。
n
max Z
a i x i
i 1
n
a i x i 1
i 1
x i 是整数
4. 一艘货轮分前、中、后三个舱位,它们的与最大允许载重量如表
3.1 所示。现有三
种货物待运,已知有相关数据列于表
3.2 。
表 3.1
项目
前舱 中舱 后舱 最大允许载重量( t )
2000 3000 1500
容积( m 2)
4000
5400
1500
表 3.2
商品 数量(件)
3
运价(元 / 件)
每件体积(m/ 件) 每件重量( t/ 件)
A 600 10 8 1000
B 1000 5 6 700 C
800
7
5
600
又为了航海安全,前、中、后舱实际载重量大体保持各舱最大允许载重量的比例关系。
具体要求:前、后舱分别与中舱之间载重量比例的偏差不超过
15%,前、后舱之间不超
过 10%。问该货轮应该载 A,B,C 各多少件运费收入才最大?试建立这个问题的线性规划模型。
解:设 x ij 表示第 i 件商品在舱 j 的装载量, i,j=1,2,3
max Z
1000( x 11 x 12 x 13 ) 700( x 21 x 22 x 23 ) 600( x 31 x 32 x 33 )
1) 商品的数量约束:
x 11 x 12
x 13
600 x 21
x 22
x
23
1000 x
31 x
32
x
33
800
2) 商品的容积约束:
10 x 11 5x 21 7 x 31 4000 10 x 12 5x 22
7x 32 5400
10 x 13 5x 23 7 x 33 1500
3) 最大载重量约束:
8x 11 6x 21 5x 31 2000 8x 12 6x 22 5x 32 3000
8x 13 6x 23 5x 33 1500
4) 重量比例偏差的约束:
8x11 6x21 5x31 2
(1 0.15)(8x12 6x22 5x32 ) 3
8x11 6x21 5x31 2
(1 0.15)(8x12 6x22 5x32 ) 3
8x13 6x23 5x33 1
(1 0. 15)(8x12 6x22 5x32 ) 2
8x13 6x23 5x33 1
(1 0. 15)(8x12 6x22 5x32 ) 2
8x13 6x23 5x33 3
0. 1)(8x11 6x21 5x31 )
(1
4
8x13 6x23 5x33 3
(1 0. 1)(8x11 6x21 5x31 ) 4
5.篮球队需要选择 5 名队员组成出场阵容参加比赛。 8 名队员的身高及擅长位置见表
5.
表 5
队员 1 2 3 4 5 6 7 8 身高( m) 1.92 1.9 1.88 1.86 1.85 1.83 1.8 1.78 擅长位置中锋中锋前锋前锋前锋后卫后卫后卫出场阵容应满足以下条件:
(1)只能有一名中锋上场;
(2)至少一名后卫;
(3)如 1 号和 4 号均上场,则 6 号不出场;
(4) 2 号和 8 号至少有一个不出场。
问应当选择哪 5 名队员上场,才能使出场队员平均身高最高,试建立数学模型。
解:设 x i 1表示第i个队员出场,i=1,2 8.
max Z 1 8
x i 5 i 1
8
x i 5
i 1
x1 x2 1, x6 x7 x8 1
x2 x8 1, x1 x4 x6 2
x i是 0 — 1变量
6. 时代服装公司生产一款新的时装,据预测今后 6 个月的需求量如表4 所示,每件时
装用工 2h 和 10 元原材料费,售价 40 元。该公司 1 月初有 4 名工人,每人每月可工作 200h ,月薪 2000 元。该公司可于任一个月初新雇工人, 但每雇 1 人需一次性额外支出 1500 元,也可辞退工人,但每辞退 1 人需补偿 1000 元。如当月生产数超过需
求,可留到后面月份销售,但需付库存费每件每月
5 元,当供不应求时,短缺数不
需补上。试帮组该公司决策,如何使用
6 个月的总利润最大。
表 4
单位:件
月份
1
2 3 4 5 6 需求
500
600
300
400
500
800
解:设 x i1 为第 i 月现有工人人数, x i 2 为新雇工人人数, x i3 为辞退工人人数, y i 为每月 的需求。 i=1,2 , , 6。则有:
6
200
(x i1
6
6
j
max Z
(40
10)
x i 2 )
(2000 x i 1 3500 x i 2 1000x i3 ) 5
( n i y i ) f (n i y i )
i 1
2
i 1
j 1
k 1
其中 f ( x)
1, x 0
0, x
x
11
4
x
i1
x
i 3
x i1
,
,, ,
x
i 2
i 1 2
5
s.t.
200 ( x i1 x i 2 ) 2
n i
x
ik
, ,, ,; ,
0 i 1 2 ,
6 k 1 2
7. 童心玩具厂下一年度的现金流(万元)如表 6 所示,表中负号表示该月现金流出大于流入,为此该厂需借款。借款有两种方式:一是于上一年末借一年期贷款,一次
得全部贷款额, 从 1 月底起每月还息 1%,于 12 月归还本金和最后一次利息; 二是得
到短期贷款,每月初获得,于月底归还,月息
1.5%。当该厂有多余现金时,可短期
存款,月初存入,月末取出,月息
0.4%。问该厂应如何进行存贷款操作,既能弥补
可能出现的负现金流,又可使年末现金总量为最大。
表 6
月份 1 2 3 4 5 6 7 8 9 10 11 12 现金流
-12
-10
-8
-10
-4
5
-7
-2
15
12
-7
45
解:设长期存款为 y , 为第 i 个月的短期贷款额, z i 为第 i 个月短期存款额, i=1,2, ,
w i
n 。则有:
max Z 1.
004z 12 1.01y 1.015w 12 y w 1 z 1 12
1.004z 1 0.01y 1.015w 1 z 2 w 2 10 1.004z 2 0.01y 1.015w 2 z 3 w 3 8 1.004z 3 0.01y 1.015w 3 z 4 w 4 10 1.004z 4
0.01y 1.015w 4 z 5 w 5 4
1.004z 5
0.01y 1.015w 5 z 6 w 6 5 s.t.
0.01y 1.015w 6 z 7 w 7 7 1.004z 6 1.004z 7 0.01y 1.015w 7 z 8 w 8 2
1.004z 8 0.01y 1.015w 8 z 9 w 9
15 1.004z 9
0.01y 1.015w 9
z
10 w
10 12 1.004z 10 0.01y 1.015w 10
z
11
w
11
7
1.004z 11 0.01y 1.015w 11 z 12 w
12 45
8. 某地准备投资 D 元建民用住宅, 可以建住宅的地点有 n 处: A 1, A 2, A n 。 A n 处每幢
住宅的造价为 d ,最多可造 a 幢。问应当在哪几处建住宅,分别建几幢,才能使建造
的住宅总数最多,试建立问题的数学模型。
解:设 x i 表示在 A 处所建住宅的数量, i=1,2
, n 。
n
max Z
x i
i 1
n
d i x i
D ,
x i a i , ,,
i 1 2 n
i 1
x i 是整数
9. 有一批每根长度为 l 的圆钢,需截取 n 种不同长度的零件毛坯。长度为 a j 的毛坯必须有
m j 段( j=1 , 2, n ),为了方便,每根圆钢只截取一种长度的毛坯。应当怎样
截取,才能使动用的圆钢数目最少,要求建立数学模型。
解:设 x i 表示各种毛坯使用圆钢的数量, y i 表示各种毛坯在一根圆钢上可得到的数量。
i=1,2 , n 。
n
min Z
x i
i 1
a j x i l , i ,, , n
1 2
y i x i m j , i ,, , n
1 2 , y i ,且都是整数 x i 0 i 1,2, , n
10. 一个旅行者要在其背包里装一些最有用的旅行用品。背包容积为 a ,携带物品总重量最
多为 b 。现有物品 m 件,第 i 件物品体积为 a i ,重量为 b i ( i=1,2 ,m )。为了比
较物品的有用程度,假设第 i 件物品的价值为 c i (i=1,2 ,m )。若每件物品只能整件
携带,每件物品都能放入包中,并且不考虑物品放入包后相互的间隙。问旅行者应
当携带几件物品,才能使携带物品的总价值最大,要求建立数学模型。
解:设 x i 1表示携带第 i 件物品, i=1,2 , , m 。
m
max Z
c i x i
i 1
m
a i x i a
i 1 m
b i x i b
i 1
x 是0 — 1变量
i 1,2, m
11. 宏银公司承诺为谋建设项目从 2003 年起的 4 年中每年初分别提供以下数额贷款:
2003 年——100 万元, 2004 年——150 万元,2005 年——120 万元,2006——110 万元。
以上贷款资金均需 2002 年底前筹集齐。但为了充分发挥这笔资金的作用,在满足每年贷款额情况下,可将多余资金分别用于下列投资项目:
( 1) 于 2003 年初购买 A 种债卷,期限 3 年,到期后本息合计为投资额的
140%,
但限购 60 万元。
( 2) 于 2003 年初购买 B 种债卷,期限 2 年,到期后本息合计为投资额的
125%,
且限购 90 万元。
( 3) 于 2004 年初购买 C 种债卷,期限 2 年,到期后本息合计为投资额的
130%,
但限购 50 万元。
求宏银公司应如何运用好这笔筹集到的资金,使
2002 年底需要筹集到的资金数额为最
少。
解:设 x 为 2002 年底该公司需要筹集到的资金额;
y 1, y 2, y 3 分别为 2003、2004、2005
年初存放到银行的资金数; w A , w B , w C 分别为购买 A 、B 、C 债卷的数额。则有:
min Z x
x y 1 w A w B 100 1.04 y 1 y 2 w C 150
1.04 y 2 1.25w B y 3 120
1.04 y 3 1.40w A 1.30w C 110 s.t . , 、 、 y 3 ,
x 0 y 1 y 2 0
0 w A ,
60
0 w B ,
90
0 w C 50
第一章线性规划1、 由图可得:最优解为 2、用图解法求解线性规划: Min z=2x1+x2 ? ? ? ? ? ? ? ≥ ≤ ≤ ≥ + ≤ + - 10 5 8 24 4 2 1 2 1 2 1 x x x x x x 解: 由图可得:最优解x=1.6,y=6.4
Max z=5x 1+6x 2 ? ?? ??≥≤+-≥-0 ,23222212 121x x x x x x 解: 由图可得:最优解Max z=5x 1+6x 2, Max z= + ∞
Maxz = 2x 1 +x 2 ????? ? ?≥≤+≤+≤0,5242261552121211x x x x x x x 由图可得:最大值?????==+35121x x x , 所以?????==2 3 21x x max Z = 8.
12 12125.max 2328416412 0,1,2maxZ .j Z x x x x x x x j =+?+≤? ≤?? ≤??≥=?如图所示,在(4,2)这一点达到最大值为2 6将线性规划模型化成标准形式: Min z=x 1-2x 2+3x 3 ????? ??≥≥-=++-≥+-≤++无约束 321 321321321,0,05232 7x x x x x x x x x x x x 解:令Z ’=-Z,引进松弛变量x 4≥0,引入剩余变量x 5≥0,并令x 3=x 3’-x 3’’,其中x 3’≥ 0,x 3’’≥0 Max z ’=-x 1+2x 2-3x 3’+3x 3’’ ????? ? ?≥≥≥≥≥≥-=++-=--+-=+-++0 ,0,0'',0',0,05 232 '''7'''543321 3215332143321x x x x x x x x x x x x x x x x x x x
一、不定向选择 1、若线性规划问题有可行解则: A其可行域可能无界 B其可行域为凸集 C至少有一个可行解为基本可行解 D可行域边界上点都为基本可行解 E一定存在某一可行解使目标函数达最优值 F任一可行解均能表示为所有可行域顶点线性组合表示 G某一可行解为最优解必要条件为它是一个基本解。 2、线性规划问题和其对偶问题关系: A对偶问题的对偶问题为原问题 B若原问题无解,其对偶问题有无界解 C若原问题无界解,其对偶问题无解或者无界解 D即使原问题有最优解,其对偶问题也未必有最优解 E原问题目标函数达到最大时,其对偶问题取最小值 F只有原问题达最优解时,其对偶问题才有可行解 G若原问题有无穷多最优解,其对偶问题有无界解。 二、已知线性规划问题,如下: max z=x1+x2-x3 -x1+2x2+x3<=2 st. -2x1+x2-x3<=3 x1,x2,x3>=0 据对偶理论分析此问题有解的情况(最优,无界或无解)三、已知线性规划问题 max z=x1+4x2+x3+2x4 x1+2x2 +x4<=8 x2 +2x4<=6 st. x2+x3+x4<=9 x1+x2+x3 <=6 x1,x2,x3,x4>=0 最优解为(0,2,4,2)据对偶理论找出其对偶问题最优解四、单纯形法解下列线性规划问题 max z=3x1+2x2
x1+2x2<=6 st. 2x1+x2<=8 -x1+x2<=1 x2<=2 x1,x2>=0 1)第一、二、四约束的影子价格为多少? 2)变量x1价值系数增加2,最优解是否变化? 五、运输问题单价表如下,确定总运费最小的调运方案 B1 B2 B3 B4 产量 A1 3 10 3 11 14 A2 2 8 1 9 8 A3 10 6 7 4 18 销量10 12 6 12 40 六、设备更新题:某设备收益r(万元),维修保养费w(万元) 更新费g(万元)与役龄t(年)关系如下: r(t)=10-1/2 t w(t)=1+5/4 t g(t)=1/2+4/5 t 考虑资金占用利率I ,试建立10年更新计划动态规划模型
《运筹学》习题答案 一、单选题 1.用动态规划求解工程线路问题时,什么样的网络问题可以转化为定步数问题求解()B A.任意网络 B.无回路有向网络 C.混合网络 D.容量网络 2.通过什么方法或者技巧可以把工程线路问题转化为动态规划问题?()B A.非线性问题的线性化技巧 B.静态问题的动态处理 C.引入虚拟产地或者销地 D.引入人工变量 3.静态问题的动态处理最常用的方法是?B A.非线性问题的线性化技巧 B.人为的引入时段 C.引入虚拟产地或者销地 D.网络建模 4.串联系统可靠性问题动态规划模型的特点是()D A.状态变量的选取 B.决策变量的选取 C.有虚拟产地或者销地 D.目标函数取乘积形式 5.在网络计划技术中,进行时间与成本优化时,一般地说,随着施工周期的缩短,直接费用是( )。C A.降低的 B.不增不减的 C.增加的 D.难以估计的 6.最小枝权树算法是从已接接点出发,把( )的接点连接上C A.最远 B.较远 C.最近 D.较近 7.在箭线式网络固中,( )的说法是错误的。D A.结点不占用时间也不消耗资源 B.结点表示前接活动的完成和后续活动的开始 C.箭线代表活动 D.结点的最早出现时间和最迟出现时间是同一个时间 8.如图所示,在锅炉房与各车间之间铺设暖气管最小的管道总长度是( )。C A.1200 B.1400 C.1300 D.1700 9.在求最短路线问题中,已知起点到A,B,C三相邻结点的距离分别为15km,20km,25km,则()。D A.最短路线—定通过A点 B.最短路线一定通过B点 C.最短路线一定通过C点 D.不能判断最短路线通过哪一点 10.在一棵树中,如果在某两点间加上条边,则图一定( )A A.存在一个圈 B.存在两个圈 C.存在三个圈 D.不含圈 11.网络图关键线路的长度( )工程完工期。C A.大于 B.小于 C.等于 D.不一定等于
运筹学基础课后习题答案 [2002年版新教材] 第一章导论 P5 1.、区别决策中的定性分析和定量分析,试举例。 定性——经验或单凭个人的判断就可解决时,定性方法 定量——对需要解决的问题没有经验时;或者是如此重要而复杂,以致需要全面分析(如果涉及到大量的金钱或复杂的变量组)时,或者发生的问题可能是重复的和简单的,用计量过程可以节约企业的领导时间时,对这类情况就要使用这种方法。 举例:免了吧。。。 2、. 构成运筹学的科学方法论的六个步骤是哪些? .观察待决策问题所处的环境; .分析和定义待决策的问题; .拟定模型; .选择输入资料; .提出解并验证它的合理性(注意敏感度试验); .实施最优解; 3、.运筹学定义: 利用计划方法和有关许多学科的要求,把复杂功能关系表示成数学模型,其目的是通过定量分析为决策和揭露新问题提供数量根据 第二章作业预测P25 1、. 为了对商品的价格作出较正确的预测,为什么必须做到定量与定性预测的结合?即使在定量预测法诸如加权移动平均数法、指数平滑预测法中,关于权数以及平滑系数的确定,是否也带有定性的成分? 答:(1)定量预测常常为决策提供了坚实的基础,使决策者能够做到心中有数。但单靠定量预测有时会导致偏差,因为市场千变万化,影响价格的因素很多,有些因素难以预料。调查研究也会有相对局限性,原始数据不一定充分,所用的模型也往往过于简化,所以还需要定性预测,在缺少数据或社会经济环境发生剧烈变化时,就只能用定性预测了。(2)加权移动平均数法中权数的确定有定性的成分;指数平滑预测中的平滑系数的确定有定性的成分。 2.、某地区积累了5 个年度的大米销售量的实际值(见下表),试用指数平滑法,取平滑系数α= 0.9,预测第6年度的大米销售量(第一个年度的预测值,根据专家估计为4181.9千公斤) 年度 1 2 3 4 5 大米销售量实际值 (千公斤)5202 5079 3937 4453 3979 。 答: F6=a*x5+a(1-a)*x4+a(1-a)~2*x3+a(1-a)~3*x2+a(1-a)~4*F1 F6=0.9*3979+0.9*0.1*4453+0.9*0.01*3937+0.9*0.001*5079+0.9*0.0001*4181.9
运筹学(胡运权)第五版课后答案-运筹作业
47页1.1b 用图解法找不到满足所有约束条件的公共范围,所以该问题无可行解47页1.1d 无界解 1 2 3 4 5 4 3 2 1 - 1 -6 -5 -4 -3 -2 X2 X1 2x1- -2x1+3x 1 2 3 4 4 3 2 1 X1 2x1+x2=2 3x1+4x2= X
1.2(b) 约束方程的系数矩阵A= 1 2 3 4 2 1 1 2 P1 P2 P3 P4 基 基解 是否可行解目标函数值X1 X2 X3 X4 P1 P2 -4 11/2 0 0 否 P1 P3 2/5 0 11/5 0 是43/5 P1 P4 -1/3 0 0 11/6 否 P2 P3 0 1/2 2 0 是 5 P2 P4 0 -1/2 0 2 否 P3 P4 0 0 1 1 是 5 最优解A=(0 1/2 2 0)T和(0 0 1 1)T 49页13题 设Xij为第i月租j个月的面积 minz=2800x11+2800x21+2800x31+2800x41+4500x12+4500x22+4500x32+6000x1 3 +6000x23+7300x14 s.t. x11+x12+x13+x14≥15 x12+x13+x14+x21+x22+x23≥10 x13+x14+x22+x23+x31+x32≥20 x14+x23+x32+x41≥12 Xij≥0 用excel求解为: ( )
用LINDO求解: LP OPTIMUM FOUND AT STEP 3 OBJECTIVE FUNCTION V ALUE
2015年清华大学826运筹学与统计学(数学规划、应用随机模型、统计学各占1/3)考研复习参考书 科目:826 运筹学与统计学(数学规划、应用随机模型、统计学各占1/3)参考书:《运筹学(数学规划)(第3版)清华大学出版社,2004年1月 W.L.Winston 《运筹学》(应用随机模型)清华大学出版社,2004年2月 V.G. Kulkarni 《概率论与数理统计》(第1~9章)高等教育出版社,2001年盛聚等 考研复习方法,这里不详细展开。简单归纳为: 新祥旭考研提醒:首先,清楚考试明细,掌握真题,真题为本。通过真题,了解和熟知:考什么、怎么考、考了什么、没考什么;通过练习真题,了解:目前我的能力、复习过程中我的进步、我的考试目标。提醒一句:千万不要浪费大量时间做不相关的模拟题;千万不要把考研复习等同于做题目,搞题海战术。 其次,把握参考书,参考书为锚。弄懂、弄熟。考研复习如何才能成功?借用《卖油翁》里的一句话,那就是:手熟而已。明确考试之后,考研就基本上是一个熟悉吃透的过程。无论何时,参考书第一,不能轻视。所以,千万不要本末倒置,把做题凌驾于看书之上。如何才叫熟悉?我认为,要打破“讲速度,不讲效率”的做法,看了多少遍并不是检验熟悉与否的指标,合上书本,随时自我检测,能否心中有数、一问便知,这才是关键。 再次,制定计划,合理分配时间。不是每一本参考书都很重要,都一样重要,所以,在了解真题的基础上,要了解每一本书占多少分,如何命题考试,在此基础上,每一本参考书的主次轻重、复习方略也就清楚了,复习才不会像开摊卖药,平均用力。一个月制定一份计划书,每天写一句话鼓励自己,一个月调整一次复习重点,这都是必要的。 最后,快乐复习。考研复习是以什么样状态进行的,根源在于能否克服不良情绪。第一,报考对外汉语,你是因为喜欢这个专业吗?如果是,那么,就继续给自己这种暗示,那么你一定会发现,复习再紧张,也是愉悦的,因为你是为了兴趣而考研的;第二,规律的作息,不大时间战,消耗战,养精蓄锐。运动加休息,如果能每天都很规律,那么成功也就有了保障,负面情绪少了,效率也就高了。 总结为几个关键词,就是:知己知彼、本末分明。
1.某饲养场饲养动物出售,设每头动物每天至少需700g蛋白质、30g矿物质、100mg 维生素。现有五种饲料可供选用,各种饲料每kg营养成分含量及单价如表1所示。表1 要求确定既满足动物生长的营养需要,又使费用最省的选用饲料的方案。 x表示满足动物生长的营养需要时,解:设总费用为Z。i=1,2,3,4,5代表5种饲料。 i 第i种饲料所需的数量。则有: 2.某医院护士值班班次、每班工作时间及各班所需护士数如表2所示。每班护士值班 开始时间向病房报道,试决定: (1)若护士上班后连续工作8h,该医院最少需要多少名护士,以满足轮班需要; (2)若除22:00上班的护士连续工作8h外(取消第6班),其他班次护士由医院排定上1~4班的其中两个班,则该医院又需要多少名护士满足轮班需要。表2 x第i班开始上班的人数,i=1,2,3,4,5,6 解:(1)设 i x第i 解:(2)在题设情况下,可知第五班一定要30个人才能满足轮班需要。则设设 i 班开始上班的人数,i=1,2,3,4。
a 3.要在长度为l的一根圆钢上截取不同长度的零件毛坯,毛坯长度有n种,分别为 j (j=1,2,…n)。问每种毛坯应当截取多少根,才能使圆钢残料最少,试建立本问题的数学模型。 解:设 x表示各种毛坯的数量,i=1,2,…n。 i 4.一艘货轮分前、中、后三个舱位,它们的与最大允许载重量如表3.1所示。现有三 种货物待运,已知有相关数据列于表3.2。 表3.1 表3.2 又为了航海安全,前、中、后舱实际载重量大体保持各舱最大允许载重量的比例关系。具体要求:前、后舱分别与中舱之间载重量比例的偏差不超过15%,前、后舱之间不超过10%。问该货轮应该载A,B,C各多少件运费收入才最大?试建立这个问题的线性规划模型。 x表示第i件商品在舱j的装载量,i,j=1,2,3 解:设 ij 1)商品的数量约束: 2)商品的容积约束: 3)最大载重量约束: 4)重量比例偏差的约束: 5.篮球队需要选择5名队员组成出场阵容参加比赛。8名队员的身高及擅长位置见表 5. 表5
《运筹学》试题(答案) 一、单项选择题。下列每题给出的四个答案中只有一个是正确的,将表示正确答案的字母填入题后的括号中。(20分) 1.对一个极大化的线性规划问题用单纯形法求解,若对所有的检验数0 ≤j σ,但对某个 非基变量j x ,有0 =j σ,则该线性规划问题( B ) A .有唯一的最优解; B .有无穷多个最优解; C .为无界解; D .无可行解。 2.使用人工变量法求解极大化线性规划问题时,当所有的检验数0 ≤j σ,在基变量中仍含有非零的人工变量,表明该线性规划问题( D ) A .有唯一的最优解; B .有无穷多个最优解; C .为无界解; D .无可行解。 3.在对偶问题中,若原问题与对偶问题均具有可行解,则( A ) A .两者均具有最优解,且它们最优解的目标函数值相等; B .两者均具有最优解,原问题最优解的目标函数值小于对偶问题最优解的目标函数值; C .若原问题有无界解,则对偶问题无最优解; D .若原问题有无穷多个最优解,则对偶问题只有唯一最优解; 4.在用对偶单纯形法解最大化线性规划问题时,每次迭代要求单纯形表中( D ) A .b 列元素不小于零; B .检验数都大于零; C .检验数都不小于零; D .检验数都不大于零。 5.在产销平衡运输问题中,设产地为m 个,销地为n 个,那么解中非零变量的个数( A )。 A .不能大于(m +n -1);B .不能小于(m +n -1);C .等于(m +n -1);D .不确定。 6.在运输问题中,每次迭代时,如果有某非基变量的检验数等于零,则该运输问题( B )。 A .无最优解;B .有无穷多个最优解;C .有唯一最优解;D .出现退化解。 7.在目标规划中,求解的基本原则是首先满足高级别的目标,但当高级别目标不能满足时( D )。 A .其后的所有低级别目标一定不能被满足; B .其后的所有低级别目标一定能被满足; C .其后的某些低级别目标一定不能被满足; D .其后的某些低级别目标有可能被满足。 8.若一个指派问题的系数矩阵的某行各元素都加上常数k 得到一个新的矩阵,这一新矩阵对应着一个新的指派问题,则( A )。 A .新问题与原问题有相同的最优解; B .新问题最优目标值大于原问题最优目标函数值; C .新问题最优解等于原问题最优解加上k ; D .新问题最优解小于原问题最优解。 9.如果要使目标规划实际实现值不超过目标值,则相应的偏离变量应满足( B )。 A .0>+d ; B .0=+d ; C .0=-d ; D . .0,0>>+-d d 10.动态规划问题中最优策略具有性质:( C ) A .每个阶段的决策都是最优的; B .当前阶段以前的各阶段决策是最优的; C .无论初始状态与初始决策如何,对于先前决策所形成的状态而言,其以后的所有决策应
47页1.1b 用图解法找不到满足所有约束条件的公共范围,所以该问题无可行解47页1.1d 无界解
1.2(b) 约束方程的系数矩阵 A= 1 2 3 4 ( ) 2 1 1 2 P1 P2 P3 P4 最优解A=(0 1/2 2 0)T和(0 0 1 1)T 49页13题 设Xij为第i月租j个月的面积 minz=2800x11+2800x21+2800x31+2800x41+4500x12+4500x22+4500x32+6000x13 +6000x23+7300x14 s.t. x11+x12+x13+x14≥15 x12+x13+x14+x21+x22+x23≥10 x13+x14+x22+x23+x31+x32≥20 x14+x23+x32+x41≥12 Xij≥0 用excel求解为:
用LINDO求解: LP OPTIMUM FOUND AT STEP 3 OBJECTIVE FUNCTION VALUE 1) 118400.0 VARIABLE VALUE REDUCED COST Z 0.000000 1.000000 X11 3.000000 0.000000
X21 0.000000 2800.000000 X31 8.000000 0.000000 X41 0.000000 1100.000000 X12 0.000000 1700.000000 X22 0.000000 1700.000000 X32 0.000000 0.000000 X13 0.000000 400.000000 X23 0.000000 1500.000000 X14 12.000000 0.000000 ROW SLACK OR SURPLUS DUAL PRICES 2) 0.000000 -2800.000000 3) 2.000000 0.000000 4) 0.000000 -2800.000000 5) 0.000000 -1700.000000 NO. ITERATIONS= 3 答若使所费租借费用最小,需第一个月租一个月租期300平方米,租四个月租期1200平方米,第三个月租一个月租期800平方米,
《运筹学教程》第三章习题答案 1.影子价格是根据资源在生产中作出的贡献而做的估价。它是一种边际价格, 其值相当于在资源得到最有效利用的生产条件下,资源每变化一个单位时目标函数的增量变化。又称效率价格。 影子价格是指社会处于某种最优状态下,能够反映社会劳动消耗、资源稀缺程度和最终产品需求状况的价格,是社会对货物真实价值的度量。 只有在完善的市场条件下才会出现,然而这种完善的市场条件是不存在的,因此现成的影子价格也是不存在的。市场价格是物品和服务在市场上销售的实际价格,是由供求关系决定的。 2.证明:当原问题约束条件右端变为b i′时, 原问题变为: maxz=∑C i X j s.t. ∑a ij X i≤b i′(i=1,2,3,……,m) X j≥0 (j=1,2,3,……,n) 对偶问题为: minp=∑b i′y i s.t. ∑a ij y i≥C i y i≥0 (i=1,2,3,……,m) (j=1,2,3,……,n) 设,当b i变为b i′原问题有最优解(X1′X2′X3′……X n-1′X n′)时,对偶问题的最优解为(y1′y2′y3′……y n-1′y n′),则有: 又因为当原问题有最优解时,对偶问题也有最优解,且相等,则有: 所以
3(1).minp=6y1 + 2y2 s.t. -y1+2y2≥-3 3y1+3y2≥4 y1,y2≥0 (2)解:令X2=X2′-X2〞,X4= X4′-X4〞,X2′,X2〞,X4′,X4〞≥0 ,原式化为: maxz=2X1 +2X2′-2X2〞-5X3 +2X4′-2X4〞 s.t. 2X1 -X2′+X2〞+3X3 +3X4′-3X4〞≤-5 -2X1 +X2′-X2〞-3X3 -3X4′+3X4〞≤5 -6X1 -5X2′+5X2〞+X3 -5X4′+5X4〞≤-6 10X1 -9X2′+9X2〞+6X3 +4X4′-4X4〞≤12 X1, X2′,X2〞,X3, X4′,X4〞≥0 则对偶规划为:. minp= -5y1′+ 5y1〞-6y2 + 12y3 s.t. 2y1′-2y1〞-6y2 + 10y3≥2 -y1′+y1〞-5y2 -9y3≥2 y1′-y1〞+5y2 + 9y3≥-2 3y1′-3y1〞+y2 + 6y3≥-5 3y1′-3y1〞-5y2 + 4y3≥2 -3y1′+3y1〞+5y2 -4y3≥-2 即: minp= -5y1′+ 5y1〞-6y2 + 12y3
47页 用图解法找不到满足所有约束条件的公共范围,所以该问题无可行解47页 无界解
(b) 约束方程的系数矩阵 A= 1 2 3 4 () 2 1 1 2 P1 P2 P3 P4 最优解A=(0 1/2 2 0)T和(0 0 1 1)T 49页13题 设Xij为第i月租j个月的面积 minz=2800x11+2800x21+2800x31+2800x41+4500x12+4500x22+4500x32+6000x13 +6000x23+7300x14 . x11+x12+x13+x14≥15 x12+x13+x14+x21+x22+x23≥10 x13+x14+x22+x23+x31+x32≥20 x14+x23+x32+x41≥12 Xij≥0 用excel求解为:
用LINDO求解: LP OPTIMUM FOUND AT STEP 3 OBJECTIVE FUNCTION VALUE 1) VARIABLE VALUE REDUCED COST Z X11 X21 X31 X41 X12 X22 X32 X13 X23 X14 ROW SLACK OR SURPLUS DUAL PRICES 2) 3) 4) 5) NO. ITERATIONS= 3 答若使所费租借费用最小,需第一个月租一个月租期300平方米,租四个月租期1200平方米,第三个月租一个月租期800平方米, 50页14题 设a1,a2,a3, a4, a5分别为在A1, A2, B1, B2, B3加工的Ⅰ产品数量,b1,b2,b3分别为在A1, A2, B1加工的Ⅱ产品数量,c1为在A2,B2上加工的Ⅲ产品数量。则目标函数为‘ maxz= a1+a2+a3)+( b3+( (a1+b1)- (a2+b2+c1)- (a3+b3)(a4+c1)-0.05a5 =0. 95a1+0. 97a2+0. 94a3++2.1c-0.11a-0.05a . 5a1+10b1≤6000 7a2+b2+12c1≤10000
清华第三版 运筹学 答案[键入文字] [键入文字] [键入文字] 运筹学教程 1. 某饲养场饲养动物出售,设每头动物每天至少需700g 蛋白质、30g 矿物质、100mg 维生素。现有五种饲料可供选用,各种饲料每kg 营养成分含量及单价如表1所示。 表1 要求确定既满足动物生长的营养需要,又使费用最省的选用饲料的方案。 解:设总费用为Z 。i=1,2,3,4,5代表5种饲料。i x 表示满足动物生长的营养需要时,第i 种饲料所需的数量。则有: ????? ? ?=≥≥++++≥++++≥++++++++=5,4,3,2,1,01008.022.05.0305.022.05.07008623..8.03.04.07.02.0min 54321543215432154321i x x x x x x x x x x x x x x x x t s x x x x x Z i 2. 某医院护士值班班次、每班工作时间及各班所需护士数如表2所示。每班护士值班 开始时间向病房报道,试决定: (1) 若护士上班后连续工作8h ,该医院最少需要多少名护士,以满足轮班需要; (2) 若除22:00上班的护士连续工作8h 外(取消第6班),其他班次护士由医院 排定上1~4班的其中两个班,则该医院又需要多少名护士满足轮班需要。 表2
6 2:00~6:00 30 解:(1)设x 第i 班开始上班的人数,i=1,2,3,4,5,6 ???????????=≥≥+≥+≥+≥+≥+≥++++++=且为整数 6,5,4,3,2,1,030 2050607060..min 655443 322161 654321i x x x x x x x x x x x x x t s x x x x x x Z i 解:(2)在题设情况下,可知第五班一定要30个人才能满足轮班需要。则设设i x 第i 班开始上班的人数,i=1,2,3,4。 ??? ????? ?? ??? ??=≥=+++=≥+++=+++=≥+++=+++=≥+++=+++=≥+++++++=4 ,3,2,1,1002 1502 16021702 ,160..30 min i 444342414444433422411434 33323133 443333223113242322212244233222211214131211114413312211114321j i y x y y y y y x y x y x y x y y y y y y x y x y x y x y y y y y y x y x y x y x y y y y y y x y x y x y x y t s x x x x Z ij 变量,—是,,,第四班约束,,第三班约束,,第二班约束,第一班约束 3. 要在长度为l 的一根圆钢上截取不同长度的零件毛坯,毛坯长度有n 种,分别为j a (j=1,2,…n )。问每种毛坯应当截取多少根,才能使圆钢残料最少,试建立本问题的数学模型。 解:设i x 表示各种毛坯的数量,i=1,2,…n 。
运筹学[胡运权]第五版课后 答案,运筹作业 -标准化文件发布号:(9456-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII
47页1.1b 用图解法找不到满足所有约束条件的公共范围,所以该问题无可行解47页1.1d 无界解
1.2(b) 约束方程的系数矩阵 A= 1 2 3 4 ( ) 2 1 1 2 P1 P2 P3 P4 最优解A=(0 1/2 2 0)T和(0 0 1 1)T 49页13题 设Xij为第i月租j个月的面积 minz=2800x11+2800x21+2800x31+2800x41+4500x12+4500x22+4500x32+6000x13 +6000x23+7300x14 s.t. x11+x12+x13+x14≥15 x12+x13+x14+x21+x22+x23≥10 x13+x14+x22+x23+x31+x32≥20 x14+x23+x32+x41≥12 Xij≥0 用excel求解为:
用LINDO求解: LP OPTIMUM FOUND AT STEP 3 OBJECTIVE FUNCTION VALUE 1) 118400.0 VARIABLE VALUE REDUCED COST Z 0.000000 1.000000 X11 3.000000 0.000000
X21 0.000000 2800.000000 X31 8.000000 0.000000 X41 0.000000 1100.000000 X12 0.000000 1700.000000 X22 0.000000 1700.000000 X32 0.000000 0.000000 X13 0.000000 400.000000 X23 0.000000 1500.000000 X14 12.000000 0.000000 ROW SLACK OR SURPLUS DUAL PRICES 2) 0.000000 -2800.000000 3) 2.000000 0.000000 4) 0.000000 -2800.000000 5) 0.000000 -1700.000000 NO. ITERATIONS= 3 答若使所费租借费用最小,需第一个月租一个月租期300平方米,租四个月租期1200平方米,第三个月租一个月租期800平方米,
1. 某饲养场饲养动物出售,设每头动物每天至少需700g 蛋白质、30g 矿物质、100mg 维生素。现有五种饲料可供选用,各种饲料每kg 营养成分含量及单价如表1所示。 表1 要求确定既满足动物生长的营养需要,又使费用最省的选用饲料的方案。 解:设总费用为Z 。i=1,2,3,4,5代表5种饲料。i x 表示满足动物生长的营养需要时,第i 种饲料所需的数量。则有: ????? ? ?=≥≥++++≥++++≥++++++++=5,4,3,2,1,01008.022.05.0305.022.05.07008623..8.03.04.07.02.0min 54321543215432154321i x x x x x x x x x x x x x x x x t s x x x x x Z i 2. 某医院护士值班班次、每班工作时间及各班所需护士数如表2所示。每班护士值班 开始时间向病房报道,试决定: (1) 若护士上班后连续工作8h ,该医院最少需要多少名护士,以满足轮班需要; (2) 若除22:00上班的护士连续工作8h 外(取消第6班),其他班次护士由医院 排定上1~4班的其中两个班,则该医院又需要多少名护士满足轮班需要。 表2
解:(1)设x 第i 班开始上班的人数,i=1,2,3,4,5,6 ???????????=≥≥+≥+≥+≥+≥+≥++++++=且为整数 6,5,4,3,2,1,030 2050607060..min 655443 322161 654321i x x x x x x x x x x x x x t s x x x x x x Z i 解:(2)在题设情况下,可知第五班一定要30个人才能满足轮班需要。则设设i x 第i 班开始上班的人数,i=1,2,3,4。 ??? ????? ?? ??? ??=≥=+++=≥+++=+++=≥+++=+++=≥+++=+++=≥+++++++=4 ,3,2,1,1002 1502 16021702 ,160..30 min i 444342414444433422411434 33323133 443333223113242322212244233222211214131211114413312211114321j i y x y y y y y x y x y x y x y y y y y y x y x y x y x y y y y y y x y x y x y x y y y y y y x y x y x y x y t s x x x x Z ij 变量,—是,,,第四班约束,,第三班约束,,第二班约束,第一班约束 3. 要在长度为l 的一根圆钢上截取不同长度的零件毛坯,毛坯长度有n 种,分别为j a (j=1,2,…n )。问每种毛坯应当截取多少根,才能使圆钢残料最少,试建立本问题的数学模型。 解:设i x 表示各种毛坯的数量,i=1,2,…n 。 ?????≤= ∑∑==是整数i 1 1 1max x x a x a Z i i n i i i n i
《运筹学》第五章习题 1.思考题 (1)试述动态规划的“最优化原理”及它同动态规划基本方程之间的关系。(2)动态规划的阶段如何划分? (3)试述用动态规划求解最短路问题的方法和步骤。 (4)试解释状态、决策、策略、最优策略、状态转移方程、指标函数、最优值函数、边界函数等概念。 (5)试述建立动态规划模型的基本方法。 (6)试述动态规划方法的基本思想、动态规划的基本方程的结构及正确写出动态规划基本方程的关键步骤。 2.判断下列说法是否正确 (1)动态规划分为线性动态规划和非线性动态规划。 (2)动态规划只是用来解决和时间有关的问题。 (3)对于一个动态规划问题,应用顺推法和逆推法可能会得到不同的最优解。 (4)在用动态规划的解题时,定义状态时应保证各个阶段中所做的决策的相互独立性。 (5)在动态规划模型中,问题的阶段等于问题的子问题的数目。 (6)动态规划计算中的“维数障碍”,主要是由于问题中阶段数的急剧增加 而引起的。 3.计算下图所示的从A 到E 的最短路问题 4.计算下图所示的从A 到E 的最短路问题 5.计算从A 到B、C、D 的最短路线。已知各线段的长度如下图所示。
6.设某油田要向一炼油厂用管道供应油料,管道铺设途中要经过八个城镇,各 城镇间的路程如下图所示,选择怎样的路线铺设,才使总路程最短? 7.用动态规划求解下列各题 (1).2 22211295m a x x x x x z -+-=; ?? ?≥≤+0,52 121x x x x ; (2). 3 3 221m a x x x x z = ?? ?≥≤++0,,6321 321x x x x x x ; 8.某人外出旅游,需将3种物品装入背包,但背包重量有限制,总重量不超过 10千克。物品重量及其价值等数据见下表。试问每种物品装多少件,使整个 背包的价值最大? 913 千克。物品重量及其价值的关系如表所示。试问如何装这些物品,使整个背包 价值最大? 10 量和相应单位价值如下表所示,应如何装载可使总价值最大? 30 30
运筹学习题答案 第一章(39页) 1.1用图解法求解下列线性规划问题,并指出问题是具有唯一最优解、无穷多最优解、无界解还是无可行解。 (1)max 12z x x =+ 51x +102x ≤50 1x +2x ≥1 2x ≤4 1x ,2x ≥0 (2)min z=1x +1.52x 1x +32x ≥3 1x +2x ≥2 1x ,2x ≥0 (3)max z=21x +22x 1x -2x ≥-1 -0.51x +2x ≤2 1x ,2x ≥0 (4)max z=1x +2x 1x -2x ≥0 31x -2x ≤-3 1x ,2x ≥0 解: (1)(图略)有唯一可行解,max z=14 (2)(图略)有唯一可行解,min z=9/4 (3)(图略)无界解 (4)(图略)无可行解 1.2将下列线性规划问题变换成标准型,并列出初始单纯形表。
(1)min z=-31x +42x -23x +54x 41x -2x +23x -4x =-2 1x +2x +33x -4x ≤14 -21x +32x -3x +24x ≥2 1x ,2x ,3x ≥0,4x 无约束 (2)max k k z s p = 11 n m k ik ik i k z a x ===∑∑ 1 1(1,...,)m ik k x i n =-=-=∑ ik x ≥0 (i=1…n; k=1,…,m) (1)解:设z=-z ',4x =5x -6x , 5x ,6x ≥0 标准型: Max z '=31x -42x +23x -5(5x -6x )+07x +08x -M 9x -M 10x s. t . -41x +2x -23x +5x -6x +10x =2 1x +2x +33x -5x +6x +7x =14 -21x +32x -3x +25x -26x -8x +9x =2 1x ,2x ,3x ,5x ,6x ,7x ,8x ,9x ,10x ≥0
运筹学作业2(第二章部分习题)答案 2.1 题 (P . 77) 写出下列线性规划问题的对偶问题: (1)123123123123123max 224..34223343500,z x x x s t x x x x x x x x x x x x =++??++≥??++≤??++≤?≥≥??无约束 ,; 解:根据原—对偶关系表,可得原问题的对偶规划问题为: 123123123123123max 235..22342 4334,0,0w y y y s t y y y y y y y y y y y y =++??++≤??++≤??++=?≥≤≤?? (2)1111min ,1,,,1,,0,1,,;1,,m n ij ij i j n ij ij i j n ij ij j j ij z c x c x a i m c x b j n x i m j n ====?=???==????==??≥==??∑∑∑∑L L L L 解:根据原—对偶关系表,可得原问题的对偶规划问题为: 11max 1,,;1,,m n i i j j i j i j ij i w a u b v u v c i m j n u ==?=+???+≤??==???∑∑L L j 无约束,v 无约束 2.2判断下列说法是否正确,为什么 (1) 如果线性规划的原问题存在可行解,则其对偶问题也一定存在可行解; 答:错。 因为:若线性规划的原问题存在可行解,且其对偶问题有可行解,则原问题和可行问题都将有最优解。但,现实中肯定有一些问题是无最优解的,故本题说法不对。
例如原问题12 1221 2max 31..3 0,0z x x x x s t x x x =++≥??≤??≥≥?有可行解,但其对偶问题 12 1121 2min 33..1 0,0w y y y s t y y y y =+≥??+≥??≤≥?无可行解。 (2) 如果线性规划的对偶问题无可行解,则原问题也一定无可行解; 答:错,如(1)中的例子。 (3) 在互为对偶的一对原问题与对偶问题中,不管原问题是求极大或求极小,原问题可 行解的目标函数值一定不超过其对偶问题可行解的目标函数值。 答:错。正确说法是:在互为对偶的一对原问题与对偶问题中,求极大的问题可行解的目标函数值一定不超过求极小的问题可行解的目标函数值。 (4) 任何线性规划问题具有唯一的对偶问题。 答:正确。 2.5给出线性规划问题 123 123123123123max 221.. 22 0,0,0z x x x x x x x x x s t x x x x x x =+++-≤??-+=??++≥??≥≥≥? 写出其对偶问题;(2)利用对偶问题性质证明原问题目标函数值1z ≤ 解:(1)原问题的对偶问题为: 123 123123123123min 22212..10,,0 w y y y y y y y y y s t y y y y y y =++++≥??-+≤??-++=??≥≤?无约束 (2)取()011T y =,既1230,1,0y y y ===,经验证,()011T y =是对偶问题的 一个可行解,并且1w =。由对偶问题的性质可得1z w ≤= 2.9 用对偶单纯形法求解下列线性规划问题: (2)123 123123123min 524324..63510,,0z x x x x x x s t x x x x x x =++++≥??++≥??≥? ,
第一章 线性规划 1、 由图可得:最优解为 2、用图解法求解线性规划: Min z=2x 1+x 2 ????? ??≥≤≤≥+≤+-01058 2442 12121x x x x x x 解: 由图可得:最优解x=1.6,y=6.4
Max z=5x 1+6x 2 ? ?? ??≥≤+-≥-0 ,23222212 121x x x x x x 解: 由图可得:最优解Max z=5x 1+6x 2, Max z= +∞
Maxz = 2x 1 +x 2 ????? ? ?≥≤+≤+≤0,5242261552121211x x x x x x x 由图可得:最大值?????==+35121x x x , 所以?????==2 3 21x x max Z = 8.
12 12125.max 2328416412 0,1,2maxZ .j Z x x x x x x x j =+?+≤? ≤?? ≤??≥=?如图所示,在(4,2)这一点达到最大值为2 6将线性规划模型化成标准形式: Min z=x 1-2x 2+3x 3 ????? ??≥≥-=++-≥+-≤++无约束 321 321321321,0,05232 7x x x x x x x x x x x x 解:令Z ’=-Z,引进松弛变量x 4≥0,引入剩余变量x 5≥0,并令x 3=x 3’-x 3’’,其中 x 3’≥0,x 3’’≥0 Max z ’=-x 1+2x 2-3x 3’+3x 3’’ ????? ? ?≥≥≥≥≥≥-=++-=--+-=+-++0 ,0,0'',0',0,05 232 '''7'''543321 3215332143321x x x x x x x x x x x x x x x x x x x
计算题一一 1. 下列线性规划问题化为标准型。 (10分) mi nZ x-|+5x 2-2x 3 min Z 4为 2x 2+3x 3 4x ,+5x 2 6X 3=7 8% 9x 2 10x 3 11 12% 13x 2 14 X 1 0,X 2 无约束,X 3 B1 B2 B3 B4 产量 A1 10 6 7 12 4 16 10 & 9 9 A3 5 4 10 10 4 销S 5 2 4 6 i (i 1,2,3)的投资额为x 时,其收益分别为 g 1(x 1) 4禺4区) g (x 3) 2x3 ,问应如何分配投资数额才能使总收益最大? (15分) 5.求图中所示网络中的最短路。 (15分) 计算题二 X 1 X 2 X 3 6 2x 1 X 2 3x 3 5 X 1 X 2 10 X 1 0,X 2 0,X 3符号不 限 满足 〈 2. 写出下列问题的对偶问题 (10分) 9x 2,
5.某项工程有三个设计方案。 据现有条件,这些方案不能按期完成的概率分别为 0.5,0.7,0.9, 1某工厂拥有 A,B,C 三种类型的设备,生产甲、乙两种产品,每件产品在生产中需要使用 的机时数, (2)利用单纯形法求最优解;(15分) 2、用对偶理论判断下面缰性规划是否存在最优解:〔10分)屮 maxz = 2孔 +2x 3 * 满足: J 対+ 2皿叫 3. 判断下表中的启案能否作为恚上作业法求解运输间题的初始启宪,说朋理由.ho 分 n 4.如图所示的单行线交通网,每个弧旁边的数字表示这条单行线的长度。现在有一个人要 从V l 出发,经过这个交通网到达 V8,要寻求使总路程最短的线路。 (15分) ■.■'2 1