1.实验7-1 传染病模型2

河北大学《数学模型》实验实验报告

一、实验目的

二、实验要求

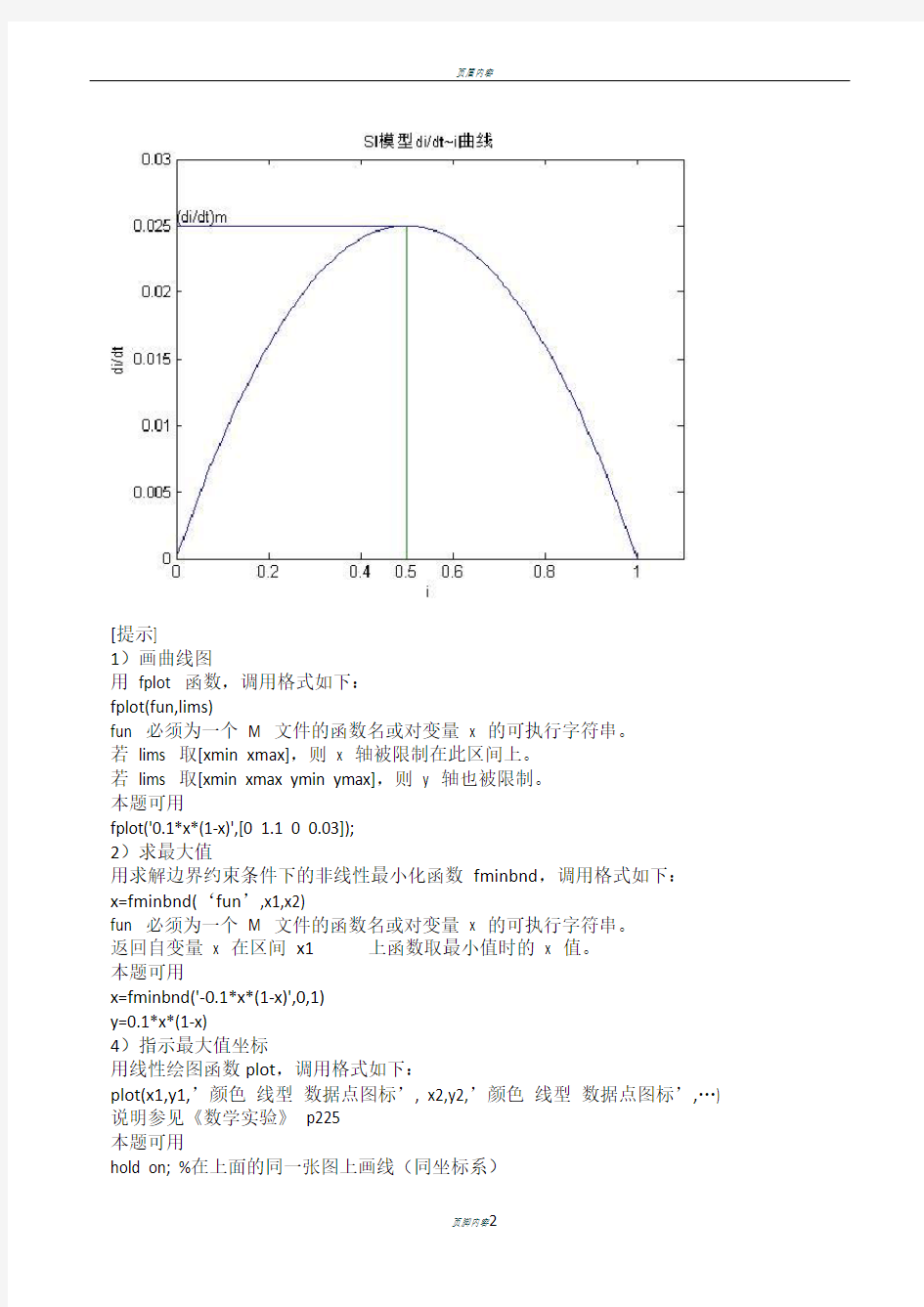
1.实验7-1 传染病模型2（SI模型）——画di/dt~ i曲线图

（参考教材p137-138）

传染病模型2（SI 模型）：

di/dt=ki(1-i),i(0)=i0;

其中，i(t)是第t 天病人在总人数中所占的比例。

λ是每个病人每天有效接触的平均人数（日接触率）。

i0是初始时刻（t=0）病人的比例。

取k=0.1，画出di/dt~ i 曲线图，求i 为何值时di/dt达到最大值，并在曲线图上标注。试编写一个m 文件来实现。

参考程序运行结果（在图形窗口菜单选择Edit/Copy Figure，复制图形）：

[提示]

1）画曲线图

用fplot 函数，调用格式如下：

fplot(fun,lims)

fun 必须为一个M 文件的函数名或对变量x 的可执行字符串。

若lims 取[xmin xmax]，则x 轴被限制在此区间上。

若lims 取[xmin xmax ymin ymax]，则y 轴也被限制。

本题可用

fplot('0.1*x*(1-x)',[0 1.1 0 0.03]);

2）求最大值

用求解边界约束条件下的非线性最小化函数fminbnd，调用格式如下：

x=fminbnd(‘fun’,x1,x2)

fun 必须为一个M 文件的函数名或对变量x 的可执行字符串。

返回自变量x 在区间x1

本题可用

x=fminbnd('-0.1*x*(1-x)',0,1)

y=0.1*x*(1-x)

4）指示最大值坐标

用线性绘图函数plot，调用格式如下：

plot(x1,y1,’颜色线型数据点图标’, x2,y2,’颜色线型数据点图标’,…) 说明参见《数学实验》p225

本题可用

hold on; %在上面的同一张图上画线（同坐标系）

plot([0,x],[y,y],':',[x,x],[0,y],':');

3）图形的标注

使用文本标注函数text，调用格式如下：

格式 1

text(x,y,文本标识内容,’HorizontalAlignment’,’字符串1’)

x,y 给定标注文本在图中添加的位置。

’HorizontalAlignment’为水平控制属性，控制文本标识起点位于点(x,y)同一水平线

上。

’字符串1’为水平控制属性值，取三个值之一：

‘left’，点(x,y)位于文本标识的左边。

‘center’，点(x,y)位于文本标识的中心点。

‘right’，点(x,y)位于文本标识的右边。

格式 2

text(x,y, 文本标识内容,’VerticalAlignment’,’字符串2’)

x,y 给定标注文本在图中添加的位置。

’VerticalAlignment’为垂直控制属性，控制文本标识起点位于点(x,y)同一垂直线上。

’字符串1’为垂直控制属性值，取四个值之一：

‘middle’，’top’，’cap’，’baseline’，’bottom’。（对应位置可在命令窗口应用确

定）

本题可用

text(0,y,'(di/dt)m','VerticalAlignment','bottom');

text(x,-0.001,num2str(x),'HorizontalAlignment','center');

4）坐标轴标注

调用函数xlabel，ylabel 和title

本题可用

title('SI模型di/dt~i曲线');

xlabel('i');

ylabel('di/dt');

2.实验7-2 传染病模型2（SI模型）——画i~t曲线图

（参考教材p137-138）

传染病模型2（SI 模型）：

di/dt=ki(1-i),i(0)=i0;

其中，

i(t)是第t 天病人在总人数中所占的比例。

k 是每个病人每天有效接触的平均人数（日接触率）。

i0是初始时刻（t=0）病人的比例

求出微分方程的解析解i(t)，画出如下所示的i~t 曲线（i(0)=0.15, k=0.2,

t=0~30）。试编写一个m 文件来实现。（在图形窗口菜单选择Edit/Copy Figure，复制图形）

[提示]

1）求解微分方程

常微分方程符号解用函数dsolve,调用格式如下：

dsolve(‘equ1’,’equ2’,…,’变量名’)

以代表微分方程及初始条件的符号方程为输入参数，多个方程或初始条件可在一个输入变量内联立输入，且以逗号分隔。

默认的独立变量为t，也可把t 变为其他的符号变量。

字符 D 代表对独立变量的微分，通常指d/dt。

本题可用

x=dsolve(‘Dx=k*x*(1-x)’,’x(0)=x0’)

2) 画出i~t 曲线（i(0)=0.15, λ=0.2, t=0~30）

用for 循环，函数length, eval, plot, axis, title, xlabel, ylabel

3.实验7-3 传染病模型3（SIS模型）——画di/dt~ i曲线图

（参考教材p138-139）

已知传染病模型3（SIS 模型）：

di/dt=- i[i-(1-1/ )],i(0)=i0

其中，

i(t)是第t 天病人在总人数中所占的比例。

λ是每个病人每天有效接触的平均人数（日接触率）。

i0是初始时刻（t=0）病人的比例。

σ是整个传染期内每个病人有效接触的平均人数（接触数）。

取λ=0.1，σ=1.5，画出如下所示的di/dt~ i曲线图。试编写一个m 文件来实现。（在图

形窗口菜单选择Edit/Copy Figure，复制图形）

[提示]

用fplot函数画出di/dt~ i曲线图；

在上图上用plot函数画一条过原点的水平

用title, xlabel, ylabel标注。

4.实验7-4 传染病模型3（SIS模型）——画i~t曲线图

（参考教材p138-139）

已知传染病模型3（SIS 模型）：

di/dt=- i[i-(1-1/ )],i(0)=i0

其中，

i(t)是第t 天病人在总人数中所占的比例。

λ 是每个病人每天有效接触的平均人数（日接触率）。

i0是初始时刻（t=0）病人的比例。

σ 是整个传染期内每个病人有效接触的平均人数（接触数）。

实验要求:

求出微分方程的解析解i(t)。取λ =0.2, σ =3, t=0~40，画出如下所示的图形。试编写一个m 文件来实现。

其中

蓝色实线为i(0)=0.2 时的i~t 曲线（第 1 条）；

黑色虚点线为过点（0, 1-1/σ ）的水平线（第 2 条）；

红色虚线为i(0)=0.9 时的i~t 曲线（第 3 条）。

[提示]

图例标注可用

legend('i(0)=0.2','1-1/|σ ','i(0)=0.9');

5.实验7-5 传染病模型4（SIR模型）

（参考教材p140-141）

SIR 模型的方程:di/dt= si- i i(0)=i0

ds/dt=- si s(0)=s0

实验要求：

1．设λ =1，μ =0.3，i(0)=0.02，s(0)=0.98。输入p139 的程序，并修改程序中

的[t,x]，使得输出的数据格式如下（提示：取 4 位小数，使用四舍五入取整函数round，矩阵剪裁和拼接）：

ans =

Columns 1 through 6

0 1 2 3 4 5

0.02 0.039 0.0732 0.1285 0.2033 0.2795

0.98 0.9525 0.9019 0.8169 0.6927 0.5438

Columns 7 through 12

6 7 8 9 10 15

0.3312 0.3444 0.3247 0.2863 0.2418 0.0787

0.3995 0.2839 0.2027 0.1493 0.1145 0.0543

Columns 13 through 18

20 25 30 35 40 45

三、实验内容

1.实验7-1 传染病模型2（SI模型）——画di/dt~ i曲线图在matlab中建立M文件fun1.m

代码如下：

function y=fun(x)

k=0.1;

y=k*x*[1-x];

Fun2.m

代码如下：

function y=fun(x)

k=0.1;

y=-k*x*[1-x];

在命令行输入以下代码：

fplot('fun1',[0 1.1 0 0.03]);

x=fminbnd('fun2',0,1);

y=0.1*x*(1-x);

hold on;

plot([0,x],[y,y],'-',[x,x],[0,y],'-');

text(0,y,'(di/dt)m','VerticalAlignment','bottom');

text(x,-0.001,num2str(x),'HorizontalAlignment','center');

title('SI模型di/dt~i曲线');

xlabel('i');

ylabel('di/dt');

hold off

2.实验7-2 传染病模型2（SI模型）——画i~t曲线图

在matlab中建立M文件fun22.m

代码如下：

k=0.2;

x0=0.15;

x=dsolve('Dx=k*x*(1-x)','x(0)=x0');

tt=linspace(0,31,1001);

for i=1:1001

t=tt(i);

xx(i)=eval(x);

end

plot(tt,xx)

axis([0,31,0,1.1]);

title('图1 SI模型i~t曲线');

xlabel('t(天)');

ylabel('i（病人所占比例）');

在命令行输入以下代码：

fun22;

3.实验7-3 传染病模型3（SIS模型）——画di/dt~ i曲线图在matlab中建立M文件fun3.m

代码如下：

function y=fun(x)

a=0.1;

b=1.5;

y=-a*x*[x-(1-1/b)];

在命令行输入以下代码：

fplot('fun3',[0 0.4 -0.0005 0.003]);

x=fminbnd('fun3',0,1);

title('SIS模型di/dt~i曲线');

xlabel('i');

ylabel('di/dt');

>> hold on

>> plot([0,0.4],[0,0])

4.实验7-4 传染病模型3（SIS模型）——画i~t曲线图

在matlab中建立M文件fun4.m

代码如下：

function y=fun(x)

x=dsolve('Dx=-0.2*x*(x-(1-1/3))','x(0)=0.2');

tt=linspace(0,41,1001);

for i=1:1001

t=tt(i);

xx(i)=eval(x);

end

plot(tt,xx);

hold on;

plot([0,40],[1-1/3,1-1/3],'-k');

x=dsolve('Dx=-0.2*x*(x-(1-1/3))','x(0)=0.9');

tt=linspace(0,41,1001);

for i=1:1001

t=tt(i);

xx(i)=eval(x);

end

plot(tt,xx,'-r');

axis([0,40,0,1]);

title('图1 SI模型i~t曲线(λ=0.2, σ=3)');

xlabel('t(天)');

ylabel('i（病人所占比例）');

legend('i(0)=0.2','1-1/σ','i(0)=0.9');

在命令行输入以下代码：

fun4;

5.实验7-5 传染病模型4（SIR模型）

在matlab中建立M文件fun5.m

代码如下：

function y=fun(t,x)

a=1;

b=0.3;

y=[a*x(1)*x(2)-b*x(1),-a*x(1)*x(2)]';

在命令行输入以下代码：

>> ts=0:50;

>> x0=[0.02,0.98];

>> [t,x]=ode45('fun5',ts,x0);

>> plot(t,x(:,1),t,x(:,2)),grid,pause

>> plot(x(:,2),x(:,1)),grid,

四、实验结果及其分析

1.实验7-1 传染病模型2（SI模型）——画di/dt~ i曲线图

分析：

当i=1/2时di/dt达到最大值(di/dt)m ,这时病人增加得在最快，可以认为是医院的门诊量最大的一天，预示着传染病高潮的到来，是医疗卫生部门关注的时刻。当t趋近于无穷时i趋近于1，即所有人终将被传染，全部变成病人，着显然不符合实际。原因是模型中没有考虑到病人可以治愈，人群中的健康者只能变成病人，病人不会再变成健康者。

2.实验7-2 传染病模型2（SI模型）——画i~t曲线图

分析：

当i=1/2时di/dt达到最大值(di/dt)m ,这时病人增加得在最快，可以认为是医院的门诊量最大的一天，预示着传染病高潮的到来，是医疗卫生部门关注的时刻。当t趋近于无穷时i趋近于1，即所有人终将被传染，全部变成病人，着显然不符合实际。原因是模型中没有考虑到病人可以治愈，人群中的健康者只能变成病人，病人不会再变成健康者。

3.实验7-3 传染病模型3（SIS模型）——画di/dt~ i曲线图

分析：

是一个阈值，当>1时,i(t)的增减性取决于i0的大小，但其极限值i(无穷)=1-1/,随的增加而增加（试从的含义给予解释）；当<=1时，病人的比例i(t)越来越小。最终趋近于0，这是由于传染期内经有效接触从而使健康者变成病人数不超过原来的病人数的缘故。

4.实验7-4 传染病模型3（SIS模型）——画i~t曲线图

分析：

是一个阈值，当>1时,i(t)的增减性取决于i0的大小，但其极限值i(无穷)=1-1/,随的增加而增加（试从的含义给予解释）；当<=1时，病人的比例i(t)越来越小。最终趋近于0，这是由于传染期内经有效接触从而使健康者变成病人数不超过原来的病人数的缘故。

5.实验7-5 传染病模型4（SIR模型）

ans =

0 0.0200 0.9800

1.0000 0.0390 0.9525

2.0000 0.0732 0.9019

3.0000 0.1285 0.8169

4.0000 0.2033 0.6927

5.0000 0.2795 0.5438

6.0000 0.3312 0.3995

7.0000 0.3444 0.2839

8.0000 0.3247 0.2027

9.0000 0.2863 0.1493

10.0000 0.2418 0.1145

11.0000 0.1986 0.0917

12.0000 0.1599 0.0767

13.0000 0.1272 0.0665

14.0000 0.1004 0.0593

15.0000 0.0787 0.0543

16.0000 0.0614 0.0507

17.0000 0.0478 0.0480

18.0000 0.0371 0.0460

19.0000 0.0287 0.0445

20.0000 0.0223 0.0434

21.0000 0.0172 0.0426

22.0000 0.0133 0.0419

23.0000 0.0103 0.0415

24.0000 0.0079 0.0411

25.0000 0.0061 0.0408

26.0000 0.0047 0.0406

27.0000 0.0036 0.0404

28.0000 0.0028 0.0403

29.0000 0.0022 0.0402

30.0000 0.0017 0.0401

31.0000 0.0013 0.0400

32.0000 0.0010 0.0400

33.0000 0.0008 0.0400

34.0000 0.0006 0.0399

35.0000 0.0005 0.0399

36.0000 0.0004 0.0399

37.0000 0.0003 0.0399

38.0000 0.0002 0.0399

39.0000 0.0002 0.0399

40.0000 0.0001 0.0399

41.0000 0.0001 0.0399

42.0000 0.0001 0.0399

43.0000 0.0001 0.0399

44.0000 0.0000 0.0398

45.0000 0.0000 0.0398

46.0000 0.0000 0.0398

47.0000 0.0000 0.0398

48.0000 0.0000 0.0398

49.0000 0.0000 0.0398

50.0000 0.0000 0.0398

分析：

如果仅当病人比例i（t）有一段增长的时期才认为传染病在蔓延，那么1/σ是一个阈值，当

s0>1/σ时传染病就会蔓延，而减小传染期接触数σ，即提高阈值1/σ，是的s0<=1/σ，传染病就不会蔓延。σ减小时，s∞增加，im降低，也控制了蔓延的程度。在σ=λ/μ中，人们的卫生水平提高，日接触率λ越小；医疗水平越高，日治愈率μ越大，于是σ越小，所以提高卫生水平和医疗水平有助于控制传染病的蔓延。

数学建模之传染病模型

第五章 微 分 方 程 模 型 如果实际对象的某特性是随时间（或空间）变化的，那么分析它的变化规律，预测它的未来性态时，通常要建立此实际对象的动态模型，这就是微分方程模型. §1 传 染 病 模 型 建立传染病的数学模型来描述传染病的传播过程，分析受感染人数的变化规律，预报传染病高潮的到来等，一直是各国有关专家和官员关注的课题. 考虑某地区的传染病的传染情况，设该地区人口总数为N ，既不考虑生死，也不考虑迁移，时间以天为计量单位. 一. SI 模 型 假设条件： 1. 人群分为易感染者(Susceptible )和已感染者(Infective )两类人，简称为健康人 和病人，在时刻t 这两类人在总人数中所占比例分别记作()t s 和()t i . 2. 每个病人每天有效接触的平均人数是λ(常数)，λ称为日接触率，当病人与健康 人有效接触时，使健康者受感染变为病人. 试建立描述()t i 变化的数学模型. 解： ()()1=+t i t s ()()N N t i N t s =+∴ 由假设2知，每个病人每天可使()t s λ个健康者变为病人，又由于病人数为 ()t i N ，∴每天共有()()t i N t s λ个健康人被感染. 于是i s N λ就是病人数i N 的增加率，即有 i s N dt di N λ= (1)

i s dt di λ=∴ 而1=+i s . 又记初始时刻(0=t )病人的比例为0i ，则 ()()?????=-=0 01i i i i dt di λ 这就是Logistic 模型，其解为 ()t e i t i λ-??? ? ??-+= 11110 ［结果分析］ 作出()t t i ~和i dt di ~的图形如下： 1. 当2 1=i 时，dt di 取到最大值m dt di ?? ? ??，此时刻为 ??? ? ??-=-11ln 01i t m λ 2. 当∞→t 时，1→i 即所有人终将被传染，全变为病人（这是不实际的）. 二. SIS 模 型 在前面假设1、2之下，再考虑病人可以医治，并且有些传染病如伤风、痢疾等愈后免疫力很低，可以假定无免疫性，于是病人被治愈后变成健康者，健康者还可以被感染再变成病人，此模型称SIS 模型.

数学建模 传染病模型

传染病模型 摘要 当今社会，人们开始意识到通过定量地研究传染病的传播规律，建立传染病的传播模型，可以为预测和控制传染病提供可靠、足够的信息。本文利用微分方程稳定性理论对传统传染病动力学建模方式进行综述，且针对甲流，SARS等新生传染病模型进行建模和分析。 不同类型的传染病的传播过程有其各自不同的特点，我们不是从医学的角度一一分析各种传染病的传播，而是从一般的传播机理分析建立各种模型，如简单模型，SI模型，SIS模型，SIR模型等。本文中，我们应用传染病动力学模型来描述疾病发展变化的过程和传播规律，运用联立微分方程组体现疫情发展过程中各类人的内在因果联系，并在此基础上建立方程求解算法。然后，通过借助Matlab程序拟合出与实际较为符合的曲线并进行了疫情预测，评估各种控制措施的效果，从而不断完善文中的模型。 本文由简到难、全面地评价了该模型的合理性与实用性，而后对模型和数据也做了较为扼要的分析，进一步改进了模型的不妥之处。同时，在对问题进行较为全面评价的基础上又引入更为全面合理的假设，运用双线性函数模型对卫生部的措施进行了评价并给出建议，做好模型的完善与优化工作。 关键词：传染病模型,简单模型，SI，SIS,SIR，微分方程，Matlab。

一、问题重述 有一种传染病（如SARS、甲型H1N1）正在流行，现在希望建立适当的数学模型，利用已经掌握的一些数据资料对该传染病进行有效地研究，以期对其传播蔓延进行必要的控制，减少人民生命财产的损失。考虑如下的几个问题，建立适当的数学模型，并进行一定的比较分析和评价展望。 1、不考虑环境的限制，设单位时间内感染人数的增长率是常数，建立模型求t 时刻的感染人数。 2、假设单位时间内感染人数的增长率是感染人数的线性函数，最大感染时的增长率为零。建立模型求t时刻的感染人数。 3、假设总人口可分为传染病患者和易感染者，易感染者因与患病者接触而得病，而患病者会因治愈而减少且对该传染病具有很强的免疫功能，建立模型分析t 时刻患病者与易感染者的关系，并对传染情况（如流行趋势，是否最终消灭）进行预测。 二、问题分析 1、这是一个涉及传染病传播情况的实际问题，其中涉及传染病感染人数随时间的变化情况及一些初始资料，可通过建立相应的微分方程模型加以解决。 2、问题表述中已给出了各子问题的一些相应的假设。 3、在实际中，感染人数是离散变量，不具有连续可微性，不利于建立微分方程模型。但由于短时间内改变的是少数人口，这种变化与整体人口相比是微小的。 因此，为了利用数学工具建立微分方程模型，我们还需要一个基本假设：感染人数是时间的连续可微函数。 三、模型假设 模型二和模型三的假设条件： 假设一：在疾病传播期内所考察地区的总人数N不变，即不考虑生死，也不考虑迁移。人群分为易感染者（Susceptible）和已感染者（Infective）两类（取两个词的第一个字母，称之为SI模型），以下简称健康者和病人。时刻t这两类人在总人数中所占比例分别记作s(t)和i(t)。 假设二：每个病人每天有效接触的平均人数是常数，称为日接触率。当病人

数学建模 传染病模型

传染病模型 医学科学的发展已经能够有效地预防和控制许多传染病，但是仍然有一些传染病暴发或流行，危害人们的健康和生命。 社会、经济、文化、风俗习惯等因素都会影响传染病的传播，而最直接的因素是：传染者的数量及其在人群中的分布、被传染者的数量、传播形式、传播能力、免疫能力等。 一般把传染病流行范围内的人群分成三类：S类，易感者(Susceptible)，指未得病者，但缺乏免疫能力，与感染者接触后容易受到感染；I类，感病者(Infective)，指染上传染病的人，它可以传播给S类成员；R类，移出者(Removal)，指被隔离或因病愈而具有免疫力的人。 问题提出 请建立传染病模型，并分析被传染的人数与哪些因素有关？如何预报传染病高潮的到来?为什么同一地区一种传染病每次流行时，被传染的人数大致不变？ 关键字:传染病模型、建模、流行病 摘要：随着卫生设施的改善、医疗水平的提高以及人类文明的不断发展，诸如霍 乱、天花等曾经肆虐全球的传染性疾病已经得到有效的控制。但是一些新的、不断变异着的传染病毒却悄悄向人类袭来。20世纪80年代十分险恶的爱滋病毒开始肆虐全球，至今带来极大的危害。还有最近的SARS病毒和禽流感病毒，都对人类的生产生活造成了重大的损失。长期以来，建立制止传染病蔓延的手段等，一直是各国有关专家和官员关注的课题。 不同类型传染病的传播过程有其各自不同的特点，弄清这些特点需要相当多的病理知识，这里不可能从医学的角度一一分析各种传染病的传播，而只是按照一般的传播模型机理建立几种模型。 模型1 在这个最简单的模型中，设时刻t的病人人数x(t)是连续、可微函数， 方程（1）的解为 结果表明，随着t的增加，病人人数x(t)无限增长，这显然是不符合实际的。 建模失败的原因在于：在病人有效接触的人群中，有健康人也有病人，而其中只有健康人才可以被传染为病人，所以在改进的模型中必须区别健康人和病人这两种人。 模型2 SI模型 假设条件为 1.在疾病传播期内所考察地区的总人数N不变，即不考虑生死，也不考虑迁移。人群分为易感染者即健康人（Susceptible）（S）和已感染者即病人（Infective）（i）两类（取两个词的第一个字母，称之为SI模型），以下简称健康者和病人。时刻t这两类人在总人数中所占比例分别记作s(t)和i(t)。 2.每个病人每天有效接触的平均人数是常数 ，称为日接触率。当病人与健康者接触时，使健康者受感染变为病人。

数学建模传染病模型剖析

传染病的传播 摘要：本文先根据材料提供的数据建立了指数模型，并且全面地评价了该模型的合理性与实用性。而后对模型与数据做了较为扼要地分析了指数模型的不妥之处。并在对问题进行较为全面评价的基础上引入更为全面合理的假设和建立系统分析模型。运用联立微分方程组体现疫情发展过程中各类人的内在因果联系，并在此基础上建立方程求解算法结合

MATLAB 编程(程序在附件二)拟合出与实际较为符合的曲线并进行了疫情预测。同时运用双线性函数模型对卫生部的措施进行了评价并给出建议以及指出建立一个真正能够预测以及能为预防和控制提供可靠、足够的信息的模型，这样做的困难本文的最后，通过本次建模过程中的切身体会，说明建立如SARS 预测模型之类的传染病预测模型的重要意义。 关键词：微分方程 SARS 数学模型 感染率 1问题的重述 SARS （Severe Acute Respiratory Syndrome ，严重急性呼吸道综合症, 俗称：非典型肺炎）是21世纪第一个在世界范围内传播的传染病。SARS 的爆发和蔓延给我国的经济发展和人民生活带来了很大影响，我们从中得到了许多重要的经验和教训，认识到定量地研究传染病的传播规律、为预测和控制传染病蔓延创造条件的重要性。请你们对SARS 的传播建立数学模型，具体要求如下： 1)建立传染病传播的指数模型，评价其合理性和实用性。 2)建立你们自己的模型，说明为什么优于指数模型；特别要说明怎样才能建立一个真正能够预测以及能为预防和控制提供可靠、足够的信息的模型，这样做的困难在哪里？对于卫生部门所采取的措施做出评论，如：提前或延后5天采取严格的隔离措施，对疫情传播所造成的影响做出估计。附件1提供的数据供参考。 3)说明建立传染病数学模型的重要性。 2 定义与符号说明 N …………………………………表示为SARS 病人的总数； K （感染率）……………………表示为平均每天每人的传染他人的人数； L …………………………………表示为每个病人可能传染他人的天数； dt d N(t)………………………… 表示为每天（单位时间）发病人数； N(t)-N(t-L)………………………表示可传染他人的病人的总数减去失去传染能力的病人数； t …………………………………表示时间； R 2 ………………………………表示拟合的均方差； 3 建立传染病传播的指数模型 3.1模型假设 1) 该疫情有很强的传播性，病人（带菌者）通过接触（空气，食物，……）将病菌传播给健康者。单位时间（一天）内一个病人能传播的人数是常数k ； 2) 在 所传染的人当中不考虑已治愈的人是否被再次被传播，治愈的人数占该地区的总人数是绝对的少数，治愈者不会再被传播并不影响疫情在该时间内的感染率常数k; 3) 病者在潜伏期传播可能性很小， 仍按健康人处理； 4) SARS 对不同的年龄组的感染率略有不同（相差不大），但我们只考虑它健康人的感染率是一样的；

数学建模论文资料传染病模型)

传染病模型 摘要 “传染病的传播过程”数学模型是通过控制已感染人群来实现的。利用隔离等手段来保护未被感染的人群，减少其对健康人群的危害。由于传染病具有研究新型病例有着重要的意义，利用数学知识联系实际问题，作出相应的解答和处理。问题一：描述传染病的传播过程，将分析受感染人数的变化规律，预报传染病高潮到来的时刻，在传染病过程中，建立传染病影响健康人的数学模型。问题二，在区分健康人群和已经感染人群的情况下，要建立适合总人数不变，区分已经感染的人群和的数学模型，必须在问题一的条件下作出合理假设，同时得出该模型，最后结合已知数据可算出每个已感染人群每天接触健康人群的函数和数学模型。问题三，传染病无免疫性——病人治愈成为健康人，健康人可再次被感染，问题三加入健康人可以再次感染，一个感染期内每个病人的有效接触人数，称为接触数。 一种疾病的传播过程是一种非常复杂的过程，它受很多社会因素的制约和影响，如传染病人的多少，易受传染者的多少，传染率的大小，排除率的大小，人口的出生和死亡，还有人员的迁入和迁出，潜伏期的长短，预防疾病的宣传以及人的个体差异等。如何建立一个与实际比较吻合的数学模型，开始显然不能将所有因素都考虑进去。为此，必须从诸多因素中，抓住主要因素，去掉次要因素。先把问题简化，建立相应的数学模型。将所得结果与实际比较，找出问题，修改原有假设，再建立一个与实际比较吻合的模型。从而使模型逐步完善。下面是一个由简单到复杂的建模过程，很有代表性，读者应从中体会这一建模过程的方法和思路。

一．问题的提出 描述传染病的传播过程，将分析受感染人数的变化规律，预报传染病高潮到来的时刻，在传染病过程中，建立传染病影响健康人的数学模型。问题二，在区分健康人群和已经感染人群的情况下，要建立适合总人数不变，区分已经感染的人群和的数学模型，必须在问题一的条件下作出合理假设，同时得出该模型，最后结合已知数据可算出每个已感染人群每天接触健康人群的函数和数学模型。问题三，传染病无免疫性——病人治愈成为健康人，健康人可再次被感染，问题三加入健康人可以再次感染，一个感染期内每个病人的有效接触人数，称为接触数。 二．问题的分析 2.1 问题分析 描述传染病的传播过程，将分析受感染人数的变化规律，预报传染病高潮到来的时刻，在传染病过程中，建立传染病影响健康人的数学模型。 2.2模型分工

数学模型实验报告传染病

《数学模型实验》实验报告 姓名：学院：地点： 学号：专业：时间：年月日 一、实验名称： 传染病SIR模型 二、实验目的： 探讨传染病的SIR模型。通过微分方程的解的特征，分析受感染人数的变化规律，预报感染病的高潮时间，得出控制感染病蔓延的方法。三、实验任务： 大多数传染病如天花、流感、肝炎、荨麻等治愈后均有很强的免疫力，所以对于病愈后即非健康者（易感染者）、也非病人（已感染者）的人，他们已经退出了传染系统。假设：总人数N不变，人群分为健康者、病人和病愈免疫的移出者三类。三类人在总人数N中占的比例分别为s(t),i(t)和r(t)。建立相关模型，进行求解分析 四、实验步骤： 1.模型假设 2.模型构成 3.数值计算 4.结果分析 五、实验内容： （一）模型假设

1.总人数N不变，人群分为健康者、病人和病愈免疫的移出者三类，称SIR模型。时刻t三类人在总人数中所占的比例分别为s(t),i(t)和r(t)。 2.病人的日接触率为λ，日治愈率为μ，传染期接触数为β=λ/μ。（二）模型构成 由假设1显然有s（t）+i（t）+r（t）=1；由假设2,对于病愈免疫的移出者而言应有：Ndi/dt=λNsi-μNi; Ndr/dt=μNi。再记初始时刻的健康者和病人的比例分别是s0（s0>0）和i0（i0>0），则由此得到SIR模 型的方程可以写作 （三）数值计算 设方程中λ=1，μ=0.3，i（0）=0.02，s（0）=0.98，MATLAB编程语言如下： 建立函数： 引用： 得到轨迹图如下：

i(t),s(t)图像 i-s图像(相轨线) （四）结果分析 由图可看出，i(t)由初值增长至约t=7时达到最大值，然后减少，t趋

传染病传播数学模型

第二节传染病传播的数学模型很多医学工作者试图从医学的不同角度来解释传染病传播时的一种现象，这种现象就是在某一民族或地区，某种传染病传播时，每次所涉及的人数大体上是一常数。结果都不能令人满意，后来由于数学工作者的参与，用建立数学模型来对这一现象进行模拟和论证，得到了较满意的解答。 一种疾病的传播过程是一种非常复杂的过程，它受很多社会因素的制约和影响，如传染病人的多少，易受传染者的多少，传染率的大小，排除率的大小，人口的出生和死亡，还有人员的迁入和迁出，潜伏期的长短，预防疾病的宣传以及人的个体差异等。如何建立一个与实际比较吻合的数学模型，开始显然不能将所有因素都考虑进去。为此，必须从诸多因素中，抓住主要因素，去掉次要因素。先把问题简化，建立相应的数学模型。将所得结果与实际比较，找出问题，修改原有假设，再建立一个与实际比较吻合的模型。从而使模型逐步完善。下面是一个由简单到复杂的建模过程，很有代表性，读者应从中体会这一建模过程的方法和思路。 一.最简单的模型 假设：(1) 每个病人在单位时间内传染的人数是常数k；(2) 一个人得病后经久不愈，并在传染期内不会死亡。 以i(t)表示t时刻的病人数， k表示每个病人单位时间内传染的人 数，i(0)= i表示最初时有0i个传染病人，则在t?时间内增加的病人 数为 ()()() i t t i t k i t t +?-=?

两边除以t ?，并令t ?→0得微分方程 ()()()000di t k i t dt i i ?=???=? ………… （2.1） 其解为 ()00 k t i t i e = 这表明传染病的转播是按指数函数增加的。这结果与传染病传播初期比较吻合，传染病传播初期，传播很快，被传染人数按指数函数增长。但由(2.1)的解可知，当t →∞时，i(t)→∞，这显然不符合实际情况。最多所有的人都传染上就是了。那么问题在那里呢？问题是就出在于两条假设对时间较长时不合理。特别是假设(1)，每个病人单位时间内传染的人数是常数与实际情况不符。因为随着时间的推移，病人越来越多，而未被传染的人数却越来越少，因而不同时期的传播情况是不同的。为了与实际情况较吻合，我们在原有的基础上修改假设建立新的模型。 二. 模型的修改 将人群分成两类：一类为传染病人，另一类为未被传染的人，分别用i(t)和s(t)表示t 时刻这两类人的人数。i (0)= 0i 。 假设：(1) 每个病人单位时间内传染的人数与这时未被传染的人数成正比。即()0k ks t =； (2) 一人得病后，经久不愈，并在传染期内不会死亡。 由以上假设可得微分方程

传染病的数学模型

传染病模型详解 /,SI SIS SIR 经典模型 经典的传播模型大致将人群分为传播态S ，易感染态I 和免疫态R 。S 态表示该个体带有病毒或谣言的传播能力，一旦接触到易感染个体就会以一定概率导致对方成为传播态。I 表示该个体没有接触过病毒或谣言，容易被传播态个体感染。R 表示当经过一个或多个感染周期后，该个体永远不再被感染。 SI 模型考虑了最简单的情况，即一个个体被感染，就永远成为感染态，向周围邻居不断传 播病毒或谣言等。假设个体接触感染的概率为β，总人数为 N ，在各状态均匀混合网络中建立传播模型如下： dS SI dt N I SI d t N ββ?=-????=?? 从而得到 (1)di i i dt β=- 对此方程进行求解可得： 0000(),01t t i e i t i i i i e ββ==-+（） 可见，起初绝大部分的个体为I 态，任何一个S 态个体都会遇到I 态个体并且传染给对方，网络中的S 态个数随时间成指数增长。与此同时，随着I 态个体的减少，网络中S 态个 数达到饱和，逐渐网络中个体全部成为S 态。 然而在现实世界中，个体不可能一直都处于传播态。有些节点会因为传播的能力和意愿 的下降，从而自动转变为永不传播的R 态。而有些节点可能会从S 态转变I 态，因此简单的SI 模型就不能满足节点具有自愈能力的现实需求，因而出现SIS 模型和SIR 模型。 SIR 是研究复杂网络谣言传播的经典的模型。采用与病毒传播相似的过程中的S ，I ，R 态 代表传播过程中的三种状态。Zanetee ，Moreno 先后研究了小世界传播过程中的谣言传播。 Moreno 等人将人群分为S （传播谣言）、I （没有听到谣言），R （对谣言不再相信也不传播）。 假设没有听到谣言I 个体与S 个体接触，以概率()k λ变为S 个体，S 个体遇到S 个体 或R 个体以概率()k α变为R ，如图 所示。建立的平均场方程：

1.实验7-1传染病模型2

河北大学《数学模型》实验实验报告 一、实验目的 二、实验要求 1.实验7-1 传染病模型2（ SI模型）——画di/dt~ i曲线图 （参考教材 p137-138） 传染病模型 2（ SI 模型）： ; di/dt=ki(1-i),i(0)=i 其中， i(t)是第 t 天病人在总人数中所占的比例。 λ是每个病人每天有效接触的平均人数（日接触率）。 i0是初始时刻（ t=0）病人的比例。 取 k=0.1，画出 di/dt~ i 曲线图，求 i 为何值时di/dt达到最大值，并在曲线图上标注。试编写一个 m 文件来实现。 参考程序运行结果（在图形窗口菜单选择 Edit/Copy Figure，复制图形）：

[提示] 1）画曲线图 用 fplot 函数，调用格式如下： fplot(fun,lims) fun 必须为一个 M 文件的函数名或对变量 x 的可执行字符串。 若 lims 取[xmin xmax]，则 x 轴被限制在此区间上。 若 lims 取[xmin xmax ymin ymax]，则 y 轴也被限制。 本题可用 fplot('0.1*x*(1-x)',[0 1.1 0 0.03]); 2）求最大值 用求解边界约束条件下的非线性最小化函数 fminbnd，调用格式如下： x=fminbnd(‘fun’,x1,x2) fun 必须为一个 M 文件的函数名或对变量 x 的可执行字符串。 返回自变量 x 在区间 x1

传染病传播的数学模型_上课

微分方程模型 [学习目的] 1.加深对微分方程概念的理解，掌握针对一些问题通过建立微分方程 的方法及微分方程的求解过程； 2.了解微分方程模型解决问题思维方法及技巧； 3.领会建立微分方程模型的逐步改进法的核心及优点，并掌握该方法； 4.理解微分方程的解的稳定性的意义，会用稳定性判定模型的解是否 有效； 5.体会微分方程建摸的艺术性。 在自然学科（如物理、化学、生物、天文）以及在工程、经济、军事、社会等学科量的问题可以用微分方程来描述。正如列宁所说：“自然界的统一性显示在关于各种现象领域的微分方程式的‘惊人的类似中’．”（列宁选集第二卷，人民1972年版第295页）。要建立微分方程模型，读者必须掌握元素法（有关元素法，在高等数学中已有介绍）。所谓元素法，从某种角度上讲，就是分析的方法，它是以自然规律的普遍性为根据并且以局部规律的独立的假定为基础。在解决各种实际问题时，微分方程用得极其广泛。读者通过下面的几个不同领域中的模型介绍便有所体会，要想掌握好它，在这方面应作大量的练习。 §17.1、传染病传播的数学模型 [学习目标] 1.通过学习建立传染病传播的数学模型的思维方法，能归纳出该类建模的关键 性步骤及思维方法；并能指出求解传染病传播的数学模型的方法技巧； 2.能用已知的传染病传播的数学模型，预报某种传染病的传播； 3.学会从简单到复杂的处理问题的方法。 由于人体的疾病难以控制和变化莫测，因此医学中的数学模型较为复杂。生物医学中的数学模型分为两大类：传染病传播的数学模型和疾病数学模型。 以下仅讨论传染病的传播问题。人们将传染病的统计数据进行处理和分析，发现在某一民族或地区，某种传染病传播时，每次所涉及的人数大体上是一常数。这一现象如何解释呢？关于这个问题，医学工作者试图从医学的不同角度进行解释都得不到令人满意的解释。最后由于数学工作者的参与，在理论上对上述结论进行了严格的证明。同时又由于传染病数学模型的建立，分析所得结果与

matlab传染病模型

传染病模型实验 实验目的： 理解传染病的四类模型，学会利用Matlab软件求解微分方程（组）。 实验题目： 利用Matlab求解传染病的SIS微分方程模型，并绘制教材P139页图3-图6。 SIS模型 假设： (1)、t时刻人群分为易感者(占总人数比例的s(t))和已感染者(占总人数比例的i(t))。 (2)、每个病人每天有效接触的平均人数是常数λ，λ称为日接触率，当健康者与病人接触时，健康者受感染成为病人。 (3)、病人每天被治愈的占病人总数的比例为μ，称为日治愈率，显然1 为这种传染病的平均传染期。 μ 则建立微分方程模型为： 令，则模型可写作 分别作图： 页脚内容1

当sigma>1时 Step1:先定义函数 function y=pr1(i,lambda,sigma) y=-lambda.*i.*(i-(1-1./sigma)) step2:作图 lambda=0.3;sigma=2; i=0:0.01:1; y=pr1(i,lambda,sigma) plot(i,y) 页脚内容2

页脚内容3 00.10.20.30.40.50.60.70.80.91 -0.16 -0.14-0.12-0.1-0.08-0.06-0.04-0.020 0.02 当sigma<1时 Step1:先定义函数 function y=pr1(i,lambda,sigma) y=-lambda.*i.*(i-(1-1./sigma)) step2:作图 lambda=0.3;sigma=0.5; i=0:0.01:1; y=pr1(i,lambda,sigma) plot(i,y)

传染病的数学模型

222 SI/SIS,SIR 经典模型 经典的传播模型大致将人群分为传播态 S ,易感染态I 和免疫态R 。S 态表示该个体 带有病毒或谣言的传播能力，一旦接触到易感染个体就会以一定概率导致对方成为传播态。 I 表示该个体没有接触过病毒或谣言，容易被传播态个体感染。 R 表示当经过一个或多个 感染周期后，该个体永远不再被感染。 SI 模型考虑了最简单的情况， 即一个个体被感染， 就永远成为感染态， 向周围邻居不断传 播病毒或谣言等。假设个体接触感染的概率为 Γι ,总人数为 N ,在各状态均匀混合网络中 建立传播模型如下: dS - SI dU ：SI .t N 从而得到 对此方程进行求解可得: ∣o e ∣(t) ------- —∣o +i °e 可见，起初绝大部分的个体为 I 态，任何一个S 态个体都会遇到I 态个体并且传染给对 方，网络中的S 态个数随时间成指数增长。 与此同时，随着I 态个体的减少，网络中S 态个 数达到饱和，逐渐网络中个体全部成为 S 态。 然而在现实世界中，个体不可能一直都处于传播态。有些节点会因为传播的能力和意愿 的下降，从而自动转变为永不传播的 R 态。而有些节点可能会从 S 态转变I 态，因此简单 的SI 模型就不能满足节点具有自愈能力的现实需求，因而出现 SIS 模型和SIR 模型。 SIR 是研究复杂网络谣言传播的经典的模型。 采用与病毒传播相似的过程中的 S , I , R 态 代表传播过程中的三种状态。 Zanetee, Moreno 先后研究了小世界传播过程中的谣言传播。 Moreno 等人将人群分为 S （传播谣言）、I （没有听到谣言），R （对谣言不再相信也不传 播）。 假设没有听到谣言I 个体与S 个体接触，以概率,（k ）变为S 个体，S 个体遇到S 个体 或R 个体以概率: （k ）变为R ,如图2.9所示。建立的平均场方程: 传染病模型详解 [,i ° =K O ) BI 1 9 SlR 權峑眄优■业趨图

传染病传播地数学模型

传染病传播的数学模型 很多医学工作者试图从医学的不同角度来解释传染病传播时的一种现象，这种现象就是在某一民族或地区，某种传染病传播时，每次所涉及的人数大体上是一常数。结果都不能令人满意，后来由于数学工作者的参与，用建立数学模型来对这一现象进行模拟和论证，得到了较满意的解答。 一种疾病的传播过程是一种非常复杂的过程，它受很多社会因素的制约和影响，如传染病人的多少，易受传染者的多少，传染率的大小，排除率的大小，人口的出生和死亡，还有人员的迁入和迁出，潜伏期的长短，预防疾病的宣传以及人的个体差异等。如何建立一个与实际比较吻合的数学模型，开始显然不能将所有因素都考虑进去。为此，必须从诸多因素中，抓住主要因素，去掉次要因素。先把问题简化，建立相应的数学模型。将所得结果与实际比较，找出问题，修改原有假设，再建立一个与实际比较吻合的模型。从而使模型逐步完善。下面是一个由简单到复杂的建模过程，很有代表性，读者应从中体会这一建模过程的方法和思路。 一.最简单的模型 假设：(1) 每个病人在单位时间内传染的人数是常数k；(2) 一个人得病后经久不愈，并在传染期内不会死亡。 以i(t)表示t时刻的病人数，表示每个病人单位时间内传染的人数，i(0)= 表示最初时有个传染病人，则在时间内增加的病人数为

两边除以，并令→0得微分方程 …………（2.1） 其解为 这表明传染病的转播是按指数函数增加的。这结果与传染病传播初期比较吻合，传染病传播初期，传播很快，被传染人数按指数函数增长。但由(2.1)的解可知，当t→∞时，i(t)→∞，这显然不符合实际情况。最多所有的人都传染上就是了。那么问题在那里呢？问题是就出在于两条假设对时间较长时不合理。特别是假设(1)，每个病人单位时间内传染的人数是常数与实际情况不符。因为随着时间的推移，病人越来越多，而未被传染的人数却越来越少，因而不同时期的传播情况是不同的。为了与实际情况较吻合，我们在原有的基础上修改假设建立新的模型。 二. 模型的修改 将人群分成两类：一类为传染病人，另一类为未被传染的人，分别用i(t)和s(t)表示t时刻这两类人的人数。i (0)= 。 假设：(1) 每个病人单位时间内传染的人数与这时未被传染的人数成正比。即； (2) 一人得病后，经久不愈，并在传染期内不会死亡。 由以上假设可得微分方程

传染病模型数学建模论文

甲型H1N1流感传播模型研究 摘要 本文采用了SIR模型对的甲型h1n1流感病毒的传播规律进行了研究和预测，文章收集了美国地区的甲流实验室确认病例数量的数据，对模型进行了验证，并提出了如何降低流感在人群中发病率的俩种可靠方法。 一、问题重述 近年来由墨西哥发端的甲型h1n1型流感（又称猪流感）正成为人们关注的焦点，通过相关网站获得数据，建立一个模型对甲型h1n1流感的走势进行预测。 二、问题分析 甲型h1n1流感的传播是一道传染病问题。在数学建模领域已经有很多关于这方面的研究，其中SIR模型是比较完整的模型。SIR模型通过建立微分方程组，按照一般的传播机理建立集中模型。本文选取美国地区的甲流实验室确认病例数量，建立SIR模型，对甲型h1n1流感的传播规律进行预测。

三、建立模型 （一）、不考虑潜伏期的数学模型 1、模型假设 （1）、在甲型H1N1流感传播期内，美国境内的总人数为N 亿不变，既不考虑生死，也不 考虑迁移，人群分为易感染者S ，发病人群I 和退出人群R(括死亡者和治愈者)四类，时刻t 内这三类人在总人数中所占比例分别为s(t)、i(t)、r(t)。 （2）、i(t)关于时间的增长率与s(t)成正比，比例常数为λ。 病人的数量减少速度与当时的病人总人数成正比，比例常数为ν。治愈 的病人具有了免疫力，即治愈后不再会成为二次患者。 （3）、s(t)、r(t)、i(t)之和是一个常数1。 2、模型构成 易感者和发病者有效接触后成为发病者者。设每个发病者平均每天有效接触的易感者数为()S t λ，()NI t 个发病者平均每天能使()()S t NI t λ个易感者成为病毒潜伏者。 所以有： ()()()dS t S t I t dt λ=- （1） 单位时间内退出者的变化等于发病人群的减少，即 ()()dR t I t dt ν= （2） 发病人群的变化等于易感人群转入的数量，即 ()()()()dI t S t I t I t dt λν=- （3） 记初始时刻的健康者和病人的比例分别为0S 、0R （不妨设0R =0）。 3、模型求解 方程组（1）、（2）、（3）无法求出解析解，我们定义一个新的变量 /σλν=，于是可以求出方程的解为： 000 1()ln s i s i s s σ=+-+ （4） 下面分析s(t)、i(t)、r(t)的变化情况： a 、不论初始条件0S 、0R 如何，病人最终将消失，即0i ∞=。 b 、最终未被感染者的健康者的比例是s ∞，是方程 0001()ln 0s s i s s σ +-+=在(0,1/)σ内的根。

数学建模_传染病模型 (1)

传染病模型 医学科学的发展已经能够有效地预防和控制许多传染病，但是仍然有一些传染病暴发或流行，危害人们的健康和生命。 社会、经济、文化、风俗习惯等因素都会影响传染病的传播，而最直接的因素是：传染者的数量及其在人群中的分布、被传染者的数量、传播形式、传播能力、免疫能力等。 一般把传染病流行范围内的人群分成三类：S 类，易感者(Susceptible)，指未得病者，但缺乏免疫能力，与感染者接触后容易受到感染；I 类，感病者(Infective)，指染上传染病的人，它可以传播给S 类成员；R 类，移出者(Removal)，指被隔离或因病愈而具有免疫力的人。 问题提出 请建立传染病模型，并分析被传染的人数与哪些因素有关？如何预报传染病高潮的到来?为什么同一地区一种传染病每次流行时，被传染的人数大致不变？ 关键字:传染病模型、建模、流行病 摘要：随着卫生设施的改善、医疗水平的提高以及人类文明的不断发展，诸如霍乱、 天花等曾经肆虐全球的传染性疾病已经得到有效的控制。但是一些新的、不断变异着的传染病毒却悄悄向人类袭来。20世纪80年代十分险恶的爱滋病毒开始肆虐全球，至今带来极大的危害。还有最近的SARS 病毒和禽流感病毒，都对人类的生产生活造成了重大的损失。长期以来，建立制止传染病蔓延的手段等，一直是各国有关专家和官员关注的课题。 不同类型传染病的传播过程有其各自不同的特点，弄清这些特点需要相当多的病理知识，这里不可能从医学的角度一一分析各种传染病的传播，而只是按照一般的传播模型机理建立几种模型。 模型1 在这个最简单的模型中，设时刻t 的病人人数x(t)是连续、可微函数， 病人人数的增加，就有 到考察的人数为常数足使人致病接触并且每天每个病人有效t t t ?+λ)(t t x t x t t x ?=-?+)()()(λ 程有个病人，即得微分方时有再设00x t = )1()0(,d d 0x x x t x ==λ 方程（1）的解为 )2()(0t e x t x λ= 结果表明，随着t 的增加，病人人数x(t)无限增长，这显然是不符合实际的。 建模失败的原因在于：在病人有效接触的人群中，有健康人也有病人，而其中只有健康人

传染病的数学模型-数学建模-论文Word版

数 学 建 模 论 文 班级：商英1002班 学号：14号 姓名：谭嘉坤 指导老师：周爱群

由于人体的疾病难以控制和变化莫测，医学中的数学模型也是较为复杂的。在研究传染病传播问题时，人们发现传染病传播所涉及的因素很多，例如，传染病人的多少，易受感染者的多少，免疫者(或感染后痊愈者)的多少等。在将某一地区，某种传染病的统计数据进行处理和分析后，人们发现了以下的规律性： 设S k表示在开始观察传染病之后第k天易受感染者的人数，H k表示在开始观察后第k天传染病人的人数，I k表示在开始观察后第k天免疫者(或感染后痊愈者)的人数，那么 S k+1=S k-0.01S k (1) H k+1=H k-0.2H k＋0.01S k (2) I k+1=I k+0.2H k (3) 其中(1)式表示从第k天到第k＋1天有1％的易受感染者得病而离开了易受感染者的人群；(2)式表示在第k+1天的传染病人的人数是第k天的传染病人的人数减去痊愈的人数0.2H k(假设该病的患病期为5 (3)式表示在第k＋1天免疫者的人数是第k天免疫者的人数加上第k 天后病人痊愈的人数。 将(1)，(2)和(3)式化简得 如果已知S0，H0，I0的值，利用上式可以求得S1，H1，I1的值，将这组值再代入上式，又可求得S2，H2，I2的值，这样做下去，我们可以逐个地，递推地求出各组S k，H k，I k的值。因此，我们把S k+1，H k＋1，I k+1和S k，H k，I k之间的关系式叫做递推关系式。 现在假设开始观察时易受感染者，传染病人和免疫者的人数分别为 将上述数据(5)代入(4)式右边得

传染病传播的数学模型

传染病传播的数学模型 Company Document number：WUUT-WUUY-WBBGB-BWYTT-1982GT

传染病传播的 数学模型 很多医学工作者试图从医学的不同角度来解释传染病传播时的一种现象，这种现象就是在某一民族或地区，某种传染病传播时，每次所涉及的人数大体上是一常数。结果都不能令人满意，后来由于数学工作者的参与，用建立数学模型来对这一现象进行模拟和论证，得到了较满意的解答。 一种疾病的传播过程是一种非常复杂的过程，它受很多社会因素的制约和影响，如传染病人的多少，易受传染者的多少，传染率的大小，排除率的大小，人口的出生和死亡，还有人员的迁入和迁出，潜伏期的长短，预防疾病的宣传以及人的个体差异等。如何建立一个与实际比较吻合的数学模型，开始显然不能将所有因素都考虑进去。为此，必须从诸多因素中，抓住主要因素，去掉次要因素。先把问题简化，建立相应的数学模型。将所得结果与实际比较，找出问题，修改原有假设，再建立一个与实际比较吻合的模型。从而使模型逐步完善。下面是一个由简单到复杂的建模过程，很有代表性，读者应从中体会这一建模过程的方法和思路。 一.最简单的模型 假设：(1) 每个病人在单位时间内传染的人数是常数k ；(2) 一个人得病后经久不愈，并在传染期内不会死亡。 以i(t)表示t 时刻的病人数，0k 表示每个病人单位时间内传染的人数，i(0)= 0i 表示最初时有0i 个传染病人，则在t ?时间内增加的病人数为 ()()()0i t t i t k i t t +?-=?

两边除以t ?，并令t ?→0得微分方程 ()()()000di t k i t dt i i ?=???=? ………… （） 其解为 ()00k t i t i e = 这表明传染病的转播是按指数函数增加的。这结果与传染病传播初期比较吻合，传染病传播初期，传播很快，被传染人数按指数函数增长。但由的解可知，当t →∞时，i(t)→∞，这显然不符合实际情况。最多所有的人都传染上就是了。那么问题在那里呢问题是就出在于两条假设对时间较长时不合理。特别是假设(1)，每个病人单位时间内传染的人数是常数与实际情况不符。因为随着时间的推移，病人越来越多，而未被传染的人数却越来越少，因而不同时期的传播情况是不同的。为了与实际情况较吻合，我们在原有的基础上修改假设建立新的模型。 二. 模型的修改 将人群分成两类：一类为传染病人，另一类为未被传染的人，分别用i(t)和s(t)表示t 时刻这两类人的人数。i (0)= 0i 。 假设：(1) 每个病人单位时间内传染的人数与这时未被传染的人数成 正比。即()0k ks t =； (2) 一人得病后，经久不愈，并在传染期内不会死亡。 由以上假设可得微分方程

传染病模型 SI SIR

数学模型实验—实验报告10 学院： 专 业： 姓 名： 学号：___ ____ 实验时间：__ ____ 实验地点： 一、实验项目：传染病模型求解 二、实验目的和要求 a.求解微分方程的解析解 b.求解微分方程的数值解 三、实验内容 问题的描述 各种传染病给人类带来的巨大的灾难，长期以来，建立传染病的数学模型来描述传染病的的传播过程，分析受感染人数的变化规律，探索制止传染病蔓延的手段等，一直是各国有关专家和官员关注的课题。 不同类型传染病有各自不同的特点，在此以一般的传播机理建立几种3模型。分别对3种建立成功的模型进行模型分析，便可以了解到该传染病在人类间传播的大概情况。 模型一（SI 模型）： （1）模型假设 1.在疾病传播期内所考察地区的总人数N 不变，人群分为健康人和病人，时刻t 这两类人在总人数中所占比例为s （t ）和i （t ）。 2.每个病人每天有效接触的平均人数是常数a ，a 成为日接触率，当病人与健康者有效接触时，可使其患病。 （2）建立模型 根据假设，每个病人每天可使as （t ）个健康人变成病人，t 时刻病人数为Ni （t ），所以每天共有aNs （t ）i （t ）个健康者被感染，即病人的增加率为： Ndi/dt=aNsi 又因为s （t ）+i （t ）=1 再记时刻t=0时病人的比例为i0 则建立好的模型为： ) 1(i ai dt di -= i(0)=i0 （3）模型求解 （代码、计算结果或输出结果） syms a i t i0 % a ：日接触率，i ：病人比例， s ：健康人比例，i0：病人比例在t=0时的值 i=dsolve('Di=a*i*(1-i)','i(0)=i0','t'); y=subs(i,{a,i0},{,}); ezplot(y,[0,100])

传染病模型数学建模论文

甲型H1N1流感传播模型研究 小组成员：宋科康张晓鹏姚步泉 摘要 本文采用了SIR模型对的甲型h1n1流感病毒的传播规律进行了研究和预测，文章收集了美国地区的甲流实验室确认病例数量的数据，对模型进行了验证，并提出了如何降低流感在人群中发病率的俩种可靠方法。

一、问题重述 近年来由墨西哥发端的甲型h1n1型流感（又称猪流感）正成为人们关注的焦点，通过相关网站获得数据，建立一个模型对甲型h1n1流感的走势进行预测。 二、问题分析 甲型h1n1流感的传播是一道传染病问题。在数学建模领域已经有很多关于这方面的研究，其中SIR模型是比较完整的模型。SIR模型通过建立微分方程组，按照一般的传播机理建立集中模型。本文选取美国地区的甲流实验室确认病例数量，建立SIR模型，对甲型h1n1流感的传播规律进行预测。 美国甲型H1N1流感实验室确认病例数量： 三、建立模型 （一）、不考虑潜伏期的数学模型

1、模型假设 （1）、在甲型H1N1流感传播期内，美国境内的总人数为N 亿不变，既不考虑生 死，也不考虑迁移，人群分为易感染者S ，发病人群I 和退出人群R(括死亡者和治愈者)四类，时刻t 内这三类人在总人数中所占比例分别为s(t)、i(t)、r(t)。 （2）、i(t)关于时间的增长率与s(t)成正比，比例常数为λ。 病人的数量减少速度与当时的病人总人数成正比，比例常数为ν。治愈 的病人具有了免疫力，即治愈后不再会成为二次患者。 （3）、s(t)、r(t)、i(t)之和是一个常数1。 2、模型构成 易感者和发病者有效接触后成为发病者者。设每个发病者平均每天有效接触的易感者数为()S t λ，()NI t 个发病者平均每天能使()()S t NI t λ个易感者成为病毒潜伏者。所以有： () ()()dS t S t I t dt λ=-（1） 单位时间内退出者的变化等于发病人群的减少，即 () ()dR t I t dt ν=（2） 发病人群的变化等于易感人群转入的数量，即 () ()()()dI t S t I t I t dt λν=-（3） 记初始时刻的健康者和病人的比例分别为0S 、0R （不妨设0R =0）。 3、模型求解 方程组（1）、（2）、（3）无法求出解析解，我们定义一个新的变量 /σλν=，于是可以求出方程的解为： 0001()ln s i s i s s σ=+-+（4） 下面分析s(t)、i(t)、r(t)的变化情况： a 、不论初始条件0S 、0R 如何，病人最终将消失，即0i ∞=。 b 、最终未被感染者的健康者的比例是s ∞，是方程 0001()ln 0s s i s s σ +-+=在(0,1/)σ内的根。 C 、若01/s σ>，则开始有：()i t 先增加。当01/s σ=时，()i t 达到最大值，然后() i t