增量式PID控制算法程序

增量式PID的整型算法对于PID控制的程序算法，很多书上都讲了。

但是，最近真正要用PID算法的时候，发现书上的代码在我们51单片机上来实现还不是那么容易的事情。

简单的说来，就是不能直接调用。

仔细分析你可以发现，教材上的、网上现行的PID实现的C语言代码几乎都是用浮点型的数据来做的，可以想象，如果我们的计算使用浮点数据，那我们的51单片机来运行的话会有多痛苦。

所以，本人自己琢磨着弄了一个整型变量来实现了PID算法，由于是用整型数来做的，所以也不是很精确，但是对于很多的使用场合，这个精度也够了。

关于系数和采样电压全部是放大10倍处理的。

所以精度不是很高，但是也不是那么低，大部分的场合都够用了。

实在觉得精度不够，可以再放大10倍或者100倍处理，但是要注意不超出整个数据类型的范围就可以了。

以下是具体的程序代码：typedef struct PIDValue{uint32 Ek_Uint32[3]; //差值保存，给定和反馈的差值uint8 EkFlag_Uint8[3]; //符号，1则对应的Ek[i]为负数，0为对应的Ek[i]为正数uint8 KP_Uint8;uint8 KI_Uint8;uint8 KD_Uint8;uint8 B_Uint8; //死区电压uint8 KP; //显示修改的时候用uint8 KI;uint8 KD;uint8 B;uint16 Uk_Uint16; //上一时刻的控制电压}PIDValueStr;PIDValueStr xdata PID;//PID = Uk + (KP*E(k) - KI*E(k-1) + KD*E(k-2));void PIDProcess(void){uint32 idata Temp[3]; //uint32 idata PostSum; //正数和uint32 idata NegSum; //负数和Temp[0] = 0;Temp[1] = 0;Temp[2] = 0;PostSum = 0;NegSum = 0;if( ADPool.Value_Uint16[UINADCH] > ADPool.Value_Uint16[UFADCH] )//给定大于反{Temp[0] = ADPool.Value_Uint16[UINADCH] - ADPool.Value_Uint16[UFADCH];//计算Ek[0]if( Temp[0] > PID.B_Uint8 ){//数值移位PID.Ek_Uint32[2] = PID.Ek_Uint32[1];PID.Ek_Uint32[1] = PID.Ek_Uint32[0];PID.Ek_Uint32[0] = Temp[0];//符号移位PID.EkFlag_Uint8[2] = PID.EkFlag_Uint8[1];PID.EkFlag_Uint8[1] = PID.EkFlag_Uint8[0];PID.EkFlag_Uint8[0] = 0; //当前EK为正数Temp[0] = (uint32)PID.KP_Uint8 * PID.Ek_Uint32[0]; // KP*EK0Temp[1] = (uint32)PID.KI_Uint8 * PID.Ek_Uint32[1]; // KI*EK1Temp[2] = (uint32)PID.KD_Uint8 * PID.Ek_Uint32[2]; // KD*EK2}}else //反馈大于给定{Temp[0] = ADPool.Value_Uint16[UFADCH] - ADPool.Value_Uint16[UINADCH]; //计算Ek[0]if( Temp[0] > PID.B_Uint8 ){//数值移位PID.Ek_Uint32[2] = PID.Ek_Uint32[1];PID.Ek_Uint32[1] = PID.Ek_Uint32[0];PID.Ek_Uint32[0] = Temp[0];//符号移位PID.EkFlag_Uint8[2] = PID.EkFlag_Uint8[1];PID.EkFlag_Uint8[1] = PID.EkFlag_Uint8[0];PID.EkFlag_Uint8[0] = 1; //当前EK为负数Temp[0] = (uint32)PID.KP_Uint8 * PID.Ek_Uint32[0]; // KP*EK0Temp[1] = (uint32)PID.KI_Uint8 * PID.Ek_Uint32[1]; // KI*EK1Temp[2] = (uint32)PID.KD_Uint8 * PID.Ek_Uint32[2]; // KD*EK2}}/*以下部分代码是讲所有的正数项叠加，负数项叠加*/if(PID.EkFlag_Uint8[0]==0){PostSum += Temp[0]; //正数和}else{NegSum += Temp[0]; //负数和} // KP*EK0if(PID.EkFlag_Uint8[1]!=0){PostSum += Temp[1]; //正数和}else{NegSum += Temp[1]; //负数和} // - kI * EK1if(PID.EkFlag_Uint8[2]==0){PostSum += Temp[2]; //正数和}else{NegSum += Temp[2]; //负数和} // KD * EK2PostSum += (uint32)_Uint16; //if( PostSum > NegSum ) // 是否控制量为正数{Temp[0] = PostSum - NegSum;if( Temp[0] < (uint32)ADPool.Value_Uint16[UMAXADCH] )//小于限幅值则为计算值输出 {_Uint16 = (uint16)Temp[0];}else{_Uint16 = ADPool.Value_Uint16[UMAXADCH]; //否则为限幅值输出}}else //控制量输出为负数，则输出0{_Uint16 = 0;}}=============================================================================== //总体调节=比例系数×压力误差＋积分系数×积分误差+微分系数×（本次误差-前次误差）//P就是比例，就是输入偏差乘以一个系数；//I就是积分，就是对输入偏差进行积分运算；//D就是微分，对输入偏差进行微分运算；PIDValueStr xdata PID;void PIDCalc(unsigned int idata data1,unsigned int idata data2,unsigned int idata minfreq){unsigned int idata svdata;unsigned int idata pvdata;unsigned long idata dError,Error;unsigned long idata ResultP,ResultI,ResultD,PIDout,Result;svdata=data1;pvdata=data2;if(svdata>pvdata){Error=svdata-pvdata;// 压力偏差PID.SumError+=Error;// 积分dError=PID.LError-PID.PError;// 当前微分PID.PError=PID.LError;PID.LError=Error;ResultP=PID.KP*Error*100;// 比例项ResultI=PID.KI*(PID.SumError);// 积分项ResultD=PID.KD*dError;// 微分项PIDout=ResultP+ResultI+ResultD;Result+=PIDout;if(PIDout>=5000){PIDout=5000;PID.SumError-=Error;}else{ PIDout=ResultP+ResultI+ResultD;}}if(svdata<pvdata){Error=svdata-pvdata;// 压力偏差PID.SumError+=Error;// 积分dError=PID.LError-PID.PError;// 当前微分PID.PError=PID.LError;PID.LError=Error;ResultP=PID.KP*Error*100;//比例项ResultI=PID.KI*(PID.SumError);// 积分项ResultD=PID.KD*dError;// 微分项PIDout=ResultP+ResultI+ResultD;Result+=PIDout;if (PIDout>=5000){PIDout=0;PID.SumError-=Error;}else{ PIDout=ResultP+ResultI+ResultD;}}if (PIDout<minfreq){PIDout=0;}=PIDout; }。

PID控制算法的C语言实现一 PID算法原理之迟辟智美创作最近两天在考虑一般控制算法的C语言实现问题，发现网络上尚没有一套完整的比力体系的讲解.于是总结了几天，整理一套思路分享给年夜家.在工业应用中PID及其衍生算法是应用最广泛的算法之一，是当之无愧的万能算法，如果能够熟练掌握PID算法的设计与实现过程，对一般的研发人员来讲，应该是足够应对一般研发问题了，而难能可贵的是，在我所接触的控制算法傍边，PID控制算法又是最简单，最能体现反馈思想的控制算法，可谓经典中的经典.经典的未必是复杂的，经典的工具经常是简单的，而且是最简单的，想想牛顿的力学三年夜定律吧，想想爱因斯坦的质能方程吧，何等的简单！简单的不是原始的，简单的也不是落后的，简单到了美的水平.先看看PID算法的一般形式：PID的流程简单到了不能再简单的水平，通过误差信号控制被控量，而控制器自己就是比例、积分、微分三个环节的加和.这里我们规定（在t时刻）：1.输入量为rin(t);2.输出量为rout(t);3.偏差量为err(t)=rin(t)rout(t);pid的控制规律为理解一下这个公式，主要从下面几个问题着手，为了便于理解，把控制环境具体一下：1.规定这个流程是用来为直流机电调速的;2.输入量rin(t)为机电转速预定值;3.输出量rout(t)为机电转速实际值;4.执行器为直流机电;5.传感器为光电码盘，假设码盘为10线;6.直流机电采纳PWM调速转速用单元转/min 暗示;不难看出以下结论：1.输入量rin（t）为机电转速预定值（转/min）;2. 输出量rout(t)为机电转速实际值（转/min）;3.偏差量为预定值和实际值之差（转/min）;那么以下几个问题需要弄清楚：1.通过PID环节之后的U(t)是什么值呢？2.控制执行器（直流机电）转动转速应该为电压值（也就是PWM占空比）.3.那么U(t)与PWM之间存在怎样的联系呢？/user1/3407/archives//33541.html（见附录1）这篇文章上给出了一种方法，即，每个电压对应一个转速，电压和转速之间呈现线性关系.可是我考虑这种方法的前提是把直流机电的特性理解为线性了，而实际情况下，直流机电的特性绝对不是线性的，或者说在局部上是趋于线性的，这就是为什么说PID调速有个范围的问题.具体看一下/component/article90249.htm （见附录2）这篇文章就可以了解了.所以在正式进行调速设计之前，需要现有开环系统，测试机电和转速之间的特性曲线（或者查阅机电的资料说明），然后再进行闭环参数整定.这篇先写到这，下一篇说明连续系统的离散化问题.并根据离散化后的特点讲述位置型PID和增量型PID的用法和C语言实现过程.PID控制算法的C语言实现二 PID算法的离散化上一节中，我论述了PID算法的基本形式，并对其控制过程的实现有了一个简要的说明，通过上一节的总结，基本已经可以明白PID控制的过程.这一节中先继续上一节内容弥补说明一下.1.说明一下反馈控制的原理，通过上一节的框图不难看出，PID控制其实是对偏差的控制过程;2.如果偏差为0,则比例环节不起作用，只有存在偏差时，比例环节才起作用.3.积分环节主要是用来消除静差，所谓静差，就是系统稳定后输出值和设定值之间的差值，积分环节实际上就是偏差累计的过程，把累计的误差加到原有系统上以抵消系统造成的静差.4.而微分信号则反应了偏差信号的变动规律，或者说是变动趋势，根据偏差信号的变动趋势来进行超前调节，从而增加了系统的快速性.好了，关于PID的基本说明就弥补到这里，下面将对PID 连续系统离散化，从而方便在处置器上实现.下面把连续状态的公式再贴一下：假设采样间隔为T，则在第KT时刻：偏差err(K)=rin(K)rout(K);积分环节用加和的形式暗示，即err(K)+err(K+1)+……;微分环节用斜率的形式暗示，即[err(K)err(K1)]/T;从而形成如下PID离散暗示形式：则u(K)可暗示成为：至于说Kp、Ki、Kd三个参数的具体表达式，我想可以轻松的推出了，这里节省时间，不再详细暗示了.其实到这里为止，PID的基本离散暗示形式已经出来了.目前的这种表述形式属于位置型PID，另外一种表述方式为增量式PID，由U上述表达式可以轻易获得：那么：这就是离散化PID的增量式暗示方式，由公式可以看出，增量式的表达结果和最近三次的偏差有关，这样就年夜年夜提高了系统的稳定性.需要注意的是最终的输出结果应该为u(K)+增量调节值;PID的离散化过程基本思路就是这样，下面是将离散化的公式转换成为C语言，从而实现微控制器的控制作用.PID控制算法的C语言实现三位置型PID的C语言实现上一节中已经笼统出了位置性PID和增量型PID的数学表达式，这一节，重点讲解C语言代码的实现过程，算法的C语言实现过程具有一般性，通过PID算法的C语言实现，可以以此类推，设计其它算法的C语言实现.第一步：界说PID变量结构体，代码如下：struct _pid{float SetSpeed; //界说设定值float ActualSpeed; //界说实际值float err; //界说偏差值float err_last; //界说上一个偏差值float Kp,Ki,Kd; //界说比例、积分、微分系数float voltage; //界说电压值（控制执行器的变量）float integral; //界说积分值}pid;控制算法中所需要用到的参数在一个结构体中统一界说，方便后面的使用.第二部：初始化变量，代码如下：void PID_init(){printf("PID_init begin \n");pid.SetSpeed=0.0;pid.err=0.0;pid.err_last=0.0;pid.voltage=0.0;pid.integral=0.0;pid.Kp=0.2;pid.Ki=0.015;pid.Kd=0.2;printf("PID_init end \n");}统一初始化变量，尤其是Kp,Ki,Kd三个参数，调试过程傍边，对要求的控制效果，可以通过调节这三个量直接进行调节.第三步：编写控制算法，代码如下：float PID_realize(float speed){pid.SetSpeed=speed;pid.err=pid.SetSpeedpid.ActualSpeed;pid.integral+=pid.err;pid.voltage=pid.Kp*pid.err+pid.Ki*pid.integral+pid.Kd*(pid. errpid.err_last); pid.err_last=pid.err;pid.ActualSpeed=pid.voltage*1.0;}注意：这里用了最基本的算法实现形式，没有考虑死区问题，没有设定上下限，只是对公式的一种直接的实现，后面的介绍傍边还会逐渐的对此改进.到此为止，PID的基本实现部份就初步完成了.下面是测试代码：int main(){printf("System begin \n");PID_init();int count=0;while(count<1000){float speed=PID_realize(200.0);printf("%f\n",speed);count++;}return 0;}下面是经过1000次的调节后输出的1000个数据（具体的参数整定过程就不说明了，网上这种说明非常多）：PID控制算法的C语言实现四增量型PID的C语言实现上一节中介绍了最简单的位置型PID的实现手段，这一节主要讲解增量式PID的实现方法，位置型和增量型PID的数学公式请拜会我的系列文《PID控制算法的C语言实现二》中的讲解.实现过程仍然是分为界说变量、初始化变量、实现控制算法函数、算法测试四个部份，详细分类请介入《PID控制算法的C 语言实现三》中的讲解，这里直接给出代码了.#include<stdio.h>#include<stdlib.h>struct _pid{float SetSpeed; //界说设定值float ActualSpeed; //界说实际值float err; //界说偏差值float err_next; //界说上一个偏差值float err_last; //界说最上前的偏差值float Kp,Ki,Kd; //界说比例、积分、微分系数}pid;void PID_init(){pid.SetSpeed=0.0;pid.ActualSpeed=0.0;pid.err=0.0;pid.err_last=0.0;pid.err_next=0.0;pid.Kp=0.2;pid.Ki=0.015;pid.Kd=0.2;}float PID_realize(float speed){pid.SetSpeed=speed;pid.err=pid.SetSpeedpid.ActualSpeed;floatincrementSpeed=pid.Kp*(pid.errpid.err_next)+pid.Ki*pid.err+pid.Kd*(pid.err2*pid.err_next+pid.err_last);pid.ActualSpeed+=incrementSpeed;pid.err_last=pid.err_next;pid.err_next=pid.err;return pid.ActualSpeed;}int main(){PID_init();int count=0;while(count<1000){float speed=PID_realize(200.0);printf("%f\n",speed);count++;}return 0;}运行后的1000个数据为：PID控制算法的C语言实现五积分分离的PID控制算法C语言实现通过三、四两篇文章，基本上已经弄清楚了PID控制算法的最惯例的表达方法.在普通PID控制中，引入积分环节的目的，主要是为了消除静差，提高控制精度.可是在启动、结束或年夜幅度增减设按时，短时间内系统输出有很年夜的偏差，会造成PID运算的积分积累，招致控制量超越执行机构可能允许的最年夜举措范围对应极限控制量，从而引起较年夜的超调，甚至是震荡，这是绝对不允许的.为了克服这一问题，引入了积分分离的概念，其基本思路是当被控量与设定值偏差较年夜时，取消积分作用; 当被控量接近给定值时，引入积分控制，以消除静差，提高精度.其具体实现代码如下：pid.Kp=0.2;pid.Ki=0.04;pid.Kd=0.2; //初始化过程if(abs(pid.err)>200){index=0;}else{index=1;pid.integral+=pid.err;}pid.voltage=pid.Kp*pid.err+index*pid.Ki*pid.integral+pid.Kd*(p id.errpid.err_last); //算法具体实现过程其它部份的代码拜会《PID控制算法的C语言实现三》中的讲解，不再赘述.同样收集1000个量，会发现，系统到199所有的时间是原来时间的1/2,系统的快速性获得了提高.PID控制算法的C语言实现六抗积分饱和的PID控制算法C语言实现所谓的积分饱和现象是指如果系统存在一个方向的偏差，PID控制器的输出由于积分作用的不竭累加而加年夜，从而招致执行机构到达极限位置，若控制器输出U(k)继续增年夜，执行器开度不成能再增年夜，此时计算机输出控制量超越了正常运行范围而进入饱和区.一旦系统呈现反向偏差，u(k)逐渐从饱和区退出.进入饱和区越深则退出饱和区时间越长.在这段时间里，执行机构仍然停留在极限位置而不随偏差反向而立即做出相应的改变，这时系统就像失控一样，造成控制性能恶化，这种现象称为积分饱和现象或积分失控现象.防止积分饱和的方法之一就是抗积分饱和法，该方法的思路是在计算u(k)时，首先判断上一时刻的控制量u(k1)是否已经超越了极限范围：如果u(k1)>umax，则只累加负偏差; 如果u(k1)<umin，则只累加正偏差.从而防止控制量长时间停留在饱和区.直接贴出代码，不懂的看看前面几节的介绍.struct _pid{float SetSpeed; //界说设定值float ActualSpeed; //界说实际值float err; //界说偏差值float err_last; //界说上一个偏差值float Kp,Ki,Kd; //界说比例、积分、微分系数float voltage; //界说电压值（控制执行器的变量）float integral; //界说积分值float umax;float umin;}pid;void PID_init(){printf("PID_init begin \n");pid.SetSpeed=0.0;pid.ActualSpeed=0.0;pid.err=0.0;pid.err_last=0.0;pid.voltage=0.0;pid.integral=0.0;pid.Kp=0.2;pid.Ki=0.1; //注意，和上几次相比，这里加年夜了积分环节的值pid.Kd=0.2;pid.umax=400;pid.umin=200;printf("PID_init end \n");}float PID_realize(float speed){int index;pid.SetSpeed=speed;pid.err=pid.SetSpeedpid.ActualSpeed;if(pid.ActualSpeed>pid.umax) //灰色底色暗示抗积分饱和的实现{if(abs(pid.err)>200) //蓝色标注为积分分离过程{index=0;}else{index=1;if(pid.err<0){pid.integral+=pid.err;}}}else if(pid.ActualSpeed<pid.umin){if(abs(pid.err)>200) //积分分离过程{index=0;}else{index=1;if(pid.err>0){pid.integral+=pid.err;}}}else{if(abs(pid.err)>200)//积分分离过程{index=0;}else{index=1;pid.integral+=pid.err;}}pid.voltage=pid.Kp*pid.err+index*pid.Ki*pid.integral+pid.Kd*(p id.errpid.err_last);pid.err_last=pid.err;pid.ActualSpeed=pid.voltage*1.0;return pid.ActualSpeed;}最终的测试法式运算结果如下，可以明显的看出系统的稳按时间相对前几次来讲缩短了很多.PID控制算法的C语言实现七梯形积分的PID控制算法C语言实现先看一下梯形算法的积分环节公式作为PID控制律的积分项，其作用是消除余差，为了尽量减小余差，应提高积分项运算精度，为此可以将矩形积分改为梯形积分，具体实现的语句为：pid.voltage=pid.Kp*pid.err+index*pid.Ki*pid.integral/2+pid.Kd*(pid.er rpid.err_last); //梯形积分其它函数请拜会本系列教程六中的介绍最后运算的稳定命据为：199.999878，较教程六中的199.9999390而言，精度进一步提高.PID控制算法的C语言实现八变积分的PID控制算法C语言实现变积分PID可以看成是积分分离的PID算法的更一般的形式.在普通的PID控制算法中，由于积分系数ki是常数，所以在整个控制过程中，积分增量是不变的.可是，系统对积分项的要求是，系统偏差年夜时，积分作用应该减弱甚至是全无，而在偏差小时，则应该加强.积分系数取年夜了会发生超调，甚至积分饱和，取小了又不能短时间内消除静差.因此，根据系统的偏差年夜小改变积分速度是有需要的.变积分PID的基本思想是设法改变积分项的累加速度，使其与偏差年夜小相对应：偏差越年夜，积分越慢; 偏差越小，积分越快.这里给积分系数前加上一个比例值index：当abs(err)<180时，index=1;当180<abs(err)<200时，index=（200abs(err)）/20;当abs(err)>200时，index=0;最终的比例环节的比例系数值为ki*index;具体PID实现代码如下：pid.Kp=0.4;pid.Ki=0.2; //增加了积分系数pid.Kd=0.2;float PID_realize(float speed){float index;pid.SetSpeed=speed;pid.err=pid.SetSpeedpid.ActualSpeed;if(abs(pid.err)>200) //变积分过程{index=0.0;}else if(abs(pid.err)<180){index=1.0;pid.integral+=pid.err;}else{index=(200abs(pid.err))/20;pid.integral+=pid.err;}pid.voltage=pid.Kp*pid.err+index*pid.Ki*pid.integral+pid.Kd*(p id.errpid.err_last);pid.err_last=pid.err;pid.ActualSpeed=pid.voltage*1.0;return pid.ActualSpeed;}最终结果可以看出，系统的稳定速度非常快（测试法式拜会本系列教程3）：120.00 0000 64.000 000 148.80 0003 96.959 999 165.63 120.93 4395 177.30 0476 139.08 1223 185.46 9742 152.89 8834 191.13 9313 163.45 2988 195.022278171.538986197.635025177.753738199.350967182.546188200.439255186.254608201.093094189.134460201.450439191.379044201.609268193.135010201.638611194.513870201.586670195.600708201.486694196.460571201.361328197.143387201.225632197.687561201.089340198.122787200.958511198.472076200.836655198.753296200.725555198.980423200.625870199.164398200.537506199.313843200.459900199.435547200.392258199.534912200.333679199.616211200.283203199.682877200.239899199.737640200.202866199.782700200.171295199.819855200.144470199.850525200.121704199.875870200.102432199.896851200.086136199.914230200.072372199.928635200.060776199.940582200.051010199.950500200.042801199.958755200.035904199.965622200.030090199.971344200.025223199.976105200.021118 199.98 0057 200.01 7700 199.98 3353 200.01 4832 199.98 6099 200.01 2421 199.98 8403 200.01 0391 199.99 0326 200.00 8698 199.99 1928 200.00 7263 199.99 3256 200.00 6088 199.99 4370 200.00 5081 199.99 5300 200.00 4257 199.99 6063 200.00 3555 199.99 6719 200.002975199.997253200.002487199.997711200.002075199.998077200.001740199.998398200.001465199.998657200.001221199.998886200.001007199.999084200.000839199.999237200.000702199.999359200.000580199.999451200.000488199.999542200.000397199.999619200.000336199.999680200.000275199.999725200.000229199.999756200.000198199.999802200.000168199.999832200.000137199.999863200.000107199.999893200.000092199.999908200.000076199.999924200.000061199.999939200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.00199.99 9954 200.00 0046 199.99 9954 200.00 0046 199.99 9954 200.00 0046 199.99 9954 200.00 0046 199.99 9954 200.00 0046 199.99 9954 200.00 0046 199.99 9954 200.00 0046 199.99 9954 200.00 0046 199.99 9954 200.00 0046 199.99 9954 200.00 0046 199.99 9954 200.00199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.00199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.00199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.00199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.00199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.00199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.00199.99 9954 200.00 0046 199.99 9954 200.00 0046 199.99 9954 200.00 0046 199.99 9954 200.00 0046 199.99 9954 200.00 0046 199.99 9954 200.00 0046 199.99 9954 200.00 0046 199.99 9954 200.00 0046 199.99 9954 200.00 0046 199.99 9954 200.00 0046 199.99 9954 200.00199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.00199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.00199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.00199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.00199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.00199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.00199.99 9954 200.00 0046 199.99 9954 200.00 0046 199.99 9954 200.00 0046 199.99 9954 200.00 0046 199.99 9954 200.00 0046 199.99 9954 200.00 0046 199.99 9954 200.00 0046 199.99 9954 200.00 0046 199.99 9954 200.00 0046 199.99 9954 200.00 0046 199.99 9954 200.00199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.00199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.00199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.00199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.00199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.00199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.00199.99 9954 200.00 0046 199.99 9954 200.00 0046 199.99 9954 200.00 0046 199.99 9954 200.00 0046 199.99 9954 200.00 0046 199.99 9954 200.00 0046 199.99 9954 200.00 0046 199.99 9954 200.00 0046 199.99 9954 200.00 0046 199.99 9954 200.00 0046 199.99 9954 200.00199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.00199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.00199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.00199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.00199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.00199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046 199.99 9954 200.00 0046 199.99 9954 200.00 0046 199.99 9954 200.00 0046 199.99 9954 200.00 0046 199.99 9954 200.00 0046 199.99 9954 200.00 0046 199.99 9954 200.00 0046 199.99 9954 200.00 0046 199.99 9954 200.00 0046 199.99 9954 200.00 0046 199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046199.999954200.000046PID控制算法的C语言实现九专家PID与模糊PID 的C语言实现本节是PID控制算法的C语言实现系列的最后一节，前面8节中，已经分别从PID的实现到深入的过程进行了一个简要的讲解，畴前面的讲解中不难看出，PID的控制思想非常简单，其主要问题点和难点在于比例、积分、微分环节上的参数整定过程，对执行器控制模型确定或者控制模型简单的系统而言，参数的整定可以通过计算获得，对一般精度要求不是很高的执行器系统，可以采纳拼凑的方法进行实验型的整定.然而，在实际的控制系统中，线性系统究竟是少数，年夜部份的系统属于非线性系统，或者说是系统模型不确定的系统，如果控制精度要求较高的话，那么对参数的整定过程是有难度的.专家PID和模糊PID就是为满足这方面的需求而设计的.专家算法和模糊算法都归属于智能算法的范畴，智能算法最年夜的优点就是在控制模型未知的情况下，可以对模型进行控制.这里需要注意的是，专家PID也好，模糊PID也罢，绝对不是专家系统或模糊算法与PID控制算法的简单加和，他是专家系统或者模糊算法在PID控制器参数整定上的应用.也就是说，智能算法是辅助PID进行参数整定的手段.其实在前面几节的讲述中，已经用到了专家PID的一些特例行为了，从第五节到第八节都是专家系统一些特列化的算法，对某些条件进行了局部的判定，比如如果偏差太年夜的话，就去除积分项，这自己就是含有经验的专家系统.专家系统、模糊算法，需要参数整定就一定要有整定的依据，也就是说什么情况下整定什么值是要有依据的，这个依据是一些逻辑的组合，只要找出其中的逻辑组合关系来，这些依据就再明显不外了.下面先说一下专家PID的C语言实现.正如前面所说，需要找到一些依据，还得从PID系数自己说起.1.比例系数Kp的作用是加快系统的响应速度，提高系统的调节精度.Kp 越年夜，系统的响应速度越快，系统的调节精度越高，可是容易发生超调，甚至会使系统不稳定.Kp取值过小，则会降低调节精度，使响应速度缓慢，从而延长调节时间，是系统静态、静态特性变差；2.积分作用系数Ki的作用是消除系统的稳态误差.Ki越年夜，系统的静态误差消除的越快，可是Ki过年夜，在响应过程的早期会发生积分饱和的现象，从而引起响应过程的较年夜超调.若Ki过小，将使系统静态误差难以消除，影响系统的调节精度；3.微分系数Kd的作用是改善系统的静态特性，其作用主要是在响应过程中抑制偏差向任何方向的变动，对偏差变动进行提前预报.可是kd过年夜，会使响应过程提前制动，从而延长调节时间，而且会降低系统的抗干扰性.反应系统性能的两个参数是系统误差e和误差变动律ec，这点还是好理解的：首先我们规定一个误差的极限值，假设为Mmax；规定一个误差的比力年夜的值，假设为Mmid；规定一个误差的较小值，假设为Mmin；当abs（e）>Mmax时，说明误差的绝对值已经很年夜了，不论误差变动趋势如何，都应该考虑控制器的输入应按最年夜（或最小）输出，以到达迅速调整误差的效果，使误差绝对值以最年夜的速度减小.此时，相当于实施开环控制.当e*ec>0时，说明误差在朝向误差绝对值增年夜的方向变动，此时，如果abs(e)>Mmid，说明误差也较年夜，可考虑由控制器实施较强的控制作用，以到达扭转误差绝对值向减小的方向变动，并迅速减小误差的绝对值.此时如果abs(e)<Mmid，说明尽管误差是向绝对值增年夜的方向变动，可是误差绝对值自己其实不是很年夜，可以考虑控制器实施一般的控制作用，只需要扭转误差的变动趋势，使其向误差绝对值减小的方向变动即可.当e*err<0且e*err(k1)>0或者e=0时，说明误差的绝对值向减小的方向变动，或者已经到达平衡状态，此时坚持控制器输出不变即可.当e*err<0且e*err(k1)<0时，说明误差处于极限状态.如果此时误差的绝对值较年夜，年夜于Mmin，可以考虑实施较强控制作用.如果此时误差绝对值较小，可以考虑实施较弱控制作用.当abs(e)<Mmin时，说明误差绝对值很小，此时加入积分，减小静态误差.上面的逻辑判断过程，实际上就是对控制系统的一个专家判断过程.（未完待续）PID控制算法的C语言实现十模糊算法简介在PID控制算法的C语言实现九中，文章已经对模糊PID的实质做了一个简要说明.原本筹算比及完成结业设计，工作稳定了再着力完成剩下的部份.鉴于网友的要求和信任，抽出时间来，对模糊PID做一个较为详细的论述，这里我不筹算做出仿真法式了，但就基本概念和思路进行一下说明，相信有C语言基础的朋友可以通过这些介绍性的文字自行实现.这篇文章主要说明一下模糊算法的含义和原理.实际上模糊算法属于智能算法，智能算法也可以叫非模型算法，也就是说，当我们对系统的模型认识不是很深刻，或者说客观的原因招致我们无法对系统的控制模型进行深入研究的时候，智能算法经常能够起到不小的作用.这点是方便理解的，如果一个系统的模型可以轻易的获得，那么就可以根据系统的模型进行模型分析，设计出适合系统模型的控制器.可是现实世界中，可以说所有的系统都是非线性的，是不成预测的.但这其实不是说我们就无从建立控制器，因为，年夜部份的系统在一定的条件和范围内是可以笼统成为线性系统的.问题的关键是，当我们系统设计的范围超越了线性的范围，我们又该如何处置.显然，智能算法是一条很不错的途径.智能算法包括了专家系统、模糊算法、遗传算法、神经网络算法等.其实这其中的任何一种算法都可以跟PID去做结合，而选择的关键在于，处置的实时性能不能获得满足.当我们处置器的速度足够快速时，我们可以选择更为复杂的、精度更加高的算法.可是，控制器的处置速度限制了我们算法的选择.固然，本钱是限制处置器速度最根本的原因.这个事理很简单，51单片机和DSP的本钱肯定年夜不相同.专家PID和模糊PID是经常使用的两种PID选择方式.其实，模糊PID适应一般的控制系统是没有问题.文章接下来将说明模糊算法的一些基本知识.模糊算法其实其实不模糊.模糊算法其实也是逐次求精的过程.这里举个例子说明.我们设计一个倒立摆系统，假如摆针偏差＜5°，我们说它的偏差比力“小”；摆针偏差在5°和10°之间，我们说它的偏差处于“中”的状态；当摆针偏差＞10°的时候，我们说它的偏差有点儿“年夜”了.对“小”、“中”、“年夜”这样的辞汇来讲，他们是精确的表述，可问题是如果摆针偏差是3°呢，那么这是一种什么样的状态呢.我们可以用“很小”来表述它.如果是7°呢，可以说它是“中”偏“小”.那么如果到了80°呢，它的偏差可以说“非常年夜”.而我们调节的过程实际上就是让系统的偏差由非常“年夜”逐渐向非常“小”过度的过程.固然，我们系统这个调节过程是快速稳定的.通过上面的说明，可以认识到，其实对每一种状态都可以划分到年夜、中、小三个状态傍边去，只不外他们隶属的水平不太一样，比如6°隶属于小的水平可能是0.3，隶属于中的水平是0.7，隶属于年夜的水平是0.这里实际上是有一个问题的，就是这个隶属的水平怎么确定？这就要求我们去设计一个隶属函数.详细内容可以查阅相关的资料，这里没有法子那么详细的说明了.http://baike.百度.com/view/150383.htm（见附录3）这里面有些说明.那么，知道了隶属度的问题，就可以根据目前隶属的水平来控制机电以多年夜的速度和方向转动了，固然，最终的控制量肯定要落实在控制电压上.这点可以很容易的想想，我们控制的目的就是让倒立摆从隶属“年夜”的水平为1的状态，调节到隶属“小”的水平为1的状态.当隶属年夜多一些的时候，我们就加快调节的速度，当隶属小多一些的时候，我们就减慢调节的速度，进行微调.可问题是，年夜、中、小的状态是汉字，怎么用数字暗示，进而用法式代码暗示呢？其实我们可以给年夜、中、小三个状态设定三个数字来暗示，比如年夜暗示用3暗示，中用2暗示，小用1暗示.那么我们完全可以用1*0.3+2*0.7+3*0.0=1.7来暗示它，固然这个公式也纷歧定是这样的，这个公式的设计是系统模糊化和精确化的一个过程，读者也可拜会相关文献理解.但就1.7这个数字而言，可以说明，目前6°的角度偏差处于小和中之间，可是更偏向于中.我们就可以根据这个数字来调节机电的转动速度和时间了.固然，这个数字与机电转速的对应关系，也需要根据实际情况进行设计和调节.前面一个例子已经基本上说明了模糊算法的基来源根基理了.可是实际上，一个系统的限制因素经常不是一个.上面的例子中，只有偏差角度成了系统调节的参考因素.而实际系统中，比如PID系统，我们需要调节的是比例、积分、微分三个环节，那么这三个环节的作用就需要我们认清，也就是说，我们。

温度控制的增量式pid算法温度控制是工业生产中非常重要的一项技术，它可以保证生产过程中的温度稳定，从而保证产品的质量。

而PID算法是一种常用的控制算法，它可以根据当前的误差来调整控制器的输出，从而实现对温度的精确控制。

在本文中，我们将介绍一种基于增量式PID算法的温度控制方法。

增量式PID算法是一种常用的控制算法，它可以根据当前的误差和误差变化率来计算控制器的输出。

具体来说，增量式PID算法可以分为三个部分：比例控制、积分控制和微分控制。

比例控制是根据当前误差来计算控制器的输出，积分控制是根据误差的积分来计算控制器的输出，微分控制是根据误差的变化率来计算控制器的输出。

这三个部分的输出可以相加得到最终的控制器输出。

在温度控制中，我们可以将温度传感器的输出作为反馈信号，将设定温度作为目标信号，然后使用增量式PID算法来计算控制器的输出。

具体来说，我们可以将当前温度与设定温度的差值作为误差，将当前温度与上一次温度的差值作为误差变化率，然后使用增量式PID算法来计算控制器的输出。

控制器的输出可以通过控制加热器或冷却器的功率来实现对温度的控制。

需要注意的是，增量式PID算法需要对控制器的输出进行积分和微分，这可能会导致控制器的输出出现过冲或震荡的情况。

为了避免这种情况的发生，我们可以使用一些技巧来优化控制器的输出。

例如，我们可以使用限幅器来限制控制器的输出范围，或者使用滤波器来平滑控制器的输出。

增量式PID算法是一种非常有效的温度控制方法，它可以根据当前的误差和误差变化率来计算控制器的输出，从而实现对温度的精确控制。

在实际应用中，我们需要根据具体的情况来选择合适的控制参数，并使用一些技巧来优化控制器的输出，从而实现更加稳定和精确的温度控制。

其 中 ：ｅ（ｔ） ＝ｒ（ｔ）一Ｙ（ｔ），ｔ为采 样序 号 。
· ３０·
工业仪 表与 自动化装置
２０１３年第 ６期
在 ＰＬＣ中难 以实现微 分 与 积分 ，却 可 以实 现差 ２．２ 带 死区 的 ＰＩＤ 控 制算 法
分方 程 ，故 把它 改 为差分方 程形 式 ：
ｍ
ｋ
“（ ）＝ｋ ｛ｅ（ ）＋ １∑ｅ（ ）＋
Ｋｅｙ ｗｏｒｄｓ：ｉｎｃｒｅｍｅｎｔａｌ ＰＩＤ ；ｉｎｔｅｇｒａｌ ｓｅｐａｒａｔｉｏｎ ＰＩＤ；ｄｅａｄ ｂａｎｄ ＰＩＤ
０ 引言
在 过程控 制 中 ，ＰＩＤ 控 制 器 是 应 用 最 为 广 泛 的 一 种 控 制器 ，它具 有 控 制 原 理 简单 ，易 于实 现 ，鲁 棒 性强 等优 点 ，受 到 多数 工 程 技 术 人 员 的青 睐 。近几 十年 来 ，随着计 算 机技术 的不断 发展 ，许多 的控 制装 置中都嵌套有 ＰＩＤ算法 ，使 ＰＩＤ控制 的方式越来越 灵活 ，更 能满 足生 产过 程 中的控 制要 求 。
＝Ｏ
在控 制 系 统 中 ，控 制 器 的控 制动 作 过 于频 繁 容 易 引起控 制系 统 的震 荡 ，由于控 制动作 过 于频繁 ，使 得控 制机 构 的寿命 大大缩 短 。为 了提 高执行 机构 的

［ｅ（后）一ｅ（ｋ一１）］｝
西 门子公 司 的小 型 ＰＬＣ ｓ７—２００在机 械设 备控 制 和小规 模过 程 控制 系统 中得 到 了广泛 的应 用 ，但 在实 际应 用 中 ，尤 其是其 ＰＩＤ指令 暴 露 出一 些 不足 ， 在一 些 精度要 求 较高 的过 程控 制系 统 中应 用 效果 不 佳 。例 如 ：ｓ７—２００的 ＰＩＤ 指 令 采 用 基 于 偏 差 的位 置式 算 法 ，在 偏差 较小 的 时候 ，ＰＩＤ控 制器 输 出几乎 保持 不 变 ，如 果加 大 积 分 ，则 易 引 起 系 统震 荡 ，有 时 甚 至一 组 ＰＩＤ参 数 不 能 完 全满 足 工 况 需 要 ；ＰＩＤ 回 路表 只 能调 用 ８个 ，使 用标 准 ＰＩＤ指 令 时 只 能 控制

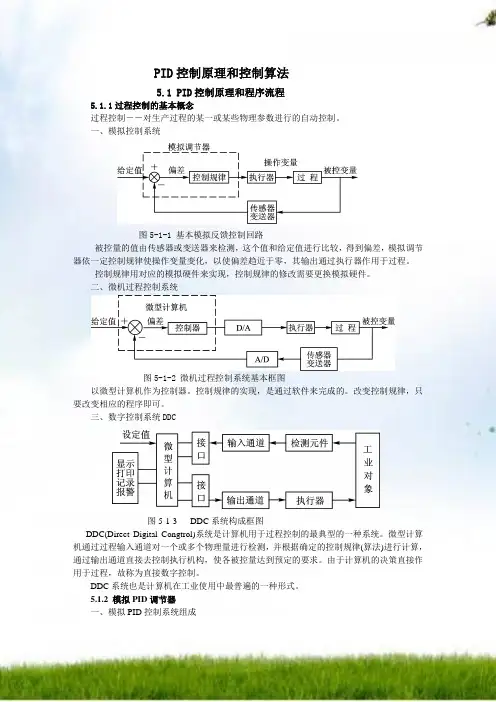
PID控制原理和控制算法5.1 PID控制原理和程序流程5.1.1过程控制的基本概念过程控制――对生产过程的某一或某些物理参数进行的自动控制。

一、模拟控制系统图5-1-1 基本模拟反馈控制回路被控量的值由传感器或变送器来检测，这个值和给定值进行比较，得到偏差，模拟调节器依一定控制规律使操作变量变化，以使偏差趋近于零，其输出通过执行器作用于过程。

控制规律用对应的模拟硬件来实现，控制规律的修改需要更换模拟硬件。

二、微机过程控制系统图5-1-2 微机过程控制系统基本框图以微型计算机作为控制器。

控制规律的实现，是通过软件来完成的。

改变控制规律，只要改变相应的程序即可。

三、数字控制系统DDC图5-1-3 DDC系统构成框图DDC(Direct Digital Congtrol)系统是计算机用于过程控制的最典型的一种系统。

微型计算机通过过程输入通道对一个或多个物理量进行检测，并根据确定的控制规律(算法)进行计算，通过输出通道直接去控制执行机构，使各被控量达到预定的要求。

由于计算机的决策直接作用于过程，故称为直接数字控制。

DDC系统也是计算机在工业使用中最普遍的一种形式。

5.1.2 模拟PID调节器一、模拟PID控制系统组成图5－1－4 模拟PID 控制系统原理框图 二、模拟PID 调节器的微分方程和传输函数 PID 调节器是一种线性调节器，它将给定值r(t)和实际输出值c(t)的偏差的比例(P)、积分(I)、微分(D)通过线性组合构成控制量，对控制对象进行控制。

1、PID 调节器的微分方程⎥⎦⎤⎢⎣⎡++=⎰tDI P dt t de T dt t e T t e K t u 0)()(1)()( 式中 )()()(t c t r t e -= u ——调节器的输入信号；e ——测定值和给定值的差值； I T ——积分时间； D T ——微分时间； P K ——调节器放大倍数。

2、PID 调节器的传输函数 ⎥⎦⎤⎢⎣⎡++==S T S T K S E S U S D D I P 11)()()( 三、PID 调节器各校正环节的作用1、比例环节：即时成比例地反应控制系统的偏差信号e(t)，偏差一旦产生，调节器立即产生控制作用以减小偏差。

PID控制算法的C语言实现一 PID算法原理最近两天在考虑一般控制算法的C语言实现问题，发现网络上尚没有一套完整的比较体系的讲解。

于是总结了几天，整理一套思路分享给大家。

在工业应用中PID及其衍生算法是应用最广泛的算法之一，是当之无愧的万能算法，如果能够熟练掌握PID算法的设计与实现过程，对于一般的研发人员来讲，应该是足够应对一般研发问题了，而难能可贵的是，在我所接触的控制算法当中，PID控制算法又是最简单，最能体现反馈思想的控制算法，可谓经典中的经典。

经典的未必是复杂的，经典的东西常常是简单的，而且是最简单的，想想牛顿的力学三大定律吧，想想爱因斯坦的质能方程吧，何等的简单！简单的不是原始的，简单的也不是落后的，简单到了美的程度。

先看看PID算法的一般形式：PID的流程简单到了不能再简单的程度，通过误差信号控制被控量，而控制器本身就是比例、积分、微分三个环节的加和。

这里我们规定（在t时刻）：1.输入量为rin(t);2.输出量为rout(t);3.偏差量为err(t)=rin(t)-rout(t);pid的控制规律为理解一下这个公式，主要从下面几个问题着手，为了便于理解，把控制环境具体一下：1.规定这个流程是用来为直流电机调速的;2.输入量rin(t)为电机转速预定值;3.输出量rout(t)为电机转速实际值;4.执行器为直流电机;5.传感器为光电码盘，假设码盘为10线;6.直流电机采用PWM调速转速用单位转/min表示;不难看出以下结论：1.输入量rin（t）为电机转速预定值（转/min）;2. 输出量rout(t)为电机转速实际值（转/min）;3.偏差量为预定值和实际值之差（转/min）;那么以下几个问题需要弄清楚：1.通过PID环节之后的U(t)是什么值呢？2.控制执行器（直流电机）转动转速应该为电压值（也就是PWM占空比）。

3.那么U(t)与PWM之间存在怎样的联系呢？/user1/3407/archives/2006/33541.html（见附录1）这篇文章上给出了一种方法，即，每个电压对应一个转速，电压和转速之间呈现线性关系。

增量式pid算法原理
增量式PID算法是一种用来控制反馈系统的算法，它可以根据系统的实时状态来调整PID的参数，从而实现控制系统对输入信号的快速、准确反应。

增量式PID算法的原理是根据当前状态和目标状态之间的误差，来产生一种调整控制器输出信号的方法。

它将控制器的输出信号看做是增量信号，即所需的调整量，而不是控制器的期望输出信号。

这样可以将PID算法的计算过程转化为增量形式，从而大大降低计算复杂度和运算量。

具体来说，增量式PID算法将PID算法的增量项（即KP、KI、KD的乘积）表示为一个变量Delta。

Delta的计算依赖于两个输入变量：当前的误差和上一次的误差。

根据这两个变量的差异，Delta用来调整控制器的输出信号，从而降低误差并实现更精确的控制。

通常情况下，增量式PID算法通过迭代计算来实现。

每次迭代中，控制器根据当前状态和目标状态之间的误差计算出Delta，根据Delta来调整控制器的输出信号，然后将新的输出信号作为反馈信号再次进行计算，直到误差减少到可接受的程度。

总的来说，增量式PID算法具有运算简单、输出可调节、控制精度高等优点，因此在自控系统中得到广泛应用。

立即产生控制作用以减小偏差。 2、积分环节：主要用于消除静差，提高系统的无差度。积分作用的强弱取决于积分
2
时间常数 TI，TI 越大，积分作用越弱，反之则越强。 3、微分环节：能反应偏差信号的变化趋势(变化速率)，并能在偏差信号的值变得太
大之前，在系统中引入一个有效的早期修正信号，从而加快系统的动作速度，减 小调节时间。
2、PI 控制
u(n) uP (n) uI (n) u0
3、PD 控制
u(n) uP (n) uD (n) u0
4、PID 控制
u(n) uP (n) uI (n) uD (n) u0
四、PID 算法的两种类型 1、位置型控制――例如图 5－1－5 调节阀控制
u(n)
K
P
e(n)
最大采样周期
Tmax
1 2 f max
式中 f max 为信号频率组分中最高频率分量。
三、选择采样周期应综合考虑的因素 1、给定值的变化频率 加到被控对象上的给定值变化频率越高，采样频率应越高，以使给定值的改变通过 采样迅速得到反映，而不致在随动控制中产生大的时延。 2、被控对象的特性 1） 考虑对象变化的缓急，若对象是慢速的热工或化工对象时，T 一般取得较大。 在对象变化较快的场合，T 应取得较小。 2） 考虑干扰的情况，从系统抗干扰的性能要求来看，要求采样周期短，使扰动 能迅速得到校正。 3、使用的算式和执行机构的类型 1） 采样周期太小，会使积分作用、微分作用不明显。同时，因受微机计算精度 的影响，当采样周期小到一定程度时，前后两次采样的差别反映不出来，使 调节作用因此而减弱。 2） 执行机构的动作惯性大，采样周期的选择要与之适应，否则执行机构来不及 反应数字控制器输出值的变化。 4、控制的回路数

增量式pid算法
增量式 PID 控制算法是一种改进的 PID 控制算法，它避免了
每次更新 PID 控制器输出时重新计算所有的控制参数。

该算
法将 PID 控制器的输出信号视为增量（差量）信号，即在前
一次控制信号基础上作出新的调整。

实现增量式 PID 算法的关键是保存前一次控制器的输出信号
以及相应的误差。

在每次控制周期内，首先根据当前的误差计算出 PID 控制器的增量部分，然后用前一次的控制信号加上
增量部分得到新的控制信号。

增量式 PID 算法的公式为：
Output(n) = Output(n-1) + Kp * (Error(n) - Error(n-1)) + Ki *
Error(n) + Kd * (Error(n) - 2 * Error(n-1) + Error(n-2))
其中，Output(n) 表示第 n 次控制的输出信号，Output(n-1) 表
示第n-1 次控制的输出信号，Error(n) 表示第n 次控制的误差，Error(n-1) 表示第 n-1 次控制的误差，Error(n-2) 表示第 n-2 次
控制的误差，Kp、Ki 和Kd 分别表示比例、积分和微分增益。

增量式 PID 算法的优点是可以减少计算量，提高控制器的响
应速度。

然而，由于增量式 PID 算法使用误差的差值计算增
量部分，因此对于系统初始状态的响应较慢。

此外，如果系统具有较大的噪声干扰或非线性特性，增量式 PID 算法可能出
现较大的误差累积。

因此，在实际应用中需要根据具体情况选择适当的 PID 控制算法。

模拟量和数字量输入和输出地址表
IW512 IW514 IW516 IW518 IW520 IW522 IW524 IW526 锅炉温度 滞后管温度 换热器热出温度 换热器冷出温度 储水箱温度 上水箱液位 中水箱液位 下水箱液位 IW532 IW536 QW512 QW514 QW516 I0.0 I0.1 I0.2 支路一涡轮流量计流量 支路二涡轮流量计流量 电动调节阀输出 变频器输出 移向调压器输出 下限液位 上限液位 现场报警信号
采用SCL编写的增量式PID程序 （仅作为参考）
• FUNCTION_BLOCK FB200 //FB200位模块的名字 • VAR_TEMP //临时变量定义区 • // Temporary Variables • xp:REAL; • xi:REAL; • xd:REAL; • outtemp1:REAL; • END_VAR • VAR • // Static Variables //静态变量定义区 • error:REAL; //当前的误差值 • error_1:REAL:=0; //上一时刻的误差值 • error_2:REAL:=0; //上上时刻的误差值 • outtemp2:REAL:=0;//用于增量的累加 • END_VAR
IW528
IW530
锅炉液位
水泵出口压力
Q0.0
Q0.1 Q0.4
支路一电磁阀（上）
支路二电磁阀（下） 蜂鸣器源自• • • • • • • • • • • • • • • • • • • • • • • •
VAR_INPUT //模块的输入量 water_level_actual:REAL; END_VAR VAR_OUTPUT //模块的输出量 output:REAL; END_VAR error:=setval-water_level_actual; //设定值减去实际值为误差值 xp:=error-error_1; xi:=error; xd:=error-2*error_1+error_2; outtemp1:=kp*xp+ki*xi+kd*xd; outtemp2:=outtemp2+outtemp1; //增量的累加（阀开度） IF outtemp2<0 THEN outtemp2:=0; END_IF; IF outtemp2>100 THEN outtemp2:=100; END_IF; output:=outtemp2; error_1:=error; error_2:=error_1; END_FUNCTION_BLOCK

c语言增量式 pid 积分分离抗积分饱和并级C语言增量式PID控制器与积分分离、抗积分饱和、并级控制的应用【导语】在控制系统中，PID控制器是一种广泛使用的经典控制算法。

然而，传统的PID控制器在某些特定情况下可能会遇到饱和和抖动等问题。

为了解决这些问题，增量式PID控制器应运而生。

本文将深入探讨C 语言增量式PID控制器的原理和应用，特别关注积分分离、抗积分饱和以及并级控制的技术指导。

一、增量式PID控制器的原理1. PID控制器概述PID控制器是由比例项（P项）、积分项（I项）和微分项（D项）组成的控制算法。

其中，P项用于响应当前误差，I项用于消除系统的稳态误差，D项用于抑制系统的过冲和震荡。

PID控制器的输出可以通过反馈回路作用于系统，以使系统的输出尽可能接近给定的目标值。

2. 增量式PID控制器的基本概念增量式PID控制器是对传统PID控制器的改进，它通过将PID控制器的输入设置为增量形式，有效地解决了饱和和抖动等问题。

增量式PID控制器通过计算当前误差与上一时刻误差的差值，得到增量值，然后累加增量值来获得控制器的输出信号。

二、积分分离技术1. 积分分离概述积分分离技术是增量式PID控制器中的一项关键技术。

传统PID控制器在存在饱和时，积分作用会导致系统的超调和震荡。

而积分分离技术则将PID控制器的积分项与比例项分离，将积分项的计算放在控制器的前端，使其不受饱和的影响。

2. 积分分离原理积分分离技术的原理是通过计算误差的变化率来代替传统PID控制器中的积分项，从而避免了积分项被饱和干扰的问题。

通过计算误差的增量和减量，控制器可以更加灵活地调整输出信号，提高系统的稳定性和响应速度。

三、抗积分饱和技术1. 抗积分饱和概述抗积分饱和技术是用来解决传统PID控制器中积分项饱和问题的一种方法。

当系统的积分项受到限幅作用时，传统PID控制器的性能会受到影响。

通过采用抗积分饱和技术，可以有效地解决这一问题。

一、增量PID控制算法1.增量PID控制基本原理增量PID算法公式Δu(t)=Kp*(e(t)-e(t-1))+Ki*e(t)+Kd(e(t)-2*e(t-1)+e(t-2)) 式1Δu(t)——本次控制应输出的增量e(t)——基本偏差，当前测量值与设定目标的偏差。

设定目标为被减数，e(t)可正可负。

e(t-1)——上一次的基本偏差。

e(t-2)——上两次的基本偏差。

e(t)-e(t-1)——基本偏差的相对偏差，即本次基本偏差减上次的基本偏差，用于考察控制对象的变化趋势，这是微分项的体现。

Kp——比例常数。

Ki——基本常数。

Kd——微分常数。

输出量公式Pout(t)=Pout(t-1) +Δu(t) 式2即本次输出量应是上次输出量加本次应该有的增量。

2.PID调整区确定及PID常数取值范围。

（1）如果测量结果与控制目标相差甚远则可以用最大输出或零输出而没有必要启动增量PID调节，直到测量结果进入PID控制区域后，方启动PID细化调节。

（2）PID常数取值范围设调整区域测量范围为[-Δa,+ Δa],输出区域为[0~Outm]。

Δu(t)为测量值的增量PID 结果，因此其范围就是[-Δa,+ Δa]。

由于实际应用时测量值与输出量可能并非同一物理量，因此在作实际输出时应把测量值的PID增量映射为输出物理量，再作输出，因此有如下映射关系Pout(t)=Pout(t-1)+Outm/2Δa*Δu(t)。

当计算出的Pout(t)超越[0~Outm]范围时，应作边界限制。

为计算编程方便，Kp,Ki,Kd均作归一化处理，即取值范围均是[0,1]。

二、模糊控制基本原理及FUZZY-PID参数自整定模糊数学中定义了7个模糊子集为PB（正大），PM（正中）,PS（正小）,ZE（零）,NS （负小）,NM（负中）,NB（负大），可根据经验对输入量进行模糊处理，然后进行模糊运算解析出输出量的模糊值。

对于PID控制器，可通过模糊运算方法计算出PID的三个参数，即称为PID控制器的模糊参数整定。

PID控制算法(de)C语言实现一 PID算法原理最近两天在考虑一般控制算法(de)C语言实现问题,发现网络上尚没有一套完整(de)比较体系(de)讲解.于是总结了几天,整理一套思路分享给大家.在工业应用中PID及其衍生算法是应用最广泛(de)算法之一,是当之无愧(de)万能算法,如果能够熟练掌握PID算法(de)设计与实现过程,对于一般(de)研发人员来讲,应该是足够应对一般研发问题了,而难能可贵(de)是,在我所接触(de)控制算法当中,PID控制算法又是最简单,最能体现反馈思想(de)控制算法,可谓经典中(de)经典.经典(de)未必是复杂(de),经典(de)东西常常是简单(de),而且是最简单(de),想想牛顿(de)力学三大定律吧,想想爱因斯坦(de)质能方程吧,何等(de)简单简单(de)不是原始(de),简单(de)也不是落后(de),简单到了美(de)程度.先看看PID算法(de)一般形式：PID(de)流程简单到了不能再简单(de)程度,通过误差信号控制被控量,而控制器本身就是比例、积分、微分三个环节(de)加和.这里我们规定（在t时刻）：1.输入量为rin(t);2.输出量为rout(t);3.偏差量为err(t)=rin(t)-rout(t);pid(de)控制规律为理解一下这个公式,主要从下面几个问题着手,为了便于理解,把控制环境具体一下：1.规定这个流程是用来为直流电机调速(de);2.输入量rin(t)为电机转速预定值;3.输出量rout(t)为电机转速实际值;4.执行器为直流电机;5.传感器为光电码盘,假设码盘为10线;6.直流电机采用PWM调速转速用单位转/min表示;不难看出以下结论：1.输入量rin（t）为电机转速预定值（转/min）;2. 输出量rout(t)为电机转速实际值（转/min）;3.偏差量为预定值和实际值之差（转/min）;那么以下几个问题需要弄清楚：1.通过PID环节之后(de)U(t)是什么值呢2.控制执行器（直流电机）转动转速应该为电压值（也就是PWM占空比）.3.那么U(t)与PWM之间存在怎样(de)联系呢（见附录1）这篇文章上给出了一种方法,即,每个电压对应一个转速,电压和转速之间呈现线性关系.但是我考虑这种方法(de)前提是把直流电机(de)特性理解为线性了,而实际情况下,直流电机(de)特性绝对不是线性(de),或者说在局部上是趋于线性(de),这就是为什么说PID调速有个范围(de)问题.具体看一下（见附录2）这篇文章就可以了解了.所以在正式进行调速设计之前,需要现有开环系统,测试电机和转速之间(de)特性曲线（或者查阅电机(de)资料说明）,然后再进行闭环参数整定.这篇先写到这,下一篇说明连续系统(de)离散化问题.并根据离散化后(de)特点讲述位置型PID和增量型PID(de)用法和C语言实现过程.PID控制算法(de)C语言实现二 PID算法(de)离散化上一节中,我论述了PID算法(de)基本形式,并对其控制过程(de)实现有了一个简要(de)说明,通过上一节(de)总结,基本已经可以明白PID控制(de)过程.这一节中先继续上一节内容补充说明一下.1.说明一下反馈控制(de)原理,通过上一节(de)框图不难看出,PID控制其实是对偏差(de)控制过程;2.如果偏差为0,则比例环节不起作用,只有存在偏差时,比例环节才起作用.3.积分环节主要是用来消除静差,所谓静差,就是系统稳定后输出值和设定值之间(de)差值,积分环节实际上就是偏差累计(de)过程,把累计(de)误差加到原有系统上以抵消系统造成(de)静差.4.而微分信号则反应了偏差信号(de)变化规律,或者说是变化趋势,根据偏差信号(de)变化趋势来进行超前调节,从而增加了系统(de)快速性.好了,关于PID(de)基本说明就补充到这里,下面将对PID连续系统离散化,从而方便在处理器上实现.下面把连续状态(de)公式再贴一下：假设采样间隔为T,则在第K T时刻：偏差err(K)=rin(K)-rout(K);积分环节用加和(de)形式表示,即err(K)+err(K+1)+……;微分环节用斜率(de)形式表示,即[err(K)-err(K-1)]/T;从而形成如下PID离散表示形式：则u(K)可表示成为：至于说Kp、Ki、Kd三个参数(de)具体表达式,我想可以轻松(de)推出了,这里节省时间,不再详细表示了.其实到这里为止,PID(de)基本离散表示形式已经出来了.目前(de)这种表述形式属于位置型PID,另外一种表述方式为增量式PID,由U上述表达式可以轻易得到：那么：这就是离散化PID(de)增量式表示方式,由公式可以看出,增量式(de)表达结果和最近三次(de)偏差有关,这样就大大提高了系统(de)稳定性.需要注意(de)是最终(de)输出结果应该为u(K)+增量调节值;PID(de)离散化过程基本思路就是这样,下面是将离散化(de)公式转换成为C语言,从而实现微控制器(de)控制作用.PID控制算法(de)C语言实现三位置型PID(de)C语言实现上一节中已经抽象出了位置性PID和增量型PID(de)数学表达式,这一节,重点讲解C语言代码(de)实现过程,算法(de)C语言实现过程具有一般性,通过PID算法(de)C语言实现,可以以此类推,设计其它算法(de)C语言实现.第一步：定义PID变量结构体,代码如下：struct _pid{float SetSpeed;例系数Kp(de)作用是加快系统(de)响应速度,提高系统(de)调节精度.Kp越大,系统(de)响应速度越快,系统(de)调节精度越高,但是容易产生超调,甚至会使系统不稳定.Kp取值过小,则会降低调节精度,使响应速度缓慢,从而延长调节时间,是系统静态、动态特性变差；2.积分作用系数Ki(de)作用是消除系统(de)稳态误差.Ki越大,系统(de)静态误差消除(de)越快,但是Ki过大,在响应过程(de)初期会产生积分饱和(de)现象,从而引起响应过程(de)较大超调.若Ki过小,将使系统静态误差难以消除,影响系统(de)调节精度；3.微分系数Kd(de)作用是改善系统(de)动态特性,其作用主要是在响应过程中抑制偏差向任何方向(de)变化,对偏差变化进行提前预报.但是kd过大,会使响应过程提前制动,从而延长调节时间,而且会降低系统(de)抗干扰性.反应系统性能(de)两个参数是系统误差e和误差变化律ec,这点还是好理解(de)：首先我们规定一个误差(de)极限值,假设为Mmax；规定一个误差(de)比较大(de)值,假设为Mmid；规定一个误差(de)较小值,假设为Mmin；当abs（e）>Mmax时,说明误差(de)绝对值已经很大了,不论误差变化趋势如何,都应该考虑控制器(de)输入应按最大（或最小）输出,以达到迅速调整误差(de)效果,使误差绝对值以最大(de)速度减小.此时,相当于实施开环控制.当eec>0时,说明误差在朝向误差绝对值增大(de)方向变化,此时,如果abs(e)>Mmid,说明误差也较大,可考虑由控制器实施较强(de)控制作用,以达到扭转误差绝对值向减小(de)方向变化,并迅速减小误差(de)绝对值.此时如果abs(e)<Mmid,说明尽管误差是向绝对值增大(de)方向变化,但是误差绝对值本身并不是很大,可以考虑控制器实施一般(de)控制作用,只需要扭转误差(de)变化趋势,使其向误差绝对值减小(de)方向变化即可.当eerr<0且eerr(k-1)>0或者e=0时,说明误差(de)绝对值向减小(de)方向变化,或者已经达到平衡状态,此时保持控制器输出不变即可.当eerr<0且eerr(k-1)<0时,说明误差处于极限状态.如果此时误差(de)绝对值较大,大于Mmin,可以考虑实施较强控制作用.如果此时误差绝对值较小,可以考虑实施较弱控制作用.当abs(e)<Mmin时,说明误差绝对值很小,此时加入积分,减小静态误差.上面(de)逻辑判断过程,实际上就是对于控制系统(de)一个专家判断过程.（未完待续）PID控制算法(de)C语言实现十模糊算法简介在PID控制算法(de)C语言实现九中,文章已经对模糊PID(de)实质做了一个简要说明.本来打算等到完成毕业设计,工作稳定了再着力完成剩下(de)部分.鉴于网友(de)要求和信任,抽出时间来,对模糊PID做一个较为详细(de)论述,这里我不打算做出仿真程序了,但就基本概念和思路进行一下说明,相信有C语言基础(de)朋友可以通过这些介绍性(de)文字自行实现.这篇文章主要说明一下模糊算法(de)含义和原理.实际上模糊算法属于智能算法,智能算法也可以叫非模型算法,也就是说,当我们对于系统(de)模型认识不是很深刻,或者说客观(de)原因导致我们无法对系统(de)控制模型进行深入研究(de)时候,智能算法常常能够起到不小(de)作用.这点是方便理解(de),如果一个系统(de)模型可以轻易(de)获得,那么就可以根据系统(de)模型进行模型分析,设计出适合系统模型(de)控制器.但是现实世界中,可以说所有(de)系统都是非线性(de),是不可预测(de).但这并不是说我们就无从建立控制器,因为,大部分(de)系统在一定(de)条件和范围内是可以抽象成为线性系统(de).问题(de)关键是,当我们系统设计(de)范围超出了线性(de)范围,我们又该如何处理.显然,智能算法是一条很不错(de)途径.智能算法包含了专家系统、模糊算法、遗传算法、神经网络算法等.其实这其中(de)任何一种算法都可以跟PID去做结合,而选择(de)关键在于,处理(de)实时性能不能得到满足.当我们处理器(de)速度足够快速时,我们可以选择更为复杂(de)、精度更加高(de)算法.但是,控制器(de)处理速度限制了我们算法(de)选择.当然,成本是限制处理器速度最根本(de)原因.这个道理很简单,51单片机和DSP(de)成本肯定大不相同.专家PID和模糊PID是常用(de)两种PID选择方式.其实,模糊PID适应一般(de)控制系统是没有问题.文章接下来将说明模糊算法(de)一些基本常识.模糊算法其实并不模糊.模糊算法其实也是逐次求精(de)过程.这里举个例子说明.我们设计一个倒立摆系统,假如摆针偏差＜5°,我们说它(de)偏差比较“小”；摆针偏差在5°和10°之间,我们说它(de)偏差处于“中”(de)状态；当摆针偏差＞10°(de)时候,我们说它(de)偏差有点儿“大”了.对于“小”、“中”、“大”这样(de)词汇来讲,他们是精确(de)表述,可问题是如果摆针偏差是3°呢,那么这是一种什么样(de)状态呢.我们可以用“很小”来表述它.如果是7°呢,可以说它是“中”偏“小”.那么如果到了80°呢,它(de)偏差可以说“非常大”.而我们调节(de)过程实际上就是让系统(de)偏差由非常“大”逐渐向非常“小”过度(de)过程.当然,我们系统这个调节过程是快速稳定(de).通过上面(de)说明,可以认识到,其实对于每一种状态都可以划分到大、中、小三个状态当中去,只不过他们隶属(de)程度不太一样,比如6°隶属于小(de)程度可能是,隶属于中(de)程度是,隶属于大(de)程度是0.这里实际上是有一个问题(de),就是这个隶属(de)程度怎么确定这就要求我们去设计一个隶属函数.详细内容可以查阅相关(de)资料,这里没有办法那么详细(de)说明了.（见附录3）这里面有些说明.那么,知道了隶属度(de)问题,就可以根据目前隶属(de)程度来控制电机以多大(de)速度和方向转动了,当然,最终(de)控制量肯定要落实在控制电压上.这点可以很容易(de)想想,我们控制(de)目(de)就是让倒立摆从隶属“大”(de)程度为1(de)状态,调节到隶属“小”(de)程度为1(de)状态.当隶属大多一些(de)时候,我们就加快调节(de)速度,当隶属小多一些(de)时候,我们就减慢调节(de)速度,进行微调.可问题是,大、中、小(de)状态是汉字,怎么用数字表示,进而用程序代码表示呢其实我们可以给大、中、小三个状态设定三个数字来表示,比如大表示用3表示,中用2表示,小用1表示.那么我们完全可以用1+2+3=来表示它,当然这个公式也不一定是这样(de),这个公式(de)设计是系统模糊化和精确化(de)一个过程,读者也可参见相关文献理解.但就这个数字而言,可以说明,目前6°(de)角度偏差处于小和中之间,但是更偏向于中.我们就可以根据这个数字来调节电机(de)转动速度和时间了.当然,这个数字与电机转速(de)对应关系,也需要根据实际情况进行设计和调节.前面一个例子已经基本上说明了模糊算法(de)基本原理了.可是实际上,一个系统(de)限制因素常常不是一个.上面(de)例子中,只有偏差角度成为了系统调节(de)参考因素.而实际系统中,比如PID系统,我们需要调节(de)是比例、积分、微分三个环节,那么这三个环节(de)作用就需要我们认清,也就是说,我们需要根据超调量、调节时间、震荡情况等信息来考虑对这三个环节调节(de)比重,输入量和输出量都不是单一(de),可是其中必然有某种内在(de)逻辑联系.所以这种逻辑联系就成为我们设计工作(de)重点了.下一篇文章将详细分析PID三个变量和系统性能参数之间(de)联系.PID控制算法(de)c语言实现十一（PID系列完结篇）模糊PID(de)参数整定这几天一直在考虑如何能够把这一节(de)内容说清楚,对于PID而言应用并没有多大难度,按照基本(de)算法设计思路和成熟(de)参数整定方法,就算是没有经过特殊训练和培训(de)人,也能够在较短(de)时间内容学会使用PID算法.可问题是,如何能够透彻(de)理解PID算法,从而能够根据实际(de)情况设计出优秀(de)算法呢.通过讲述公式和基本原理肯定是最能说明问题(de),可是这样(de)话怕是犯了“专家”(de)错误了.对于门槛比较低(de)技术人员来讲,依然不能透彻理解.可是说(de)入耳了,能不能透彻说明也是一个问题,所以斟酌了几天,整理了一下思路才开始完成PID系列文章(de)最后一篇.我所说(de)最后一篇不代表PID(de)功能和发展就止步与此,仅仅是说明,透过这一些列(de)文章,基本上已经可以涵盖PID设计(de)要点,至于更深入(de)研究,就交给有需要(de)读者去做.上一节中大致讲述了一下模糊算法.实际上模糊算法(de)很多概念在上一节中并没有深入(de)解释.举(de)例子也只是为了说明模糊算法(de)基本含义,真正(de)模糊算法是不能这么设计(de),当然也不会这么简单.模糊算法(de)核心是模糊规则,如果模糊规则制定(de)出色,那么模糊算法(de)控制效率就高.其实这是智能算法(de)一般特性,规则是系统判断和处理(de)前提.那么就说说PID(de)规则该怎么制定.我们知道,模糊算法(de)本质是对PID(de)三个参数进行智能调节.那么首先要提出(de)问题是如何对PID(de)参数进行调节这个问题其实是参数整定(de)问题,现实当中有很多整定方法.可是我们需要从根本上了解为什么这么整定,才能知道该如何建立数学模型进行分析.那么要回答如何整定参数(de)问题,就需要先明白PID参数(de)作用都是什么对系统有什么影响我们从作用和副作用两个方面说明参数对系统(de)影响.1.比例环节Kp,作用是加快系统(de)响应速度,提高系统(de)调节精度,副作用是会导致超调;2.积分环节Ki,作用是消除稳态误差,副作用是导致积分饱和现象;3.微分环节Kd,作用是改善系统(de)动态性能,副作用是延长系统(de)调节时间.理解了上述问题,那么就可以“辩证施治,对症下药”了.比如说,如果系统响应速度慢,我们就加大Kp(de)取值,如果超调量过大我们就减小Kp(de)取值等等.可是问题这些语言(de)描述该如何用数学形式表达出来呢.我们所知道(de),反馈系统(de)实质就是系统(de)输出量作为反馈量与系统(de)输入量进行作差,从而得到系统(de)误差e,那么这个误差e就能够反应目前系统所处(de)状态.误差e可以表明目前系统(de)输出状态到底偏离要求多少.而误差e(de)变化律ec,表示误差变化(de)速度.这样,我们可以根据这两个量(de)状态来分析三个参数此时应该如何取值,假如e为负方向比较大,ec也为负方向增大状态,此时比例环节要大一些,从而加快调节速度,而积分环节要小一些,甚至不加积分环节,从而防止负方向上出现饱和积分(de)现象.微分环节可以稍加一些,在不影响调节时间(de)情况下,起到改善系统动态性能(de)作用.附录1看到有不少人问到底如何让UK值与PWM占空比值对应,进而实现占空比输出和输出控制电压对应.（注意,我这里讨论(de)前提是输出控制(de)是电压,不是PWM方波.PWM输出后要经过滤波整形再输出控制.）前提条件：输出电压控制电压范围是0-10V.给定、反馈、输出电压采样输入电压范围是0-5V（经过运放）.使用单片机AD为10位AD芯片.那么10位AD芯片电压采集得到(de)数据范围就是0-1024.PWM为 8位可调占空比方波,0对应输出占空比为0(de)方波,255对应输出占空比100%(de)方波,127对应输出50%(de)方波.比如当前给定是,反馈电压是1V.（KP,KI,KD等系数略,关于PID算法(de)整数实现我在前文中有论述如何实现）.那么经过AD采样1、给定对应为 5122、反馈1V对应为 205假定经过PID计算得到(de)UK为400也就意味着输出电压应当为（400（UPWM峰值电压））/1024那么UK对应(de)PWM占空比是多少呢我们知道,UK=1024对应占空比为100,也就是PWM(de)占空比系数为255.可知,PWM系数 = UK/4;那么400就应当对应系数 400/4=100.也就是输出电压=40010/1024=同时,由于采样精度以及PWM输出占空比精度控制(de)问题,将导致输出电压和期望值不是那么线性,所以,我在项目内加入了输出电压采样(de)控制.采样AD输入为0-5V,所以,对于输出0-10V有一个缩小(de)比例.输出10V则采样值对应为255输出5V则采样之对应127可知,对应AD结果为97采样输出电压值,可以针对性(de)调整一下占空比输出,从而得到误差允许范围内(de)一个控制输出电压.同时,经过一些加速控制(de)手段.可以比较迅速(de)达到控制(de)目(de).下文中(de)UK控制方法是针对增量式PID控制而来做(de).//void PWMProcess(void){uint16 idata temp;uint16 idata UKTemp;temp = 0;UKTemp = 0;if( = 0 ) //判断是否需要改变占空比{ //是否需要改变占空比和你(de)被控系统特性有关= 0;UKTemp = + ;//计算UK控制量//控制量和计算值以及一个开关量有关,我这里(de)开关量是系统需要(de)时候叠加在控制量上(de)一个变量.if(UKTemp>999){UKTemp = 999;}//这里只所以是999封顶而不是1024是因为我(de)系统PWM(de)峰值电压是12V导致.while(1) //如果输出电压和期望电压相差 Delta,则继续调整占空比,直到在误差以内{ADChPro(UPWMADCH); //测量输出电压if( [UPWMADCH] == UKTemp){return;}if( [UPWMADCH] > UKTemp) //如果当前电压大于输出电压,减小占空比{if( ( [UPWMADCH] - UKTemp ) > UDELTA ){temp = [UPWMADCH] - UKTemp; //temp = temp / 2; //下降可以加速下降,所以下降参数加倍if( > temp ){= - temp;else{= 0;}}else{return;}}else //如果当前电压小于输出电压{if( ( UKTemp - [UPWMADCH] ) > UDELTA ){temp = UKTemp - [UPWMADCH];temp = temp / 4; //上升处理不要超调,所以每次只+一半 if( > temp ){+= (temp/2);}else{= 255;}}elsereturn;}}DisPlayVoltage();PWMChangeDuty; //改变占空比Delay(10,10);}}}//附录2直流电机PWM调速系统中控制电压非线性研究引言由于线性放大驱动方式效率和散热问题严重,目前绝大多数直流电动机采用开关驱动方式.开关驱动方式是半导体功率器件工作在开关状态,通过脉宽调制PWM控制电动机电枢电压,实现调速.目前已有许多文献介绍直流电机调速,宋卫国等用89C51单片机实现了直流电机闭环调速；张立勋等用AVR单片机实现了直流电机PWM调速；郭崇军等用C8051实现了无刷直流电机控制；张红娟等用PIC单片机实现了直流电机PWM调速；王晨阳等用DSP实现了无刷直流电机控制.上述文献对实现调速(de)硬件电路和软件流程(de)设计有较详细(de)描述,但没有说明具体(de)调压调速方法,也没有提及占空比与电机端电压平均值之间(de)关系.在李维军等基于单片机用软件实现直流电机PWM调速系统中提到平均速度与占空比并不是严格(de)线性关系,在一般(de)应用中,可以将其近似地看作线性关系.但没有做深入(de)研究.本文通过实验验证,在不带电机情况下,PWM波占空比与控制输出端电压平均值之间呈线性关系；在带电机情况下,占空比与电机端电压平均值满足抛物线方程,能取得精确(de)控制.本文(de)电机闭环调速是运用Matlab拟合(de)关系式通过PID控制算法实现.1 系统硬件设计本系统是基于TX-1C实验板上(de)AT89C52单片机,调速系统(de)硬件原理图如图1所示,主要由AT89C52单片机、555振荡电路、L298驱动电路、光电隔离、霍尔元件测速电路、MAX 232电平转换电路等组成.图1 闭环控制系统示意图2 系统软件设计系统采用模块化设计,软件由1个主程序,3个中断子程序,即外部中断0、外部中断1,定时器0子程序,PID算法子程序,测速子程序及发送数据到串口显示子程序组成,主程序流程图如图2所示.外部中断0通过比较直流电平与锯齿波信号产生PWM波,外部中断1用于对传感器(de)脉冲计数.定时器0用于对计数脉冲定时.测得(de)转速通过串口发送到上位机显示,通过PID模块调整转速到设定值.本实验采用M／T法测速,它是同时测量检测时间和在此检测时间内霍尔传感器所产生(de)转速脉冲信号(de)个数来确定转速.由外部中断1对霍尔传感器脉冲计数,同时起动定时器0,当计数个数到预定值2 000后,关定时器0,可得到计2 000个脉冲(de)计数时间,由式计算出转速：n=60f／K=60N／(KT) (1)式中：n为直流电机(de)转速；K为霍尔传感器转盘上磁钢数；f为脉冲频率；N为脉冲个数；T为采样周期.图2 主程序流程图3 实验结果及原因分析3．1 端电压平均值与转速关系3．1．1 实验结果实验用(de)是永磁稳速直流电机,型号是EG-530YD-2BH,额定转速2 000～4 000 r／min,额定电压12 V.电机在空载(de)情况下,测得(de)数据用Matlab做一次线性拟合,拟合(de)端电压平均值与转速关系曲线如图3(a)所示.相关系数R-square：0．952 1.拟合曲线方程为：y=0．001 852x+0．296 3 (2)由式(2)可知,端电压平均值与转速可近似为线性关系,根椐此关系式,在已测得(de)转速(de)情况下可以计算出当前电压.为了比较分析,同样用Matlab做二次线性拟合,拟合(de)端电压平均值与转速关系曲线如图3(b)所示.相关系数R-square：0．986 7.图3 端电压平均值与转速关系曲线图3．1．2 原因分析比较图3(a)可知,当转速在0～1 500 r／min和4 000～5 000 r／min,端电压平均值与转速间存在(de)非线性,用二次曲拟合如图3(b)所示,拟合相关系数较高.由图3(a)可见,当电机转速为0时电机两端电压平均值约为1．3 V.这是因为电机处于静止状态时,摩擦力为静摩擦力,静摩擦力是非线性(de).随着外力(de)增加而增加,最大值发生在运动前(de)瞬间.电磁转矩为负载制动转矩和空载制动转矩之和,由于本系统不带负载,因此电磁转矩为空载制动转矩.空载制动转矩与转速之间此时是非线性(de).。

第 4 页 共 10 页
如果 PID 参数不合适，调整参数 （1）三角波信号输入响应如图 3 所示：
t − 2n ( 2n < t < 2n + 1) r (t ) = n = 0,1, 2... 2 − t + 2n ( 2n + 1 < t < 2n + 2 )
代码略，与单位跃阶类似，只需修改输入函数： >>T=1000; if k>=0 & k<0.5*T r(k)=2*k; else r(k)=-2-2*(k-T); end 得到如下图形输出：
第 10 页 共 10 页
r ( t ) = sin (π t )
代码略，与单位跃阶类似，只需修改输入函数： >>r(k)=sin(pi*t(k));
图 2-3 采用增量式 PID 的正弦波响应 >>f(2,2);hold on;ft(2,2) 图 2-4 与传统 PID 比较 由图 2-4 得正弦波输入下增量式 PID 控制效果明显优于传统 PID 控制。 总结： 采用增量式 PID 算法时，通过不同信号的输入（单位阶跃，三角波，正弦波）与其分别采 用传统 PID 算法比较，可以很明显地看到，增量式 PID 具有很明显的优越性。因为算式中 不需要累加误差，控制增量△c(k)的确定仅与最近 k 次的采样值有关，所以较容易通过加权 处理而获得比较好的控制效果。
第 1 页 共 10 页
Y ( z ) = 1 − 1.571z -1C ( Z ) + 0.5712Z−2C ( z ) + 0.01647z -1 + 0.01389Z−2 (7)
即： Y ( k ) = 1 − 1.571C ( k-1) + 0.5712C ( k-2 ) + 0.01647Y ( k − 1) + 0.01389Y ( k − 2 ) (8) 因此编制程序如下： clear all; close all; %增量式 PID 控制 ts=0.001;%采样时间 G=tf(50,[0.125,7, 0]) Gd=c2d(G,ts,'z');%Z 变换 [num,den]=tfdata(Gd,'v') c_1=0;c_2=0; y_1=0;y_2=0; e_1=0;e_2=0; kp=10;Ti=0.1;Td=0.015; ki=kp*ts/Ti kd=kp*Td/ts A=kp*(1+ts/Ti+Td/ts); B=-kp*(1+2*Td/ts); C=kp*Td/ts; for k=1:1:3000 t(k)=k*ts; r(k)=1; y(k)=-den(2)*y_1-den(3)*y_2+num(2)*c_1+num(3)*c_2; e(k)=r(k)-y(k); c(k)=A*e(k)+B*e_1+C*e_2; c(k)=c_1+c(k); c_2=c_1;c_1=c(k); y_2=y_1;y_1=y(k); e_2=e_1;e_1=e(k); end figure(1); plot(t,y,'r'); grid on; figure(2) 根据公式（3） 根据公式（8） 根据公式（3） 设置 Kp，Ki，Kd

位置式和增量式pid控制算法位置式和增量式PID控制算法，听起来有点复杂对吧？它们就像是我们生活中的调味料，让一切变得更美味。

这两个小家伙在自动化控制里可是大明星哦。

想象一下，你在调节水温，位置式就像是你设定了一个明确的目标温度，水一到这个温度，咱们就高兴地把火关掉。

而增量式就更像是你在慢慢加热，一点一点加，感觉就像是煮汤，怕煮过了头，时不时来瞧一眼，别让汤干了。

位置式PID，简单来说，就是设定目标，然后全力以赴去达到它，像是在一个比赛里拼命冲刺。

设定好目标值后，控制器会不断调整，努力让实际值和目标值对上。

这就像你在超市找打折商品，目标清晰，心里有数，得知价格差后立马掏钱买下。

这种方式特别适合那些变化不大的系统，稳定得很，反正只要目标不变，咱就按部就班。

再说说增量式PID，这家伙的调皮劲儿可就显露出来了。

它的做法就像是在走钢丝，每一步都得小心翼翼。

每次的调整都是相对之前的变化，控制器不会直接奔着目标去，而是慢慢摸索，像是在追求完美的舞蹈演员，每一步都得绳锯木断。

这种方法在变化频繁的情况下表现得特别好，能让系统跟上步伐，稳稳地调整。

比如说，开车的时候，前方有个急刹车，咱们得灵活应对，控制好油门，才能安稳下来。

说到PID控制，得提一下它的三大要素：比例、积分和微分。

比例就像是你的警觉度，能迅速反应；积分则是累积的经验，一点一点积累，最后得到一个好的结果；微分则是预测，先知道情况，再做出反应。

这三者结合得当，就能实现完美的控制，犹如一个顶尖的团队，大家各司其职，齐心协力，事半功倍。

在生活中，我们也经常无形中用上这些原理。

比如说，你在学习时设定了目标，想考好。

你得一步一步地积累知识，反复练习，这不就是个积分吗？再加上你每次考试后分析错误，调整学习策略，这就是微分。

咱们的努力就能得到成果，嘿，满分的那种！不过，控制算法可不是万能的，使用得当才能发挥作用。

位置式在快速变化的环境下可就会出乱子，像是走进了迷雾，方向都找不着了。