中考数学几何专题训练含答案
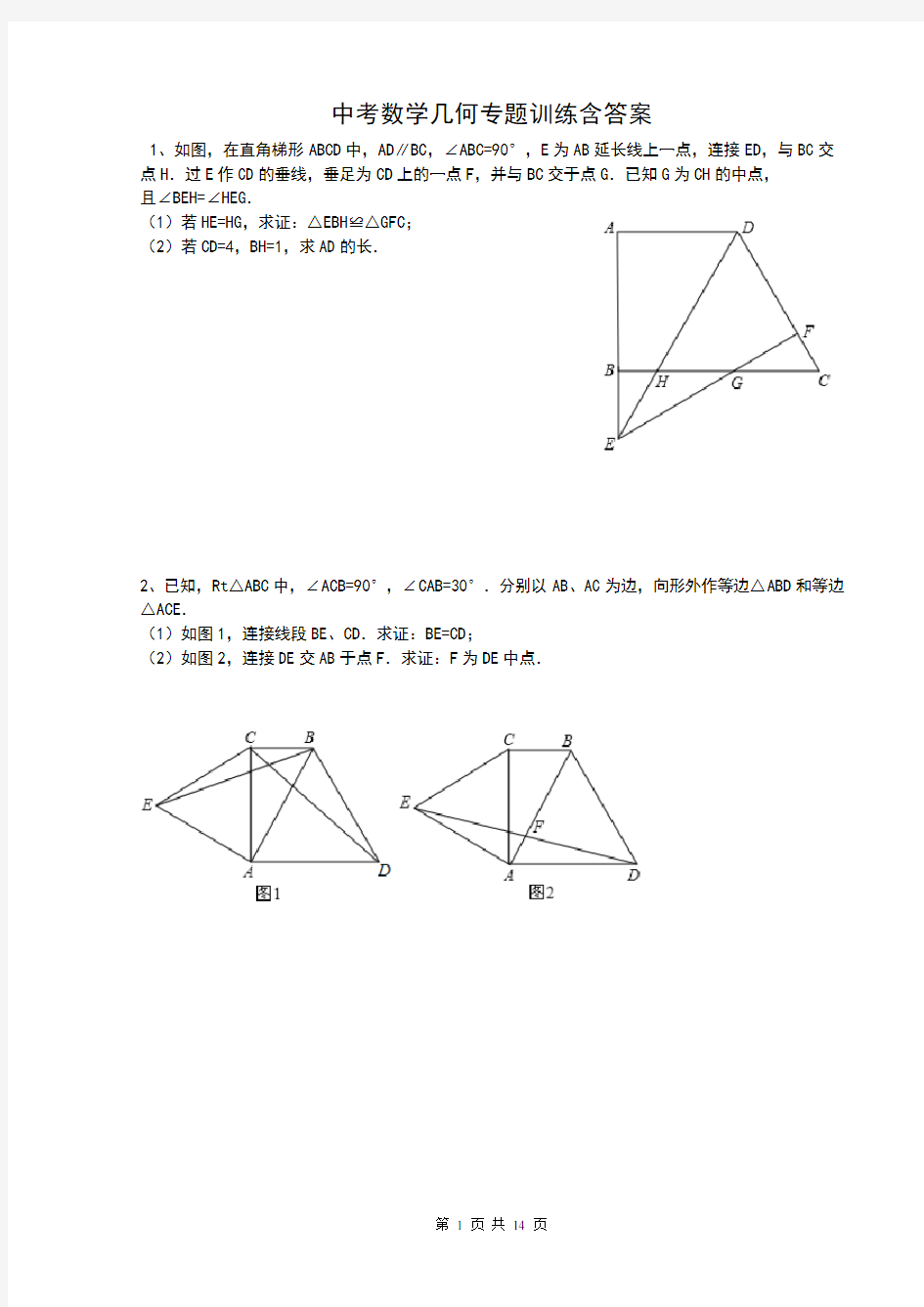
1、如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,E为AB延长线上一点,连接ED,与BC交点H.过E作CD的垂线,垂足为CD上的一点F,并与BC交于点G.已知G为CH的中点,
且∠BEH=∠HEG.
(1)若HE=HG,求证:△EBH≌△GFC;
(2)若CD=4,BH=1,求AD的长.
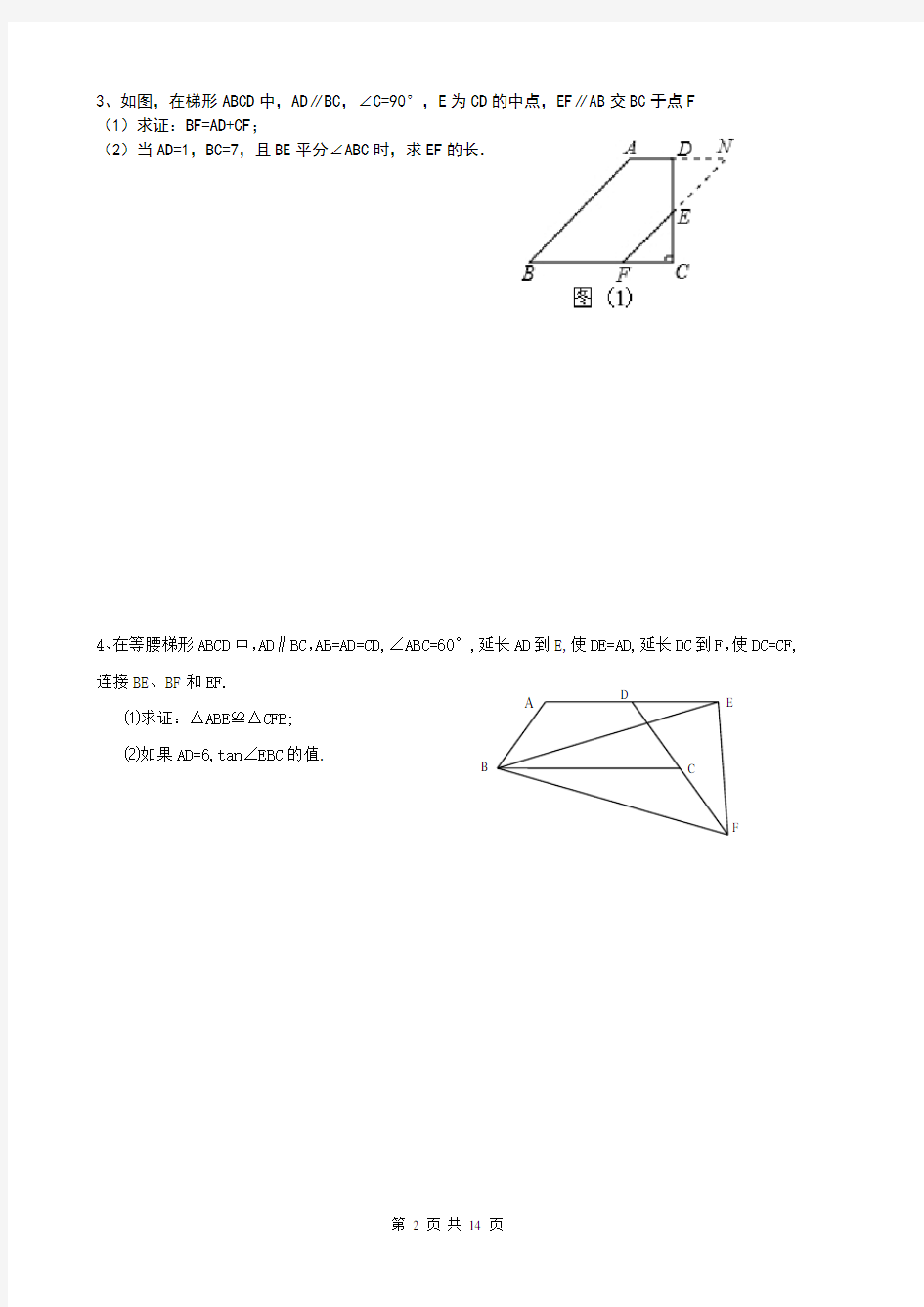
2、已知,Rt△ABC中,∠ACB=90°,∠CAB=30°.分别以AB、AC为边,向形外作等边△ABD和等边△ACE.
(1)如图1,连接线段BE、CD.求证:BE=CD;
(2)如图2,连接DE交AB于点F.求证:F为DE中点.
3、如图,在梯形ABCD 中,AD ∥BC ,∠C=90°,E 为CD 的中点,EF ∥AB 交BC 于点F
(1)求证:BF=AD+CF ;
(2)当AD=1,BC=7,且BE 平分∠ABC 时,求EF 的长.
4、在等腰梯形ABCD 中,AD ∥BC ,AB=AD=CD,∠ABC=60°,延长AD 到E,使DE=AD,延长DC 到F ,使DC=CF,连接BE 、BF 和EF.
⑴求证:△ABE ≌△CFB;
⑵如果AD=6,tan ∠EBC 的值.
A
B D E
C F
5、已知:AC是矩形ABCD的对角线,延长CB至E,使CE=CA,F是AE的中点,连接DF、CF 分别交AB于G、H点(1)求证:FG=FH;(2)若∠E=60°,且AE=8时,求梯形AECD的面积.
6、如图,直角梯形ABCD中,AD∥BC,∠BCD=90°,且CD=2AD,tan∠ABC=2,过点D作DE ∥AB,交∠BCD的平分线于点E,连接BE.
(1)求证:BC=CD;
(2)将△BCE绕点C,顺时针旋转90°得到△DCG,连接EG.求证:CD垂直平分EG;
(3)延长BE交CD于点P.求证:P是CD的中点.
7、如图,直角梯形ABCD中,∠DAB=90°,AB∥CD,AB=AD,∠ABC=60度.以AD为边在直角梯形ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.
(1)求证:EB=EF;
(2)延长FE交BC于点G,点G恰好是BC的中点,若AB=6,求BC的长.
(1)证明:∵△ADF为等边三角形,
8、已知,矩形ABCD中,延长BC至E,使BE=BD,F为DE的中点,连结AF、CF.求证:
(1)∠ADF=∠BCF;
(2) AF⊥CF.
9、如图,在直角梯形ABCD中,AD⊥DC,AB∥DC,AB=BC,AD与BC延长线交于点F,G是DC延长线上一点,AG⊥BC于E.
(1)求证:CF=CG;
(2)连接DE,若BE=4CE,CD=2,求DE的长.
10、如图,在正方形ABCD中,E、F分别为BC、AB上两点,且BE=BF,过点B作AE的垂线交AC于点G,过点G作CF的垂线交BC于点H延长线段AE、GH交于点M.
(1)求证:∠BFC=∠BEA;
(2)求证:AM=BG+GM.
11、直角梯形ABCD中,AB∥CD,∠C=90°,AB=BC,M为BC边上一点.
(1)若∠DMC=45°,求证:AD=AM.(2)若∠DAM=45°,AB=7,CD=4,求BM的值.
12、如图,AC是正方形ABCD的对角线,点O是AC的中点,点Q是AB上一点,连接CQ,DP ⊥CQ于点E,交BC于点P,连接OP,OQ;
求证:
(1)△BCQ≌△CDP;
(2)OP=OQ.
中考数学几何专题训练(24)答案
1、如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,E为AB延长线上一点,连接ED,与BC交于点H.过E作CD的垂线,垂足为CD上的一点F,并与BC交于点G.已知G为CH的中点,且∠BEH=
∠HEG.
(1)若HE=HG,求证:△EBH≌△GFC;
(2)若CD=4,BH=1,求AD的长.
(1)证明:∵HE=HG,
∴∠HEG=∠HGE,
∵∠HGE=∠FGC,∠BEH=∠HEG,
∴∠BEH=∠FGC,
∵G是HC的中点,
∴HG=GC,
∴HE=GC,
∵∠HBE=∠CFG=90°.
∴△EBH≌△GFC;
(2)解:过点H作HI⊥EG于I,
∵G为CH的中点,
∴HG=GC,
∵EF⊥DC,
HI⊥EF,
∴∠HIG=∠GFC=90°,
∠FGC=∠HGI,∴△GIH≌△GFC,∵△EBH≌△EIH(AAS),∴
FC=HI=BH=1,∴AD=4-1=3.
2、已知,Rt△ABC中,∠ACB=90°,∠CAB=30°.分别以AB、AC
为边,向形外作等边△ABD和等边△ACE.
(1)如图1,连接线段BE、CD.求证:BE=CD;
(2)如图2,连接DE交AB于点F.求证:F为DE中点.
证明:(1)∵△ABD和△ACE是等边三角形,∴AB=AD,AC=AE,∠DAB=∠EAC=60°,∴∠DAB+∠BAC=
∠EAC+∠BAC,即∠DAC=∠BAE,在△DAC和△BAE中, AC=AE ∠DAC=∠BAE AD=AB ,∴△DAC≌△BAE(SAS),∴DC=BE;
(2)如图,作DG∥AE,交AB于点G,由∠EAC=60°,∠CAB=30°得:∠FAE=∠EAC+∠CAB=90°,∴∠DGF=∠FAE=90°,又∵∠ACB=90°,∠CAB=30°,∴∠ABC=60°,又∵△ABD为等边三角形,∠DBG=60°,DB=AB,∴∠DBG=∠ABC=60°,在△DGB和△ACB中,∠DGB=∠ACB ∠DBG=∠ABC DB=AB ,∴△DGB≌△ACB(AAS),∴DG=AC,又∵△AEC为等边三角形,∴AE=AC,∴DG=AE,在△DGF和△EAF 中,∠DGF=∠EAF ∠DFG=∠EFA DG=EA ,∴△DGF≌△EAF(AAS),∴DF=EF,即F为DE中点.
3、如图,在梯形ABCD中,AD∥BC,∠C=90°,E为CD的中点,EF∥AB交BC于点F
(1)求证:BF=AD+CF;
(2)当AD=1,BC=7,且BE平分∠ABC时,求EF的长.
(1)证明:如图(1),延长AD交FE的延长线于N
∵∠NDE=∠FCE=90°
∠DEN=∠FECDE=EC∴△NDE≌△FCE
∴DN=CF∵AB∥FN,AN∥BF∴四边形ABFN是平行四边形
∴BF=AD+DN=AD+FC
(2)解:∵AB∥EF,∴∠ABN=∠EFC,即∠1+∠2=∠3,又∵∠2+∠BEF=∠3,∴∠1=∠BEF,∴BF=EF,∵∠1=∠2,∴∠BEF=∠2,∴EF=BF,又∵BC+AD=7+1∴BF+CF+AD=8而由(1)知CF+AD=BF∴BF+BF=8∴2BF=8,∴BF=4,
∴BF=EF=4
4、在等腰梯形ABCD中,AD∥BC,
AB=AD=CD,∠ABC=60°,延长AD到E,使DE=AD,延长DC到F,使DC=CF,连接BE、BF和EF.
⑴求证:△ABE≌△CFB;
⑵如果AD=6,tan∠EBC的值.
解:(1)证明:连结CE,
在△BAE与△FCB中,
∵ BA=FC,∠A=∠BCF,, AE=BC,
∴△BAE≌△FCB;
(2)延长BC交EF于点G,作AH⊥BG于H,作AM⊥BG,∵△BAE≌△FCB,
∴∠AEB=∠FBG,BE=BF,
∴△BEF为等腰三角形,A
B D
E
C
F
又∵AE ∥BC ,
∴∠AEB=∠EBG ,
∴∠EBG=∠FBG ,
∴BG ⊥EF ,
∵∠AMG=∠EGM=∠AEG=90°,
∴四边形AMGE 为矩形,
∴AM=EG ,
在Rt △ABM 中,
AM=AB ?sin60°=6× 2
3 =33 , ∴EG=AM=33,
BG=BM+MG=6×2+6×cos60°=15,
∴tan ∠EBC=
5
31533==BG EG 5、已知:AC 是矩形ABCD 的对角线,延长CB 至E ,使CE=CA ,F 是AE 的中点,连接DF 、CF 分别交AB 于G 、H 点(1)求证:FG=FH ;(2)若∠E=60°,且AE=8时,求梯形AECD 的面积. (1)证明:连接BF
∵ABCD 为矩形
∴AB ⊥BC AB ⊥AD AD=BC
∴△ABE 为直角三角形
∵F 是AE 的中点
∴AF=BF=BE
∴∠FAB=∠FBA
∴∠DAF=∠CBF
∵ AD=BC, ∠DAF=∠CBF ,AF=BF ,
∴△DAF ≌△CBF
∴∠ADF=∠BCF
∴∠FDC=∠FCD
∴∠FGH=∠FHG
∴FG=FH ;
(2)解:∵AC=CE ∠E=60°
∴△ACE 为等边三角形
∴CE=AE=8
∵AB ⊥BC
∴BC=BE=CE 2
1=4 ∴根据勾股定理AB=34
∴梯形AECD 的面积=21×(AD+CE)×CD=2
1×(4+8)×34=324
6、如图,直角梯形ABCD 中,AD ∥BC ,∠BCD=90°,且CD=2AD ,tan ∠ABC=2,过点D 作DE ∥AB ,交∠BCD 的平分线于点E ,连接BE .
(1)求证:BC=CD ;
(2)将△BCE 绕点C ,顺时针旋转90°得到△DCG ,连接EG .求证:CD 垂直平分EG ;
(3)延长BE 交CD 于点P .求证:P 是CD 的中点.
证明:(1)延长DE 交BC 于F ,
∵AD ∥BC ,AB ∥DF ,
∴AD=BF ,∠ABC=∠DFC .
在Rt △DCF 中,
∵tan ∠DFC=tan ∠ABC=2, ∴CF
CD =2, 即CD=2CF ,
∵CD=2AD=2BF ,
∴BF=CF ,
∴BC=BF+CF=21CD+2
1 CD=CD . 即BC=CD .
(2)∵CE 平分∠BCD ,
∴∠BCE=∠DCE ,
由(1)知BC=CD ,
∵CE=CE ,
∴△BCE ≌△DCE ,
∴BE=DE ,
由图形旋转的性质知CE=CG ,BE=DG ,
∴DE=DG ,
∴C ,D 都在EG 的垂直平分线上,
∴CD 垂直平分EG .
(3)连接BD ,
由(2)知BE=DE ,
∴∠1=∠2.
∵AB ∥DE ,
∴∠3=∠2.∴∠1=∠3.
∵AD ∥BC ,∴∠4=∠DBC .
由(1)知BC=CD ,
∴∠DBC=∠BDC ,∴∠4=∠BDP .
又∵BD=BD ,∴△BAD ≌△BPD(ASA)
∴DP=AD .
∵AD=21CD ,∴DP=2
1CD . ∴P 是CD 的中点.
7、如图,直角梯形ABCD 中,∠DAB=90°,AB ∥CD ,AB=AD ,∠ABC=60度.以AD 为边在直角梯形ABCD 外作等边三角形ADF ,点E 是直角梯形ABCD 内一点,且∠EAD=∠EDA=15°,连接EB 、EF .
(1)求证:EB=EF ;
(2)延长FE 交BC 于点G ,点G 恰好是BC 的中点,若AB=6,求BC 的长.
(1)证明:∵△ADF 为等边三角形,
∴AF=AD ,∠FAD=60°
∵∠DAB=90°,∠EAD=15°,AD=AB
∴∠FAE=∠BAE=75°,AB=AF ,
∵AE 为公共边
∴△FAE ≌△BAE
∴EF=EB
(2)过C 作CQ ⊥AB 于Q ,
∵CQ=AB=AD=6,
∵∠ABC=60°,
∴BC=6÷ 2
3 =34.
8、已知,矩形ABCD 中,延长BC 至E ,使BE=BD ,F 为DE 的中点,连结AF 、CF.求证:
(1)∠ADF=∠BCF ;
(2) AF ⊥CF.
证明:(1)在矩形ABCD 中,
∵∠ADC=∠BCD=90°,
∴∠DCE=90°,
在Rt △DCE 中,
∵F 为DE 中点,
∴DF=CF ,
∴∠FDC=∠DCF ,
∴∠ADC+∠CDF=∠BCD+∠DCF ,
即∠ADF=∠BCF ;
(2)连接BF ,
∵BE=BD ,F 为DE 的中点,
∴BF ⊥DE ,
∴∠BFD=90°,即∠BFA+∠AFD=90°,
在△AFD 和△BFC 中 AD=BC ∠ADF=∠BCF CF=DF ,
∴△ADF ≌△BCF ,
∴∠AFD=∠BFC ,
∵∠AFD+∠BFA=90°,
∴∠BFC+∠BFA=90°,
即∠AFC=90°,
∴AF ⊥FC .
9、如图,在直角梯形ABCD 中,AD ⊥DC ,AB ∥DC ,AB=BC ,AD 与BC 延长线交于点F ,G 是DC 延长线上一点,AG ⊥BC 于E .
(1)求证:CF=CG ;
(2)连接DE ,若BE=4CE ,CD=2,求DE 的长.
解答:(1)证明:连接AC ,
∵DC ∥AB ,AB=BC ,
∴∠1=∠CAB ,∠CAB=∠2,
∴∠1=∠2;
∵∠ADC=∠AEC=90°,AC=AC ,
∴△ADC ≌△AEC ,
∴CD=CE ;
∵∠FDC=∠GEC=90°,∠3=∠4,
∴△FDC ≌△GEC ,
∴CF=CG .
(2)解:由(1)知,CE=CD=2,
∴BE=4CE=8,
∴AB=BC=CE+BE=10,
∴在Rt △ABE 中,AE= AB 2-BE 2 =6,
∴在Rt △ACE 中,AC= AE 2+CE 2 =102
由(1)知,△ADC ≌△AEC ,
∴CD=CE ,AD=AE ,
∴C 、A 分别是DE 垂直平分线上的点,
∴DE ⊥AC ,DE=2EH ;(8分)
在Rt △AEC 中,S △AEC =21 AE ?CE=21 AC ?EH , ∴EH=AC CE AE ? =10
226? =5103 ∴DE=2EH=2×5103=5
106
10、如图,在正方形ABCD 中,E 、F 分别为BC 、AB 上两点,且BE=BF ,过点B 作AE 的垂线交AC 于点G ,过点G 作CF 的垂线交BC 于点H 延长线段AE 、GH 交于点M .
(1)求证:∠BFC=∠BEA ;
(2)求证:AM=BG+GM.
证明:(1)在正方形ABCD中,AB=BC,∠ABC=90°,
在△ABE和△CBF中,
AB=BC ∠ABC=∠ABC BE=BF ,
∴△ABE≌△CBF(SAS),
∴∠BFC=∠BEA;
(2)连接DG,在△ABG和△ADG中,
AB=AD ∠DAC=∠BAC=45°AG=AG ,
∴△ABG≌△ADG(SAS),
∴BG=DG,∠2=∠3,
∵BG⊥AE,
∴∠BAE+∠2=90°,
∵∠BAD=∠BAE+∠4=90°,
∴∠2=∠3=∠4,
∵GM⊥CF,
∴∠BCF+∠1=90°,
又∠BCF+∠BFC=90°,
∴∠1=∠BFC=∠2,
∴∠1=∠3,
在△ADG中,∠DGC=∠3+45°,
∴∠DGC也是△CGH的外角,
∴D、G、M三点共线,
∵∠3=∠4(已证),
∴AM=DM,
∵DM=DG+GM=BG+GM,
∴AM=BG+GM.
11、直角梯形ABCD中,AB∥CD,∠C=90°,AB=BC,M为BC边上一点.
(1)若∠DMC=45°,求证:AD=AM.(2)若∠DAM=45°,AB=7,CD=4,求BM的值.(1)证明:作AF⊥CD交延长线于点F.
∵∠DMC=45°,∠C=90°
∴CM=CD,
又∵∠B=∠C=∠AFD=90°,AB=BC,
∴四边形ABCF为正方形,
∴BC=CF,
∴BM=DF,
在Rt△ABM和Rt△AFD中,AB=AF,∠B=∠AFD=90°,BM=DF,
∴△ABM≌△AFD,
∴AD=AM.
(2)解:把Rt△ABM绕点A顺时针旋转90°,使AB与AE重合,得Rt△AFN.
∵∠DAM=45°,
∴∠BAM+∠DAF=45°,
由旋转知∠BAM=∠NAF ,∴∠DAF+∠NAF=45°,
即∠DAM=∠DAN ,
由旋转知AM=AN ,
∴△ADM ≌△ADN ,
∴DM=DN ,
设BM=x ,
∵AB=BC=CF=7,
∴CM=7-x
又∵CD=4,
∴DF=3,BM=FN=x ,
∴MD=DN=3+x ,
在Rt △CDM 中,(7-x )2+42=(3+x )2,
解得:x=5
14 ∴BM 的值为
5
14. 答:BM 的值为514.
12、如图,AC 是正方形ABCD 的对角线,点O 是AC 的中点,点Q 是AB 上一点,连接CQ ,DP ⊥CQ 于点E ,交BC 于点P ,连接OP ,OQ ;
求证:
(1)△BCQ ≌△CDP ;
(2)OP=OQ .
证明:∵四边形ABCD 是正方形,
∴∠B=∠PCD=90°,BC=CD ,
∴∠2+∠3=90°,
又∵DP ⊥CQ ,
∴∠2+∠1=90°,
∴∠1=∠3,
在△BCQ 和△CDP 中,
∠B=∠PCD BC=CD ∠1=∠3 .
∴△BCQ ≌△CDP .
(2)连接OB .
由(1):△BCQ ≌△CDP 可知:BQ=PC ,
∵四边形ABCD 是正方形,
∴∠ABC=90°,AB=BC ,
而点O 是AC 中点,
∴BO=21AC=CO ,∠4=2
1∠ABC=45°=∠PCO , 在△BCQ 和△CDP 中, BQ=CP ∠4=∠PCO BO=CO
∴△BOQ≌△COP,∴OQ=OP.
人教版初中数学几何图形初步经典测试题及答案 一、选择题 1.下列图形中1∠与2∠不相等的是( ) A . B . C . D . 【答案】B 【解析】 【分析】 根据对顶角,平行线,等角的余角相等等知识一一判断即可. 【详解】 解:A 、根据对顶角相等可知,∠1=∠2,本选项不符合题意. B 、∵∠1+∠2=90°,∠1与∠2不一定相等,本选项符合题意. C .根据平行线的性质可知:∠1=∠2,本选项不符合题意. D 、根据等角的余角相等,可知∠1=∠2,本选项不符合题意. 故选:B . 【点睛】 本题考查平行线的性质对顶角的性质,等角的余角相等等知识,解题的关键是熟练掌握基本知识,属于中考常考题型. 2.如图,是某个几何体从不同方向看到的形状图(视图),这个几何体的表面能展开成下面的哪个平面图形?( ) A . B .
C.D. 【答案】D 【解析】 【分析】 根据三视图可判断这个几何体的形状;再由平面图形的折叠及立体图形的表面展开图的特点解题. 【详解】 解:根据三视图可判断这个几何体是圆柱;D选项平面图一个长方形和两个圆折叠后,能围成的几何体是圆柱.A选项平面图折叠后是一个圆锥;B选项平面图折叠后是一个正方体;C选项平面图折叠后是一个三棱柱. 故选:D. 【点睛】 本题考查由三视图判断几何体及展开图折叠成几何体,熟记常见几何体的平面展开图的特征,是解决此类问题的关键. 3.如图是由四个正方体组合而成,当从正面看时,则得到的平面视图是() A.B. C.D. 【答案】D 【解析】 【分析】 根据从正面看到的图叫做主视图,从左面看到的图叫做左视图,从上面看到的图叫做俯视图.根据图中正方体摆放的位置判定则可. 【详解】 解:从正面看,下面一行是横放3个正方体,上面一行最左边是一个正方体. 故选:D. 【点睛】
圆的综合大题 1.如图,⊙O是△ABC的外接圆,FH是⊙O的切线,切点为F,FH∥BC,连接AF交BC于E,∠ABC的平分线BD交AF于D,连接BF. (1)证明:AF平分∠BAC; (2)证明:BF=FD; (3)若EF=4,DE=3,求AD的长. 2.如图,AB是⊙O的直径,过点B作⊙O的切线BM,点P在右半圆上移动(点P与点A,B不重合),过点P作PC⊥AB,垂足为C;点Q在射线BM上移动(点M在点B的右边),且在移动过程中保持OQ∥AP. (1)若PC,QO的延长线相交于点E,判断是否存在点P,使得点E恰好在⊙O上?若存在,求出∠APC的大小;若不存在,请说明理由; (2)连接AQ交PC于点F,设,试问:k的值是否随点P的移动而变化?证明你的结论.
3.已知:如图1,把矩形纸片ABCD折叠,使得顶点A与边DC上的动点P重合(P不与点D,C重合),MN为折痕,点M,N分别在边BC,AD上,连接AP,MP,AM,AP与MN相交于点F.⊙O过点M,C,P. (1)请你在图1中作出⊙O(不写作法,保留作图痕迹); (2)与是否相等?请你说明理由; (3)随着点P的运动,若⊙O与AM相切于点M时,⊙O又与AD相切于点H.设AB为4,请你通过计算,画出这时的图形.(图2,3供参考) 4.在⊙O中,弦AB与弦CD相交于点G,OA⊥CD于点E,过点B作⊙O的切线BF交CD的延长线于点F. (I)如图①,若∠F=50°,求∠BGF的大小; (II)如图②,连接BD,AC,若∠F=36°,AC∥BF,求∠BDG的大小.
5.如图,在⊙O中,半径OD⊥直径AB,CD与⊙O相切于点D,连接AC交⊙O 于点E,交OD于点G,连接CB并延长交⊙于点F,连接AD,EF. (1)求证:∠ACD=∠F; (2)若tan∠F= ①求证:四边形ABCD是平行四边形; ②连接DE,当⊙O的半径为3时,求DE的长. 6.如图,⊙O的直径AB为10cm,弦BC为6cm,D、E分别是∠ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE. (1)求AC、AD的长; (2)试判断直线PC与⊙O的位置关系,并说明理由.
2016年北京中考专题突破几何综合 在北京中考试卷中,几何综合题通常出现在后两题,分值为8分或7分.几何综合题主要包含三角形(全等、相似)、四边形、锐角三角函数、圆等知识,主要研究图形中的数量关系、位置关系、几何计算以及图形的运动、变换等规律. 求解几何综合题时,关键是抓住“基本图形”,能在复杂的几何图形中辨认、分解出基本图形,或通过添加辅助线补全、构造基本图形,或运用图形变换的思想将分散的条件集中起来,从而产生基本图形,再根据基本图形的性质,合理运用方程、三角函数的运算等进行推理与计算. 1.[2015·北京] 在正方形ABCD中,BD是一条对角线,点P在射线CD上(与点C,D 不重合),连接AP,平移△ADP,使点D移动到点C,得到△BCQ,过点Q作QH⊥BD于点H,连接AH,PH. (1)若点P在线段CD上,如图Z9-1(a). ①依题意补全图(a); ②判断AH与PH的数量关系与位置关系,并加以证明. (2)若点P在线段CD的延长线上,且∠AHQ=152°,正方形ABCD的边长为1,请写出求DP长的思路.(可以不写出计算结果 .........) 图Z9-1 2.[2014·北京] 在正方形ABCD外侧作直线AP,点B关于直线AP的对称点为E,连接BE,DE,其中DE交直线AP于点F. (1)依题意补全图Z9-2①; (2)若∠PAB=20°,求∠ADF的度数; (3)如图②,若45°<∠PAB<90°,用等式表示线段AB,FE,FD之间的数量关系,并证明.
图Z9-2 3.[2013·北京] 在△ABC中,AB=AC,∠BAC=α(0°<α<60°),将线段BC绕点B 逆时针旋转60°得到线段B D. (1)如图Z9-3①,直接写出∠ABD的大小(用含α的式子表示); (2)如图②,∠BCE=150°,∠ABE=60°,判断△ABE的形状并加以证明; (3)在(2)的条件下,连接DE,若∠DEC=45°,求α的值. 图Z9-3 4.[2012·北京] 在△ABC中,BA=BC,∠BAC=α,M是AC的中点,P是线段BM上的动点,将线段PA绕点P顺时针旋转2α得到线段PQ. (1)若α=60°且点P与点M重合(如图Z9-4①),线段CQ的延长线交射线BM于点D,请补全图形,并写出∠CDB的度数; (2)在图②中,点P不与点B,M重合,线段CQ的延长线与射线BM交于点D,猜想∠CDB 的大小(用含α的代数式表示),并加以证明; (3)对于适当大小的α,当点P在线段BM上运动到某一位置(不与点B,M重合)时,能使得线段CQ的延长线与射线BM交于点D,且PQ=DQ,请直接写出α的范围. 图Z9-4
新初中数学几何图形初步技巧及练习题 一、选择题 1.如图,已知ABC ?的周长是21,OB ,OC 分别平分ABC ∠和ACB ∠,OD BC ^于D ,且4OD =,则ABC ?的面积是( ) A .25米 B .84米 C .42米 D .21米 【答案】C 【解析】 【分析】 根据角平分线的性质可得点O 到AB 、AC 、BC 的距离为4,再根据三角形面积公式求解即可. 【详解】 连接OA ∵OB ,OC 分别平分ABC ∠和ACB ∠,OD BC ^于D ,且4OD = ∴点O 到AB 、AC 、BC 的距离为4 ∴ABC AOC OBC ABO S S S S =++△△△△ ()142 AB BC AC =??++ 14212 =?? 42=(米) 故答案为:C . 【点睛】 本题考查了三角形的面积问题,掌握角平分线的性质、三角形面积公式是解题的关键.
2.∠1与∠2互余,∠1与∠3互补,若∠3=125°,则∠2=() A.35°B.45°C.55°D.65° 【答案】A 【解析】 【分析】 【详解】 解:根据题意得:∠1+∠3=180°,∠3=125°,则∠1=55°,∵∠1+∠2=90°,则∠2=35° 故选:A. 【点睛】 本题考查余角、补角的计算. 3.将如图所示的Rt△ACB绕直角边AC旋转一周,所得几何体的主视图(正视图)是() A.B.C. D. 【答案】D 【解析】 解:Rt△ACB绕直角边AC旋转一周,所得几何体是圆锥,主视图是等腰三角形. 故选D. 首先判断直角三角形ACB绕直角边AC旋转一周所得到的几何体是圆锥,再找出圆锥的主视图即可. 4.如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,当△ABC的周长最小时,点C的坐标是
如图 8,在Rt ABC中,CAB 90,AC 3 , AB 4 ,点 P 是边 AB 上任意一点,过点 P 作PQ AB 交BC于点E,截取 PQ AP ,联结 AQ ,线段 AQ 交BC于点D,设 AP x ,DQ y .【2013徐汇】 (1)求y关于x的函数解析式及定义域;( 4 分) (2)如图 9,联结CQ,当CDQ和ADB相似时,求x的值;( 5 分) (3)当以点C为圆心,CQ为半径的⊙C和以点B为圆心,BQ为半径的⊙B相交的另一个交点在边 AB 上时,求 AP 的长.( 5 分) C Q D E A P B (图 8) C Q D E A (图 9) P B C A B (备用图) 【2013 奉贤】如图,已知AB是⊙O的直径,AB=8,点C在半径OA上(点C与点O、A不重合),过点 C作 AB的垂线交⊙ O于点 D,联结 OD,过点 B 作 OD的平行线交⊙ O于点 E、交射 线CD于点 F. (1)若 ⌒ ED BE⌒ ,求∠ F 的度数; (2)设CO x, EF y,写出y 与x之间的函数解析式,并写出定义域;
(3)设点 C 关于直线 OD 的对称点为 P ,若△ PBE 为等腰三角形,求 OC 的长. 第 25 题 【 2013 长宁】△ ABC 和△ DEF 的顶点 A 与 D 重合,已知∠ B = 90 . ,∠ BAC = 30 . , BC=6,∠ FDE = 90 , DF=DE=4. (1)如图①, EF 与边 、 分别交于点 ,且 . 设 DF a ,在射线 上取 AC AB G 、H FG=EH DF 一点 P ,记: DP xa ,联结 CP. 设△ DPC 的面积为 y ,求 y 关于 x 的函数解析式,并写 出定义域; (2)在( 1)的条件下,求当 x 为何值时 PC // AB ; ( 3)如图②,先将△ DEF 绕点 D 逆时针旋转,使点 E 恰好落在 AC 边上,在保持 DE 边与 AC 边完 全重合的条件下, 使△ DEF 沿着 AC 方向移动 . 当△ DEF 移动到什么位置时, 以线段 AD 、FC 、BC 的长度为边长的三角形是直角三角形. 图① 图② 【 2013 嘉定】已知 AP 是半圆 O 的直径,点 C 是半圆 O 上的一个动点 (不与点 A 、P 重合),联结 AC ,以直线 AC 为对称轴翻折 AO ,将点 O 的对称点记为 O 1 ,射线 AO 1 交半圆 O 于 点 B ,联结 OC . (1)如图 8,求证: AB ∥ OC ; (2)如图 9,当点 B 与点 O 1 重合时,求证: AB CB ;
初中数学几何图形初步技巧及练习题 一、选择题 1.如图是由若干个大小相同的小正方体堆砌而成的几何体,那么其三种视图中面积最小的是() A.主视图B.俯视图C.左视图D.一样大 【答案】C 【解析】 如图,该几何体主视图是由5个小正方形组成, 左视图是由3个小正方形组成, 俯视图是由5个小正方形组成, 故三种视图面积最小的是左视图, 故选C. 2.如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,当△ABC的周长最小时,点C的坐标是 A.(0,0)B.(0,1)C.(0,2)D.(0,3) 【答案】D 【解析】 【详解】 解:作B点关于y轴对称点B′点,连接AB′,交y轴于点C′, 此时△ABC的周长最小,
∵点A 、B 的坐标分别为(1,4)和(3,0), ∴B ′点坐标为:(-3,0),则OB′=3 过点A 作AE 垂直x 轴,则AE=4,OE=1 则B′E=4,即B′E=AE ,∴∠EB ′A=∠B ′AE , ∵C ′O ∥AE , ∴∠B ′C ′O=∠B ′AE , ∴∠B ′C ′O=∠EB ′A ∴B ′O=C ′O=3, ∴点C ′的坐标是(0,3),此时△ABC 的周长最小. 故选D . 3.如图,在正方形ABCD 中,E 是AB 上一点,2,3BE AE BE ==,P 是AC 上一动点,则PB PE +的最小值是( ) A .8 B .9 C .10 D .11 【答案】C 【解析】 【分析】 连接DE ,交AC 于P ,连接BP ,则此时PB+PE 的值最小,进而利用勾股定理求出即可. 【详解】 解:如图,连接DE ,交AC 于P ,连接BP ,则此时PB PE +的值最小 ∵四边形ABCD 是正方形 B D ∴、关于A C 对称 PB PD =∴
中考数学压轴题(几何综合题) 1、如图1,△ABC中,∠ACB=90°,AC=4厘米,BC=6厘米,D是BC的中点.点E从A 出发,以a厘米/秒(a>0)的速度沿AC匀速向点C运动,点F同时以1厘米/秒的速度从C出发,沿CB匀速向点B运动,其中一个动点到达端点时,另一个动点也随之停止运动,过点E作AC的垂线,交AD于点G,连接EF,FG.设它们运动的时间为t秒(t>0).(1)当t=2时,△ECF∽△BCA,求a的值; (2)当a=1 2 时,以点E、F、D、G为顶点的四边形是平行四边形,求t的值; (3)当a=2时,是否存在某个时间,使△DFG是直角三角形?若存在,请求出t的值; 若不存在,请说明理由. 解:(1)∵t=2,∴CF=2厘米,AE=2a厘米, ∴EC=(4-2a ) 厘米. ∵△ECF∽△BCA.∴EC CF CB AC = ∴422 64 a - =.∴ 1 2 a=. (2)由题意,AE=1 2 t厘米,CD=3厘米,CF=t厘米. ∵EG∥CD,∴△AEG∽△ACD.∴EG AE CD AC =, 1 2 34 t EG =.∴EG= 3 8 t. ∵以点E、F、D、G为顶点的四边形是平行四边形,∴EG=DF. 当0≤t<3时,3 3 8 t t =-, 24 11 t=. 当3<t≤6时,3 3 8 t t=-, 24 5 t=. 综上 24 11 t=或 24 5 (3)由题意,AE=2t厘米,CF=t厘米,可得:△AEG∽△ACD AG=5 2 t厘米,EG= 3 2 t,DF=3-t厘米,DG=5- 5 2 t(厘米). G D B A C F E (第27题) D B A C 备用图 图1
如图8,在ABC Rt ?中,?=∠90CAB ,3=AC ,4=AB ,点P 是边AB 上任意一点,过点P 作AB PQ ⊥交BC 于点E ,截取AP PQ =,联结AQ ,线段AQ 交BC 于点D ,设x AP =,y DQ =.【2013徐汇】 (1)求y 关于x 的函数解析式及定义域; (4分) (2)如图9,联结CQ ,当CDQ ?和ADB ?相似时,求x 的值; (5分) (3)当以点C 为圆心,CQ 为半径的⊙C 和以点B 为圆心,BQ 为半径的⊙B 相交的另一 个交点在边AB 上时,求AP 的长. (5分) 【2013奉贤】如图,已知AB 是⊙O 的直径,AB =8, 点C 在半径OA 上(点C 与点O 、A 不重合),过点C 作AB 的垂线交⊙O 于点D ,联结OD ,过点B 作OD 的平行线交⊙O 于点E 、交射线CD 于点F . (1)若 ,求∠F 的度数; (2)设,,y EF x CO ==写出y 与x 之间的函数解析式,并写出定义域; (图8) C A B D E P Q C A B D E P Q (图9) (备用图) C A B BE ED =⌒ ⌒
第25题 (3)设点C 关于直线OD 的对称点为P ,若△PBE 为等腰三角形,求OC 的长. 【2013长宁】△ABC 和△DEF 的顶点A 与D 重合,已知∠B =?90. ,∠BAC =?30. ,BC=6,∠ FDE =?90,DF=DE=4. (1)如图①,EF 与边AC 、AB 分别交于点G 、H ,且FG=EH . 设a DF =,在射线DF 上取一点P ,记:a x DP =,联结CP. 设△DPC 的面积为y ,求y 关于x 的函数解析式,并写出定义域; (2)在(1)的条件下,求当x 为何值时 AB PC //; (3)如图②,先将△DEF 绕点D 逆时针旋转,使点E 恰好落在AC 边上,在保持DE 边与AC 边完全重合的条件下,使△DEF 沿着AC 方向移动. 当△DEF 移动到什么位置时,以线段 AD 、FC 、BC 的长度为边长的三角形是直角三角形. 【2013嘉定】已知AP 是半圆O 的直径,点C 是半圆O 上的一个动点(不与点A 、P 重合),联结AC ,以直线AC 为对称轴翻折AO ,将点O 的对称点记为1O ,射线1AO 交半圆O 于点B ,联结OC . (1)如图8,求证:AB ∥OC ; (2)如图9,当点B 与点1O 重合时,求证:CB AB =; 图① 图②
最全初中数学几何动点问题专题分类归纳汇总 近几年有关“线段最值”的中考试题层出不穷,形式多样,往往综合了几何变换、函数等方面的知识,具有一定的难度,具有很强的探索性,通过研究发现,这些问题尽管形式多样、背景复杂、变化不断,但都可以通过几何变换转化为常见的基本问题. 最值题目类型多:作图、计算;有求差最大,求和最小;求周长最小、求时间最短;求最值、已知最值求待定系数等;对称载体多:几乎涉及到初中全部的轴对称图形(角、线段、等腰三角形、等腰梯形、菱形、正方形、抛物线、圆、坐标轴). 我们知道“对称、平移、旋转” 是三种保形变换。通过这三种几何变换可以实现图形在保持形状、大小不变的前提下而使其位置发生变化,具有更紧凑的位置关系或组合成新的有利论证的基本图形.通过几何变换移动线段的位置是解决最值问题的有效手段,题目是千变万化的,但是运用几何变换把最值问题转化为基本问题却是不变的。 数学问题是千变万化的,几何变换的应用也不是单一的,有些问题需要多种变换的组合才能解决,看看以下策略对解决问题能否奏效。 (1)去伪存真。刨去不变的线段,看清楚究竟是几段和的最小值问题,必须仔细研究题目的背景,搞清楚哪些是动点、哪些是定点、哪些是定长。 (2)科学选择。捕捉题目的信号,探索变换的基础,选择变换的手段.平移把不“连”的线段“接”起来,旋转把“碰头”的线段“展”开来重“接”,对称把在同侧的线段翻折过去重组,因此“不连——平移、碰头——旋转、同侧——对称”是一般的思路;对称变换的基础是轴对称图形,平移变换的基础是平行线,旋转变换的基础是等线段,所以选择哪种几何变换还要看题目中具备何种变换的基础信息。 (3)怎么变换?对称变换一般以动点所在直线为对称轴,构建定点(直线)的对称点(直线),如有多个动点就必须作多次变换;平移一般是移动没有公共端点的两条线段中的某一条,与另一条对“接”;旋转变换一般以定点为旋转中心旋转60°或90°。 (4)怎么求值?几何变换成了“两折线”或“三折线”后,根据“两点之间线段最
2019年中考数学几何综合型试题分类汇编及答案 各位读友大家好,此文档由网络收集而来,欢迎您下载,谢谢 1.重庆,11,4分)据报道,重庆主城区私家车拥有量近380000辆.将数380000用科学记数法表示为________ 【解析】科学记数法的正确写法是:a×。 【答案】×105 【点评】通常易犯的错误是a的整数位数不对。 2.过度包装既浪费资源又污染环境.据测算,如果全国每年减少10%的过度包装纸用量,那么可减排二氧化碳3120000吨.把数3120000用科学记数法表示为 ×105 ×106 ×105 ×107
【解析】3120000是一个7位整数,所以3120000用科学记数法可表示为×1000000=×106,故选B. 【答案】B 【点评】科学记数法是将一个数写成a×10n的形式,其中1≤|a|1时,n是正数;当原数的绝对值1时,n是正数;当原数的绝对值<1时,n是负数.学生在学习科学记数法时最不容易掌握的就是n的确定,查准是10的几次方。还有的学生容易把“×10n”忘记而丢失,要明确记清. 其方法是确定a,a是只有一位整数的数;确定n;当原数的绝对值≥10时,n 为正整数,n等于原数的整数位数减1;当原数的绝对值<1时,n为负整数,n 的绝对值等于原数中左起第一个非零数前零的个数. 16. 2011年安徽省棉花产量约378000吨,将378000用科学计数法表示应是______________. 【解析】科学记数法形式:a×10n 中n的值是易错点,由于378 000有6
位,所以可以确定n=6﹣1=5,所以378 000=×105 【答案】×105 【点评】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值大于10时,n是正数;当原数的绝对值小于1时,n是负数.表示时关键要正确确定a 的值以及n的值. 17.从权威部门获悉,中国海洋面积是万平方公里,约为陆地面积的三分之一, 万平方公里用科学计数法表示为平方公里 A. B. C. D. 【解析】∵万平方公里=×106平方公里,且结果保留两位有效数字 ∴×106平方公里≈ 【答案】C. 【点评】此题考查对科学计数法和有效数字的理解,把一个绝对值大于10
【典例1】如图,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC 边上的动点,将△EBF沿EF所在直线折叠得到△EB′F,连结B′D,则B′D的最小值是(). B.6 C. D.4 A. 【解析】∵AE=BE,BE=B′E,由圆的定义可知,A、B、B′在以点E为圆心, AB长为直径的圆上,如图所示. B′D的长最小值= DE =. 22故选A. 【启示】此题属于动点(B′)到一定点(E)的距离为定值(“定点定长”),联想到以E为圆心,EB′为半径的定圆,当点D到圆上的最小距离为点D到圆心的距离-圆的半径.当然此题也可借助三角形三边关系解决,如B D DE B E '' ≤-,当且仅当点E、B′、D三点共线时,等号成立. 【典例2】如图,E、F是正方形ABCD的边AD上两个动点,满足AE=DF,连接CF交BD于点G,连结BE交AG于点H,若正方形的边长是2,则线段DH长度的最小值是 . 【思路探究】根据正方形的轴对称性易得∠AHB=90°,故点H在以AB为直径的圆上.取AB中点O,当D、H、O三点共线时,DH的值最小,此时DH=OD-OH,问
题得解. 【解析】由△ABE≌△DCF,得∠ABE=∠DCF,根据正方形的轴对称性,可得∠DCF=∠DAG,∠ABE=∠DAG,所以∠AHB=90°,故点H在以AB为直径的圆弧上.取AB中点O,OD交⊙O于点H,此时DH最小,∵OH=1 AB=,OD=,∴DH的最 1 2 小值为OD-OH 1. 【启示】此题属于动点是斜边为定值的直角三角形的直角顶点,联想到直径所对圆周角为直角(定弦定角),故点H在以AB为直径的圆上,点D在圆外,DH的最小值为DO-OH.当然此题也可利用DH OD OH ≤-的基本模型解决. 【针对训练】 1. 如图,在△ABC中,∠ACB=90°,AC=2,BC=1,点A,C分别在x轴,y轴上,当点A在x轴正半轴上运动时,点C随之在y轴上运动,在运动过程中,点B到原点O的最大距离为(). B.1.3 A 2.如图,在矩形ABCD中,AB=4,BC=6,E是矩形内部的一个动点,且AE⊥BE,则线段CE的最小值为(). B. C. D.4 A.3 3. 如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P、Q分别是边BC和半圆上的运点,连接PQ,则PQ长的最大值与最小值的和是().
最新初中数学几何图形初步知识点 一、选择题 1.如图将两块三角板的直角顶点重叠在一起,DOB ∠与DOA ∠的比是2:11,则BOC ∠的度数为( ) A .45? B .60? C .70? D .40? 【答案】C 【解析】 【分析】 设∠DOB=2x ,则∠DOA=11x ,可推导得到∠AOB=9x=90°,从而得到角度大小 【详解】 ∵∠DOB 与∠DOA 的比是2:11 ∴设∠DOB=2x ,则∠DOA=11x ∴∠AOB=9x ∵∠AOB=90° ∴x=10° ∴∠BOD=20° ∴∠COB=70° 故选:C 【点睛】 本题考查角度的推导,解题关键是引入方程思想,将角度推导转化为计算的过程,以便简化推导 2.如图为一直棱柱,其底面是三边长为5、12、13的直角三角形.若下列选项中的图形均由三个矩形与两个直角三角形组合而成,且其中一个为如图的直棱柱的展开图,则根据图形中标示的边长与直角记号判断,此展开图为何?( )
A.B.C.D. 【答案】D 【解析】 分析:三棱柱的侧面展开图是长方形,底面是三角形,据此进行判断即可. 详解:A选项中,展开图下方的直角三角形的斜边长为12,不合题意; B选项中,展开图上下两个直角三角形中的直角边不能与其它棱完全重合,不合题意; C选项中,展开图下方的直角三角形中的直角边不能与其它棱完全重合,不合题意; D选项中,展开图能折叠成一个三棱柱,符合题意; 故选:D. 点睛:本题主要考查了几何体的展开图,从实物出发,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键. ⊥,从A地测得B地在A地的北偏东43?3.如图,有A,B,C三个地点,且AB BC 的方向上,那么从B地测得C地在B地的() A.北偏西43?B.北偏西90?C.北偏东47?D.北偏西47? 【答案】D 【解析】 【分析】 根据方向角的概念和平行线的性质求解. 【详解】 如图,过点B作BF∥AE,则∠DBF=∠DAE=43?, ∴∠CBF=∠DBC-∠DBF=90°-43°=47°, ∴从B地测得C地在B地的北偏西47°方向上, 故选:D.
页眉内容 中考数学复习--几何综合题 Ⅰ、综合问题精讲: 几何综合题是中考试卷中常见的题型,大致可分为几何计算型综合题与几何论证型综合题,它主要考查学生综合运用几何知识的能力,这类题往往图形较复杂,涉及的知识点较多,题设和结论之间的关系较隐蔽,常常需要添加辅助线来解答.解几何综合题,一要注意图形的直观提示;二要注意分析挖掘题目的隐含条件、发展条件,为解题创造条件打好基础;同时,也要由未知想需要,选择已知条件,转化结论来探求思路,找到解决问题的关键. 解几何综合题,还应注意以下几点: ⑴ 注意观察、分析图形,把复杂的图形分解成几个基本图形,通过添加辅助线补全或构造基 本图形. ⑵ 掌握常规的证题方法和思路. ⑶ 运用转化的思想解决几何证明问题,运用方程的思想解决几何计算问题.还要灵活运用数 学思想方法伯数形结合、分类讨论等). Ⅱ、典型例题剖析 【例1】(南充,10分)⊿ABC 中,AB =AC ,以AC 为直径的⊙O 与AB 相交于点E ,点F 是BE 的中点. (1)求证:DF 是⊙O 的切线.(2)若AE =14,BC =12,求BF 的长. 解:(1)证明:连接OD ,AD . AC 是直径, ∴ AD⊥BC. ⊿ABC 中,AB =AC , ∴ ∠B=∠C,∠BAD=∠DAC. 又∠BED 是圆内接四边形ACDE 的外角, ∴∠C =∠BED . 故∠B =∠BED ,即DE =DB . 点F 是BE 的中点,DF ⊥AB 且OA 和OD 是半径, 即∠DAC =∠BAD =∠ODA . 故OD ⊥DF ,DF 是⊙O 的切线. (2)设BF =x ,BE =2BF =2x . 又 BD =CD =21 BC =6, 根据BE AB BD BC ?=?,2(214)612x x ?+=?. 化简,得 27180x x +-=,解得 122,9x x ==-(不合题意,舍去).
第四章图形的认识 本章思维导图 第一节图形初步 考点精要解析 考点一、平面展开图和三视图 1.平面展开图:将立体图形的表面适当剪开,可以展开成平面图形,这样的平面图形称为相应立体图形的展开图. 2.正方体的常见展开图 (1)“1-4-1”型,如图4-1-1所示. (2)“2-3-1”型,如图4-1-2所示.
(3)“3-3”型,如图4-1-3所示(4)“2-2-2”型,如图4-1-4所示 3.三视图 (1)主视图:从物体的前面向后面投射所得的视图称主视图——能反映物体的前面形状.(2)俯视图:从物体的上面向下面投射所得的视图称俯视图——能反映物体的上面形状.(3)左视图:从物体的左面向右面投射所得的视图称左视图——能反映物体的左面形状.注:画三视图时应注意一视图的位置要准确,看得见的部分的轮廓线通常画成实线,看不见的轮廓线通常画成虚线,主俯长对正、主左高平齐、俯左宽相等.即主视图和俯视图的长要相等;主视图和左视图的高相等;左视图和俯视图的宽要相等. 考点二:线与角 1.直线、射线与线段 (1)两个重要公理: ①经过两点有且只有一条直线,也称为“两点确定一条直线”. ②两点之间的连线中,线段最短,简称“两点之间,线段最短”. (2)两点之间的距离:连接两点的线段的长度. (3)线段的中点:把一条线段分成两条相等的线段的点叫作这条线段的中点. 2.角 (1)由公共端点的两条射线组成的图形叫作角. (2)角的分类 ①锐角——小于直角的角(0o<α<90o) ②直角——等于90o的角(α=90o). ③钝角——大于直角而小于平角的角(90o<α<180o).
(3)角的换算:1度=60分(1o=60'),1分=60秒(1'60" ). (4)角平分线:从一个角的顶点出发,把这个角分成两个相等的角的射线叫作这个角的平分线. (5)余角和补角 ①如果两个角的和是一个平角,那么这两个角互为补角,简称“互补”. ②如果两个角的和是一个直角,那么这两个角互为余角,简称“互余”. ③补角、余角的性质:同角或等角的余(补)角相等. 考点三:相交线与平行线 1.两条直线的位置关系 在同一平面内,两条直线的位置关系只有两种:(1)相交;(2)平行. 2.相交线 (1)对顶角与邻补角 ①对顶角:两条直线相交所成的四个角中,一个角的两边与另一个角的两边互为反向延长线,这两个角叫作对顶角.对顶角相等. ②邻补角:两条直线相交所成的四个角中,两个角有一条公共边,另一边互为反向延长线,这两个角叫作邻补角.邻补角互补. (2)垂线 ①定义:两条直线相交所成的四个角中,有一个角是直角,就说这两条直线互相垂直. ②垂线的性质 性质1:在同一平面内,过一点有且只有一条直线与已知直线垂直. 性质2:连接直线外一点与直线上各点的所有线段中,垂线段最短.简称:垂线段最短. ③点到直线的距离:直线外一点到这条直线的垂线段的长度,叫作点到直线的距离. 3.平行线 (1)定义:在同一平面内,不相交的两条直线叫作平行线. (2)平行公理:经过直线外一点,有且只有一条直线与已知直线平行. (3)平行公理的推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行.即“平行于同一条直线的两条直线平行”. 4.两直线平行的判定方法 (1)平行公理的推论. (2)同位角相等,两直线平行.
几何最值 一、选择题 1.(2020·泰安)如图,点A ,B 的坐标分别为A (2,0),B (0,2),点C 为坐标平面内一点,BC ﹦1,点M 为线段AC 的中点,连接OM ,则OM 的最大值为( ) A . 2 +1 B . 2 +1 2 C .2 2 +1 D .2 2 —1 2 {答案} B {解析}本题考查了圆的概念、勾股定理、三角形中位线的性质以及动点运动最值问题,因为点C 为坐标平面内一点,BC ﹦1,所以点C 在以点B 为圆心、1长为半径的圆上,在x 轴上取OA ′=OA=2,当A ′、B 、C 三点共线时,A ′C 最大,则A ′C=2 2 +1,所以OM 的最大值为 2 +1 2 ,因此本题选B . 2.(2020·无锡)如图,等边△ABC 的边长为3,点D 在边AC 上,AD =12,线段PQ 在边BA 上运动,PQ =1 2, 有下列结论: ①CP 与QD 可能相等; ②△AQD 与△BCP 可能相似; ③四边形PCDQ 面积的最大值为31316; ④四边形PCDQ 周长的最小值为3+37 2. 其中,正确结论的序号为( ) A .①④ B .②④ C .①③ D .②③ {答案} D {解析}设AQ =x ,则BP =5 2 —x ①如图1,当点P 与B 重合时,此时QD 为最大,过点Q 作QE ⊥AC ,∵AQ =52,∴AE =54,QE =53 4,∴DE = 34,∴此时QD =212,即0≤QD ≤212;而33 2≤CP ≤3,两个范围没有交集,即不可能相等;①错误 ②若△AQD ∽△BCP ,则AD BP =AQ BC ,代入得2x 2—5x +3=0,解得x 1=1,x 2=3 2,∴都存在,∴②正确; ③如图2,过点D 作DE ⊥AB ,过点P 作PF ⊥BC ,S 四边形PCDQ =S △ABC —S △AQD —S △BPC = 34×32-12?x ?34-1 2 ×3 × D Q P C B A
初中数学几何图形初步知识点 一、选择题 1.一把直尺和一块三角板ABC(含30°,60°角)的摆放位置如图,直尺一边与三角板的两直角边分别交于点D、点E,另一边与三角板的两直角边分别交于点F、点A,且∠CED=50°,那么∠BAF=() A.10°B.50°C.45°D.40° 【答案】A 【解析】 【分析】 先根据∠CED=50°,DE∥AF,即可得到∠CAF=50°,最后根据∠BAC=60°,即可得出∠BAF的大小. 【详解】 ∵DE∥AF,∠CED=50°, ∴∠CAF=∠CED=50°, ∵∠BAC=60°, ∴∠BAF=60°﹣50°=10°, 故选:A. 【点睛】 此题考查平行线的性质,几何图形中角的和差关系,掌握平行线的性质是解题的关键. 2.下列图形经过折叠不能围成棱柱的是(). A.B.C.D. 【答案】B 【解析】 试题分析:三棱柱的展开图为3个矩形和2个三角形,故B不能围成. 考点:棱柱的侧面展开图. ⊥,从A地测得B地在A地的北偏东43?3.如图,有A,B,C三个地点,且AB BC 的方向上,那么从B地测得C地在B地的()
A.北偏西43?B.北偏西90?C.北偏东47?D.北偏西47? 【答案】D 【解析】 【分析】 根据方向角的概念和平行线的性质求解. 【详解】 如图,过点B作BF∥AE,则∠DBF=∠DAE=43?, ∴∠CBF=∠DBC-∠DBF=90°-43°=47°, ∴从B地测得C地在B地的北偏西47°方向上, 故选:D. 【点睛】 此题考查方位角,平行线的性质,正确理解角度间的关系求出能表示点位置的方位角是解题的关键. 4.下列图形中,是正方体表面展开图的是() A.B.C.D. 【答案】C 【解析】 【分析】 利用正方体及其表面展开图的特点解题. 【详解】 解:A、B、D经过折叠后,下边没有面,所以不可以围成正方体,C能折成正方体.
几何综合题 1.已知△ABC中,AD是的平分线,且AD=AB,过点C作AD的垂线,交AD的延长线于点H. (1)如图1,若 ①直接写出B ∠和ACB ∠的度数; ②若AB=2,求AC和AH的长; (2)如图2,用等式表示线段AH与AB+AC之间的数量关系,并证明. 答案: (1)①75 B ∠=?,45 ACB ∠=?; ②作DE⊥AC交AC于点E. Rt△ADE中,由30 DAC ∠=?,AD=2可得DE=1,AE3 =. Rt△CDE中,由45 ACD ∠=?,DE=1,可得EC=1. ∴AC31 =+. Rt△ACH中,由30 DAC ∠=?,可得AH33 + =; (2)线段AH与AB+AC之间的数量关系:2AH=AB+AC 证明:延长AB和CH交于点F,取BF中点G,连接GH. BAC ∠ 60 BAC ∠=?
易证△ACH ≌△AFH . ∴AC AF =,HC HF =. ∴GH BC ∥. ∵AB AD =, ∴ ABD ADB ∠=∠. ∴ AGH AHG ∠=∠ . ∴ AG AH =. ∴()2222AB AC AB AF AB BF AB BG AG AH +=+=+=+==. 2.正方形ABCD 的边长为2,将射线AB 绕点A 顺时针旋转α,所得射线与线段BD 交于点M ,作CE AM ⊥于点E ,点N 与点M 关于直线CE 对称,连接CN . (1)如图1,当045α?<
几何综合题复习 几何综合题是中考试卷中常见的题型,大致可分为几何计算型与几何论证型综合题,它主要考查考生综合运用几何知识的能力。 一、几何论证型综合题 例1、()如图,已知:⊙O1与⊙O2是等圆,它们相交于A、B两点,⊙O2在⊙O1上,AC 是⊙O2的直径,直线CB交⊙O1于D,E为AB延长线上一点,连接DE。 (1)请你连结AD,证明:AD是⊙O1的直径; (2)若∠E=60°,求证:DE是⊙O1的切线。 分析:解几何综合题,一要注意图形的直观提示,二要注意分析挖掘题目的隐含条件,不断地由已知想可知,发展条件,为解题创条件打好基础。 证明: (1)连接AD,∵AC是⊙O2的直径,AB⊥DC Array∴∠ABD=90°, ∴AD是⊙O1的直径 (2)证法一:∵AD是⊙O1的直径, ∴O1为AD中点 连接O1O2, ∵点O2在⊙O1上,⊙O1与⊙O2的半径相等, ∴O1O2=AO1=AO2 ∴△AO1O2是等边三角形, ∴∠AO1O2=60° 由三角形中位线定理得:O1O2∥DC, ∴∠ADB=∠AO1O2=60° ∵AB⊥DC,∠E=60, ∴∠BDE=30,∠ADE=∠ADB+∠BDE=60°+30°=90° 又AD是直径, ∴DE是⊙O1的切线 证法二:连接O1O2, ∵点O2在⊙O1上,O1与O2的半径相等, ∴点O1在⊙O2 ∴O1O2=AO1=AO2, ∴∠O1AO2=60° ∵AB是公共弦, ∴AB⊥O1O2, ∴∠O1AB=30° ∵∠E=60° ∴∠ADE=180°-(60°+30°)=90° 由(1)知:AD是的⊙O1直径, ∴DE是⊙O1的切线. 说明:本题考查了三角形的中位线定理、圆有关概念以及圆的切线的判定定理等。
中考压轴题突破:几何最值问题大全(将军饮马、造桥选址、胡 不归、阿波罗尼斯圆等) 一、基本图形 所有问题的老祖宗只有两个:①[定点到定点]:两点之间,线段最短;②[定点到定线]:点线之间,垂线段最短。 由此派生:③[定点到定点]:三角形两边之和大于第三边;④[定线到定线]:平行线之间,垂线段最短;⑤[定点到定圆]:点圆之间,点心线截距最短(长);⑥[定线到定圆]:线圆之间,心垂线截距最短;⑦[定圆到定圆]:圆圆之间,连心线截距最短(长)。 余不赘述,下面仅举一例证明:[定点到定圆]:点圆之间,点心线截距最短(长)。 已知⊙O半径为r,AO=d,P是⊙O上一点,求AP的最大值和最小值。
证明:由“两点之间,线段最短”得AP≤AO+PO,AO≤AP+PO,得d-r≤AP≤d+r,AP最小时点P在B处,最大时点P在C处。即过圆心和定点的直线截得的线段AB、AC分别最小、最大值。(可用“三角形两边之和大于第三边”,其实质也是由“两点之间,线段最短”推得)。 上面几种是解决相关问题的基本图形,所有的几何最值问题都是转化成上述基本图形解决的。 二、考试中出现的问题都是在基本图形的基础上进行变式,如圆与线这些图形不是直接给出,而是以符合一定条件的动点的形式确定的;再如过定点的直线与动点所在路径不相交而需要进行变换的。类型分三种情况:(1)直接包含基本图形;(2)动点路径待确定;(3)动线(定点)位置需变换。 (一)直接包含基本图形 例1.在⊙O中,圆的半径为6,∠B=30°,AC是⊙O的切线,则CD的最小值是。
简析:由∠B=30°知弧AD一定,所以D是定点,C是直线AC上的动点,即为求定点D到定线AC的最短路径,求得当CD⊥AC时最短为3。 (二)动点路径待确定 例2.,如图,在△ABC中,∠ACB=90°,AB=5,BC=3,P是AB边上的动点(不与点B重合),将△BCP沿CP所在的直线翻折,得到△B′CP,连接B′A,则B′A长度的最小值是。 简析:A是定点,B'是动点,但题中未明确告知B'点的运动路径,所以需先确定B'点运动路径是什么图形,一般有直线与圆两类。此题中B'的路径是以C为圆心,BC为半径的圆弧,从而转化为定点到定圆的最短路径为AC-B'C=1。 例3.在△ABC中,AB=AC=5,cos∠ABC=3/5,将△ABC绕点C顺时针旋转,得到△A'B'C,点E是BC上的中点,点F为线段AB上
中考数学几何模型11:阿氏圆最值模型 名师点睛拨开云雾开门见山在前面的“胡不归”问题中,我们见识了“kPA+PB”最值问题,其中P点轨迹是直线,而当P点轨迹变为圆时,即通常我们所说的“阿氏圆”问题. 【模型来源】 “阿氏圆”又称为“阿波罗尼斯圆”,如下图,已知A、B两点,点P满足PA:PB=k(k≠1),则满足条件的所有的点P的轨迹构成的图形为圆.这个轨迹最早由古希腊数学家阿波罗尼斯发现,故称“阿氏圆”. B P O
【模型建立】 如图1 所示,⊙O 的半径为R,点A、B 都在⊙O 外,P为⊙O上一动点,已知R=2 5 OB, 连接PA、PB,则当“PA+2 5 PB”的值最小时,P 点的位置如何确定? 解决办法:如图2,在线段OB 上截取OC使OC=2 5 R,则可说明△BPO与△PCO相似,则有 2 5 PB=PC。 故本题求“PA+2 5 PB”的最小值可以转化为“PA+PC”的最小值,其中与A与C为定点,P为动点,故当A、 P、C 三点共线时,“PA+PC”值最小。 【技巧总结】 计算PA k PB +g的最小值时,利用两边成比例且夹角相等构造母子型相似三角形 问题:在圆上找一点P使得PA k PB +g的值最小,解决步骤具体如下: 1.如图,将系数不为1的线段两端点与圆心相连即OP,OB
2. 计算出这两条线段的长度比 OP k OB = 3. 在OB 上取一点C ,使得OC k OP =,即构造△POM ∽△BOP ,则PC k PB =,PC k PB =g 4. 则=PA k PB PA PC AC ++≥g ,当A 、P 、C 三点共线时可得最小值 典题探究 启迪思维 探究重点 例题1. 如图,在Rt △ABC 中,∠C=90°,AC=4,BC=3,以点C 为圆心,2为半径作圆C ,分别交AC 、BC 于D 、E 两点,点P 是圆C 上一个动点,则12 PA PB +的最小值为__________. E A B C D P 【分析】这个问题最大的难点在于转化12 PA ,此处P 点轨迹是圆,注意到圆C 半径为2,CA=4,