5三角形全等的判定HL

三角形全等的判定方法6种
1、SSS（Side-Side-Side）（边边边）：三边对应相等的三角形是全等三角形。

2、SAS（Side-Angle-Side）（边角边）：两边及其夹角对应相等的三角形是全等三角形。

3、ASA（Angle-Side-Angle）（角边角）：两角及其夹边对应相等的三角形全等。

4、AAS（Angle-Angle-Side）（角角边）：两角及其一角的对边对应相等的三角形全等。

5、RHS（Rightangle-Hypotenuse-Side）（直角、斜边、边）（又称HL定理（斜边、直角边））：在一对直角三角形中，斜边及另一条直角边相等。

（它的证明是用SSS原理）
下列两种方法不能验证为全等三角形：
1、AAA（Angle-Angle-Angle）（角角角）：三角相等，不能证全等，但能证相似三角形。

2、SSA（Side-Side-Angle）（边边角）：其中一角相等，且非夹角的两边相等。

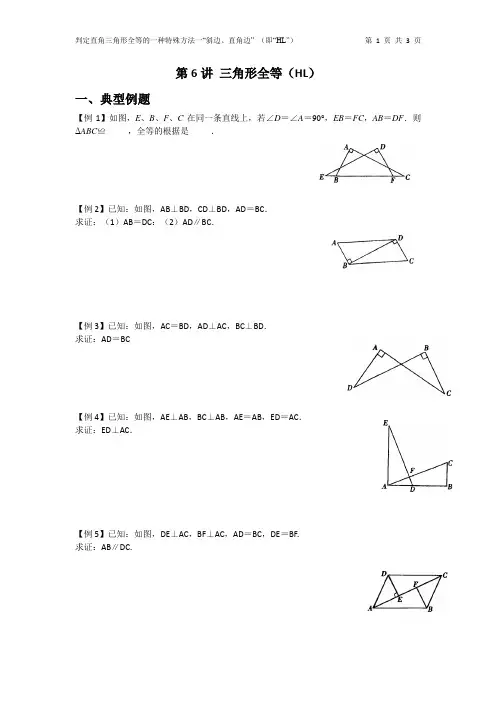
第6讲三角形全等（HL）一、典型例题【例1】如图，E、B、F、C在同一条直线上，若∠D＝∠A＝90°，EB＝FC，AB＝DF．则ΔABC≌_____，全等的根据是_____．【例2】已知：如图，AB⊥BD，CD⊥BD，AD＝BC．求证：（1）AB＝DC：（2）AD∥BC．【例3】已知：如图，AC＝BD，AD⊥AC，BC⊥BD．求证：AD＝BC【例4】已知：如图，AE⊥AB，BC⊥AB，AE＝AB，ED＝AC．求证：ED⊥AC．【例5】已知：如图，DE⊥AC，BF⊥AC，AD＝BC，DE＝BF.求证：AB∥DC.二、课堂练习（一）填空题1．判定两直角三角形全等的“HL”这种特殊方法指的是_____．2．直角三角形全等的判定方法有_____ （用简写）．3．判断满足下列条件的两个直角三角形是否全等，不全等的画“×”，全等的注明理由：（1）一个锐角和这个角的对边对应相等；（）（2）一个锐角和这个角的邻边对应相等；（）（3）一个锐角和斜边对应相等；（）（4）两直角边对应相等；（）（5）一条直角边和斜边对应相等．（）（二）选择题4．下列说法正确的是（）A．一直角边对应相等的两个直角三角形全等B．斜边相等的两个直角三角形全等C．斜边相等的两个等腰直角三角形全等D．一边长相等的两等腰直角三角形全等5．如图，AB＝AC，AD⊥BC于D，E、F为AD上的点，则图中共有（）对全等三角形．A．3 B．4 C．5 D．6（三）解答题1、如图，AB=CD，DF⊥AC于F，BE⊥AC于E，DF=BE，求证：AF=CE.2、如图，△ABC中，∠C=90°，AB=2AC，M是AB的中点，点N在BC上，MN⊥AB。

求证:AN平分∠BAC。

3、如图，A、E、F、B四点共线，AC⊥CE、BD⊥DF、AE=BF、AC=BD，求证：△ACF≌△BDE.4、已知在ABC ∆中，AD 平分BAC ∠，BD=CD.求证：AB=AC1．如图，点C 在∠DAB 的内部，CD ⊥AD 于D ，CB ⊥AB 于B ，CD=CB 那么Rt △ADC ≌Rt △ABC 的理由是（ ）A ．SSSB. ASAC. SASD. HL2．如图，CE ⊥AB ，DF ⊥AB ，垂足分别为E 、F ，AC ∥DB ，且AC=BD ，那么Rt △AEC ≌Rt △BFC 的理由是（ ）.A ．SSSB. AASC. SASD. HL3.下列说法正确的个数有（ ）.①有一角和一边对应相等的的两个直角三角形全等；②有两边对应相等的两个直角三角形全等；③有两边和一角对应相等的两个直角三角形全等；④有两角和一边对应相等的两个直角三角形全等.A ．1个 B. 2个 C. 3个 D. 4个4．如图，△ABC 中，∠C= 90，AM 平分∠CAB ，CM=20cm ，那么M 到AB 的距离是（ ）cm.5.如图，在△ABC 中，∠ACB=90。

12.2.5三角形全等的判定HL用HL判定三角形全等概念题型一：判定使用HL证明全等【例题1】（2020·广东期末）如图，OD AB⊥于D，OP AC⊥于P，且OD OP=，则AOD与AOP 全等的理由是()A．SSS B．ASA C．SSA D．HL【点睛】本题考查三角形全等的判定方法HL.根据已知结合图形，找到已经有的条件，然后结合判定方法选择条件是正确解答本题的关键．特别注意题目要求利用HL判定全等,需要的是两个直角三角形的斜边和一直角边对应相等.变式训练【变式1-1】（2021·四川期末）如图，AB BD⊥，CD BD⊥，AD BC=，则能直接判断Rt RtABD CDB△△≌的理由是（）A．HL B．ASA C．SAS D．SSS知识点管理归类探究在两个直角三角形中，有斜边和一条直角边对应相等的两个直角三角形全等（可以简写成“斜边、直角边”或“HL”）.应用“斜边、直角边”判定两个直角三角形全等的过程中要突出直角三角形这个条件，书写时必须在两个三角形前加上“Rt”【变式1-2】（2021·全国八年级）如图，AB BC ⊥，CD BC ⊥，AC BD =，则能证明ABC DCB ≅的判定法是( )A ．SASB ．AASC ．SSSD ．HL【变式1-3】（2020·东莞市东莞中学初中部八年级期中）如图，CE AB ⊥，DF AB ⊥，垂足分别为点E ，F ，且CE DF =，AC BD =，那么Rt Rt AEC BFD △≌△的理由是（ ）．A ．HLB ．SSSC ．SASD ．AAS题型二：通过添加条件利用SSS ，判定三角形全等【例题2】（2020·河南期末）如图，ABC 中，AD BC ⊥于D ，要使ABD ACD △≌△，若根据“HL ”判定，还需要加条件__________【点睛】本题考查选条件补齐使用HL 证明三角形全等.注意要两个直角三角形+斜边+一直角边. 变式训练【变式2-1】（2020·东莞期中）如图，已知AB⊥CD ，垂足为B ，BC=BE ，若直接应用“HL”判定⊥ABC ⊥⊥DBE ，则需要添加的一个条件是__________．【变式2-2】（2021·江苏期末）结合如图，用符号语言表达定理“斜边和一条直角边分别相等的两个直角三角形全等”的推理形式：在Rt ABC ∆和Rt DEF ∆中，90C F ∠=∠=︒，AC DF =，_______Rt ABC Rt DEF ∴∆≅∆．【变式2-3】（2020·永善县墨翰中学八年级月考）如图，要用“HL ”判定Rt ABC 和Rt A B C '''全等的条件是（ ）A ．AC AC ''=，BCBC ''= B ．A A '∠=∠，AB A B ''=C ．AC AC ''=，AB A B ''=D ．B B '∠=∠，BC B C ''= 题型三：直接利用SSS 证明三角形全等【例题3】（2020·沭阳县修远中学七年级期末）已知：BE⊥CD ，BE ＝DE ，BC ＝DA ，求证：⊥BEC⊥⊥DAE【点睛】HL 证明全等需要两个直角三角形+两个条件，在此类简单的证明题中往往题目中给出两个明显的条件，第三个条件可能隐藏在公共边或者线段的和差得到；此外还可能需要寻找题目中已知条件或者图形中隐含条件通过等量代换达到证明全等的目的.变式训练【变式3-1】（2021·湖北武汉市·八年级期中）如图，已知AB ＝CD ，CE ＝BF ，AE ⊥BC ，DF ⊥BC ，垂足分别为E ，F ，求证：CD ⊥AB ．【变式3-2】（2020·云南红河哈尼族彝族自治州·九年级学业考试）已知：如图，AB=CD ，DE⊥AC ，BF⊥AC ，E ，F 是垂足，AE=CF ．求证：⊥ABF⊥⊥CDE【变式3-3】（2020·荣县留佳初级中学校八年级期中）已知：如图，DE⊥AC ，BF⊥AC ，AD=BC ，DE=BF ，求证：AD⊥BCHL 证明全等的应用题型四：全等三角形性质与HL 判定的综合运用【例题4】（2021·全国八年级专题练习）如图，Rt ABC 与Rt DEF △的顶点A ，F ，C ，D 共线，AB 与EF 交于点G ，BC 与DE 相交于点H ，90B E ∠=∠=︒，AF CD =，AB DE =．（1）求证：Rt ABC Rt DEF ≌；（2）若1GF =，求线段HC 的长．【点睛】方法总结:证明线段相等或角相等可以通过证明三角形全等而得到，所以可以根据题目给出的已知条件，考虑证明三角形全等，还需要什么条件这些条件怎样可以得到.由对应边角相等的条件边得到三角形全等，这是全等三角形的判定;由三角形全等得到对应的边角相等，这是全等三角形的性质.变式训练【变式4-1】 （2019·江苏苏州市·七年级期末）已知:如图，AB BC ⊥，CD DA ⊥，AB CD =．求证:OB OD =．【变式4-2】（2019·河南开封市·八年级月考）在ABC 中，,90AB CB ABC ︒=∠=，F 为AB 延长线上一点，点E 在BC 上，且AE CF =.（1）求证：Rt ABE Rt CBF ≅△△（2）若30EAB ︒∠=，求BFC ∠度数.【变式4-3】（2020·贵州省施秉县第二中学八年级期末）如图所示，C 、D 分别位于路段A 、B 两点的正北处与正南处，现有两车分别从E 、F 两处出发，以相同的速度直线行驶，相同时间后分别到达C 、D 两地，休整一段时间后又以原来的速度直线行驶，最终同时到达A 、B 两点，那么CE 与DF 平行吗？为什么？题型五：角平分线与HL 的综合【例题5】（2019·江苏南通市·南通第一初中七年级月考）如图，PD ⊥AB ，PE ⊥AC ，垂足分别为D 、E ，且PD ＝PE ，则⊥APD 与⊥APE 全等的理由是（ ）A ．SASB ．AAAC ．SSSD ．HL【点睛】此题型考查全等三角形的判定和性质，角平分线的性质与判定，熟练掌握HL 全等三角形的判定和性质是解题的关键．注意灵活使用角平分线上的点到角两边距离相等.变式训练【变式5-1】（2019·浙江台州市·八年级期末）用三角尺画角平分线：如图，先在AOB ∠的两边分别取OM ON =，再分别过点M ，N 作OA ，OB 的垂线，交点为P ．得到OP 平分AOB ∠的依据是（ ）A ．HLB ．SSS B ．C ．SASD ．ASA 【变式5-2】（2020·吉林市亚桥第一九年制学校八年级期中）如图，四边形ABCD 中，90D ∠=︒，AB AC =，BEAC ⊥于点E ，=AE AD ．求证：AC 平分DAB ∠．3.（2018·郴州市第五中学八年级期末）如图，AC平分⊥BAD，CE⊥AB于E，CF⊥AD的延长线于F，且BC=DC．求证：BE=DF．【真题1】（2014·江苏南京市）（问题提出）学习了三角形全等的判定方法（即“SAS”、“ASA”、“AAS”、“SSS”）和直角三角形全等的判定方法（即“HL”）后，我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究．（初步思考）我们不妨将问题用符号语言表示为：在⊥ABC和⊥DEF中，AC=DF，BC=EF，⊥B=⊥E，然后，对⊥B进行分类，可分为“⊥B是直角、钝角、锐角”三种情况进行探究．（深入探究）第一种情况：当⊥B是直角时，⊥ABC⊥⊥DEF．（1）如图⊥，在⊥ABC和⊥DEF，AC=DF，BC=EF，⊥B=⊥E=90°，根据，可以知道Rt⊥ABC⊥Rt⊥DEF．第二种情况：当⊥B是钝角时，⊥ABC⊥⊥DEF．（2）如图⊥，在⊥ABC和⊥DEF，AC=DF，BC=EF，⊥B=⊥E，且⊥B、⊥E都是钝角，求证：⊥ABC⊥⊥DEF．第三种情况：当⊥B是锐角时，⊥ABC和⊥DEF不一定全等．（3）在⊥ABC和⊥DEF，AC=DF，BC=EF，⊥B=⊥E，且⊥B、⊥E都是锐角，请你用尺规在图⊥中作出⊥DEF，使⊥DEF和⊥ABC不全等．（不写作法，保留作图痕迹）（4）⊥B还要满足什么条件，就可以使⊥ABC⊥⊥DEF？请直接写出结论：在⊥ABC和⊥DEF中，AC=DF，链接中考BC=EF，⊥B=⊥E，且⊥B、⊥E都是锐角，若，则⊥ABC⊥⊥DEF．【拓展1】（2019·辽宁大连市·八年级月考）阅读下面材料，完成（1）-（3）题数学课上，老师出示了这样一道题：如图，⊥ABD和⊥ACE中，AB＝AD，AC＝AE，⊥DAB＝⊥CAE＝α，连接DC、BE交于点F，过A作AG⊥DC于点G，探究线段FG、FE、FC之间的数量关系，并证明．同学们经过思考后，交流了自己的想法：小明：“通过观察和度量，发现线段BE与线段DC相等．”小伟：“通过观察发现，⊥AFE与α存在某种数量关系．”老师：“通过构造全等三角形，从而可以探究出线段FG、FE、FC之间的数量关系．”（1）求证：BE＝CD；（2）求⊥AFE的度数（用含α的式子表示）；（3）探究线段FG、FE、FC之间的数量关系，并证明．【拓展2】（2020·湖北黄石市·黄石八中八年级期中）如图1，AB=12，AC⊥AB，BD⊥AB，AC=BD=8．点P在线段AB上以每秒2个单位的速度由点A向点B运动，同时，点Q在线段BD上由B点向点D运动．它们的运动时间为t(s).（1）若点Q的运动速度与点P的运动速度相等，当t=2时，⊥ACP与⊥BPQ是否全等，请说明理由，并判断此时线段PC和线段PQ的位置关系；（2）如图2，将图1中的“AC⊥AB，BD⊥AB”改为“⊥CAB=⊥DBA=60°”，其他条件不变．设点Q的运动速度为每秒x个单位，是否存在实数x，使得⊥ACP与⊥BPQ全等？若存在，求出相应的x,t的值；若不存在，满分冲刺请说明理由．。

1.38全等三角形判定（5）HL班级__________ 姓名__________ 学号__________【学习目标】1．利用尺规作图，掌握已知斜边、直角边画直角三角形的画图方法；2．经历操作、实验、观察、归纳，证明斜边、直角边（HL）定理；运用HL定理及其他三角形全等的判定方法进行证明和计算【课堂前测】1.如何将一个等腰三角形变成两个全等的直角三角形？2.如图，在Rt△ABC、Rt△DEF中，∠B＝∠E＝90°，（1）若∠A＝∠D，AB＝DE，则△ABC≌△DEF（）．（2）若∠A＝∠D，BC＝EF，则△ABC≌△DEF（）．（3）若AB＝DE，BC＝EF，则△ABC≌△DEF（）．上面的每一小题，都只添加了两个条件，就使两个直角三角形全等，你还能添加哪两个不同的条件使这两个直角三角形全等？【教学过程】一、探索新知1.议一议由前测2，我们可以得到什么？直角三角形是特殊的三角形，判定两个三角形全等，有没有特殊的方法？你有怎样的猜想？2.画一画用直尺和圆规作Rt△ABC，使∠C＝90°，CB＝a，AB＝c．（可以参阅书中的作法）F想一想：你作的直角三角形和其他同学所作的三角形能完全重合吗？你发现了什么？3．讨论、证明已知：在△ABC 和△A′B′C′中，∠C ＝∠C′ ＝ 90°，AB ＝A′B′，AC ＝A′C′．证明：△ABC ≌△A′B′C′．二、提炼归纳基本事实: （简写成“HL”）． 几何语言：∵在△ABC 和△DEF 中，＝，＝ ，∴△ABC ≌△DEF （HL ）．三、例题解析例1： 已知：如图，AD 、BC 相交于点O ，AD ＝BC ，∠C ＝∠D ＝ 900，求证： AO= BO ，CO ＝ DO ．四、巩固练习1. 如图，∠C ＝∠D ＝90°，请你再添加一个条件，使△ABD ≌△BAC ，并在添加的条件后的（ ）内写出判定全等的依据．（1） （ ） （2） （ ） （3） （ ） （4） （ ）2．已知：如图，△ABC 中，AB ＝AC ，AD 是高，则______≌______．依据是______，BD ＝______，∠BAD ＝______．3. 如图，AB ＝AE ，BC ＝ED ，∠B ＝∠E ，AF ⊥CD ，F 为垂足，求证：CF ＝DF ．五、归纳小结ABDB E六、【拓展提升】如图，OC平分∠AOB，点D，E分别在OA，OB上，点P在OC上且有PD=PE．求证：∠PDO=∠PEB．。

D C B
A
全等三角形判定条件ＨＬ
姓名：
【自主学习，探究新知】
全等三角形的判定：HL
文字语言表述为：斜边与一直角边对应相等的两个直角三角形 （可以简写成“ ”或“ ”）
用数学语言表述： 作图作法：
在Rt △ABC 和Rt '''A B C ∆中, ∵''BC B C AB =⎧⎨=⎩ ∴Rt △ABC ≌Rt △
注：直角三角形是特殊的三角形，所以不仅有一般三角形判定全等的方法
“ ”、“ ”、 “ ”、 “ ”、 还有直角三角形特殊的判定方法 “ ”
【例题讲析】
如图，AC=AD ，∠C ，∠D 是直角，将上述条件标注在图中，你能说明BC 与BD 相等吗？
【巩固训练】
１、 如图，CD ⊥AB ，BE ⊥AC ，垂足分别为D 、E ，BE 交CD 于F ，且AD=DF ，AC= BF
求证：Rt △ＡＤＣ≌Ｒｔ△ＦＤＢ
B A 1
1 C 1
A D C
B A E F
C
D
２、如图，AC ⊥BC ，BD ⊥AD ，AC=BD. 求证：BC=AD.
【拓展能力】
如图，B 、E 、F 、C 在同
一直线上，AF ⊥BC 于F ，DE ⊥BC 于E ， AB=DC ，BE=CF ，求证：AB ∥
CD。

三角形全等的判定条件
全等三角形判定条件(六种)是：
1、定义法：两个完全重合的三角形全等。

2、SSS：三个对应边相等的三角形全等。

3、SAS：两边及其夹角对应相等的三角形全等。

4、ASA：两角及其夹边对应相等的三角形全等。

5、AAS：两角及其中一角的对边对应相等的三角形全等。

6、HL：斜边和一条直角边对应相等的两个直角三角形全等。

经过翻转、平移、旋转后，能够完全重合的两个三角形叫做全等三角形，而该两个三角形的三条边及三个角都对应相等。

全等三角形指两个全等的三角形，它们的三条边及三个角都对应相等。

第一章三角形的证明2．直角三角形全等的“HL”的判定定理希望学校吕淑霞一、学情分析学生在学习直角三角形全等判定定理“HL”之前，已经掌握了一般三角形全等的判定方法，在本章的前一阶段的学习过程中接触到了证明三角形全等的推论，在本节课要掌握这个定理的证明以及利用这个定理解决相关问题还是一个较高的要求。

二、教学任务分析本节课是三角形全等的最后一部分内容，也是很重要的一部分内容，凸显直角三角形的特殊性质。

在探索证明直角三角形全等判定定理“HL”的同时，进一步巩固命题的相关知识也是本节课的任务之一。

因此本节课的教学目标定位为：1．知识目标：①能够证明直角三角形全等的“HL”的判定定理，进一步理解证明的必要性②利用“HL’’定理解决实际问题2．能力目标：①进一步掌握推理证明的方法，发展演绎推理能力三、教学过程分析本节课设计了六个教学环节：第一环节：复习提问；第二环节：引入新课；第三环节：做一做；第四环节：议一议；第五环节：课时小结；第六环节：课后作业。

1：复习提问1.判断两个三角形全等的方法有哪几种？2.已知一条边和斜边，求作一个直角三角形。

想一想，怎么画？同学们相互交流。

3、有两边及其中一边的对角对应相等的两个三角形全等吗？如果其中一个角是直角呢？请证明你的结论。

我们曾从折纸的过程中得到启示，作了等腰三角形底边上的中线或顶角的角平分线，运用公理，证明三角形全等，从而得出“等边对等角”。

那么我们能否通过作等腰三角形底边的高来证明“等边对等角”．要求学生完成，一位学生的过程如下：已知：在△ABC 中， AB=AC ．求证：∠B=∠C ．证明：过A 作AD ⊥BC ，垂足为C ，∴∠ADB=∠ADC=90°又∵AB=AC ，AD=AD ，∴△ABD ≌△ACD ．∴∠B =∠C （全等三角形的对应角相等）在实际的教学过程中，有学生对上述证明方法产生了质疑。

质疑点在于“在证明△ABD ≌△ACD 时，用了“两边及其中一边的对角对相等的两个三角形全等”．而我们在前面学习全等的时候知道，两个三角形，如果有两边及其一边的对角相等，这两个三角形是不一定全等的．可以画图说明．(如图所示在ABD 和△ABC 中，AB=AB ，∠B=∠B ，AC=AD ，但△ABD 与△ABC 不全等)” ．也有学生认同上述的证明。

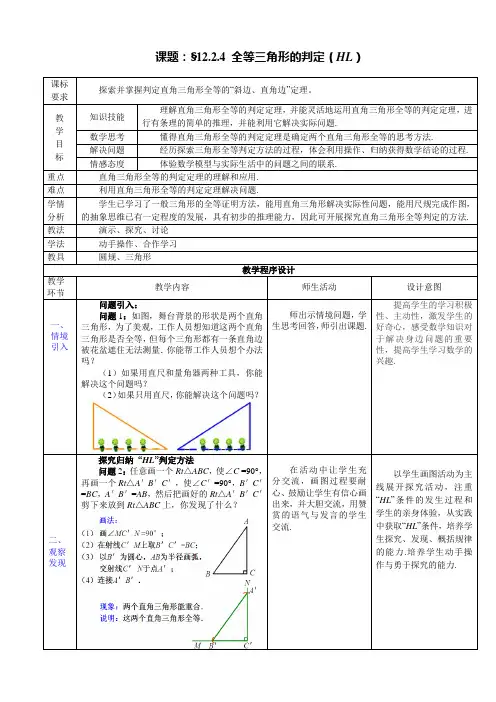
课题：§12.2.4 全等三角形的判定（HL）课标要求探索并掌握判定直角三角形全等的“斜边、直角边”定理。

教学目标知识技能理解直角三角形全等的判定定理，并能灵活地运用直角三角形全等的判定定理，进行有条理的简单的推理，并能利用它解决实际问题.数学思考懂得直角三角形全等的判定定理是确定两个直角三角形全等的思考方法.解决问题经历探索三角形全等判定方法的过程，体会利用操作、归纳获得数学结论的过程. 情感态度体验数学模型与实际生活中的问题之间的联系.重点直角三角形全等的判定定理的理解和应用. 难点利用直角三角形全等的判定定理解决问题.学情分析学生已学习了一般三角形的全等证明方法，能用直角三角形解决实际性问题，能用尺规完成作图，的抽象思维已有一定程度的发展，具有初步的推理能力，因此可开展探究直角三角形全等判定的方法.教法演示、探究、讨论学法动手操作、合作学习教具圆规、三角形教学程序设计教学环节教学内容师生活动设计意图一、情境引入问题引入：问题1：如图，舞台背景的形状是两个直角三角形，为了美观，工作人员想知道这两个直角三角形是否全等，但每个三角形都有一条直角边被花盆遮住无法测量．你能帮工作人员想个办法吗？（1）如果用直尺和量角器两种工具，你能解决这个问题吗？（2）如果只用直尺，你能解决这个问题吗？师出示情境问题，学生思考回答，师引出课题.提高学生的学习积极性、主动性，激发学生的好奇心，感受数学知识对于解决身边问题的重要性，提高学生学习数学的兴趣.二、观察发现探究归纳“HL”判定方法问题2：任意画一个Rt△ABC，使∠C =90°，再画一个Rt△A＇B＇C＇，使∠C＇=90°，B＇C＇=BC，A＇B＇=AB，然后把画好的Rt△A＇B＇C＇剪下来放到Rt△ABC上，你发现了什么？在活动中让学生充分交流，画图过程要耐心、鼓励让学生有信心画出来，并大胆交流，用赞赏的语气与发言的学生交流.以学生画图活动为主线展开探究活动，注重“HL”条件的发生过程和学生的亲身体验，从实践中获取“HL”条件，培养学生探究、发现、概括规律的能力.培养学生动手操作与勇于探究的能力.教学环节教学内容师生活动设计意图直角三角形全等判定定理：斜边和一条直角边分别相等的两个直角三角形全等.（简写为“斜边、直角边”或“HL”）几何语言：师生共同概括直角三角形全等的判定定理，及符号表示方法.明了“HL”判断全等的条件，规范符号语言表达形式.三、应用提高“HL”判定方法的运用：例5：如图，AC⊥BC，BD⊥AD，垂足分别为C、D，AC =BD．求证：BC =AD．变式1：如图，AC⊥BC，BD⊥AD，要证△ABC≌△BAD，需要添加一个什么条件？请说明理由．例（补充）：如图，有两个长度相同的滑梯，左边滑梯的高度AC 与右边滑梯水平方向的长度DF 相等，两个滑梯的倾斜角∠ABC 和∠DFE 的大小有什么关系？为什么？∴∠ABC =∠DEF.∵∠DEF +∠DFE=90°，师出示例题，小组探究，全班交流，师点评总结并板书.小组交流，师参与其中，并适时引导.让学生初步学会运用HL公理，掌握HL公理证题的规范格式；并通过种变换，加强学生的应用能力，活跃学生的思维.理解模型“双垂图”，并能应用全等的性质进行进一步的探究，培养学生的发散性思维、综合运用的能力.附：板书设计教学反思：成功之处：本节课教学，主要是让学生在回顾全等三角形判定的基础上，进一步研究特殊的三角形全等的判定的方法，让学生充分认识特殊与一般的关系，加深他们对公理的多层次的理解。