机器人避障路径探索

机器人避障的最优路径探索

摘要

本文研究了机器人避障最短路径的问题。基于定积分理论，我们提出并建立了一种选择最短路径的模型，即用起始点与目标点的连线将障碍物分割，并通过连接顶点的方式创建几何图形并比较分割线两边的包含障碍物在内的新创建的几何图形的面积。通过比较创建的几何图形面积来选择最短路径的方向。即从面积较小的新创建的几何图形一侧绕过障碍物抵达目标点所走的路径最短。

同时我们研究了在一个区域中存在多个障碍物，由出发点经过障碍物到达目标点所需最短路径的问题。我们通过证明具有圆形限定区域的最短路径是由两部分组成的：一部分是平面上的自然最短路径（即直线段），另一部分是限定区域的部分边界，这两部分是相切的，互相连接的。依据这个结果，我们可以认为最短路径一定是由线和圆弧做组成，因此我们建立了线圆结构，这样无论路径多么复杂，我们都可以将路径划分为若干个这种线圆结构来求解。对于途中经过节点再到达目标点的状况，我们采用了两种方案，一种是在拐点和节点都采用最小转弯半径的形式，另一种是适当扩大拐点处的转弯半径，使得机器人能够沿平滑曲线通过途中的目标点。然后建立了模型对两种方案分别进行求解。

关键词避障路径选择最短路径定积分

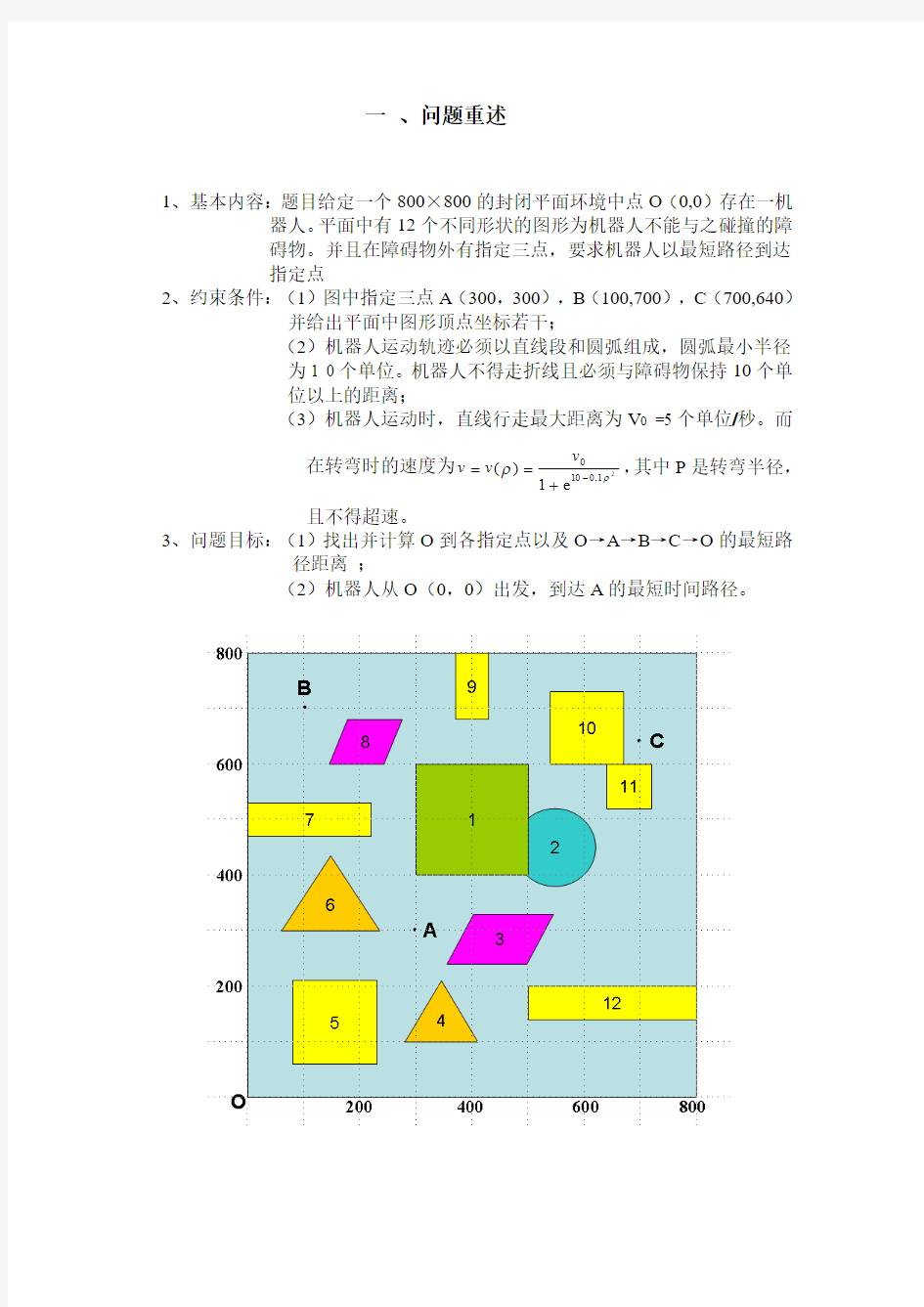
1、基本内容：题目给定一个800×800的封闭平面环境中点O （0,0）存在一机

器人。平面中有12个不同形状的图形为机器人不能与之碰撞的障碍物。并且在障碍物外有指定三点，要求机器人以最短路径到达指定点

2、约束条件：（1）图中指定三点A （300，300），B （100,700），C （700,640） 并给出平面中图形顶点坐标若干；

（2）机器人运动轨迹必须以直线段和圆弧组成，圆弧最小半径

为1 0个单位。机器人不得走折线且必须与障碍物保持10个单位以上的距离；

（3）机器人运动时，直线行走最大距离为V 0 =5个单位/秒。而

在转弯时的速度为2

1.0100

e

1)(ρ

ρ-+=

=v v v ，其中P 是转弯半径，

且不得超速。

3、问题目标：（1）找出并计算O 到各指定点以及O →A →B →C →O 的最短路

径距离 ；

（2）机器人从O （0，0）出发，到达A 的最短时间路径。

问题一:

1、问题一中要求从定点O（0, 0）按照一定的行走规则绕过障碍物到达目标

的最短路径。

2、因为障碍物的关系，机器人运动的路径不可能是直线，而且要求机器人要

是终与障碍物保持10单位以上的距离。

3、因此，我们先可以用包络线画出机器人行走的危险区域，这样的话，拐角

处就是一个半径为10的四分之一圆弧，然后采用拉绳子的方法寻找可能的最短路径。

问题二：

1、问题二中要求定点O（0， 0）经过中间的5号障碍物到达目标点A所需的

最短时间路径。

2、这时我们考虑的就不仅仅是经过障碍物拐点的问题，也应该考虑机器人沿

路径运动速度的问题。

3、我们在拐点及途中目标点处都采用最小转弯半径的形式，也可以适当的改

变拐点处的拐弯半径，使机器人能够以更接近直线运动速度的轨迹通过途中的障碍物而到达目标点。

三、模型假设

1、假设机器人始终以最大速度运动。

2、假设机器人变速可在瞬间完成，这样我们不必考虑机器人加速度的问题。

3、假设机器人能够抽象成点来处理。

四、符号说明

五、模型的建立

1、路径的选择模型

1）模型一：将起始点与目标点用一条直线连接起来，则两点间的障

碍物被直线分割成两部分。由起始点和目标点分别连接被分割图形顶点，所构成图形面积越大，则绕过该部分所需运动路径距离越大。（当被分割图形有两个或两个以上顶点时，若顶点在三角形内则连接同一顶点距离最短；若顶点在三角形外则分别连接最近顶点距离最短）。

L（AOa）当S△AOa＜S△AOb

MIN（L）=

L(AOb) 当S△AOa＞S△Aob

图5-1 边长面积比较示意图

证明:将a与b分别与O，A相连，得到△OaA与△ObA。由于两点之间直线最短，所以如果要从O经过矩形障碍物至A ，则最短路径为O→a→A或O→b→A。

解：Oa2+aA2=Ae2+Oe2+2ae2

Ob2+Ab2=Od2+Ad2+2bd2

设 Oe为X 则Ae为OA-X

则有Oe2+Ae2=2X2+OA2-2OAX

可知当Oe=Ae时 Oe2+Ae2取得最大值

同理Od=Ad时取得最大值

当Oe=Ae=Od=Ad时

Oa2+Aa2-（Ob2+Ab2）=2ae2-2bd2

因为ae＜bd

所以Oa+Aa＜Ob+Ab

当被分割图形不止一个顶点时，连接一个顶点必然小于连接两个顶点。

如图：ObA必然小于ObcA。

由上述思想我们可以建立一般模型，我们可以把问题简化为已知S△OAa ＜S△OAb，求证Oa+Aa＜Ob+Ab，证明如下：

将三角形用等宽矩形填充，设△OAa中矩形长hi，有n个，△OAb中矩形长Hj ,有n个。设OA=l

将△OAa分成△Oae和△Aae；将△OAb分成△Obd和△Abd；

则S△Oae=0.5*{2*（h1+h2+……+h e）/e }*el/n =l/n(h1+h2+……+h e)

S△Aae=0.5*{2*（h e+1+h e+2……+h n）/（n-e）}*（n-e）l/n =l/n （h e+1+h e+2+……+h n）

同理S△Obd=l/n（H1+H2+……+H d）

S△Abd=l/n（H d+1+H d+2+……+H n）

∴S△OAa=l/n*（h1+h2+……+h n）

S△OAb=l/n*（H1+H2+……+H n）

又∵S△OAa＜S△OAb

∴∑h＜∑H

且Oa2=（el/n）2+{2*（h1+h2+……+h e）/e}2,

Aa2={（n-e）l/n}2+{2*（h e+1+h e+2……+h n）/（n-e）}2

Ob2=（dl/n）2+{2*（H1+H2+……+H d）/d}2

Ab2={（n-d）l/n}2+{2*（H d+1+H d+2+……+H n）/（n-d）}2

用Oa+Aa-（Od+Ad）

当Oa=Aa=Od=Ad时

Oa+Aa和Ob+Ab取得最大值

又∵∑h＜∑H

∴Oa+Aa＜Od+Ad

由此可得出结论：当S△AOa＜S△AOb时l△AOa＜l△AOb

2）模型的推广

1.由上述分析我们有了这样一个想法：将连接端点后构成的新图形用等宽的矩形填充。然后相邻矩形间的高度差与矩形的宽可以与连线构成一个小型三角形

△a1b2a1。因为图形的面积越大，则矩形间的高度差a2b1越大，且因为矩形的宽

是固定的，所以被矩形顶点截出的连接线段a1b2会随着高度差的增加而增加。从而证明连接线会随着面积的增大而增大。如图5-2所示：

图 5-2 多顶点图形证明示意图

2.根据模型一的分析我们可以把全部有顶点的直边图形连接成三角形或多边形。接下来我们分析当被分割图形不存在顶点且边不为直线时的情况。我们过起始点与目标点做关于被分割曲线图形的切线，于是我们创建的新图形是一个由直线段与曲线组合成的图形。我们可以将其分解为两个部分，即由直线段包含的部分以及由曲线包含的部分。关于直线段的部分我们可以参照之前的方式证明，在此我们着重探讨曲线部分的面积与边长的关系。

我们如果将图放大，如果填充的矩形足够细密的话，则相邻矩形顶点所截曲线段a1a2可近似的看做直线段，于是我们可以将曲线图形转化为直边的多边形来对待。因此，对于没有顶点的曲线图形也适用与模型一的证明范围。

图5-3 曲边图形证明示意图

除此之外，我们还注意到凹形图的存在。因为我们是将被分割图形的顶点与起始点和目标点相连，因此创建的新的图形总不会是凹形图。因而无论凹形图还是凸形图都适用于此方法。

2、路径的计算模型

1）模型二：具有圆形限定区域的最短路径是由两部分组成的：一部分是平面上的自然最短路径（即直线段），另一部分是限定区域的部分边界，这两部分是相切的，互相连接的。（即问题分析中的拉绳子拉到最紧时的状况）

证明：如图5-4所示，假设在平面中有A （a ，0）和B （-a ，0）两点，中间

有一个半圆形的障碍物，证明从A 到B 的最路径为A

B 。

图5-4 最短路径计算示意图

平面上连接两点最短的路径是通过这两点的直线段，但是连接两点的线段于障碍物相交，所以设法尝试折线路径。在y 轴上取一点C （0，y ），若y 适当大，则折线ACB 与障碍物不相交，折线ACB 的长度为：

||ACB =显然||ACB 随着y 的减小而减小，减小y 得y →1y ，即1C C →,使得1AC 与1C B 与障碍物相切，切点分别为E 和F,显然1A C B 是这种折线路径中最短的。由于满足

0<

<

2

π

的角满足<

,所以易知弧度EF 小于1E C F 的长， 即

A E +

+FB<1A C B ,记线段AE 、弧度EF 、线段FB 为AEFB,那么AEFB 比任何折线

路径都短。

下面在考察一条不穿过障碍物的任何一条路径，设其分别于OE 和OF 的延长线交与P 、Q 两点，记A 和P 之间的路径长度为，显然

>|AP|,又由AE ⊥EO,

所以|AP|>AE,从而

>AE,同理可得

>BF 。

再来比较PQ 之间路径长度和圆弧EF 的长度的大小。若PQ 之间的路径可有极坐标方程

,则有

,可得：

=

≥

-

3

π

-

亦即路径APQB 的长度超过路径AEFB 的长度。以上证明足以说明了AEFB 是满足条件A 到B 的最短路径。

2)模型二的推广

根据模型二中的定理，我们就可以这样认为，起点到目标点无论中间障碍物有多少，最短路径都应该是若干个线圆结构所组成。在本题中存在障碍物的状况，且障碍物在拐点处的危险区域是一个半径为10的圆弧，，我们易知，求两点之间的最短路径中的转弯半径我们应该按照最小的转弯半径来算才能达到最优。

图5-5 线圆结构图

3、路径模型

根据模型二的分析，在有若干个障碍物的区域中，我们把按照线圆结构画出从出发点到目标点的路径图依据模型二中的想法转换成以下图示（仅以示意），图中的O和A点就是添加的源点和终点，其它节点均是出发点和目标点到圆弧的切线和圆弧与圆弧之间的切线转化而成。

图5-6

对于最短路径的求解，有以下步骤：

1）我们画出出发点和目标点和各个圆弧的切线，以及圆弧与圆弧之间的切线，但是切线有可能经过障碍物的内部或危险区域，也可能出现切线重复的状况，既有很多不合法的切线。于是我们对模型做了以下修正：

1．检验切线两个端点是否在障碍物内部。

2．检验切线是否障碍物的对角线相交。

3．检验圆弧所对应的圆心，即障碍物的顶点到切线的距离是否小于10。

如果以上三种情况满足其一，我们规定对应这段切线的顶点为M（M为无

穷大）。

另外还有如下图所示的一种特殊情况：

两个大小相同在同一水平或者竖直位置上，不考虑切线满足1、2、3的状况它们由2条内公切线，8条外公切线，但是有6条外公切线是重复的。因此我们作如下规定:如果某条切线与某段圆弧相切，且切点不在切线的端点上，

则该切线为不合法。权值矩阵中表示它的顶点也为M 。

图5-7

2） 然后把合法的切线与这些切线之间的劣弧转化成如5-7所示的形式。假设转化过后有m 条合法切线，那么就有m 个顶点，设这些点的权值i E （1i m ≤≤），即第i 条合法曲线的长度。j D 为边的权值，即第j 条弧的长度。

3）然后把路径图转化成如图5-6所示，按照求得权值矩阵给图中的顶点及边长

赋值。

4）最后依据Dijkstra 算法求得最短路径。

六、模型的求解

1、问题一

以下给出了O点到各目标点的可能的最短路径：

1）如图6-1，解决的就是O到目标点A的最短路径问题。图6-1中，粗黑线就为机器人隔出的区域，我们用细红线和细黑线表示两条由O至A的可能的最短路径。红线表示通过5号障碍顶点的圆为支撑而拉紧的绳子，这样计算出绳子的长度就是O到A的最短路径。

图6-1 O→A路径示意图

我们运用模型一中的方法，通过比较OA与两条路径所围成图形的面积来判断哪条路径更短。

由于两条路径均为直线段与圆弧的组合，但由于圆弧较小，且我们只是用来判断大小，细微误差不会对结果造成影响，为了便于计算我们假设所围成的图形是以圆心为第三顶点的三角形。（如图细黑线所示），结果如下：左上方三角形面积为OA与该顶点距离的积，通过计算，求得结果为39000 右下方三角形面积为51000，

因为39000/51000＜1

所以左上方路径更短。

接下来我们通过计算证明判断： 解：

设 半径=r=10 5号障碍左上顶点为O 1 11α=∠O AO 21α=∠M OO

31α=∠N AO

O(0,0) O 1(80,210) A(300,300) OA=a OO 1=b AO 1=c a=2

2

300

300

+

b=2

221080+

c=22)210300()80300(-+- 在1AOO ?中，

)2arccos(

2

221bc

a

c b -+=α

在Rt M AO 1?中， b

r arccos

2=α

在Rt N AO 1?中， c

r arccos

3=α

3212αααπθ---=

L=θ+-+-2

22

2

r

c r

b r

将相关数据带入得

上方路径长 473.82 右下方路径长 550.25

2）如图6-2，解决的是O到目标点B的最短路径问题，图中给出了可能的三条路径的最短路径（图中的红、绿、紫线所示），我们可以分别计算出三条可能路径的最短路径的长度，然后进行比较，取最小者就是O到目标点B的最优路径。最终得到最短路线为红色所示。

解法同前，最终求得O到B的最短路径距离为828.36

绿色路径距离为851.37

紫色路径距离为928.07

图6-2 O→B路径示意图

3)如图6-3，解决的是O到目标点C的最短路径问题。由于其间有多个障碍物且可供选择的路线较多，所以把路径分解为两部分。由于最短路径应尽量选取直线且避免折返，所以可知路径最终应经由11号障碍物右下顶点向上到右上顶点最后到达C点。我们选取三个特殊点作为“阶段点”即3号障碍物的左上顶点a、右下顶点b以及4号障碍物的右下顶点c。阶段点以前我们讨论由O点到三个特殊点的路径，而后讨论由“阶段点”到C点的最短路径。之后对三条路径相比较从而得出最短路径。

最终求得过c点的路径为1092.97

过b点的路径为1089.14

过a点的路径为1173.51

图6-3 O→C路径示意图

4）如图6-4，O→A→B→C→O的最短路径，解法同前。

可求得为最短路径为2698.12。

图6-4 O→A→B→C→O最短路径示意图

2、问题二

我们先按照中的思想来进行求解，这样我们可以做出路线如图6-5所示：

图6-5 O →A 最短时间路径示意图

由猜想一可知O 点经由5号障碍物上方至A 必然比从下方至A 距离短且经过的圆弧一定比从下方的短，所以我们着重讨论如图6-5所示路径。

由于机器人直线行走的最大速度为50=v 个单位/秒。机器人转弯时，最大转弯速度为2

1.0100e

1)(ρ

ρ-+=

=v v v ，其中ρ是转弯半径。即转弯速度受圆弧半径影响，当

半径足够大时，机器人在圆弧上的运动速度可以无限接近于5个单位/秒。但是由于机器

人在圆弧上的运行速度始终小于直线，因此我们还是要尽可能的减少机器人的弧线运动。因此我们取两个可能的最短时间路径，即如图6-5蓝、红线所示。

利用matlab 求解得出结果如下：

红线路径所需时间为：94.41 蓝色路径所需时间为：89.23

显然，蓝色路径所用时间更短。

七、模型评价

一、模型优点

1、模型简单，易用。

2、模型优化后用解析几何进行求解，精确度较高。

二、模型缺陷

1、此模型只能对单个障碍进行分析，当区域内有多个不相连障碍时，需要

对空间进行分割并选取某些点来辅助分析，较为繁琐。

2、此模型只能应对与固定且可预知障碍物的路线选择。当出现探索型最短

路径时，此模型需要改进。

八、参考文献

[1]卓金武，MATLAB在数学建模中的应用，北京，北京航空航天大学出版社2011；

[2]邦迪，图论及其应用，西安，西安科学出版社 1984

[3]胡海星，RPG游戏中精灵的移动问题，杂志《程序员》 2011；

[4]尤承业，解析几何，北京，北京大学出版社，2004

[5]周培德，计算几何—算法与设计，北京清华大学出版社，2005

九、附录

1）%求解一次转弯所经路线总长

%T：初始点 V:转弯圆弧圆心 W:到达点

function result=zongchang(T,W,V,r)

TV=sqrt((T(1)-V(1))^2+(T(2)-V(2))^2);

TW=sqrt((T(1)-W(1))^2+(T(2)-W(2))^2);

VW=sqrt((V(1)-W(1))^2+(V(2)-W(2))^2);

alpha1=acos((TV^2+VW^2-TW^2)/(2*TV*VW));

alpha2=acos(r/TV);

alpha3=acos(r/VW);

alpha4=2*pi-alpha1-alpha2-alpha3;%alpha4为转弯圆心角

TS1=sqrt(TV^2-r^2);%TS1,TS2均为圆弧切线%

S2W=sqrt(VW^2-r^2);

S1S2hu=r*alpha4;

result=TS1+S1S2hu+S2W;

2）%求解O经过中间节点到达目标点的最短路径

model:

min=d1+b+d3+u+v+t;

a=@sqrt(40^2+15^2);

b=@sqrt((x1-40)^2+(y1-15)^2);

c=@sqrt(x1^2+y1^2);

d1=3*3.1415926/2-@acos((a^2+b^2-c^2)/(2*a*b))-@acos(1/a);

(x1-50)^2+(y1-40)^2=1;

x1>49;

x1<50;

d2=@acos(@abs((50-x1+(1600-40*x1-40*y1+x1*y1)/(y1-15))/(@sqrt(1+(x1-4 0)^2/(y1-15)^2)*@sqrt((50-x1)^2+(40-y1)^2))));

e=@sqrt(55^2+55^2);

3)

>> clear all

>> Xo=[50 500];

>> k=1;

>> K=0;

>> m=5e6;

>> Po=105;

>> n=1;

>> a=0.5;

>> l=1;

>> J=200;

>> %end

>> %给出障碍和目标信息

>> Xsum=[500 50;300 300];

>> Xj=Xo;

>> for j=1:

Goal(j,1)=Xj(1);

Goal(j,2)=Xj(2);

Theta=compute_angle(Xj,Xsum,n);

ngle=Theta(1);

Angle=Theta(1);

angle_at=Theta(1);

[Fatx,Faty]=compute_Attract(Xj,Xsum,k,Angle,0,Po,n);

for i=1:n

angle_re(i)=Theta(i+1);

end

[Frerxx,Freryy,Fataxx,Fatayy]=compute_repulsion(Xj,Xsum,m,ang le_at,angle_re,n,Po,a);

Fsumyj=Faty+Freryy+Fatayy;

Fsumxj=Fatx+Frerxx+Fataxx;

Position_angle(j)=atan(Fsumyj/Fsumxj);

Xnext(2)=Xj(2)+l*sin(Position_angle(j));

Xj=Xnext;

if ((Xj(1)-Xsum(1,1))>0)&((Xj(2)-Xsum(1,2))>0)

K=j;

break;

%记录此时的j值

end%如果不符合if的条件，重新返回循环，继续执行.

end%大循环结束'.

>> K=j;

>> Goal(K,1)=Xsum(1,1);

>> Goal(K,2)=Xsum(1,2);

>> X=Goal(:,1);

>> Y=Goal(:,2);

>> %路径向量Goal是二维数组,X,Y分别是数组的x,y元素的集合，是两个一维数组。

>> x=[300];%障碍的x坐标

>> y=[300];

>> plot(x,y,'o',500,50,'v',0,0,'ms',X,Y,'.r');

>> plot(x,y,'o',500,50,'v',0,0,'ms',X,Y,'.r');

2012年数学建模机器人避障问题

机器人避障问题 摘要 本文主要运用直线逼近法等规律来解决机器人避障问题.对于问题一：要求最短路径运用直线逼近法证得圆弧角三角形定理，得出结论：若一大圆弧角三角形完全包括另一小圆弧角三角形，则该三角形曲线周长必大于小的三角形周长.那么可知机器人在曲线过弯时，选择最小半径可满足路径最短，即为10个单位半径，通过观察可得可能的所有曲线，通过仅考虑直线段的大致筛选选出总长较小、长度相近（之差小于100）的曲线，然后利用平面几何知识对相关切点，进而求出各直线、曲线的长度，求和可得最段路线.对于问题二：通过对机器人过弯规律2 1.0100 e 1)(ρ ρ-+= =v v v 的分析可知，当过弯 半径13ρ=时，机器人速度达最大速度为50=v 个单位/秒，再大就无变化了，那么可分两种情况考虑：1）当13ρ>时，过弯速度无变化，但由圆弧角三角形定理可知，此时随着ρ的不断变大，其路线总长不断变大，这时ρ越小O A →所用时间最短；2）当13ρ≤时，统计计算ρ分别为10、11、12、13时，过弯速度v 也不断变化，计算所用时间发现随ρ不断变大，O A →所用时间越短，此时当13ρ=时，时间最短.综合上述可知：当 13ρ=时，时间最短. 关键词： 质点机器人 安全范围 直线逼近法 圆弧角三角形定理 10单位半径

1 问题重述 在一个800×800的平面场景中，在原点O(0, 0)点处有一个机器人，它只能在该平面场景范围内活动，其中有12个不同形状的区域是机器人不能与之发生碰撞的障碍物， 物的距离至少超过10个单位）.规定机器人的行走路径由直线段和圆弧组成，其中圆弧是机器人转弯路径.机器人不能折线转弯，转弯路径由与直线路径相切的一段圆弧组成，也可以由两个或多个相切的圆弧路径组成，但每个圆弧的半径最小为10个单位.为了不与障碍物发生碰撞，同时要求机器人行走线路与障碍物间的最近距离为10个单位. 机器人直线行走的最大速度为50=v 个单位/秒.机器人转弯时，最大转弯速度为 2100.11 0()(1e ) v v v ρρ--==+，其中ρ是转弯半径.如果超过该速度，机器人将发 生侧翻，无法完成行走. 下面建立机器人从区域中一点到达另一点的避障最短路径和最短时间路径的数学模型.对场景图中4个点O(0, 0)，A(300, 300)，B(100, 700)，C(700, 640)，具体计算： (1) 机器人从O(0, 0)出发，O→A 、O→B 、O→C 和O→A→B→C→O 的最短路径. (2) 机器人从O (0, 0)出发，到达A 的最短时间路径. 2 问题分析 2.1问题一： 该问题要求路径最短，即不要求速度与时间，则可认为以最小半径10的圆过弯. 如图2.1所示：由圆弧角三角形定理（简单证明见模型准备5.3）可知过弯时，只有采用10单位半径过弯时，才会使得过弯路径最短，因此解决问题一的过弯拐角问题均采用10单位半径过弯路径. 2.2问题二： 由于O→A 过程中，机器人至少要经过一

机器人避障问题的解题分析(建模集训)

机器人避障问题的解题分析 摘要：本文对2012年全国大学生数学建模竞赛D题机器人避障问题进行了全面分析，对最短路的设计进行了理论分析和证明，建立了机器人避障最短路径的几何模型，对最短时间路径问题通过建立非线性规划模型，有效地解决了转弯半径、圆弧圆心位置和行走时间等问题。 关键词：机器人避障；最短路径；Dijkstra算法；几何模型；非线性规划模型 1 引言 随着科学技术的进步和计算机技术的发展，机器人的应用越来越广泛，在机器人的应用中如何使机器人在其工作范围内为完成一项特定的任务寻找一条安全高效的行走路径，是人工智能领域的一个重要问题。本文主要针对在一个场景中的各种静态障碍物，研究机器人绕过障碍物到达指定目的地的最短路径问题和最短时间问题。 本文以2012年“高教社”杯全国大学生数学建模竞赛D题“机器人避障问题”为例进行研究。假设机器人的工作范围为800×800的平面正方形区域（如图1），其中有12个不同形状的静态障碍物，障碍物的数学描述（如表1）： 图1 800×800平面场景图

表1 在原点O(0, 0)点处有一个机器人，它只能在该平面场景范围内活动，机器人不能与障碍物发生碰撞，障碍物外指定一点为机器人要到达的目标点。规定机器人的行走路径由直线段和圆弧组成，其中圆弧是机器人转弯路径。机器人不能折线转弯，转弯路径由与直线路径相切的一段圆弧组成，也可以由两个或多个相切的圆弧路径组成，但每个圆弧的半径最小为10个单位。为了不与障碍物发生碰撞，同时要求机器人行走线路与障碍物间的最近距离为10个单位，否则将发生碰撞，若碰撞发生，则机器人无法完成行走。机器人直线行走的最大速度为50=v 个单位/秒。机器人转弯时，最大转弯速度为2 1.0100 e 1)(ρρ-+==v v v （ρ是转弯 半径）。如果超过该速度，机器人将发生侧翻，无法完成行走。 场景图中有4个目标点O(0, 0)，A(300, 300)，B(100, 700)，C(700, 640)，下面我们

机器人避障问题——国家一等奖论文 推荐

D题机器人避障问题 摘要 本文综合运用分析法、图论方法、非线性规划方法，讨论了机器人避障最短路径和最短时间路径求解问题。 针对问题一，首先，通过分析，建立了靠近障碍物顶点处转弯得到的路径最短、转弯时圆弧的半径最小时和转弯圆弧的圆心为障碍物的顶点时路径最短、转弯在中间目标点附近时，中间目标点位于弧段中点有最短路径的三个原理，基于三个原理，其次对模型进行变换，对障碍物进行加工，扩充为符合条件的新的区域并在转弯处圆角化构成障碍图，并通过扩充的跨立实验，得到切线和圆弧是否在可避障区的算法，第三，计算起点、中间目标点和最终目标点和各圆弧及圆弧之间的所有可避障切线和圆弧路径，最后给这些定点赋一个等于切线长度或弧度的权值构成一个网络图，然后利用Dijkstra算法求出了O-A、O-B，O-C的最短路径为O-A：471.0372个单位，O-B：853.7001个单位，O-C：1086.0677个单位；对于需要经中间目标点的路径，可运用启发规则分别以相邻的目标点作为起点和终点计算，确定路径的大致情况，在进一步调整可得到O-A-B-C-O的最短路径为2748.699个单位。 针对问题二，主要研究的是由出发点到达目标点A点的最短时间路径，我们在第一问的基础上考虑路径尽可能短且圆弧转弯时的圆弧尽量靠近障碍物的顶点，即确定了圆弧半径最小时的圆弧内切于要确定的圆弧时存在最小时间路径，建立以总时间最短为目标函数，采用非线性规划模型通过Matlab编程求解出最短时间路径为最短时间路程为472.4822个单位，其中圆弧的圆心坐标为(81.430,209.41)，最短时间为94.3332秒。圆弧两切点的坐标分别为（70.88,212.92）、（77.66,219.87）。 关键字：Dijkstra算法跨立实验分析法非线性规划模型

避障机器人设计报告

开放性实验报告 ——避障机器人设计 系别：智能科学与技术 姓名：唐继鹏 姚武浩 姜飞鹏 郑光旭 指导老师：袁立行、王曙光、亢红波时间：2011.9.16——2012.4.28

目录 1 系统功能介绍 (1) 2 设计任务与要求 (1) 3 系统硬件设计 (1) 3.1系统总体设计框图 (1) 3.2寻线模块(ST188) (2) 3.3电机控制模块 (3) 3.4单片机最小模块 (4) 3.5数码管显示模块 (6) 4 系统软件实现 (7) 4.1 设计思路 (7) 4.2 软件程序流程图 (8) 4.3程序代码见附录Ⅰ (8) 5 调试结果 (8) 6 实验总结 (9) 附录Ι (10) 附录Ⅱ (18) 附录Ⅲ (19)

1 系统功能介绍 本设计以单片机作为控制核心，电路分为最小系统模块，黑线检测模块，电机驱动模块，数码管显示模块。黑线检测模块采用反射式关电传感器st188，并且接相应的三级管来规划传感器的输出，当输出高电平为正常情况。电机为伺服电机，给定脉宽为1.5ms的信号电机保持不动，给定脉宽为1.7ms的信号电机正向转到给定脉宽为1.3ms的信号电机逆向转到。数码管动态显示机器人行进过程所用的时间。 2 设计任务与要求 ◆熟悉51系列单片机的原理及应用。 ◆掌握ST188设计电路和传感器的使用。 ◆掌握直流电机的驱动方法。 ◆掌握动态数码管显示的方法。 ◆设计机器人的硬件电路及软件程序。 ◆制作机器人的硬件电路，并调试软件，最后实现机器人的自动测量黑线。 3 系统硬件设计 3.1系统总体设计框图 该系统中51单片机作为主微控芯片，其外多个I/O口作为通用I/O口接受传感器的信号并输出相应的控制信号。 系统硬件总体设计框图如下图3.1-1所示。

高教社杯数学建模D题机器人避障问题论文

机器人避 障问题 摘要 本文研究了机器人避障最短路径和最短时间路径的问题。主要研究了在一个区域中存在12个不同形状障碍物，由出发点到达目标点以及由出发点经过途中的若干目标点到达最终目标点的多种情形，寻找出一条恰当的从给出发点到目标点的运动路径使机器人在运动中能安全、无碰撞的绕过障碍物而使用的路径和时间最短。由于规定机器人的行走路径由直线段和圆弧组成，其中圆弧是机器人转弯路径，机器人不能折线转弯。所以只要给定的出发点到目标点存在至少一个障碍物，我们都可以认为最短路径一定是由线和圆弧所组成，因此我们建立了切线圆结构，这样无论路径多么复杂，我们都可以将路径划分为若干个这种切线圆结构来求解。在没有危险碰撞的情况下，圆弧的半径越小，路径应该越短，因此我们尽量选择最小的圆弧半径以达到最优。对于途中经过节点的再到达目标点的状况，我们采用了两种方案，一种是在拐点和节点都采用最小转弯半径的形式，另一种是适当扩大拐点处的转弯半径，使得机器人能够沿直线通过途中的目标点。然后建立了最优化模型对两种方案分别进行求解，把可能路径的最短路径采用穷举法列举出来，用lingo 工具箱求解得出了机器人从O(0,0)出发，O→A、O→B、O→C 和O→A→B→C→O 的最短路径；利用matlab 中的fminbnd 函数求极值的方法求出了机器人从O(0,0)出发，到达A 的最短时间路径。本文提出一种最短切线圆路径的规划方法，其涉及的理论并不高深，只是应用了几何知识和计算机程序、数学工具计算，计算简易，便于实现，能搞提高运行效率。 问题一 O→A 最短路径为：OA L =471.0372 O→B 最短路径为：=1OB L 853.8014 O→C 最短路径为：4OC L =1054.0 O→A→B→C→O 最短路径为： 问题二机器人从O(0,0)出发，到达A 的最短时间路径： 最短时间是94.5649，圆弧的半径是11.5035,路径长4078 .472=OA L 关键词最短路径；避障路径；最优化模型；解析几何；数学工具 一、问题重述 图1是一个800×800的平面场景图，在原点O(0,0)点处有一个机器人，它只能在该平面场景范围内活动。图中有12个不同形状的区域是机器人不能与之发生碰撞的障碍

机器人避障问题的最短路径分析

机器人避障问题的最短路径分析 摘要 本论文研究了机器人避障最短路径和最短时间路径的问题。主要讨论了在一个区域中存在12个障碍物，由出发点到达目标点以及由出发点经过若干目标点最终到达出发点的两种情况。采用传统的避障方法——切线图法。建立了线圆结构，这样任何路径，我们都可以将路径划分为若干个这种线圆结构来求解。对于途中经过节点再到达目标点的状况，我们采用在转弯点和节点都采用最小转弯半径，以节点为切点的形式。然后建立了最优化模型，利用MATLAB软件对方案进行求解。 问题一：把路径分解成若干个线圆结构来求解，然后把可能的最短路径采用穷举法列举出来，最终得出最短路径： A O→最短路径为：471.0 O→最短路径为：869.5 B O→最短路径为：1093.3 C 对于O → → →我们将A、B、C看作切点，同样采用线圆结构 C B A O→ 计算。 O→ → → →最短路径为：2827.1 A O C B 问题二：考虑避障路径和转弯速度，我们建立时间与路径之间的模型，用MATLAB软件求出最优解。当转弯半径为11.5的时候，可以得出最短时间为：T=94.3 关键词最优化模型避障路径线圆结构切线图法

一、问题重述 本文是求一个机器人在800×800的平面场景图中避开障碍物，建立从原点O(0, 0)点处出发达到终点的最短路径和最短时间路径的模型。即求：1、O→A 、O→B 、O→C 和O→A→B→C→O 的最短路径。2、O →A 的最短时间路径。 机器人在行走时的要求是：1、它只能在该平面场景范围内活动2、图中有12个不同形状的区域是机器人不能与之发生碰撞的障碍物（障碍物的分布如图1）3、障碍物外指定一点为机器人要到达的目标点（要求目标点与障碍物的距离至少超过10个单位）。4、规定机器人的行走路径由直线段和圆弧组成，其中圆弧是机器人转弯路径。机器人不能折线转弯，转弯路径由与直线路径相切的一段圆弧组成，也可以由两个或多个相切的圆弧路径组成，但每个圆弧的半径最小为10个单位。5、为了不与障碍物发生碰撞，同时要求机器人行走线路与障碍物间的最近距离为10个单位，否则将发生碰撞。 机器人直线行走的最大速度为50=v 个单位/秒。机器人转弯时，最大转弯速 度为2 1.0100 e 1)(ρρ-+==v v v ，其中ρ是转弯半径。 已知场景图中4个点O(0, 0)，A(300, 300)，B(100, 700)，C(700, 640)。图中各个点 的坐标见下表。 图1 编号 障碍物名称 左下顶点坐标 其它特性描述 1 正方形 (300, 400) 边长200 2 圆形 圆心坐标(550, 450)，半径70 3 平行四边形 (360, 240) 底边长140，左上顶点坐标(400, 330)

机器人避障问题

精心整理 机器人避障问题 摘要 本文研究了在一个800800?平面场景里，机器人通过直线和圆弧转弯，绕过障碍物，到达目标点的问题，解决了到达目标点路径最短，以及到达A 点时间最短的问题。文章将路径划分为若干个这种线圆结构来求解。对于途中经过节点的再到达目标点的状况，我们采用了在拐点和节点最小转弯半径的形式. O A →O →B O →C O →A →B 10个单位为50=v 对场景图中4(1)(2)1.出发，分别做圆的切线，直到终点。对于经过路径中的目标点的问题，我们采用最小转弯模式，建立优化模型，最终求的最短路径。 2．问题二要求从起始点到达A 点所用的时间最短，从题意以及生活经验可得，拐弯半径越大，所用时间越短，拐弯半径越小，所用时间越大。半径最小不低于10，取最大值时机器人应刚好未碰到4、6三角形，可通过几何解法计算出来，并对时间进行优化处理。 三、模型假设 假设机器人可以抽象成点来处理 假设机器人的能源充足，且在整个行走过程中无故障发生 四,符号说明

】 5（为起点，，OA 圆弧的切点，角度 1OO A ∠=,11OO M ∠=,11AO N ∠=，111M O N θ∠=.设这段路程机器人的总路程为L. 解法如下： 如上图可得有以下关系： 1 AOO ?在中： 在11Rt OO M ?： 222arccos(2b c a bc α+-=

在11Rt AO N 中： 所以： 从而可得： 结果如下： 机器人行走路线 1OM =1N A 弧11M N = 224.7221； b= 237.6973 c= O 同理了解 比较可得， O 从上面绕到到目标点A 的距离最短，最短路径为471.0372。

本科毕业论文-—基于向量场直方图的移动机器人避障方法研究

本科毕业设计（论文） 题目：（中文）基于向量场直方图的移动机器人避 障方法研究 （英文）STUDY OF OBSTACLE AVOIDANCE FOR THE MOBILE ROBOT BASED ON VECTOR FIELD HISTOGRAM

诚信承诺 我谨在此承诺：本人所写的毕业论文《基于向量场直方图的移动机器人避障方法研究》均系本人独立完成，没有抄袭行为，凡涉及其他作者的观点和材料，均作了注释，若有不实，后果由本人承担。 承诺人（签名）： 年月日

基于向量场直方图的移动机器人避障方法研究 摘要 【摘要】移动机器人广泛应用于工业生产加工制造中，尤其在危险和恶劣的环境中可以用机器人代替人工操作减少损失。避障技术在移动机器人的发展中起着至关重要的作用，避障方法有很多种，本文是基于向量场直方图的移动机器人避障方法。由于传统的向量场直方图法在给定值太大或太小时都无法安全避障，本文在此基础上，利用激光测距仪所或得的数据首先确定一个可以安全行驶的范围，然后通过算法自动的改变给定值的大小，最终选择最优给定值，通过差分驱动控制使机器人安全避障。并在Robotic Studio仿真系统中建立场景和编程来实现。 【关键词】移动机器人；激光测距仪；向量场直方图；差分驱动；避障

STUDY OF OBSTACLE A VOIDANCE FOR THE MOBILE ROBOT BASED ON VECTOR FIELD HISTOGRAM Abstract 【ABSTRACT】Mobile robots are widely used in industrial production and manufacturing，especially in dangerous and harsh environments they can replace manual operations to reduce losses. Obstacle avoidance technology plays a vital role in the development of mobile robot , There are many ways about obstacle avoidance, this article is the obstacle avoidance method for mobile robot based on the vector field histogram.If the given value is too large or too small the robot can not go through obstacles safely using traditional vector field histogram method. Basing on the VFH, firstly ,determining a range of safe driving use the data from laser range finders.Then changing the given value automatically and choosing the optimal value , finally using the differential drive control method make the robot avoid obstacles successfully.And make it come ture in the Robotic Studio simulated system. 【KEYWORDS】mobile robot；LRF；VFH ; differential drive; obstacle avoidance

小车自动避障与路径规划

第3章系统总体结构及工作原理 该系统主要以超声波测距为基本测距原理，并在相应的硬件和软件的支持下，达到机器人避障的效果。 3.1机器人总体硬件设计 3.1.1传感器的分布要求 为了全方位检测障物的分布状况，并及时为机器人系统提供全面的数据，可将所需的八个传感器均匀排列在机器人周围，相邻每对传感器互成45度角。为了避免相互干扰，八个传感器以程序运行周期为周期，进行循环测距。传感器排列示意图如下： 图3.1.1 传感器分布图

图3.1.2 硬件设计总体框架图 上图为支持机器人运行实用程序的硬件部分的总体设计框架图，由负责相关任务的同学提供。在超声波信号输入单片机以后，由存储在单片机中的主程序调用避障子程序，根据输入信号执行避障指令，并使相关数据返回主程序，转而提供给电机和LED显示器的驱动程序使用，最后，由电机执行转向指令，结果则显示在LED显示器上。

图3.1.3 软件总体框架图 由上图可知，本文作者负责的超声波避障程序为软件总体设计中的子程序部分。在主程序运行过程中，若调用超声波避障程序，机器人在自行轨迹规划后，将程序处理所得数据送给电机处理成立程序，控制电机动作。具体的避障程序设计将在第4章进行。 3.2超声波测距原理 测距原理：超声波是指频率高于20KHz的机械波。为了以超声波作为检测

手段，必须产生超生波和接收超声波。完成这种功能的装置就是超声波传感器，习惯上称为超声波换能器或超声波探头。超声波传感器有发送器和接收器，但一个超声波传感器也可具有发送和接收声波的双重作用。超声波传感器是利用压电效应的原理将电能和超声波相互转化即在发射超声波的时候，将电能转换，发射超声波；而在收到回波的时候，则将超声振动转换成电信号。[8]超声波测距的原理一般采用渡越时间法TOF（time of flight）。首先测出超声波从发射到遇到障碍物返回所经历的时间，再乘以超声波的速度就得到二倍的声源与障碍物之间的距离，即：[8] D=ct/2 其中D为传感器与障碍物之间的距离，以m计，c为超声波速度，这里以340m/s计，t为超声波从发送到接收的总时间，以s计。据此原理可以用超声波传感器测得的距离为避障程序提供所需的数据。[8] 第4章轨迹规划算法的实现方案 4.1轨迹规划算法的层次化设计 根据上述材料分析，可以将机器人轨迹规划算法设计分为基础控制层、行为控制层和坐标计算层，三个层次进行。 4.1.1基础控制层设计 基础控制层可定义为基本行为层，这层算法的任务是寻找目标点，并确保机器人可以顺利到达指定目标位。在确定目的地位置的情况下，为了达到上述目的，计算机必须对机器人的方位进行时实计算。应用人工势场法原理，可以将目标点设为引力极，牵引机器人运动。对此动作建立相应的模型，可以使用建立平面坐标作为虚拟势场的方法来给机器人定义方位，将机器人关于目标点的时实偏角作为虚拟引力方向，以确定机器人下一步所需转过的角度，并时实检测，是否已到达目的地，若已到达，则可认为虚拟引力此刻为0，并发出信号控制程序终止运行总体程序。 由此，可确定基础控制层所需的各参数： (1)机器人的时实坐标x, y值，由专门的坐标计算层提供，为了提高精 确度，可以采用厘米为单位制。 (2)机器人的速度v，测量后设为定值使用。 (3)周期T，直接设置为定值使用。 (4)偏转角de，可通过机器人与横坐标之间的夹角pe，减去机器人到目 标点连线与横坐标的夹角E得到。

机器人避障问题论文

机器人避障问题 【摘要】 本文主要是对机器人在一个平面区域内通过不同障碍物到指定目标点进行研究，通过建立机器人与障碍物的最小安全距离的禁区模型，进而建立从区域一点到另一点的最短距离、最短时间的数学模型。在最优转弯顶点为障碍物，最优转弯半径为安全距离10的基础上，把路径概括为基本的三种数学模型。利用穷举的算法找出最短路径和最短时间。 针对区域中从一点到另一点避障的最优路径问题，把障碍物划分为有顶点和无顶点两大类。首先本文证明对于有顶点障碍物，机器人以障碍物顶点为圆心且转弯的圆弧半径为10时路径最优，我们还注意到在某些路径中适当增加圆的半径可以把曲线路线转换为直线路径，进一步优化行进路径；对于无顶点障碍物通过论证找出以障碍物圆心为转弯圆心，以障碍物半径与安全距离的和为转弯半径的最优转弯圆弧。其次本文将寻找最短路径的的问题转换为最短路径的优选问题。本文巧妙的将优化模型转变为研究不与障碍物边界相交、不与圆弧相交的路线中的最优解的问题。在这个数学模型的基础上进行相应的改善并且使用穷举的算法找出最优路径。 针对不同的目标点，我们将机器人的行进分为单目标点和多目标点两种情况针对多目标点问题，由于机器人不能直线转向，所以在经过目标点时，应该提前转向，且中间目标点应该在转弯弧上。因此先建立优化模型（模型三）对行进时中间目标点处转弯圆弧圆心搜索求解。求出中间目标点转弯圆心后，用把中间目标点的圆心看做“障碍物”的办法把问题转化为单目标点问题。然后根据模型二和模型一利用MATLAB软件编程求得了O→A、O→B、O→C、O→A→B→A→C的最短路径，最短路径长分别为 471.0372、857.6778、1094.5、2799.0121,其中O-->A的最短路径对应圆弧的圆心坐标为(80,210)；O→B的最短路径对应圆弧的圆心坐标：(60,300)、(150,435)、（220、470）、(220,530)、(150,600)；O→C经过的圆心：(230，60)、(410,100)、(500,200)、(720,520)， （720,600）；对于多目标点问题利用模型三进行分割求解得到O→A→B→C→O最短路径对应圆心坐标（80,210）、（307.7715）、（306.2932）、（220,530）、（150,600）、（109.8478,701.7379）、（270,680）、（370,680）、（430,680）、（540,730）、（670,730）、（709.7933）、（642.0227）、（720,600）、（720,520）（500,200），（410,100），（230,60）。对于最短时间路径问题，根据转弯半径和速度的关系，在问题一求出的最短路径的模型的基础上，进行路线优化，建立以最短时间为目标的非线性规划模型，利用lingo 求解最短时间获得了机器人从O点出发，到达A的最短时间路径，求得最短时间路径下转弯半径为12.9885 ，同时最短时间路径时间长为94.2283个单位，路径长为471.129个单位。相应圆弧的圆心坐标为（82.1414，207.9153）。 关键词：机器人避障覆盖法穷举法非线性规划

移动机器人常用传感器及相关避障技术介绍

移动机器人常用传感器及相关避障技术介绍 移动机器人是机器人的重要研究领域，人们很早就开始移动机器人的研究。世界上第一台真正意义上的移动机器人是斯坦福研究院（SRI）的人工智能中心于1966年到1972年研制的，名叫Shakey，它装备了电视摄像机、三角测距仪、碰撞传感器、驱动电机以及编码器，并通过无线通讯系统由二台计算机控制，可以进行简单的自主导航。Shakey的研制过程中还诞生了两种经典的导航算法：A*算法（the A* search algorithm）和可视图法（the visibility graph method）。虽然Shakey只能解决简单的感知、运动规划和控制问题，但它却是当时将AI应用于机器人的最为成功的研究平台，它证实了许多通常属于人工智能（AriTIficial Intelligence，AI）领域的严肃的科学结论。从20世纪70年代末开始，随着计算机的应用和传感技术的发展，以及新的机器人导航算法的不断推出，移动机器人研究开始进入快车道。 移动机器人智能的一个重要标志就是自主导航，而实现机器人自主导航有个基本要求避障。下面让我们来了解一下移动机器人的避障，避障是指移动机器人根据采集的障碍物的状态信息，在行走过程中通过传感器感知到妨碍其通行的静态和动态物体时，按照一定的方法进行有效地避障，最后达到目标点。 实现避障与导航的必要条件是环境感知，在未知或者是部分未知的环境下避障需要通过传感器获取周围环境信息，包括障碍物的尺寸、形状和位置等信息，因此传感器技术在移动机器人避障中起着十分重要的作用。避障使用的传感器主要有超声传感器、视觉传感器、红外传感器、激光传感器等。 移动机器人避障常用的传感器 1、激光传感器 激光测距传感器利用激光来测量到被测物体的距离或者被测物体的位移等参数。比较常用的测距方法是由脉冲激光器发出持续时间极短的脉冲激光，经过待测距离后射到被测目标，回波返回，由光电探测器接收。根据主波信号和回波信号之间的间隔，即激光脉冲从

行走机器人避障问题

机器人行走问题 摘要 本文研究了机器人避障最短路径的问题。主要研究了在一个区域中存在四个障碍物，由出发点到达目标点以及由出发点经过途中的若干目标点到达最终目标点的两种情形。我们通过证明具有圆形限定区域的最短路径是由两部分组成的：一部分是平面上的自然最短路径（即直线段），另一部分是限定区域的部分边界，这两部分是相切的，互相连接的。依据这个结果，我们可以认为最短路径一定是由线和圆弧做组成，因此我们建立了线圆结构，这样无论路径多么复杂，我们都可以将路径划分为若干个这种线圆结构来求解。对于途中经过节点的再到达目标点的状况，我们采用了两种方案，一种是在拐点和节点都采用最小转弯半径的形式，另一种是适当扩大拐点处的转弯半径，使得机器人能够沿直线通过途中的目标点。然后建立了最优化模型对两种方案分别进行求解。 问题一，我们很容易分解成线圆结构来求解，然后把可能路径的最短路径采用穷举法列举出来，最终得出最短路径： R→A 最短路径为：70.5076 R→B 最短路径为：107.9587 R→C 最短路径为：102.0514 问题二，我们方案都进行优化，求得最终结果： 第一种方案最短路径为：156.471 第二种方案最短路径为：157.752 关键词最短路径最优化模型避障路径解析几何

一、问题重述 下图是一个100×80的平面场景图，在R（0，0）点处有一个机器人，机器人只能在该100×80的范围内活动，图中四个矩形区域是机器人不能与之发生碰撞的障碍物，障碍物的数学描述分别为B1（20，40；5，10）、B2（30，30；10，15）、B3（70，50；15，5）、B4（85，15；5，10），其中B1（20，40；5，10）表示一个矩形障碍物，其中心坐标为（20，40），5表示从中心沿横轴方向左右各5个单位，即矩形沿横轴方向长5×2=10个单位，10表示从中心沿纵轴方向上下各10个单位，即矩形沿纵轴方向长10×2=20个单位，所以，障碍物B1的中心在（20，40），大小为10×20个单位的矩形，其它三个障碍物的描述完全类似。 在平面场景中、障碍物外指定一点为机器人要到达的目标点（要求目标点与障碍物的距离至少超过1个单位），为此，须要确定机器人的最优行走路线——由直线段和圆弧线段组成的光滑曲线，其中圆弧线段是机器人转弯路线，机器人不能折线转弯，转弯路径是与直线相切的一圆形曲线段，也可以是两个或多个相切的圆弧曲线段组成，但每个圆形路线的半径都必须大于某个最小转弯半径，假设为1个单位。另外，为了不与障碍物发生碰撞，要求机器人行走线路与障碍物间的最短距离为1个单位，越远越安全，否则将发生碰撞，若碰撞发生，则机器人无法到达目标点，行走失败。请回答如下问题： 1.场景图中有三个目标点A（50，40）、B（75，60）、C（95，20），请用数学建 模的方法给出机器人从R（0，0）出发安全到达每个目标点的最短路线。 2.求机器人从R（0，0）出发，依次安全通过A、B到达C的最短路线。

机器人避障问题的MATLAB解法探析

机器人避障问题的MATLAB解法探析 摘要：本文对2012年全国大学生数学建模竞赛D题“机器人行走避障问题”，给出了利用matlab这一数学软件进行求解的方法，并对该方法的优缺点进行了分析。 关键词：机器人避障matlab 2012年全国大学生数学建模竞赛D题“机器人行走避障问题”如下： 在一个800×800的平面场景图中，原点O（0，0）点处有一个机器人，它只能在该平面场景范围内活动。图中有12个不同形状的区域是机器人不能与之发生碰撞的障碍物。规定机器人的行走路径由直线段和圆弧组成，其中圆弧是机器人转弯路径。机器人不能折线转弯，转弯路径由与直线路径相切的圆弧组成，每个圆弧的半径最小为10个单位。为了不与障碍物发生碰撞，同时要求机器人行走线路与障碍物间的最近距离为10个单位。计算机器人从O（0，0）出发，O→A、O→B、O→C和O→A→B→C→O的最短路径。 一、问题的分析 为达到要求，我们按照以下原则选择路径： （1）在障碍物拐点处的圆弧半径为临界半径个单位； （2）因为直线速度大于转弯速度，所以在不转弯的地方尽可能走直线； 按照上述原则，我们选取以下步骤求最短路径： （1）穷举出起始点与目标点的所有可能直线路径，判断出最短直线路径； （2）针对上述最短直线路径，在障碍物拐点处加入弧线转弯，然后计算实际最短行走路径。 二、问题的求解 按照上述步骤，逐步求最短路径： （1）首先画出O到A允许行走所有直线路线，如图所示。 （2）计算出各节点到下一节点的距离作为权值给各条边赋权，可以求解出最优直线路径。用MATLAB软件，程序如下： sets： cities/O，B1，B2，C1，C2，A/； roads（cities，cities）/O，B1 O，B2 O，C1 B1，A B1，C2 C1，B1 C1，B2 B2，C2 B2，A C2，A /：w，x； data： w= 224.7 237.7 100 237.7 150 150 150 150 250 114； n=@size（cities）； min=@sum（roads：w*x）； @for（cities（i）|i #ne# 1 #and# i #ne# n： @sum（roads（i，j）：x（i，j））=@sum（roads（j，i）：x（j，i）））； @sum（roads（i，j）|i #eq# 1：x（i，j））=1； end 计算出结果（只列出有用部分）： Global optimal solution found. Total solver iterations：0 Variable Value Reduced Cost

智能避障机器人设计外文翻译

INTELLIGENT VEHICLE Our society is awash in “machine intelligence” of various kinds.Over the last century, we have witnessed more and more of the “drudgery” of daily living being replaced by devices such as washing machines. One remaining area of both drudgery and danger, however, is the daily act ofdriving automobiles 1.2 million people were killed in traffic crashes in 2002, which was 2.1% of all globaldeaths and the 11th ranked cause of death . If this trend continues, an estimated 8.5 million people will be dying every year in road crashes by 2020. In fact, the U.S. Department of Transportation has estimated the overall societal cost of road crashes annually in the United States at greater than $230 billion. When hundreds or thousands of vehicles are sharing the same roads at the same time, leading to the all too familiar experience of congested traffic. Traffic congestion undermines our quality of life in the same way air pollution undermines public health.Around 1990, road transportation professionals began to apply them to traffic and road management. Thus was born the intelligent transportation system(ITS). Starting in the late 1990s, ITS systems were developed and deployed. In developed countries, travelers today have access to signifi-cant amounts of information about travel conditions, whether they are driving their own vehicle or riding on public transit systems. As the world energy crisis, and the war and the energy consumption of oil -- and are full of energy, in one day, someday it will disappear without a trace. Oil is not in resources. So in oil consumption must be clean before finding a replacement. With the development of science and technology the progress of the society, people invented the electric car. Electric cars will become the most ideal of transportation. In the development of world each aspect is fruitful, especially with the automobile electronic technology and computer and rapid development of the information age. The electronic control technology in the car on a wide range of

基于弹性绳索拉伸的机器人避障问题

基于弹性绳索拉伸的机器人避障问题 摘要 本文研究了机器人避障的相关问题。在一个已知区域中存在12个障碍物，使用基于弹性绳索拉伸的方法，求解了由出发点到目标点的最短路径和最短时间路径。我们在禁区顶点以最小转弯半径转向为最优的前提下，对障碍物进行了加工，即将限定区域向外扩展并将顶点圆角化。那么最短路径就由两部分组成：一部分是平面上的直线段，另一部分是限定区域上部分弧构成。由于最短路径一定是由直线线段和圆弧做组成，而弹性绳索紧贴障碍物时，弹性绳索与直线线段和圆弧重合，并且弹性绳索有自然缩短的趋势，弹性绳处于紧绷状态，此时弹性绳长就是最短路径。 问题一，将绳索系与起点和终点，使用拉伸弹性绳索的方法，找到所有符合要求的绳索连结成的路径并计算路径长度，最终最短的绳长即为所求。由于符合要求的路径可能比较多，我们又使用了尺规作图进行简化了以及一般情况下的Dijkstra求解最短路径的方法。 最终求得： O→A最短路径长度为471.037 O→B最短路径长度为 853.13 O→C最短路径长度为1092.82 O→A→B→C→O最短路径长度为2714.31 问题二，由于机器人转弯时所行走的速度和转弯半径有关。而当转弯半径最小时相应的速度也最小。就必须平衡转弯半径和转弯时速度的这一对矛盾。本文通过极限状态的求解，计算出可能的最短时间路径。 关键字：最短路径切线长弧长

一、问题的重述 图1是一个800×800的平面场景图，在原点O(0, 0)点处有一个机器人，它只能在该平面场景范围内活动。图中有12个不同形状的区域是机器人不能与之发生碰撞的障碍物，障碍物的数学描述如下表： 编号 障碍物名称 左下顶点坐标 其它特性描述 1 正方形 (300, 400) 边长200 2 圆形 圆心坐标(550, 450)，半径70 3 平行四边形 (360, 240) 底边长140，左上顶点坐标(400, 330) 4 三角形 (280, 100) 上顶点坐标(345, 210)，右下顶点坐标(410, 100) 5 正方形 (80, 60) 边长150 6 三角形 (60, 300) 上顶点坐标(150, 435)，右下顶点坐标(235, 300) 7 长方形 (0, 470) 长220，宽60 8 平行四边形 (150, 600) 底边长90，左上顶点坐标(180, 680) 9 长方形 (370, 680) 长60，宽120 10 正方形 (540, 600) 边长130 11 正方形 (640, 520) 边长80 12 长方形 (500, 140) 长300，宽60 在图1的平面场景中，障碍物外指定一点为机器人要到达的目标点(要求目标点与障碍物的距离至少超过10个单位)。规定机器人的行走路径由直线段和圆弧组成，其中圆弧是机器人转弯路径。机器人不能折线转弯，转弯路径由与直线路径相切的一段圆弧组成，也可以由两个或多个相切的圆弧路径组成，但每个圆弧的半径最小为10个单位。为了不与障碍物发生碰撞，同时要求机器人行走线路与障碍物间的最近距离为10个单位，否则将发生碰撞，若碰撞发生，则机器人无法完成行走。 机器人直线行走的最大速度为50=v 个单位/秒。机器人转弯时，最大转弯速度为 2 1.0100 e 1)(ρρ-+==v v v ，其中ρ是转弯半径。如果超过该速度，机器人将发生侧 翻，无法完成行走。 请建立机器人从区域中一点到达另一点的避障最短路径和最短时间路径的数学模型。对场景图中4个点O(0, 0)，A(300, 300)，B(100, 700)，C(700, 640)，具体计算： (1) 机器人从O(0, 0)出发，O→A 、O→B 、O→C 和O→A→B→C→O 的最短路径。 (2) 机器人从O (0, 0)出发，到达A 的最短时间路径。 注：要给出路径中每段直线段或圆弧的起点和终点坐标、圆弧的圆心坐标以及机器人行走的总距离和总时间。

2012年高教社杯数学建模D题--机器人避障问题论文设计

机器人避障问题 摘要 本文研究了机器人避障最短路径和最短时间路径的问题。主要研究了在一个区域中存在12个不同形状障碍物，由出发点到达目标点以及由出发点经过途中的若干目标点到达最终目标点的多种情形，寻找出一条恰当的从给出发点到目标点的运动路径使机器人在运动中能安全、无碰撞的绕过障碍物而使用的路径和时间最短。由于规定机器人的行走路径由直线段和圆弧组成，其中圆弧是机器人转弯路径，机器人不能折线转弯。所以只要给定的出发点到目标点存在至少一个障碍物，我们都可以认为最短路径一定是由线和圆弧所组成，因此我们建立了切线圆结构，这样无论路径多么复杂，我们都可以将路径划分为若干个这种切线圆结构来求解。在没有危险碰撞的情况下，圆弧的半径越小，路径应该越短，因此我们尽量选择最小的圆弧半径以达到最优。对于途中经过节点的再到达目标点的状况，我们采用了两种方案，一种是在拐点和节点都采用最小转弯半径的形式，另一种是适当扩大拐点处的转弯半径，使得机器人能够沿直线通过途中的目标点。然后建立了最优化模型对两种方案分别进行求解，把可能路径的最短路径采用穷举法列举出来，用lingo 工具箱求解得出了机器人从O(0, 0)出发，O →A 、O →B 、O →C 和O →A →B →C →O 的最短路径；利用matlab 中的fminbnd 函数求极值的方法求出了机器人从O (0, 0)出发，到达A 的最短时间路径。本文提出一种最短切线圆路径的规划方法，其涉及的理论并不高深，只是应用了几何知识和计算机程序、数学工具计算，计算简易，便于实现，能搞提高运行效率。 问题一 O →A 最短路径为：OA L =471.0372 O →B 最短路径为：=1OB L 853.8014 O →C 最短路径为：4OC L =1054.0 O →A →B →C →O 最短路径为： 问题二机器人从O (0, 0)出发，到达A 的最短时间路径： 最短时间是94.5649，圆弧的半径是11.5035,路径长4078.472=OA L 关键词 最短路径；避障路径；最优化模型；解析几何；数学工具