
第二章插值法
2.在区间[-1,1]上分别取n=10,20用两组等距节点对龙哥函数f(x)=1/(1+25*x^2)做多项式插值及三次样条插值,对每个n值,分别画出插值函数及f(x)的图形。
(1)多项式插值
①先建立一个多项式插值的M-file;
输入如下的命令(如牛顿插值公式):
function [C,D]=newpoly(X,Y)
n=length(X);
D=zeros(n,n)
D(:,1)=Y'
for j=2:n
for k=j:n
D(k,j)=(D(k,j-1)- D(k-1,j-1))/(X(k)-X(k-j+1));
end
end
C=D(n,n);
for k=(n-1):-1:1
C=conv(C,poly(X(k)))
m=length(C);
C(m)= C(m)+D(k,k);
end
②当n=10时,我们在命令窗口中输入以下的命令:
clear,clf,hold on;
X=-1:0.2:1;
Y=1./(1+25*X.^2);
[C,D]=newpoly(X,Y);
x=-1:0.01:1;
y=polyval(C,x);
plot(x,y,X,Y,'.');
grid on;
xp=-1:0.2:1;
z=1./(1+25*xp.^2);
plot(xp,z,'r')
得到插值函数和f(x)图形:
③当n=20时,我们在命令窗口中输入以下的命令:clear,clf,hold on;
X=-1:0.1:1;
Y=1./(1+25*X.^2);
[C,D]=newpoly(X,Y);
x=-1:0.01:1;
y=polyval(C,x);
plot(x,y,X,Y,'.');
grid on;
xp=-1:0.1:1;
z=1./(1+25*xp.^2);
plot(xp,z,'r')
得到插值函数和f(x)图形:
(2)三次样条插值
①先建立一个多项式插值的M-file;
输入如下的命令:
function S=csfit(X,Y,dx0,dxn)
N=length(X)-1;
H=diff(X);
D=diff(Y)./H;
A=H(2:N-1);
B=2*(H(1:N-1)+H(2:N));
C=H(2:N);
U=6*diff(D);
B(1)=B(1)-H(1)/2;
U(1)=U(1)-3*(D(1));
B(N-1)=B(N-1)-H(N)/2;
U(N-1)=U(N-1)-3*(-D(N));
for k=2:N-1
temp=A(k-1)/B(k-1);
B(k)=B(k)-temp*C(k-1);
U(k)=U(k)-temp*U(k-1);
end
M(N)=U(N-1)/B(N-1);
for k=N-2:-1:1
M(k+1)=(U(k)-C(k)*M(k+2))/B(k);
end
M(1)=3*(D(1)-dx0)/H(1)-M(2)/2;
M(N+1)=3*(dxn-D(N))/H(N)-M(N)/2;
for k=0:N-1
S(k+1,1)=(M(k+2)-M(k+1))/(6*H(k+1));
S(k+1,2)=M(k+1)/2;
S(k+1,3)=D(k+1)-H(k+1)*(2*M(k+1)+M(k+2))/6;
S(k+1,4)=Y(k+1);
end
②当n=10时,我们在命令窗口中输入以下的命令:clear,clc
X=-1:0.2:1;
Y=1./(25*X.^2+1);
dx0= 0.14201;dxn= -0.14201;
S=csfit(X,Y,dx0,dxn)
x1=-1:0.01:-0.5;y1=polyval(S(1,:),x1-X(1));
x2=-0.5:0.01:0;y2=polyval(S(2,:),x2-X(2));
x3=0:0.01:0.5; y3=polyval(S(3,:),x3-X(3));
x4=0.5:0.01:1;y4=polyval(S(4,:),x4-X(4));
plot(x1,y1,x2,y2,x3,y3,x4,y4, X,Y,'.')
结果如图:
②当n=20时,我们在命令窗口中输入以下的命令:clear,clc
X=-1:0.1:1;
Y=1./(25*X.^2+1);
dx0= 0.14201;dxn= -0.14201;
S=csfit(X,Y,dx0,dxn)
x1=-1:0.01:-0.5;y1=polyval(S(1,:),x1-X(1));
x2=-0.5:0.01:0;y2=polyval(S(2,:),x2-X(2));
x3=0:0.01:0.5; y3=polyval(S(3,:),x3-X(3));
x4=0.5:0.01:1;y4=polyval(S(4,:),x4-X(4));
plot(x1,y1,x2,y2,x3,y3,x4,y4, X,Y,'.')
结果如图:
第三章函数逼近与快速傅里叶变换
2.
x 0.0 0.1 0.2 0.3 0.5 0.8 1.0
y 1.0 0.41 0.50 0.61 0.91 2.02 2.46
试求3次、4次多项式的曲线拟合,再根据数据曲线形状,求一个另外函数的拟合曲线,用图示数据曲线及相应的三种拟合曲线。
(1)、三次拟合曲线:
命令如下:
x=[0.0 0.1 0.2 0.3 0.5 0.8 1.0];
y=[1.0 0.41 0.50 0.61 0.91 2.02 2.46];
cc=polyfit(x,y,3);
xx=x(1):0.1:x(length(x));
yy=polyval(cc,xx);
plot(xx,yy,'--');
hold on;
plot(x,y,'x');
xlabel('x');
ylabel('y');
结果如图:
(2)、4次拟合曲线
输入命令:
x=[0.0 0.1 0.2 0.3 0.5 0.8 1.0];
y=[1.0 0.41 0.50 0.61 0.91 2.02 2.46];
cc=polyfit(x,y,4);
xx=x(1):0.1:x(length(x));
yy=polyval(cc,xx);
plot(xx,yy,'r');
hold on;
plot(x,y,'x');
xlabel('x');
ylabel('y');
结果如图:
(3)、另一个拟合曲线:
新建一个M-file:
输入如下命令:
function [C,L]=lagran(x,y)
w=length(x);
n=w-1;
L=zeros(w,w);
for k=1:n+1
V=1;
for j=1:n+1
if k~=j
V=conv(V,poly(x(j)))/(x(k)-x(j));
end
end
L(k,:)=V;
end
C=y*L
在命令窗口中输入以下的命令:
x=[0.0 0.1 0.2 0.3 0.5 0.8 1.0];
y=[1.0 0.41 0.50 0.61 0.91 2.02 2.46];
cc=polyfit(x,y,4);
xx=x(1):0.1:x(length(x));
yy=polyval(cc,xx);
plot(xx,yy,'r');
hold on;
plot(x,y,'x');
xlabel('x');
ylabel('y');
x=[0.0 0.1 0.2 0.3 0.5 0.8 1.0];
y=[0.94 0.58 0.47 0.52 1.00 2.00 2.46]; %y中的值是根据上面两种拟合曲线而得到的估计数据,不是真实数据
[C,L]=lagran(x,y);
xx=0:0.01:1.0;
yy=polyval(C,xx);
hold on
plot(xx,yy,'b',x,y,'.');
第五章 解线性方程组的直接方法
1.用LU 分解及列主元消去法解线性方程组
12341070183 2.09999962 5.9000015151521031x x x x -??????
??????-??????=??????--????????????
输出Ax=b 中系数A=LU 分解的矩阵L 及U ,解向量x 及detA ;列主元法的行交换次序,解向量x 及detA ;比较两种方法所得的结果。 解:程序如下:
clear;
A=[10 -7 0 1;-3 2.099999 6 2;5 -1 5 -1;2 1 0 2]; B=[8;5.900001;5;1]; [L,U]=lu(A); X=U\(L\B) 输出的结果如下:
求det (A ):
输入:det(A);
输出:
列主元素消去法:程序如下:
function X =Gauss(A, b)
[n, m] = size(A);
X = zeros(n, 1);
temp = zeros(1, m);
temp_b = 0;
i = 1;
for j = 1: (m - 1)
if (A(i, j) ~= 0)
for k = (i + 1):n
if (A(k, j) ~= 0)
temp = A(k, :) + A(i, :) * (-A(k, j) / A(i, j));
temp_b = b(k) + b(i) * (-A(k, j) / A(i, j));
A(k, :) = temp;
b(k) = temp_b;
end
end
end
i = i + 1;
end;
A
b
disp('det(A) is ...');
x = det(A);
disp(x);
disp('cond(A) is ...');
x = cond(A);
disp(x);
X(n) = b(n) / A(n, n);
for i = (n - 1):-1:1
temp_b = 0;
for j = (i + 1):n
temp_b = temp_b + A(i, j) * X(j);
end
X(i) = (b(i) - temp_b) / A(i, i);
end
end
输出结果为:
A=[10 -7 0 1;-3 2.099999 6 2;5 -1 5 -1;2 1 0 2]
第八章矩阵特征值的计算
1.已知矩阵A=
10787
7565
86109
75910
??
??
??
??
??
??,B=
23456
44567
03678
00289
00010
??
??
??
??
??
??
??
??
,=
11/21/31/41/51/6
1/21/31/41/51/61/7
1/31/41/51/61/71/8
1/41/51/61/71/81/9
1/51/61/71/81/91/10
1/61/71/81/91/101/11
??
??
??
??
??
??
??
??
??
(1)用MATLAB函数“eig”求矩阵全部特征值。
(2)用基本QR算法求全部特征值(可用MATLAB函数“qr”实现矩阵的QR分解)。解:MATLAB程序如下:
求矩阵A的特征值:
clear;
A=[10 7 8 7;7 5 6 5;8 6 10 9;7 5 9 10];
E=eig(A)
输出结果:
求矩阵B的特征值:
clear;
B=[2 3 4 5 6;4 4 5 6 7;0 3 6 7 8;0 0 2 8 9;0 0 0 1 0];
E=eig(B)
输出结果:
求矩阵的特征值:
clear;
=[1 1/2 1/3 1/4 1/5 1/6; 1/2 1/3 1/4 1/5 1/6 1/7; 1/3 1/4 1/5 1/6 1/7 1/8; 1/4 1/5 1/6 1/7 1/8 1/9;1/5 1/6 1/7 1/8 1/9 1/10; 1/6 1/7 1/8 1/9 1/10 1/11];
E=eig()
输出结果:
(2)A=10787 7565 86109 75910
第一步:A0=hess(A);[Q0,R0]=qr(A0);A1=R0*Q0 返回得到:
第二部:
[Q1,R1]=qr(A1);A2=R1*Q1
第三部:
[Q2,R2]=qr(A2);A3=R2*Q2
现在收缩,继续对A3的子矩阵=29.8329 3.44110.0000 3.4411 4.30530.1611
00.16110.8516
-
-
进行累世变换,得到(假设收缩后的矩阵为C6)
C6=29.8329 3.44110.0000 3.4411 4.30530.1611
00.16110.8516
-
-
这是进行了6步qr算法所得的结果。故求的A的近似特征值为30.2886,,,0.0102。而A的特征值是0.0102
30.2886
同理,用类似的方法可求矩阵B 和的特征值,但过程过于繁琐,不再一一求解。
数值分析参考答案(第 二章)
第二章 插值法 1.当1,1,2x =-时,()0,3,4f x =-,求()f x 的二次插值多项式。 解: 0120121200102021101201220211,1,2, ()0,()3,()4;()()1 ()(1)(2)()()2()()1 ()(1)(2) ()()6 ()()1 ()(1)(1) ()()3 x x x f x f x f x x x x x l x x x x x x x x x x x l x x x x x x x x x x x l x x x x x x x ==-===-=--==-+-----==------= =-+-- 则二次拉格朗日插值多项式为 2 20()()k k k L x y l x ==∑ 0223()4() 14 (1)(2)(1)(1)23537623l x l x x x x x x x =-+=---+-+=+- 2.给出()ln f x x =的数值表 用线性插值及二次插值计算ln0.54的近似值。 解:由表格知, 01234012340.4,0.5,0.6,0.7,0.8;()0.916291,()0.693147()0.510826,()0.356675()0.223144 x x x x x f x f x f x f x f x ======-=-=-=-=- 若采用线性插值法计算ln0.54即(0.54)f , 则0.50.540.6<<
2 112 1 221 11122()10(0.6)()10(0.5)()()()()() x x l x x x x x x l x x x x L x f x l x f x l x -==----= =---=+ 6.93147(0.6) 5.10826(0.5)x x =--- 1(0.54)0.62021860.620219L ∴=-≈- 若采用二次插值法计算ln0.54时, 1200102021101201220212001122()() ()50(0.5)(0.6) ()() ()() ()100(0.4)(0.6) ()()()() ()50(0.4)(0.5) ()() ()()()()()()() x x x x l x x x x x x x x x x x l x x x x x x x x x x x l x x x x x x x L x f x l x f x l x f x l x --==------==-------= =----=++ 500.916291(0.5)(0.6)69.3147(0.4)(0.6)0.51082650(0.4)(0.5) x x x x x x =-?--+---?--2(0.54)0.615319840.615320L ∴=-≈- 3.给全cos ,090x x ≤≤的函数表,步长1(1/60),h '==若函数表具有5位有效数字,研究用线性插值求cos x 近似值时的总误差界。 解:求解cos x 近似值时,误差可以分为两个部分,一方面,x 是近似值,具有5位有效数字,在此后的计算过程中产生一定的误差传播;另一方面,利用插值法求函数cos x 的近似值时,采用的线性插值法插值余项不为0,也会有一定的误差。因此,总误差界的计算应综合以上两方面的因素。 当090x ≤≤时, 令()cos f x x = 取0110,( )606018010800 x h ππ ===?=
数值分析 第二章 2.当1,1,2x =-时,()0,3,4f x =-,求()f x 的二次插值多项式。 解: 0120121200102021101201220211,1,2, ()0,()3,()4;()()1 ()(1)(2)()()2()()1 ()(1)(2) ()()6 ()()1 ()(1)(1) ()()3 x x x f x f x f x x x x x l x x x x x x x x x x x l x x x x x x x x x x x l x x x x x x x ==-===-=--==-+-----==------= =-+-- 则二次拉格朗日插值多项式为 2 20 ()()k k k L x y l x ==∑ 0223()4() 14 (1)(2)(1)(1)23 537623 l x l x x x x x x x =-+=---+ -+= +- 6.设,0,1,,j x j n =L 为互异节点,求证: (1) 0()n k k j j j x l x x =≡∑ (0,1,,);k n =L (2)0 ()()0n k j j j x x l x =-≡∑ (0,1,,);k n =L 证明 (1) 令()k f x x = 若插值节点为,0,1,,j x j n =L ,则函数()f x 的n 次插值多项式为0 ()()n k n j j j L x x l x == ∑。 插值余项为(1)1() ()()()()(1)! n n n n f R x f x L x x n ξω++=-= + 又,k n ≤Q
(1)()0 ()0 n n f R x ξ+∴=∴= 0()n k k j j j x l x x =∴=∑ (0,1,,);k n =L 0 000 (2)()() (())()()(()) n k j j j n n j i k i k j j j i n n i k i i k j j i j x x l x C x x l x C x x l x =-==-==-=-=-∑∑∑∑∑ 0i n ≤≤Q 又 由上题结论可知 ()n k i j j j x l x x ==∑ ()()0 n i k i i k i k C x x x x -=∴=-=-=∑原式 ∴得证。 7设[]2 (),f x C a b ∈且()()0,f a f b ==求证: 21 max ()()max ().8 a x b a x b f x b a f x ≤≤≤≤''≤- 解:令01,x a x b ==,以此为插值节点,则线性插值多项式为 10 101010 ()() ()x x x x L x f x f x x x x x --=+-- =() () x b x a f a f b a b x a --=+-- 1()()0()0 f a f b L x ==∴=Q 又 插值余项为1011 ()()()()()()2 R x f x L x f x x x x x ''=-= -- 011 ()()()()2 f x f x x x x x ''∴= --
课题一:拉格朗日插值法 1.实验目的 1.学习和掌握拉格朗日插值多项式。 2.运用拉格朗日插值多项式进行计算。 2.实验过程 作出插值点(1.00,0.00),(-1.00,-3.00),(2.00,4.00)二、算法步骤 已知:某些点的坐标以及点数。 输入:条件点数以及这些点的坐标。 输出:根据给定的点求出其对应的拉格朗日插值多项式的值。 3.程序流程: (1)输入已知点的个数; (2)分别输入已知点的X坐标; (3)分别输入已知点的Y坐标; 程序如下: #include
插值算法*/ { int i,j; float *a,yy=0.0; /*a作为临时变量,记录拉格朗日插值多项*/ a=(float*)malloc(n*sizeof(float)); for(i=0;i<=n-1;i++) { a[i]=y[i]; for(j=0;j<=n-1;j++) if(j!=i) a[i]*=(xx-x[j])/(x[i]-x[j]); yy+=a[i]; } free(a); return yy; } int main() { int i; int n; float x[20],y[20],xx,yy; printf("Input n:");
scanf("%d",&n); if(n<=0) { printf("Error! The value of n must in (0,20)."); getch();return 1; } for(i=0;i<=n-1;i++) { printf("x[%d]:",i); scanf("%f",&x[i]); } printf("\n"); for(i=0;i<=n-1;i++) { printf("y[%d]:",i);scanf("%f",&y[i]); } printf("\n"); printf("Input xx:"); scanf("%f",&xx); yy=lagrange(x,y,xx,n); printf("x=%f,y=%f\n",xx,yy); getch(); } 举例如下:已知当x=1,-1,2时f(x)=0,-3,4,求f(1.5)的值。
数值分析报告 班级: 专业: 流水号: 学号: 姓名:
常用的插值方法 序言 在离散数据的基础上补插连续函数,使得这条连续曲线通过全部给定的离散数据点。插值是离散函数逼近的重要方法,利用它可通过函数在有限个点处的取值状况,估算出函数在其他点处的近似值。 早在6世纪,中国的刘焯已将等距二次插值用于天文计算。17世纪之后,牛顿、拉格朗日分别讨论了等距和非等距的一般插值公式。在近代,插值法仍然是数据处理和编制函数表的常用工具,又是数值积分、数值微分、非线性方程求根和微分方程数值解法的重要基础,许多求解计算公式都是以插值为基础导出的。 插值问题的提法是:假定区间[a,b〕上的实值函数f(x)在该区间上n+1个互不相同点x0,x1……x n处的值是f(x0),……f(x n),要求估算f(x)在[a,b〕中某点的值。其做法是:在事先选定的一个由简单函数构成的有n+1个参数C0, C1,……C n的函数类Φ(C0,C1,……C n)中求出满足条件P(x i)=f(x i)(i=0,1,……n)的函数P(x),并以P(x)作为f(x)的估值。此处f(x)称为被插值函数,x0,x1,……xn 称为插值结(节)点,Φ(C0,C1,……C n)称为插值函数类,上面等式称为插值条件,Φ(C0,……C n)中满足上式的函数称为插值函数,R(x)=f(x)-P(x)称为插值余项。
求解这类问题,它有很多种插值法,其中以拉格朗日(Lagrange)插值和牛顿(Newton)插值为代表的多项式插值最有特点,常用的插值还有Hermit 插值,分段插值和样条插值。 一.拉格朗日插值 1.问题提出: 已知函数()y f x =在n+1个点01,,,n x x x L 上的函数值01,,,n y y y L ,求任意一点 x '的函数值()f x '。 说明:函数()y f x =可能是未知的;也可能是已知的,但它比较复杂,很难计算其函数值()f x '。 2.解决方法: 构造一个n 次代数多项式函数()n P x 来替代未知(或复杂)函数()y f x =,则 用()n P x '作为函数值()f x '的近似值。 设()2012n n n P x a a x a x a x =++++L ,构造()n P x 即是确定n+1个多项式的系数 012,,,,n a a a a L 。 3.构造()n P x 的依据: 当多项式函数()n P x 也同时过已知的n+1个点时,我们可以认为多项式函数 ()n P x 逼近于原来的函数()f x 。根据这个条件,可以写出非齐次线性方程组: 20102000 20112111 2012n n n n n n n n n n a a x a x a x y a a x a x a x y a a x a x a x y ?++++=?++++=?? ? ?++++=?L L L L L 其系数矩阵的行列式D 为范德萌行列式: ()20 0021110 2111n n i j n i j n n n n x x x x x x D x x x x x ≥>≥= = -∏L L M M M M L
数值分析 报告 班级: 专业: 流水号: 学号: 姓名:
常用的插值方法 序言 在离散数据的基础上补插连续函数,使得这条连续曲线通过全部给定的离散数据点。插值是离散函数逼近的重要方法,利用它可通过函数在有限个点处的取值状况,估算出函数在其他点处的近似值。 早在6世纪,中国的刘焯已将等距二次插值用于天文计算。17世纪之后,牛顿、拉格朗日分别讨论了等距和非等距的一般插值公式。在近代,插值法仍然是数据处理和编制函数表的常用工具,又是数值积分、数值微分、非线性方程求根和微分方程数值解法的重要基础,许多求解计算公式都是以插值为基础导出的。 插值问题的提法是:假定区间[a,b〕上的实值函数f(x)在该区间上 n+1 个互不相同点x 0,x 1 (x) n 处的值是f(x ),……f(x n ),要求估算f(x)在[a,b〕 中某点的值。其做法是:在事先选定的一个由简单函数构成的有n+1个参数C , C 1,……C n 的函数类Φ(C ,C 1 ,……C n )中求出满足条件P(x i )=f(x i )(i=0,1,…… n)的函数P(x),并以P(x)作为f(x)的估值。此处f(x)称为被插值函数,x 0,x 1 ,……xn 称为插值结(节)点,Φ(C 0,C 1 ,……C n )称为插值函数类,上面等式称为插值条件, Φ(C 0,……C n )中满足上式的函数称为插值函数,R(x)= f(x)-P(x)称为 插值余项。
求解这类问题,它有很多种插值法,其中以拉格朗日(Lagrange)插值和牛顿(Newton)插值为代表的多项式插值最有特点,常用的插值还有Hermit 插值,分段插值和样条插值。 一.拉格朗日插值 1.问题提出: 已知函数()y f x =在n+1个点01,, ,n x x x 上的函数值01,, ,n y y y ,求任意一点 x '的函数值()f x '。 说明:函数()y f x =可能是未知的;也可能是已知的,但它比较复杂,很难计算其函数值()f x '。 2.解决方法: 构造一个n 次代数多项式函数()n P x 来替代未知(或复杂)函数()y f x =,则 用()n P x '作为函数值()f x '的近似值。 设()2012n n n P x a a x a x a x =+++ +,构造()n P x 即是确定n+1个多项式的系数 012,,,,n a a a a 。 3.构造()n P x 的依据: 当多项式函数()n P x 也同时过已知的n+1个点时,我们可以认为多项式函数 ()n P x 逼近于原来的函数()f x 。根据这个条件,可以写出非齐次线性方程组: 20102000 201121112012n n n n n n n n n n a a x a x a x y a a x a x a x y a a x a x a x y ?+++ +=?++++=??? ?+++ +=? 其系数矩阵的行列式D 为范德萌行列式: () 200021110 2 111n n i j n i j n n n n x x x x x x D x x x x x ≥>≥= = -∏
第一章绪论(1-4) 一、误差来源及分类 二、误差的基本概念 1.绝对误差及绝对误差限 2.相对误差及相对误差限 3.有效数字 三、数值计算的误差估计 1.函数值的误差估计 2.四则运算的误差估计 四、数值计算的误差分析原则 第二章插值(1.2.4-8) 一、插值问题的提法(定义)、插值条件、插值多项式的存在唯一性 二、拉格朗日插值 1.拉格朗日插值基函数的定义、性质 2.用拉格朗日基函数求拉格朗日多项式 3.拉格朗日插值余项(误差估计) 三、牛顿插值 1.插商的定义、性质 2.插商表的计算 3.学会用插商求牛顿插值多项式 四、等距节点的牛顿插值 1.差分定义、性质及计算(向前、向后和中心) 2.学会用差分求等距节点下的牛顿插值公式 五、学会求低次的hermite插值多项式 六、分段插值 1.分段线性插值 2.分段三次hermite插值 3.样条插值 第三章函数逼近与计算(1-6) 一、函数逼近与计算的提法(定义)、常用两种度量标准(一范数、二范数\平方逼近) 二、基本概念 连续函数空间、最佳一次逼近、最佳平方逼近、内积、内积空间、偏差与最小偏差、偏差点、交错点值、平方误差 三、学会用chebyshev定理求一次最佳一致逼近多项式,并估计误差(最大偏差) 四、学会在给定子空间上通过解方程组求最佳平方逼近,并估计误差(平方误差) 五、正交多项式(两种)定义、性质,并学会用chebyshev多项式性质求特殊函数的(降阶)最佳一次逼近多项式 六、函数按正交多项式展开求最佳平方逼近多项式,并估计误差 七、一般最小二乘法(多项式拟合)求线性拟合问题 第四章数值分析(1-4) 一、数值求积的基本思想及其机械求积公式
第二章插值法 2.在区间[-1,1]上分别取n=10,20用两组等距节点对龙哥函数f(x)=1/(1+25*x^2)做多项式插值及三次样条插值,对每个n值,分别画出插值函数及f(x)的图形。 (1)多项式插值 ①先建立一个多项式插值的M-file; 输入如下的命令(如牛顿插值公式): function [C,D]=newpoly(X,Y) n=length(X); D=zeros(n,n) D(:,1)=Y' for j=2:n for k=j:n D(k,j)=(D(k,j-1)- D(k-1,j-1))/(X(k)-X(k-j+1)); end end C=D(n,n); for k=(n-1):-1:1 C=conv(C,poly(X(k))) m=length(C); C(m)= C(m)+D(k,k); end ②当n=10时,我们在命令窗口中输入以下的命令: clear,clf,hold on; X=-1:0.2:1; Y=1./(1+25*X.^2); [C,D]=newpoly(X,Y); x=-1:0.01:1; y=polyval(C,x); plot(x,y,X,Y,'.'); grid on; xp=-1:0.2:1; z=1./(1+25*xp.^2); plot(xp,z,'r') 得到插值函数和f(x)图形:
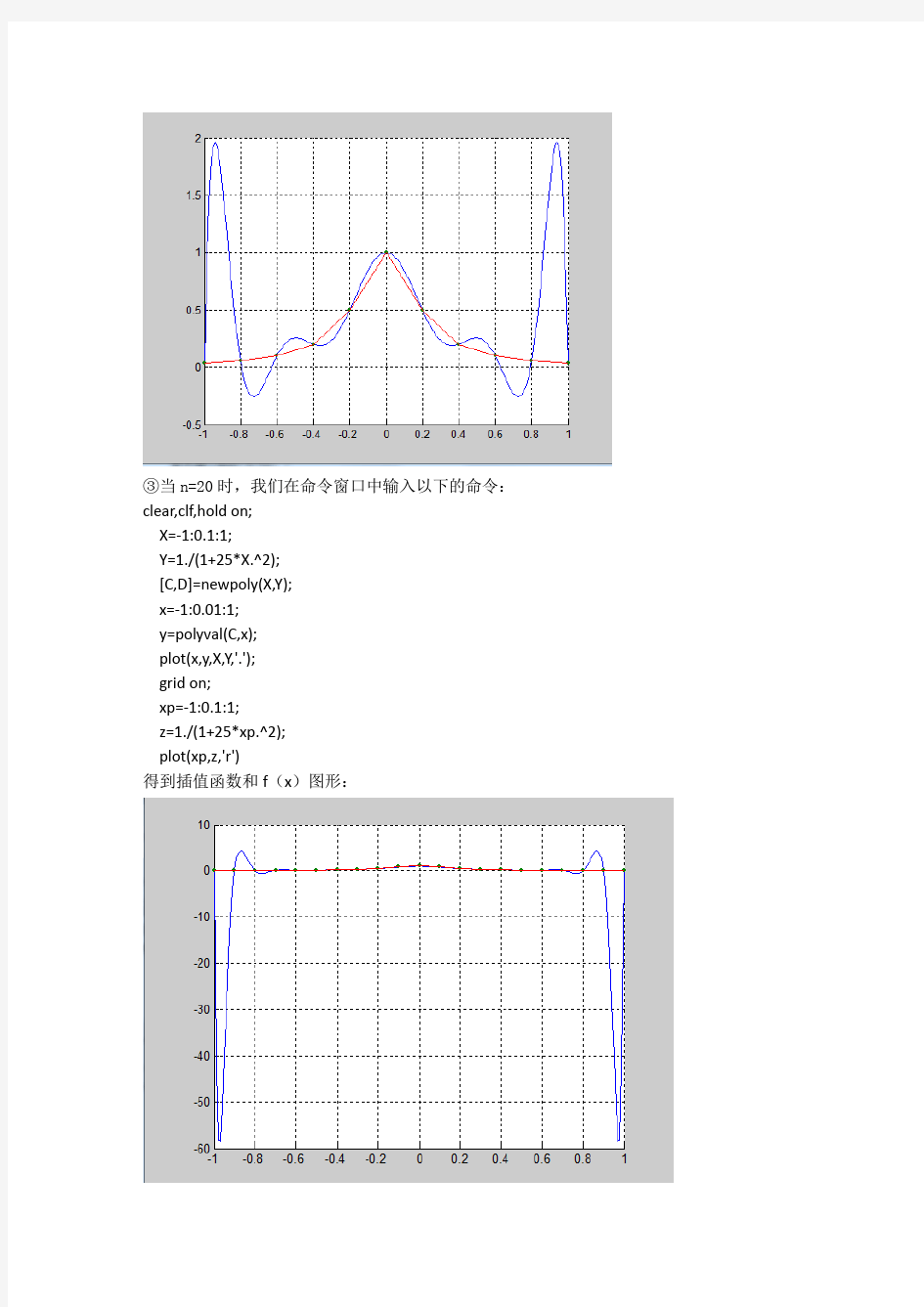
③当n=20时,我们在命令窗口中输入以下的命令:clear,clf,hold on; X=-1:0.1:1; Y=1./(1+25*X.^2); [C,D]=newpoly(X,Y); x=-1:0.01:1; y=polyval(C,x); plot(x,y,X,Y,'.'); grid on; xp=-1:0.1:1; z=1./(1+25*xp.^2); plot(xp,z,'r') 得到插值函数和f(x)图形:
第二章复习与思考题 1.什么是拉格朗日插值基函数它们是如何构造的有何重要性质 答:若n 次多项式()),,1,0(n j x l j Λ=在1+n 个节点n x x x <<<Λ10上满足条件 (),,,1,0,, ,0, ,1n k j j k j k x l k j Λ=?? ?≠== 则称这1+n 个n 次多项式()()()x l x l x l n ,,,10Λ为节点n x x x ,,,10Λ上的n 次拉格朗日插值基函数. 以()x l k 为例,由()x l k 所满足的条件以及()x l k 为n 次多项式,可设 ()()()()()n k k k x x x x x x x x A x l ----=+-ΛΛ110, 其中A 为常数,利用()1=k k x l 得 ()()()()n k k k k k k x x x x x x x x A ----=+-ΛΛ1101, 故 ()()()() n k k k k k k x x x x x x x x A ----= +-ΛΛ1101 , 即 ()()()()()()()()∏ ≠=+-+---=--------=n k j j j k j n k k k k k k n k k k x x x x x x x x x x x x x x x x x x x x x l 0110110)(ΛΛΛΛ. 对于()),,1,0(n i x l i Λ=,有 ()n k x x l x n i k i k i ,,1,00 Λ==∑=,特别当0=k 时,有 ()∑==n i i x l 0 1. 2.什么是牛顿基函数它与单项式基{ }n x x ,,,1Λ有何不同 答:称()()()(){ }10100,,,,1------n x x x x x x x x x x ΛΛ为节点n x x x ,,,10Λ上的牛顿基函数,利用牛顿基函数,节点n x x x ,,,10Λ上的n 次牛顿插值多项式()x P n 可以表示为 ()()()()10010---++-+=n n n x x x x a x x a a x P ΛΛ 其中[]n k x x x f a k k ,,1,0,,,,10ΛΛ==.与拉格朗日插值多项式不同,牛顿插值基函数在增加节点时可以通过递推逐步得到高次的插值多项式,例如 ()()()()k k k k x x x x a x P x P --+=++Λ011,
第二章 习 题 1. 已知函数()f x 在3,1,4x =的值分别为4,2,5,求Lagrange 插值多项式的表达式. 2. 已知函数 ()f x 在3x =和 4的值分别为0.5和0.64,用线性插值求此函数在 3.8x =的函数值. 3. 证明:对于 ()f x 的以01x x <为节点的一次插值多项式1()p x ,有 2 101()()()8 x x f x p x M ??≤,01x x x ≤≤, 其中01 max ()x x x M f x ≤≤′′= . 4. 已知函数 ()f x 的函数值表: x 0.1 0.2 0.3 0.4 0.5 ()f x 0.70010 0.40160 0.10810 -0.17440 -0.43750 试利用这个函数表求函数()f x 在0.3和0.4之间的零点. 5. 设 01,,,n x x x ???为1n +个互异的节点,()k l x 为n 阶 Lagrange 插值基函数, 0()()n k k x x x ω==?∏.证明: (1) 0()1n k k l x =≡∑; (2) 0(),0,1,2,,k n j j k k x l x x j n =≡=???∑; (3) ()()0,0,1,2,,n j k k k x x l x j n =?≡=???∑; (4)() ()()() k k k x l x x x x ωω= ′?.
6. 若73()1f x x x =?+,求0172,2,,2f ???????和018 2,2,,2f ???????. 7. 设 53()1f x x x =++,求以1x =?,-0.8,0,0.5,1为插值节点的Newton 插值多 项式和插值余项. 8. 已知函数值表: x 0 1 4 3 6 ()f x -7 8 5 14 求Newton 插值多项式的表达式. 9. 分别在下列情况下计算 1n ?次多项式()p t 在指定点t 的的值,各需要多少次乘 法运 算? (a)多项式()p t 按照单项式基函数展开; (b)多项式()p t 按照Lagrange 基函数展开; (c)多项式()p t 按照Newton 基函数展开. 10. 在区间[]0,/2π上使用5个等距节点对函数sin t 进行插值,试计算最大误差. 在 []0,/2π上选取若干点,比较函数值和插值多项式的值,验证误差界. 如果希望最大误 差为10 10 ?,需要多少个插值节点? 11. 一直平面曲线()y f x =过点(0,1) ,(1,3),(2,4),试求一个三次多项式3()p x ,使其经过这3个点,并且满足3(1)1p ′=;然后给出余项3()()()R x f x p x =?的表达式. 12. 试求一个四次多项式4()p x ,使其满足44 44(0)(0)0(1)(1)1p p p p ′′====,,4(2)1p =. 13. 能否通过使用分段二次多项式进行插值,使插值函数是二次连续可微的?为什么? 14. 设[]4 (),f x C a b ∈. 求三次多项式()p x ,使之满足插值条件 11 ()(),0,1,2, ()(),i i p x f x i p x f x ==?? ′′=?
《数值分析》课程实验一:插值与拟合 一、实验目的 1. 理解插值的基本原理,掌握多项式插值的概念、存在唯一性; 2. 编写MATLAB 程序实现Lagrange 插值和Newton 插值,验证Runge 现象; 3. 通过比较不同次数的多项式拟合效果,理解多项式拟合的基本原理; 4. 编写MATLAB 程序实现最小二乘多项式曲线拟合。 二、实验内容 1. 用Lagrange 插值和Newton 插值找经过点(-3, -1), (0, 2), (3, -2), (6, 10)的三次插值公式,并编写MATLAB 程序绘制出三次插值公式的图形。 2. 设 ]5,5[,11 )(2 -∈+= x x x f 如果用等距节点x i = -5 + 10i /n (i = 0, 1, 2, …, n )上的Lagrange 插值多项式L n (x )去逼近它。不妨取n = 5和n = 10,编写MATLAB 程序绘制出L 5(x )和L 10(x )的图像。 3. 在某冶炼过程中,根据统计数据的含碳量与时间关系如下表,试求含碳量与时间t 的拟合曲线。
(1) 用最小二乘法进行曲线拟合; (2) 编写MATLAB 程序绘制出曲线拟合图。 三、实验步骤 1. (1) Lagrange 插值法:在线性空间P n 中找到满足条件: ?? ?≠===j i j i x l ij j i , 0,, 1)(δ 的一组基函数{}n i i x l 0)(=,l i (x )的表达式为 ∏ ≠==--= n i j j j i j i n i x x x x x l ,0),,1,0()( 有了基函数{}n i i x l 0)(=,n 次插值多项式就可表示为 ∑==n i i i n x l y x L 0)()( (2) Newton 插值法:设x 0, x 1, …, x n 是一组互异的节点,y i = f (x i ) (i = 0, 1, 2, …, n ),f (x )在处的n 阶差商定义为 1102110] ,,,[],,,[],,,[x x x x x f x x x f x x x f n n n n --= - 则n 次多项式 ) ())(](,,[) )(](,,[)](,[)()(11010102100100----++--+-+=n n n x x x x x x x x x f x x x x x x x f x x x x f x f x N 差商表的构造过程:
数值分析作业 第二章 1、用Gauss消元法求解下列方程组: 2x 1-x 2 +3x 3 =1, (1) 4x 1+2x 2 +5x 3 =4, x 1+2x 2 =7; (2) 解: A=[2 -1 3 1;4 2 5 4;1 2 0 7] n=size(A,1);x=zeros(n,1);flag=1; % 消元过程 for k=1:n-1 for i=k+1:n if abs(A(k,k))>eps A(i,k+1:n+1)= A(i,k+1:n+1)-A(k,k+1:n+1)*A(i,k)/A(k,k); else flag=0; return end end end % 回代过程 if abs(A(n,n))>eps x(n)=A(n,n+1)/A(n,n); else flag=0; return end for i=n-1:-1:1 x(i)=(A(i,n+1)-A(i,i+1:n)*x(i+1:n))/A(i,i); end return x A = 2 -1 3 1 4 2 5 4 1 2 0 7
x = 9 -1 -6 11x1-3x2-2x3=3, (2)-23x 1+11x 2 +1x 3 =0, x 1+2x 2 +2x 3 =-1; (2) 解: A=[11 -3 -2 3;-23 11 1 0;1 2 2 -1] n=size(A,1);x=zeros(n,1);flag=1; % 消元过程 for k=1:n-1 for i=k+1:n if abs(A(k,k))>eps A(i,k+1:n+1)= A(i,k+1:n+1)-A(k,k+1:n+1)*A(i,k)/A(k,k); else flag=0; return end end end % 回代过程 if abs(A(n,n))>eps x(n)=A(n,n+1)/A(n,n); else flag=0; return end for i=n-1:-1:1 x(i)=(A(i,n+1)-A(i,i+1:n)*x(i+1:n))/A(i,i); end return x A = 11 -3 -2 3 -23 11 1 0 1 2 2 -1 x = 0.2124 0.5492 -1.1554 4、用Cholesky分解法解方程组 3 2 3 x1 5 2 2 0 x2 3 3 0 12 x3 7
数值分析--第2章插值法
第2章 插值法 在科学研究与工程技术中,常常遇到这样的问题:由实验或测量得到一批离散样点,要求作出一条通过这些点的光滑曲线,以便满足设计要求或进行加工。反映在数学上,即已知函数在一些点上的值,寻求它的分析表达式。此外,一些函数虽有表达式,但因式子复杂,不易计算其值和进行理论分析,也需要构造一个简单函数来近似它。 解决这种问题的方法有两类:一类是给出函数)(x f 的一些样点,选定一个便于计算的函数)(x ?形式,如多项式、分式线性函数及三角多项式等,要求它通过已知样点,由此确定函数)(x ?作为)(x f 的近似,这就是插值法;另一类方法在选定近似函数的形式后,不要求近似函数过已知样点,只要求在某种意义下在这些样点上的总偏差最小。这类方法称为曲线(数据)拟合法。 设已知函数f 在区间],[b a 上的1+n 个相异点i x 处的函数值(),0,,i i f f x i n ==,要求构造一个简单函数()x ?作为函数()f x 的近似表达式()()f x x ?≈,使得 ()(),0,1,,i i i x f x f i n ?=== (2-1) 这类问题称为插值问题。称f 为被插值函数;()x ?为插值函数;n x x ,,0 为插值节点;(2-1)为插值条件。 若插值函数类{()}x ?是代数多项式,则相应的插值问题为代数插值。若{()}x ?是三角多项式,则相应的插值问题称为三角插值。若{()}x ?是有理分式,则相应的插值问题称为有理插值。
§1 Lagrange 插值 1.1 Lagrange 插值多项式 设函数f 在1+n 个相异点0 1 ,,,n x x x 上的值n i x f f i i ,,1,0),( ==是已知的,在次数不超过n 的多项式集合n P 中,求()n L x 使得 (),0,1,,n i i L x f n n == (2-2) 定理2.1 存在惟一的多项式n n P L ∈满足插值条件(2-2)。 证明 我们采用构造性的证明方法。假如我们能够构造出n 次多项式()i l x ,使得 1,(),0,1,,0,i j ij i j l x i j n i j δ=?===?≠? , (2-3) 那么 ∑==n i i i n x l f x L 0) ()( (2-4) 是满足插值条件(2-2)的插值多项式。 余下的问题就是如何构造出满足式(2-3)的n 次多项式(),0,1,,i l x i n =。由于当j i ≠时,()0,0,1,,i j l x i j n ==,,即111,,,,,i i n x x x x -+是()i l x 的零点,因此()i l x 必然具有形式 ∏≠=+--=----=n i j j j i n i i i i x x c x x x x x x x x c x l 0110)()())(()()( 又因1)(=i i x l ,故∏≠=-=n i j j j i i x x c 0)(,因此 ∏ ∏∏≠=≠=≠=--=--= n i j j j i j n i j j j i n i j j j i x x x x x x x x x l 000) () () () ()( (2-5)
第二章 习题 1. 当x=1,-1,2时,f(3)=0,-3,4,求f(x)的二次插值多项式。 解:利用二次Lagrange 插值多项式公式, 这里403311210210==-=-==-=y y y x x x ,,,,,,得 ()()()() ()()()()()() ()() ()() 3 723651 34 23211212114021112132222211002-+=-++--=-+-+?++------? -=++=x x x x x x x x x x l y x l y x l y x L 2. 给出()()x x f ln =的数值表,(见表2.1),用线性插值及二次插值计算ln0.54的近似值。 表2.1 解:选取54.06.05.010===x x x ,,代入Lagrange 线性插值多项式,得 ()()()620219 .0510826.05 .06.05.054.0693147 .060.050.060 .054.054.054.0ln 1-≈-?--+-?--= ≈L 又选取54.06.05.04.0210====x x x x ,,,代入Lagrange 二次插值多项式,得 ()()()615320 .0)510826.0() 5.06.0)(4.06.0() 5.054.0)(4.054.0(693147 .0)6.05.0)(4.05.0() 6.054.0)(4.054.0(916291 .0)6.04.0)(5.04.0() 6.054.0)(5.054.0(54.054.0ln 2-≈-?----+-?----+-?----= ≈L 3. 设()x l k kh x x x x x k 203 0max 10≤≤=+=,求, ,,2,3。 解:由题意知 ()()()() ()()() 3212023102x x x x x x x x x x x x x l ------= 令()0'2=x l ,得 ()0383632 02 002 =++++-h h x x x h x x ,
4.1 设(0.4)0.38942,(0.5)0.47943,(0.6)0.56464f f f ===,使用一次、二次 Lagrange 插值多项式计算(0.5789)f 的近似值. 解:(0.4)0.38942,(0.5)0.47943,(0.6)0.56464f f f === 一次Lagrange 插值多项式公式 05338.08521.06 .05.06 .0)5.0(5.06.05.0) 6.0()(1+=--+--=x x f x f x P 故 546669.005338.057891.08521.0)57891 .0(1≈+?=P . 二次Lagrange 插值多项式公式: ) 5.04.0)( 6.04.0() 5.0)( 6.0() 4.0()4.0 5.0)( 6.05.0()4.0)(6.0()5.0()4.06.0)(5.06.0()4.0)(5.0() 6.0()(2----+----+----=x x f x x f x x f x P 即 01862.01161.124.0)(22-+-=x x x P 故 5470686 .001862.057891.01161.157891.024.0)57891.0(2 2=-?+?-=P 4.2 设01(),(), ,()n l x l x l x 是以为节点的01,,,n x x x 的n 次Lagrange 插值基函数,试 证明; (),0,1, ,n j j k k k x l x x j n ===∑ 证:假设在对应于01,,,n x x x 节点的函数值为,...)1,0(=i y i ,则应有: ),...,1,0()()(1 n i x l y x P n i i i ==∑= 取n j x y j i i ,...,1,0,==,由插值条件有: j i i j x y x P ==)( 故0 ()n j j i i i i x x l x ==∑,即0 ()n j j k k i x x l x ==∑