
实验二线性规划模型及灵敏度分析(一)实验目的:掌握使用Excel软件进行灵敏度分析的操作方法。
(二)实验内容和要求:用Excel软件完成案例。
(三)实例操作:
(1)建立电子表格模型;
(2)使用Excel规划求解功能求解问题并生成“敏感性报告”;
(3)结果分析:哪些问题可以直接利用“敏感性报告”中的信息求解,哪些问题需要重新规划求解,并对结果提出你的看法;
(4)在Word文档中书写实验报告,包括线性规划模型、电子表格模型、敏感性报告和结果分析等。
案例1 市场调查问题
某市场调查公司受某厂的委托,调查消费者对某种新产品的了解和反应情况。该厂对市场调查公司提出了以下要求:
(1)共对500个家庭进行调查;
(2)在被调查家庭中,至少有200个是没有孩子的家庭,同时至少有200个是有孩子的家庭;
(3)至少对300个被调查家庭采用问卷式书面调查,对其余家庭可采用口头调查;
(4)在有孩子的被调查家庭中,至少对50%的家庭采用问卷式书面调查;
(5)在没有孩子的被调查家庭中,至少对60%的家庭采用问卷式书面调查。
对不同家庭采用不同调查方式的费用如下表所示:
市场调查费用表
家庭类型调查费用(元)
问卷式书面调查口头调查
有孩子的家庭50 30
没有孩子的家庭40 25
问:市场调查公司应如何进行调查,使得在满足厂方要求的条件下,使得总调查费用最少?
案例2 经理会议建议的分析
某公司生产三种产品A1,A2,A3,它们在B1,B2两种设备上加工,并耗用C1,C2两种原材料,已知生产单位产品耗用的工时和原材料以及设备和原材料的每天最多可使用量
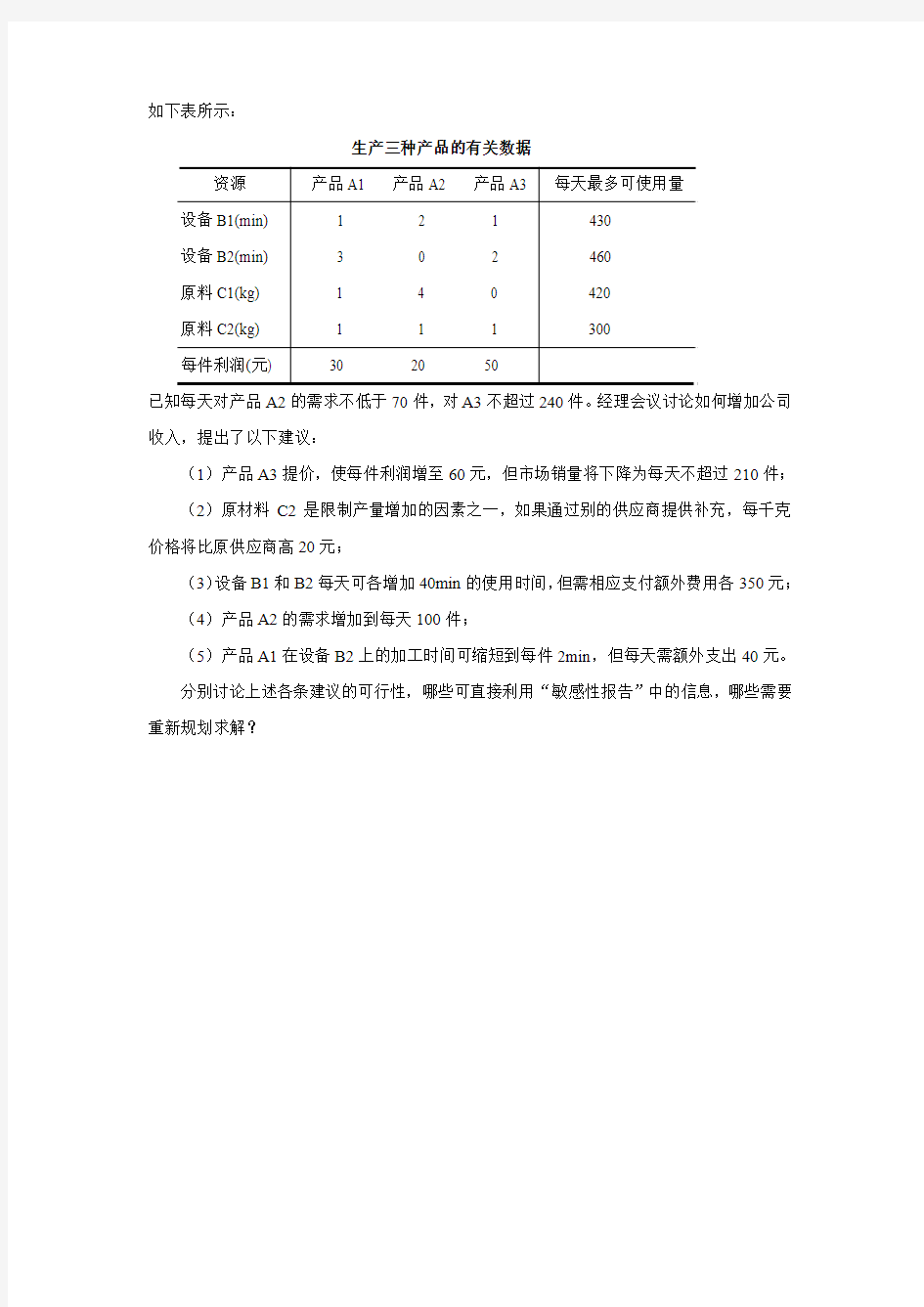
如下表所示:
生产三种产品的有关数据
资源产品A1 产品A2 产品A3 每天最多可使用量设备B1(min) 1 2 1 430
设备B2(min) 3 0 2 460
原料C1(kg) 1 4 0 420
原料C2(kg) 1 1 1 300
每件利润(元) 30 20 50
已知每天对产品A2的需求不低于70件,对A3不超过240件。经理会议讨论如何增加公司收入,提出了以下建议:
(1)产品A3提价,使每件利润增至60元,但市场销量将下降为每天不超过210件;
(2)原材料C2是限制产量增加的因素之一,如果通过别的供应商提供补充,每千克价格将比原供应商高20元;
(3)设备B1和B2每天可各增加40min的使用时间,但需相应支付额外费用各350元;
(4)产品A2的需求增加到每天100件;
(5)产品A1在设备B2上的加工时间可缩短到每件2min,但每天需额外支出40元。
分别讨论上述各条建议的可行性,哪些可直接利用“敏感性报告”中的信息,哪些需要重新规划求解?
一个实例理解Lingo的灵敏性分析 线性规划问题的三个重要概念: 最优解就是反应取得最优值的决策变量所对应的向量。 最优基就是最优单纯形表的基本变量所对应的系数矩阵如果其行列式是非奇异的,则该系数矩阵为最优基。 最优值就是最优的目标函数值。 Lingo的灵敏性分析是研究当目标函数的系数和约束右端项在什么范围(此时假定其它系数不变)时,最优基保持不变。灵敏性分析给出的只是最优基保持不变的充分条件,而不一定是必要条件。下面是一道典型的例题。 一奶制品加工厂用牛奶生产A1,A2两种奶制品,1桶牛奶可以在甲车间用12小时加工成3公斤A1,或者在乙车间用8小时加工成4公斤A2。根据市场需求,生产的A1,A2全部能售出,且每公斤A1获利24元,每公斤A2获利16元。现在加工厂每天能得到50桶牛奶的供应,每天正式工人总的劳动时间480小时,并且甲车间每天至多能加工100公斤A1,乙车间的加工能力没有限制。试为该厂制订一个生产计划,使每天获利最大,并进一步讨论以下3个附加问题: 1)若用35元可以买到1桶牛奶,应否作这项投资?若投资,每天最多购买多少桶牛奶?2)若可以聘用临时工人以增加劳动时间,付给临时工人的工资最多是每小时几元? 3)由于市场需求变化,每公斤A1的获利增加到30元,应否改变生产计划? 模型代码: max=72*x1+64*x2; x1+x2<=50; 12*x1+8*x2<=480; 3*x1<=100; 运行求解结果: Objective value: 3360.000 Variable Value Reduced Cost X1 20.00000 0.000000 X2 30.00000 0.000000 Row Slack or Surplus Dual Price 1 3360.000 1.000000 2 0.000000 48.00000 3 0.000000 2.000000 4 40.00000 0.000000 这个线性规划的最优解为x1=20,x2=30,最优值为z=3360,即用20桶牛奶生产A1, 30桶牛奶生产A2,可获最大利润3360元。输出中除了告诉我们问题的最优解和最优值以外,还有许多对分析结果有用的信息。 其中,“Reduced Cost”列出最优单纯形表中判别数所在行的变量的系数,表示当变量有微小变动时, 目标函数的变化率。其中基变量的reduced cost值应为0,对于非基变量Xj, 相应的reduced cost值表示当某个变量Xj 增加一个单位时目标函数减少的量( max型问题)。本例中X1,X2均为基变量。 “Slack or Surplus”给出松驰变量的值,模型第一行表示目标函数,所以第二行对应第一个约束。3个约束条件的右端不妨看作3种“资源”:原料、劳动时间、车间甲的加工能力。输出中Slack or Surplus给出这3种资源在最优解下是否有剩余:原料、劳动时间的剩余均为
题目 如何利用EXC E L求解线性规划 问题及其灵敏度分析 第 8 组 姓名学号 乐俊松 090960125 孙然 090960122 徐正超 090960121 崔凯 090960120王炜垚 090960118 蔡淼 090960117南京航空航天大学(贸易经济)系 2011年(5)月(3)日
摘要 线性规划是运筹学的重要组成部分,在工业、军事、经济计划等领域有着广泛的应用,但其手工求解方法的计算步骤繁琐复杂。本文以实际生产计划投资组合最优化问题为例详细介绍了Excel软件的”规划求解”和“solvertable”功能辅助求解线性规划模型的具体步骤,并对其进行了灵敏度分析。
目录 引言 (4) 软件的使用步骤 (4) 结果分析 (9) 结论与展望 (10) 参考文献 (11)
1. 引言 对于整个运筹学来说,线性规划(Linear Programming)是形成最早、最成熟的一个分支,是优化理论最基础的部分,也是运筹学最核心的内容之一。它是应用分析、量化的方法,在一定的约束条件下,对管理系统中的有限资源进行统筹规划,为决策者提供最优方案,以便产生最大的经济和社会效益。因此,将线性规划方法用于企业的产、销、研等过程成为了现代科学管理的重要手段之一。[1] Excel中的线性规划求解和solvertable功能并不作为命令直接显示在菜单中,因此,使用前需首先加载该模块。具体操作过程为:在Excel的菜单栏中选择“工具/加载宏”,然后在弹出的对话框中选择“规划求解”和“solvertable”,并用鼠标左键单击“确定”。加载成功后,在菜单栏中选择“工具/规划求解”,便会弹出“规划求解参数”对话框。在开始求解之前,需先在对话框中设置好各种参数,包括目标单元格、问题类型(求最大值还是最小值)、可变单元格以及约束条件等。 2 软件的使用步骤 “规划求解”可以解决数学、财务、金融、经济、统计等诸多实 际问题,在此我们只举一个简单的应用实例,说明其具体的操作 方法。 某人有一笔资金可用于长期投资,可供选择的投资机会包括购买国库券、公司债券、投资房地产、购买股票或银行保值储蓄等。投资者希望投资组合的平均年限不超过5年,平均的期望收益率不低于13%,风险系数不超过4,收益的增长潜力不低于10%。问在满足上述要求的前提下投资者该如何选择投资组合使平均年收益率最高?(不同的投资方式的具体参数如下表。)
线性规划问题及灵敏度分析在LINGO软件中的实现 (龙少波李东阳罗添元) 一、问题的提出: 某公司饲养实验用的动物以出售给动物研究所,已知这些动物的生长对饲 料中3种营养成分(蛋白质、矿物质和维生素)特别敏感,每个动物每周至少需 要蛋白质60g,矿物质3g,维生素8mg,该公司能买到5种不同的饲料,每种饲 料1kg所含各种营养成分和成本如下表所示,如果每个小动物每周食用饲料不超 过52kg,才能满足动物生长需要。 A1 A2 A3 A4 A5 营养最 低 要求蛋白质(g) 0.3 2 1 0.6 1.8 60 矿物质(g) 0.1 0.05 0.02 0.2 0.05 3 维生素(mg) 0.05 0.1 0.02 0.2 0.08 8 成本(元/ kg)0.2 0.7 0.4 0.3 0.5 问题: 1.求使得总成本最低的饲料配方? 2.如果另一个动物研究对蛋白质的营养要求变为59单位, 但是要求动物的价格比现在的价格便宜0.3元,问该养殖所 值不值得接受? 3.由于市场因素的影响,X2的价格降为0.6元每千克, 问是否要改变饲料配方? 二、建立线性规划数学模型 解答: (1)设需要饲料A1, A2, A3, A4分别为X1, X2, X3, X4kg,则建立线 性规划数学模型如下: 目标函数:MinS=0.2X1+0.7X2+0.4X3+0.3X4+0.5X5 约束条件:0.3X1+2X2+X3+0.6X4+1.8X5>=60 0.1X1+0.05X2+0.02X3+0.2X4+0.05X5>=3 005X1+0.1X2+0.02X3+0.2X4+0.08X5>=8
淮北师范大学 2011届学士学位论文 线性规划灵敏度分析 学院、专业数学科学学院数学与应用数学 研究方向运筹学 学生姓名陈红 学号20071101008 指导教师姓名张发明 指导教师职称副教授 2011年4月10日
线性规划的灵敏度分析 陈 红 (淮北师范大学数学科学学院,淮北,235000) 摘 要 本文主要从价值系数j c 的变化,技术系数ij a 的变化,右端常数i b 的变化以及增加新的约束条件和增加一个新变量的灵敏度这几个方面来进行研究;资源条件是线性规划灵敏度分析中的主要应用内容,而对于资源条件b 的一个重要应用是:“影子价格问题”的实际应用,最后简述了线性规划在经济及管理问题上的典型应用和从求解例题的图解法揭示了最优解的一些重要特征。 关键词 单纯形法,灵敏度分析,最优解,资源条件,价值系数
Sensitivity Analysis of Linear Programming Chen Hong (School of Mathematical Science,Huaibei Normal University ,Huaibei,235000) Abstract This thesis is mainly from the variety of the cost coefficient …j c ?, the variety of technology coefficient …ij a ?, the variety of the resources condition…i b ?and increase the new restraint and new variable to analytical linear programming of sensitivity analysis.This thesis is mainly based on the simplex method and dual simplex method of linear programming to system analytical the influence of the variety upon the optical solution of the coefficient of the simplex table.Linear programming of sensitivity analysis in physically of application is mainly about application of the variety of resources c ondition…i b ?in the economic management …shadow price problem?. Keywords simplex method, sensitivity analysis, optimum solution , resources condition ,cost coefficient
实验三灵敏度分析的应用 「、实验目的 (1) 掌握数学建模和用软件求解数学模型。 (2) 掌握在软件上分析问题和改进数学模型的方法。二、实验内容 1、(工作安排问题)人员在时段开始上班,连续工作8小时问该公交线路至少需要多少人。 问:要求在第5,6时段不能有多余人员上班,如何排班
在第i时段开始上班的人数为X i 。 模型: min Z 6 X i i 1 X6X160 ; X i X 70 ; X2X3 60 ; X3X4 50 ; X4X5 20 ; X5X6 30 ; X i0
min x1+x2+x3+x4+x5+x6 subject to x6+x1>60 x1+x2>70 x2+x3>60 x3+x4>50 x4+x5=20 x5+x6=30 end gin x1 gin x2 gin x3 gin x4 gin x5 gin x6 问:要求在第5,6时段不能有多余人员上班,如何排班。
保本点 盈亏平衡点又称零利润点、保本点、盈亏临界点、损益分歧点、收益转折点。通常是指全部销售收入等于全部成本时(销售收入线与总成本线的交点)的产量。 以盈亏平衡点的界限,当销售收入高于盈亏平衡点时企业盈利,反之,企业就亏损。盈亏平衡点可以用销售量来表示,即盈亏平衡点的销售量;也可以用销售额来表示,即盈亏平衡点的销售额。 单位售价-单位销售成本=单位毛利 可变成本=0时,保本点=每月固定成本/单位毛利(每月销售量)(不亏不赚) 可变成本0时, 估计的单位可变成本=每月可变成本/每月销售量 保本点=每月固定成本/ (单位毛利-估计的单位可变成本) 产品1销量50;每月固定成本=1000;计算保本点 产品利润贡献率的计算 对产品1的利润贡献率的计算:1,求解模型A的最优解X1,及最优解值Z1 2,增加约束X 0,得到模型B o 3,求解模型B的最优解X2,及最优解值Z24,设X1中分量X1的值为X*,贝V产品1的利润贡献率: Z1 Z2 * X 例如,(4280-3600) /20=34 2、(2)计算产品利润贡献率
线性规划练习题 1、用单纯形表求解以下线性规划问题 (1) max z= x1-2x2+x3 s.t. x1+x2+x3≤12 2x1+x2-x3≤ 6 -x1+3x2≤9 x1, x2, x3≥0 (2) min z= -2x1-x2+3x3-5x4 s.t x1+2x2+4x3-x4≤ 6 2x1+3x2-x3+x4≤12 x1+x3+x4≤ 4 x1, x2, x3, x4≥0 (3) min z= 3x1-x2 s.t. -x1-3x2≥-3 -2x1+3x2≥-6 2x1+x2≤8 4x1-x2≤16 x1, x2≥0 二、配料问题 某工厂要用四种合金T1,T2,T3和T4为原料,经熔炼成为一种新的不锈钢G。这四种原料含元素铬(Cr),锰(Mn)和镍(Ni)的含量(%),这四种原料的单价以及新的不锈钢材料G所要求的Cr,Mn和Ni的最低含量(%)如下表所示: 表错误!文档中没有指定样式的文字。-1 设熔炼时重量没有损耗,要熔炼成100公斤不锈钢G,应选用原料T1,T2,T3和T4各多少公斤,使成本最小。 灵敏度分析练习题 一、已知以下线性规划问题
max z= 2x1+x2-x3 s.t. x1+2x2+x3≤8 -x1+x2-2x3≤4 x1, x2, x3≥0 及其最优单纯形表如下: z x1 x6 (1)求使最优基保持不变的c2=1的变化范围。如果c2从1变成5,最优基是否变化,如果变化,求出新的最优基和最优解。 (2)对c1=2进行灵敏度分析,求出c1由2变为4时的最优基和最优解。 (3)对变量x3在第二个约束中的系数a23=-2进行灵敏度分析,求出a23从-2变为1时新的最优基和最优解。 (4)增加一个新的变量x6,它在目标函数中的系数c6=4,在约束条件中的系数向量为a6 1 2 = ? ? ? ? ? ?, 求新的最优基和最优解。 (5)增加一个新的约束x2+x3≥2,求新的最优基和最优解。 (6)设变量x1在约束条件中的系数向量由 1 1 - ? ? ? ? ? ?变为 -? ? ? ? ? ? 1 2 ,求出新的最优基和最优解。 二、某工厂用甲、乙、丙三种原料生产A、B、C、D四种产品,每种产品消耗原料定额以及三种原料 的数量如下表所示: (1)求使总利润最大的生产计划和按最优生产计划生产时三种原料的耗用量和剩余量。 (2)求四种产品的利润在什么范围内变化,最优生产计划不会变化。 (3)求三种原料的影子价格和四种产品的机会成本,并解释最优生产计划中有的产品不安排生产的原因。 (4)在最优生产计划下,哪一种原料更为紧缺?如果甲原料增加120吨,这时紧缺程度是否有变化?
lingo 软件求解线性规划及灵敏度分析 注:以目标函数最大化为例进行讨论,对求最小的问题,有类似的分析方法!所有程序运行环境为lingo10。 一、用lingo 软件求解线性规划 例1: m a x 23..4310 3512,0 z x y s t x y x y x y =++≤+≤≥ 在模型窗口输入: model: max=2*x+3*y; 4*x+3*y<=10; 3*x+5*y<12; ! the optimal value is :7.454545 ; End 如图所示: 运行结果如下(点击 工具栏上的‘solve ’或点击菜单‘lingo ’下的‘solve ’即可): Global optimal solution found. Objective value: 7.454545(最优解函数值) Infeasibilities: 0.000000 Total solver iterations: 2(迭代次数)
Variable (最优解) Value Reduced Cost X 1.272727 0.000000 Y 1.636364 0.000000 Row Slack or Surplus Dual Price 1 7.454545 1.000000 2 0.000000 0.9090909E-01 3 0.000000 0.5454545 例2: 12123124125m a x 54.. 390280450 z x x s t x x x x x x x x x x =+++=++=++=≥ 在模型窗口输入: model: max=5*x1+4*x2; x1+3*x2+x3=90; 2*x1+x2+x4=80; x1+x2+x5=45; end 运行(solve )结果如下: Global optimal solution found. Objective value: 215.0000 Infeasibilities: 0.000000 Total solver iterations: 3 Variable Value Reduced Cost X1 35.00000 0.000000 X2 10.00000 0.000000 X3 25.00000 0.000000 X4 0.000000 1.000000 X5 0.000000 3.000000 Row Slack or Surplus Dual Price 1 215.0000 1.000000 2 0.000000 0.000000 3 0.000000 1.000000 4 0.000000 3.000000 例3
线性规划模型的应用与灵敏度分析 第一章线性规划问题 1.线性规划简介及发展 线性规划(Linear Programming)是运筹学中研究最早、发展最快、应用广泛、方法成熟的一个重要分支,它是辅助人们进行科学管理的一种数学方法,研究线性约束条件下线性目标函数的极值问题的数学理论和方法,英文缩写为LP。它是运筹学的一个重要分支,广泛应用于军事作战、经济分析、经营管理和工程技术等方面,为合理利用有限的人力、物力、财力等资源做出的最优决策,提供科学的依据。 线性规划及其通用解法——单纯形法是由美国G.B.Dantzig在1947年研究空军军事规划提出来的。法国数学家傅里叶和瓦莱-普森分别于1832和1911年独立地提出线性规划的想法,但未引起注意。1939年苏联数学家康托罗维奇在《生产组织与计划中的数学方法》一书中提出线性规划问题,也未引起重视[1]。1947年美国数学家丹齐克提出线性规划的一般数学模型和求解线性规划问题的通用方法──单纯形法,为这门学科奠定了基础。1947年美国数学家诺伊曼提出对偶理论,开创了线性规划的许多新的研究领域,扩大了它的应用范围和解题能力[2]。1951年美国经济学家库普曼斯把线性规划应用到经济领域,为此与康托罗维奇一起获1975年诺贝尔经济学奖。50年代后对线性规划进行大量的理论研究,并涌现出一大批新的算法。例如,1954年莱姆基提出对偶单纯形法,1954年加斯和萨迪等人解决了线性规划的灵敏度分析和参数规划问题,1956年塔克提出互补松弛定理,1960年丹齐克和沃尔夫提出分解算法等。线性规划的研究成果还直接推动了其他数学规划问题包括整数规划、随机规划和非线性规划的算法研究[3]。由于数字电子计算机的发展,出现了许多线性规划软件,如MPSX,OPHEIE,UMPIRE等,可以很方便地求解几千个变量的线性规划问题。1979年苏联数学家提出解线性规划问题的椭球算法,并证明它是多项式时间算法。1984年美国贝尔电话实验室的印度数学家N.卡马卡提出解线性规划问题的新的多项式时间算法。用这种方法求解线性规划问题在变量个数为5000时只要单纯形法所用时间的1/50。现已形成线性规划多项式算法理论。50年代后线性规划的应用范围不断扩大。建立线性规
【2017年整理】lingo灵敏度分析实例一个实例理解Lingo的灵敏性分析 线性规划问题的三个重要概念: 最优解就是反应取得最优值的决策变量所对应的向量。 最优基就是最优单纯形表的基本变量所对应的系数矩阵如果其行列式是非奇异的,则该系数矩阵为最优基。 最优值就是最优的目标函数值。 Lingo的灵敏性分析是研究当目标函数的系数和约束右端项在什么范围(此时假定其它系数不变)时,最优基保持不变。灵敏性分析给出的只是最优基保持不变的充分条件,而不一定是必要条件。下面是一道典型的例题。 一奶制品加工厂用牛奶生产A1,A2两种奶制品,1桶牛奶可以在甲车间用12小时加工成3公斤A1,或者在乙车间用8小时加工成4公斤A2。根据市场需求,生产的A1,A2全部能售出,且每公斤A1获利24元,每公斤A2获利16元。现在加工厂每天能得到50桶牛奶的供应,每天正式工人总的劳动时间480小时,并且甲车间每天至多能加工100公斤A1,乙车间的加工能力没有限制。试为该厂制订一个生产计划,使每天获利最大,并进一步讨论以下3个附加问题: 1) 若用35元可以买到1桶牛奶,应否作这项投资,若投资,每天最多购买多少桶牛奶, 2) 若可以聘用临时工人以增加劳动时间,付给临时工人的工资最多是每小时几元, 3) 由于市场需求变化,每公斤A1的获利增加到30元,应否改变生产计划, 模型代码: max=72*x1+64*x2; x1+x2<=50; 12*x1+8*x2<=480;
3*x1<=100; 运行求解结果: Objective value: 3360.000 Variable Value Reduced Cost X1 20.00000 0.000000 X2 30.00000 0.000000 Row Slack or Surplus Dual Price 1 3360.000 1.000000 2 0.000000 48.00000 3 0.000000 2.000000 4 40.00000 0.000000 这个线性规划的最优解为x1=20,x2=30,最优值为z=3360,即用20桶牛奶生产A1, 30桶牛奶生产A2,可获最大利润3360元。输出中除了告诉我们问题的最优解和最优值以外,还有许多对分析结果有用的信息。 其中,“Reduced Cost”列出最优单纯形表中判别数所在行的变量的系数,表示当变量有微小变动时, 目标函数的变化率。其中基变量的reduced cost值应为0,对于非基变量 Xj, 相应的 reduced cost值表示当某个变量Xj 增加一个单位时目标函数减少的量( max型问题)。本例中X1,X2均为基变量。 “Slack or Surplus”给出松驰变量的值,模型第一行表示目标函数,所以第二行对应第一个约束。3个约束条件的右端不妨看作3种“资源”:原料、劳动时间、车间甲的加工能力。输出中Slack or Surplus给出这3种资源在最优解下是否有剩余:原料、劳动时间的剩余均为 零,车间甲尚余40(公斤)加工能力。
. . . .. . . . 2011——2012学年第二学期 合肥学院数理系 实验报告 课程名称:运筹学 实验项目:线性规划的灵敏度分析 实验类别:综合性□设计性□验证性□√ 专业班级: 09级数学与应用数学(1)班 姓名:王秀秀学号: 0907021006 实验地点: 9#503 实验时间: 2012-4-25 指导教师:管梅成绩:
一.实验目的 熟悉LINDO软件的灵敏度分析功能; 二.实验内容 1、求解线性规划 。 12 12 12 12 max z x2x 2x5x12 s.t.x2x8 x,x0 =+ +≥ ? ? +≤ ? ?≥ ? 并对价值系数、右端常量进行灵敏度分析 2、已知某工厂计划生产I,II,III三种产品,各产品需要在A、B、C设备上加工,有关数据如下: 试问答: (1)如何发挥生产能力,使生产盈利最大? (2)若为了增加产量,可租用别工厂设备B,每月可租用60台时,租金1.8万元,租用B设备是否合算?
(3)若另有二种新产品IV 、V ,其中新产品IV 需用设备A 为12台时、B 为5台时、C 为10台时,单位产品盈利2.1千元;新产品V 需用设备A 为4台时、B 为4台时、C 为12台时,单位产品盈利1.87千元。如A 、B 、C 的设备台时不增加,这两种新产品投产在经济上是否划算? (4)对产品工艺重新进行设计,改进结构。改进后生产每件产品I 需用设备A 为9台时、设备B 为12台时、设备C 为4台时,单位产品盈利4.5千元,这时对原计划有何影响? 三. 模型建立 1、数学模型为 12121212 max z x 2x 2x 5x 12 s.t.x 2x 8x ,x 0=++≥?? +≤??≥? 2、设分别生产I ,II ,III 三种产品1x ,2x ,3x 件, (1)数学模型为: 123122123123123 123max z 3x 2x 2.9x 8x 2x 10x 30010x 5x 8x 400s.t.2x 13x 10x 420x x x 0 x ,x x =++++≤?? ++≤?? ++≤??≥???,,,,为整数 (2)数学模型为: 123122123123123123max z 3x 2x 2.9x 188x 2x 10x 30010x 5x 8x 460s.t.2x 13x 10x 420x x x 0x ,x x =++-++≤?? ++≤?? ++≤??≥???,,,,为整数
实验二___线性规划灵敏度分析
实验二线性规划模型及灵敏度分析 (一)实验目的:掌握使用Excel软件进行灵敏度分析的操作方法。 (二)实验内容和要求:用Excel软件完成案例。 (三)实例操作: (1)建立电子表格模型; (2)使用Excel规划求解功能求解问题并生成“敏感性报告”; (3)结果分析:哪些问题可以直接利用“敏感性报告”中的信息求解,哪些问题需要重新规划求解,并对结果提出你的看法; (4)在Word文档中书写实验报告,包括线性规划模型、电子表格模型、敏感性报告和结果分析等。 案例1 市场调查问题 某市场调查公司受某厂的委托,调查消费者对某种新产品的了解和反应情况。该厂对市场调查公司提出了以下要求: (1)共对500个家庭进行调查;
(2)在被调查家庭中,至少有200个是没有孩子的家庭,同时至少有200个是有孩子的家庭; (3)至少对300个被调查家庭采用问卷式书面调查,对其余家庭可采用口头调查; (4)在有孩子的被调查家庭中,至少对50%的家庭采用问卷式书面调查; (5)在没有孩子的被调查家庭中,至少对60%的家庭采用问卷式书面调查。 对不同家庭采用不同调查方式的费用如下表所示: 市场调查费用表 家庭类型调查费用(元) 问卷式书面调查口头调查 有孩子的家庭50 30 没有孩子的家庭40 25 问:市场调查公司应如何进行调查,使得在
满足厂方要求的条件下,使得总调查费用最少? 案例2 经理会议建议的分析 某公司生产三种产品A1,A2,A3,它们在B1,B2两种设备上加工,并耗用C1,C2两种原材料,已知生产单位产品耗用的工时和原材料以及设备和原材料的每天最多可使用量如下表所示: 生产三种产品的有关数据 资源产品A1 产品A2 产品A3 每天最多可使用量 设备B1(min) 1 2 1 430 设备B2(min) 3 0 2 460 原料C1(kg) 1 4 0 420 原料C2(kg) 1 1 1 300 每件利润(元) 30 20 50
lingo结果分析及灵敏性分析 问题描述 程序代码: max = 60*desks + 30*tables + 20*chairs; 8*desks + 6*tables + chairs <= 48; 2*desks + 1.5*tables + 0.5*chairs <= 8; 4*desks + 2*tables + 1.5*chairs <= 20; tables<= 5; 部分结果一: Variable Value Reduced Cost DESKS 2.000000 0.000000 TABLES 0.000000 5.000000 CHAIRS 8.000000 0.000000 ⑴Value:给出最优解中各变量的值,Value=0(非基变量),反之为基变量。
⑵Reduced Cost:表示当非基变量有微小变动时, 目标函数的变化率。本例中: 变量tables 对应的reduced cost 值为5,表示当非基变量tables 的值从0 变为1 时(此时假定其他非基变量保持不变,但为了满足约束条件,基变量显然会发生变化),最优的目标函数值= 280 - 5 = 275。 部分结果二: Row Slack or Surplus Dual Price 1 280.0000 1.000000 2 24.00000 0.000000 3 0.000000 10.00000 4 0.000000 10.00000 5 5.000000 0.000000 ⑴“Slack or Surplus”――松驰变量。 ⑵“Dual Price”――对偶价格表示当对应约束有微小变动时, 目标函数的变化 率。若其数值为p,表示对应约束中不等式右端项若增加1个单位,目标函数将增加p个单位(max 型问题)。 ⑶如果在最优解处约束正好取等号(紧约束,也称为有效约束或起作用约束), 对偶价格值才可能不是0。本例中:第3、4 行是紧约束,对应的对偶价格值为10,表示当紧约束4) 4 DESKS + 2 TABLES + 1.5 CHAIRS <= 20 变为4) 4 DESKS + 2 TABLES + 1. 5 CHAIRS <= 21 时,目标函数值= 280 +10 = 290。
Max 123234z x x x =++ S.t 123412351523234,,0x x x x x x x x x x +++=?? -+-=??≥? 基变量x1=2,x2=3;非基变量x3=x4= x5=0; 由约束条件得基变量用非基变量表示为71112 1345 2121 23455555x x x x x x x x =--+??=+--? 目标函数中基变量用非基变量代入后981 345 14z x x x =---。 (1)当目标函数中系数i c 变化时(只要考虑最优性条件): 设目标函数变为Max 123'34z cx x x =++ 目标函数中基变量用非基变量代入672361111234555555555()()()z c c x c x c x =+---+-- 所以如果72355c -,6155c +,1 2 55c -0≥,则符合最优解判别条件,所以目标函数最优性不变611'z c =+,由723c -,6155c +,1 2 55c -0≥解得最优性不变的c 的范围。 否则,即如果超出该范围,则重新用单纯形法求解。 (2)当约束条件右边常数i b 变化时(先考虑可行性条件看最优基是否变化,再考虑): 设约束条件变为12341235152234,,0x x x x b x x x x x x +++=?? -+-=??≥? 先假设基没有变,所以令非基变量x3=x4= x5=0代入约束条件解得为8 15 8 2 24b b x x ++=??=-? 根据可行性条件,必须12,0x x ≥,解得b 的范围,即在此范围内最优基不变(最优解可能变化,要另外去求)。 否则,即如果超出该范围,则重新用单纯形法求解。 (3)当约束条件中价值系数ij a 变化时(先看可行性条件看最优基是否变化,再考虑最优值): 设约束条件变为11123412351523 234,,0a x x x x x x x x x x +++=?? -+-=??≥?
熟悉LINGO软件的灵敏度分析功能
2012——2013学年第一学期 合肥学院数理系 实验报告 课程名称:运筹学 实验项目:熟悉LINGO软件的灵敏度分析功能实验类别:综合性□设计性□√验证性□专业班级: 姓名:学号: 实验地点: 实验时间: 2012年11月22日 指导教师:管梅成绩:
一.实验目的 1、学会使用LINGO 软件求解线性规划问题的灵敏度分析。 2、学会分析LINGO 软件求解的结果。 二.实验内容 1、求解线性规划: 12 1212max 2251228Z x x x x x x =++≥?? +≤? 并对价值系数、右端常量进行灵敏度分析。 2、已知某工厂计划生产I ,II ,III 三种产品,各产品需要在A 、B 、C 设备上加 I II III 设备有效台时 (每月) A 8 2 10 300 B 10 5 8 400 C 2 13 10 420 单位产品利润 (千元) 3 2 2.9 (1)如何发挥生产能力,使生产盈利最大? (2)若为了增加产量,可租用别工厂设备B ,每月可租用60台时,租金1.8万元,租用B 设备是否合算? (3)若另有二种新产品IV 、V ,其中新产品IV 需用设备A 为12台时、B 为5台时、C 为10台时,单位产品盈利2.1千元;新产品V 需用设备A 为4台时、B 为4台时、C 为12台时,单位产品盈利1.87千元。如A 、B 、C 的设备台时不增加,这两种新产品投产在经济上是否划算? (3)对产品工艺重新进行设计,改进结构。改进后生产每件产品I 需用设备A 为9台时、设备B 为12台时、设备C 为4台时,单位产品盈利4.5千元,这时对原计划有何影响? 三. 模型建立 1、模型略
灵敏度分析 简介: 研究与分析一个系统(或模型)的状态或输出变化对系统参数或周围条件变化的敏感程度的方法。在最优化方法中经常利用灵敏度分析来研究原始数据不准确或发生变化时最优解的稳定性。通过灵敏度分析还可以决定哪些参数对系统或模型有较大的影响。因此,灵敏度分析几乎在所有的运筹学方法中以及在对各种方案进行评价时都是很重要的。 用途: 主要用于模型检验和推广。简单来说就是改变模型原有的假设条件之后,所得到的结果会发生多大的变化。 举例(建模五步法): 一头猪重200磅,每天增重5磅,饲养每天需花费45美分。猪的市场价格为每磅65美分,但每天下降1美分,求出售猪的最佳时间。 建立数学模型的五个步骤: 1.提出问题 2.选择建模方法 3.推到模型的数学表达式 4.求解模型 5.回答问题 第一步:提出问题 将问题用数学语言表达。例子中包含以下变量:猪的重量w(磅),从现在到出售猪期间经历的时间t(天),t天内饲养猪的花费C(美元),猪的市场价格p(美元/磅),出售生猪所获得的收益R(美元),我们最终要获得的净收益P(美元)。还有一些其他量,如猪的初始重量200磅。 (建议先写显而易见的部分) 猪从200磅按每天5磅增加 (w磅)=(200磅)+(5磅/天)*(t天) 饲养每天花费45美分 (C美元)=(0.45美元/天)*(t天) 价格65美分按每天1美分下降 (p美元/磅)=(0.65美元/磅)-(0.01美元/磅)*(t天) 生猪收益 (R美元)=(p美元/磅)*(w磅) 净利润 (P美元)=(R美元)-(C美元) 用数学语言总结和表达如下: 参数设定: t=时间(天)
w=猪的重量(磅) p=猪的价格(美元/磅) C=饲养t天的花费(美元) R=出售猪的收益(美元) P=净收益(美元) 假设: w=200+5t C=0.45t p=0.65-0.01t R=p*w P=R-C t>=0 目标:求P的最大值 第二步:选择建模方法 本例采用单变量最优化问题或极大—极小化问题 第三步:推导模型的数学表达式子 P=R-C (1) R=p*w (2) C=0.45t (3) 得到R=p*w-0.45t p=0.65-0.01t (4) w=200+5t (5) 得到P=(0.65-0.01t)(200+5t)-0.45t 令y=P是需最大化的目标变量,x=t是自变量,现在我们将问题转化为集合S={x:x>=0}上求函数的最大值: y=f(x)=(0.65-0.01x)(200+5x)-0.45x (1-1) 第四步:求解模型 用第二步中确定的数学方法解出步骤三。例子中,要求(1-1)式中定义的y=f (x)在区间x>=0上求最大值。下图给出了(1-1)的图像和导数(应用几何画板绘制)。在x=8为全局极大值点,此时f(8)=133.20。因此(8,133.20)为f在整个实轴上的全局极大值点,同时也是区间x>=0上的最大值点。 第五步:回答问题 根据第四步,8天后出售生猪的净收益最大,可以获得净收益133.20美元。只要第一步中的假设成立,这一结果正确。
实验报告 课程名称:运筹学 实验项目名称:应用Excel对线性规划进行灵敏度分析班级与班级代码: 实验室名称(或课室): 专业: 任课教师: 学号: 姓名: 实验日期:2010 年10 月18 日 广东商学院教务处制
姓名实验报告成绩 评语: 指导教师(签名) 年月日说明:指导教师评分后,实验报告交院(系)办公室保存。
实验二应用Excel对线性规划的灵敏度分析 一、实验目的与要求 1.了解线性规划模型中各参数的变化对最优解的影响。 2.会用Excel中提供的敏感性报告对目标函数系数进行灵敏度分析。 3.会用Excel中提供的敏感性报告对约束条件右端值的灵敏度分析。 二、实验步骤与方法 1.可以在电子表格中采取试验的方法,不断增加或减少的 c值,直到最优 j 解发生改变,以找到最优解发生变化时对应的 c值.但是,这样计算太 j 麻烦了。 2.在Excel求得最优解之后,在其右边列出了它可以提供的三个报告。 选择第二项敏感性报告的选项,就可以得到灵敏度的分析报告,它显示在模型的工作表之前。 3.当几个价值系数同时变动时,注意使用百分之百法则。 4.对约束条件限定数的灵敏度分析同上:选择第二项“敏感性报告”的 选项,就可以得到灵敏度的分析报告,其中“约束”表即是。 5.若几个约束限定数同时变动,也要注意使用百分之百法则。 三、实验内容 第1题. 医院放射科目前可以开展X线平片检查和CT检查业务,现拟购买磁共振仪,以增A 设磁共振检查业务。为此A医院收集了有关信息,从医院获取最大利润角度出发,问是否应购买磁共振仪?经过资料收集,A医院估计今后放射科如果开展此3项业务,在现有放射科医务人员力量和病人需求的情况下,每月此3项业务的最多提供量为1800人次。平均每人次检查时间、每月机器实际可使用时间、平均每人次检查利润如下表 放射科业务 项目X线平片检查CT检查磁共振检查平均每人次检查时间(小时/次)0.1 0.25 0.5 每月机器实际可使用时间(小时)300 120 120 平均每人次检查利润(元/次)20 60 10
一个实例理解Lingo 的灵敏性分析 线性规划问题的三个重要概念: 最优解就是反应取得最优值的决策变量所对应的向量。最优基就是最优单纯形表的基本变量所对应的系数矩阵如果其行列式是非奇异的,则该系数矩阵为最优基。 最优值就是最优的目标函数值。 Lingo 的灵敏性分析是研究当目标函数的系数和约束右端项在什么范围(此时假定其它系数不变)时,最优基保持不变。灵敏性分析给出的只是最优基保持不变的充分条件,而不一定是必要条件。下面是一道典型的例题。 一奶制品加工厂用牛奶生产A1,A2 两种奶制品,1 桶牛奶可以在甲车间用12小时加工成3 公斤A1,或者在乙车间用8小时加工成4公斤A2。根据市场需求,生产的A1,A2全部能售出,且每公斤A1 获利24 元,每公斤A2 获利16 元。现在加工厂每天能得到50 桶牛奶的供应,每天正式工人总的劳动时间480小时,并且甲车间每天至多能加工100公斤A1,乙 车间的加工能力没有限制。试为该厂制订一个生产计划,使每天获利最大,并进一步讨论以下3 个附加问题: 1 )若用35 元可以买到1 桶牛奶,应否作这项投资?若投资,每天最多购买多少桶牛奶? 2)若可以聘用临时工人以增加劳动时间,付给临时工人的工资最多是每小时几元? 3)由于市场需求变化,每公斤A1 的获利增加到30 元,应否改变生产计划?模型代码: max=72*x1+64*x2; x1+x2<=50; 12*x1+8*x2<=480; 3*x1<=100; 运行求解结果: Objective value: 3360.000 Variable Value Reduced Cost X120.000000.000000 X230.000000.000000 Row Slack or Surplus Dual Price 13360.000 1.000000 0.00000048.00000 2 30.000000 2.000000 440.000000.000000 这个线性规划的最优解为x1=20,x2=30,最优值为z=3360,即用20桶牛奶生产A1, 30 桶牛奶生产A2 ,可获最大利润3360 元。输出中除了告诉我们问题的最优解和最优值以外,还有许多对分析结果有用的信息。 其中,“ Reduced Cost列'出最优单纯形表中判别数所在行的变量的系数,表示当变量有微 小变动时,目标函数的变化率。其中基变量的reduced cost值应为0,对于非基变量Xj,相应的reduced cost值表示当某个变量Xj增加一个单位时目标函数减少的量(max型问题)。本例中X1 , X2 均为基变量。 “ Slack or Surplus给出松驰变量的值,模型第一行表示目标函数,所以第二行对应第一个约束。3个约束条件的右端不妨看作3种“资源”:原料、劳动时间、车间甲的加工能力。输出中Slack or Surplus 给出这3 种资源在最优解下是否有剩余:原料、劳动时间的剩余均为零,车间甲尚余40(公斤)加工能力。 “DUAL PRICE”(对偶价格)表示当对应约束有微小变动时,目标函数的变化率。输出结 果中对应于每一个约束有一个对偶价格。若其数值为p,表示对应约束中不等式右端项若 增加1个单位,目标函数将增加p个单位(max型问题)。显然,如果在最优解处约束正好取等号(也就是“紧约束”,也称为有效约束或起作用约束),对偶价格值才可能不是0。上 例中,第一、二个约束是紧约束”。当“x1+x2<=50'改为“x1+x2<=51"时,目标函数的值为
基于线性规划的灵敏度分析问题的研究 摘要:本文主要研究的是线性规划的灵敏度分析问题。讨论线性规划价值系数和资源系数中单个系数在什么区间变化时能保证最优解或最优基不变,以及多系数同时变化时最优解或者最优基不变的判定定理。最后通过实例进行说明验证。 本文对线性规划的灵敏度分析问题进行研究,主要内容如下: 第一章主要是简单的介绍了线性规划的发展历程,在线性规划的灵敏度分析的含义,灵敏度分析在其他方面的应用。 第二章,技术系数矩阵A发生变化时,最优解的变化。举例验证,应用LINGO 软件,进行灵敏度分析,确定在什么范围内,最优解不变。 第三章,资源向量b发生变化时,讨论最优解的变化情况。并举例验证其理论知识,应用LINGO软件,确定在什么变化范围内,最优解不变。 第四章,价值系数C发生变化时,最优解的变化情况。举例验证其理论实施过程,应用LINGO软件,分析其灵敏度。 第五章,对本文研究内容进行总结,指出一些不足之处,并提出进一步研究的方向。 关键词:运筹学;线性规划;灵敏度分析;技术系数;资源向量;价值系数;LINGO
The inventory model under uncertain demand Abstract:
第一章 绪论 随着运筹学的发展,线性规划方面的知识也得到了逐步的完善,并广泛地运用到实际的生活中,尤其给经济管理和决策提供了强有力的理论根据.管理部门和企业在进行生产或投资决策时,一般通过建立数学模型和对模型的求解,做出具体的决策方案.在建立模型和求解的过程中,都是以价值系数j c 、资源系数j b 和消耗系数ij a 为基础的,这些数据不但难以确定,而且市场价格的变动、资源供应的波动、工人技术的提高、设备的改进等,都会使这些数据变动.本文讨论线性规划价值系数和资源系数中单个系数在什么区间变化时能保证最优解或最优基不变,以及多系数同时变化时最优解或者最优基不变的判定定理。 线性规划发展史 1)1939年,前苏联数学家康托洛维奇发表了《生产组织与计划中的数学方法》学术报告,首次提出了线性规划问题,但是他没有找到一个统一的求解这类问题的方法。 2)美国学者希奇柯克(Hitchcock ,1941)独立的提出了运输问题这样一类特殊的线性规划问题。 3)1947年,美国学者丹捷格(Dantzig )提出求解线性规划的单纯形法和许多相关的理论,为线性规划奠定了理论基础,推动了线性规划的发展。 灵敏度分析的概念 研究与分析一个系统(或模型)的状态或输出变化对系统参数或周围条件变化的敏感程度的方法。在最优化方法中经常利用灵敏度分析来研究原始数据不准确或发生变化时最优解的稳定性。通过灵敏度分析还可以决定哪些参数对系统或模型有较大的影响。因此,灵敏度分析几乎在所有的运筹学方法中以及在对各种方案进行评价时都是很重要的。 灵敏度分析的应用领域 线性规划中灵敏度分析 对于线性规划问题: 1 max n j j j X c x ==∑公式