
第十一章质点动力学
1.质点动力学的基本方程为
矢量形式的微分方程为
经常应用的为直角坐标形式和自然坐标形式的微分方程。
2.质点动力学的两类问题
★已知质点的运动规律,求作用于质点的力,通常是求约束力;
★已知质点所受的作用力,求其运动规律。
一般一个问题中同时包含以上两类问题。求解动力学问题,建立动力学微分方程是关键的一步。对质点的运动及受力作初步的分析后,应选定合适的坐标系,将质点放在任意位置上,画受力图,写出它所受主动力的函数式,然后建立相对应坐标系的运动微分方程。求解运动微分方程要根据初始条件确定积分常数,即质点的运动是由质点的受力和初始条件同时决定。
3.质点相对非惯性参考系矢量形式的微分方程为
其中为相对非惯性参考系的矢径,为牵连惯性力,为科式惯性力。具体应用时取适当形式的投影方程。
质点是具有一定质量而几何形状和尺寸大小可以忽略不计的物体。
本章根据牛顿第二定律建立了质点运动微分方程,应用此方程可求解质点动力学的两类问题。牛顿定律不适用于非惯性坐标系。本章应用复合运动的分析方法,建立非惯性坐标系与惯性坐标系运动量之间的关系,进而得到适用非惯性坐标系的动力学基本定律。
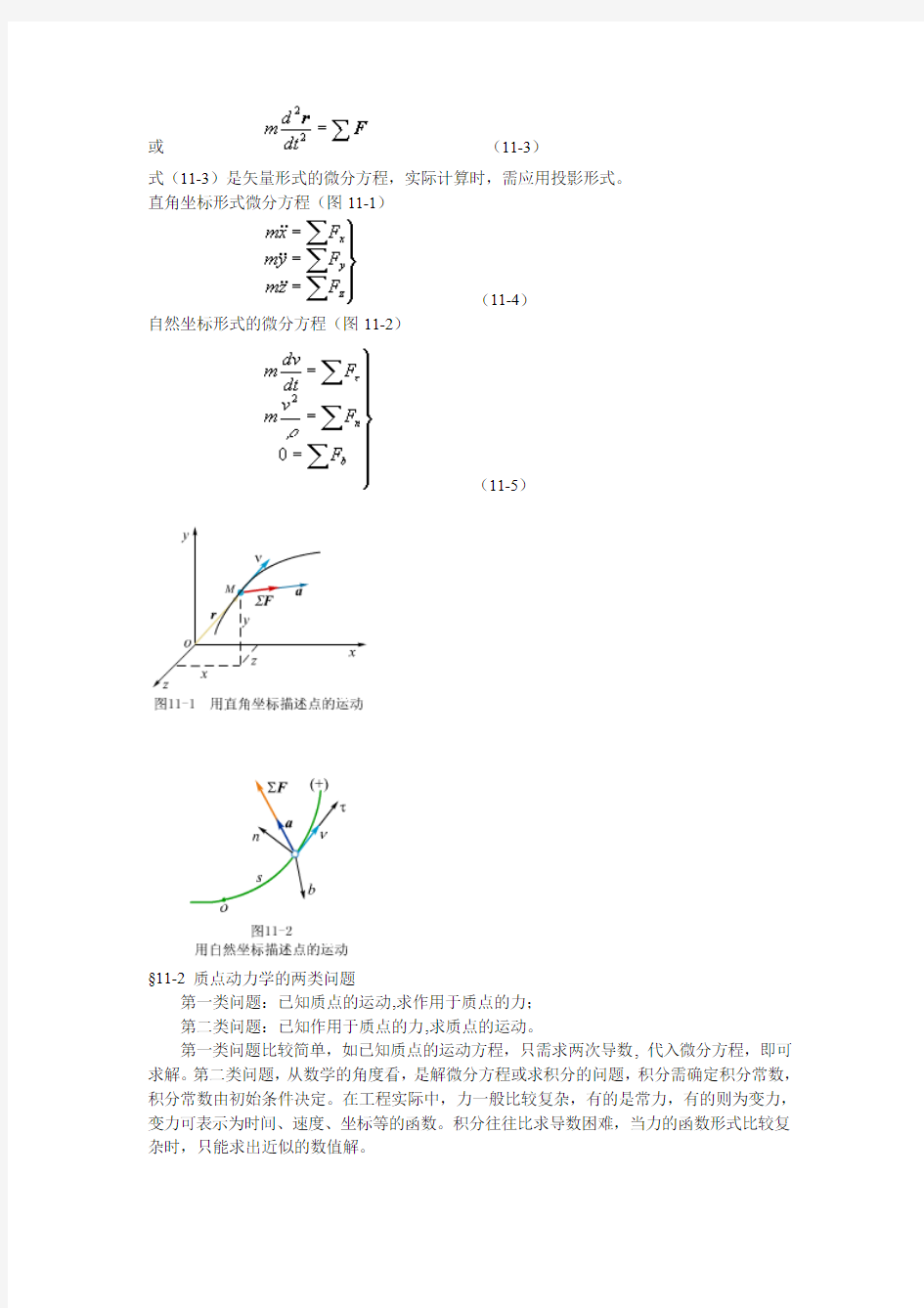
§11-1质点运动微分方程
1.动力学基本定律--牛顿三定律第一定律--惯性定律:任何质点如不受力作用,则将保持原来静止或等速直线运动状态。
物体保持其运动状况不变的固有属性,称为惯性。质量为物体惯性的度量。
第二定律--在力的作用下物体所获得的加速度的大小与作用力的大小成正比,与物体的质量成反比,方向与力的方向相同。即
(11-1)
在国际单位中,质量的单位为kg(千克),长度的单位为m(米),时间的单位为s(秒)。力的单位为N(牛顿)是导出单位:1N=1kg×1m/s
第三定律--作用反作用定律:两物体之间的作用力和反作用力大小相等,方向相反,并沿同一条直线分别作用在两个物体上。
2.运动微分方程当物体受几个力作用时,式(11-1)的右端应为这几个力的合力。即
(11-2)
或(11-3)
式(11-3)是矢量形式的微分方程,实际计算时,需应用投影形式。
直角坐标形式微分方程(图11-1)
(11-4)
自然坐标形式的微分方程(图11-2)
(11-5)
§11-2质点动力学的两类问题
第一类问题:已知质点的运动,求作用于质点的力;
第二类问题:已知作用于质点的力,求质点的运动。
第一类问题比较简单,如已知质点的运动方程,只需求两次导数,代入微分方程,即可求解。第二类问题,从数学的角度看,是解微分方程或求积分的问题,积分需确定积分常数,积分常数由初始条件决定。在工程实际中,力一般比较复杂,有的是常力,有的则为变力,变力可表示为时间、速度、坐标等的函数。积分往往比求导数困难,当力的函数形式比较复杂时,只能求出近似的数值解。
例11-1在简谐力作用下质点沿直线的运动
质量为m的质点在已知力作用下沿轴运动,设时,,
,求质点的运动规律。
解:这是一个求质点的直线运动规律的问题,已知力为时间函数。
图11-3为质点在任意位置的受力图。
质点的运动微分方程为:
或
上式可分离变量积分,由运动的初始条件,,确定积分的下限,即:
得
上式可分离变量积分,有
得
图11-4为质点沿x轴的运动图。
例11-2抛射体在与速度一次方成正比的阻尼介质中的运动
在重力作用下,以仰角、初速v0抛射出一物体。假设空气阻力与速度一次方成正比,
方向与之相反,即为阻力系数。试求抛射体的运动方程。
解:作用于质点上的为:重力(常力)和阻力(变力,速度的函数)。取直角坐标系如图示,坐标原点为质点开始运动的位置。列出质点直角坐标形式的运动微分方程:
令,上式可写为:
这是两个独立的线性微分方程,一般解为:
积分常数由运动起始条件时,,,确定,即
求得
将积分常数代入一般解后,得到质点的运动方程为:
上式是以时间t为参数的轨迹方程。质点的速度公式为:
由轨迹方程可看出当时,轨迹以铅垂线为其渐近线。如图11-6所示。由速度公式可看出质点在水平方向的速度不是常数,而是随时间的增加不断地减小,当
时,,。所以当,质点将以其极限速度沿渐近线降落。图11-5中虚线为抛射体在真空中的运动轨迹,对于速度小、射程短的物体来说,忽略空气阻力的影响是合理的。但对于象导弹、火箭等高速、远射程的物体,如略去阻力,理论结果与实际情形就相差甚远。因此研究弹道问题时必须考虑空气阻力。实验证明,空气
阻力值与速度大小的n次方成正比,n又决定于速度大小的范围,可写成。比例系
数决定于空气密度、物体的形状和迎风面面积。
例11-3单摆的大摆动球磨机
图11-7为一单摆。设球的质量为m,杆的质量不计,杆长为l。当杆在
铅垂位置时,球因受冲击,具有水平初速v0。不计空气阻力,研究球的运动和杆对球的约束力。
解:这是非自由质点动力学问题。本题应先由已知的主动力P求质点的运动规律,再根据求得的运动求未知约束力,故同时包含第一类问题和第二类问题。
由于质点运动轨迹是圆弧,故用自然轴系研究较方便。如图11-8所示
,。建立小球的运动微分方程:
上式中第一式建立了主动力与切向加速度的关系,这是非线性的运动微分方程;第二式建立了法向加速度与约束力的关系。
下面分两种情况讨论:(1)微幅摆动
当杆的摆角很小时(),,运动微分方程即成
或
令,则
这是一个常系数二阶线性微分方程,其通解为:
积分常数由起始条件决定。将时,代入后得:
于是,摆角随时间变化的规律为:
小球的运动方程为:
这表明小球沿圆弧作简谐运动,其周期为:
即微幅摆动的周期与摆动的初始条件无关,这种性质称为单摆微幅摆动的等时性。
(2)大幅摆动或圆周运动
如起始速度较大,则不能用代替,质点的运动微分方程的切向投影式为
这是一个常系数二阶非线性微分方程,其解为一椭圆积分,现仅研究其首次积分。
用分离变量后得:
代入时,,得
求得速度后,应用运动微分方程中的法向投影式可求得未知的约束力。
上式中右边的第一项是由重力的法向分量引起的,称为静约束力;第二项是由质点的运动引起的,称为动约束力。经整理可写成
对于刚性杆一类的双面约束,由速度公式可知,欲使球摆动至时,有,则
其初速有,球就可作圆周运动。但对于绳索一类的单面约束,作圆周运动的条件,
即不脱离约束的条件为,则其初始条件。
当时,
当时,
则
如,则有
且有
在此情形下,不同位置时约束力的变化曲线如图11-9所示。
若为单面约束,球运动至位置A时,将失去约束作用,小球将脱离圆轨道而沿抛物线ADC自由飞行,如图11-10所示。在工程实际中常利用物体受单面约束时的运动特点,
例如化工、机械中常用的球磨机。当转筒带动钢球旋转到一定角度处,钢球即脱离约束沿抛物线飞落下来,打击筒内的物料或矿石,以达到粉碎的目的(图11-11)。钢球恰好能随
筒转整圈而不脱离时,转筒的转速称为临界转速,运行时应使球磨机转筒的转速。为了提高粉碎效率,设计时要计算脱离角、打击速度和飞行时间,据此计算出转筒合理的转速和尺寸参数。
§11-3质点相对运动动力学的基本方程
1.基本方程牛顿第二定律只适用于惯性参考系,对于非惯性参考系,质点的运动微分方程将具有不同的形式。
如图11-12所示,质量为m的质点M相对非惯性参考系O'x'y'z'运动,Oxyz为惯性参考系,设作用于质点上的力为,在惯性参考系内,有
为质点相对定参考系Oxyz的绝对加速度。设为质点相对动参考系O'x'y'z'的相对加速度,由加速度合成定理有:
其中为牵连加速度,为科式加速度。代入前式后得
或(11-6)
式中具有力的量纲,分别称为牵连惯性力和科氏惯性力。
令
由此,式(11-6)变为
(11-7)
此式称为质点相对运动动力学基本方程,它在形式上与惯性参考系中的牛顿第二定律相似。
只是在方程的右边,除了作用在质点上的合力外,还应附加牵连惯性力和科氏惯性力
。式(11-7)为矢量形式的方程,具体应用时应取适当形式的投影方程。
下面讨论几种特殊情形:
(1)质点相对动参考系作等速直线运动,有,式(11-7)成为
称为相对平衡状态。
若,且有,此时称为相对静止状态。
(2)动参考系相对定参考系作平动,有,式(11-7)成为
(3)动参考系相对定参考系作等速直线运动,有,,式(11-7)成为
上式说明相对于惯性参考系作等速直线运动的参考系也是惯性参考系。
例11-4图11-13所示单摆,摆长为l,小球质量为m,其悬挂点O以加速度向上运动,求此时单摆作微振动的周期。
解:小球受力分析:重力,绳子张力;还应加牵
连惯性力。相对运动动力学方程为:;切线方向的运动微分方程为
作微振动时,有,代入,上式成为
令,上式成为微振动微分方程的标准形式
其解为,周期为
例11-5如图所示,水平圆盘绕O轴转动,角速度,盘上有一光滑直槽,离O的距离为s,求小球的运动和槽对小球的横向作用力。
解:取固结于圆盘上的坐标系为动坐标系。
因此,牵连惯性力为:
科氏惯性力为:
相对运动微分方程为:
由第一式得
如果给定初始条件:可得
由第二式得出槽对小球的横向作用力
2.质点相对地球的运动工程中大多数问题是以地球作为惯性参考系直接应用牛顿定律,计算所得结果与实际情况符合良好。但不是所有的力学现象都能以地球为惯性参考系来解释的,例如,讨论物体相对地球的运动,在精度要求高,或时间间隔长的情况下,就必须考虑地球的自转的影响,即把地心系作为惯性参考系,而地球就是非惯性参考系。下面以“落体偏东现象”为例说明这一问题。
例11-6在地球表面北纬角处,一质量为m的质点,自高度为h处自由下落,求由
于地球自转的影响,落体对于铅垂线的偏离。
解:选取固结于地球的非惯性参考系为,其中z 轴近似通过地球中心,铅直向上,x轴水平向东,y轴水平向北,如图11-15所示。
分析质点受力:质点受地球引力,分析质点相对地球的运动时,应再加上牵连惯性
力和科氏惯性力。其中地球引力和牵连惯性力之合,就是物体在地球表面表
现出的重力,即:
而科氏惯性力为
其中为地球的自转角速度矢量,方向如图所示。的矢量积可展开为
列出质点的相对运动微分方程
①
采用逐次近似法解上述微分方程,由于地球自转的角速度很小,在最初的计算中,
可取,则式①的零次近似方程为
②
初始条件为,时
式②积分一次得零次近似的速度为
③
将上式代入式①,得一次近似的微分方程
④
上式积分一次,得一次近似速度为
⑤
再积分一次,得一次近似的运动方程为
由此解可看出落体已不再沿z轴下落,而在x方向有偏离。偏距与时间t的三次方成正比。因此,下落距离愈大,偏距也就愈大。以北京地区为
例,,下落高度为。则偏离为
由于偏离沿x正向,即东偏,称为落体偏东。如图11-16
《动力学I 》第一章 运动学部分习题参考解答 1-3 解: 运动方程:θtan l y =,其中kt =θ。 将运动方程对时间求导并将0 30=θ代入得 34cos cos 22lk lk l y v ====θ θθ 938cos sin 22 3 2lk lk y a =-==θ θ 1-6 证明:质点做曲线运动,所以n t a a a +=, 设质点的速度为v ,由图可知: a a v v y n cos ==θ,所以: y v v a a n = 将c v y =,ρ 2 n v a = 代入上式可得 ρ c v a 3 = 证毕 1-7 证明:因为n 2 a v =ρ,v a a v a ?==θsin n 所以:v a ?= 3 v ρ 证毕 1-10 解:设初始时,绳索AB 的长度为L ,时刻t 时的长度 为s ,则有关系式: t v L s 0-=,并且 222x l s += 将上面两式对时间求导得: 0v s -= ,x x s s 22= 由此解得:x sv x -= (a ) (a)式可写成:s v x x 0-= ,将该式对时间求导得: 2 02 v v s x x x =-=+ (b) 将(a)式代入(b)式可得:32 20220x l v x x v x a x -=-== (负号说明滑块A 的加速度向上) 1-11 解:设B 点是绳子AB 与圆盘的切点,由于绳子相对圆盘无滑动,所以R v B ω=,由于绳子始终处 于拉直状态,因此绳子上A 、B 两点的速度在 A 、B 两点连线上的投影相等,即: θcos A B v v = (a ) 因为 x R x 2 2cos -= θ (b ) 将上式代入(a )式得到A 点速度的大小为: 2 2 R x x R v A -=ω (c ) 由于x v A -=,(c )式可写成:Rx R x x ω=--22 ,将该式两边平方可得: 222222)(x R R x x ω=- 将上式两边对时间求导可得: x x R x x R x x x 2232222)(2ω=-- 将上式消去x 2后,可求得:2 22 42) (R x x R x --=ω 由上式可知滑块A 的加速度方向向左,其大小为 2 22 42) (R x x R a A -=ω 1-13 解:动点:套筒A ; 动系:OA 杆; 定系:机座; 运动分析: 绝对运动:直线运动; 相对运动:直线运动; 牵连运动:定轴转动。 根据速度合成定理 r e a v v v += 有:e a cos v v =?,因为AB 杆平动,所以v v =a , o v o v a v e v r v x o v x o t
第三篇 动力学 一、选择题(每题2分,共20分) 1.在铅直面内的一块圆板上刻有三道直槽AO ,BO ,CO ,三个质量相等的小球M 1,M 2,M 3在重力作用下自静止开始同时从A ,B ,C 三点分别沿各槽运动,不计摩擦,则________到达O 点。 (A )M 1小球先; (B )M 2小球先; (C )M 3小球先; (D )三球同时。 题1 题2 题3 2.质量分别为m 1=m ,m 2=2m 的两个小球M 1,M 2用长为L 而重量不计的刚杆相连。现将M 1置于光滑水平面上,且M 1M 2与水平面成?60角。则当无初速释放,M 2球落地时,M 1球移动的水平距离为____________。 (A )3L ; (B )4L ; (C )6L ; (D )0。 3.质量为m ,长为b 的匀质杆OA ,以匀角速度ω绕O 轴转动。图示位置时,杆的动量及对O 轴的动量矩的大小为________。 (A )2 ωmb p =,122ωmb L O =; (B )0=p ,122ωmb L O =; (C )2ωmb p =,22ωmb L O =; (D )2 ωmb p =,32ωmb L O =。 4.在_____情况下,跨过滑轮的绳子两边张力相等,即F 1=F 2(不计轴承处摩擦)。 (A )滑轮保持静止或以匀速转动或滑轮质量不计; (B )滑轮保持静止或滑轮质量沿轮缘均匀分布; (C )滑轮保持静止或滑轮质量均匀分布; (D )滑轮质量均匀分布。 题4 题5 5.均质杆长L ,重P ,均质圆盘直径D =L ,亦重P ,均放置在铅垂平面内,并可绕O 轴转动。初始时杆轴线和圆盘直径均处于水平位置,而后无初速释放,则在达到图示位置瞬时,杆的角速度ω1________圆盘的角速度ω2。 (A )大于; (B )小于; (C )等于; (D )小于或等于。
本篇接着阐述理论力学动力学中的核心观念。阐述的方式依旧是回答几个问题。 问题1:动力学的基本问题是什么? 答案:虽然书上有关于动力学问题的许多说法,但是就实际应用而言,对于我们机械专业而言,我们所遇到的最常见的动力学问题是,在一个机构上的原动件受到了力(偶),我们要得到机构上各构件的速度和加速度。或者已知了速度和加速度,要反推这个力(偶)是多少。 下图就是这样一个例子。在OA杆上施加一个驱动力偶,各个杆件都有重力,我们要计算此时各约束处的约束力的大小,还需要计算CD杆的速度和加速度。 该问题中,力与运动交织在一起,这就是机构的动力学问题,也是机械中经常遇到的问题。 问题2:如何求解动力学问题? 答案: 解决动力徐问题的方法很多。我们只要谈两种方法:第一种是通用解法,第二种是动静法(达朗伯原理)。 通用解法,是指面对一个动力学问题,我们总是有一套很程序化的思路来求解它,这套思路中,我们会使用刚体平面运动的微分方程。使用这种方法,我们几乎不用思考,就可以列出所有的方程,解决所有的未知数。例如,对上面这个问题,如果它已知M,要求CD杆的加速度。则使用通用解法,我们可以同时求出AB杆,BE,CD杆的加速度,也可以求出A,B,C,D,E 处所有的约束力。使用通用解法,我们几乎不用关注题目要求什么,而总是可以求出所有的未知数。 动静法,是说把这个动力学问题从形式上变成静力学问题,然后再借用静力学的求解方法来计算所需要的未知数。动静法之所以能够把动力学问题变成静力学问题,是因为它把加速度变成了惯性力,然后对于系统中的每一个构件,形成了一个力系平衡的问题。而我们之所以使用动静法,是因为对于静力学问题,我们有很多解题技巧,例如取整体为对象,或者取某几个构件一起为对象,或者对任何一个点取力矩,这些优越性,都是刚体平面运动微分方程所不具备的。 问题3:如何使用通用解法求解动力学问题?
质点动力学的基本方程 知识总结 1.牛顿三定律适用于惯性参考系。 质点具有惯性,以其质量度量; 作用于质点的力与其加速度成比例; 作用与反作用力等值、反向、共线,分别作用于两个物体上。 2.质点动力学的基本方程。 质点动力学的基本方程为,应用时取投影形式。 3.质点动力学可分为两类基本问题。 质点动力学可分为两类基本问题: (1). 已知质点的运动,求作用于质点的力; (2). 已知作用于质点的力,求质点的运动。 求解第一类问题,需先求得质点的加速度;求解第二类问题,一般是积分的过程。质点的运动规律不仅决定于作用力,也与质点的运动初始条件有关,这两类的综合问题称为混合问题。 动量定理 知识点总结 1.牛顿三定律适用于惯性参考系。 质点具有惯性,以其质量度量; 作用于质点的力与其加速度成比例; 作用与反作用力等值、反向、共线,分别作用于两个物体上。 2.质点动力学的基本方程。 质点动力学的基本方程为,应用时取投影形式。 3.质点动力学可分为两类基本问题。 质点动力学可分为两类基本问题: (1). 已知质点的运动,求作用于质点的力; (2). 已知作用于质点的力,求质点的运动。
求解第一类问题,需先求得质点的加速度;求解第二类问题,一般是积分的过程。质点的运动规律不仅决定于作用力,也与质点的运动初始条件有关,这两类的综合问题称为混合问题。 常见问题 问题一在动力学中质心意义重大。质点系动量,它只取决于质点系质量及质心速度。 问题二质心加速度取决于外力主失,而与各力作用点无关,这一点需特别注意。 动量矩定理 知识点总结 1.动量矩。 质点对点O 的动量矩是矢量。 质点系对点O 的动量矩是矢量。 若z 轴通过点O ,则质点系对于z 轴的动量矩为 。 若 C 为质点系的质心,对任一点O 有。 2.动量矩定理。 对于定点O 和定轴z 有 若 C 为质心,C z 轴通过质心,有
第一章 静力学公理和物体的受力分析 一、选择题与填空题 1.C 2.ACD 3.A ,B 两处约束力的方向如图所示。 4.5F ,方向与5F 方向相反。 5.60°。 6. 铅直向上。 第二章 平面力系 一、选择题与填空题 1.B ;D 。 2.B 。3. 2 F ;向上。4.B 。5.L M 334;方向与水平线成?60角,指向 右下。6.10kN ;10kN ;5kN ;5kN 。7. 100kN ;水平向右。 二.计算题 1. 70-=B F KN 70=Ax F KN ,120=Ay F KN ,30A M KN m =-? 2. qa F Ax -= qa F F Bx += F qa F Ay += F qa F By -= 3. kN 5-=Dx F kN 33.4=Dy F kN 33.4=E F kN 41.24=C F kN 08.17-=By F kN 5-='=Bx Ax F F kN 08.14-=Ay F m kN 66.14?-=A M 4.
5. N 10=Ax F N 20=Ay F m N 15?=A M N 1.14=CD F 6. kN 5.2=Ax F kN 16.2-=Ay F m kN 8?-=A M kN 33.20=C F 7. kN 40=B F kN 10-=Ax F kN 20-=Ay F m kN 50?-=A M kN 40=Cx F 0 =Cy F 8. N 100-=Ax F N 300-=Ay F N 300-=Ex F N 100=Ey F N 200=Dy F N 300=Hx F N 100=Hy F 第三章 空间力系 一、选择题与填空题 1.B 。 2.B 。 3. 0)(=F M x ;2)(Fa F M y -= ;4 6)(Fa F M z = 。 4. F x =240-N ;F y =302N ;M z =2402m N ?。 5. sin z F F ?=;cos cos y F F ?β=; ()(cos cos sin )x M F F c b ?β?=+。 6. ?sin )(Fa F M AB = 。 7. 6 R x C - =;0C y =。
习 题 12–1 一刚度系数为k 的弹簧,放在倾角为θ的斜面上。弹簧的上端固定,下端与质量为m 的物块A 相连,图12-23所示为其平衡位置。如使重物A 从平衡位置向下沿斜面移动了距离s ,不计摩擦力,试求作用于重物A 上所有力的功的总和。 图12-23 ))((2 sin 2st 2 st s k s mg W +-+ ?=δδθ 2st 2 sin s k s k mgs --=δθ 22 s k -= 12–2 如图12-24所示,在半径为r 的卷筒上,作用一力偶矩M=a ?+b ?2 ,其中?为转角,a 和b 为常数。卷筒上的绳索拉动水平面上的重物B 。设重物B 的质量为m ,它与水平面之间的滑动摩擦因数为μ。不计绳索质量。当卷筒转过两圈时,试求作用于系统上所有力的功的总和。 图12-24 3 22π40 π3 64π8d )+ (d b a b a M W M + ===? ????? mgr r mg W F π4π4μμ-=?-= )3π16π6π(3 4 π4π364π8232mgr b a mgr b a W μμ-+=-+=∑ 12–3 均质杆OA 长l ,质量为m ,绕着球形铰链O 的铅垂轴以匀角速度ω转动,如图12-25所示。如杆与铅垂轴的夹角为θ,
试求杆的动能。 图12-25 x x l m x x l m v m E d )sin 2()sin )(d (21)(d 21d 2222k θωθω=== θωθω2220222k sin 6 1 d )sin 2(ml x x l m E l ?== 12–4 质量为m 1的滑块A 沿水平面以速度v 移动,质量为 m 2的物块B 沿滑块A 以相对速度u 滑下,如图12-26所示。试求 系统的动能。 图12-26 ])30sin ()30cos [(2 1 2 122221k ?++?+=u v u m v m E )30cos 2(212 122221?+++=uv v u m v m )3(2 1 2122221uv v u m v m +++= 12–5 如图12-27所示,滑块A 质量为m 1,在滑道内滑动,其上铰接一均质直杆AB ,杆AB 长为l ,质量为m 2。当AB 杆与铅垂线的夹角为?时,滑块A 的速度为A v ,杆AB 的角速度为ω。试求在该瞬时系统的动能。 图12-27 AB A E E E k k k += 22222221)12 1(21])sin 2()cos 2[(2121ω?ω?ωl m l l v m v m A A ++++= )12 1cos 41(212122222 221ω?ωωl lv l v m v m A A A ++++= )cos 3 1(2121222 221?ωωA A A lv l v m v m +++= 12–6 椭圆规尺在水平面内由曲柄带动,设曲柄和椭圆规
(a ) 第11章 达朗贝尔原理及其应用 11-1 均质圆盘作定轴转动,其中图(a ),图(c )的转动角速度为常数,而图(b ),图(d )的角速度不为常量。试对图示四种情形进行惯性力的简化。 r , 0 ,α I ( d ) I =F , αα2 I 2 1mr J M O O = = 11-2矩形均质平板尺寸如图,质量27kg ,由两个销子 A 、 B 悬挂。若突然撤去销子B ,求在撤 去的瞬时平板的角加 速度和销子A 的约束力。 解:如图(a ):设平板的质量为m ,长和宽分别为a 、b 。 αα375.3I =?=AC m F ααα5625.0])(12 1 [222I =?++==AC m b a m J M A A ∑=0)(F A M ;01.0I =-mg M A ;2rad/s 04.47=α ∑=0x F ;0sin I =-Ax F F θ;其中:6.05 3sin ==θ N 26.956.004.47375.3=??=Ax F ∑=0y F ;0cos I =-+mg F F Ay θ;8.05 4sin ==θ N 6.1378.004.47375.38.927=??-?=Ay F 11-3在均质直角构件ABC 中,AB 、BC 两部分的质量各为3.0kg ,用连杆AD 、DE 以及绳子AE 保持在图示位置。若突然剪断绳子,求此瞬时连杆AD 、BE 所受的力。连杆的质量忽略不计,已知l = 1.0m ,φ = 30o。 解:如图(a ):设AB 、BC 两部分的质量各为m 直角构件ABC 作平移,其加速度为a = a A ,质心在O 处。 ma F 2I = ∑=0)(F O M ; 04 sin )(43 cos 4cos =+--l F F l F l F B A A B ??? (1) ∑=0AD F ; 0cos 2=-+?mg F F B A (2) 联立式(1)和式(2),得:A B F mg F 3+= 习 题 ( (
第6章 刚体的平面运动分析 6-1 图示半径为r 的齿轮由曲柄OA 带动,沿半径为R 的固定齿轮滚动。曲柄OA 以等角加速度α绕轴O 转动,当运动开始时,角速度0ω= 0,转角0?= 0。试求动齿轮以圆心A 为基点的平面运动方程。 解:?cos )(r R x A += (1) ?sin )(r R y A += (2) α为常数,当t = 0时,0ω=0?= 0 22 1t α?= (3) 起始位置,P 与P 0重合,即起始位置AP 水平,记θ=∠OAP ,则AP 从起始水平位置至图示AP 位置转过 θ??+=A 因动齿轮纯滚,故有? ? =CP CP 0,即 θ?r R = ?θr R = , ??r r R A += (4) 将(3)代入(1)、(2)、(4)得动齿轮以A 为基点的平面运动方程为: ??? ? ?? ??? +=+=+=22 2212sin )(2cos )(t r r R t r R y t r R x A A A α?αα 6-2 杆AB 斜靠于高为h 的台阶角C 处,一端A 以匀速v 0沿水平向右运动,如图所示。试以杆与铅垂 线的夹角 表示杆的角速度。 解:杆AB 作平面运动,点C 的速度v C 沿杆AB 如图所示。作速度v C 和v 0的垂线交于点P ,点P 即为杆AB 的速度瞬心。则角速度杆AB 为 6-3 图示拖车的车轮A 与垫滚B 的半径均为r 。试问当拖车以速度v 前进时, 轮A 与垫滚B 的角速度A ω与B ω有什么关系?设轮A 和垫滚B 与地面之间以及垫滚B 与拖车之间无滑动。 解:R v R v A A ==ω R v R v B B 22==ω B A ωω2= 6-4 直径为360mm 的滚子在水平面上作纯滚动,杆BC 一端与滚子铰接,另一端与滑块C 铰接。设杆BC 在水平位置时,滚子的角速度=12 rad/s ,=30,=60,BC =270mm 。试求该瞬时杆BC 的角速度和点C 的速度。 习题6-1图 A B C v 0 h 习题6-2图 P AB v C A B C v o h 习题6-2解图 习题6-3解图 习题6-3图 v A = v v B = v
y 第十一章 动量矩定理 习题解 [习题11-1] 刚体作平面运动。已知运动方程为:2 3t x C =,24t y C =,3 2 1t = ?,其中长度以m 计,角度以rad 计,时间以s 计。设刚体质量为kg 10,对于通过质心C 且垂直于图平面的惯性半径m 5.0=ρ,求s t 2=时刚体对坐标原点的动量矩。 解: )(1223|22m x t C =?== )(1624|2 2m y t C =?== t t dt d dt dx v C Cx 6)3(2=== )/(1226|2s m v t Cx =?== t t dt d dt dy v C Cy 8)4(2=== )/(1628|2s m v t Cy =?== 2323)21(t t dt d dt d === ?ω )/(622 3 |22s rad t =?==ω → →→+=k v m M J L C Z Cz O )]([ω → → -+=k y mv x mv m L C Cx C Cy O ][2 ωρ → =→ ?-?+??=k L t O ]1612121665.0[10|2 2 → =→ =k L t O 15|2 )/(2 s m kg ?,→ k 是z 轴正向的单位向量。 [习题11-2] 半径为R ,重为W 的均质圆盘固结在长l ,重为P 的均质水平直杆AB 的B 端,绕铅垂轴Oz 以角速度ω旋转,求系统对转轴的动量矩。 解: g Pl l g P J AB z 3312 2,=??=
平动 )(a O 转动 绕定轴C )( b 转动 绕定轴1 )(O c O 在圆弧上作纯滚动 )(d g l R W l g W g J l z 4)4(R W 412222,+=?+??=圆盘 ωω?+?=圆盘,,z AB z z J J L ω4) 4(3[222g l R W g Pl L z ++= ω)4443(2 22g WR g Wl g Pl L z ++= ω)4333(2 22g WR g Wl g Pl L z ++= ω)433( 2 2R g W l g W P L z ++= [习题11-3] 已知均质圆盘质量为m ,半径为R ,当它作图示四种运动时,对固定点1O 的动量矩分别为多大?图中l C O =1。 解:)(a 因为圆盘作平动,所以 ωω2 11ml J L z O O == 解:)(b → →→→?+=p r L L C C O 1 其中,质心C 的动量为0 ωω22 1 1mR J L Cz O = = 解:)(c ωω)2 1 (2211ml mR J L z O O +== 解:)(d 因为圆盘作平面运动,所以: )(11→ +=C Z O Cz O v m M J L ω
第12章 虚位移原理及其应用 12-1 图示结构由8根无重杆铰接成三个相同的菱形。试求平衡时,主动力F 1与F 2的大小关系。 解:应用解析法,如图(a ),设OD = l θsin 2l y A =;θsin 6l y B = θθδcos 2δl y A =;θθδcos 6δl y B = 应用虚位移原理:0δδ12=?-?A B y F y F 02612=-F F ;213F F = 12-2图示的平面机构中,D 点作用一水平力F 1,求保持机构平衡时主动力F 2之值。已知:AC = BC = EC = DE = FC = DF = l 。 解:应用解析法,如图所示: θcos l y A =;θsin 3l x D = θθδsin δl y A -=;θθδcos 3δ l x D = 应用虚位移原理:0δδ12=?-?-D A x F y F 0cos 3sin 12=-θθF F ;θcot 312F F = 12-3 图示楔形机构处于平衡状态,尖劈角为θ和β,不计楔块自重与摩擦。求竖向力F 1与F 2的大小关系。 解:如图(a ),应用虚位移原理:0δδ2211=?+?r F r F 如图(b ): β θtan δδtan δ2 a 1r r r ==;12 δ tan tan δr r θ β = 0δtan tan δ1211=? -?r θβF r F ;θ β tan tan 21?=F F 12-4 图示摇杆机构位于水平面上,已知OO 1 = OA 。机构上受到力偶矩M 1和M 2的作用。机构在可能的任意角度θ下处于平衡时,求M 1和M 2之间的关系。 习题12-1图 (a ) 习题12-2解图 习题12-3 (a ) r a (b )
理论力学动力学知识点汇总
————————————————————————————————作者:————————————————————————————————日期:
质点动力学的基本方程 知识总结 1.牛顿三定律适用于惯性参考系。 质点具有惯性,以其质量度量; 作用于质点的力与其加速度成比例; 作用与反作用力等值、反向、共线,分别作用于两个物体上。 2.质点动力学的基本方程。 质点动力学的基本方程为,应用时取投影形式。 3.质点动力学可分为两类基本问题。 质点动力学可分为两类基本问题: (1). 已知质点的运动,求作用于质点的力; (2). 已知作用于质点的力,求质点的运动。 求解第一类问题,需先求得质点的加速度;求解第二类问题,一般是积分的过程。质点的运动规律不仅决定于作用力,也与质点的运动初始条件有关,这两类的综合问题称为混合问题。 动量定理 知识点总结 1.牛顿三定律适用于惯性参考系。 质点具有惯性,以其质量度量; 作用于质点的力与其加速度成比例; 作用与反作用力等值、反向、共线,分别作用于两个物体上。 2.质点动力学的基本方程。 质点动力学的基本方程为,应用时取投影形式。 3.质点动力学可分为两类基本问题。 质点动力学可分为两类基本问题: (1). 已知质点的运动,求作用于质点的力; (2). 已知作用于质点的力,求质点的运动。
求解第一类问题,需先求得质点的加速度;求解第二类问题,一般是积分的过程。质点的运动规律不仅决定于作用力,也与质点的运动初始条件有关,这两类的综合问题称为混合问题。 常见问题 问题一在动力学中质心意义重大。质点系动量,它只取决于质点系质量及质心速度。 问题二质心加速度取决于外力主失,而与各力作用点无关,这一点需特别注意。 动量矩定理 知识点总结 1.动量矩。 质点对点O 的动量矩是矢量。 质点系对点O 的动量矩是矢量。 若z 轴通过点O ,则质点系对于z 轴的动量矩为 。 若 C 为质点系的质心,对任一点O 有。 2.动量矩定理。 对于定点O 和定轴z 有 若 C 为质心,C z 轴通过质心,有
y x 第十一章 动量矩定理 习题解 [习题11-1] 刚体作平面运动。已知运动方程为:23t x C =,24t y C =,3 2 1t = ?,其中长度以m 计,角度以rad 计,时间以s 计。设刚体质量为kg 10,对于通过质心C 且垂直于图平面的惯性半径m 5.0=ρ,求s t 2=时刚体对坐标原点的动量矩。 解: )(1223|2 2m x t C =?== )(1624|22m y t C =?== t t dt d dt dx v C Cx 6)3(2=== )/(1226|2s m v t Cx =?== t t dt d dt dy v C Cy 8)4(2=== )/(1628|2s m v t Cy =?== 2323)21(t t dt d dt d === ?ω )/(622 3 |22s rad t =?==ω → →→+=k v m M J L C Z Cz O )]([ω → → -+=k y mv x mv m L C Cx C Cy O ][2 ωρ → =→ ?-?+??=k L t O ]1612121665.0[10|2 2 → =→ =k L t O 15|2 )/(2 s m kg ?,→ k 是z 轴正向的单位向量。 [习题11-2] 半径为R ,重为W 的均质圆盘固结在长l ,重为P 的均质水平直杆AB 的B 端,绕铅垂轴Oz 以角速度ω旋转,求系统对转轴的动量矩。 解: g Pl l g P J AB z 3312 2,= ??=
平动 )(a O 转动 绕定轴C )( b 转动 绕定轴1 )(O c 1 O 在圆弧上作纯滚动 )(d g l R W l g W g J l z 4) 4(R W 412222,+= ?+??=圆盘 ωω?+?=圆盘,,z AB z z J J L ω4) 4(3[222g l R W g Pl L z ++= ω)4443( 2 2 2 g WR g Wl g Pl L z ++= ω4333(2 22g WR g Wl g Pl L z ++= ω)433( 2 2R g W l g W P L z ++= [习题11-3] 已知均质圆盘质量为m ,半径为R ,当它作图示四种运动时,对固定点1O 的动量矩分别为多大?图中l C O =1。 解:)(a 因为圆盘作平动,所以 ωω211ml J L z O O == 解:)(b → → → →?+=p r L L C C O 1 其中,质心C 的动量为0 ωω22 1 1mR J L Cz O = = 解:)(c ωω)2 1 (2211ml mR J L z O O +== 解:)(d 因为圆盘作平面运动,所以: )(11→ +=C Z O Cz O v m M J L ω
一、 是非题 1. 只要知道作用在质点上的力,那么质点在任一瞬时的运动状态就完全确定了。 (错) 2. 在惯性参考系中,不论初始条件如何变化,只要质点不受力的作用,则该质点应 保持静止或等速直线运动状态。 (对) 3. 作用于质点上的力越大,质点运动的速度越高。 (错) 4. 牛顿定律适用于任意参考系。 (错) 5. 一个质点只要运动,就一定受有力的作用,而且运动的方向就是它受力的方向。 (错) 6. 圆盘在光滑的水平面上平动,其质心作等速直线运动。若在此圆盘平面上作用一 力偶,则此后圆盘质心的运动状态是变速直线运动。(错) 7. 若系统的总动量为零,则系统中每个质点的动量必为零。(错) 8. 质系动量对于时间的变化率,只与作用于系统的外力有关,而与内力无关。(对) 9. 刚体在一组力作用下运动,只要各个力的大小和方向不变,不管各力的作用点如 何变化,刚体质心的加速度的大小和方向不变。 (对) 10. 冲量的量纲与动量的量纲相同。 (对) 11. 平动刚体各点的动量对一轴的动量矩之和可以用质心对该轴的动量矩表示。(对) 12. 质点系对于任意动点的动量矩对时间的导数,等于作用于质点系的所有外力对于 同一点的矩的矢量和。(错) 13. 因为质点系的动量为m C p v =,所以质点系对O 点的动量矩为 ()M m O C O L v =。 (错) 14. 质点系的内力不能改变质点系的动量与动量矩。(对) 15. 刚体的质量是刚体平动时惯性大小的度量,刚体对某轴的转动惯量则是刚体绕该 轴转动时惯性大小的度量。(对) 16. 机械能守恒定理是,当质点系不受外力作用时,则动能与势能之和等于零。 (错) 17. 系统内力所做功之代数和总为零。 (错) 18. 如果某质点系的动能很大,则该质点系的动量也很大。(错) 19. 在使用动静法时,凡是运动着的质点都应加上惯性力。 (错) 20. 平移刚体惯性力系可简化为一个合力,该合力一定作用在刚体的质心上。 ( 对) 21. 具有垂直于转轴的质量对称面的转动刚体,其惯性力系可简化为一个通过转轴的 力和一个力偶,其中力偶的矩等于对转轴的转动惯量与刚体角加速度的乘积,转向与角加速度相反。(对) 22. 应用达朗贝尔原理时,在质点系的每一质点上加上惯性力Ii F 后,作用于每一质 点的主动力i F 、约束力 Ni F ,与惯性力 Ii F 成平衡,即i F +Ni F +Ii F =0,因此, 只须写出方程i F ∑+F Ni ∑+Ii F ∑=0即可求解。(错)
第11章
第11章
虚位移原理
§11.1 位形、约束方程及其分类 §11.2 虚位移 §11.3 虚功 §11.4 虚位移原理及其应用 §11.5 通过广义力研究质点系的平衡问题 §11.6 关于虚位移原理与静力平衡条件 求解平衡问题的对比
第11.4节
§11.4 虚 位 移 原 理 解题步骤: 1. 选取研究对象 2. 受力分析:分析作虚功的主动力 ? 求主动力之间的关系或平衡位置:只画主动力 ? 求约束力:解除约束,约束力作虚功,为“主动力” 3. 给出虚位移,找出它们之间的关系 ? 虚速度法(几何法):根据约束的几何关系,通过虚速 度关系直接找出各点虚位移之间的关系 ? 分析法:选取适当的坐标系,写出约束方程并进行变分 ,即可求得各点的虚位移;或直接由广义坐标表示所求 点的坐标,变分得到广义虚位移表示的点的虚位移 4. 列出虚功方程,并求解
例题11.10 图示滑块连杆机构,已知杆长曲柄OA=r,杆受力偶矩 为M的力偶作用,试求平衡时M和F的数量关系。
O
B
30°
M
C
30 °
A
O1
D
30°
r F
例题11.10解答
60°
O
B M 解:1)研究系统 r δ r δθ C 2)作虚功的力如图示 r r C δ r δ r 3)给出虚位移,找出它们之间的关系。 A D A 30 ° 这是单自由度系统,约束许可杆 OA,O1D作转动;杆AB,CD作 D O1 r 一般平面运动,图示瞬时杆AB作瞬时平移。 F
设杆OA虚位移δθ 转向如图,则相应点的虚位移方向如图。
o o 3 rδθ Q δrA = δrC = rδθ ,δrC cos60 = δrD cos30 ∴ δrD = 3 4)列出虚功方程,并求解 r r Q ∑ δ ′W = δ ′W F + δ ′W M = 0 ,即:F ? δrD + M O ( M )δθ = 0
F cos150 δrD + M δθ = 0
o
1 Qδθ ≠ 0 ∴? Fr + M = 0 2
( ? 1 Fr + M ) δθ = 0 2
F = 2M r
习 题 11-1 质量为m 的质点在平面Oxy 内运动,其运动方程为:t b y t a x ωω2sin ,cos ==。其中a 、b 和w 均为常量。试求质点对坐标原点O 的动量矩。 t a x v x ωωsin -== t b y v y ωω2cos 2== x mv y mv L y x O +-= )cos 2cos 22sin sin (t a t b t b t a m ωωωωωω?+?= )cos 2cos 22sin (sin t t t t mab ωωωωω?+?= )cos 2cos 2cos sin 2(sin t t t t t mab ωωωωωω?+?= )2cos (sin cos 22t t t mab ωωωω+= t mab ωω3cos 2= 11-2 C 、D 两球质量均为m ,用长为2 l 的杆连接,并将其中点固定在轴AB 上,杆CD 与轴AB 的交角为θ,如图11-25所示。如轴AB 以角速度w 转动,试求下列两种情况下,系统对AB 轴的动量矩。(1)杆重忽略不计;(2)杆为均质杆,质量为2m 。 图11-25 (1) θθ222sin 2)sin (2ml l m J z =?= θω22sin 2l m L z = (2) θθ2202sin 32d )sin (2ml x x l m J l z ==? 杆 θ22sin 3 8 ml J z = θ ω22sin 3 8 l m L z = 11-3 试求图11-26所示各均质物体对其转轴的动量矩。各物体质量均为m 。 图11-26 (a) ω2 3 1ml L O = (b) 22291)6(121ml l m ml J O =+= ω29 1ml L O -=
动量矩定理 12-1 质量为m 的点在平面Oxy 内运动,其运动方程为: t b y t a x ωω2sin cos == 式中a 、b 和ω为常量。求质点对原点O 的动量矩。 解:由运动方程对时间的一阶导数得原点的速度 t b t y v t a t x v y x ωωωω2cos 2d d sin d d ==-== 质点对点O 的动量矩为 t a t b m t b t a m x mv y mv m M m M L y x O O ωωωωωωcos 2cos 22sin )sin ()()(0??+?-?-=?+?-=+=y x v v t mab ωω3 cos 2= 12-3 如图所示,质量为m 的偏心轮在水平面上作平面运动。轮子轴心为A ,质心为C ,AC = e ;轮子半径为R ,对轴心A 的转动惯量为J A ;C 、A 、B 三点在同一铅直线上。(1)当轮子只滚不滑时,若v A 已知,求轮子的动量和对地面上B 点的动量矩。(2)当轮子又滚又滑时,若v A 、ω已知,求轮子的动量和对地面上B 点的动量矩。 解:(1)当轮子只滚不滑时B 点为速度瞬心。 轮子角速度 R v A =ω 质心C 的速度 )(e R R v C B v A C += =ω 轮子的动量 A C mv R e R mv p += =(方向水平向右) 对B 点动量矩 ω?=B B J L 由于 222)( )( e R m me J e R m J J A C B ++-=++= 故 [] R v e R m me J L A A B 22)( ++-= (2)当轮子又滚又滑时由基点法求得C 点速度。 e v v v v A CA A C ω+=+= 轮子动量 )(e v m mv p A C ω+== (方向向右) 对B 点动量矩 ) ( )()()( )( 2e mR J e R mv me J e R e v m J BC mv L A A A A C C B +++=-+++=+=ωωωω 12-13 如图所示,有一轮子,轴的直径为50 mm ,无初速地沿倾角?=20θ的轨道滚下,设只滚不滑,5秒内轮心滚动的距离为s = 3 m 。试求轮子对轮心的惯性半径。 解:取轮子为研究对象,轮子受力如图(a )所示,根据刚体平面运动微分方程有 F mg ma C -=θsin (1) J C α = Fr (2) 因轮子只滚不滑,所以有 a C =αr (3)
(a ) 习题11-1图 第11章 达朗贝尔原理及其应用 11-1 均质圆盘作定轴转动,其中图(a ),图(c )的转动角速度为常数,而图(b ),图(d )的角速度不为常量。试对图示四种情形进行惯性力的简化。 解:设圆盘的质量为m ,半径为r ,则如习题11-1解图: (a )2I ωmr F =,0I =O M (b )2n I ωmr F =,αmr F =t I ,αα2 I 2 3mr J M O O = = (c )0I =F ,0I =O M (d )0I =F ,αα2 I 2 1mr J M O O = = 11-2矩形均质平板尺寸如图,质量27kg ,由两个销子 A 、B 悬挂。若突然撤去销子B ,求在撤去的瞬时平板的角加 速度和销子A 的约束力。 解:如图(a ):设平板的质量为m ,长和宽分别为a 、b 。 αα375.3I =?=AC m F ααα5625.0])(12 1 [222I =?++==AC m b a m J M A A ∑=0)(F A M ;01.0I =-mg M A ;2rad/s 04.47=α ∑=0x F ;0sin I =-Ax F F θ;其中:6.05 3sin ==θ N 26.956.004.47375.3=??=Ax F ∑=0y F ;0cos I =-+mg F F Ay θ;8.05 4sin ==θ 习题11-2图 习题11-1解图 (a ) (a )
N 6.1378.004.47375.38.927=??-?=Ay F 11-3在均质直角构件ABC 中,AB 、BC 两部分的质量各为3.0kg ,用连杆AD 、DE 以及绳子AE 保持在图示位置。若突然剪断绳子,求此瞬时连杆AD 、BE 所受的力。连杆的质量忽略不计,已知l = 1.0m ,φ = 30o。 解:如图(a ):设AB 、BC 两部分的质量各为m = 3.0kg 直角构件ABC 作平移,其加速度为a = a A ,质心在O 处。 ma F 2I = ∑=0)(F O M ; 04 sin )(43cos 4cos =+--l F F l F l F B A A B ??? (1) ∑=0AD F ; cos 2=-+?mg F F B A (2) 联立式(1)和式(2),得:A B F mg F 3+= N 38.5)13(4 1 =-=mg F A ; N 5.4538.53=?+=mg F B 11-4 两种情形的定滑轮质量均为m ,半径均为 r 。图a 中的绳所受拉力为W ;图b 中块重力为W 。 试分析两种情形下定滑轮的角加速度、绳中拉力和定滑轮轴承处的约束反力是否相同。 解:1、图(a ): ① Wr J O =a α Wr mr =a 22 1α mr W 2a =α (1) ②绳中拉力为W (2) ③∑=0x F ,0=Ox F (3) ∑=0y F ,W F Oy = (4) 2、图(b ): ① b 2I 2 1 αmr M O = (5) b I αr g W a g W F == (6) ∑=0O M ,0I I =-+W r r F M O (5)、(6)代入,得 ) 2(2b W mg r Wg +=α (7) ②绳中拉力(图c ): ∑=0y F ,W F T =+I b W W mg mg a g W W T 2b +=- = (8) ③轴承反力: ∑=0x F ,0=Ox F (9) ∑=0y F ,0I =-+W F F Oy W mg mgW F Oy 2+= (10) 习题11-3图 (a ) a I F (a) 习题11-4图 αa F Oy F Ox F Oy F Ox αb M I O F I W a
动力学 (MADE BY 水水) 1-3 解: 运动方程:θtan l y =,其中kt =θ。 将运动方程对时间求导并将030=θ代入得 34cos cos 22lk lk l y v = ===θθθ 938cos sin 22 32lk lk y a = -==θ θ 1-6 证明:质点做曲线运动, 所以质点的加速度为:n t a a a +=, 设质点的速度为v ,由图可知: a a v v y n cos ==θ,所以: y v v a a n = 将c v y =,ρ 2 n v a = 代入上式可得 ρ c v a 3 = 证毕 1-7 证明:因为n 2 a v =ρ,v a a v a ?==θsin n 所以:v a ?=3 v ρ 证毕 1- 10 x o y
解:设初始时,绳索AB 的长度为L ,时刻t 时的长度 为s ,则有关系式: t v L s 0-=,并且 222x l s += 将上面两式对时间求导得: 0v s -= ,x x s s 22= 由此解得:x sv x 0 -= (a ) (a)式可写成:s v x x 0-= ,将该式对时间求导得: 2002v v s x x x =-=+ (b) 将(a)式代入(b)式可得:32 20220x l v x x v x a x -=-== (负号说明滑块A 的加速度向上) 取套筒A 为研究对象,受力如图所示,根据质点矢量形式的运动微分方程有: g F F a m m N ++= 将该式在y x ,轴上投影可得直角坐标形式的运动微分方程: N F F y m F mg x m +-=-=θθsin cos 其中: 2 22 2sin ,cos l x l l x x += += θθ0,32 20=-=y x l v x 将其代入直角坐标形式的运动微分方程可得: 2 3220)(1)(x l x l v g m F ++= 1-11 o v o v F N F g m y θ