ARCGIS多边形重心
方法一:
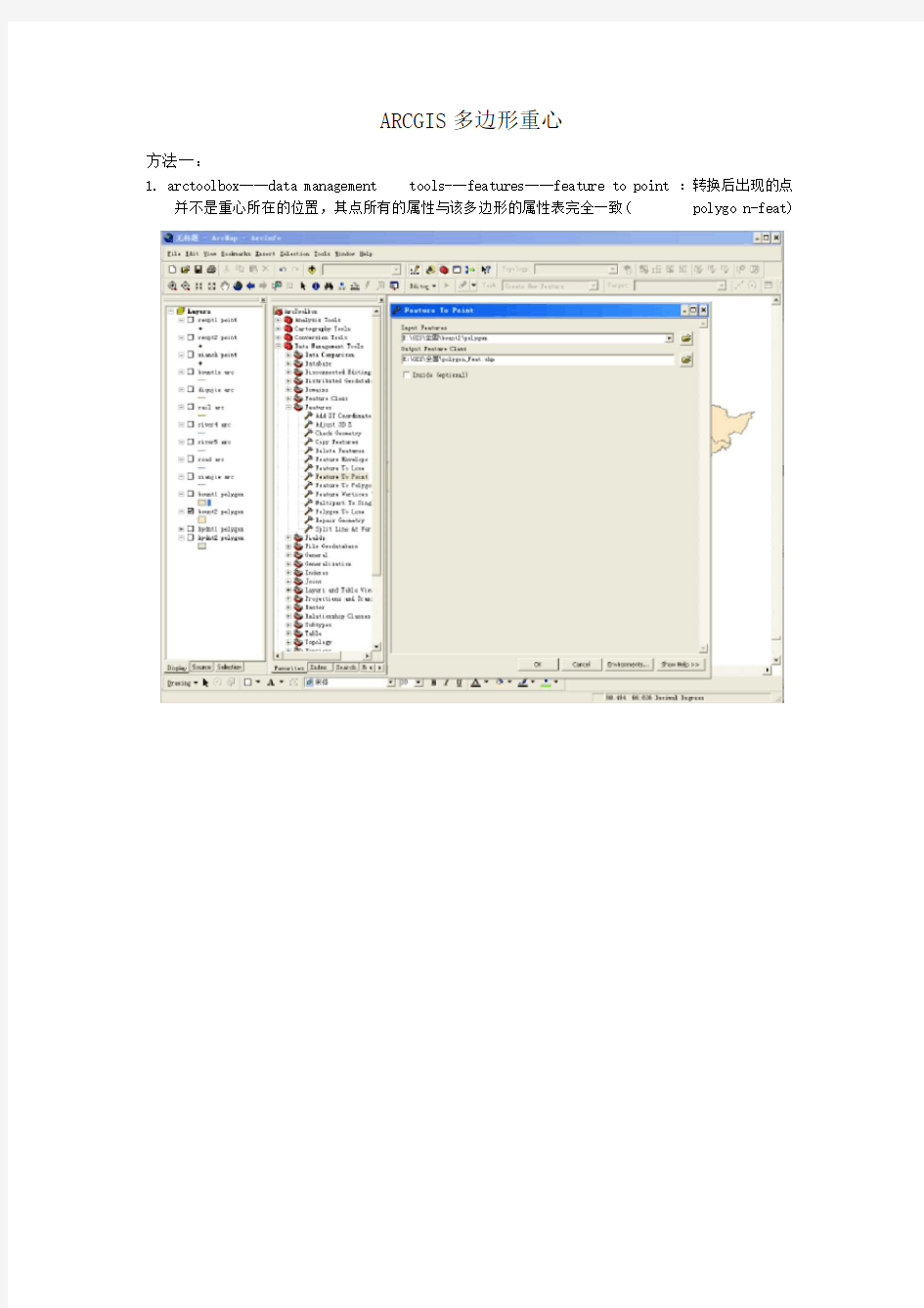
1. arctoolbox----data management tools---features----feature to point :转换后出现的点
并不是重心所在的位置,其点所有的属性与该多边形的属性表完全一致( polygo n-feat)
仓库选址重心法在物流实训教学中的研究与应用 一、仓库选址重心法在物流实训教学中研究与应用的前期准备 1设定实训初始条件仓库选址重心法是一个相当复杂的问题,影响因素相当多,完全现实的仓库选址重心法是难于进行实训的, 所以不妨假设在该实训教学过程中单位货品运入和运 出成本是相等的,不考虑在不满载的情况下增加的特殊配送费用,使用数学位置坐标系 (在国际选址中,经常采用经度和纬度建立坐标标出各个地点的位置,根据各点在坐标系中的横纵坐标值求出总配送成本最低的位置坐标 X 和 Y ,具体公式是:库选址的理论最佳选址位置, ( X0 ,Y0 现有需求点 i 的位置坐标, Ti --第 i 个需求点的配送量。 2.物流实训班级的学生分组假设物流实训班级的学生人数为 40名,将全班学生分成 8个组,每组 5人,每组设置选址决策分析员 1名、选址实施员 3名、选址记录计算员 1名,其中决策分析员的主要职责是确定选址方法、选用选址工具、分析选址结果、分析理论仓库选址位置与实际实训结果仓库选址位置差异等,选址实施员主要职责是确定坐标系位置、标出需求点位置、凿洞穿线、确定配送量的模拟硬币数量、绑定硬币、标出实训的仓库选址具体位置等, 选址记录计算员的主要职责是记录决策分析员所提供的决策数据与决策结果, 记录选址实施员实施过程所产生的相关数据与结果、利用位置坐标系与仓库选址重心法公式 计算仓库理论位置坐标。 3.准备物流实训教学所需的工具深圳地图模型图纸 A3纸每组一张; A3纸大小的硬纸板每组一张,要求能在硬纸板上至少凿穿 6个细小光滑的洞;重量可忽略不计且长度为 0.5 米的白色细线每组至少 6条, 重量可近似为零的小型薄膜袋每组至少 8个,学生自备硬币每人至少 9枚,透明胶每组 1卷,宣传类大白纸每组一张,小图钉至少每组10枚,小钻笔每组一支, 直尺与铅笔每组一支, 白板笔每组一支, 清晰的实训内容与实训要求每组一份。
正多边形的有关计算 一、素质教育目标 (一)知识教学点 使学生学会将正多边形的边长、半径、边心距和中心角、周长、面积等有关的计算问题转化为解直角三角形的问题. (二)能力训练点 1.通过定理的证明过程培养学生观察能力、推理能力、概括能力; 2.通过一定量的计算,培养学生正确迅速的运算能力; 3.通过用不同方法求正多边形的内角,培养学生的发散思维能力和选优意识; 4.从具体边数的正n边形得到一般正n边形的计算图培养学生化归、转化的数学思想. (三)德育渗透点 1.由具体边数的正多边形计算图过渡到一般计算图,渗透了“从特殊到一般,再由一般到特殊”的辩证唯物主义认识观; 2.正多边形计算图的得出渗透了化繁为简、化难为易二矛盾相互依存、相互转化的思想; 3.通过正多边形的有关计算,培养学生仔细认真、一丝不苟、严谨的科学态度; 4.通过正多边形有关计算公式的推导,培养学生不断探索科学奥秘的创新精神. 二、教学重点、难点、疑点及解决方法 1.重点:1.化正多边形的有关计算为解直角三角形问题定理.2.正多边形计算图及其应用. 2.难点:正确地将正多边形的有关计算问题转化为解直角三角形的问题解决、综合运用几何知识准确计算.
3.疑点及解决方法:学生对只画出正n边形的一部分图形的计算图生疏,用它分析、计算有疑虑.为此计算图的抽象应由具体边数的正多边形计算图逐步过渡. 三、教学步骤 (一)明确目标 前几课我们学习了正多边形的定义、概念、性质,今天我们来学习正多边形的有关计算. (二)整体感知 大家知道正多边形在生产和生活中有广泛的应用性,伴随而来的有关正多边形计算问题必然摆在大家的面前,如何解决正多边形的计算问题,正是本堂课研究的课题. (三)重点、难点的学习与目标完成过程 哪位同学回答,什么叫正多边形.(安排中下生回答:各边相等,各角相等的多边形.) 什么是正多形的边心距、半径?(安排中下生回答:正多边形内切圆的半径叫做边心距.正多边形外接圆的半径叫做正多边形的半径.) 正多边形的边有什么性质、角有什么性质?(安排中下生回答:边都相等,角都相等.) 什么叫正多边形的中心角?(安排中下生回答:正多边形的一边所对正多边形外接圆的圆心角.) 正n边形的中心角度数如何计算?(安排中下生回答:中心角的度数 正n边形的一个外角度数如何计算?(安排中下生回答:一个外角度 哪位同学有所发现?(安排举手学生:正n边形的中心角度数=正n边形的一个外角度数.)
四边形重心的探索 四边形重心的探索是人教版八年级数学第十九章的一节内容,课文中论述了线段,三角形以及一些其他规则平面图形的重心确定方法,多边形重心一般用悬挂法确定其重心。 对于四边形,除此之外,还可用以下方法来确定其重心,方法如下: 如图1,在四边形ABCD 中,先连接它的一条对角线AD ,这个四边形被分成了两个三角形⊿ADC 和⊿ABC ,取AD 中点E ,DC 中点M ,BC 中点N ,连接AM, DE 相交于P , 连接AN,BE 相交于点Q ,连接PQ 相交于点F, 在PQ 上截取QO=PF , 则O 点为四边形ABCD 的重心。 图1 这样作图的依据是:因为M,E,N 都是中点,所以P 和Q 分别是⊿ADC 和⊿ABC 的重心。,这时可将这两个三角形看作两个质点,如图2,则四边形ABCD 的重心必在PQ 的连 图2 线上,可将连线段视作杠杆,两个三角形的面积视为重量,那么支点就是四边,若O 点为四边形重心,则必有下式成立::S ⊿ABC ×OQ=S ⊿ADC ×OP 。 因为P ,Q 分别是两个三角形的重心,由重心性质可知 32==AN AQ AM AP ,所以P Q ∥MN ,由三角形相似得NE QF ME PF =,所以NE ME QF PF =,由中位线定理MN ∥BD,所以PQ ∥BD,设BD 和AC 相交于T ,所以PF:DT=QF:BT 即PF :QF=DT :BT=S ⊿ADC:S ⊿ABC,而S ⊿ADC:S ⊿ABC=OQ:OP,故只须PF:QF=OQ:OP 即可。因为PF+QF=OQ+OP,所以PF=OQ,QF=OP. A B C D N M E P Q F ·O T P Q ·F ·O
谈谈平面图形的重心 宝坻三中杨春来 在新人教版八年级“课题学习重心”一节,在教学中学生通过实验很容易得到:线段的重心是线段的中点;平行四边形的重心是它的对角线的交点。通过悬挂法又可以得到三角形的重心是它的三条中线的交点。而对于任意多边形的重心也可以用悬挂法得到。问题是,用悬挂法无法找出课本上或作业本上多边形的重心。怎么画出课本上或作业本上多边形的重心呢? 课本一开始就告诉我们:“在一块均匀的木板上,找到一个点,如果用一个手指顶住这点,木板会保持平衡,这个平衡点就是这块木板的重心。”其实找重心的问题就是找平衡点的问题。由平衡我们自然可以想到杠杆原理,想到阿基米德。阿基米德在《论平面图形的平衡》一书中最早提出了杠杆原理。怎样使杠杆保持平衡?阻力×支点到阻力作用线的距离=动力×支点到动力作用线的距离,即阻力×阻力臂=动力×动力臂,即F1×L1=F2×L2。动力作用点、阻力作用点和支点在同一直线上。 我们以四边形ABCD为例来研究如何找多边形的重心。重心就是平衡点,也就是杠杆原理中的支点。如果我们把四边形ABCD的木板支起来,保持平衡,那么支点周围一定存在着很多对“动力作用点和阻力作用点”,并且这个支点一定在连接两个作用点的线段上。我们不妨先连接四边形的一条对角线,把四边形ABCD分成两个三角形,分别作出它们的重心G1,G2,并把这两个重心连起来,得到线段G1G2;再连接四边形的另一条对角线,再把四边形ABCD 分成两个三角形,分别作出它们的重心G3,G4,再把这两个重心连起来。得到线段G3G4;线段G1G2与线段G3G4的交点就是四边形ABCD的重心。
GG4?BCD 的面积() = 22.93 厘米3 GG3?ABD 的面积() = 22.93 厘米3GG2?ACD 的面积() = 28.71 厘米 3 GG1?ABC 的面积() = 28.71 厘米3ACD 的面积 = 15.46 厘米2 ABC 的面积 = 22.61 厘米2BCD 的面积 = 25.68 厘米2ABD 的面积 = 12.40 厘米2GG2 = 1.86厘米 GG1 = 1.27厘米GG4 = 0.89厘米GG3 = 1.85厘米 B 可见:GG 1*△ABC 的面积=GG 2*△ACD 的面积, GG 3*△ABD 的面积=GG 4*△BCD 的面积。 木板的面积*厚度h*密度ρ就是木板的重量,由于木板质地相同即密度均为ρ,薄厚均匀即厚度均为h ,因此上面的两个等式就可以转化为 GG 1*△ABC 木板的重力=GG 2*△ACD 木板的重力, GG 3*△ABD 木板的重力=GG 4*△BCD 木板的重力。 所以我们用手指顶住G 点,四边形ABCD 木板就能平衡了。 我们改变一下四边形ABCD 的形状,再看看 B
质心: 质量中心简称质心,指物质系统上被认为质量集中于此的一个假想点。与重心不同的是,质心不一定要在有重力场的系统中。值得注意的是,除非重力场是均匀的,否则同一物质系统的质心与重心通常不在同一假想点上。
重心 重心,是在重力场中,物体处于任何方位时所有各组成支点的重力的合力都通过的那一点。规则而密度均匀物体的重心就是它的几何中心。不规则物体的重心,可以用悬挂法来确定。物体的重心,不一定在物体上。另外,重心可以指事情的中心或主要部分。 三角形的重心即为中线交点。 物体的重心位置,质量均匀分布的物体(均匀物体),重心的位置只跟物体的形状有关。有规则形状的物体,它的重心就在几何中心上,例如,均匀细直棒的中心在棒的中点,均匀球体的重心在球心,均匀圆柱的重心在轴线的中点。不规则物体的重心,可以用悬挂法来确定.物体的重心,不一定在物体上。
如果一个任意几何图形,其实没有中心的定义正多边形有中心,平行四边形有对称中心。 这个中心的意义其实并不很严谨。数学上本身也并没有所谓的几何中心的定义。探讨几何图形的中心一词,实际是来源于中心对称这个概念。就是说这个几何图形首先应该是中心对称的图形,那么这个图形各部分围绕某个点呈中心对称时,这个点就是这个几何图形的中心。那么后来有人把这个概念扩大了,认为所有的正多边形的重心都可以看做是这个几何图形的中心。 垂心是三角形三条高的交点 内心是三角形三条内角平分线的交点即内接圆的圆心 重心是三角形三条中线的交点 外心是三角形三条边的垂直平分线的交点即外接圆的圆心 旁心,是三角形两条外角平分线和一条内角平分线的交点 正三角形中,中心和重心,垂心,内心,外心重合! 垂心定理:三角形的三条高交于一点。该点叫做三角形的垂心 内心定理:三角形的三内角平分线交于一点。该点叫做三角形的内心。旁心定理:三角形一内角平分线和另外两顶点处的外角平分线交于一点。该点叫做三角形的旁心。三角形有三个旁心。 重心定理:三角形的三条中线交于一点,这点到顶点的 离是它到对边中点距离的2倍。该点叫做三角形的重心。 外心定理:三角形的三边的垂直平分线交于一点。该点叫做三角形的
模型的建立与求解 一、计算凸多边形的重心 对于任意凸多边形,我们以其重心为蛛网的中枢区中心,也即蜘蛛的等待猎物点,以此点出发,先发出放射丝,再织捕丝。 1.计算任意凸多边形重心的理论基础 1. 四边形的重心作法:连接出四边形的一条对角线,这样四边形就变成两个三角形的组合体,分别作出两个三角形的重心,并连接两个重心成一条线段AB ,同样,连接出四边形的另一条对角线,四边形就变成另外两个三角形的组合体,分别作出这两个三角形的重心,并连接两个重心成一条线段CD ,则线段AB ,CD 的交点就是四边形的重心。 2.五边形的重心作法:连接出五边形的任一条对角线,将五边形分为1个三角形与一个四边形组合体,分
别作出三角形的重心,和四边形的重心,并连成线段AB;连接五边形的另外一条对角形,将五边形分为另1个三角形与四边形的组合体,分别作出三角形与四边形的重心,并连接成线段CD;则AB、CD的交点就是五边形的重心。 3、用数学归纳法,对于六边形、七边形,N边形,都可以用上述方法,先连接出一条对角线,将N边形化为一个三角形与(N-1)边形,或四边形与(N-2)边形,然后分别作出重心,并连接成线段,然后再连接另外一条对象线,分别作出两个组合体的重心并连接成线段,两条线段的交点就是N边形的重心。 2.重心计算的算法程序实现: 有了以上理论基础,我们通过C++语言编写了一个计算任意凸多边形的程序,算法思想如下,算法程序见附录一。
○1在平面上取一点(一般取原点)得到N个三角形OP[i]P[i+1](其中点的顺序为逆时针) ○2分别求出这N个三角形的重心Ci和面积Ai(注意此处面积是有向面积, 就是用叉乘求面积时保留其正负号) ○3求出A = A1+A2+...+AN(同样保留正负号的代数相加) ○4重心C = sigma(Ai+Ci)/A; 附录一:任意凸多边形重心C++算法 #include
正多边形的计算之万法归宗解直角三角形 仪陇县银山初级中学董兴胜各边相等、各角也相等的多边形叫做正多边形,正多边形的外接圆和内切圆的圆心重合叫正多边形的中心。外接圆半径叫正多边形的半径.内切圆的半径叫正多边形的边心距。正多边形的每 一边所对的圆心角叫中心角,中心角的度数是 n 360。 笔者在教学中,发现学生对涉及有关正多边形的计算时,比如计算正多边形的边长,半径,正多边形的周长,正多边形的面积,或者是两个正多边形有关比值的计算,往往无从下手,表现在一遇到题就去画图,下手就算,既费时,又方向不清,结果往往是无功而返。通过多年的教学经验总结,提出了化归思想,即任何正多边形的计算问题都可以转化为一个重要的直角三角形,从而将正多边形的问题转化为解直角三角形的问题。 首先来认识一下正多边形的基本知识,仅以N=3,456为例。 一计算正N边形的内角(如下图) 很容易知道正n边形的每个内角都等于 二将正N边形分割成等腰三角形(如下图所示) 设O为各正多边形的中心,即外接圆和内切圆的圆心,正n边形的n条半径分正n边形为n个全等的等腰三角形. 三将正N边形分割成直角三角形(如下图所示)
这一步只需要作正多边形的边心距,边心距又把上一步n 个等腰三角形分成了个2N 个直角三角形,这些直角三角形也是全等 的.因此正n 边形的半径和边心距把正n 边形分成2n 个全等的直角三角形。 通过这三步,实质是把正多边形的问题向直角三角形转化.由于这些直角三角形的斜边都是正n 边形的半径R ,一条直角边是正n 边形的边心距r n ,另一条直角边是正n 边形边长a n 的一半,一 个锐角是正n 边形中心角 的一半,即 ,所以,就把正n 边形的有关计算归结为解直角三角形问题.为了让学生理解深刻,容易记忆,笔者特总结出如下的口诀和图形: 一个中心,两条半径, 两半径之夹角等于中心角之一半,半径夹角之对边等于边长之一半
一、简单重心法(运输量重心法) 单一物流中心选址---重心法 公式:x0 = ( ∑ xiwi ) / ( ∑ wi) y0 = ( ∑ yiwi ) / ( ∑ wi) ( x0 , y0 ) ----新设施的地址 ( xi , yi ) ----现有设施的位置 wi ----第i个供应点的运量 例题:某物流园区,每年需要从P1地运来铸铁,从P2地运来钢材,从P3地运来煤炭,从P4地运来日用百货,各地与某城市中心的距离和每年的材料运量如表 所示。请用重心法确定分厂厂址。 解: x0 = ( 20×2000+60×1200+20×1000+50×2500 ) / ( 2000+1200+1000+2500) = 35.4 y0 = ( 70×2000+60×1200+20×1000+20×2500 ) / ( 2000+1200+1000+2500) = 42.1 所以,分厂厂址的坐标为(35.4 , 42.1) 二、迭代重心法(“运输量—运输距离—运输费率”重心法) 单一物流中心选址---迭代重心法 单一物流中心选址---迭代重
公式:X = ( ∑Q i R i X i/D i) / ( ∑Q i R i/D i ) Y= ( ∑Q i R i Y i/D i) / ( ∑Q i R i/D i ) D i= ( ( X i-X)2+(Y i-Y)2 )1/2 F = ∑Q i R i D i (Xi , Yi)----现有目标的坐标位置 Qi----运输量 Ri----运输费率 F----总运费 (X , Y)----新仓库的位置坐标 Di----现有目标到新仓库的距离 解题方法: (1)令Di=1 A、求出仓库的初始位置; B、将求出的仓库位置(X,Y)代入Di公式中,求出客户到仓库初始位置的距离; C、计算出仓库初始位置的总运费ΣQiRiDi; ( 2 ) 迭代计算: A、将Di代入原公式,求出仓库的新位置坐标(X ,Y); B、将求出的(X ,Y)代入Di公式中求出Di; C、计算出仓库新位置的总运费ΣiQiRiDi …不断迭代,直到求出的仓库位置和总运费越来越接近于不 变,即为所得; 注意:牵涉到运输费率要用重心法做;但如无费率,又要求 用迭代重心法计算,则令费率为1。 例题:某企业的两个工厂P1、P2分别生产A、B两种产品,供应三个市场M1、M2、M3。已知条件如表一所示。现需设置一个中转仓库,A、B两种产品通过该仓库间接向三个市场供货。请使用迭代重心法求出仓库的最优选址。 表一
。 选址重心法模型 文章来源:宝库企业管理网更新时间: 2007-11-13 16:28:50 重心法是一种布置单个设施的方法,这种方法要考虑现有设施之间的距离和要运输的货物量。它经常用于中间仓库的选择。在最简单的情况下,这种方法假设运入和运出成本是相等的,它并未考虑在不满载的情 况下增加的特殊运输费用。 重心法首先要在坐标系中标出各个地点的位置,目的在于确定各点的相对距离。坐标系可以随便建立。 在国际选址中,经常采用经度和纬度建立坐标。 然后,根据各点在坐标系中的横纵坐标值求出成本运输最低的位置坐标X 和 Y ,重心法使用的公式是: 式中 CX-- 重心的 x 坐标; Cy-- 重心的 y 坐标; Dix-- 第 i 个地点的 x 坐标; Diy-- 第 i 个地点的 y 坐标; Vi-- 运到第 i 个地点或从第I 个地点运出的货物量。 最后,选择求出的重心点坐标值对应的地点作为我们要布置设施的地点。 重心法: 1 、现假设有五个工厂,坐标分别为P1( 1, 2 ),P2( 7,4 ),P3( 3,1 ),P4( 5,5 ),P5( 2,6 )。 现要建立一个中心仓库为五个工厂服务。工厂到中心仓库的运输由载货汽车来完成,运
量按车次计算,分别为 3 , 5, 2, 1 , 6 次每天。求这个中心仓库的位置。 解:设物流费用与车次数量成正比,则相应的物流费用系数为:3,5,2, 1,6。在坐标轴上标出各个点的相应位置,设总运输费用最低的位置坐标为X 和 Y,根据重心法的计算方法,可求得中心仓库的坐标。计算过程如下: 6 P5(2, 6):6 5 P4(5, 5):1 4 P2(7, 4):5 3 2 P1(1, 2):3 1 P3(3, 1):2 0 1 2 3 4 5 6 7 (3 1) (5 7) (2 3) (1 5) (6 2) 61 X 3 5 2 1 6 3.588 17 (3 2) (5 4) (2 1) (1 5) (6 6) 69 Y 3 5 2 1 6 4.059 17 故所求中心仓库的理论位置在原坐标系里的位置为( 3.588 ,4.059 )。 2 、易出莲花超市要在江西省南昌市建立一所地区级中央配送中心,要求该配送中心能够覆 盖该地区五个连锁店,连锁店的坐标及每月的销售量数据如表所示,要求求出一个理论 上的配送中心的位置。 位置坐标月销售额连锁店 A ( 325,75 )1500 连锁店 B (400,150 )250 连锁店 C (450,350 )450
单一物流中心选址重心法程序设计 重心法是一种模拟方法。这种方法将物流系统中的需求点和资源点看成是分布在某一平面范围内的物流系统,各点的需求量和资源量分别看成是物体的重量,物体系统的重心作为物流网点的最佳设置点,利用求物体系统重心的方法来确定物流网点的位置。 i d i R n m i i V TC ∑+==1 min 运输总费用(1) 式中:V i —i 点运输量; R i —待定物流中心到i 点的运输费率; d i —待定物流中心到i 点的距离。 求解算法—数值分析法(重心法) 1) 设供应点和需求点所在地的坐标为(X i ,Y i ),待定物流中心的位置坐标为(X 0,Y 0) 则 ()()2020Y Y X X d i i i -+-=(2) 2) 将(2)式代入(1)式,然后求运输总费用TC 对X 0和Y 0的偏导数,并令其等于 零。 ∑-+-=2020)()(Y Y X X R V TC i i i i 0)(00=--=??∑i i i i d X X R V X TC
00=-∑∑i i i i i i i d R V X d X R V ∑ ∑= )()(0 i i i i i i i d R V d X R V X (3) ∑∑= ) ()(0i i i i i i i d R V d Y R V Y (4) 上述两式中仍含有未知数d i ,因此一次不能求得X 0和Y 0(解析解),需要通过迭代收敛法得到数值解。 迭代收敛法具体步骤: 1、先用重心公式估算初始选址点(大致位置): ∑ ∑= )()(0 i i i i i R V X R V X (5) ∑ ∑= )()(0 i i i i i R V Y R V Y (6) 2、将X 0和Y 0代入公式2,计算d i (i=1,2,…,m+n ); 3、将d i 代入公式3和4,解出修正值X 0和Y 0; 4、根据修正值X 0和Y 0,再重新计算d i ; 5、重复步骤3和4,直至X 0和Y 0的值在连续迭代过程中不再变化,即△X 0≈0,△Y 0≈0,即得到精确仓库选址位置,继续计算无意义。 程序设计具体步骤: Step1: 利用几何重心公式(5)和(6)估算初始点X 0,Y 0 ∑∑= ) ()(0i i i i i R V X R V X ∑ ∑=)()(0 i i i i i R V Y R V Y Step2: 将X 0,Y 0代入距离公式(2),计算d i (i=1,2, (5) 2012011)()(Y Y X X d -+-=
几何中心 三角形的中心 几何学中,n维空间中一个对象X的几何中心或中心、重心、形心是将X分成矩相等的两部分的所有超平面的交点。非正式地说,它是X中所有点的平均。 如果一个对象具有一致的密度,或者其形状和密度具有某种对称性足以确定几何中心,那么它的几何中心和质量中心重合。该条件是充分但不是必要的。 有限个点总存在几何中心,可以通过计算这些点的每个坐标分量的算术平均值得到。这个中心是空间中一点到这有限个点距离的平方和的惟一最小值点。点集的几何中心在仿射变换下保持不变。 一个凸对象的几何中心总在其内部。一个非凸对象的几何中心可能在外部,比如一个环或碗的几何中心不在内部。 地理学中,地球表面一个区域的几何中心也称为地理中心。 三角形的中心 形心是三角形的幾何中心,通常也称为重心,三角形的三條中线(頂點和對邊的中點的連線)交點,此點即為重心[1]。 三條中線共點證明
三條中線共點證明 用西瓦定理逆定理可以直接證出: 因此三線共點。[2] 中心分每条中线比为2:1,这就是说距一边的距离是该边相对顶点距该边的1/3。如右图所示: 如果三角形是由均匀材料做成的薄片,那么几何中心也就是质量中心。它的笛卡尔坐标是三个顶点的坐标算术平均值。也就是说,如果三顶点位于(xa,ya),(xb,yb),和(xc,yc),那么几何中心位于: 三角形的中心一般用字母G 表示。在任何一个三角形中,外心O、中心M、九点圆圆心F 和垂心H 四点共线,且。这个定理最早由欧拉证明, 故称为欧拉定理,这条线称为欧拉线。类似的有,内心I、中心G 和奈格尔点N 三点共 线,且。 三角形中心的等角共轭点称为类似重心。 中心分中线为2:1的证明 设三角形ABC 的中线AD,BE 和CF 交于三角形的中心G,延长AD 至点O 使得 那么三角形AGE 和AOC 相似(公共角A,AO = 2 AG,AC = 2 AE),所以OC 平行于GE。但是GE 是BG 的延长,所以OC 平行于BG。同样的,OB 平行于CG。 从而图形GBOC 是一个平行四边形。因为平行四边形对角线互相平分,对角线GO 和BG 的交点使得GD = DO,这样 所以,,或,这对任何中线都成立。 性質
19.3梯形 等腰梯形的性质 【导学目标】 1.知道梯形、等腰梯形、直角梯形的有关概念;能说出并证明等腰梯形的两个性质;等腰梯形同一底上的两个角相等;两条对角线相等。 2.会运用梯形的有关概念和性质进行有关问题的论证和计算。 3.通过添加辅助线,把梯形的问题转化成平行四边形或三角形问题,体会图形变换的方法和转化的思想。 【导学重点】 探索梯形的有关概念、性质及其应用。 【导学难点】 探索等腰梯形的性质。 【导学指导】 学习教材P106-P107相关内容,完成下列问题: 一、自主学习 1.什么是梯形?什么是梯形的上底?什么是梯形的下底?什么是梯形是高?什么是梯形 的腰? 2.什么是等腰梯形?什么是直角梯形? 二、合作学习 等腰梯形有哪些性质?你是如何发现的?你能证明它吗?三、训练为能 1、在梯形ABCD中,已知AD∥BC,∠B=50°,∠C=80°,AD=a,BC=b,则DC= 。 2、直角梯形的高为6cm,有一个角是30°,则这个梯形的两腰分别是和。 3、等腰梯形ABCD中,AB∥CD,AC平分∠DAB,∠DAB=60°,若梯形周长为8cm,则AD= . 4、等腰梯形ABCD中,AB=2CD,AC平分∠DAB,AB=4√3, (1)求梯形的各角。 (2)求梯形的面积。 5、如图在等腰梯形ABCD中,AD∥BC,AD=DC=AB,BD=BC,求∠A的度数. D C B A A B C D 6、.①在梯形ABCD中,AD∥BC,对角线AC⊥BD,且AC=5,BD=12,求梯形中位线的长②若AD=2,BC=3,E、F分别为AC、BD中点,求EF. 7、下列命题中,真命题是() A、有一组对边平行但不相等的四边形是梯形 B、直角梯形中只有一个直角 C、等腰梯形的对角线相等且互相垂直 D、等腰梯形是轴对称图形,有两条对称轴 8、如图,在梯形ABCD中,∠D=90°,AD=DC=4,AB=1,E为AD的中点,则点E到BC的距离为___________. 四、小结反思 本节课你有哪些收获,与同伴交流一下。 五、拓展练习 如图:已知在等腰梯形ABCD中,对角线AC=BC+AD,求∠DBC的度数。 B C
重心法选址项目分析实例 例题一:某物流园区,每年需要从P1地运来水果,从P2地运来蔬菜,从P3地运来乳制品,从P4地运来日用百货,各地与某城市中心的距离和每年的材料运量如表所示。见书本30页 1、物流中心选址的原则? 2、物流中心选址的主要影响因素? 3、重心法的计算原理? 4、根据表中数据,使用重心法确定分厂厂址。 (1)物流中心选址的原则答:不同的物流系统对物流中心的选址要求不同,但总体来说物流中心的选址应遵从以下原则:充分考虑服务对象的分布、经济发展中心地区或城市、各种交通方式重叠和交会地区、物流资源较优地区、土地开发资源较好地区、有利于整个物流网络的优化、有利于各类节点的合理分工和协调配合、地区管理及人才资源较好地区。 (2)物流中心选址的主要影响因素答:物流中心选扯的影响因素可分为外部因素和内部因素两个方面。外部因素包括:(a)土地的可得性和成本。由于一般物流中心规划占地面积都较大,所以在选址时必须考虑能否在备选区域得到足够面积的土地,同时由于土地的稀缺性,所以地价的高低将直接影响物流中心的选址以及网点布局,这些都是选址时必须注意的。(b)交通的便利性。运输成本在物流中心运营成本中的占有比例很高,所以在物流中心选址时,必须考虑对外运输渠道的便利性,以及未来交通与邻近地区的发展状况等因素。(c)政治及经济因素。在物流选址时应综合考虑那些政治稳定、政策优惠、税收合理的国家或地区。(d)劳动力因素。物流中心属于劳动密集型作业,所以存在对一定量劳动力资源的依赖;同时,随着机械化、信息化水平的提高,对劳动力素质的要求也提高了。所以在选址时,还必须考虑劳动力资源的来源、技术水平、工作习惯、工资水平等因素。(e)货品供应和需求等市场因素。原材料与货品的来源、数量、用户对象的分布、需求层次和需求量等因素,也会影响物流中心的选址。企业的内部因素往往是物流中心选址决策考虑的主要因素。物流中心的选址决策首先要与企业的发展战略相适应为。其次,物流中心的选址和数量受到企业的产品特点、销售区域、营销策略等因素的影响。 (3)重心法的计算原理答:重心法包括基于需求量的重心法和基于吨距离的重心法等两种方法。基于需求量的重心解法:把需求量作为考察因素,它的主要步骤是首先将一个经济区域内的各需求点在坐标系中表示,并将各需求点看成一个物理系统,然后将各需求点的需求量视为物体的质量,最后通过求该物理系统的重心来确定物流中心的最佳坐落点。基于吨距离的重心法解法:因是单一设施选址,物流中心的建设以及运营成本均可以视为固定不变的,而运输费用随距离和货运量而变化,所以可以考虑在不同地点设置的物流中心因距各用户距离变化和需求量而引起运输费用的变化,找出使运输总费用最小的点,并将其作为最佳选址点。(4)重心法选址计算: x0 = ( 30×2200+70×1800+30×1500+60×2500 ) / ( 2200+1800+1500+2500) = 48.38 y0 = ( 80×2200+70×1800+30×1500+30×2500 ) / (2200+1800+1500+2500) = 52.75 所以,分厂厂址的坐标为(48.38 , 52.75) 例题二:某汽车公司,每年需要从A ,地运来橡胶,从AZ 地运来玻璃,从A :地运来发动机,从A 、地运来零配件,各地与某城市中心的距离和每年的材料运量如表
问:土方10m*10m,挖深2m,放坡系数1:0.5,旁边有个土方5m*5m,挖深2m,放坡系数1:0.5,求总体积? 答:V=(s1+s2+根下s1*s2)h/3 s1上底面积 S2下底面积, V1=(10*10+8*8+12.8)*2/3= V2=(5*5+3*3+5.8)*2/3= V=V1+V2 土方量计算方法 土方量的计算是建筑工程施工的一个重要步骤。工程施工前的设计阶段必须对土石方量进行预算,它直接关系到工程的费用概算及方案选优。在现实中的一些工程项目中,因土方量计算的精确性而产生的纠纷也是经常遇到的。如何利用测量单位现场测出的地形数据或原有的数字地形数据快速准确的计算出土方量就成了人们日益关心的问题。比较经常的几种计算土方量的方法有:方格网法、等高线法、断面法、DTM法、区域土方量平衡法和平均高程法等。 1、断面法 当地形复杂起伏变化较大,或地狭长、挖填深度较大且不规则的地段,宜选择横断面法进行土方量计算。 上图为一渠道的测量图形,利用横断面法进行计算土方量时,可根据渠LL,按一定的长度L设横断面A1、A2、A3……Ai等。 断面法的表达式为 (1) 在(1)式中,Ai-1,Ai分别为第i单元渠段起终断面的填(或挖)方面积;Li为渠段长;Vi为填(或挖)方体积。 土石方量精度与间距L的长度有关,L越小,精度就越高。但是这种方法计算量大, 尤其是在范围较大、精度要求高的情况下更为明显;若是为了减少计算量而加大断面间隔,就会降低计算结果的精度; 所以断面法存在着计算精度和计算速度的矛盾。 2、方格网法计算 对于大面积的土石方估算以及一些地形起伏较小、坡度变化平缓的场地适宜用格网法。
精确重心法 问题描述 假设有一系列点代表生产地和需求地,各自有一定量货物需要以一定的运输费率运向待定的仓库,或从仓库运出,现在要确定仓库应该位于何处才能使总运输成本最小?这是一类单设施选址问题,精确重心法是求解这类问题最有效的算法之一。 我们以该点的运量乘以到该点的运输费率再乘以到该点的距离,求出上述乘积之和最小的点,即: n i i i i 1 m in T C V R d == ∑ 其中:T C ——总运输成本 i V ——i 点的运输量 i R ——到i 点的运输费率 i d ——从位置待定的仓库到i 点的距离 i d K =其中k 代表一个度量因子,将坐标轴上的一单位指标转换为通用的距离单位,如英里等。 传统的精确重心法是对上述目标函数求偏微分,然后再使用迭代的方法,计算过程繁琐,在这里我们使用excel 软件求解。 算例:假设有两个工厂向一个仓库供货,由仓库供应三个需求中心,工厂一生产A 产品,工厂二生产B 产品。工厂和需求地的坐标、货运量和运输费率见表1,k 值取10。 表一 工厂和需求地的坐标、货运量和运输费率 第一步:建立excel 模型,输入已知数据,如图1所示 第二步:在第一步基础上,利用excel 提供的函数,分别求出各个地点到仓库的运输成本和总成本。如图2(1)和2(2)所示
第三步:用excel的“规划求解”工具求解。点击“工具”菜单,选择“规划求解”(如果没有此菜单,选择“工具——加载宏”,选择加载“规划求解”即可。),此时出现一个“规划求解参数”对话框,如图3所示。在此对话框中输入“规划求解”的参数,其中目标单元格为$J$10,目标函数求的是最小值,可变单元格为$D$5、$E$9,即仓库坐标值x和y所在的单元格。最后点击“求解”按钮求解。 第四步:保存计算结果。计算机计算完成后将会提示是否将结果保存,点击“确定”保存结果。本算例的求解结果如图4所示。求得的仓库最优坐标值为(4.910,5.058),总运输成本为21425.136美元。 分析:(1)在上述excel模型中,仓库坐标值的初始值不能为0,即D5和E5单元格均不能为0。 (2)excel的“规划求解”实际上包含一个非线性优化模块,对于求解小型问题很有效。
不规则多边形的重心如何找 平面多边形,不管多复杂,理论上都可以用尺规作图,作出它的重心 三角形的重心作法很容易,我就不多说了,(三角形三条中线的交点即是) 对于任意多边形,甚至是几个彼此分开的多边形组成的复杂图案,重心作图法就比较复杂,需要用到一些复杂的定理 首先来看下面的几个定理(它们的证明比较复杂,你可以自己尝试证明) 定理1:由两个图形A,B合并而成的一个图形C,则C的重心必在A的重心与B的重心连接的线段上。(注意,此定理也适用于A B彼此分开,没有公共点的情形) 定理2:由两个A,B合并而成的一个图形C,A的重心为点a, B的重心为点b, C的重心为点c, A的面积为Sa, B的面积为Sb,则下面条件成立: (1)点c 必在线段ab 上 (2) ac * Sa = bc * Sb 根据以上定理,特别是定理1,我们就可以从理论上用尺规作图作出作任意多边形的重心. 1.四边形的重心作法:连接出四边形的一条对角线,这样四边形就变成两个三角形的组合体,分别作出两个三角形的重心,并连接两个重心成一条线段AB,同样,连接出四边形的另一条对角线,四边形就变成另外两个三角形的组合体,分别作出这两个三角形的重心,并连接两个重心成一条线段CD,则线段AB,CD的交点就是四边形的重心。(根据定理1) 2.五边形的重心作法:连接出五边形的任一条对角线,将五边形分为1个三角形与一个四边形组合体,分别作出三角形的重心,和四边形的重心,并连成线段AB;连接五边形的另外一条对角形,将五边形分为另1个三角形与四边形的组合体,分别作出三角形与四边形的重心,并连接成线段CD;则AB、CD的交点就是五边形的重心。 3、用数学归纳法,对于六边形、七边形,N边形,都可以用上述方法,先连接出一条对角线,将N边形化为一个三角形与(N-1)边形,或四边形与(N-2)边形,然后分别作出重心,并连接成线段,然后再连接另外一条对象线,分别作出两个组合体的重心并连接成线段,两条线段的交点就是N边形的重心。
3.1仓库选址 3.1.1 重心法求最佳仓库选址的原理 重心法是根据几何的方法确定在一个平面或空间内分布有若干的点,求出一点到这若干的点的总距离最短。重心法是一种模拟方法,它将物流系统中的需求点和资源点看成是分布在某一平面范围内的物流系统,各点的需求量和资源量分别看成是物体的重量,物体系统的重心作为物流网点的最佳设置点,利用求物体系统重心的方法来确定物流网点的位置。通常重心法可以用于解决仓库的选址、配送中心的选址等问题。 重心法在解决配送中心的选址问题时,它把运输成本看成现有配送点之间的运输距离和运输的货物量的线性函数。重心法首先要在坐标系中标出各个地点的位置,目的在于确定各点的相对距离。坐标系采用经度和纬度建立坐标。这样就确定了各个配送点的具体地理位置。同时考虑各段运输路线的运输成本。 设拟建的配送中心有N 个需要收件的配送点,它们所在的位置坐标为(i i y x ,),其中i=1,2,···n ,拟建的配送中心的坐标为(x,y),如下图所示:
Y 根据在中国地图上查找各城市的经纬度得到每个城市的地理坐标(保留小数点后
货物从i 地运至配送中心所在地的运输费用是i c ,设i h 为运输费率即单位货物运输单位距离的费用,且假设配送点与配送中心所在地之间的道路为直线,距离为i d ,i w 为运输量。 则i i i i d w h c ??= ...........................(1) 且i d =22)()(i i y y x x -+- (2) 总运输费用H 为: H=i i n i i n i i d w h c ??=∑∑==1 1 (3) 由于i d 与配送中心位置(x,y)有关,因此总运输费用是x,y 的函数,将式(2)带入式(3),得: 221)()(),(i i i n i i y y x x w h y x H -+-??=∑= (4) (1)根据以上公式和案例给定的各个分拨中心的业务量求出配送中心的初始地理坐标(假设一级分拨中心的运输费率为0.05,二级分拨中心的运输费率为0.075)
计算几何-多边形的重心 1. 1 累加和求重心 设平面上有N 个离散数据点( xi , yi ) ( i = 1, 2, ., n) , 其 多边形重心G( . x1, . y1) 为: 这是求多边形最简单直观的方法。可以直接利用离散数据点的x, y坐标就能求图形重心。但是缺陷在于没有对离散数据点所围图形做任何处理和分析,精度不够。 1. 2算法一:在讲该算法时,先要明白下面几个定理。 定理1已知三角形△A1A2A3的顶点坐标Ai ( xi , yi ) ( i =1, 2, 3) 。它的重心坐标为: xg = (x1+x2+x3) / 3 ; yg = (y1+y2+y3) / 3 ; 定理2已知三角形△A1A2A3的顶点坐标Ai ( xi , yi ) ( i =1, 2, 3) 。该三角形的面积为: S = ( (x2 - x1) * (y3 - y1) - (x3 - x1) * (y2 - y1) ) / 2 ; △A1A2A3 边界构成逆时针回路时取+ , 顺时针时取-。 另外在求解的过程中,不需要考虑点的输入顺序是顺时针还是逆时针,相除后就抵消了。 原理:将多边形划分成n个小区域, 每个小区域面积为σi ,重心为Gi ( xi , yi ) ,利用求平面薄板重心公式把积分变成累加和:
由前面所提出的原理和数学定理可以得出求离散数据点所围多边形的一般重心公式:以Ai ( xi , yi ) ( i = 1, 2, ., n) 为顶点的任意N边形A1A2 .An ,将它划分成N - 2个三角形(如图1) 。每个三角形的重心为Gi (xi , . yi ) ,面积为σi。那么多边形的重心坐标G( x2, .y2) 为: 图1 多边形分解 例题:HDU 1115 Lifting the Stone 代码:如下。 1 #include
重心法 重心法是将物流系统的需求点看成是分布在某一平面范围内的物体系统,各点的需求量和资源量分别看成是物体的重量,物体系统的重心将作为物流网点的最佳设置点,利用确定物体中心的方法来确定物流网点的位置。具体过程如下。 设在某计划区域内,有N 个资源点和需求点,各点的资源量或需求量为 ) ,,2,1(n j W j =,它们各自的坐标是 ) ,,2,1)(,(n j y x j j =。该网络用图5-2示如 下: 在计划区域内准备设置一个配送中心,设该配送中心的坐标是),(y x ,配送中心至资源点或需求点的运费率是 j C 。根据求平面中物体重心的方法,可以得到: ??????? ==∑∑∑∑====n j n j j j j j j n j n j j j j j j W C Y W C y W C X W C x 1111 (5-15) 代入数值,实际求得),(y x 的值,即为所求得配送网点位置的坐标。 必须指出的是,通过上述方法求得的配送中心坐标还不是最优的,因为它没有考虑设置一个配送中心后现有资源点和需求点之间将不再直接联系而要通过该配送中心中转,运输距离将发生变化,从而运输成本也将变化。所以必须将以上方法加以如下优化。 假设配送中心的地理坐标是 ) ,(00y x 。配送中心到资源点或者需求点的发送费用为 j C ,总的发送费用为 D ,则有: ∑==n j j C D 1 (5-16) 而 j C 又可以用下面的式子来表示: j j j j d W r C = (5-17) 式(5-17)中:j r ——从配送中心到资源点或者需求点的发送费率(即单位吨公里的发送费); j W ——资源点的供应量或者需求点的发送量;