
第一章:Monte Carlo 方法概述
讲课人:Xaero Chang | 课程主页: https://www.doczj.com/doc/b36885148.html,/notes/intro2mc 本章主要概述 Monte Carlo 的一些基础知识,另外包括一个最简单的用 Monte Carlo 方法计算数值积分的例子。
一、Monte Carlo 历史渊源
Monte Carlo 方法的实质是通过大量随机试验,利用概率论解决问题的一种数值方法, 基本思想是基于概率和体积间的相似性。它和 Simulation 有细微区别。单独的 Simulation 只 是模拟一些随机的运动,其结果是不确定的;Monte Carlo 在计算的中间过程中出现的数是 随机的,但是它要解决的问题的结果却是确定的。 历史上有记载的 Monte Carlo 试验始于十八世纪末期 (约 1777 年) 当时布丰 , (Buffon) 为了计算圆周率,设计了一个“投针试验”。(后文会给出一个更加简单的计算圆周率的例 子)。虽然方法已经存在了 200 多年,此方法命名为 Monte Carlo 则是在二十世纪四十年, 美国原子弹计划的一个子项目需要使用 Monte Carlo 方法模拟中子对某种特殊材料的穿透作 用。 出于保密缘故, 每个项目都要一个代号, 传闻命名代号时, 项目负责人之一 von Neumann 灵犀一点选择摩洛哥著名赌城蒙特卡洛作为该项目名称, 自此这种方法也就被命名为 Monte Carlo 方法广为流传。
十一、Monte Carlo 方法适用用途 (一)数值积分
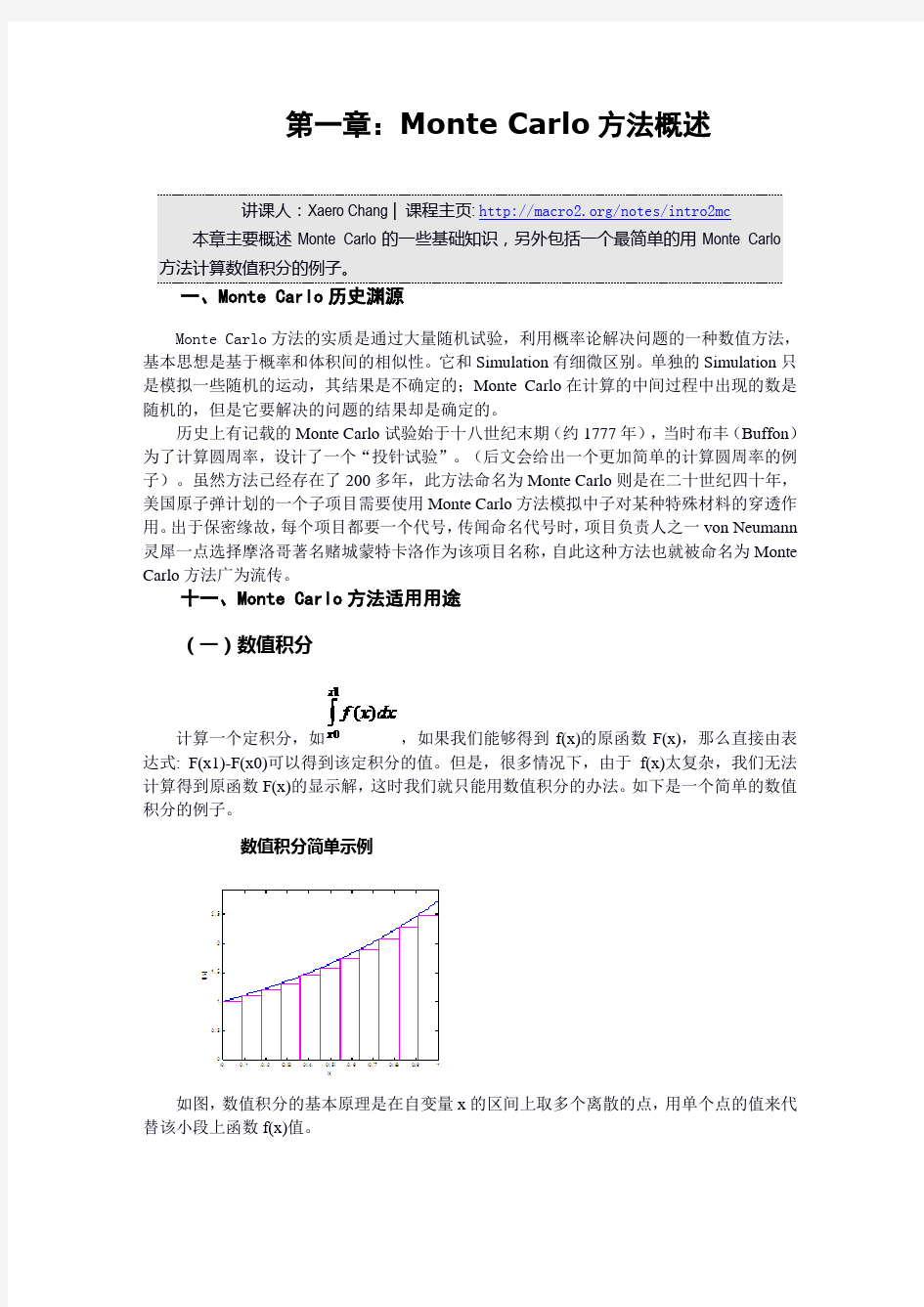
计算一个定积分,如 ,如果我们能够得到 f(x)的原函数 F(x),那么直接由表 达式: F(x1)-F(x0)可以得到该定积分的值。但是,很多情况下,由于 f(x)太复杂,我们无法 计算得到原函数 F(x)的显示解, 这时我们就只能用数值积分的办法。 如下是一个简单的数值 积分的例子。 数值积分简单示例
如图, 数值积分的基本原理是在自变量 x 的区间上取多个离散的点, 用单个点的值来代 替该小段上函数 f(x)值。 常规的数值积分方法是在分段之后,将所有的柱子(粉红色方块)的面积全部加起来, 用这个面积来近似函数 f(x)(蓝色曲线)与 x 轴围成的面积。这样做当然是不精确的,但是 随着分段数量增加,误差将减小,近似面积将逐渐逼近真实的面积。
Monte Carlo 数值积分方法和上述类似。差别在于,Monte Carlo 方法中,我们不需要 将所有方柱的面积相加, 而只需要随机地抽取一些函数值, 将他们的面积累加后计算平均值 就够了。通过相关数学知识可以证明,随着抽取点增加,近似面积也将逼近真实面积。 在金融产品定价中, 我们接触到的大多数求基于某个随机变量的函数的期望值。 考虑一 个欧式期权, 假定我们已经知道在期权行权日的股票服从某种分布 (理论模型中一般是正态 分布),那么用期权收益在这种分布上做积分求期望即可。
(五)随机最优化
Monte Carlo 在随机最优化中的应用包括:模拟退火(Simulated Annealing)、进化策略 (Evolution strategy)等等。一个最简单的例子是,已知某函数,我们要求此函数的最大值,那 么我们可以不断地在该函数定义域上随机取点,然后用得到的最大的点作为此函数的最大 值。这个例子实质也是随机数值积分,它等价于求此函数的无穷阶范数( -Norm)在定义 域上的积分。 由于在金融产品定价中, 这部分内容用的相对较不常见, 所以此课程就不介绍随机最优 化方法了。
十二、Monte Carlo 形式与一般步骤 (一)积分形式
做 Monte Carlo 时,求解积分的一般形式是:
X 为自变量,它应该是随机的,定义域为(x0, x1),f(x)为被积函数,ψ (x)是 x 的概率密 度。在计算欧式期权例子中,x 为期权到期日股票价格,由于我们计算期权价格的时候该期 权还没有到期,所以此时 x 是不确定的(是一随机变量),我们按照相应的理论,假设 x 的概率密度为ψ (x)、最高可能股价为 x1(可以是正无穷)、最低可能股价为 x0(可以是 0), 另外,期权收益是到期日股票价格 x 和期权行权价格的函数,我们用 f(x)来表示期权收益。
(二)一般步骤
我将 Monte Carlo 分为三加一个步骤: 1.依据概率分布ψ (x)不断生成随机数 x, 并计算 f(x) 由于随机数性质,每次生成的 x 的值都是不确定的,为区分起见,我们可以给生成的 x 赋予下标。如 xi 表示生成的第 i 个 x。生成了多少个 x,就可以计算出多少个 f(x)的值 2.将这些 f(x)的值累加,并求平均值 例如我们共生成了 N 个 x,这个步骤用数学式子表达就是
3.到达停止条件后退出 常用的停止条件有两种,一种是设定最多生成 N 个 x,数量达到后即退出,另一种是检 测计算结果与真实结果之间的误差,当这一误差小到某个范围之内时退出。 有趣的类比:积分表达式中的积分符合类比为上式中累加符号,dx 类比为 1/N(数 学知识告诉我们积分实质是极限意义下的累加;f(x)还是它自己,积分中的ψ (x)可类比 为依据ψ (x)生成随机数 4.误差分析
Monte Carlo 方法得到的结果是随机变量,因此,在给出点估计后,还需要给出此估计 值的波动程度及区间估计。严格的误差分析首先要从证明收敛性出发,再计算理论方差,最 后用样本方差来替代理论方差。 在本课程中我们假定此方法收敛, 同时得到的结果服从正态 分布,因此可以直接用样本方差作区间估计。详细过程在例子中解释。 这个步骤的理论意义很重要,但在实际应用中,它的重要性有所淡化,倘若你的老板不 太懂这些知识,你报告计算结果时可以只告诉他点估计即可。 注意, 前两大步骤还可以继续细分, 例如某些教科书上的五大步骤就是将此处的前两步 细分成四步。
十三、最简单的例子
举个例子:
计算从
函数从 0 到 2 的定积分值
。 =6.38905609893065 。
数学方法: 我们已知 的原函数是 , 那么定积分值就是: 计算这个数值可以在 Matlab 中输入代码: exp(2)-exp(0) 上面得到的值是此不定积分的真实值。
常规数值积分:在 区间内取 N 个点,计算各个点上的函数值,然后用函数值乘 以每个区间宽度,最后相加。Matlab 代码: N=100;x=linspace(0,2,N);sum(exp(x).*2/N) 试着调大 N 的值,你会发现,最后的结果将更接近真实值。 Monte Carlo 数值积分法:在 内随机取 N 个点,计算各个点上的函数值,最后 求这些函数值的平均值再乘以 2(为何要乘以 2 在后面小节详细讲)。看 Matlab 代码: N=100;x=unifrnd(0,2,N,1);mean(2*exp(x)) 同样的,通过增大 N,这种方法得到的结果也将越来越接近真实值。
解释
这个例子要求的积分形式是:
, 还不完全是
形式,我们先做变
换, ,这里 是 f(x);1/2 是ψ (x),它表示,在取值范围(0,2)区间内,x 服 从均匀分布。 前一例子共三条语句,逐句解释如下: N=100; 设定停止条件,共做 N 次 Monte Carlo 模拟。 x=unifrnd(0,2,N,1); 按照(0,2)区间均匀分布概率密度对 x 随机抽样,共抽取 N 个 xi。此句相当于第一个步 骤中的前半部分。 mean(2*exp(x)) 2*exp(x)作用是对每个 xi 计算 f(xi)的值,共可得到 N 个值, 这个相当于第一个步骤后半 部分;Mean()函数的作用是将所有的 f(xi)加起来取平均值,相当于第二个步骤。
这段代码中的停止条件隐含于 N 值设定中,它一次性生成 N 个 x 值,完成此次计算后 整个程序就结束了。
十四、Monte Carlo 方法的优点
对比前面常规数值积分和 Monte Carlo 数值积分代码, 同样数量的 N 值——也就意味这 几乎相同的计算量——常规数值积分结果的精确度要高于 Monte Carlo 数值积分的结果。那 么,我们为何还需要用 Monte Carlo 来算数值积分呢? 答案的关键在于,常规数值积分的精度直接取决于每个维度上取点数量,维度增加了, 但是每个维度上要取的点却不能减少。在多重积分中,随着被积函数维度增加,需要计算的
函数值数量以指数速度递增。例如在一重积分
中,只要沿着 x 轴取 N 个点;
要达到相同大小的精确度,在 s 重积分 s 中,仍然需要在每个维度上取 N 个点,s 个纬度的坐标相组合,共需要计算 N 个坐标对应 的 f()函数值。取点越多,会占用计算机大量内存,也需要更长运算时间,最终导致这种计 算方法不可行! Monte Carlo 方法却不同, 不管是积分有多少重, N 个点计算的结果精确度都差不多。 取 因此,即使在一重积分的情形下,Monte Carlo 方法的效率比不过常规数值积分,但随着积 分维度增加,常规数值积分的速度呈指数下降,Monte Carlo 方法的效率却基本不变。经验 表明,当积分重数达到 4 重积分甚至更高时,Monte Carlo 方法将远远优于常规数值积分方 法。 现在回到金融产品定价,欧式期权理论定价公式只需要一重积分,此时 Monte Carlo 方 法的效果不明显,但是如果我们考虑一个亚式期权:期限为 1 年期,期权价格基于此 1 年内 每天某个时点时的价格,全年共 252 个交易日,这样此亚式期权理论定价公式是一个 252 252 重积分。常规的数值积分方法,需要取 N 个点,这个数有多大,你自己去计算一下就知道 了(注意:N 取值要远远大于 2),常规数值积分方法不可行,只能用 Monte Carlo。 综上,如果计算高维度多重积分,如路径依赖的 exotic options(奇异期权)等金融产品 定价,我们一般用的方法都是 Monte Carlo。
十五、Monte Carlo 方法原理(选读)
Monte Carlo 方 法 计 算 的 结 果 收 敛 的 理 论 依 据 来 自 于 大 数 定 律 , 且 结 果 渐 进 地 (Asymptotically)服从正态分布的理论依据是中心极限定理。 以上两个属性都是渐进性质,要进行很多次抽样,此属性才会比较好地显示出来,如果 Monte Carlo 计算结果的某些高阶距存在,即使抽样数量不太多,这些渐进属性也可以很快 地达到。 这些原理在理论上意义重大,但由于我们一般遇上的 Monte Carlo 问题都是收敛的、结 果也都是渐进正态分布,所以工作中使用时可以不加考虑。 详细推导见相关书籍。
第二章:随机数的生成
讲课人:Xaero Chang | 课程主页: https://www.doczj.com/doc/b36885148.html,/notes/intro2mc 本章第一节会简要复习随机变量的一些概念,但学习本章最好要有一定的数学基 础。 第二节主要介绍如何生成一维概率分布的随机数, 第三节介绍如何生成高维分布的 随机数。最后略提及伪随机数问题的应对策略。
由前文可知, Monte Carlo 积分解决的问题形如 , f(x)值只需由 x 值决定, 因此此处最重要的就是如何生成服从ψ (x)概率分布的随机数。可以说,正确生成随机数, Monte Carlo 方法就做完了一半。
一、随机变量基本概念 (一)随机变量
现实世界中有很多可以用数字来衡量的事物, 站在当前时间点来看, 它们在未来时刻的 值是不确定的。例如,我们掷一骰子,在它停稳前,我们不可能知道掷出多少点(传说中的 赌王除外,哈哈);例如某只股票在明天的股价,没有人能准确知晓第二天股票的价格(不 然他就发惨了!)。但是,我们却可以描述这些事物未来各种值的可能性。
(二)离散型随机变量
离散型随机变量最重要的是分布律,即每个取值的概率是多少。例如掷骰子,我们认为 扔出任何一个点的概率都是 1/6。那么掷骰子得到的点数的分布律如下表: 骰子点数 1 2 3 4 5 6 概率 1/6 1/6 1/6 1/6 1/6 1/6
(三)连续性随机变量
连续型随机变量有两个重要的概念。概率密度函数(PDF)和累积概率分布函数(CDF), 具体定义见数学书籍。
PDF 函数本身不是概率,只有对 x 的某段区间中的 PDF 积分得到的数值才有概率的含 义。CDF 是概率的意思,点 x 上 CDF 的值表示该随机变量可能取值小于 x 的概率的大小。 如图是正态分布的 PDF 和 CDF
(四)多元分布
在这个课程里面, 我不将多维的随机变量拆分成多个一维的随机变量来表述, 而是将各 个维度组合成一个随机变量向量。 多元随机变量分布需要掌握联合分布、 边缘分布和条件分 布。 联合分布和单变量 PDF 类似,如果将其对随机变量某个取值范围做积分就可以得到随 机变量最终取值落在该区间内的概率。 边缘分布是只考虑多维随机变量中的某一维,其他维度不考虑情况下的 PDF 条件分布是固定随机变量在其他维度的取值,再考虑剩余那个维度上的 PDF。
如图是一个二维正态分布(两个维度间相关系数为 0.3)的示意图。两个小图分别是第一 和第二维度的边缘分布 PDF 图(都是标准正态分布 PDF)。右上角的大图是依据此二维正 态联合分布生成的随机数。从随机数的疏密程度可以看出联合分布 PDF 函数在该区域的大 小。 研究这些分布不是我们的目的, 只是达到目的的手段。 我们所需要做的事情是生成符合 各种分布的随机数。由分布的不同类型——连续型和离散型,常规型(Matlab 中有内置函 数)和特殊型(Matlab 中无内置函数),一维分布和多维分布——我们接下来就各种情况 分别讲述如何在 Matlab 中生成各种各样的随机数。
十六、一维随机数
两个注意事项: 1.生成随机数有两种选择,可以每次只生成一个随机数,直接用此数计算 f(x),然后循 环重复此过程,最后求平均值;另一种方法是每次生成全部循环所需的随机数,利用 Matlab 矩阵运算语法计算 f(x),不需要写循环,直接即可求平均值。前一种方法代码简单,但速度 慢;后一种方法代码相对更难写。此处一定要掌握如何生成随机数组成的向量和矩阵(单个 随机数就是一个 1*1 的矩阵) 在后面章节的例子里面一般会有两个版本的代码分别讲述这 , 两种生成方法。 2.生成了一维的随机数后,可以用 hist()函数查看这些数服从的大致分布情况。
(一)Matlab 内部函数
a. 基本随机数 Matlab 中有两个最基本生成随机数的函数。 1.rand() 生成(0,1)区间上均匀分布的随机变量。基本语法: rand([M,N,P ...]) 生成排列成 M*N*P... 多维向量的随机数。如果只写 M,则生成 M*M 矩阵;如果参数 为[M,N]可以省略掉方括号。一些例子: rand(5,1) %生成 5 个随机数排列的列向量,一般用这种格式 rand(5) %生成 5 行 5 列的随机数矩阵 rand([5,4]) %生成一个 5 行 4 列的随机数矩阵 生成的随机数大致的分布。 x=rand(100000,1); hist(x,30); 由此可以看到生成的随机数很符合均匀分布。(视频教程会略提及 hist()函数的作用) 2.randn() 生成服从标准正态分布(均值为 0,方差为 1)的随机数。基本语法和 rand()类似。 randn([M,N,P ...]) 生成排列成 M*N*P... 多维向量的随机数。如果只写 M,则生成 M*M 矩阵;如果参数 为[M,N]可以省略掉方括号。一些例子: randn(5,1) %生成 5 个随机数排列的列向量,一般用这种格式 randn(5) %生成 5 行 5 列的随机数矩阵 randn([5,4]) %生成一个 5 行 4 列的随机数矩阵 生成的随机数大致的分布。 x=randn(100000,1); hist(x,50); 由图可以看到生成的随机数很符合标准正态分布。 b. 连续型分布随机数 如果你安装了统计工具箱 (Statistic Toolbox), 除了这两种基本分布外, 还可以用 Matlab 内部函数生成符合下面这些分布的随机数。 3.unifrnd() 和 rand()类似,这个函数生成某个区间内均匀分布的随机数。基本语法 unifrnd(a,b,[M,N,P,...]) 生成的随机数区间在(a,b)内,排列成 M*N*P... 多维向量。如果只写 M,则生成 M*M 矩阵;如果参数为[M,N]可以省略掉方括号。一些例子: unifrnd(-2,3,5,1) %生成 5 个随机数排列的列向量,一般用这种格式 unifrnd(-2,3,5) %生成 5 行 5 列的随机数矩阵 unifrnd(-2,3,[5,4]) %生成一个 5 行 4 列的随机数矩阵 %注:上述语句生成的随机数都在(-2,3)区间内. 生成的随机数大致的分布。 x=unifrnd(-2,3,100000,1); hist(x,50); 由图可以看到生成的随机数很符合区间(-2,3)上面的均匀分布。
4.normrnd() 和 randn()类似,此函数生成指定均值、标准差的正态分布的随机数。基本语法 normrnd(mu,sigma,[M,N,P,...]) 生成的随机数服从均值为 mu,标准差为 sigma(注意标准差是正数)正态分布,这些 随机数排列成 M*N*P... 多维向量。如果只写 M,则生成 M*M 矩阵;如果参数为[M,N]可 以省略掉方括号。一些例子: normrnd(2,3,5,1) %生成 5 个随机数排列的列向量,一般用这种格式 normrnd(2,3,5) %生成 5 行 5 列的随机数矩阵 normrnd(2,3,[5,4]) %生成一个 5 行 4 列的随机数矩阵 %注:上述语句生成的随机数所服从的正态分布都是均值为 2,标准差为 3. 生成的随机数大致的分布。 x=normrnd(2,3,100000,1); hist(x,50);
如图,上半部分是由上一行语句生成的均值为 2,标准差为 3 的 10 万个随机数的大致 分布,下半部分是用小节“randn()”中最后那段语句生成 10 万个标准正态分布随机数的大 致分布。 注意到上半个图像的对称轴向正方向偏移(准确说移动到 x=2 处),这是由于均值为 2 的结果。 而且, 由于标准差是 3, 比标准正态分布的标准差 (1) 要高, 所以上半部分图形更胖(注 意 x 轴刻度的不同)。 5.chi2rnd() 此函数生成服从卡方(Chi-square)分布的随机数。卡方分布只有一个参数:自由度 v。 基本语法 chi2rnd(v,[M,N,P,...]) 生成的随机数服从自由度为 v 的卡方分布,这些随机数排列成 M*N*P... 多维向量。如 果只写 M,则生成 M*M 矩阵;如果参数为[M,N]可以省略掉方括号。一些例子: chi2rnd(5,5,1) %生成 5 个随机数排列的列向量,一般用这种格式 chi2rnd(5,5) %生成 5 行 5 列的随机数矩阵 chi2rnd(5,[5,4]) %生成一个 5 行 4 列的随机数矩阵 %注:上述语句生成的随机数所服从的卡方分布的自由度都是 5
生成的随机数大致的分布。 x=chi2rnd(5,100000,1); hist(x,50); 6.frnd() 此函数生成服从 F 分布的随机数。F 分布有 2 个参数:v1, v2。基本语法 frnd(v1,v2,[M,N,P,...]) 生成的随机数服从参数为(v1,v2)的卡方分布,这些随机数排列成 M*N*P... 多维向量。 如果只写 M,则生成 M*M 矩阵;如果参数为[M,N]可以省略掉方括号。一些例子: frnd(3,5,5,1) %生成 5 个随机数排列的列向量,一般用这种格式 frnd(3,5,5) %生成 5 行 5 列的随机数矩阵 frnd(3,5,[5,4]) %生成一个 5 行 4 列的随机数矩阵 %注:上述语句生成的随机数所服从的参数为(v1=3,v2=5)的 F 分布 生成的随机数大致的分布。 x=frnd(3,5,100000,1); hist(x,50); 从结果可以看出来, F 分布集中在 x 正半轴的左侧,但是它在极端值处也很可能有一 些取值。 7.trnd() 此函数生成服从 t(Student's t Distribution, 这里 Student 不是学生的意思, 而是 Cosset.W.S. 的笔名)分布的随机数。t 分布有 1 个参数:自由度 v。基本语法 trnd(v,[M,N,P,...]) 生成的随机数服从参数为 v 的 t 分布,这些随机数排列成 M*N*P... 多维向量。如果只 写 M,则生成 M*M 矩阵;如果参数为[M,N]可以省略掉方括号。一些例子: trnd(7,5,1) %生成 5 个随机数排列的列向量,一般用这种格式 trnd(7,5) %生成 5 行 5 列的随机数矩阵 trnd(7,[5,4]) %生成一个 5 行 4 列的随机数矩阵 %注:上述语句生成的随机数所服从的参数为(v=7)的 t 分布 生成的随机数大致的分布。 x=trnd(7,100000,1); hist(x,50); 可以发现 t 分布比标准正太分布要“瘦”,不过随着自由度 v 的增大,t 分布会逐渐变 胖,当自由度为正无穷时,它就变成标准正态分布了。 接下来的分布相对没有这么常用, 同时这些函数的语法和前面函数语法相同, 所以写得 就简略一些——在视频中也不会讲述, 你只需按照前面那几个分布的语法套用即可, 应该不 会有任何困难——时间足够的话这是一个不错的练习机会。 8.betarnd() 此函数生成服从 Beta 分布的随机数。Beta 分布有两个参数分别是 A 和 B。下图是 A=2,B=5 的 beta 分布的 PDF 图形。
生成 beta 分布随机数的语法是: betarnd(A,B,[M,N,P,...]) 9.exprnd() 此函数生成服从指数分布的随机数。指数分布只有一个参数: mu, 下图是 mu=3 时指数 分布的 PDF 图形
生成指数分布随机数的语法是: betarnd(mu,[M,N,P,...]) 10.gamrnd() 生成服从 Gamma 分布的随机数。Gamma 分布有两个参数:A 和 B。下图是 A=2,B=5 Gamma 分布的 PDF 图形
生成 Gamma 分布随机数的语法是: gamrnd(A,B,[M,N,P,...]) 11.lognrnd() 生成服从对数正态分布的随机数。其有两个参数:mu 和 sigma,服从这个这样的随机 数取对数后就服从均值为 mu,标准差为 sigma 的正态分布。下图是 mu=-1, sigma=1/1.2 的 对数正态分布的 PDF 图形。
生成对数正态分布随机数的语法是: lognrnd(mu,sigma,[M,N,P,...])
12.raylrnd() 生成服从瑞利(Rayleigh)分布的随机数。其分布有 1 个参数:B。下图是 B=2 的瑞利 分布的 PDF 图形。
生成瑞利分布随机数的语法是: raylrnd(B,[M,N,P,...]) 13.wblrnd() 生成服从威布尔(Weibull)分布的随机数。其分布有 2 个参数:scale 参数 A 和 shape 参数 B。下图是 A=3,B=2 的 Weibull 分布的 PDF 图形。
生成 Weibull 分布随机数的语法是: wblrnd(A,B,[M,N,P,...]) 还有非中心卡方分布(ncx2rnd),非中心 F 分布(ncfrnd),非中心 t 分布(nctrnd), 括号 中是生成服从这些分布的函数,具体用法用:
help 函数名
查找。 c. 离散型分布随机数 离散分布的随机数可能的取值是离散的,一般是整数。 14.unidrnd() 此函数生成服从离散均匀分布的随机数。Unifrnd 是在某个区间内均匀选取实数(可为 小数或整数),Unidrnd 是均匀选取整数随机数。离散均匀分布随机数有 1 个参数:n, 表示 从{1, 2, 3, ... N}这 n 个整数中以相同的概率抽样。基本语法: unidrnd(n,[M,N,P,...]) 这些随机数排列成 M*N*P... 多维向量。如果只写 M,则生成 M*M 矩阵;如果参数为 [M,N]可以省略掉方括号。一些例子: unidrnd(5,5,1) %生成 5 个随机数排列的列向量,一般用这种格式 unidrnd(5,5) %生成 5 行 5 列的随机数矩阵 unidrnd(5,[5,4]) %生成一个 5 行 4 列的随机数矩阵 %注:上述语句生成的随机数所服从的参数为(10,0.3)的二项分布 生成的随机数大致的分布。 x=unidrnd(9,100000,1); hist(x,9); 可见,每个整数的取值可能性基本相同。 15.binornd() 此函数生成服从二项分布的随机数。二项分布有 2 个参数:n,p。考虑一个打靶的例子, 每枪命中率为 p,共射击 N 枪,那么一共击中的次数就服从参数为(N,p)的二项分布。注 意 p 要小于等于 1 且非负,N 要为整数。基本语法: binornd(n,p,[M,N,P,...]) 生成的随机数服从参数为(N,p)的二项分布,这些随机数排列成 M*N*P... 多维向量。如 果只写 M,则生成 M*M 矩阵;如果参数为[M,N]可以省略掉方括号。一些例子: binornd(10,0.3,5,1) %生成 5 个随机数排列的列向量,一般用这种格式 binornd(10,0.3,5) %生成 5 行 5 列的随机数矩阵 binornd(10,0.3,[5,4]) %生成一个 5 行 4 列的随机数矩阵 %注:上述语句生成的随机数所服从的参数为(10,0.3)的二项分布 生成的随机数大致的分布。 x=binornd(10,0.45,100000,1); hist(x,11); 我们可以将此直方图解释为,假设每枪射击命中率为 0.45,每论射击 10 次,共进行 10 万轮,这个图就表示这 10 万轮每轮命中成绩可能的一种情况。 16.geornd() 此函数生成服从几何分布的随机数。几何分布的参数只有一个:p。几何分布的现实意 义可以解释为,打靶命中率为 p,不断地打靶,直到第一次命中目标时没有击中次数之和。 注意 p 是概率,所以要小于等于 1 且非负。基本语法: geornd(p,[M,N,P,...])
这些随机数排列成 M*N*P... 多维向量。如果只写 M,则生成 M*M 矩阵;如果参数为 [M,N]可以省略掉方括号。一些例子: geornd(0.4,5,1) %生成 5 个随机数排列的列向量,一般用这种格式 geornd(0.4,5) %生成 5 行 5 列的随机数矩阵 geornd(0.4,[5,4]) %生成一个 5 行 4 列的随机数矩阵 %注:上述语句生成的随机数所服从的参数为(0.4)的二项分布 生成的随机数大致的分布。 x=geornd(0.4,100000,1); hist(x,50); 17.poissrnd() 此函数生成服从泊松(Poisson)分布的随机数。泊松分布的参数只有一个:lambda。此参 数要大于零。基本语法: geornd(p,[M,N,P,...]) 这些随机数排列成 M*N*P... 多维向量。如果只写 M,则生成 M*M 矩阵;如果参数为 [M,N]可以省略掉方括号。一些例子: poissrnd(2,5,1) %生成 5 个随机数排列的列向量,一般用这种格式 poissrnd(2,5) %生成 5 行 5 列的随机数矩阵 poissrnd(2,[5,4]) %生成一个 5 行 4 列的随机数矩阵 %注:上述语句生成的随机数所服从的参数为(2)的泊松分布 生成的随机数大致的分布。 x=poissrnd(2,100000,1); hist(x,50); 其他离散分布还有超几何分布(Hyper-geometric, 函数是 hygernd)等,详细见 Matlab 帮 助文档。
(六)特殊连续分布
这里我将 Matlab 中没有对应函数的分布称为特殊分布。有多种方法可以用于生产服从 这些分布的随机数。这里主要介绍两种最常见的。 1.逆 CDF 函数法 如果我们已知某特定一维分布的 CDF 函数,经过如下几个步骤即可生成符合该分布的 随机数。(其中数学推导等在此处略去,详见相关数学书籍) 1. 计算 CDF 函数的反函数: 2. 生成服从(0,1)区间上均匀分布的初始随机数 a 3. 令 x= ,则 x 即服从我们需要的特定分布的随机数。 为了更形象解说这种方法,这里选取柯西(Cauchy)分布作为例子。有时也称其为洛 仑兹分布或者 Breit-Wigner 分布。柯西分布有一大特点就是,它是肥尾(Fat-tail,又译作 胖尾)分布。在金融市场中,肥尾分布越来越受到重视,因为在传统的正态分布基本不考虑 像当前次贷危机等极端情况,而肥尾分布则能很好地将很极端的情形考虑进去。
上图是 Cauchy 分布和标准正态分布 PDF 图对比,看看是不是 Cauchy 分布的尾巴(x 轴两端)更“胖”一点? 柯西分布的 PDF 函数是:
简化起见我们只考虑 x0=0, γ =1 情形。此时 PDF 函数是:
PDF 函数对 x 作积分,就得到 CDF 函数(推导过程略):
现在我们套用这三个步骤来生成服从 Cauchy 分布的随机数:
1. 计算得到 Cauchy 分布 CDF 函数的反函数为: 2. 使用 rand()函数生成(0,1)区间上均匀分布的初始随机数。我习惯一次生成一 堆这种随机数。 original_x=rand(1,100000); 3. 将初始随机数代入 CDF 反函数即可得到我们需要的 Cauchy 随机数。。 cauchy_x=tan((original_x-1/2)*pi); 上面这两句代码结合起来就生成了 10 万个服从参数为(x0=0, γ =1)Cauchy 分布的随机 数。 这种方法生成随机数与 Cauchy 分布有多大相似之处呢?这里有一个图可以说明:
蓝色的图形就是用 hist 画出的随机数的样本分布情况,红色线条是 Cauchy 分布理论的 PDF 图形。由此可看出生成的随机数挺符合 Cauchy 分布。 注意:上图中,我略去了 x 轴小于-12.5 和大于 12.5 部分的图形——因为 Cauchy 是胖 尾分布, 会生成出的不少取值很大的随机数,而那些很大的值使得我们不方便用 hist 函数来 画随机数分布图。 注意,这种方法本身虽然很简单,效率也很高,但有如下受限之处: 1.它有个可能会出错的地方,有的 CDF 函数的反函数在 0 或者 1 处的值是正/ 负无穷,例如此处的 Cauchy 分布就是这样,倘若用(0,1)均匀分布产生的初始随机数 中包含 0 或者 1,那么这个程序会出错。幸运的是,迄今为止,我用 Matlab 的 rand() 函数生成的随机数中还没有出现过 0 或者 1。但不同版本的 Matlab 的这种情况也许 会改变。此处提醒你,如果程序出错,不要忘记检查是否是这个错误。 2.CDF 函数必须严格单调递增,这也就意味着,PDF 函数在 x 定义域内必须处 处严格大于零,否则 CDF 的反函数不存在。 3.即使 CDF 函数存在,如果它太复杂,可能导致计算速度太慢,甚至无法计算 的后果。 2.接受/拒绝法 Acceptance-Rejection Method Accelptence-Rejection 方法的精髓在于“形似”,可以形象地将其比喻为制作冰雕— —二者相同之处在于都要首先堆砌出雏形,然后再用将多出的部分削去。用此法生成服从 f(x)分布的随机数,分为如下几大步骤: 1. 首先, 选用某个分布, pdf 为 g(x)的分布, 如 此时要计算一个常数 c, 使得 , 对 x 定义域内任意的 x 都成立——这相当于使 cg(x)图形完全“覆盖”住 f(x)图形,容易理 解,做冰雕时,最初堆出来的那堆冰块要比最终得到的雕塑大。 2.生成服从 pdf 为 g(x)分布的随机数,假设生成的随机数为 x0。 3.再生成一个服从(0,1)间的均匀分布的随机数 y 4.如果 的随机数。 ,丢弃生成的 x0;反之,生成的 x0 就是我们需要的、服从 f(x)分布
下面用一个例子结合图形解释这种方法,假设我们要生成的分布 是: ,此 pdf 图形如下图的蓝色曲线。 1.我们选用(0,2)之间的均匀分布作为原始分布,即 g(x)=0.5,此分布的 pdf 图见
下图中的绿色线。由条件:无论哪个 x, 都要成立,我们计算得到 c 要大于等 于 10.8。这种情况下,我们一般选择 c=1.875。因为 c 选得越大,意味着我们堆砌的原始雏 形越大,需要削去的部分越多,效率越低,所以我们要使得 c 尽量地小。 2.生成服从(0,2)之间的均匀分布的随机数,设它为 x0 X0=unifrnd(0,2); 3.然后再生成一个服从(0,1)间的均匀分布的随机数 y Y=rand; 4.如果 ,丢弃生成的 x0,重新生成;反之,生成的 x0 就是我们需要的、 服从 f(x)分布的随机数,用于做后续计算。
以上步骤每次只能处理一个随机数, 效率较低, 下面这段代码可以一次性生成一堆随机 数。 N=400000;c=1.875;gx=0.5 x0=unifrnd(0,2,1,N); y=rand(1,N); fx0=(x0-0.5).*(x0-0.5)/2.4; final_x=x0(y<=fx0./c/gx); 在视频教程中我会逐句解释每句含义,如果没听懂,一般是因为你对 Matlab 向量运算 不熟悉,请参照 Matlab 基础教程学习此部分的内容,后面章节会有很多地方用得上。 这段语句生成的变量 final_x 即为服从 f(x)分布的随机数组成的一个行向量。我们可以 用 hist 查看这些随机数大致的分布。 hist(final_x,50);title('f(x)=(x-0.5)^2/2.4');
如图所示,生成的随机数挺符合 f(x)分布。 这种方法很简单,也不需要计算 CDF 函数的反函数,但它也有如下受限之处: 1.由于我们用随机数 y 来控制是否削去某个随机数 x0,所以我们无法准确预知 最终得到的随机数数量多少。 2.选择合适的 g(x)分布是此方法最关键的技巧所在。g(x)的选择原则是在完全 覆盖 f(x)的前提下尽可能与 f(x)形似,二者形状越相似,需要削去的部分就越少,这 种方法的效率就越高。需要记住的是:很多时候,人们不选用这种方法的原因几乎都 在于它的效率过低。
(七)特殊离散分布
离散分布关键在获得它的分布律, 有了分布律我们计算骰子掷出点数小于等于某个数字 的累积概率分布。一个简单的例子,假设我们有一个不均匀的骰子,获得六个点数的概率分 别是: 点数 1 2 3 4 5 6 概率 .1 累积点数 1 累积概率 .1 0 .3 2 0 .4 3 0 .6 4 0 .8 5 0 6 1 0 .2 0 .1 0 .2 0 .2 0 .2 0
生成符合该分布随机数的步骤是: 1.生成一个(0,1)间均匀分布的随机数 x0。 2.依据 x0 介于累积概率哪个区间来决定掷出骰子的点数 x。如 0
elseif x=2; elseif x=3 elseif x=4 elseif x=5 else x=6 end
x0<0.3 x0<0.4 x0<0.6 x0<0.8
这段语句能生成一个服从上表中离散分布的随机数 x,如果生成多个 x,可以用循环语 句,也可以考虑将上述代码向量化。下图是我用上述代码生成 10 万个随机数所画出的分布 直方图,可见这些随机数很符合上表中的分布律。
十七、生成多维联合分布随机数
一维随机变量是标量(也就是指单独的一个数字),而多维随机变量是一个向量。一个 n 维随机变量 x 是有 n 个分量的向量,(X0,X1,...,Xn),用 f(X0,X1,...,Xn)表示联合分布,用 fk(Xk)表示第 k 维的边缘分布,用 fk(Xk|X1=x1,X2=x2,....Xk-1=xk-1, Xk+1=xk+1,...,Xn=xn)表示当 分量 X1=x1,X2=x2,....Xk-1=xk-1, Xk+1=xk+1,...,Xn=xn 时第 k 个分量 xk 的分布。这里大写 X 表示 随机变量某个维度上的分量,小写 x 表示具体的数值。关于边缘分布、条件分布、联合分布 一定要明白,这些都是基础数学知识,非本课程内容。如果手头没有书,通过 google 搜索 或上维基百科临阵磨枪也是可以的。 各种生成多维分布随机数的方法一般步骤都是, 逐个维度生成随机数分量, 最后将这些 分量依次组合起来——如先生成 x0,再 x1,...,最后 xn,,最终写成(x0,x1,...,xn)。 在详细讲如何生成这些分量前,我们讲讲如何储存生成的随机数。 如果一次生成一个 n 维的随机数向量, 可以用 n 变量来储存这个随机数的 n 个分量, 也 可以将这 n 个分量按照次序(次序不能乱)存于一个 1*n 的行向量中。如果一次生成随机数 的数量很多,例如 N 个随机数,前面两种办法都可以用,即可用 n 个变量来储存这些随机 数的每个分量,此时每个变量是 N*1 的列向量;也可以只用一个 N*n 矩阵储存随机数所有
分量,这个矩阵每一行是一个服从规定的联合分布的随机数,共有 N 行即表示共储存 N 个 这样的随机数,矩阵的每一列表示这 N 个随机数的一个维度上的分量,共有 n 个维度。
(一)最简单的——各维度独立
各维度独立的联合分布随机数的生成最为方便, 由于联合分布函数就是每个维度边缘分 布函数的直接乘积, 所以只要分别生成每个维度的随机数分量, 然后组合成随机数向量即可 得到服从该联合分布的随机数。 例子 1,生成一个在 0≤x≤2,0≤y≤2,正方形区域上的二维均匀分布。二维均匀分布 在每个维度上都是均匀分布(即两个维度的边缘分布都是(0,2)上的均匀分布),且两个维度 互相独立。 用第一种存储方法, x=unifrnd(0,2); y=unifrnd(0,2); 则每个维度上分别生成一个服从(0,2)均匀分布并分别储存在 x,y 这两个变量中。如果一 次生成多个随机数,如 N 个,可用 N=400; x=unifrnd(0,2,N,1); y=unifrnd(0,2,N,1); 这里 x,y 都是 N*1 大小的列向量, 分布存储着这 N 个随机数的第一维和第二维两个分 量。我们看看这些随机数是否很好得符合二维均匀分布特性。 scatter(x,y); 接着,我们看看用上述第二种存储方法, X=[x,y]; 紧接着第一种存储方法中的语句,我们将生成的两个分量组合起来储存到一个变量中。 当然这里还有一种取巧的办法, 由于两个维度的边缘分布都相同且独立, 我们只需用 unifrnd 函数一次性生成一个 N*n 大小的矩阵就可以了。 X=unifrnd(0,2,N,2); 例子 2, 我们要生成的随机数服从一个三维联合分布, 其第一维边缘分布服从标准正太, 第二维边缘分布是自由度为 4 的 t 分布,第三维边缘分布是自由度为(7,8)的 F 分布,各个维 度边际的边缘分布之间相互独立。我们只要用如下代码: x1=rand x2=trnd(4) x3=frnd(7,8) x=[x1,x2,x3] x1,x2,x3 分布储存三个维度的分量(第一种存储方法),将这些分量组合起来存入 x 中(第二种存储方法)。 如果要一次就能生成一堆这样的随机数。可以用如下的代码: N=1000; x=[rand(N,1),trnd(4,[N,1]),frnd(7,8,[N,1])]; 这段代码略过了中间过程, 直接生成第二种存储方法所说的矩阵, 这个矩阵大小为 N*3, 我们可以大致观察该联合分布在每个区域内的概率密度的大小。 scatter3(x(:,1),x(:,2),x(:,3),'marker','.','sizedata',1); 注:x(:,1)表示将 x 矩阵的第一列(也即随机数第一维上的分量)提取出来。
#《算法竞赛入门经典》勘误 关于勘误?下面的勘误很多来自于热心读者,再次向他们表示衷心的感谢!我并不清楚这些错误实际是在哪个版本中改正过来的,所以麻烦大家都看一下。 有发现新错误的欢迎大家在留言中指出,谢谢! 一些一般性的问题?运算符?已经被废弃,请用min、max代替(代码仓库中的代码已更新,g++ 4.6.2下编译通过) 重大错误?p24. 最后一行,“然后让max=INF,而min=-INF”应该是“然后让max=-INF, 而min=INF”。 (感谢imxivid) p43. 最后,判断s[i..j]是否为回文串的方法也不难写出:int ok = 1; for(k = i; i<=j; i++)应该为for(k = i; k<=j; k++) (感谢imxivid) p45. 第七行和第九行i-j+1应为i+j+1。修改后: 1. { 2. for (j = 0; i - j >= 0 && i + j < m; j++) 3. { 4. if (s[i - j] != s[i + j]) break; 5. if (j*2+1 > max) { max = j*2+1; x = p[i - j]; y = p[i + j];} 6. } 7. for (j = 0; i - j >= 0 && i + j + 1 < m; j++) 8. { 9. if (s[i - j] != s[i + j + 1]) break; 10. if (j*2+2 > max) 11. {max = j*2+2; x = p[i - j]; y = p[i + j + 1]; } 12. } 13. }p53. 例题4-1. 组合数. 输入非负整数n和m,这里的n和m写反了。应是“输入非负整数m和n”。 p54. 举例中的m和n也写反了(真是个悲剧),且C(20,1)=20。 p71. 《周期串》代码的第8行,j++应为i++。 p72. 代码的第7行,“return”改为“break”以和其他地方一致。 p81. k为奇数和偶数的时候,分子和分母的顺序是不一样的。正确代码为: #include
Monte Carlo 方法法 §1 概述 Monte Carlo 法不同于确定性数值方法,它是用来解决数学和物理问题的非确定性的(概率统计的或随机的)数值方法。Monte Carlo 方法(MCM ),也称为统计试验方法,是理论物理学两大主要学科的合并:即随机过程的概率统计理论(用于处理布朗运动或随机游动实验)和位势理论,主要是研究均匀介质的稳定状态。它是用一系列随机数来近似解决问题的一种方法,是通过寻找一个概率统计的相似体并用实验取样过程来获得该相似体的近似解的处理数学问题的一种手段。运用该近似方法所获得的问题的解in spirit 更接近于物理实验结果,而不是经典数值计算结果。 普遍认为我们当前所应用的MC 技术,其发展约可追溯至1944年,尽管在早些时候仍有许多未解决的实例。MCM 的发展归功于核武器早期工作期间Los Alamos (美国国家实验室中子散射研究中心)的一批科学家。Los Alamos 小组的基础工作刺激了一次巨大的学科文化的迸发,并鼓励了MCM 在各种问题中的应用[2]-[4]。“Monte Carlo ”的名称取自于Monaco (摩纳哥)内以赌博娱乐而闻名的一座城市。 Monte Carlo 方法的应用有两种途径:仿真和取样。仿真是指提供实际随机现象的数学上的模仿的方法。一个典型的例子就是对中子进入反应堆屏障的运动进行仿真,用随机游动来模仿中子的锯齿形路径。取样是指通过研究少量的随机的子集来演绎大量元素的特性的方法。例如,)(x f 在b x a <<上的平均值可以通过间歇性随机选取的有限个数的点的平均值来进行估计。这就是数值积分的Monte Carlo 方法。MCM 已被成功地用于求解微分方程和积分方程,求解本征值,矩阵转置,以及尤其用于计算多重积分。 任何本质上属随机组员的过程或系统的仿真都需要一种产生或获得随机数的方法。这种仿真的例子在中子随机碰撞,数值统计,队列模型,战略游戏,以及其它竞赛活动中都会出现。Monte Carlo 计算方法需要有可得的、服从特定概率分布的、随机选取的数值序列。 §2 随机数和随机变量的产生 [5]-[10]全面的论述了产生随机数的各类方法。其中较为普遍应用的产生随机数的方法是选取一个函数)(x g ,使其将整数变换为随机数。以某种方法选取0x ,并按照)(1k k x g x =+产生下一个随机数。最一般的方程)(x g 具有如下形式: m c ax x g mod )()(+= (1) 其中 =0x 初始值或种子(00>x ) =a 乘法器(0≥a ) =c 增值(0≥c ) =m 模数 对于t 数位的二进制整数,其模数通常为t 2。例如,对于31位的计算机m 即可取1 312 -。这 里a x ,0和c 都是整数,且具有相同的取值范围0,,x m c m a m >>>。所需的随机数序{}n x 便可由下式得
一、蒙特卡洛算法 1、含义的理解 以概率和统计理论方法为基础的一种计算方法。也称统计模拟方法,是指使用随机数(或更常见的伪随机数)来解决很多计算问题的方法,它是将所求解的问题同一定的概率模型相联系,用计算机实现统计模拟或抽样,以获得问题的近似解。 2、算法实例 在数值积分法中,利用求单位圆的1/4的面积来求得Pi/4从而得到Pi 。单位圆的1/4面积是一个扇形,它是边长为1单位正方形的一部分。只要能求出扇形面积S1在正方形面积S 中占的比例K=S1/S 就立即能得到S1,从而得到Pi 的值。怎样求出扇形面积在正方形面积中占的比例K 呢?一个办法是在正方形中随机投入很多点,使所投的点落在正方形中每一个位置的机会相等看其中有多少个点落在扇形内。将落在扇形内的点数m 与所投点的总数n 的比m/n 作为k 的近似值。P 落在扇形内的充要条件是 221x y +≤ 。 已知:K= 1s s ,K ≈m n ,s=1,s1=4P i ,求Pi 。 由1 s m s n ≈,知s1≈*m s n =m n , 而s1=4P i ,则Pi=*4m n 程序: /* 利用蒙特卡洛算法近似求圆周率Pi*/ /*程序使用:VC++6.0 */ #include x=rand()*1.0/RAND_MAX;/*RAND_MAX=32767,包含在 第一章习题1-1 #include 习题1-3 #include 习题1-5 #include 浅析蒙特卡洛方法原理及应用 于希明 (英才学院1236103班测控技术与仪器专业6120110304) 摘要:本文概述了蒙特卡洛方法产生的历史及基本原理,介绍了蒙特卡洛方法的最初应用——蒲丰投针问题求圆周率,并介绍了蒙特卡洛方法在数学及生活中的一些简单应用,最后总结了蒙特卡洛方法的特点。 关键词:蒙特卡洛方法蒲丰投针生活应用 蒙特卡洛方法(Monte Carlo method),也称统计模拟方法,是二十世纪四十年代中期由于科学技术的发展和电子计算机的发明,而被提出的一种以概率统计理论为指导的一类非常重要的数值计算方法。它是以概率统计理论为基础, 依据大数定律( 样本均值代替总体均值) , 利用电子计算机数字模拟技术, 解决一些很难直接用数学运算求解或用其他方法不能解决的复杂问题的一种近似计算法。蒙特卡洛方法在金融工程学,宏观经济学,计算物理学(如粒子输运计算、量子热力学计算、空气动力学计算)等领域应用广泛。 一、蒙特卡洛方法的产生及原理 蒙特卡洛方法于20世纪40年代美国在第二次世界大战中研制原子弹的“曼哈顿计划”计划的成员S.M.乌拉姆和J.冯·诺伊曼首先提出。数学家冯·诺伊曼用驰名世界的赌城—摩纳哥的Monte Carlo—来命名这种方法,为它蒙上了一层神秘色彩。在这之前,蒙特卡洛方法就已经存在。1777年,法国数学家蒲丰(Georges Louis Leclere de Buffon,1707—1788)提出用投针实验的方法求圆周率π。这被认为是蒙特卡洛方法的起源。 其基本原理如下:由概率定义知,某事件的概率可以用大量试验中该事件发生的频率来估算,当样本容量足够大时,可以认为该事件的发生频率即为其概率。因此,可以先对影响其可靠度的随机变量进行大量的随机抽样,然后把这些抽样值一组一组地代入功能函数式,确定结构是否失效,最后从中求得结构的失效概率。蒙特卡洛法正是基于此思路进行分析的。 设有统计独立的随机变量Xi(i=1,2,3,…,k),其对应的概率密度函数分别为fx1,fx2,…,fxk,功能函数式为Z=g(x1,x2,…,xk)。首先根据各随机变量的相应分布,产生N组随机数x1,x2,…,xk值,计算功能函数值Zi=g(x1,x2,…,xk)(i=1,2,…,N),若其中有L组随机数对应的功能函数值Zi≤0,则当N→∞时,根据伯努利大数定理及正态随机变量的特性有:结构失效概率,可靠指标。 二、蒲丰投针问题 作为蒙特卡洛方法的最初应用, 是解决蒲丰投针问题。1777 年, 法国数学家蒲丰提出利用投针实验求解圆周率的问题。设平面上等距离( 如为2a) 画有一些平行线, 将一根长度为2l( l< a) 的针任意投掷到平面上, 针与任一平行线相交的频率为p 。针的位置可以用针的中心坐标x 和针与平行线的夹角θ来决定。任意方向投针, 便意味着x与θ可以任意取一值, 只是0≤x ≤a, 0≤θ≤π。那么, 投针与任意平行线相交的条件为x ≤ l sinθ。相交频率p 便可用下式求 大师兄教你如何过华为机试 宝典1—内功心法 大华为这个大数据时代土豪金海量式的招聘又要开始了!!! 近期听说大华为的校招机试马上就要开始了,由于华为软件岗位的招聘只有技术面跟机试是与技术有关的内容,所以机试的地位非常重要。对于机试,除了长期积累的软件基本功以外,还有很多可以短期训练的东西,类似于考试之前的突击,可以迅速提高机试成绩,就像在我西电大杨老师考前最后一堂课一定要去,那个重点就是考点阿。 这篇机试葵花宝典的内容是针对华为软件类上机准备的,如果你认真看了本宝典,如果你是真正通过自己能力考上西电的话,想不过都难。同样想拿高级题的同学,请移步 https://www.doczj.com/doc/b36885148.html,/land/或者https://www.doczj.com/doc/b36885148.html,,刷上200道题,机试不想拿满分都难。 对于机试,首先应该调整好自己的心态,不要觉得写程序很难,机试题很难,也不要去考虑,万一机试考到自己不会的内容怎么办,要相信,机试题永远是考察每个人的基础,基础是不会考的很偏的,会有人恰好做过某个题而做出来那个题,但不会有人恰好没做过一个题而做不出来那个题。 机试之前,应该做的准备有: 1、买一本《算法竞赛入门经典》,这本书不同于普通的算法或者编程语言的书籍,这 本书既讲语言,又讲算法,由浅入深,讲的很好,能看完前几章并且把例题都做 会,想通过机试就很简单了 2、调整好心态,时刻告诉自己,哪些小错误是自己以前经常犯的,最好用笔记本记录 下来,写每道题前再看一遍,如果遇到代码调不出来了,先想想自己是否犯过以 前那些错误。还有就是,看了题目以后,先仔细想清楚细节,在纸上写清楚自己 需要用到的变量,以及代码的基本框架,不要急于动手去写代码 3、不要惧怕任何一道看起来很难的题目,有不会的就去问身边会的人,让别人给自己 讲清楚 4、心中默念10遍C++跟C除了多了两个加号其实没有区别,会C就能上手C++ 5、大量的练习是必要且有效的 6、看完这篇宝典,预过机试、必练此功。 在这里推荐一个帖子,是机试归来的学长写的,写的很不错,里面的例题在后面的攻略 信息学奥赛(NOIP)必看经典书目汇总! 小编整理汇总了一下大神们极力推荐的复习资料!(欢迎大家查漏补缺) 基础篇 1、《全国青少年信息学奥林匹克分区联赛初赛培训教材》(推荐指数:4颗星) 曹文,吴涛编著,知识点大杂烩,部分内容由学生撰写,但是对初赛知识点的覆盖还是做得相当不错的。语言是pascal的。 2、谭浩强老先生写的《C语言程序设计(第三版)》(推荐指数:5颗星) 针对零基础学C语言的筒子,这本书是必推的。 3、《骗分导论》(推荐指数:5颗星) 参加NOIP必看之经典 4、《全国信息学奥林匹克联赛培训教程(一)》(推荐指数:5颗星) 传说中的黄书。吴文虎,王建德著,系统地介绍了计算机的基础知识和利用Pascal语言进行程序设计的方法 5、《全国青少年信息学奥林匹克联赛模拟训练试卷精选》 王建德著,传说中的红书。 6、《算法竞赛入门经典》(推荐指数:5颗星) 刘汝佳著,算法必看经典。 7、《算法竞赛入门经典:训练指南》(推荐指数:5颗星) 刘汝佳著,《算法竞赛入门经典》的重要补充 提高篇 1、《算法导论》(推荐指数:5颗星) 这是OI学习的必备教材。 2、《算法艺术与信息学竞赛》(推荐指数:5颗星) 刘汝佳著,传说中的黑书。 3、《学习指导》(推荐指数:5颗星) 刘汝佳著,《算法艺术与信息学竞赛》的辅导书。(PS:仅可在网上搜到,格式为PDF)。 4、《奥赛经典》(推荐指数:5颗星) 有难度,但是很厚重。 5、《2016版高中信息学竞赛历年真题解析红宝书》(推荐指数:5颗星) 历年真题,这是绝对不能遗失的存在。必须要做! 三、各种在线题库 1、题库方面首推USACO(美国的赛题),usaco写完了一等基本上就没有问题,如果悟性好的话甚至能在NOI取得不错的成绩. 2、除此之外Vijos也是一个不错的题库,有很多中文题. 3、国内广受NOIP级别选手喜欢的国内OJ(Tyvj、CodeVs、洛谷、RQNOJ) 4、BJOZ拥有上千道省选级别及以上的题目资源,但有一部分题目需要购买权限才能访问。 5、UOZ 举办NOIP难度的UER和省选难度的UR。赛题质量极高,命题人大多为现役集训队选手。 424-Integer Inquiry One of the first users of BIT's new supercomputer was Chip Diller.He extended his exploration of powers of3to go from0 to333and he explored taking various sums of those numbers. ``This supercomputer is great,''remarked Chip.``I only wish Timothy were here to see these results.''(Chip moved to a new apartment,once one became available on the third floor of the Lemon Sky apartments on Third Street.) Input The input will consist of at most100lines of text,each of which contains a single VeryLongInteger.Each VeryLongInteger will be100or fewer characters in length,and will only contain digits(no VeryLongInteger will be negative). The final input line will contain a single zero on a line by itself. Output Your program should output the sum of the VeryLongIntegers given in the input. Sample Input 123456789012345678901234567890 123456789012345678901234567890 123456789012345678901234567890 Sample Output 370370367037037036703703703670 10106–Product The Problem The problem is to multiply two integers X,Y.(0<=X,Y<10250) The Input The input will consist of a set of pairs of lines.Each line in pair contains one multiplyer. The Output For each input pair of lines the output line should consist one integer the product. Sample Input 12 12 2 222222222222222222222222 Sample Output 144 444444444444444444444444 465–Overflow Write a program that reads an expression consisting of two non-negative integer and an operator.Determine if either integer or the result of the expression is too large to be represented as a``normal''signed integer(type integer if you are working Pascal,type int if you are working in C). Input An unspecified number of lines.Each line will contain an integer,one of the two operators+or*,and another integer. Output For each line of input,print the input followed by0-3lines containing as many of these three messages as are appropriate: ``first number too big'',``second number too big'',``result too big''. Sample Input 300+3 9999999999999999999999+11 Sample Output 300+3 9999999999999999999999+11 first number too big 蒙特卡罗方法简介 蒙特卡罗模型(Monte Carlo method),又称统计模拟法、随机抽样技术。由S.M.乌拉姆和J.冯·诺伊曼在20世纪40年代为研制核武器而首先提出。在这之前,蒙特卡罗方法就已经存在。1777年,法国Buffon提出用投针实验的方法求圆周率∏。这被认为是蒙特卡罗方法的起源。是一种以概率统计理论为指导的非常重要的数值计算方法。是指使用随机数(或更常见的伪随机数)来解决很多计算问题的方法。蒙特卡罗(Monte Carlo)方法,或称计算机随机模拟方法,是一种基于“随机数”的计算方法。这一方法源于美国在第一次世界大战进研制原子弹的“曼哈顿计划”。该计划的主持人之一、数学家冯·诺伊曼用驰名世界的赌城—摩纳哥的Monte Carlo—来命名这种方法,为它蒙上了一层神秘色彩。而蒙特·卡罗方法正是以概率为基础的方法。考虑平面上的一个边长为1的正方形及其内部的一个形状不规则的“图形”,如何求出这个“图形”的面积呢?Monte Carlo方法是这样一种“随机化”的方法:向该正方形“随机地”投掷N个点落于“图形”内,则该“图形”的面积近似为M/N。 蒙特卡罗模型的基本思想是,为了求解数学、物理、工程技术以及管理等方面的问题,首先建立一个概率模型或随机过程,使它们的参数,如概率分布或数学期望等问题的解;然后通过对模型或过程的观察或抽样试验来计算所求参数的统计特征,并用算术平均值作为所求解的近似值。对于随机性问题,有时还可以根据实际物理背景的概率法则,用电子计算机直接进行抽样试验,从而求得问题的解答。从理论上来说,蒙特卡罗方法需要大量的实验。实验次数越多,所得到的结果才越精确。 科技计算中的问题比这要复杂得多。比如金融衍生产品(期权、期货、掉期等)的定价及交易风险估算,问题的维数(即变量的个数)可能高达数百甚至数千。对这类问题,难度随维数的增加呈指数增长,这就是所谓的“维数的灾 难”(Course Dimensionality),传统的数值方法难以对付(即使使用速度最快的计算机)。Monte Carlo方法能很好地用来对付维数的灾难,因为该方法的计算复杂性不再依赖于维数。以前那些本来是无法计算的问题现在也能够计算量。为提高方法的效率,科学家们提出了许多所谓的“方差缩减”技巧。 图1-1 蒙特卡罗方法学习总结 核工程与核技术2014级3班张振华20144530317 一、蒙特卡罗方法概述 1.1蒙特卡罗方法的基本思想 1.1.1基本思想 蒙特卡罗方的基本思想就是,当所求问题的解是某个事件的概率,或者是某个随机变量的数学期望,或者是与概率、数学期望有关的量时,通过某种试验方法,得出该事件发生的频率,或者该随机变量若干个具体观察值的算术平均值,通过它得到问题的解。 1.1.2计算机模拟打靶游戏 为了能更为深刻地理解蒙特卡罗方法的基本思想,我们学习了蒲丰氏问题和打靶游戏两大经典例子。下面主要对打靶游戏进行剖析、计算机模拟(MATLAB 程序)。 设某射击运动员的弹着点分布如表1-1 所示, 首先用一维数轴刻画出已知该运动员的弹 着点的分布如图1-1所示。研究打靶游戏,我 们不用考察子弹的运动轨迹,只需研究每次“扣动扳机”后的子弹弹着点。每一环数对应唯一确定的概率,且注意到概率分布函数有单调不减和归一化的性质。首先我们产生一个在(0,1)上均匀分布的随机数(模拟扣动扳机),然后将该随机数代表的点投到P 轴上(模拟子弹射向靶上的一个确定点),得到对应的环数(即子弹的弹着点),模拟打靶完成。反复进行N 次试验,统计出试验结果的样本均值。样本均值应当等于数学期望值,但允许存在一定的偏差,即理论计算值应该约等于模拟试验结果。 clear all;clc; N=100000;s=0; for n=1:N %step 4.重复N 次打靶游戏试验 x=rand(); %step 1.产生在(0,1)上均匀分布的随机数if(x<=0.1) %step 2.若随机数落在(0.0,0.1)上,则代表弹着点在7环g=7; s=s+g; %step 3.统计总环数elseif(x<=0.2) %step 2.若随机数落在(0.1,0.2)上,则代表弹着点在8环g=8;s=s+g; elseif(x<=0.5) %step 2.若随机数落在(0.2,0.5)上,则代表弹着点在9环g=9;s=s+g; else %step 2.若随机数落在(0.5,1.0)上,则代表弹着点在10环 g=10;s=s+g; end end gn_th=7*0.1+8*0.1+9*0.3+10*0.5; %step 5.计算、输出理论值fprintf('理论值:%f\n',gn_th); gn=s/N; %step 6.计算、输出试验结果 fprintf('试验结果:%f\n',gn);1.2蒙特卡罗方法的收敛性与误差 1.2.1收敛性 由大数定律可知,应用蒙特卡罗方法求近似解,当随机变量Z 的简单子样数N 趋向于无穷大(N 充分大)时,其均值依概率收敛于它的数学期望。 1.2.2误差 由中心极限定理可知,近似值与真值的误差为N Z E Z N αλ<-)(?。式中的αλ的值可以根据给出的置信水平,查阅标准正态分布表来确定。 1.2.3收敛性与误差的关系 在一般情况下,求具有有限r 阶原点矩()∞ 算法工程师成长计划 大学期间必须要学好的课程:C/C++两种语言(或JA V A)、高等数学、线性代数、数据结构、离散数学、数据库原理、操作系统原理、计算机组成原理、人工智能、编译原理、算法设计与分析。 大一上学期: 1.C语言基础语法必须全部学会,提前完成C语言课程设计。 2.简单数学题:求最大公约数、筛法求素数、康托展开、同余定理、次方求模等。 3.计算机课初步:三角形面积,三点顺序等等。 4.学会计算简单程序的时间复杂度和空间复杂度。 5.二分查找、贪心算法经典算法。 6.简单的排序算法:冒泡排序法、插入排序法。 7.高等数学。 8.操作系统应用:DOS命令,学会Windows系统的一些小知识,学会编辑注册表, 学会使用组策略管理器(gpedit.msc)管理组策略等。 大一下学期: 1.掌握C++部分语法,如引用类型、函数重载等,基本明白什么是类。 2.学会使用栈和队列等线性结构。 3.掌握BFS和DFS以及树的前序、中序、后序遍历。 4.学会分治策略。 5.掌握排序算法:选择排序、归并排序、快速排序、计数、基数排序等等。 6.动态规划:最大子串和、最长公共子序列、最长单调递增子序列、01背包、完全背 包等。 7.数论:扩展欧几里德算法、求逆元、同余方程、中国剩余定理。 8.博弈论:博弈问题与SG函数的定义、多个博弈问题SG值的合并。 9.图论:图的存储、欧拉回路的判定、单源最短路Bellman-Ford算法及Dijkstra算法、 最小生成树Kruskal算法及Prim算法。 10.学会使用C语言进行网络编程与多线程编程。 11.高等数学、线性代数:做几道“矩阵运算”分类下的题目。 12.学习matlab,如果想参加数学建模大赛,需要学这个软件。 大一假期: 1.掌握C++语法,并熟练使用STL(重要)。 2.试着实现STL的一些基本容器和函数、使自己基本能看懂STL源码。 3.数据结构:字典树、并查集、树状数组、简单线段树。 4.图论:使用优先队列优化Dijkstra算法及Prim算法,单源最短路径之SPFA,差分 约束系统,多源多点最短路径之FloydWarshall算法,求欧拉回路(圈套圈算法)。 5.拓扑排序:复杂BFS和DFS搜索、复杂模拟题训练。 6.动态规划:多重背包、分组背包、依赖背包等各种背包问题(参见背包九讲)。 7.计算几何:判断点是否在线段上、线段相交、圆与矩形的关系、点是否在多边形内、 点到线段的最近点、多边形面积、求多边形重心、求凸包、点在任意多边形内外的 判定。 8.学习使用C/C++连接数据库、学习一种C++的开发框架来编写一些窗体程序(如 MFC、Qt)。 第7章暴力求解法 【教学内容相关章节】 7.1简单枚举 7.2枚举排列 7.3子集生成 7.4回溯法 7.5隐式图搜索 【教学目标】 (1)掌握整数、子串等简单对象的枚举方法; (2)熟练掌握排列生成的递归方法; (3)熟练掌握用“下一个排列”枚举全排列的方法; (4)理解解答树,并能估算典型解答树的结点数; (5)熟练掌握子集生成的增量法、位向量法和二进制法; (6)熟练掌握回溯法框架,并能理解为什么它往往比生成-测试法高效; (7)熟练掌握解答树的宽度优先搜索和迭代加深搜索; (8)理解倒水问题的状态图与八皇后问题的解答树的本质区别; (9)熟练掌握八数码问题的BFS实现; (10)熟练掌握集合的两种典型实现——hash表和STL集合。 【教学要求】 掌握整数、子串等简单对象的枚举方法;熟练掌握排列生成的递归方法;熟练掌握用“下一个排列”枚举全排列的方法;理解子集树和排列树;熟练掌握回溯法框架;熟练掌握解答树的宽度优先搜索和迭代搜索;熟练掌握集合的两种典型实现——hash表和STL集合。【教学内容提要】 本章主要讨论暴力法(也叫穷举法、蛮力法),它要求调设计者找出所有可能的方法,然后选择其中的一种方法,若该方法不可行则试探下一种可能的方法。介绍了排列生成的递归方法;在求解的过程中,提出了解答树的概念(如子集树和排列树);介绍了回溯法的基本框架;介绍了集合的两种典型实现——hash表和STL集合。 【教学重点、难点】 教学重点: (1)熟练掌握排列生成的递归方法; (2)理解解答树,并能估算典型解答树的结点数; (3)熟练掌握子集生成的增量法、位向量法和二进制法; (4)熟练掌握回溯法框架,并能理解为什么它往往比生成-测试法高效; (5)熟练掌握解答树的宽度优先搜索和迭代搜索; (6)熟练掌握集合的两种典型实现——hash表和STL集合。 教学难点: (1)熟练掌握子集生成的增量法、位向量法和二进制法; (2)熟练掌握回溯法框架,并能理解为什么它往往比生成-测试法高效; (3)熟练掌握解答树的宽度优先搜索和迭代搜索; (4)熟练掌握集合的两种典型实现——hash表和STL集合。 【课时安排】 7.1简单枚举 7.2枚举排列 7.3子集生成 7.4回溯法 7.5隐式图搜索 Monte Carlo 法 §8.1 概述 Monte Carlo 法不同于前面几章所介绍的确定性数值方法,它是用来解决数学和物理问题的非确定性的(概率统计的或随机的)数值方法。Monte Carlo 方法(MCM ),也称为统计试验方法,是理论物理学两大主要学科的合并:即随机过程的概率统计理论(用于处理布朗运动或随机游动实验)和位势理论,主要是研究均匀介质的稳定状态[1]。它是用一系列随机数来近似解决问题的一种方法,是通过寻找一个概率统计的相似体并用实验取样过程来获得该相似体的近似解的处理数学问题的一种手段。运用该近似方法所获得的问题的解in spirit 更接近于物理实验结果,而不是经典数值计算结果。 普遍认为我们当前所应用的MC 技术,其发展约可追溯至1944年,尽管在早些时候仍有许多未解决的实例。MCM 的发展归功于核武器早期工作期间Los Alamos (美国国家实验室中子散射研究中心)的一批科学家。Los Alamos 小组的基础工作刺激了一次巨大的学科文化的迸发,并鼓励了MCM 在各种问题中的应用[2]-[4]。“Monte Carlo ”的名称取自于Monaco (摩纳哥)内以赌博娱乐而闻名的一座城市。 Monte Carlo 方法的应用有两种途径:仿真和取样。仿真是指提供实际随机现象的数学上的模仿的方法。一个典型的例子就是对中子进入反应堆屏障的运动进行仿真,用随机游动来模仿中子的锯齿形路径。取样是指通过研究少量的随机的子集来演绎大量元素的特性的方法。例如,)(x f 在b x a <<上的平均值可以通过间歇性随机选取的有限个数的点的平均值来进行估计。这就是数值积分的Monte Carlo 方法。MCM 已被成功地用于求解微分方程和积分方程,求解本征值,矩阵转置,以及尤其用于计算多重积分。 任何本质上属随机组员的过程或系统的仿真都需要一种产生或获得随机数的方法。这种仿真的例子在中子随机碰撞,数值统计,队列模型,战略游戏,以及其它竞赛活动中都会出现。Monte Carlo 计算方法需要有可得的、服从特定概率分布的、随机选取的数值序列。 §8.2 随机数和随机变量的产生 [5]-[10]全面的论述了产生随机数的各类方法。其中较为普遍应用的产生随机数的方法是选取一个函数)(x g ,使其将整数变换为随机数。以某种方法选取 0x ,并按照)(1k k x g x =+产生下一个随机数。最一般的方程)(x g 具有如下形式: m c ax x g mod )()(+= (8.1) 其中 =0x 初始值或种子(00>x ) =a 乘法器(0≥a ) =c 增值(0≥c ) =m 模数 第6章数据结构基础 【教学内容相关章节】 6.1栈和队列 6.2链表 6.3二叉树 6.4图 【教学目标】 (1)熟练掌握栈和队列及其实现; (2)了解双向链表及其实现; (3)掌握对比测试的方法; (4)掌握随机数据生成方法; (5)掌握完全二叉树的数组实现; (6)了解动态内存分配和释放方法及其注意事项; (7)掌握二叉树的链式表示法; (8)掌握二叉树的先序、后序和中序遍历和层次遍历; (9)掌握图的DFS及连通块计数; (10)掌握图的BFS及最短路的输出; (11)掌握拓扑排序算法; (12)掌握欧拉回路算法。 【教学要求】 掌握栈和队列及其实现;掌握对比测试的方法;掌握随机数据生成方法;掌握完全二叉树的数组实现和链式表示法;掌握二叉树的先序、后序和中序遍历和层次遍历;掌握图的DFS和BFS遍历;掌握拓扑排序算法;掌握欧拉回路算法。 【教学内容提要】 本章介绍基础数据结构,包括线性表、二叉树和图。有两种特殊的线性表:栈和队列。对于树型结构主要讨论二叉树,还有二叉树的先序、中序和后序的遍历方式。对于图主要讨论图的DFS和BFS的遍历方法。这些内容是很多高级内容的基础。如果数据基础没有打好,很难设计正确、高效的算法。 【教学重点、难点】 教学重点: (1)掌握栈和队列及其实现; (2)掌握对比测试的方法; (3)掌握随机数据生成方法; (4)掌握完全二叉树的数组实现和链式表示法; (5)掌握二叉树的先序、后序和中序遍历和层次遍历; (6)掌握图的DFS和BFS遍历; (7)掌握拓扑排序算法和欧拉回路算法。 教学难点: (1)掌握完全二叉树的数组实现和链式表示法; (2)掌握二叉树的先序、后序和中序遍历和层次遍历; (3)掌握图的DFS和BFS遍历; (4)掌握拓扑排序算法和欧拉回路算法。 【课时安排(共9学时)】 6.1栈和队列 6.2链表 6.3二叉树 6.4图 第一章:Monte Carlo方法概述 讲课人:Xaero Chang | 课程主页: https://www.doczj.com/doc/b36885148.html,/notes/intro2mc 本章主要概述Monte Carlo的一些基础知识,另外包括一个最简单的用Monte Carlo方法计算数值积分的例子。 一、Monte Carlo历史渊源 Monte Carlo方法的实质是通过大量随机试验,利用概率论解决问题的一种数值方法,基本思想是基于概率和体积间的相似性。它和Simulation有细微区别。单独的Simulation只是模拟一些随机的运动,其结果是不确定的;Monte Carlo 在计算的中间过程中出现的数是随机的,但是它要解决的问题的结果却是确定的。 历史上有记载的Monte Carlo试验始于十八世纪末期(约1777年),当时布丰(Buffon)为了计算圆周率,设计了一个“投针试验”。(后文会给出一个更加简单的计算圆周率的例子)。虽然方法已经存在了200多年,此方法命名为Monte Carlo则是在二十世纪四十年,美国原子弹计划的一个子项目需要使用Monte Carlo方法模拟中子对某种特殊材料的穿透作用。出于保密缘故,每个项目都要一个代号,传闻命名代号时,项目负责人之一von Neumann灵犀一点选择摩洛哥著名赌城蒙特卡洛作为该项目名称,自此这种方法也就被命名为Monte Carlo方法广为流传。 十一、Monte Carlo方法适用用途 (一)数值积分 计算一个定积分,如,如果我们能够得到f(x)的原函数F(x),那么直接由表达式: F(x1)-F(x0)可以得到该定积分的值。但是,很多情况下,由于f(x)太复杂,我们无法计算得到原函数F(x)的显示解,这时我们就只能用数值积分的办法。如下是一个简单的数值积分的例子。 数值积分简单示例 如图,数值积分的基本原理是在自变量x的区间上取多个离散的点,用单个点的值来代替该小段上函数f(x)值。 常规的数值积分方法是在分段之后,将所有的柱子(粉红色方块)的面积全部加起来,用这个面积来近似函数f(x)(蓝色曲线)与x轴围成的面积。这样做 求int的上限与下限#include return 0; } 1-3 #include 最新算法竞赛入门经典各章(第二版)前4章课后习题答案电子教案
浅析蒙特卡洛方法原理及应用
大师兄教你如何过华为机试
(完整)信息学奥赛(NOIP)必看经典书目汇总,推荐文档
BIG NUMBER 算法竞赛入门经典 刘汝佳
蒙特卡罗基本思想
蒙特卡罗方法学习总结
算法工程师本科生学习计划
算法竞赛入门经典授课教案第7章 暴力求解法
(完整版)蒙特卡洛算法详讲
算法竞赛入门经典授课教案第6章数据结构基础(精心排版,并扩充部分内容)
蒙特卡罗算法与matlab(精品教程)
算法竞赛入门经典第二版习题答案