下载文档原格式
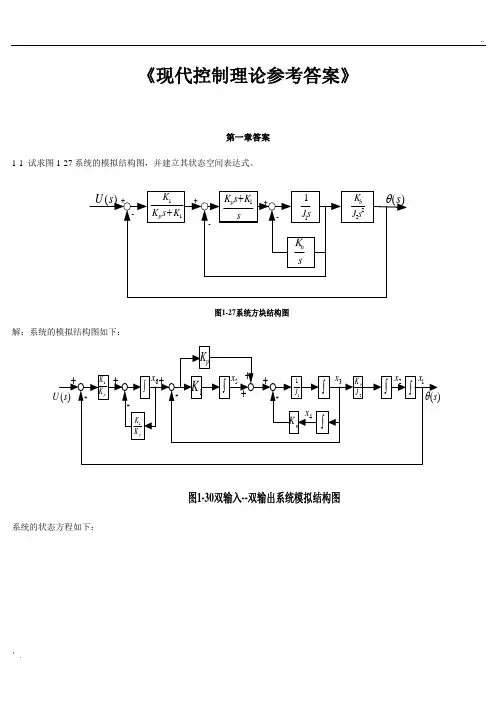
《现代控制理论参考答案》第一章答案1-1 试求图1-27系统的模拟结构图，并建立其状态空间表达式。
解：系统的模拟结构图如下： 系统的状态方程如下： 令y s =)(θ，则1x y =所以，系统的状态空间表达式及输出方程表达式为1-2有电路如图1-28所示。
以电压)(t u 为输入量，求以电感中的电流和电容上的电压作为状态变量的状态方程，和以电阻2R 上的电压作为输出量的输出方程。
解：由图，令32211,,x u x i x i c ===，输出量22x R y =有电路原理可知：•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得2221332222213*********1x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为：1-4 两输入1u ，2u ，两输出1y ，2y 的系统，其模拟结构图如图1-30所示，试求其状态空间表达式和传递函数阵。
解：系统的状态空间表达式如下所示： 1-5系统的动态特性由下列微分方程描述列写其相应的状态空间表达式，并画出相应的模拟结构图。
解：令..3.21y x y x y x ===，，，则有 相应的模拟结构图如下：1-6 （2）已知系统传递函数2)3)(2()1(6)(+++=s s s s s W ,试求出系统的约旦标准型的实现，并画出相应的模拟结构图解：ss s s s s s s s W 31233310)3(4)3)(2()1(6)(22++++-++-=+++=1-7 给定下列状态空间表达式[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡321321321100210311032010x x x y u x x x x x x ‘（1） 画出其模拟结构图（2） 求系统的传递函数 解：（2）⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+-+-=-=31103201)()(s s s A sI s W 1-8 求下列矩阵的特征矢量（3）⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=6712203010A 解：A 的特征方程 061166712230123=+++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+---=-λλλλλλλA I 解之得：3,2,1321-=-=-=λλλ当11-=λ时，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---3121113121116712203010p p p p p p 解得： 113121p p p -== 令111=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P （或令111-=p ，得⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P ） 当21-=λ时，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---32221232221226712203010p p p p p p 解得： 1232122221,2p p p p =-= 令212=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=14222122p p p P（或令112=p ，得⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=21213222122p p p P ） 当31-=λ时，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---33231333231336712203010p p p p p p 解得： 133313233,3p p p p =-= 令113=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=3313323133p p p P 1-9将下列状态空间表达式化成约旦标准型（并联分解）（2）⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡32121321321110021357213311201214x x x y y u x x x x x x解：A 的特征方程 0)3)(1(311212142=--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=-λλλλλλA I 当31=λ时，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--3121113121113311201214p p p p p p 解之得 113121p p p == 令111=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P 当32=λ时，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--1113311201214312111312111p p p p p p 解之得 32222212,1p p p p =+= 令112=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=0013222122p p p P 当13=λ时，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--23132313311201214p p p p p p解之得3323132,0p p p == 令133=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1203323133p p p P约旦标准型1-10 已知两系统的传递函数分别为W 1(s)和W 2(s)试求两子系统串联联结和并联连接时，系统的传递函数阵，并讨论所得结果 解：（1）串联联结 （2）并联联结1-11 （第3版教材）已知如图1-22所示的系统，其中子系统1、2的传递函数阵分别为 求系统的闭环传递函数 解：1-11（第2版教材） 已知如图1-22所示的系统，其中子系统1、2的传递函数阵分别为 求系统的闭环传递函数 解：1-12 已知差分方程为试将其用离散状态空间表达式表示，并使驱动函数u 的系数b(即控制列阵)为 （1）⎥⎦⎤⎢⎣⎡=11b 解法1： 解法2：求T,使得⎥⎦⎤⎢⎣⎡=-111B T 得⎥⎦⎤⎢⎣⎡=-10111T 所以 ⎥⎦⎤⎢⎣⎡-=1011T 所以，状态空间表达式为第二章习题答案2-4 用三种方法计算以下矩阵指数函数At e 。
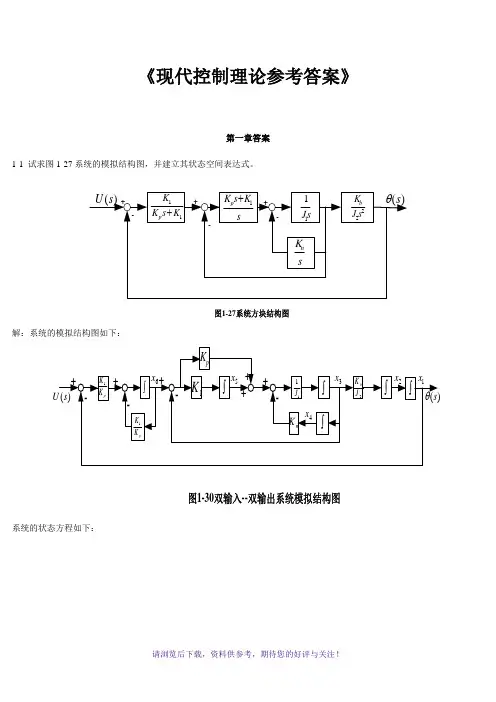
《现代控制理论参考答案》第一章答案1-1 试求图1-27系统的模拟结构图，并建立其状态空间表达式。
解：系统的模拟结构图如下： 系统的状态方程如下： 令y s =)(θ，则1x y =所以，系统的状态空间表达式及输出方程表达式为1-2有电路如图1-28所示。
以电压)(t u 为输入量，求以电感中的电流和电容上的电压作为状态变量的状态方程，和以电阻2R 上的电压作为输出量的输出方程。
解：由图，令32211,,x u x i x i c ===，输出量22x R y =有电路原理可知：•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得2221332222213*********1x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为：1-4 两输入1u ，2u ，两输出1y ，2y 的系统，其模拟结构图如图1-30所示，试求其状态空间表达式和传递函数阵。
解：系统的状态空间表达式如下所示： 1-5系统的动态特性由下列微分方程描述列写其相应的状态空间表达式，并画出相应的模拟结构图。
解：令..3.21y x y x y x ===，，，则有 相应的模拟结构图如下：1-6 （2）已知系统传递函数2)3)(2()1(6)(+++=s s s s s W ,试求出系统的约旦标准型的实现，并画出相应的模拟结构图解：ss s s s s s s s W 31233310)3(4)3)(2()1(6)(22++++-++-=+++=1-7 给定下列状态空间表达式[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡321321321100210311032010x x x y u x x x x x x ‘（1） 画出其模拟结构图（2） 求系统的传递函数 解：（2）⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+-+-=-=31103201)()(s s s A sI s W 1-8 求下列矩阵的特征矢量（3）⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=6712203010A 解：A 的特征方程 061166712230123=+++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+---=-λλλλλλλA I 解之得：3,2,1321-=-=-=λλλ当11-=λ时，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---3121113121116712203010p p p p p p 解得： 113121p p p -== 令111=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P （或令111-=p ，得⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P ） 当21-=λ时，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---32221232221226712203010p p p p p p 解得： 1232122221,2p p p p =-= 令212=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=14222122p p p P（或令112=p ，得⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=21213222122p p p P ） 当31-=λ时，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---33231333231336712203010p p p p p p 解得： 133313233,3p p p p =-= 令113=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=3313323133p p p P 1-9将下列状态空间表达式化成约旦标准型（并联分解）（2）⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡32121321321110021357213311201214x x x y y u x x x x x x解：A 的特征方程 0)3)(1(311212142=--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=-λλλλλλA I 当31=λ时，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--3121113121113311201214p p p p p p 解之得 113121p p p == 令111=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1113121111p p p P 当32=λ时，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--1113311201214312111312111p p p p p p 解之得 32222212,1p p p p =+= 令112=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=0013222122p p p P 当13=λ时，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--23132313311201214p p p p p p解之得3323132,0p p p == 令133=p 得 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1203323133p p p P约旦标准型1-10 已知两系统的传递函数分别为W 1(s)和W 2(s)试求两子系统串联联结和并联连接时，系统的传递函数阵，并讨论所得结果 解：（1）串联联结 （2）并联联结1-11 （第3版教材）已知如图1-22所示的系统，其中子系统1、2的传递函数阵分别为 求系统的闭环传递函数 解：1-11（第2版教材） 已知如图1-22所示的系统，其中子系统1、2的传递函数阵分别为 求系统的闭环传递函数 解：1-12 已知差分方程为试将其用离散状态空间表达式表示，并使驱动函数u 的系数b(即控制列阵)为 （1）⎥⎦⎤⎢⎣⎡=11b 解法1： 解法2：求T,使得⎥⎦⎤⎢⎣⎡=-111B T 得⎥⎦⎤⎢⎣⎡=-10111T 所以 ⎥⎦⎤⎢⎣⎡-=1011T 所以，状态空间表达式为第二章习题答案2-4 用三种方法计算以下矩阵指数函数At e 。
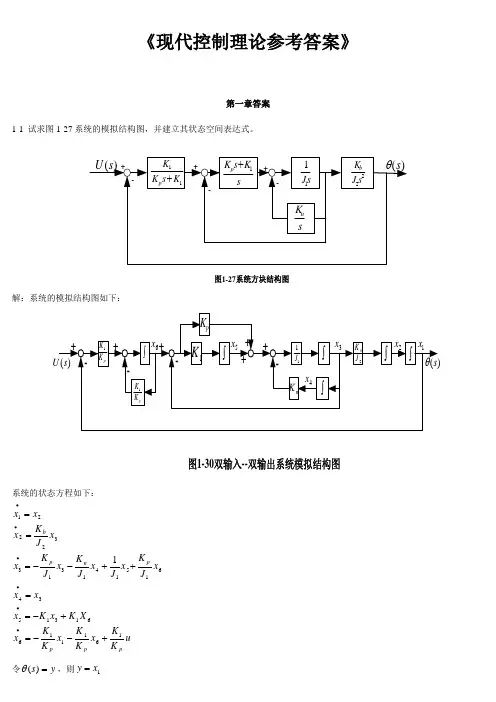
习题答案Document number : WTWYT-WYWY-BTGTT-YTTYU-2018GT《现代控制理论参考答案》第一章答案1-1试求图1-27系统的模拟结构图，并建立其状态空间表达式。
解：系统的模拟结构图如下：系统的状态方程如下：令0(s) = y,则，=册所以，系统的状态空间表达式及输出方程表达式为1-2有电路如图1-28所示。
以电压"⑴为输入量，求以电感中的电流和电容上的电压作为状态变量的状态方程，和以电阻R?上的电压作为输出量的输出方程。
解：由图,令ii =x}J2 =x2,u c =x3l输出量y = R2X2• & 1 1Rg + L, Xj + x y = u有电路原理可知:L2XI+R2X2=X3= x2 +C x3写成矢量矩阵形式为：14两输入也，两输出比，比的系统，其模拟结构图如图1-30所示，试求其状态空间表达式和传递函数阵。
解：系统的状态空间表达式如下所示：1-5系统的动态特性由下列微分方程描述列写其相应的状态空间表达式，并画出相应的模拟结构图。
解：令x, = y,吃=，，兀3 =，，则有相应的模拟结构图如下:并画岀相应的模拟结构图10 £初・ 117/ \ 6(5 + 1) -4 V 3 a解:VV (5)= ------ ---------- = --------- +— + ------------+ 丄s(s + 2)(s + 3y (s + 3y 5 + 3 s + 2 s1- 7给定下列状态空间表达式y = [0 0 1 x 2_V 3_(1) 画出其模拟结构图 (2) 求系统的传递函数解：-1 0(2) W(s) = (s/ — A)= 25 + 31 — 1 5 + 31-8求下列矩阵的特征矢量_0 1 0 _ (3)32-12 -7 -6-1 0解：A 的特征方程 |刀—A|= —3 2-2 =23+6/l 2 + lU + 6 = 0 1272 + 6解之得：入=—1,/?2 = —2,/?3 = —31-6 (2)已知系统传递函数W(s)=6(5 + 1)5(5 +2)(5+ 3)2，试求岀系统的约旦标准型的实现,■ 010 '/AiP113 0 2 P11 =— P21 -12 -7 -6_ ■皿■叽当人=一1时,令內=1Ai-1 （或令Pll =一1,得片=P21 =1 )1■ 0 1 0 ■P\2Pn 3 02 Pll =-2 P22-12 -7 _6. L/^2.解得：”22=一2卩2丿32 =>12'P22 =P\2(或令从2 T,得4 = "22“320 1当人=一3时， 3 0 -12 -71 -2£ 2解得：〃23=-3/心〃33=3门3令戸3 = 1得1・9将下列状态空间表达式化成约旦标准型（并联分解）~4 1 -2■3 fX 2 = 1 0 2X 2 + 2 7⑵-.1-1 d_5 3_得解得：P 2] =^31 =-P\\当人=一2时,令门2 = 2 得P 2 = 2 -41'4 1 -2'当人=3时， 1 02=3 "211 -13 .解之得 Pl2 = P12 + 1，P22 = “32 令 Pl2 =1并联联结(第3版教材)已知如图1・22所示的系统，其中子系统1、2的传递函数阵分别求系统的闭环传递函数_4 1 -2 P11PwT 1 0 2 "21 =3 P21 + 11 -1 3 -■叽丄 当An =3时,解：A 的特征方程2-4 -1 |27 - A| = -12 -1 1 2-2 =(2-1)(2-3)2 =02- 3解之得 P2! =Pj] =P11令/“iPw■fP21 = 1■叽丄当人=1时, 解之得 P13 = °，“23 = 2^33 令 “33 = 1约旦标准型1- 10已知两系统的传递函数分别为W|(s)和W 2(s)试求两子系统串联联结和并联连接时，系统的传递函数阵，并讨论所得结果 解： (D 串联联结MlR = 得10 -1得1-H （第2版教材）已知如图1-22所示的系统，其中子系统1、2的传递函数阵分别为求系统的闭环传递函数解：M2已知差分方程为试将其用离散状态空间表达式表示，并使驱动函数I】的系数b（即控制列阵）为⑴b=；解法1 :解法2 ：求T,使得厂，；得宀鳥所以T=所以，状态空间表达式为第二章习题答案2-4用三种方法计算以下矩阵指数函数屛‘。
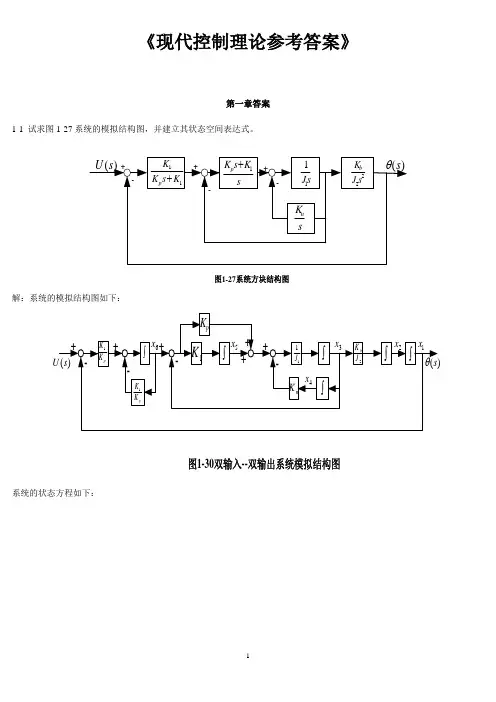
《现代控制理论》刘豹著（第3版）课后习题答案《现代控制理论》刘豹著(第3版)课后习题答案第一章习题答案1-1 试求图1-27系统的模拟结构图，并建立其状态空间表达式。
解：系统的模拟结构图如下：系统的状态方程如下：令，则所以，系统的状态空间表达式及输出方程表达式为1-2有电路如图1-28所示。
以电压为输入量，求以电感中的电流和电容上的电压作为状态变量的状态方程，和以电阻上的电压作为输出量的输出方程。
解：由图，令，输出量有电路原理可知：既得写成矢量矩阵形式为：1-3 参考例子1-3. 1-4 两输入，，两输出，的系统，其模拟结构图如图1-30所示，试求其状态空间表达式和传递函数阵。
解：系统的状态空间表达式如下所示：1-5系统的动态特性由下列微分方程描述列写其相应的状态空间表达式，并画出相应的模拟结构图。
解：令，则有相应的模拟结构图如下：1-6 已知系统传递函数,试求出系统的约旦标准型的实现，并画出相应的模拟结构图解：1-7 给定下列状态空间表达式‘画出其模拟结构图求系统的传递函数解：1-8 求下列矩阵的特征矢量解：A的特征方程解之得：当时，解得：令得当时，解得：令得当时，解得：令得1-9将下列状态空间表达式化成约旦标准型解：A的特征方程当时，解之得令得当时，解之得令得当时，解之得令得约旦标准型1-10 已知两系统的传递函数分别为W1(s)和W2(s)试求两子系统串联联结和并联连接时，系统的传递函数阵，并讨论所得结果解：串联联结并联联结1-11 已知如图1-22所示的系统，其中子系统1、2的传递函数阵分别为求系统的闭环传递函数解：1-11 已知如图1-22所示的系统，其中子系统1、2的传递函数阵分别为求系统的闭环传递函数解：1-12 已知差分方程为试将其用离散状态空间表达式表示，并使驱动函数u的系数b(即控制列阵)为解法1：解法2：求T,使得得所以所以，状态空间表达式为第二章习题答案2-4 用三种方法计算以下矩阵指数函数。
《现代控制理论参考答案》第一章答案1-1 试求图1-27系统的模拟结构图，并建立其状态空间表达式。
图1-27系统方块结构图解：系统的模拟结构图如下：图1-30双输入--双输出系统模拟结构图系统的状态方程如下：u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n p b1611166131534615141313322211+--=+-==++--===••••••令y s =)(θ，则1x y =所以，系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡••••••654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp n p b1-2有电路如图1-28所示。
以电压)(t u 为输入量，求以电感中的电流和电容上的电压作为状态变量的状态方程，和以电阻2R 上的电压作为输出量的输出方程。
U图1-28 电路图解：由图，令32211,,x u x i x i c ===，输出量22x R y =有电路原理可知：•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为：[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CC L L R L L R x x x 。
绪论为了帮助大家在期末复习中能更全面地掌握书中知识点，并且在以后参加考研考博考试直到工作中，为大家提供一个理论参考依据，我们11级自动化二班的同学们在王整风教授的带领下合力编写了这本《现代控制理论习题集》（刘豹第三版），希望大家好好利用这本辅助工具。
根据老师要求，本次任务分组化，责任到个人。
我们班整体分为五大组，每组负责整理一章习题，每个人的任务由组长具体分配，一个人大概分1~2道题，每个人任务虽然不算多，但也给同学们提出了要求：1.写清题号，抄题，画图（用CAD或word画）。
2.题解详略得当，老师要求的步骤必须写上。
3.遇到一题多解，要尽量写出多种方法。
本习题集贯穿全书，为大家展示了控制理论的基础、性质和控制一个动态系统的四个基本步骤，即建模、系统辨识、信号处理、综合控制输入。
我们紧贴原课本，强调运用统一、联系的方法分析处理每一道题，将各章节的知识点都有机地整合在一起，力争做到了对控制理论概念阐述明确，给每道题的解析赋予了较强的物理概念及工程背景。
在课后题中出现的本章节重难点部分，我们加上了必要的文字和图例说明，让读者感觉每一题都思路清晰，简单明了，由于我们给习题配以多种解法，更有助于发散大家的思维，做到举一反三！这本书是由11级自动化二班《现代控制理论》授课老师王整风教授全程监管，魏琳琳同学负责分组和发布任务书，由五个小组组组长李卓钰、程俊辉、林玉松、王亚楠、张宝峰负责自己章节的初步审核，然后汇总到胡玉皓同学那里，并由他做最后的总审核工作，绪论是段培龙同学和付博同学共同编写的。
本书耗时两周，在同学的共同努力下完成，是二班大家庭里又一份智慧和努力的结晶，望大家能够合理使用，如发现错误请及时通知，欢迎大家的批评指正！2014年6月2日第一章控制系统的状态空间表达式1-1试求图1-27系统的模拟结构图，并建立其状态空间表达式 解：系统的模拟结构图如下： 系统的状态方程如下： 令y s =)(θ，则1x y =所以，系统的状态空间表达式及输出方程表达式为1-2有电路如图1-28所示。
现代控制理论课后习题答案第⼀章习题1.2求下列多项式矩阵()s D 和()s N 的两个不同的gcrd:()2223(),()1232s s s s s s s s s ??++== ? ?+-??D N 解：()()22232321s s s s s s s++ =++ ? ?D S N S ； ()3r 2,1,2E -：223381s s s s s s ??++ ?-- ? ???；()3r 2,3,3E ：223051s s s s s ??++ ?- ? ???；()3r 1,3,2E s --：01051s s ?? ?- ? ；()3r 2,1,5E s -：01001s ?? ?；()3r 3,1,1E -：01000s ?? ? ? ???；()1r 2,3E ：01000s ?? ? ? ???；()1r 1,2E ：00100s ?? ?；所以⼀个gcrd 为001s ??；取任⼀单模矩阵预制相乘即可得另⼀个gcrd 。
1.9 求转移矩阵t A e (1)已知1141??=A ，根据拉⽒反变换求解转移矩阵tA e 。
(2) 已知412102113-?? ?= ? ?-??A ，根据C-H 有限项展开法求解转移矩阵t A e 。
解：(1)11()41s s s --??-= ?--??I A1110.50.50.250.2511(3)(1)(3)(1)13131()4141110.50.5(3)(1)(3)(1)(3)(1)3131s s s s s s s s s s s s s s s s s s s s s s s --+---+-+??-+-+ ? ?-=== ? ?---+ ?-+ ? ?-+-+-+-+?I A 3311330.5e 0.5e 0.25e 0.25e e ()e e 0.5e 0.5e t t t t t t tt t s ------??+-??=-= ??? ?-+?A L I A (2)由2412()12(1)(3)0113λλλλλλ--?? ?=--=--= ? ?--??A I -，得1,233,1λλ== 对1,23λ=，可以计算1,2()2rank λ=A I -，所以该特征值的⼏何重数为1。
《现代控制理论参考答案》第一章答案1-1 试求图1-27系统的模拟结构图，并建立其状态空间表达式。
图1-27系统方块结构图解：系统的模拟结构图如下：图1-30双输入--双输出系统模拟结构图系统的状态方程如下：u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n pb1611166131534615141313322211+--=+-==++--===••••••令y s =)(θ，则1x y =所以，系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡••••••654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp n p b1-2有电路如图1-28所示。
以电压)(t u 为输入量，求以电感中的电流和电容上的电压作为状态变量的状态方程，和以电阻2R 上的电压作为输出量的输出方程。
L1L2U图1-28 电路图解：由图，令32211,,x u x i x i c ===，输出量22x R y =有电路原理可知：•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为：[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CCL L R L L R x x x 。
《现代控制理论参考答案》第一章答案1-1 试求图1-27系统的模拟结构图，并建立其状态空间表达式。
11K s K K p +sK s K p 1+s J 11sK n 22s J K b -++-+-)(s θ)(s U 图1-27系统方块结构图解：系统的模拟结构图如下：)(s U )(s θ---+++图1-30双输入--双输出系统模拟结构图1K pK K 1pK K 1+++pK n K ⎰⎰⎰11J ⎰2J K b ⎰⎰-1x 2x 3x 4x 5x 6x系统的状态方程如下：u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n pb1611166131534615141313322211+--=+-==++--===∙∙∙∙∙∙令y s =)(θ，则1x y =所以，系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∙∙∙∙∙∙654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp n p b1-2有电路如图1-28所示。
以电压)(t u 为输入量，求以电感中的电流和电容上的电压作为状态变量的状态方程，和以电阻2R 上的电压作为输出量的输出方程。
R1L1R2L2CU---------Uc---------i1i2图1-28 电路图解：由图，令32211,,x u x i x i c ===，输出量22x R y =有电路原理可知：∙∙∙+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=∙∙∙写成矢量矩阵形式为：[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CCL L R L L R x x x 。
