
第六章 定积分
不定积分是微分法逆运算的一个侧面,本章要介绍的定积分则是它的另一个侧面。 定积分起源于求图形的面积和体积等实际问题。 古希腊的阿基米德用“穷竭法”,我国的刘徽用“割圆术”, 都曾计算过一些几何体的面积和体积,这些均为定积分的雏形。 直到17世纪中叶,牛顿和莱布尼茨先后提出了定积分的概念,并发现了积分与微分之间的内在联系,给出了计算定积分的一般方法,从而使定积分成为解决有关实际问题的有力工具,并使各自独立的微分学与积分学联系在一起,构成完整的理论体系——微积分学。
本章先从几何问题与力学问题引入定积分的定义,然后讨论定积分的性质、计算方法以及定积分在几何与其它学科中的应用。
§6.1定积分的概念与性质
6.1.1引出定积分概念的例题 一、曲边梯形的概念
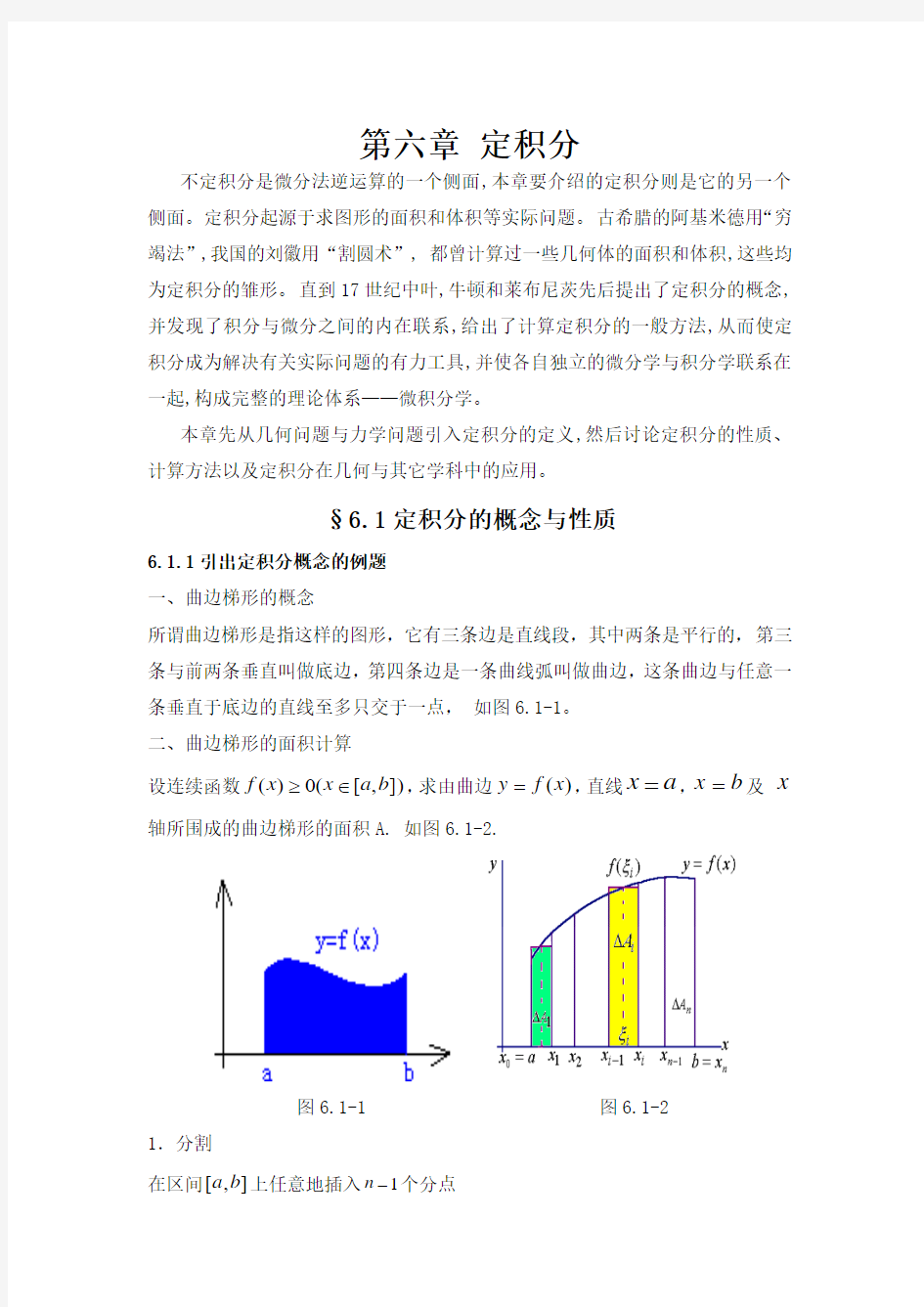
所谓曲边梯形是指这样的图形,它有三条边是直线段,其中两条是平行的,第三条与前两条垂直叫做底边,第四条边是一条曲线弧叫做曲边,这条曲边与任意一条垂直于底边的直线至多只交于一点, 如图6.1-1。 二、曲边梯形的面积计算
设连续函数]),[(0)(b a x x f ∈≥,求由曲边)(x f y =,直线x a =,x b =及 x
轴所围成的曲边梯形的面积A. 如图6.1-2.
图6.1-1 图6.1-2 1.分割
在区间],[b a 上任意地插入1-n 个分点
a x x x x x x x
b i i n n =<<<<<<<<=--01211
区间],[b a 分划成 n 个小区间],[1i i i
x x I -=,且记小区间的长度为
?x x x i n i i i =-=-112(,,,)
过每个分点作平行于y 轴的直线段,这些直线段将曲边梯形分划成n 个窄小的曲边梯形,用i A ?记第 i 个窄小的曲边梯形的面积。 2.近似
由于曲边梯形的高在],[b a 上是连续变化的,在很短小的一段区间上它的变化也很小,即可近似地视为不变。因此,在每个小区间上,可用其中某一点的高来近似代替该小区间上小曲边梯形的变化高,用相应的小矩形面积来近似小曲边梯形的面积。具体地:
对第 i 个窄小曲边梯形,在其对应区间],[1i i i x x I -=上任意地取一点i ξ,以
)(i f ξ作为近似高,以矩形面积i i x f ?)(ξ近似i A ?。
即:n i x x x f A i i i i i i ,,2,1]),[()(1 =∈??≈?-ξξ
3.求和 于是 i i
n
i n
i i
x
f A A ?≈?=∑∑==)(1
1
ξ
4.求极限
很明显地,小区间],[1i i i x x I -=的长度i x ?越小,??A f x i i i ≈()ξ近似程度
就越好;要使得i
i
n
i x f A ?≈
∑=)(1
ξ近似程度越好,只需n x x x ???,,,21 都
越来越小。因此,为了得到面积
A 的精确值,我们只需将区间],[b a 无限地细分,
使得每个小区间的长度都趋向于零。 若记},,,max{21n x x x ???= λ
,则每个小区间的长度趋向于零0→λ。
从而i
i
n
i x f A ?=∑=→)(lim
1
ξλ.
三、变速直线运动的路程
设某物体作直线运动,已知速度)(t v v =是时间间隔],[21T T 上的连续函数,且0)(≥t v ,求物体在时间间隔内所经过的路程。 在时间间隔],[21T T 内任意地插入1-n 个分点
T t t t t t t t T i i n n 1012112=<<<<<<<<=--
将分划成n 个时间区间
[,][,]
[,]
[,]t t t t t t t t i i n n 011211
--
各时间区间的长度依次为
11122011---=?-=?-=?-=?n n n i i i t t t t t t t t t t t t
记各时间区间内物体运动所经过的路程依次为
n i s s s s ???? 21
在时间间隔],[1i i t t -, 物体所经过的路程i s ?的近似值为 ??s v t t t i n i
i i i i i ≈?∈=-()([,]),,,ξξ112
即:将物体在],[1i i t t -上的速度视为不变的,以)(i v ξ来近似代替.很自然地,当],[1i i t t -这一时间间隔段很短时,这种近似是合理的。 于是可给出s 的近似值
i i n
i n i i t v s s ?≈?=∑∑==)(1
1
ξ
为得到s 的精确值, 只需让每个小时间间隔段的长n i t t t t ???? 21,均趋向于零.若记 },max{21n i t t t t ????= λ
则
i i n
i t v s ?=∑=→)(lim 1
ξλ
上述两例,尽管其实际意义不同,但有两点是一致的。
1.曲边梯形的面积值A 由高)(x f y =及x 的变化区间],[b a 来决定;变速直线运动的路程s 由速度)(t v v =及t 的变化区间],[21T T 来决定。
2.计算A 与s 的方法、步骤相同,且均归结到一种结构完全相同的和式极限。
∑=→?=n
i i
i x f A 1
0)(lim ξλ
∑=→?=n
i i
i t v s 1
0)(lim ξλ
抛开这些问题的具体实际意义, 抓住它们在数量关系上共同的本质加以概括, 我们可给出定积分定义。 6.1.2定积分的定义
定义6.1.1 设函数f(x)在],[b a 上有界, 在],[b a 中任意插入1-n 个分点
a x x x x x x x
b i i n n =<<<<<<<<=--01211
把区间分划成 n 个小区间
[,][,][,][,]x x x x x x x x i i n n 011211 --
各区间的长度依次为
11122011,,,,,---=?-=?-=?-=?n n n i i i x x x x x x x x x x x x
在每个小区间],[1i i x x -上任取一点 )(1i i i i x x ≤≤-ξξ,取函数值)(i f ξ与小
区间长度i x ?的乘积),,2,1()(n i x f i i =?ξ。作和式:i i n
i x f s ?=∑=)(1
ξ
记},,,max{21n x x x ???= λ
,如果不论对],[b a 怎样的分法, 也不论在小区
间],[1i i x x -上点i ξ怎样取法, 只要当0→λ时, 和n s 总趋于确定的极限I , 我们就称这个极限I 为函数
)(x f 在区间],[b a 上的定积分, 记为:
i i n
i b
a
x f I dx x f ?==∑?
=→)(lim )(1
ξλ
其中
)(x f 叫做被积函数;dx x f )(叫做被积表达式;x 叫做积分变量; ]
,[b a 叫做积分区间;a 叫做积分下限; b 叫做积分上限;i
i
n
i x f ?∑=)(1
ξ 叫做)
(x f 在],[b a 上的积分和式。
注意:
1.如果积分和式的极限存在,则此极限值是个常量.
2.定积分与被积函数和积分区间有关,而与积分变量的记法无关,即
???
==b
a
b a
b
a
du u f dt t f dx x f )()()(.
3.如果)(x f 在],[b a 上的定积分存在,我们就说)(x f 在],[b a 上可积。且
??
-=a
b
b
a
dx x f dx x f )()( ;0)(=?dx x f a
a
.
6.1.3定积分的几何意义
1.在],[b a 上,0)(≥x f 时,dx x f b
a ?)(表示由曲线)(x f y =,
直线x a =、x b =与x 轴所围成的曲边梯形的面积。如图6.1-3
图6.1-3 图6.1-4
2.在],[b a 上,0)(≤x f 时,dx x f b
a ?)(表示该曲边梯形面积的负值,
如图6.1-4. 3.在],[b a 上,)(x f 既有正值又有负值时,dx x f b
a
?
)(表示由曲线)(x f y =,直
线x a =、x
b =与x 轴所围成的曲边梯形的面积的代数和, 如图6.1-5.
图6.1-5
因此,定积分
dx x f b
a
?
)(是一个数值。
6.1.4定积分的性质 设函数
)()(x g x f ,在],[b a 上可积:
性质1两个函数代数和的定积分等于它们定积分的代数和,即
??
?±=±b
a
b
a
b
a
dx x g dx x f dx x g x f )()()]()([
性质2 被积函数的常数因子可以提到积分号外,即
性质3 如果积分区间],[b a 被分点c 分成区间],[c a 和],[b c ,则
当c 在区间],[b a 之外时,上面表达式也成立。性质3表明定积分对积分区间具有可加性,这个性质可以用于求分段函数的定积分。 性质4
特别的, 性质6 (定积分估值定理)
性质7 (定积分中值定理)
如果函数)(x f 在闭区间],[b a 上连续,则在积分区间],[b a 上至少存在 一个点ξ,使下式成立
()d ()d ()d =+?
??b
c
b
a
a
c
f x x f x x f x x
).
( ))((d )( b a a b f x x f b
a
≤≤-=?ξξ()d ()d =?
?
b
b
a
a
kf x x k f x x ()
是常数k ,则上恒有如果在区间1)(],[ ≡x f b a 1d d ==-?
?b
b
a
a x x
b a
性质5 (定积分比值定理) [,]()()a b f x g x ≥如果在区间上恒有,则
()d b a
f x x ≥
?
()d ?
b a
g x x
[,]()0a b f x ≥如果在区间上恒有,则()d 0
b
a
f x x ≥?
及最小值,则上的最大值在区间分别是函数及设],[)(b a x f m M ).
( )(d )()(b a a b M x x f a b m b
a
<-≤≤-?
如果函数)(x f 在闭区间],[b a 上连续,我们称 为函数)(x f
在],[b a 上的平均值。
【例题1】已知??
??
?≥-<+=0
2101)(x x
x x x f ,求
?
-2
1
)(dx x f .
解:???-++=--2
00
12
1)21()1()(dx x
dx x dx x f
利用定积分的几何意义,可分别求出
21)1(0
1
=
+?
-dx x 1)2
1(20
=-?dx x
2
3
121)(2
1=+=∴?-dx x f
【例题2】试估计定积分
?
3
6
sin π
π
xdx 的值.
解:,上,最大值在233sin )3(]3,6[==ππππf
2
1
6sin )6(==ππf 最小值 ???
??-≤≤??? ??-∴?6323632136
πππππ
πxdx
即123sin 123
6
π
π
π
π≤≤?xdx
练习6.1
1.设)(x f y =在],[b a 上连续,则定积分
?
b
a
dx x f )(的值( );
A .与区间及被积函数有关
B .与积分变量用何字母表示有关
C .与区间无关,与被积函数有关
D .与被积函数的)(x f 的形式无关
?-b
a
x x f a b d )(1
2.定积分
)(b a dx b
a
. A .线段长a b - B .线段长b a - C .矩形面积1)(?-b a D .矩形面积1)(?-a b
3.函数)(x f 在],[b a 上有界是)(x f 在],[b a 上可积的__________条件,而)(x f 在 ],[b a 上连续是)(x f 在],[b a 上可积的__________条件. 4.
_____________
sin =?-
π
πxdx ;_____________cos 22=?-π
π
xdx .
5.利用定积分的性质,比较下题中的定积分值的大小.
dx x dx x ??1
3
1
2
____)1(; dx x xdx ??2
1
221
ln _____ln )2(;
dx x dx x ??2
13
2
12
____)3( ; dx x dx e x
??+1
10)1(_____)4(.
§6.2微积分基本定理
6.2.1变上限的定积分
设函数)(x f 在区间],[b a 上连续,则对于任意的)(b x a x ≤≤,积分存在,且对于给定的)(b x a x ≤≤,就有一个积分值与之对应,所以上限为变量的积分
?
x
a
dx x f )(是上限x 的函数)()(x I dx x f x
a
=?。
注意: 积分上限x 与被积表达式dx x f )(中的积分变量x 是两个不同的概念,在求积时(或说积分过程中)上限x 是固定不变的,而积分变量x 是在下限与上限之间变化的,因此常记为
?
x
a
dt t f )(.
定理 6.2.1如果函数)(x f 在区间],[b a 上连续,则变上限的积分所确定的函数
))(()(b x a x I dt t f x
a
≤≤=?
在],[b a 上可导,且
)()()()(b x a x f dt t f dx
d x I x
a ≤≤=='? 结论:变上限积分所确定的函数
?
x
a
dt t f )(对积分上限x 的导数等于被积函数
)(t f 在积分上限x 处的值)(x f .
【例题1】)(,2sin )(0
2x f dt t x f x
'=
?
求设.
解:2
22sin ]2sin [)(x dt t x f x
='='? 【例题2】已知?-=0
2)12sin()(x
dt t x F ,求)(x F '.
])12sin([])12sin([
)(2
2
'--='-='??
dt t dt t x F x x 解:
x x 212sin 2?--
=)( )(12sin 22
--=x x
【例题3】设)(,)()()
(x G dt t f x G x '=?求βα
.
解:)()]([])([)()
(x x f dt t f x G x a
βββ'?='='?
【例题4】 求
2
arct an lim
x tdt x
x ?→.
解:这属于0
型的极限问题,利用洛必达法则,有
6.2.1牛顿-莱布尼茨公式 定理6.2.2(微积学基本定理)
设函数)(x f 在区间],[b a 上连续,且)(x F 是)(x f 在],[b a 上的任一个原函数,则
)()()(a F b F dx x f b
a
-=?
,或记作)()()()(a F b F a
b
x F dx x f b
a
-==?
.
[]
'x t t x
t t x
x x
x x
)(d arctan d d d arctan 20
2
lim lim
??
→→='x 'x x )()(arctan 21lim 0
→=
x x
x 2arctan lim
→=.2
1
111
21
2
lim =+=
→x x
上式称为牛顿-莱布尼茨公式,也称为微积分基本定理。
牛顿-莱布尼茨公式提供了计算定积分的简便的方法,即求定积分的值,只要求出被积函数)(x f 的一个原函数)(x F ,然后计算原函数在区间],[b a 上的增量
)()(a F b F -即可。该公式把计算定积分归结为求原函数的问题,揭示了定积分
与不定积分之间的内在联系。 【例题5】 求积分
?
1
2dx x .
解:因为3
3x 是被积函数2
x 的一个原函数,
根据牛顿-莱布尼茨公式,有
3
1
30310133331
02
=-==
?x dx x 【例题6】求积分?-+1
12
11
dx x
. 解: 因为x arctan 是被积函数2
11
x +的一个原函数,
根据牛顿-莱布尼茨公式,有
11arctan 11
1
12-=+?-x dx x
2
)
4
(4
)
1arctan(1arctan π
π
π
=
-
-=--=
【例题7】求积分
?
π
20
sin dx x .
解:
???
-+=π
π
π
π
20
20
)sin (sin sin dx x xdx dx x
4
2]
[cos 0]cos [=+-=ππ
πx x
练习6.2
1. 已知?=x
tdt x F 03cos )(,求___________
)(='x F . 2.(1)
?
=+2
2
_______1x dt t dx
d
;(2) ?=+32_______14x x t
dt
dx d . (3)
=
?
-x
t d t arc x d d 1
)cos (_
__________ ;(4)
=
?
20
)(x t t d e x d d
___________.
x
t
t x I x x 100
22
sin d )cos(lim
2
?-=→
___________=.
4.计算
dx x
?
-4
2
1
. 5.计算定积分 .
?
2
)(dx x f ,其中?????>≤+=12
111)(2x x x x
x f .
3.求极限
§6.3定积分的计算
6.3.1定积分的换元积分法
定理6.3.1 设函数)(x f 在区间[a ,b]上连续,而)(t x ?=满足下列条件:
(2)当t 在α与β之间变化时,)(t ?单调变化且)(t ?'连续,则
dt t t f dx x f b
a
)()]([)(??β
α
'=??
上述公式称为定积分的换元积分公式,简称换元公式。 注意:
1. 定积分的换元法在换元后,积分上、下限也要作相应的变换,
即“换元必换限”.
2. 在换元之后,按新的积分变量进行定积分运算,不必再还原为原变量. 3.新变元的积分限可能βα>,也可能βα<,但一定要求满
足 ,即α=t 对应于a x =, β=t 对应于b x =.
【例题1】求
?
20
4cos sin π
xdx
x .
解:dt xdx t x ==cos ,sin 则令 则时,当时,当,12
,00==
==t x t x π
5
1
0151cos sin 5104
20
4
=
==??
t dt t xdx x π
方法二:
?
?
=
20
42
4)(sin sin cos sin π
π
x xd xdx x
0sin 5125πx =
()5
10sin 2sin
515
5
=-??? ??=π ,
,b a ==)()()1(β?α?b a ==)(,)(β?α?
【例题2】计算dx x x e
?
+1
)
ln 1(1
.
【例题3】证明
6.3.2定积分的分部积分法
定理6.3.2
,则
是偶函数,即如果)()()()1(x f x f x f =-.
d )(2d )( 0
??
=-a
a
a
x x f x x f ,则
是奇函数,即如果)()()()2(x f x f x f -=-.
0d )( =?
-a
a
x x f ,则有、上具有连续导数在区间设函数)(' )( '],[)(),( x v x u b a x v x u .
d |??-=b
a
b
a
b
a
u v uv udv 1111
:d d(1ln )
(1ln )1ln
ln 1ln ln 2
1
e
e x x x x x e x =+++=+=??解[][].0d )( ,)()2( ,
d )(2d )( ,)()1( 0=-=-???--a a a
a
a x x f a a x f x x f x x f a a x f 则上连续,且为奇函数,在若则上连续,且为偶函数,在若证明: t
x t x x x f a
d d d )(0
-=-=?-,,令对于????
-=-=--=-a
a a
a
x
x f t t f t t f x x f 0
00
d )(d )( d )(d )([]????+-=+-=∴-a
a
a a a
x
x f x f x x f x x f x x f 0
d )()(
d )(d )(d )(???+=--a
a
a a
x
x f x x f x x f 0
0d )(d )(d )( ,有
时,,当时,则当00===-=t x a t a x
应用分部积分公式计算定积分时,只要在不定积分的结果中代入上下限作差即可。若同时使用了换元积分法,则要根据引入的变量代换相应地变换积分限。 【例题4】计算
?
1
2dx xe x .
解:令
x
x
e v dx du dx e dv x u 222
1,;,==== 代入分部积分公式,得
?
?
-
=1
221
22
10121dx e e x dx xe
x x x
)1(4
1
01
4
121222+=-=e e
e x
【例题5】计算?
e
e
dx x 1
ln .
解:先去掉绝对值符号,再用分部积分公式:
??
?
+-=
e
e
e
e
xdx dx x dx x 1
1
11ln )ln (ln
dx x x e x x dx x x x x e e e
???-+---=11
1111)ln ()1
(1
)ln (
??? ??
-=-++-=??e dx e dx e e e
1121111
【例题6】求?
1
dx e
x
.
解:令t x =,则tdt dx t x 2,2==
当
00==t x 时,,当11==t x 时,则
t
t
x
tde
dt te dx e
???
==1
1
1
22
练习6.3
1.计算下列积分.
()?+π
π
π
3)3sin(1dx x ;()?-+1
23)511(12dx x ;()?--21
2
1
2
43x
xdx
2.计算下列积分.
()?+1
011x dx ; ()?-10
242x
dx 3.计算下列积分.
()?-1
01dx xe
x
;()?10
arctan 2xdx x ;()?e
xdx 1
2
ln 3
§6.4广义积分
定积分概念的推广,主要研究积分区间无穷和被积函数在有限区间上为无界的情形。前者称为无穷限广义积分,或称无穷积分;后者称为无界函数的广义积分,或称瑕积分,也被称为反常积分。 6.4.1无穷区间上的广义积分 定义 6.4.1
设函数)(x f 在区间),[+∞a 上连续,取a b >,极限?+∞→b
a
b x x f d )(lim
称为函数)(x f 在无穷区间),[+∞a 上的广义积分,记作?+∞a
x x f d )( , 即:
??
+∞→+∞
=b
a
b a
dx x f x x f )(lim d )(
]
e 2[10
e
t -=t
t t t d e 221
1
e
?-=[].
21)e (e 2=--=
若上述等式右端的极限存在,则称广义积分?
+∞
a
x x f d )( 收敛;
如果上述极限不存在,则称广义积分
?
+∞
a
x x f d )(发散。
类似地,无穷区间],(b -∞上的广义积分定义为
)()(lim d )(b a dx x f x x f b
a
a b
<=??
-∞→∞
-
无穷区间),(+∞-∞上的广义积分定义为
??
?
∞
-+∞
+∞
∞
-+=a a
dx x f dx x f x x f )()(d )(
此时,如果上式右端的两个广义积分?
∞
-a
x x f d )(和?
+∞a
x x f d )(都收敛,则称广
义积分
?
+∞
∞
-x x f d )(收敛,否则称广义积分?+∞∞
-x x f d )(发散。
上述三种方法统称为无穷区间上的广义积分。 【例题1】 求?+∞
-0
3dx e x .
解:
=3
1
【例题2】 dx x
?+∞
∞-+2
11
. 解:根据定义有
x
x b
x b x
d e lim
d e 0
30
3?
?
-+∞→+∞
-=b
x
b 0
3e lim 31-+∞→-=)
3d(e lim 31
3x b x b --=?-+∞→x x x x x x d 11d 11d 1102022???+∞∞-+∞
∞-+++=+x x b d 1
lim d 1=+∞
x x x x a a d 11
lim d 110202??+=+-∞→∞-[]
,
2
π
)2π(0arctan lim 0
=--==-∞
→a
a x
π=+∴?
+∞
∞-dx x 2
11
6.4.2无界函数的广义积分
定义6.4.2 设函数)(x f 在],(b a 上连续,且∞=+
→)(lim x f a x ,
极限)0()(lim
0>?
+→+
εε
εb
a dx x f 称为无界函数)(x f 在],(
b a 上的积分,
记为
?
b
a
dx x f )(.
若上式右端极限存在,则称广义积分收敛.如果上述极限不存在,就称广义积分发散。
类似地,函数)(x f 在),[b a 上连续,且∞=-
→)(lim x f b
x , 广义积分定义为 如果极限
)0()(lim 0
>?-→+
εε
ε
b a
dx x f 存在,则称广义积分?b
a
dx x f )(收敛.如果
上述极限不存在,就称广义积分?
b
a
dx x f )( 发散。
函数)(x f 在],[b a 上除点),(b a c x ∈=外都连续,且∞=→)(lim x f c
x 则广义积分定义为
???
+=b
c
c
a
b
a
dx x f dx x f dx x f )()()(
此时,如果上式右端两个广义积分??
b
c
c
a
dx x f dx x f )()(和都收敛,则称
广义积分
?
b
a
dx x f )(收敛,否则称广义积分?b a
dx x f )(发散。
上述三种积分统称为无界函数的广义积分,也称为瑕积分。a ,b ,c 称为瑕点。 【例题3】 计算
dx x ?1
ln .
解:因为被积函数x ln 当+→0x 时无界,所以这是无界函数的广义积分
0).
( d )(lim d )(0
>=?
?
-→+εε
εb a
b
a
x x f x x f []
,2
π02π arctan lim 0=-=
=+∞
→b b x 0 ()d lim ()d b
b
a a f x x f x x ε
ε++→=?
?
即,x x x x d ln 0
d ln 1
10
lim ??+
→
=ε
ε
d 1ln 11
lim ?
???-=+?εεx x x x
【例题4】计算dx x
?
1
2
.
【例题5】 计算dx x ?-1
121
.
解: 因为+∞=→20
1
lim
x
x ,于是有 dx x
?-1121
?-+
=
12x dx 0
1
11011
2??????-+-??????-=?
x x x dx , 由∞=→x
x 1
lim
0可知,广义积分?
-0
1
2x dx
和?102x
dx 都发散,所以 广义积分dx x
?-1
121
发散。
注意: 若没有考虑到+∞=→2
1
lim
x x ,仍然按定积分计算,就会得到以下的错误结果:
?
-11
2x dx 2
111
-=??
? ??-=-x .
【例题6】
解:
.
1d ln 1
-=∴?x
x 1
1100000
:0 ,lim 2lim 4lim(1)4x x x +++
+→→→=====??解是瑕点于是εε
εεε101
d 1 1 .
q x q q x <≥?证明瑕积分当收敛,当时发散[]1
11
01,11 d d ln 0
lim q q x x x x x εε+→====+∞?
?当时,110
1,1
1 d d 0
lim q
q q x x x x εε+→≠=?
?当时1, 1111
q q x -+∞>??
==?当,
练习6.4
1. 计算
dx x
x e
?
+∞
ln 1
.
2. 计算
dx xe x ?
∞
-0
.
3. 计算dx x
?+∞
∞-+2
11
.
§6.5简单的微分方程
6.5.1微分方程的一般概念 一、引例
【例题1】 一曲线通过点 (1,5),且该曲线上任意点P(x,y)处的切线斜率等于 该点的横坐标平方的3倍,求此曲线的方程.
解:设所求曲线的方程为)(x y y =,由导数的几何意义得:(字母C 改为小写)
1
1 1.1q q q
<≥-故当时收敛,且其值为,当时发散 ,3d d 2x x
y
=(1)
d 3d 2x x y =即(2)
).5)1(( 5| )()5,1(1====y y x y y x 或记作应满足条件:,故又因曲线通过点(3)
).( d 3 )1(32为任意常数式两端求不定积分,得
把C C x x x y +==?,
,即=式,有
代入把条件415 )3()2(3=+C C (4)
4 3+=x y 于是,所求曲线方程为
二、微分方程的一般概念 1 .微分方程及微分方程的阶
含未知函数的导数(或微分)的方程称为微分方程; 未知函数是一元函数的微分方程,称为常微分方程; 未知函数是多元函数的微分方程,称为偏微分方程;
微分方程中未知函数的导数的最高阶数,称为微分方程的阶。 2 .微分方程的解、通解与特解
能使微分方程成为恒等式的函数,称为微分方程的解。 例如
133+=+=x y c x y 和都是dx x dy 23=的解。
如果微分方程的解中含任意常数,且独立的(即不可合并而使个数减少的)任意常数的个数与微分方程的阶数相同,这样的解为微分方程的通解。
例如c x y +=3
是dx x
dy 2
3= 的通解。
又如 g dt s d c t c gt s =++=2
2212
21是
的通解。 不包含任意常数c 的解为微分方程特解。
例如13+=x y 是dx x dy 23= 的特解。
又如g dt s d gt s ==2
22
21是
的特解。 3.微分方程的初值条件 记作000
000)(;)(0
y x y y y y x y y y
x x x x '=''='====或或 其中0
00,,y y x '都是已知值。 例1中,(1)称为一阶常微分方程;(2)称为微分方程的初值条件;
(3)称为微分方程的通解;(4)称为微分方程特解。
4.微分方程的解的几何意义
微分方程的解的图形称为微分方程的积分曲线。通解的图形是一族积分曲线,称为微分方程的积分曲线族。微分方程的某个特解的图形就是积分曲线族中满足给定初值条件的某一特定的积分曲线。
第六章 定积分的应用 第一节 定积分的元素法 教学目的:理解和掌握用定积分去解决实际问题的思想方法即定积分的元素法 教学重点:元素法的思想 教学难点:元素法的正确运用 教学内容: 一、 再论曲边梯形面积计算 设 f x ()在区间],[b a 上连续,且0)(≥x f ,求以曲线y f x =()为曲边,底为] ,[b a 的曲边梯形的面积A 。 1.化整为零 用任意一组分点 b x x x x x a n i i =<<<<<<=- 110 将区间分成 n 个小区间[,]x x i i -1,其长度为 ),,2,1(1n i x x x i i i =-=?- 并记 },,,m ax {21n x x x ???= λ 相应地,曲边梯形被划分成 n 个窄曲边梯形,第 i 个窄曲边梯形的面积记为 n i A i ,,2,1, =?。 于是 ∑=?= n i i A A 1 2.以不变高代替变高,以矩形代替曲边梯形,给出“零”的近似值
),,2,1(],[)(1n i x x x f A i i i i i i =∈??≈?-ξξ 3.积零为整,给出“整”的近似值 ∑=?≈ n i i i x f A 1 )(ξ 4.取极限,使近似值向精确值转化 ?∑=?==→b a n i i i dx x f x f A )()(lim 1 ξλ 上述做法蕴含有如下两个实质性的问题: (1)若将],[b a 分成部分区间),,2,1(],[1n i x x i i =-,则 A 相应地分成部分量 ),,2,1(n i A i =?,而 ∑=?=n i i A A 1 这表明:所求量A 对于区间],[b a 具有可加性。 (2)用i i x f ?)(ξ近似i A ?,误差应是i x ?的高阶无穷小。 只有这样,和式 ∑=?n i i i x f 1 )(ξ的极限方才是精确值A 。故关键是确定 ))()(()(i i i i i i i x o x f A x f A ?=?-??≈?ξξ 通过对求曲边梯形面积问题的回顾、分析、提炼, 我们可以给出用定积分计算某个量的条件与步骤。 二、元素法 1.能用定积分计算的量U ,应满足下列三个条件 (1) U 与变量x 的变化区间],[b a 有关; (2) U 对于区间],[b a 具有可加性; (3) U 部分量i U ?可近似地表示成i i x f ??)(ξ。 2.写出计算U 的定积分表达式步骤
定积分在经济学中的应用 摘要:定积分是微积分中重要内容,它是解决许多实际问题的重要工具,在经济学中有着广泛的应用,而且内容十分丰富。文中通过具体事例研究了定积分在经济学中的应用,如求总量生产函数、投资决策、消费者剩余和生产者剩余等方面的应用。 关键词:定积分;原函数;边际函数;最大值最小值;总量生产函数;投资;剩余 引言 积分学是微分学和积分学的总称。由于函数概念的产生和应用的加深,也由于科学技术发展的需要,一门新的数学分支就继解析几何之后产生了,这就是微积分学。微积分学这门学科在数学发展中的地位是十分重要的。可以说是继欧氏几何后,全部数学中最大的一个创造。微积分是与应用联系着并发展起来的。定积分推动了天文学、物理学、化学、生物学、工程学、经济学等自然科学、社会科学及应用科学各个分支的发展。并在这些学科中有越来越广泛的应用,微积分是一门历史悠久而又不断发展进步的学科,历史上许多著名的数学家把毕生的心血投入到微积分的研究中,从生产实际的角度上看,应用又是重中之重,随着数学的不断前进,微积分的应用也呈现前所未有的发展。本文将重点介绍定积分在经济学中的应用。
1 利用定积分求原经济函数问题 在经济管理中, 由边际函数求总函数( 即原函数) , 一般采用不定积分来解决,或求一个变上限的定积分。可以求总需求函数,总成本函数, 总收入函数以及总利润函数。 设经济应用函数u( x ) 的边际函数为)(x u ' ,则有 dx x u u x u x )()0()(0?'+= 例1 生产某产品的边际成本函数为100143)(2+-='x x x c , 固定成本 C (0) =10000, 求出生产x 个产品的总成本函数。 解 总成本函数 dx x c c x c x ?'+='0)()0()( =dx x x x )100143(1000002+-+? =x x x x 02_3|]1007[10000++ =x x x 10071000023+-+ 2 利用定积分由变化率求总量问题 如果求总函数在某个范围的改变量, 则直接采用定积分来解决。 例2 已知某产品总产量的变化率为t t Q 1240)(+=' ( 件/天) , 求从第5 天到第10 天产品的总产量。 解 所求的总产量为 dt t Q Q ?'=0 5)( 650)150200()600400(|)640()1220(10 5210 5=+-+=+=+=?t t dt t (件) 3 利用定积分求经济函数的最大值和最小值 例3 设生产x 个产品的边际成本C = 100+ 2x , 其固定成本为
第六章 定积分的应用 本章将应用第五章学过的定积分理论来分析和解决一些几何、物理中的问题,其目的不仅在于建立这些几何、物理的公式,而且更重要的还在于介绍运用元素法将一个量表达为定积分的分析方法。 一、教学目标与基本要求: 使学生掌握定积分计算基本技巧;使学生用所学的定积分的微元法(元素法)去解决各种领域中的一些实际问题; 掌握用定积分表达和计算一些几何量与物理量(平面图形的面积、平面曲线的弧长、旋转体的体积及侧面积、平行截面面积为已知的立体体积、变力作功、引力、压力及函数的平均值等) 二、本章教学内容的重点难点: 找出未知量的元素(微元)的方法。用元素法建立这些几何、物理的公式解决实际问题。运用元素法将一个量表达为定积分的分析方法 §6.1定积分的微小元素法 一、内容要点 1、复习曲边梯形的面积计算方法,定积分的定义 面积A ?∑=?==→b a n i i i dx x f x f )()(lim 1 ξλ 面积元素dA =dx x f )( 2、计算面积的元素法步骤: (1)画出图形; (2)将这个图形分割成n 个部分,这n 个部分的近似于矩形或者 扇形; (3)计算出面积元素; (4)在面积元素前面添加积分号,确定上、下限。 二、教学要求与注意点 掌握用元素法解决一个实际问题所需要的条件。用元素法解决一
个实际问题的步骤。 §6.2 定积分在几何中的应用 一、内容要点 1、在直角坐标系下计算平面图形的面积 方法一 面积元素dA =dx x x )]()([12??-,面积 A = x x x b a d )]()([12??-? 第一步:在D 边界方程中解出y 的两个表达式)(1x y ?=,)(2x y ?=. 第二步:在剩下的边界方程中找出x 的两个常数值a x =,b x =;不够时由)(1x ?)(2x ?=解出, b x a ≤≤,)()(21x y x ??≤≤,面积S =x x x b a d )]()([12??-? 方法二 面积元素dA =dy y y )]()([12??-,面积 A = y y y d c d )]()([12??-? 第一步:在D 边界方程中解出x 的两个表达式)(1y x ?=,)(2y x ?=. 第二步:在剩下的边界方程中找出y 的两个常数值c y =,d y =;不够时由)(1y ?) (2y ?=解出, d y c ≤≤,)()(21y x y ??≤≤,面积S =y y y d c d )]()([12??-? 例1 求22-=x y ,12+=x y 围成的面积 解?????+=-=1 22 2x y x y ,1222+=-x x ,1-=x ,3=x 。当31<<-x 时1222+<-x x ,于是 面积?--=+-=--+=3 1 313223 210)331 ()]2()12[(x x x dx x x 例2 计算4,22-==x y x y 围成的面积 解 由25.0y x =,4+=y x 得,4,2=-=y y ,当42<<-y 时 )
定积分与微积分基本定理(理) 基础巩固强化 1.求曲线y =x 2与y =x 所围成图形的面积,其中正确的是( ) A .S =?? ?0 1(x 2-x )d x B .S =?? ?0 1 (x -x 2)d x C .S =?? ?0 1 (y 2-y )d y D .S =??? 1 (y - y )d y [答案] B [分析] 根据定积分的几何意义,确定积分上、下限和被积函数. [解析] 两函数图象的交点坐标是(0,0),(1,1),故积分上限是1,下限是0,由于在[0,1]上,x ≥x 2,故函数y =x 2与y =x 所围成图 形的面积S =?? ?0 1 (x -x 2)d x . 2.如图,阴影部分面积等于( ) A .2 3 B .2-3 [答案] C [解析] 图中阴影部分面积为
S =??? -3 1 (3-x 2 -2x )d x =(3x -1 3x 3-x 2)|1 -3=32 3. 4-x 2d x =( ) A .4π B .2π C .π [答案] C [解析] 令y =4-x 2,则x 2+y 2=4(y ≥0),由定积分的几何意义知所求积分为图中阴影部分的面积, ∴S =1 4×π×22=π. 4.已知甲、乙两车由同一起点同时出发,并沿同一路线(假定为直线)行驶.甲车、乙车的速度曲线分别为v 甲和v 乙(如图所示).那么对于图中给定的t 0和t 1,下列判断中一定正确的是( ) A .在t 1时刻,甲车在乙车前面 B .在t 1时刻,甲车在乙车后面 C .在t 0时刻,两车的位置相同 D .t 0时刻后,乙车在甲车前面 [答案] A [解析] 判断甲、乙两车谁在前,谁在后的问题,实际上是判断在t 0,t 1时刻,甲、乙两车行驶路程的大小问题.根据定积分的几何意义知:车在某段时间内行驶的路程就是该时间段内速度函数的定积
第六章定积分的应用 教学目的 1、理解元素法的基本思想; 2、掌握用定积分表达和计算一些几何量(平面图形的面积、平面曲线的弧长、旋转体的体 积及侧面积、平行截面面积为已知的立体体积)。 3、掌握用定积分表达和计算一些物理量(变力做功、引力、压力和函数的平均值等)。教学重点: 1、计算平面图形的面积、平面曲线的弧长、旋转体的体积及侧面积、平行截面面积为已知 的立体体积。 2、计算变力所做的功、引力、压力和函数的平均值等。 教学难点: 1、截面面积为已知的立体体积。 2、引力。 §6. 1 定积分的元素法 回忆曲边梯形的面积: 设y=f (x)≥0 (x∈[a,b]).如果说积分, ?=b a dx x f A) (是以[a,b]为底的曲边梯形的面积,则积分上限函数 ?=x a dt t f x A)( ) ( 就是以[a,x]为底的曲边梯形的面积.而微分dA(x)=f (x)dx表示点x处以dx为宽的小曲边梯形面积的近似值?A≈f (x)dx, f (x)dx称为曲边梯形的面积元素. 以[a,b]为底的曲边梯形的面积A就是以面积元素f(x)dx为被积表达式,以 [a,b]为积分区间的定积分: ?=b a dx x f A) (. 一般情况下,为求某一量U,先将此量分布在某一区间[a,b]上,分布在[a,x]上的量用函数U(x)表示,再求这一量的元素dU(x),设dU(x)=u(x)dx,然后以u(x)dx为被积表达式,以[a,b]为积分区间求定积分即得 ?=b a dx x f U) (.用这一方法求一量的值的方法称为微元法(或元素法).
§6. 2 定积分在几何上的应用 一、平面图形的面积 1.直角坐标情形 设平面图形由上下两条曲线y =f 上(x )与y =f 下(x )及左右两条直线x =a 与x =b 所围成, 则面积元素为[f 上(x )- f 下(x )]dx , 于是平面图形的面积为 dx x f x f S b a ?-=)]()([下上. 类似地, 由左右两条曲线x =?左(y )与x =?右(y )及上下两条直线y =d 与y =c 所围成设平面图形的面积为 ?-=d c dy y y S )]()([左右??. 例1 计算抛物线y 2=x 、y =x 2所围成的图形的面积. 解 (1)画图. (2)确定在x 轴上的投影区间: [0, 1]. (3)确定上下曲线: 2)( ,)(x x f x x f ==下上. (4)计算积分 31]3132[)(10323102=-=-=?x x dx x x S . 例2 计算抛物线y 2=2x 与直线y =x -4所围成的图形的面积. 解 (1)画图. (2)确定在y 轴上的投影区间: [-2, 4]. (3)确定左右曲线: 4)( ,2 1)(2+==y y y y 右左??. (4)计算积分 ?--+=422)2 14(dy y y S 18]61421[4232=-+=-y y y . 例3 求椭圆12222=+b y a x 所围成的图形的面积. 解 设整个椭圆的面积是椭圆在第一象限部分的四倍, 椭圆在第一象限部分在x 轴上的投影区间为[0, a ]. 因为面积元素为ydx , 所以 ?=a ydx S 04. 椭圆的参数方程为: x =a cos t , y =b sin t , 于是 ?=a ydx S 04?=0 )cos (sin 4πt a td b
第六章 定积分的应用 §6.1 定积分的元素法 §6.2 平面图形的面积 一、填空题 1.定积分 ? b a dx x f )(的几何意义是 。 2. )(x f 、g(x)在[a,b] 上连续,则由y=f(x),y=g(x)和x=a,x=b 所围成图形的 面积A= 。 3.计算y 2=2x 与y=x-4所围成图形的面积时,选用 作积分变量较为简捷。 二、选择题 1.曲线y=x ln 与直线0,,1 === y e x e x 及所围成的区域的面积S= 。 (A )、2)11(e - (B )、e e 1- (C )、e e 1+ (D )、e 1 1+ 2.曲线r=2acos θ所围图形的面积A= 。 (A )、 θθπ d a 22 0)c o s 2(2 1 ? (B )、θθππd a 2)c o s 2(21?- (C )、 θθπ d a 2 20 )c o s 2(2 1? (D )、2θθπd a 220)cos 2(21? 3.曲线?????==t a y t x 3 3sin cos 所围图形的面积A= 。 (A )、 28a π (B )、24a π (C )、283a π (D )、22 a π 三、求下列各曲线所围成的图形的面积。 1. 曲线y=x 3-6x 与y=x 2所围成图形的面积。 2. 曲线y=-x 2+-3及共在点(0,-3)和(3,0)处的切线所围成图形的面积。
3. 曲线y=sinx 与y=sin2x(0)π≤≤x 所围成图形的面积。 4. r =3cos θθcos 1+=r 及所围成图形的面积。 5. 摆线?? ?-=-=) cos 1() sin (t a y t t a x 的一拱()20π≤≤t 与横轴所围成图形的面积。 四、在曲线族y=a(1-x 2)(a>0)中确定一条曲线,使该曲线和其在(-1,0)和(1,0)两点处 的切线所围图形的面积最小。
1.4定积分与微积分基本定理练习题及答案 1.(2011·一中月考)求曲线y =x2与y =x 所围成图形的面积,其中正确的是( ) A .S =??01(x2-x)dx B .S =??01(x -x2)dx C .S =??01(y2-y)dy D .S =??01(y -y)dy [答案] B [分析] 根据定积分的几何意义,确定积分上、下限和被积函数. [解读] 两函数图象的交点坐标是(0,0),(1,1),故积分上限是1,下限是0,由于在[0,1]上,x ≥x2,故函数y =x2与y =x 所围成图形的面积S =??0 1(x -x2)dx. 2.(2010·日照模考)a =??02xdx ,b =??02exdx ,c =??02sinxdx ,则a 、b 、c 的大小关系是 ( ) A .a 定积分在经济中的应用 一、由经济函数的边际,求经济函数在区间上的增量 根据边际成本,边际收入,边际利润以及产量x 的变动区间[,]a b 上的改变量(增量)就等于它们各自边际在区间[,]a b 上的定积分: ()()()b a R b R a R x dx '-=? (1) ()()()b a C b C a C x dx '-=? (2) ()()()b a L b L a L x dx '-=? (3) 例1 已知某商品边际收入为0.0825x -+(万元/t ),边际成本为5(万元/t ),求产量x 从250t 增加到300t 时销售收入()R x ,总成本C ()x ,利润 ()I x 的改变量(增量) 。 解 首先求边际利润 ()()()0.082550.0820L x R x C x x x '''=-=-+-=-+ 所以根据式(1)、式(2)、式(3),依次求出: 300 250 (300)(250)()R R R x dx '-=?300250(0.0825)x dx =-+?=150万元 300300250250(300)(250)()C C C x dx dx '-==? ?=250万元 300 300250250(300)(250)()(0.0820)L L L x dx x dx '-==-+??=-100万元 二、由经济函数的变化率,求经济函数在区间上的平均变化率 设某经济函数的变化率为()f t ,则称 2 121 ()t t f t dt t t -? 为该经济函数在时间间隔21[,]t t 内的平均变化率。 例2 某银行的利息连续计算,利息率是时间t (单位:年)的函数: 第五章 定积分 内容:定积分的概念和性质、微积分基本公式、换元积分法、分部积分法、广义积分。 要求:理解定积分的概念和性质。掌握牛顿-莱布尼兹公式、定积分的换元法和分部积分法,理解变上限的定积分作为其上限的函数及其求导定理,理解广义积分的概念和计算方法。 重点:定积分的概念和性质;微积分基本公式;换元积分法、分部积分法。 难点:定积分的概念;变上限积分函数及其导数;换元积分法、分部积分法。 §1.定积分的概念 一、实例分析 1.曲边梯形的面积 设函数)(x f y =∈C[a , b ], 且)(x f y =>0. 由曲线0,,),(====y b x a x x f y 围成的图形称为曲边梯形. 如何定义曲边梯形的面积 (1) 矩形面积=底高. (2) 预备一张细长条的纸, 其面积底高. (3) 预备一张呈曲边梯形状的纸, 将其撕成许多细长条. (4) 启示: 将曲边梯形分割为许多细长条, 分割得越细, 误差越小. 第i 个细长条面积)],,[()(11---=?∈??≈?i i i i i i i i i x x x x x x f S ξξ 曲边梯形面积: ∑=?≈ n i i i x f S 1 )(ξ 定积分概念示意图.ppt 定义: ),,2,1,max {()(lim 1 n i x x f S i n i i i Λ=?=?=∑=→λξλ y =f (x ) x =a x =b y =f (x ) a=x 0 x 1 x i-1 x i x n =b 抛开上述过程的几何意义,将其数学过程定义为定积分. 二、定积分的定义 1. 定义 设)(x f y =在[a , b ]有定义, 且有界. (1) 分割: 用分点b x x x a n =<<<=Λ10把[a , b ]分割成n 个小区间: } ,,2,1,max{,,,2,1],,[11n i x x x x n i x x i i i i i i ΛΛ=?=-=?=--λ记 (2) 取点: 在每个小区间],[1i i x x -上任取一点i , 做乘积: i i x f ?)(ξ. (3) 求和: ∑=?n i i i x f 1 )(ξ (4) 取极限: ∑=→?n i i i x f 1 )(lim ξλ 若极限存在, 则其为)(x f 在[a , b ]上的定积分, 记作: ? b a dx x f )(. 即: ∑? =→?=n i i i b a x f dx x f 1 )(lim )(ξλ [a , b ]: 积分区间;a :积分下限;b :积分上限; ∑=?n i i i x f 1 )(ξ积分和式. 问题: 定积分是极限值, 在求极限的过程中, 谁是常量, 谁是变量 注: (1) ∑ =?n i i i x f 1 )(ξ与区间的分割法x i 和取点法 i 有关; 而 ? b a dx x f )(与x i 和 i 无 关. (2) ? b a dx x f )(与a 、b 、f 有关,与x 无关,即: [][]???? ===b a b a b a b a d f du u f dt t f dx x f )()()()( 2.定积分存在定理 定理 若)(x f 在[a , b ]上有界且只有有限个间断点,则)(x f 在[a , b ]上可积. 推论 若)(x f 在[a , b ]上连续,则)(x f 在[a , b ]上可积. 例1. 求 ?1 xdx 专题06 定积分与微积分基本定理 1.由曲线,直线轴所围成的图形的面积为() A.B.4C.D.6 【答案】A 【解析】 联立方程得到两曲线的交点(4,2), 因此曲线y,直线y=x﹣2及y轴所围成的图形的面积为: S. 故选:A. 2.设f(x)=|x﹣1|,则=() A.5 B.6 C.7 D.8 【答案】A 【解析】 画出函数的图像如下图所示,根据定积分的几何意义可知,定积分等于阴影部分的面积,故定积分为 ,故选A. 3.曲线与直线围成的封闭图形的面积是() A.B.C.D. 【答案】D 【解析】 令,则,所以曲线围成的封闭图形面积为 ,故选D 4.为函数图象上一点,当直线与函数的图象围成区域的面积等于时,的值为 A.B.C.1D. 【答案】C 【解析】 直线与函数的图象围成区域的面积S dx = ∴ 故选:C 5.由直线与曲线所围成的封闭图形的面积为( ) A.B.1C.D. 【答案】B 【解析】 题目所求封闭图形的面积为定积分,故选B. 6.如图,矩形中曲线的方程分别是,在矩形内随机取一点,则此点取自阴影部分的概率为( ) A.B.C.D. 【答案】A 【解析】 依题意的阴影部分的面积,根据用几何概型概率计算公式有所求概率为,故选A. 7.() A.B.-1C.D. 【答案】C 【解析】 解: . 故选:C. 8.,则T的值为 A.B.C.D.1 【答案】A 【解析】 由题意得表示单位圆面积的四分之一,且圆的面积为π, ∴, ∴. 故选A. 9.下列计算错误 ..的是() A.B. C.D. 【答案】C 【解析】 在A中,, 在B中,根据定积分的几何意义,, 在C中,, 根据定积分的运算法则与几何意义,易知,故选C. 第六章定积分的应用 课后习题全解 习题6-2 ★ 1.求由曲线 x y =与直线 x y =所围图形的面积。 知识点:平面图形的面积 思路:由于所围图形无论表达为X-型还是Y-型,解法都较简单,所以选其一做即可 解: 见图6-2-1 ∵所围区域D 表达为X-型:???<<< ∵所围区域D 表达为X-型:?????<<< <1 sin 2 0y x x π, (或D 表达为Y-型:???<<< PINGDINGSHAN UNIVERSITY 院系 : 经济与管理学院 题目 : 定积分在生活中的应用 年级专业: 11级市场营销班 学生姓名 : 孙天鹏 定积分在生活中的应用 定积分作为大学里很重要的一部分,在生活有广泛的应用。微积分是与应用联系发展起来的,最初牛顿应用微积分是为了从万有引力导出行星三定律,此后,微积分极大的推动了数学的发展,同时也极大的推动了天文学、物理学、化学、工程学、经济学等自然科学的发展,而且随着人类知识的不断发展,微积分正指引着人类走向认知的殿堂。 一、定积分的概述 1、定积分的定义: 设函数()f x 在区间[],a b 上有界. ①在[],a b 中任意插入若干个分点011n n a x x x x b -=<< <<=,把区间[],a b 分成 n 个小区间[][][]01121,,,, ,,,n n x x x x x x -且各个小区间的长度依次为110x x x ?=-, 221x x x ?=-,…,1n n n x x x -?=-。 ②在每个小区间[]1,i i x x -上任取一点i ξ,作函数()i f ξ与小区间长度i x ?的乘积 ()i i f x ξ?(1,2, ,i n =) , ③作出和 ()1 n i i i S f x ξ==?∑。记{}12max ,,,n P x x x =???作极限()0 1 lim n i i P i f x ξ→=?∑ 如果不论对[],a b 怎样分法,也不论在小区间[]1,i i x x -上点i ξ怎样取法,只要当 0P →时,和S 总趋于确定的极限I ,这时我们称这个极限I 为函数()f x 在 区间[],a b 上的定积分(简称积分),记作()b a f x dx ?,即 ()b a f x dx ?=I =()0 1 lim n i i P i f x ξ→=?∑, 其中()f x 叫做被积函数,()f x dx 叫做被积表达式,x 叫做积分变量,a 叫做积分下限,b 叫做积分上限,],a b ??叫做积分区间。 定积分与微积分基本定理练习题及答案 1.(2011·宁夏银川一中月考)求曲线y =x2与y =x 所围成图形的面积,其中正确的是( ) A .S =??01(x2-x)dx B .S =??01(x -x2)dx C .S =??01(y2-y)dy D .S =??01(y -y)dy [答案] B [分析] 根据定积分的几何意义,确定积分上、下限和被积函数. [解读] 两函数图象的交点坐标是(0,0),(1,1),故积分上限是1,下限是0,由于在[0,1]上,x≥x2,故函数y =x2与y =x 所围成图形的面积S =??0 1(x -x2)dx. 2.(2010·山东日照模考)a =??02xdx ,b =??02exdx ,c =??02sinxdx ,则a 、b 、c 的大小关系 是( ) A .a 第六章 定积分的应用 习题 6-2 (A) 1. 求下列函数与 x 轴所围部分的面积: ] 3,0[,86)1(2+-=x x y ] 3,0[, 2)2(2x x y -= 2. 求下列各图中阴影部分的面积: 图 6-1 3.求由下列各曲线围成的图形的面积: ; 1,)1(===-x e y e y x x 与 ; )0(ln ,ln ,0ln )2(>>====a b b y a y x x y 与 ;0,2)3(2==-=y x y x x y 与 ; )1(,2)4(22--==x y x y ;0,2)1(4)5(2=-=-=y x y x y 与 ; 2,)6(2x y x y x y ===与 ; )0(2sin ,sin 2)7(π≤≤==x x y x y ; 8,2 )8(222 (两部分都要计算)=+=y x x y 4.的图形的面积。 所围成与直线求由曲线e x e x y x y ====-,,0ln 1 5.的面积。处的切线所围成的图形和及其在点求抛物线)0,3()3,0(342--+-=x x y 6.的面积。处的法线所围成的图形及其在点求抛物线),2 (22p p px y = 7.形的面积。与两坐标轴所围成的图求曲线a y x =+ 8.所围图形的面积。求椭圆 12 2 22 =+b y a x 9.。与横轴所围图形的面积(的一拱求由摆线)20)cos 1(),sin (π≤≤-=-=t t a y t t a x 10.轴之间的图形的面积。的切线的左方及下方与由该曲线过原点求位于曲线x e y x = 11.求由下列各方程表示的曲线围成的图形的面积: ;)0(sin 2)1(>=a a θρ ; )0()cos 2(2)2(>+=a a θρ ; 2cos 2)3(2(双纽线)θρ= 抛物体的体积。 轴旋转,计算所得旋转 所围成的图形绕及直线把抛物线x x x x ax y )0(4.12002>== 定积分与微积分基本定理 基础热身 1.已知f (x )为偶函数,且 ??0 6f(x)d x =8,则? ?6-6f(x)d x =( ) A .0 B .4 C .8 D .16 2. 设f(x)=??? x 2,x ∈[0,1], 1 x ,x ∈1,e ] (其中e 为自然对数的底数),则??0 e f(x)d x 的值为( ) B .2 C .1 3.若a =??0 2x 2d x ,b =??0 2x 3d x ,c =??0 2sin x d x ,则a 、b 、c 的大小关 系是( ) A .a A .0 B .1 C .0或1 D .以上均不对 9.如果10 N 的力能使弹簧压缩10 cm ,为在弹性限度内将弹簧拉长6 cm ,则力所做的功为( ) A . J B . J C . J D . J 10.设函数y =f(x)的定义域为R +,若对于给定的正数K ,定义函 数f K (x )=????? K ,fx ≤K ,fx ,fx >K , 则当函数f (x )=1x ,K =1时,定积分??214f K (x)d x 的值为________. (x -x 2)d x =________. 12. ∫π 20(sin x +a cos x)d x =2,则实数a =________. 13.由抛物线y 2 =2x 与直线x =12及x 轴所围成的图形绕x 轴旋转一周所得旋转体的体积为________. 14.(10分)已知函数f(x)=x 3+ax 2+bx +c 的图象如图K 15-2所示,直线y =0在原点处与函数图象相切,且此切线与函数图象所围 成的区域(阴影)面积为27 4,求f(x)的解析式. 图K 15-2 15.(13分)如图K 15-3所示,已知曲线C 1:y =x 2与曲线C 2:y =-x 2+2ax(a>1)交于点O 、A ,直线x =t (0 第六章 习题6-1 1. 利用定积分定义计算由直线y =x +1,直线x =a ,x =b (a??. (2)令()1,()1e e x x f x x f x '=--=-,因01x ≤≤,所以()0f x '>, 从而()(0)0f x f ≥=,说明1e x x ≥+,又e x 1+x .所以 1 1 (1)e d d x x x x >+??. 4. 估计下列各积分值的范围: 1利用定积分的几何意义计算」''1 - x2dx. 2. 计算定积分"2(x+ 1)dx. J i 3. 定积分"bf(x)dx的大小() ?a A .与f(x)和积分区间[a, b]有关,与E的取法无关 B.与f(x)有关,与区间[a,b]以及&的取法无关 C .与f(x)以及8的取法有关,与区间[a, b]无关 D .与f(x)、区间[a,b]和8的取法都有关 4. 在求由x= a,x= b(a 8. 10 利用定积分的几何意义求 —9 — x — 3 2dx. (1)| 2(x 2+ 2x + 1)dx ; 广n (2) 1 (sinx — cosx)dx ; (3)| J* 2 / 、 1 x — X 2 +_ 1 丿。 1 < X 丿 (4) 0-?cosx + e x )dx. ⑹p (2x + 1)dx ; ⑺ 丿0 1 2x + 一 dx x 广1 ⑺f; x (8) 1x 3dx ; ■ 0 (9) 1e x dx. 11 求 y = — x 2与 y = x — 2围成图形的面积S. 15 A.— 4 17 B.— 4 1 C.—|n 2 2 D . 2ln2 已知"2 f(x)dx = 3,贝U 2 [f(x) + 6]d 1 1 12 .由直线x =2,x =2,曲线y =严x 轴所围图形的面积为 13.已知 f 1— 1(x 3 + ax + 3a — b)dx= 2a + 6 且 f(t) = f (x 3 + ax + 3a — b)dx 为偶函数, 求下列定积分: dx ; 2 1 x 2dx 第六章 定积分的应用 (A ) 1、求由下列各曲线所围成的图形的面积 1)2 2 1x y =与822=+y x (两部分都要计算) 2)x y 1 =与直线x y =及2=x 3)x e y =,x e y -=与直线1=x 4)θρcos 2a = 5)t a x 3 cos =,t a y 3 sin = 1、求由摆线()t t a x sin -=,()t a y cos 1-=的一拱()π20≤≤t 与横轴所围成的图形的 面积 2、求对数螺线θ ρae =()πθπ≤≤-及射线πθ=所围成的图形的面积 3、求由曲线x y sin =和它在2 π= x 处的切线以及直线π=x 所围成的图形的面积和它绕 x 轴旋转而成的旋转体的体积 4、由3 x y =,2=x ,0=y 所围成的图形,分别绕x 轴及y 轴旋转,计算所得两旋转体 的体积 5、计算底面是半径为R 的圆,而垂直于底面上一条固定直径的所有截面都是等边三角形 的立体体积 6、计算曲线()x y -=33 3 上对应于31≤≤x 的一段弧的长度 7、计算星形线t a x 3 cos =,t a y 3 sin =的全长 8、由实验知道,弹簧在拉伸过程中,需要的力→ F (单位:N )与伸长量S (单位:cm ) 成正比,即:kS =→ F (k 是比例常数),如果把弹簧内原长拉伸6cm , 计算所作的功 9、一物体按规律3 ct x =作直线运动,介质的阻力与速度的平方成正比,计算物体由0 =x 移到a x =时,克服介质阻力所作的功 10、 设一锥形储水池,深15m ,口径20m ,盛满水,将水吸尽,问要作多少功? 11、 有一等腰梯形闸门,它的两条底边各长10cm 和6cm ,高为20cm ,较长的底边与 水面相齐,计算闸门的一侧所受的水压力 12、 设有一长度为λ,线密度为u 的均匀的直棒,在与棒的一端垂直距离为a 单位处 有一质量为m 的质点M ,试求这细棒对质点M 的引力 (B) 1、设由抛物线()022 >=p px y 与直线p y x 2 3 = + 所围成的平面图形为D 1) 求D 的面积S ;2)将D 绕y 轴旋转一周所得旋转体的体积(完整版)定积分在经济中的应用
高等数学第五章定积分总结
高中数学之定积分与微积分基本定理含答案
微积分 经管类 第四版 吴赣昌 习题全解 第六章定积分的应用
定积分在生活中的应用
定积分及微积分基本定理练习题及答案
高等数学定积分应用习题答案
定积分与微积分含答案
微积分(曹定华)(修订版)课后题答案第六章习题详解
微积分定积分练习题(有答案)
(完整word版)§定积分的应用习题与答案