
教 学 内 容 (教 学 时 数:2 )
一 、再论曲边梯形面积计算
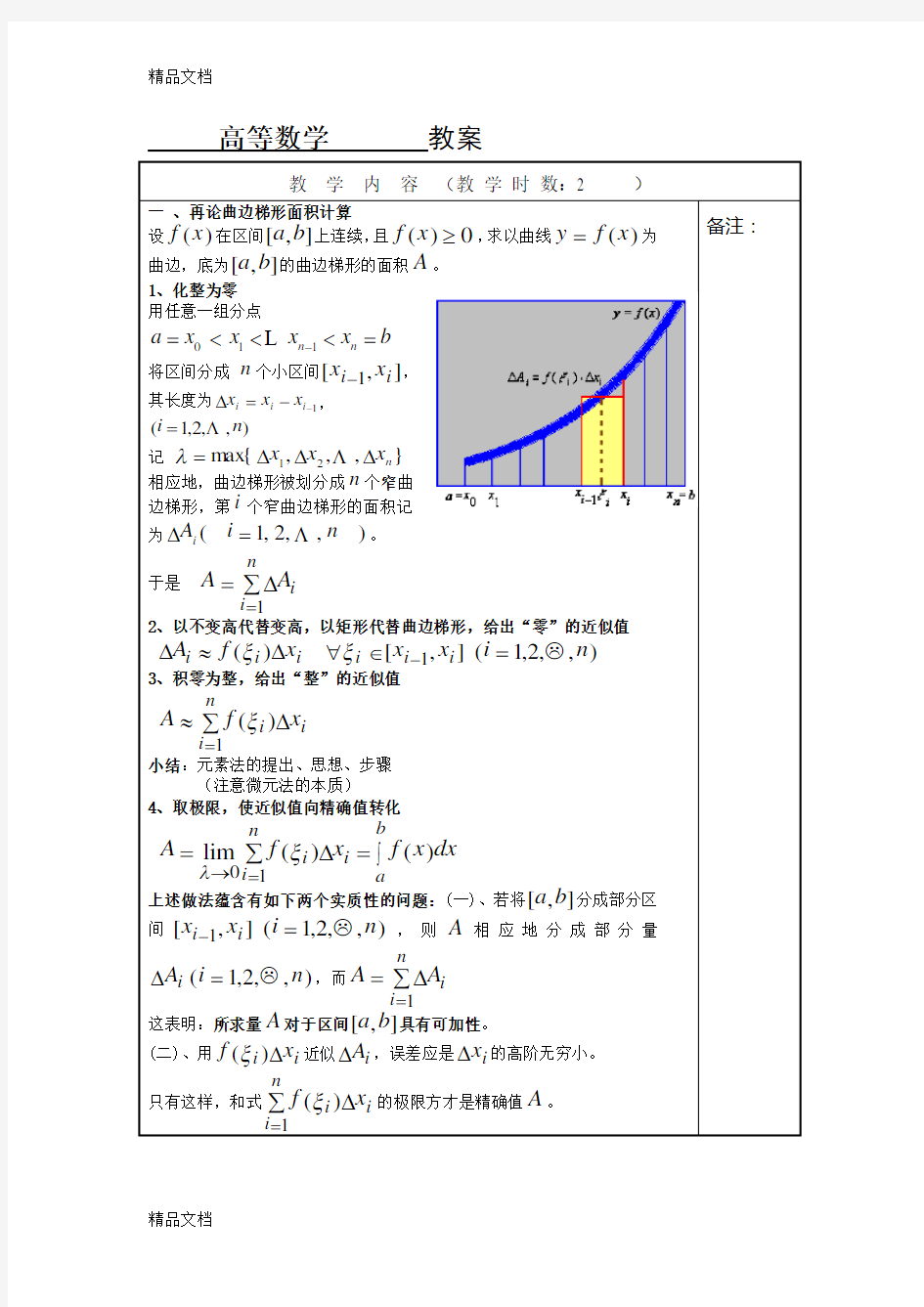
设
f x ()在区间[,]a b 上连续,且f x ()≥0,求以曲线y f x =()为曲边,底为[,]a b 的曲边梯形的面积A 。
1、化整为零 用任意一组分点
011n n a x x x x b -=<<<=L 将区间分成 n 个小区间[,]x x i i -1,
其长度为1--=?i i i x x x ,
),,2,1(n i Λ=
记 },,,m ax {21n x x x ???=Λλ
相应地,曲边梯形被划分成n 个窄曲
边梯形,第i 个窄曲边梯形的面积记为),,2,1(n i A i Λ=?。
于是 A
A i i n
=∑=?1
2、以不变高代替变高,以矩形代替曲边梯形,给出“零”的近似值 ??A f x x x i n i
i i
i i i ≈?∈=-()[,](,,,)ξξ112
3、积零为整,给出“整”的近似值
A f x i i i n
≈∑=()ξ?1
小结:元素法的提出、思想、步骤 (注意微元法的本质)
4、取极限,使近似值向精确值转化
A f x f x dx i i i n
a
b
=∑=?→=lim ()()λξ01
?
上述做法蕴含有如下两个实质性的问题:(一)、若将[,]a b 分成部分区间
[,](,,,)
x x i n i i -=112 ,则
A
相应地分成部分量
?A i n i (,,,)=12 ,而A A i i n
=∑=?1
这表明:所求量A 对于区间[,]a b 具有可加性。
(二)、用f x i i ()ξ?近似?A i ,误差应是?x i 的高阶无穷小。
只有这样,和式f x i i i n
()ξ?=∑1
的极限方才是精确值A 。
备注:
教 学 内 容 (教 学 时 数: )
确定 ))()(()(i i i i i i i
x o x f A x f A ?=?-??≈?ξξ是关键。
上述做法可进一步简化为
略去下标i ,用A ?表示任一小区间[,]x x dx +上窄曲边梯形的面积, 这样 A A =∑?一般地称()f x dx 为面积元素
记作 ()dA f x dx =
窄曲边梯形A ?叫典型面积元素。 于是 ()A f x dx dA ≈∑=∑
lim ()()b
a
A f x dx f x dx =∑=?
通过对求曲边梯形面积问题的回顾、分析、提炼, 我们可以给出用定积分计算某个量的条件与步骤。
二、元素法
1、能用定积分计算的量U ,应满足下列三个条件
(1)、U 与变量x 的变化区间[,]a b 有关; (2)、U 对于区间[,]a b 具有可加性; (3)、U 部分量?U i 可近似地表示成
f x i i ()ξ??。
2、写出计算U 的定积分表达式步骤 (1)、根据问题,选取一个变量x 为积分变量,并确定它的变化区间[,]a b ; (2)、设想将区间[,]a b 分成若干小区间,取其中的任一小区间
[,]x x dx +,
求出它所对应的部分量?U 的近似值
?U f x dx ≈() ( f x ()为[,]a b 上一连续函数) 则称f x dx ()为量U 的元素,且记作dU f x dx =()。
(3)、以U 的元素dU 作被积表达式,以[,]a b 为积分区间,得
()b
a U f x dx =?
这个方法叫做元素法,其实质是找出U 的元素dU 的微分表达式
dU f x dx a x b =≤≤()()
因此,也称此法为微元法。 【例1】已知闸门上水的压强
p (单位面积上压力的大小)是水深h 的函数,且
3(/)p h =吨米。若闸门高3米,宽2米,求水面与闸门顶相齐时闸门所承受
的水压力P 。
备注:
教 学 内 容 (教 学 时 数: )
解:选择h 为积分变量,则 03≤
≤h 位于水深h 与 h dh +之间的闸门所承受的水压力近似地为
dP h dh hdh =?=()22
故 (
3
320
29()P hdh h
=
==?
吨
( 注:这里,dP
hdh =2是水压力元素 )
备注:
作业、讨论题、思考题:
定积分的元素法
教 学 内 容 一、问题的提出 回顾:曲边梯形求面积的问题 曲边梯形由连续曲线)(x f y =)0)((≥x f 、x 轴与两条直线a x =、b x =所围 成。 ?=b a dx x f A )( 面积表示为定积分的步骤如下 (1)把区间],[b a 分成n 个长度为i x ?的小区间,相应的曲边梯形被分为n 个小窄曲边梯形,第i 个小窄曲边梯形的面积为i A ?,则∑=?=n i i A A 1. (2)计算i A ?的近似值i i i x f A ?≈?)(ξ,i i x ?∈ξ (3) 求和,得A 的近似值.)(1i i n i x f A ?≈∑=ξ (4) 求极限,得A 的精确值i i n i x f A ?=∑=→)(lim 10ξλ?=b a dx x f )( 提示: 若用A ? 表示任一小区间],[x x x ?+上的窄曲边梯形的面积,则 ∑?=A A ,并取dx x f A )(≈?,于是∑≈dx x f A )( a b x y o ) (x f y =
∑=dx x f A )(lim .)(?=b a dx x f 当所求量U 符合下列条件: (1)U 是与一个变量x 的变化区间[]b a ,有关的量; (2)U 对于区间[]b a ,具有可加性,就是说,如果把区间[]b a ,分成许多部分区间,则U 相应地分成许多部分量,而U 等于所有部分量之和; (3)部分量i U ?的近似值可表示为i i x f ?)(ξ; 就可以考虑用定积分来表达这个量U 元素法的一般步骤: 1)根据问题的具体情况,选取一个变量例如x 为积分变量,并确定它的变化区间],[b a ; 2)设想把区间],[b a 分成n 个小区间,取其中任一小区间并记为],[dx x x +,求出相应于这小区间的部分量U ?的近似值.如果U ?能近似地表示为],[b a 上的一个连续函数在x 处的值)(x f 与dx 的乘积,就把dx x f )(称为量U 的元素且记作dU ,即dx x f dU )(=; 3)以所求量U 的元素dx x f )(为被积表达式,在区间],[b a 上作定积分,得?=b a dx x f U )(,即为所求量U 的积分表达式. 这个方法通常叫做元素法. a b x y o ) (x f y =x dx x +
习题6-1定积分的元素法习题6-2定积分在几何上的应用(一) 42 4 2 4 4 1sin cos 4 (cos sin)(sin cos) (sin cos)(cos sin) 2. .x x x S x x dx x x dx x x x x ππ π π π π π == ∴=-+- =++-- = ?? 解:当时, 22 222 222 000 22 22 00 2 22 2 1 (1cos)(1cos2cos) 222 cos21 (12cos)(3cos24cos) 224 13 (3sin24sin). 422 . a a S d d d a a d d a a πππ ππ π ρθθθθθθ θ θθθθθ π θθθ ==+=++ + =++=++ =?++= ??? ?? 解:极坐标的情形 22 2 3(,0)(cos,sin), 2cos sin. 1 (2sin2)sin(sin sin cos) 2 '(cos cos sin) [cos cos(2)] (2cos cos1) 1 '0cos1. 2 cos0, .a a t b t a t b t S a t a b t ab t t t S ab t t t ab t t ab t t S t t ?? ∴=+??=+ =+- =+ =+- ==- ∴>∴ 解:设等腰梯形与椭圆在第一象限的非的交点为 则梯形的上底为,高为 令,则或 ∵交点在第一象限 max 1 cos. 2 ,sin()0 323 1 (1). 2 t t t S S a b ππ = '' ∴==< ∴=+?=
本科高等数学 第六章 定积分的应用 教学内容与基本要求:掌握用定积分表达和计算一些几何量和物理量(平面图形面积,平面曲线的弧长、体积、变力作功、引力、压力等) 第一节 定积分的元素法 ㈠.本课的基本要求 掌握掌握定积分的元素法的思想 ㈡.本课的重点、难点 元素法的思想为重点,其条件为难点 ㈢.教学内容 1.定积分的定义(略) 注:1.所求量A 与[a,b]有关且所求量对积分区间具有可加性,即积分区间分为若干个区间,总体量也分为若干部分且等于这若干部分之和 2.i i i A x f ?≈?)(ξ, i i i x x f ??是)(ξ的线性函数,且与i A ?之差是比i x ?还要高阶的无穷小──线性性 ?=b a dx x f A )( 方法:1.取典型子区间:],[dx x x +其对应的部分量为ΔA 2.dx x f A )(≈?──A 的微元(面积元素),∑?= =i A A dx x f dA ,)( 3.?=b a dx x f A )( 所求量总体I 满足下列条件才能用定积分 1.I 与某变量x 所在的区间有关 2.I 对于[a,b]具有可加性 3.部分量dx x f I )(=? (线性性) 可简化为两步: 1.分割区间[a,b],取其中任上小区间],[dx x x +,求出相应的部分量I 的近似值dx x f )(,称它为所求量I 的微元,记为I=dx x f )(,即不变代变求积分 2.对这些微分在[a,b]上无限求和,即在整个区间上求积分得所求量?=b a dx x f I )(,即微分累积成积分 上面这种“无限细分”及“无限求和”两步解决问题的方法称为微元法(或称元素法) 以下各节,我们就用微元法的思想来讨论定积分在几何、物理方面的一些应用。
定积分的元素法 一、问题的提出 回顾:曲边梯形求面积的问题 曲边梯形由连续曲线)(x f y =)0)((≥x f 、x 轴与两条直线a x =、b x =所围成。 面积表示为定积分的步骤如下 (1)把区间],[b a 分成n 个长度为i x ?的小区间,相应的曲边梯形被分为n 个小窄曲边梯形,第i 个小窄曲边梯形的面积为i A ?,则∑=?= n i i A A 1 (2)计算i A ?的近似值 (3) 求和,得A 的近似值 (4) 求极限,得A 的精确值 若用A ? 表示任一小区间],[x x x ?+上的窄曲边梯形的面积,则∑?=A A ,并取dx x f A )(≈?,于是∑≈dx x f A )( a b i i i x f A ?≈?)(ξi i x ?∈ξ.)(1i i n i x f A ?≈∑=ξi i n i x f A ?=∑=→)(lim 10ξλ? =b a dx x f )(∑=dx x f A )(lim . )(?=b a dx x f
当所求量U 符合下列条件: (1)U 是与一个变量x 的变化区间[]b a ,有关的量; (2)U 对于区间[]b a ,具有可加性,就是说,如果把区间[]b a ,分成许多部分区间,则U 相应地分成许多部分量,而U 等于所有部分量之和; (3)部分量i U ?的近似值可表示为i i x f ?)(ξ;就可以考虑用定积分来表达这个量U 元素法的一般步骤: 1) 根据问题的具体情况,选取一个变量例如x 为积分变量,并确定它的变化区间],[b a 2)设想把区间],[b a 分成n 个小区间,取其中任一小区间并记为],[dx x x +,求出相应于这小区间的部分量U ?的近似值.如果U ?能近似地表示为],[b a 上的一个连续函数在x 处的值)(x f 与dx 的乘积,就把dx x f )(称为量U 的元素且记作dU ,即dx x f dU )(=; 3)以所求量U 的元素dx x f )(为被积表达式,在区间],[b a 上作定积分,得?=b a dx x f U )(, 即为所求量U 的积分表达式. 这个方法通常叫做元素法. 应用方向:平面图形的面积;体积;平面曲线的弧长;功;水压力;引力和平均值等. §6. 2 定积分在几何上的应用 一、平面图形的面积 1.直角坐标情形 设平面图形由上下两条曲线y =f 上(x )与y =f 下(x )及左右两条直线x =a 与x =b 所围成, 则面积元素为[f 上(x )- f 下(x )]dx , 于是平面图形的面积为 dx x f x f S b a ?-=)]()([下上. 类似地, 由左右两条曲线x =?左(y )与x =?右(y )及上下两条直线y =d 与y =c 所围成设平面图