
板块一 三角形等高模型
我们已经知道三角形面积的计算公式:三角形面积=底?高2÷
从这个公式我们可以发现:三角形面积的大小,取决于三角形底和高的乘积. 如果三角形的底不变,高越大(小),三角形面积也就越大(小); 如果三角形的高不变,底越大(小),三角形面积也就越大(小);
这说明当三角形的面积变化时,它的底和高之中至少有一个要发生变化.但是,当三角形的底和高同时发生
变化时,三角形的面积不一定变化.比如当高变为原来的3倍,底变为原来的1
3
,则三角形面积与原来的一
样.这就是说:一个三角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化.同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状. 在实际问题的研究中,我们还会常常用到以下结论: ①等底等高的两个三角形面积相等;
②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; 如左图12::S S a b =
s 2s 1b
D
C
B
A
③夹在一组平行线之间的等积变形,如右上图ACD BCD S S =△△;
反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD .
④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形); ⑤三角形面积等于与它等底等高的平行四边形面积的一半;
⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比.
板块二 鸟头模型
两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.
如图在ABC △中,,D E 分别是,AB AC 上的点如图 ⑴(或D 在BA 的延长线上,E 在AC 上), 则:():()ABC ADE S S AB AC AD AE =??△△
E
D
C
B
A
D
E C
B
A
图⑴ 图⑵
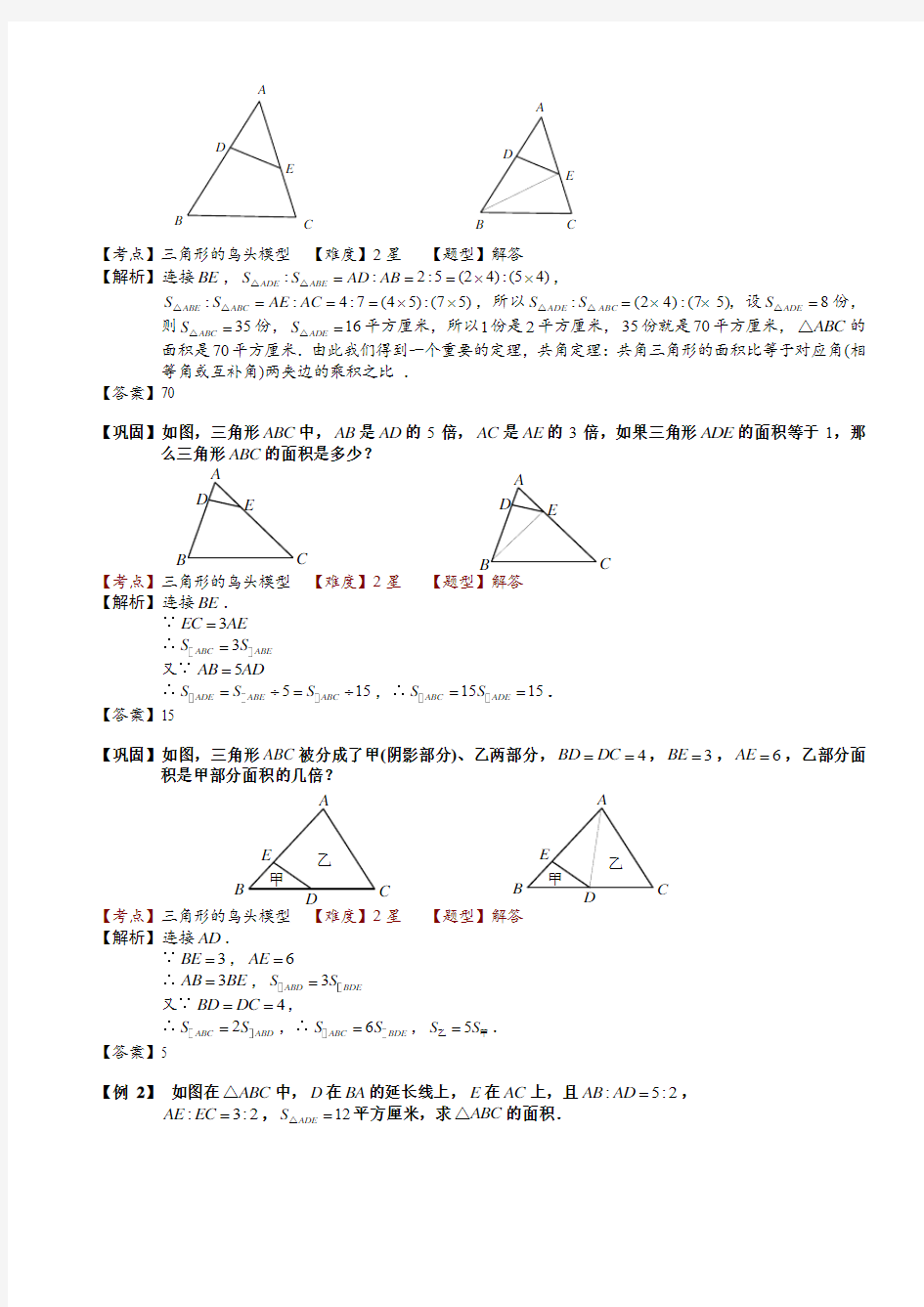
【例 1】 如图在ABC △中,,D E 分别是,AB AC 上的点,且:2:5AD AB =,:4:7AE AC =,16ADE S =△平
方厘米,求ABC △的面积.
例题精讲
4-3-2.三角形等高模型与鸟头模型
E
D
C
B
A
E
D
C
B
A
【考点】三角形的鸟头模型 【难度】2星 【题型】解答 【解析】 连接BE ,::2:5(24):(54)ADE ABE S S AD AB ===??△△,
::4:7(45):(75)ABE ABC S S AE AC ===??△△,所以:(24):(75)ADE ABC S S =??△△,设8ADE S =△份,
则35ABC S =△份,16ADE S =△平方厘米,所以1份是2平方厘米,35份就是70平方厘米,ABC △的
面积是70平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比 .
【答案】70
【巩固】如图,三角形ABC 中,AB 是AD 的5倍,AC 是AE 的3倍,如果三角形ADE 的面积等于1,那
么三角形ABC 的面积是多少?
E D
C B A A
B C D
E
【考点】三角形的鸟头模型 【难度】2星 【题型】解答 【解析】 连接BE .
∵3EC AE = ∴3ABC ABE S S = 又∵5AB AD =
∴515ADE ABE ABC S S S =÷=÷,∴1515ABC ADE S S ==.
【答案】15
【巩固】如图,三角形ABC 被分成了甲(阴影部分)、乙两部分,4BD DC ==,3BE =,6AE =,乙部分面
积是甲部分面积的几倍?
乙
甲
E D C
B
A
A B
C
D
E
甲
乙
【考点】三角形的鸟头模型 【难度】2星 【题型】解答 【解析】 连接AD .
∵3BE =,6AE =
∴3AB BE =,3ABD BDE S S = 又∵4BD DC ==,
∴2ABC ABD S S =,∴6ABC BDE S S =,5S S =乙甲.
【答案】5
【例 2】 如图在ABC △中,D 在BA 的延长线上,E 在AC 上,且:5:2AB AD =,
:3:2AE EC =,12ADE S =△平方厘米,求ABC △的面积.
E
D C
B
A E
D
C
B
A
【考点】三角形的鸟头模型 【难度】3星 【题型】解答 【解析】 连接BE ,::2:5(23):(53)ADE ABE S S AD AB ===??△△
[]::3:(32)(35):(32)5ABE ABC S S AE AC ==+=?+?△△,
所以[]:(32):5(32)6:25ADE ABC S S =??+=△△,设6ADE S =△份,则25ABC S =△份,12ADE S =△平方厘
米,所以1份是2平方厘米,25份就是50平方厘米,ABC △的面积是50平方厘米.由此我们得到
一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比
【答案】50
【例 3】 如图所示,在平行四边形ABCD 中,E 为AB 的中点,2AF CF =,三角形AFE (图中阴影部分)的
面积为8平方厘米.平行四边形的面积是多少平方厘米?
【考点】三角形的鸟头模型 【难度】2星 【题型】解答 【解析】 连接FB .三角形AFB 面积是三角形CFB 面积的2倍,而三角形AFB 面积是三角形AEF 面积的2
倍,所以三角形ABC 面积是三角形AEF 面积的3倍;又因为平行四边形的面积是三角形ABC 面积的2倍,所以平行四边形的面积是三角形AFE 面积的326?=()倍.因此,平行四边形的面积为8648?=(平方厘米).
【答案】48
【例 4】 已知DEF △的面积为7平方厘米,,2,3BE CE AD BD CF AF ===,求ABC △的面积.
F
E
D C
B
A
【考点】三角形的鸟头模型 【难度】3星 【题型】解答
【解析】
:():()(11):(23)1:6BDE ABC S S BD BE BA BC =??=??=△△,:():()(13):(24)3:8CEF ABC S S CE CF CB CA =??=??=△△:():()(21):(34)1:6ADF ABC S S AD AF AB AC =??=??=△△
设24ABC S =△份,则4BDE S =△份,4ADF S =△份,9CEF S =△份,244497DEF S =---=△份,恰好是7
平方厘米,所以24ABC S =△平方厘米
【答案】24
【例 5】 如图16-4,已知.AE=
15AC ,CD=14BC ,BF=1
6
AB ,那么DEF ABC 三角形的面积三角形的面积等于多少?
【考点】三角形的鸟头模型 【难度】3星 【题型】解答 【关键词】迎春杯,决赛,第一题,9题 【解析】 如下图,连接AD ,BE ,CF.
有△ABE ,△ABC 的高相等,面积比为底的比,则有ABE ABC
S
S
=
AE
AC
,所以ABE S =
AE
AC
×ABC S =
15
ABC S
同理有AEF S
=
AF
AB
ABE S ,即=AEF S
=
15×56ABC S =1
6
ABC S . 类似的还可以得到CDE S =14×45ABC S =15ABC S ,BDF S =16×13ABC S =1
8
ABC S .
所以有DEF S =ABC S -(AEF S +CDE S +BDF S )=(1-16-15-18)ABC S =
61
120
ABC S . 即DEF ABC 三角形的面积三角形的面积为61120
. 【答案】
61120
【例 6】 如图,三角形ABC 的面积为3平方厘米,其中:2:5AB BE =,:3:2BC CD =,三角形BDE 的面
积是多少?
A
B E
C D
D
C E
B A
【考点】三角形的鸟头模型 【难度】2星 【题型】解答 【解析】 由于180ABC DBE ?∠+∠=,所以可以用共角定理,设2AB =份,3BC =份,则5BE =份,
325BD =+=份,由共角定理:():()(23):(55)6:25ABC BDE S S AB BC BE BD =??=??=△△,设
6ABC S =△份,恰好是3平方厘米,所以1份是0.5平方厘米,25份就是250.512.5?=平方厘米,三角
形BDE 的面积是12.5平方厘米
【答案】12.5
【例 7】 如图所示,正方形ABCD 边长为6厘米,13AE AC =
,1
3
CF BC =.三角形DEF 的面积为_______平方厘米.
E
D
C
【考点】三角形的鸟头模型 【难度】3星 【题型】解答 【关键词】走美杯,五年级,初赛
【解析】 由题意知13AE AC =
、13CF BC =,可得2
3
CE AC =.根据”共角定理”可得, ():():()12:(33)2:9CEF ABC
S S CF CE CB AC =??=??=△△;而66218ABC S =?÷=△;所以4CEF S =△;
同理得,:2:3CDE ACD S S =△△;,183212CDE S =÷?=△,6CDF S =△
故412610DEF CEF DEC DFC S S S S =+-=+-=△△△△(平方厘米).
【答案】10
【例 8】 如图,已知三角形ABC 面积为1,延长AB 至D ,使BD AB =;延长BC 至E ,使2CE BC =;延
长CA 至F ,使3AF AC =,求三角形DEF 的面积.
F
E
D
C
B A
A
B C
D
E
F
【考点】三角形的鸟头模型 【难度】3星 【题型】解答 【解析】 (法1)本题是性质的反复使用.
连接AE 、CD . ∵1
1
ABC DBC S S =,1ABC S =, ∴S 1DBC =.
同理可得其它,最后三角形DEF 的面积18=.
(法2)用共角定理∵在ABC 和CFE 中,ACB ∠与FCE ∠互补, ∴111428ABC FCE S AC BC S FC CE ??===??. 又1ABC
S
=,所以8FCE
S
=.
同理可得6ADF
S =,3BDE
S =.
所以186318DEF ABC FCE ADF BDE S S S S S =+++=+++=.
【答案】18
【例 9】 如图,把四边形
ABCD 的各边都延长2倍,得到一个新四边形EFGH 如果ABCD 的面积是5平方
厘米,则EFGH 的面积是多少平方厘米?
【考点】三角形的鸟头模型 【难度】4星
【题型】解答 【解析】 方法一:如下图,连接BD ,ED ,BG ,
有EAD 、ADB 同高,所以面积比为底的比,有2EAD
ABD
ABD EA
S
S S
AB
=
=.
同理36EAH
EAD EAD ABD AH
S
S S S AD
=
==. 类似的,还可得6FCG BCD S S =,有()66EAH FCG ABD
BCD
ABCD S S
S
S
S +=+==30平方厘米.
连接AC ,AF ,HC ,还可得6EFB
ABC
S
S
=,6DHG
ACD
S
S
=,
有()66EFB
DHG
ABC
ACD
ABCD S
S
S
S
S +=+==30平方厘米
.
有四边形EFGH 的面积为EAH,FCG ,EFB,DHG ,ABCD 的面积和,即为30+30+5=65(平方厘米.) 方法二:连接BD ,有EAH 、△ABD 中∠EAD+∠BAD=180° 又夹成两角的边EA 、AH ,AB 、AD 的乘积比,
EA AH
AB AD
??=2×3=6,所以EAH
S
=6ABD
S
.
类似的,还可得FCG
S =6BCD
S
,有EAH
S
+FCG S
=6(ABD
S +BCD
S
)=6ABCD S =30平方厘米.
连接AC ,还可得EFB
S
=6ABC S
,
DHG S
=6
ACD
S
,
有EFB
S
+DHG S
=6(
ABC S +
ACD
S
)=6ABCD S =30平方厘米.
有四边形EFGH 的面积为△EAH ,△FCG ,△EFB ,△DHG ,ABCD 的面积和, 即为30+30+5=65平方厘米. 【答案】65
【例 10】 如图,平行四边形ABCD ,BE AB =,2CF CB =,3GD DC =,4HA AD =,平行四边形ABCD 的
面积是2, 求平行四边形ABCD 与四边形EFGH 的面积比.
H
G
A
B C
D E
F
H
G
A B C
D E
F
【考点】三角形的鸟头模型 【难度】4星 【题型】解答 【解析】 连接AC 、BD .根据共角定理
∵在ABC △和BFE △中,ABC ∠与FBE ∠互补,
∴111133
ABC FBE S AB BC S BE BF ??===??△△. 又1ABC S =△,所以3FBE S =△.
同理可得8GCF S =△,15DHG S =△,8AEH S =△.
所以8815+3+236EFGH AEH CFG DHG BEF ABCD S S S S S S =++++=++=△△△△.
所以213618
ABCD EFGH S S ==.
【答案】
118
【例 11】 如图,四边形EFGH 的面积是66平方米,EA AB =,CB BF =,DC CG =,HD DA =,求四边形
ABCD 的面积.
H G
F
E
D C
B A A B C
D
E
F
G
H
【考点】三角形的鸟头模型 【难度】4星 【题型】解答 【解析】 连接BD .由共角定理得:():()1:2BCD CGF S S CD CB CG CF =??=△△,即2CGF CDB S S =△△
同理:1:2ABD AHE S S =△△,即2AHE ABD S S =△△ 所以2()2AHE CGF CBD ADB ABCD S S S S S +=+=△△△△四边形 连接AC ,同理可以得到2DHG BEF ABCD S S S +=△△四边形
5AHE CGF HDG BEF EFGH ABCD ABCD S S S S S S S =++++=△△△△四边形四边形四边形
所以66513.2ABCD S =÷=四边形平方米
【答案】13.2
【例 12】 如图,将四边形ABCD 的四条边AB 、CB 、CD 、AD 分别延长两倍至点E 、F 、G 、H ,若四
边形ABCD 的面积为5,则四边形EFGH 的面积是 .
A B C
D E F G
H
A B C
D
E
F G
H
【考点】三角形的鸟头模型 【难度】4星 【题型】解答 【解析】 连接AC 、BD .
由于2BE AB =,2BF BC =,于是4BEF ABC S S ??=,同理4HDG ADC S S ??=.
于是444BEF HDG ABC ADC ABCD S S S S S ????+=+=.
再由于3AE AB =,3AH AD =,于是9AEH ABD S S ??=,同理9CFG CBD S S ??=. 于是999AEH CFG ABD CBD ABCD S S S S S ????+=+=.
那么491260EFGH BEF HDG AEH CFG ABCD ABCD ABCD ABCD ABCD S S S S S S S S S S ????=+++-=+-==.
【答案】60
【例 13】 如图,在ABC △中,延长AB 至D ,使BD AB =,延长BC 至E ,使1
2
CE BC =,F 是AC 的中点,
若ABC △的面积是2,则DEF △的面积是多少?
A B
C
D
E
F
【考点】三角形的鸟头模型 【难度】3星 【题型】解答 【解析】 ∵在ABC △和CFE △中,ACB ∠与FCE ∠互补,
∴224111
ABC FCE S AC BC S FC CE ??===??△△. 又2ABC
S
=,所以0.5FCE
S
=.
同理可得2ADF S =△,3BDE S =△.
所以20.532 3.5DEF ABC CEF DEB ADF S S S S S =++-=++-=△△△△△
【答案】3.5
【例 14】 如图,1ABC S =△,5BC BD =,4AC EC =,DG GS SE ==,AF FG =.求FGS
S
.
S
G
F E D
C
B
A
【考点】三角形的鸟头模型 【难度】3星 【题型】解答 【解析】 本题题目本身很简单,但它把本讲的两个重要知识点融合到一起,既可以看作是”当两个三角形有一
个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”的反复运用,也可以看作是找点,最妙的是其中包含了找点的3种情况.
最后求得FGS S △的面积为432111
5432210
FGS S =????=△.
【答案】1
10
【例 15】 如图所示,正方形ABCD 边长为8厘米,E 是AD 的中点,F 是CE 的中点,G 是BF 的中点,三
角形ABG 的面积是多少平方厘米?
A
B
C
D
E
F G
A
B
C D
E
F G
【考点】三角形的鸟头模型 【难度】4星 【题型】解答 【解析】 连接AF 、EG .
因为21
8164
BCF CDE S S ==?=△△,根据”当两个三角形有一个角相等或互补时,这两个三角形的面积
比等于夹这个角的两边长度的乘积比”8AEF S =,8EFG S =,再根据”当两个三角形有一个角相等或
互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”,得到16BFC
S
=,32ABFE S =,
24ABF S =,所以12ABG S =平方厘米.
【答案】12
【例 16】 四个面积为1的正六边形如图摆放,求阴影三角形的面积.
【考点】三角形的鸟头模型 【难度】4星 【题型】解答 【解析】 如图,将原图扩展成一个大正三角形DEF ,则AGF ?与CEH ?都是正三角形.
假设正六边形的边长为为a ,则AGF ?与CEH ?的边长都是4a ,所以大正三角形DEF 的边长为4217?-=,那么它的面积为单位小正三角形面积的49倍.而一个正六边形是由6个单位小正三角
形组成的,所以一个单位小正三角形的面积为16,三角形DEF 的面积为49
6
.
由于4FA a =,3FB a =,所以AFB ?与三角形DEF 的面积之比为4312
7749
?=.
同理可知BDC ?、AEC ?与三角形DEF 的面积之比都为12
49
,所以ABC ?的面积占三角形DEF 面积
的1213134949-?=,所以ABC ?的面积的面积为4913136496?=.
【答案】13
6
【巩固】已知图中每个正六边形的面积都是1,则图中虚线围成的五边形ABCDE 的面积是 .
B D
C
E
A
【考点】三角形的鸟头模型 【难度】4星 【题型】解答 【解析】 从图中可以看出,虚线AB 和虚线CD 外的图形都等于两个正六边形的一半,也就是都等于一个正六
边形的面积;虚线BC 和虚线DE 外的图形都等于一个正六边形的一半,那么它们合起来等于一个正六边形的面积;虚线AE 外的图形是两个三角形,从右图中可以看出,每个三角形都是一个正六边
形面积的16,所以虚线外图形的面积等于11132363?+?=,所以五边形的面积是12
103633
-=.
【答案】2
63
【例 17】 仅用下图这把刻度尺,最少测量 次,就能得出三角形ABC 和三角形BCD 的面积比。
【考点】三角形的鸟头模型 【难度】5星 【题型】解答 【关键词】学而思杯,6年级,第10题 【解析】 连接DA 并延长交BC 边的延长线于E 点,然后测出EA 和ED 的长度,由于EA 与ED 在一条直线上,
所以测一次就能EA 和ED 长度,根据共边定理可知,三角形ABC 与三角形BCD 的面积比就等于EA 比
ED ,故最少测量1次就可解决问题。
【答案】1次
模型二 鸟头模型 两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比. 如图在ABC △中,,D E 分别是,AB AC 上的点如图 ⑴(或D 在BA 的延长线上,E 在AC 上如图 2), 则:():()ABC ADE S S AB AC AD AE =??△△ E D C B A E D C B A 图⑴ 图⑵ 【例 1】 如图在ABC △中,,D E 分别是,AB AC 上的点,且:2:5AD AB =,:4:7AE AC =, 16ADE S =△平方厘米,求ABC △的面积. 三角形等高模型与鸟头模型
E D C B A E D C B A 【解析】 连接BE ,::2:5(24):(54)ADE ABE S S AD AB ===??△△, ::4:7(45):(75) ABE ABC S S AE AC ===??△△,所以:(24):(75)ADE ABC S S =??△△,设 8ADE S =△份,则35ABC S =△份,16ADE S =△平方厘米,所以1份是2平方厘米,35份就是70平方厘米,ABC △的面积是70平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比 . 【巩固】如图,三角形ABC 中,AB 是AD 的5倍,AC 是AE 的3倍,如果三角 形ADE 的面积等于1,那么三角形ABC 的面积是多少? E D C B A A B C D E 【解析】 连接BE . ∵3EC AE = ∴3ABC ABE S S =V V 又∵5AB AD = ∴515ADE ABE ABC S S S =÷=÷V V V ,∴1515ABC ADE S S ==V V . 【巩固】如图,三角形被分成了甲(阴影部分)、乙两部分,4BD DC ==,3BE =, 6AE =,乙部分面积是甲部分面积的几倍? 乙 甲 E D C B A A B C D E 甲 乙 【解析】 连接AD . ∵3BE =,6AE = ∴3AB BE =,3ABD BDE S S =V V 又∵4BD DC ==, ∴2ABC ABD S S =V V ,∴6ABC BDE S S =V V ,5S S =乙甲.
模型二 鸟头模型 两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比. 如图在ABC △中,,D E 分别是,AB AC 上的点如图 ⑴(或D 在BA 的延长线上,E 在AC 上如图 2), 则:():()ABC ADE S S AB AC AD AE =??△△ 图⑴ 图⑵ 【例 1】 如图在ABC △中,,D E 分别是,AB AC 上的点,且:2:5AD AB =,:4:7AE AC =,16ADE S =△平方 厘米,求ABC △的面积. 【解析】 连接BE ,::2:5(24):(54)ADE ABE S S AD AB ===??△△, ::4:7(45):(75)ABE ABC S S AE AC ===??△△,所以:(24):(75)ADE ABC S S =??△△,设8ADE S =△份, 则35ABC S =△份,16ADE S =△平方厘米,所以1份是2平方厘米,35份就是70平方厘米,ABC △的 面积是70平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比 . 【巩固】如图,三角形ABC 中,AB 是AD 的5倍,AC 是AE 的3倍,如果三角形ADE 的面积等于1,那 么三角形ABC 的面积是多少? 【解析】 连接BE . ∵3EC AE = ∴3ABC ABE S S =V V 又∵5AB AD = ∴515ADE ABE ABC S S S =÷=÷V V V ,∴1515ABC ADE S S ==V V . 【巩固】如图,三角形ABC 被分成了甲(阴影部分)、乙两部分,4BD DC ==,3BE =,6AE =,乙部分面 积是甲部分面积的几倍? 【解析】 连接AD . ∵3BE =,6AE = ∴3AB BE =,3ABD BDE S S =V V 又∵4BD DC ==, 三角形等高模型与鸟头模型
模型一 三角形等高模型 已经知道三角形面积的计算公式: 三角形面积=底?高2÷ 从这个公式我们可以发现:三角形面积的大小,取决于三角形底和高的乘积. 如果三角形的底不变,高越大(小),三角形面积也就越大(小); 如果三角形的高不变,底越大(小),三角形面积也就越大(小); 这说明当三角形的面积变化时,它的底和高之中至少有一个要发生变化.但是,当三角形的底和高同时发生变化时,三角形的面积不一定变化.比如当高变为原来的3倍,底变为原来的13 ,则三角形面积与原来的一样.这 就是说:一个三角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化.同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状. 在实际问题的研究中,我们还会常常用到以下结论: ①等底等高的两个三角形面积相等; ②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; 如图 12::S S a b = b a S 2S 1 D C B A ③夹在一组平行线之间的等积变形,如右上图ACD BCD S S =△△; 三角形等高模型与鸟头模型
反之,如果ACD BCD S S △△,则可知直线AB 平行于CD . ④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形); ⑤三角形面积等于与它等底等高的平行四边形面积的一半; ⑥两个平行四边形高相等,面积比等于它们的底之比; 两个平行四边形底相等,面积比等于它们的高之比.
【例 1】 你有多少种方法将任意一个三角形分成:⑴ 3 个面积相等的三角形; ⑵ 4个面积相等的三角形;⑶6个面积相等的三角形。 【解析】 ⑴ 如下图,D 、E 是BC 的三等分点,F 、G 分别是对应线段的中点, 答案不唯一: C E D B A F C D B A G D B A ⑵ 如下图,答案不唯一,以下仅供参考: ⑸ ⑷⑶⑵⑴ ⑶如下图,答案不唯一,以下仅供参考: 【例 2】 如图,BD 长12厘米,DC 长4厘米,B 、C 和D 在同一条直线上。 ⑴ 求三角形ABC 的面积是三角形ABD 面积的多少倍? ⑵ 求三角形ABD 的面积是三角形ADC 面积的多少倍? 【解析】 因为三角形ABD 、三角形ABC 和三角形ADC 在分别以BD 、BC 和DC 为底时,它们的高都是从A 点向BC 边上所作的垂线,也就是说三个三角形的高相等。 于是:三角形ABD 的面积12=?高26÷=?高 三角形ABC 的面积124=+?()高28÷=?高 三角形ADC 的面积4=?高22÷=?高 所以,三角形ABC 的面积是三角形ABD 面积的43 倍; 三角形ABD 的面积是三角形ADC 面积的3倍。 【例 3】 如右图,ABFE 和CDEF 都是矩形,AB 的长是4厘米,BC 的长是3厘米, 那么图中阴影部分的面积是 平方厘米。 C D B A
三角形的等高模型 例题精讲 在实际问题的研究中,我们还会常常用到以下结论: ①等底等高的两个三角形面积相等; ②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; 如左图12::S S a b = b a S 2S 1 D C B A ③夹在一组平行线之间的等积变形,如右上图ACD BCD S S =△△; 反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD . ④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形); ⑤三角形面积等于与它等底等高的平行四边形面积的一半; ⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比. 【例题1】你有多少种方法将任意一个三角形分成:⑴ 3个面积相等的三角形;⑵ 4个面积相等的三角形;⑶6个面积相等的三角形. 【解析】⑴ 如下图,D 、E 是BC 的三等分点,F 、G 分别是对应线段的中点,答案不唯一: C E D B A F C D B A G D B A ⑵ 如下图,答案不唯一,以下仅供参考: ⑸ ⑷⑶⑵⑴ ⑶如下图,答案不唯一,以下仅供参考: 【例题2】如图,BD 长12厘米,DC 长4厘米,B 、C 和D 在同一条直线上. ⑴ 求三角形ABC 的面积是三角形ABD 面积的多少倍? ⑵ 求三角形ABD 的面积是三角形ADC 面积的多少倍? C D B A
【解析】因为三角形ABD 、三角形ABC 和三角形ADC 在分别以BD 、BC 和DC 为底时, 它们的高都是从A 点向BC 边上所作的垂线,也就是说三个三角形的高相等. 于是:三角形ABD 的面积=12高÷2=6×高 三角形ABC 的面积=(12+4)×高÷2=8×高 三角形ADC 的面积=4×高÷2=2×高 所以,三角形ABC 的面积是三角形ABD 面积的4/3倍; 三角形ABD 的面积是三角形ADC 面积的3倍. 【例题3】如右图,ABFE 和CDEF 都是矩形,AB 的长是4厘米,BC 的长是3厘米,那么图中阴影部分的面积是 平方厘米. 【解析】图中阴影部分的面积等于长方形ABCD 面积的一半, 即4×3÷2=6(平方厘米). 【巩固1】如图所示,平行四边形的面积是50平方厘米,则阴影部分的面积是 平方厘米. 【解析】根据面积比例模型,可知图中空白三角形面积等于 平行四边形面积的一半,所以阴影部分的面积也等于 平行四边形面积的一半,为50÷2=25平方厘米. 【巩固2】如下图,长方形AFEB 和长方形FDCE 拼成了长方形ABCD ,长方形ABCD 的长是20,宽是12,则它 内部阴影部分的面积是 . F E C B A 【解析】 根据面积比例模型可知阴影部分面积等于长方形面积的一半, 为20×12÷120. 【例题4】如图,长方形ABCD 的面积是56平方厘米,点E 、F 、G 分别是长方形ABCD 边上的中点,H 为AD 边上的任意一点,求阴影部分的面积. E B A E B A 【解析】本题是等底等高的两个三角形面积相等的应用. 连接BH 、CH .
板块一 三角形等高模型 我们已经知道三角形面积的计算公式:三角形面积=底?高2÷ 从这个公式我们可以发现:三角形面积的大小,取决于三角形底和高的乘积. 如果三角形的底不变,高越大(小),三角形面积也就越大(小); 如果三角形的高不变,底越大(小),三角形面积也就越大(小); 这说明当三角形的面积变化时,它的底和高之中至少有一个要发生变化.但是,当三角形的底和高同时发生 变化时,三角形的面积不一定变化.比如当高变为原来的3倍,底变为原来的1 3 ,则三角形面积与原来的一 样.这就是说:一个三角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化.同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状. 在实际问题的研究中,我们还会常常用到以下结论: ①等底等高的两个三角形面积相等; ②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; 如左图12::S S a b = b a S 2S 1 D C B A ③夹在一组平行线之间的等积变形,如右上图ACD BCD S S =△△; 反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD . ④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形); ⑤三角形面积等于与它等底等高的平行四边形面积的一半; ⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比. 【例 1】 你有多少种方法将任意一个三角形分成:⑴ 3个面积相等的三角形;⑵ 4个面积相等的三角形;⑶ 6个面积相等的三角形. 【例 2】 如图,BD 长12厘米,DC 长4厘米,B 、C 和D 在同一条直线上. 例题精讲 三角形等高模型与鸟头模型 (学生版)
等高(等底)模型 【知识点分析】 1 基础知识: 三角形面积=底.K高昇 斯哄:三角形面枳的丸小,取决于三角瞪底和高的乘积. 若底不变,高越大(小),面积越大a卜); 若高不变,底越丸(小儿面积越大(小); 2. 模型结论: ①两个三角形高相等,面积比等于它们的底之比; 女!■图S] * —a * b ②两个三角形底相等,面积比等于它们的髙之比: 特殊:等底等高的两个三角形面积相等;(注意平行线) 其他常用蛀论: (1)夹在一组平行线之间的等积变形,如右上图$*=£*; 反之,如果则可知宜线曲平行于CD. (2)等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形); (3)三甫形罰积等于与它等底等高的平行四边珈圍积妁一半; (4)两个平行四边形高相等*面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比.
3、拓展结论: 拓展1: 图(1): 四边形ABCD为正方形,E、F、G是各边中点,H是是AD上任意一点,贝US阴二扌S正证明:连接BH、CH,根据等高等底知:S?=S②,S云S空S⑥三S⑥,所以正图(2):四边形ABCD为正方形,E、F、G是各边三等分点,H是是AD上任意一点、,则S阴气S正(证明方法同上) 图(3):四边形ABCD为长方形,E、F、G是各边中点,H是是AD上任意一点,则S十丄 S长(证明方法同上) 2 拓展2: 图(2): S赵S小正,证明同上(辅助线如图) 图(3): S阴二大正,证明同上(辅助线如图) 图⑷:$阴=gs中正,证明:辅助线如图,根据平行s,、RE=S住阳, 所以,S阴冷S中
【典型例题】 W 1:如右因,E在AD上.AD至直BC?ylD = 12 ^耒,DE = 3圧米.求三角 形ABC的和积是三角形EBC面积的几倍? 例2:长方形ABCD的面积为36, E> F. G为各边中点,H为AD边上任意一点, 问阴影部分面积是多少? 例3:(第6届走美杯5年级决春第8題)央如图,A. B、C都是正方形边的中 A, ACOD比AAOB大15平方厘米。AAOB的面积为多少平方厘米? D
知识框架 板块一三角形等高模型 我们已经知道三角形面积的计算公式:三角形面积=底?高2 ÷ 从这个公式我们可以发现:三角形面积的大小,取决于三角形底和高的乘积. 如果三角形的底不变,高越大(小),三角形面积也就越大(小); 如果三角形的高不变,底越大(小),三角形面积也就越大(小); 这说明当三角形的面积变化时,它的底和高之中至少有一个要发生变化.但是,当三角形的底和高同时发 生变化时,三角形的面积不一定变化.比如当高变为原来的3倍,底变为原来的 1 3,则三角形面积与原来的一样.这就是说:一个三角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化.同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状. 在实际问题的研究中,我们还会常常用到以下结论: ①等底等高的两个三角形面积相等; ②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; 如左图12 :: S S a b = ③夹在一组平行线之间的等积变形,如右上图 ACD BCD S S= △△ ; 反之,如果 ACD BCD S S= △△ ,则可知直线AB平行于CD. ④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形); ⑤三角形面积等于与它等底等高的平行四边形面积的一半; ⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比. 三角形等高模型和鸟头模型
板块二鸟头模型 两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形.共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比. 如图在ABC △中,,D E 分别是,AB AC 上的点如图⑴(或D 在BA 的延长线上,E 在AC 上),则:():() ABC ADE S S AB AC AD AE =??△ △例题精讲 【例1】如右图,E 在AD 上,AD 垂直BC,12AD =厘米,3DE =厘米.求三角形ABC 的面积是三角形 EBC 面积的几倍?欢迎关注:奥数轻松学 余老师薇芯:69039270 E D C B A 【巩固】如图30-5,设正方形ABCD 的面积为1,E,F 分别为边AB,AD 的中点,FC=3GC,则阴影部分的面 积是多少?
模型一三角形等高模型 已经知道三角形面积的计算公式 : 三角形面积二底高2 从这个公式我们可以发现:三角形面积的大小,取决于三角形底和高的乘积 ? 如果三角形的底不变,高越大(小),三角形面积也就越大(小); 如果三角形的高不变,底越大(小),三角形面积也就越大(小); 这说明当三角形的面积变化时 ,它的底和高之中至少有一个要发生变化 ?但是,当三角形的底和高同时 发生变化时,三角形的面积不一定变化?比如当高变为原来的 3倍,底变为原来的-,则三角形面积与原来 3 的一样?这就是说:一个三角形的面积变化与否取决于它的高和底的乘积 ,而不仅仅取决于高或底的变 化.同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状 ? 在实际问题的研究中,我们还会常常用到以下结论 ① 等底等高的两个三角形面积相等 ; ② 两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; 如 图 S :S 2 二a: b ④ 等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形 ); ⑤ 三角形面积等于与它等底等高的平行四边形面积的一半 ; ⑥ 两个平行四边形高相等,面积比等于它们的底之比; 两个平行四边形底相等 ,面积比等于它们的高之比 ③夹在一组平行线之间的等积变形 反之,如果 ACD = BCD , ,如右上图 ACD = S A BCD ; 则 可知直线AB 平行于CD ?
【例1】你有多少种方法将任意一个三角形分成:⑴3个面积相等的三角形:⑵4个面积相等的三角形 ⑶6个面积相等的三角形。 【解析】⑴ 如下图,D、E是BC的三等分点,F、G分别是对应线段的中点,答案不唯一: ⑵如下图,答案不唯一,以下仅供参考 【例2】如图,BD长12厘米,DC长4厘米,B、C和D在同一条直线上。 ⑴求三角形ABC的面积是三角形ABD面积的多少倍? ⑵求三角形ABD的面积是三角形ADC面积的多少倍? 【解析】因为三角形ABD、三角形ABC和三角形ADC在分别以BD、BC和DC为底时,它们的高都是从A 点向BC 边上所作的垂线,也就是说三个三角形的高相等。 于是:三角形ABD的面积=12高<2-6高 三角形ABC的面积(12 4)高"2=8高三角形ADC的面积=4高“2=2高 所以,三角形ABC的面积是三角形ABD面积的4倍; 3 三角形ABD的面积是三角形ADC面积的3倍。 【例3】如右图,ABFE和CDEF都是矩形,AB的长是4厘米,BC的长是3厘米,那么图中阴影部分的面积是_______ 平方厘米。 【解析】图中阴影部分的面积等于长方形ABCD面积的一半,即4 3一:一2=6(平方厘米)。
小学奥数-几何五大模型(等高模型)
模型一 三角形等高模型 已经知道三角形面积的计算公式: 三角形面积=底?高2÷ 从这个公式我们可以发现:三角形面积的大小,取决于三角形底和高的乘积. 如果三角形的底不变,高越大(小),三角形面积也就越大(小); 如果三角形的高不变,底越大(小),三角形面积也就越大(小); 这说明当三角形的面积变化时,它的底和高之中至少有一个要发生变化.但是,当三角形的底和高同时发生变化时,三角形的面积不一定变化.比如当高变为原来的3倍,底变为原来的13 ,则三角形面积与原来的一样.这就是说:一个三角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化.同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状. 在实际问题的研究中,我们还会常常用到以下结论: ①等底等高的两个三角形面积相等; ②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; 如图 12::S S a b = b a S 2S 1 D C B A ③夹在一组平行线之间的等积变形,如右上图ACD BCD S S =△△; 反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD . ④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形); ⑤三角形面积等于与它等底等高的平行四边形面积的一半; ⑥两个平行四边形高相等,面积比等于它们的底之比; 三角形等高模型与鸟头模型
两个平行四边形底相等,面积比等于它们的高之比.
【例 1】 你有多少种方法将任意一个三角形分成:⑴ 3个面积相等的三角形;⑵ 4个面积相等 的三角形;⑶6个面积相等的三角形。 【解析】 ⑴ 如下图,D 、E 是BC 的三等分点,F 、G 分别是对应线段的中点,答案不唯一: C E D B A F C D B A G D B A ⑵ 如下图,答案不唯一,以下仅供参考: ⑸ ⑷⑶⑵⑴ ⑶如下图,答案不唯一,以下仅供参考: 【例 2】 如图,BD 长12厘米,DC 长4厘米,B 、C 和D 在同一条直线上。 ⑴ 求三角形ABC 的面积是三角形ABD 面积的多少倍? ⑵ 求三角形ABD 的面积是三角形ADC 面积的多少倍? 【解析】 因为三角形ABD 、三角形ABC 和三角形ADC 在分别以BD 、 BC 和DC 为底时,它们的高都是从A 点向BC 边上所作的垂 线,也就是说三个三角形的高相等。 于是:三角形ABD 的面积12=?高26÷=?高 三角形ABC 的面积124=+?()高28÷=?高 三角形ADC 的面积4=?高22÷=?高 所以,三角形ABC 的面积是三角形ABD 面积的4 3 倍; 三角形ABD 的面积是三角形ADC 面积的3倍。 【例 3】 如右图,ABFE 和CDEF 都是矩形,AB 的长是4厘米,BC 的长是3厘米,那么图中阴影 部分的面积是 平方厘米。 【解析】 图中阴影部分的面积等于长方形ABCD 面积的一半,即4326?÷=(平方厘米)。 C D B A
模型一三角形等高模型 已经知道三角形面积的计算公式: 三角形面积底高2 从这个公式我们可以发现:三角形面积的大小,取决于三角形底和高的乘积. 如果三角形的底不变,高越大(小),三角形面积也就越大(小); 如果三角形的高不变,底越大(小),三角形面积也就越大(小); 这说明当三角形的面积变化时,它的底和高之中至少有一个要发生变化?但是,当三角形的底和高同时 1 发生变化时,三角形的面积不一定变化?比如当高变为原来的3倍,底变为原来的1,则三角形面积与原来 3 的一样.这就是说:一个三角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化. 同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状. 在实际问题的研究中,我们还会常常用到以下结论: ①等底等高的两个三角形面积相等; ②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; 如图S i :S2 a:b ③夹在一组平行线之间的等积变形,如右上图S A ACD S A BCD ; 反之,如果S A ACD S A BCD,则可知直线AB平行于CD ? ④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形); ⑤三角形面积等于与它等底等高的平行四边形面积的一半; ⑥两个平行四边形高相等,面积比等于它们的底之比; 两个平行四边形底相等,面积比等于它们的高之比.
你有多少种方法将任意一个三角形分成: ⑴3个面积相等的三角形; ⑵4个面积相等的三角形; ⑶ 6个面积相等的三角形。 ⑴ 如下图,D 、E 是BC 的三等分点,F 、G 分别是对应线段的中点,答案不唯一: ⑵ 如下图,答案不唯一,以下仅供参考: 如图,BD 长12厘米,DC 长4厘米,B 、C 和D 在同一条直线上。 ⑴ 求三角形ABC 的面积是三角形 ABD 面积的多少倍? ⑵求三角形ABD 的面积是三角形 ADC 面积的多少倍? 因为三角形 ABD 、三角形 ABC 和三角形ADC 在分别以BD 、BC 和DC 为底时,它们的高都是从 A 点向BC 边上所作的垂线,也就是说三个三角形的高相等。 于是:三角形ABD 的面积 12高2 6高 三角形ABC 的面积 (12 4)高2 8高 三角形ADC 的面积 4高2 2高 4 所以,三角形 ABC 的面积是三角形 ABD 面积的-倍; 3 三角形ABD 的面积是三角形 ADC 面积的3倍。 如右图,ABFE 和CDEF 都是矩形,AB 的长是4厘米,BC 的长是3厘米,那么图中阴影部分的面 积是 平方厘米。 D C 图中阴影部分的面积等于长方形 ABCD 面积的一半,即4 3 2 6(平方厘米)。 (2009年四中小升初入学测试题)如图所示,平行四边形的面积是 50平方厘米,则阴影部分的面积 是 平方厘米。 【例1】 【解 【例2】 【解析】 【例3】 【解析】 ⑶如下图,答案不唯一,以下仅供参考:
模型一 三角形等 高模型 已经知道三角形面积 的计算公式: 三角形面积=底?高2÷ 从这个公式我们可以发现:三角形面积的大小,取决于三角形底和高的乘积. 如果三角形的底不变,高越大(小),三角形面积也就越大(小); 如果三角形的高不变,底越大(小),三角形面积也就越大(小); 这说明当三角形的面积变化时,它的底和高之中至少有一个要发生变化.但是,当三角形的底和高同时 发生变化时,三角形的面积不一定变化.比如当高变为原来的3倍,底变为原来的1 3 ,则三角形面积与原来 的一样.这就是说:一个三角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化.同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状. 在实际问题的研究中,我们还会常常用到以下结论: ①等底等高的两个三角形面积相等; ②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; 如图 12::S S a b = ③夹在一组平行线之间的等积变形,如右上图ACD BCD S S =△△; 反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD . ④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形); ⑤三角形面积等于与它等底等高的平行四边形面积的一半; ⑥两个平行四边形高相等,面积比等于它们的底之比; 两个平行四边形底相等,面积比等于它们的高之比. 【例 1】 你有多少种方法将任意一个三角形分成:⑴ 3个面积相等的三角形;⑵ 4个面积相等的三角形;⑶ 6个面积相等的三角形。 【解析】 ⑴ 如下图,D 、E 是BC 的三等分点,F 、G 分别是对应线段的中点,答案不唯一: ⑵ 如下图,答案不唯一,以下仅供参考: ⑶如下图,答案不唯一,以下仅供参考: 【例 2】 如图,BD 长12厘米,DC 长4厘米,B 、C 和D 在同一条直线上。 ⑴ 求三角形ABC 的面积是三角形ABD 面积的多少倍? ⑵ 求三角形ABD 的面积是三角形ADC 面积的多少倍? 【解析】 因为三角形ABD 、三角形ABC 和三角形ADC 在分别以BD 、BC 和DC 为底时,它们的高都是从A 点向BC 边上所作的垂线,也就是说三个三角形的高相等。 于是:三角形ABD 的面积12=?高26÷=?高 三角形ABC 的面积124=+?()高28÷=?高 三角形ADC 的面积4=?高22÷=?高 所以,三角形ABC 的面积是三角形ABD 面积的 4 3 倍; 三角形ABD 的面积是三角形ADC 面积的3倍。 【例 3】 如右图,ABFE 和CDEF 都是矩形,AB 的长是4厘米,BC 的长是3厘米,那么图中阴影部分的面 积是 平方厘米。 三角形等高模型与鸟头模型
知识图谱 几何第01讲_等高模型-一、等高模型(比例关系)三角形中的等高梯形中的等高 一:等高模型(比例关系) 知识精讲 一.三角形中的面积比例关系 直线形计算中,最重要的就是找到两个三角形面积与边长之间的关系. 当两个三角形同高或等高的时候,它们面积的比等于对应底之比.如图所示: 二.梯形中的面积比例关系 在梯形中,对角线把梯形分成两个分别以上底、下底为底边的等高三角形,则它们的面积比与对应上下底之比.如图所示: 三点剖析 重难点:三角形等高模型与梯形中的等高模型 题模精讲 题模一三角形中的等高 例1.1.1、
如图,,.已知△ABC的面积是10,阴影部分的面积是__________. 答案: 2.4 解析: △ABD和△ACD是等高,它们的面积比是,所以△ACD的面积是.同理△CDE和△ADE是等高,它们的面积比是 ,所以阴影部分的面积是. 例1.1.2、 如图所示,已知△ABC的面积为1,且,,,则△DEF的面积是多少?
答案: 解析: 易知,,. 故. 例1.1.3、 如图,在△ABC中,已知△ADE、△DCE、△BCD的面积分别是89,26,28,那么△DBE的面积是_______ 答案: 解析: ,故, . 例1.1.4、
如图7,已知,,,,△BCG和△EFG的面积和是24,△AGF和△CDG的面积和是51,则△ABC与△DEF的面积和是__________. 答案: 23 解析: △ABC、△BCG、△CDG的面积比等于底边比,即,所以设它们的面积分别是2x、3x、9x;同理设△AGF、△EFG、△DEF的面积分 别是5y、4y、5y.根据条件,可列方程,所以△ABC 与△DEF的面积和是. 题模二梯形中的等高 例1.2.1、 如图,梯形ABCD的面积是10,E为CD中点,求三角形ABE的面积是 ___________.
板块一 三角形等高模型 我们已经知道三角形面积的计算公式:三角形面积=底?高2÷ 从这个公式我们可以发现:三角形面积的大小,取决于三角形底和高的乘积. 如果三角形的底不变,高越大(小),三角形面积也就越大(小); 如果三角形的高不变,底越大(小),三角形面积也就越大(小); 这说明当三角形的面积变化时,它的底和高之中至少有一个要发生变化.但是,当三角形的底和高同时发生 变化时,三角形的面积不一定变化.比如当高变为原来的3倍,底变为原来的1 3 ,则三角形面积与原来的一 样.这就是说:一个三角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化.同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状. 在实际问题的研究中,我们还会常常用到以下结论: ①等底等高的两个三角形面积相等; ②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; 如左图12::S S a b = s 2s 1b a D C B A ③夹在一组平行线之间的等积变形,如右上图ACD BCD S S =△△; 反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD . ④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形); ⑤三角形面积等于与它等底等高的平行四边形面积的一半; ⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比. 板块二 鸟头模型 两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比. 如图在ABC △中,,D E 分别是,AB AC 上的点如图 ⑴(或D 在BA 的延长线上,E 在AC 上), 则:():()ABC ADE S S AB AC AD AE =??△△ E D C B A D E C B A 图⑴ 图⑵ 【例 1】 如图在ABC △中,,D E 分别是,AB AC 上的点,且:2:5AD AB =,:4:7AE AC =,16ADE S =△平 方厘米,求ABC △的面积. 例题精讲 4-3-2.三角形等高模型与鸟头模型
模型二 鸟头模型 两个三角形中有一个角相等或互补,这两个三角形叫做共 角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比. 如图在ABC △中,,D E 分别是,AB AC 上的点如图⑴(或D 在BA 的延长线上,E 在AC 上如图2), 则:():()ABC ADE S S AB AC AD AE =??△△ E D C B A E D C B A 图⑴图⑵ 【例 1】 如图在ABC △中,,D E 分别是,AB AC 上的点,且:2:5AD AB =,:4:7AE AC =,16ADE S =△平方 厘米,求ABC △的面积. E D C B A E D C B A 【解析】 连接BE ,::2:5(24):(54)ADE ABE S S AD AB ===??△△, ::4:7(45):(75)ABE ABC S S AE AC ===??△△,所以:(24):(75)ADE ABC S S =??△△,设8ADE S =△份,则35ABC S =△份,16ADE S =△平方厘米,所以1份是2平方厘米,35份就是70平方厘米,ABC △的 面积是70平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比 . 【巩固】如图,三角形ABC 中,AB 是AD 的5倍,AC 是AE 的3倍,如果三角形ADE 的面积等于1,那 么三角形ABC 的面积是多少? E D C B A A B C D E 【解析】 连接BE . ∵3EC AE = ∴3ABC ABE S S = 又∵5AB AD = ∴515ADE ABE ABC S S S =÷=÷,∴1515ABC ADE S S ==. 【巩固】如图,三角形ABC 被分成了甲(阴影部分)、乙两部分,4BD DC ==,3BE =,6AE =,乙部分面 积是甲部分面积的几倍? 三角形等高模型与鸟头模型
模型二 鸟头模型 两个三角形中有一个角相等或互补,这两个三角形叫做共 角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比. 如图在ABC △中,,D E 分别是,AB AC 上的点如图 ⑴(或D 在BA 的延长线上,E 在AC 上如图 2), 则:():()ABC ADE S S AB AC AD AE =??△△ 图⑴ 图⑵ 【例 1】 如图在ABC △中,,D E 分别是,AB AC 上的点,且:2:5AD AB =,:4:7AE AC =,16ADE S =△平方 厘米,求ABC △的面积. 【解析】 连接BE ,::2:5(24):(54)ADE ABE S S AD AB ===??△△, ::4:7(45):(75)ABE ABC S S AE AC ===??△△,所以:(24):(75)ADE ABC S S =??△△,设8ADE S =△份, 则35ABC S =△份,16ADE S =△平方厘米,所以1份是2平方厘米,35份就是70平方厘米,ABC △的 面积是70平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比 . 【巩固】如图,三角形ABC 中,AB 是AD 的5倍,AC 是AE 的3倍,如果三角形ADE 的面积等于1,那 么三角形ABC 的面积是多少? 【解析】 连接BE . ∵3EC AE = ∴3ABC ABE S S = 又∵5AB AD = ∴515ADE ABE ABC S S S =÷=÷,∴1515ABC ADE S S ==. 【巩固】如图,三角形ABC 被分成了甲(阴影部分)、乙两部分,4BD DC ==,3BE =,6AE =,乙部分面 积是甲部分面积的几倍? 【解析】 连接AD . ∵3BE =,6AE = ∴3AB BE =,3ABD BDE S S = 又∵4BD DC ==, ∴2ABC ABD S S =,∴6ABC BDE S S =,5S S =乙甲. 【例 2】 如图在ABC △中,D 在BA 的延长线上,E 在AC 上,且:5:2AB AD =, :3:2AE EC =,12ADE S =△平方厘米,求ABC △的面积. 【解析】 连接BE ,::2:5(23):(53)ADE ABE S S AD AB ===??△△ []::3:(32)(35):(32)5ABE ABC S S AE AC ==+=?+?△△, 所以[]:(32):5(32)6:25ADE ABC S S =??+=△△,设6ADE S =△份,则25ABC S =△份,12ADE S =△平方厘 米,所以1份是2平方厘米,25份就是50平方厘米,ABC △的面积是50平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比 【例 3】 如图所示,在平行四边形ABCD 中,E 为AB 的中点,2AF CF =,三角形AFE (图中阴影部分)的面积 为8平方厘米.平行四边形的面积是多少平方厘米? 【解析】 连接FB .三角形AFB 面积是三角形CFB 面积的2倍,而三角形AFB 面积是三角形AEF 面积的2倍, 所以三角形ABC 面积是三角形AEF 面积的3倍;又因为平行四边形的面积是三角形ABC 面积的2倍,所以平行四边形的面积是三角形AFE 面积的326?=()倍.因此,平行四边形的面积为8648?=(平方厘米). 【例 4】 已知DEF △的面积为7平方厘米,,2,3BE CE AD BD CF AF ===,求ABC △的面积. 【解析】 :():()(11):(23)1:6BDE ABC S S BD BE BA BC =??=??=△△,:():()(13):(24)3:8CEF ABC S S CE CF CB CA =??=??=△△:():()(21):(34)1:6ADF ABC S S AD AF AB AC =??=??=△△ 三角形等高模型与鸟头模型
一、三角形当中的一半模型 由于三角形的面积公式S=底×高÷2,决定于底和高的长度,所以我们有了等高模型和等底模型。在等高模型中,(图1)当BD=CD时,阴影部分,SΔABD=SΔABC÷2 特别地如图2,当BE=ED,DF=FC,阴影部分面积,SΔAEF=SΔABC÷2 在等底模型中(图3),当AE=DE时,阴影部分,SΔEBC=SΔABC÷2 二、平行四边形中的一半模型 由于三角形的面积公式S=底×高÷2, 平行四边行的面积公式S=底×高 所以与平行四边形同底等高的三角形是它面积的一半! 同时,长方形是特殊的平行四边行,再根据平行线间的等积变形,可以得到如下诸图,阴影部分面积是四边形面积的一半: 知识结构 一半模型
【巩固练习】判断下面的图形中阴影部分的面积是不是整个图形面积的一半。是打“√”,不是打“×”。 ()()()() ()() 三、梯形中的一半模型 在梯形中,当三角形的底边是梯形的一个腰,顶点在另一个腰的中点处,那么三角形是梯形面积的一半。 如图4,在梯形ABCD中,BE=CE,则SΔADE=SABCD÷2 如图5,是它的变形,注意其中AF=DF,BE=CE。
四、任意四边形中的一半模型 如图6,在四边形ABCD中,AE=EB,DF=CF,则SEBFD=SABCD÷2 【能力提升】 【巩固练习】
【例1】如图,已知长方形ABCD的面积为24平方厘米,且线段EF,GH把它分成四个小长方形,求阴影部分的面积。 【巩固】已知大长方形的长是6厘米,宽是4厘米,求阴影部分的面积。 【例2】如图所示,平行四边形的面积是50 平方厘米,阴影部分面积是()平方厘米. 【例3】 如图,长方形AFEB和长方形FDCE拼成了长方形ABCD,长方形ABCD的长是20,宽是12,则它部阴影部分的面积是多少? 例题精讲 4
三角形等高模型和鸟头模型 知识框架 板块一 三角形等高模型 我们已经知道三角形面积的计算公式:三角形面积=底?高2÷ 从这个公式我们可以发现:三角形面积的大小,取决于三角形底和高的乘积. 如果三角形的底不变,高越大(小),三角形面积也就越大(小); 如果三角形的高不变,底越大(小),三角形面积也就越大(小); 这说明当三角形的面积变化时,它的底和高之中至少有一个要发生变化.但是,当三角形的底和高同时发生变化时,三角形的面积不一定变化.比如当高变为原来的3倍,底变为原来的1 3 ,则三角形面积与 原来的一样.这就是说:一个三角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化.同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状. 在实际问题的研究中,我们还会常常用到以下结论: (1) 等底等高的两个三角形面积相等; (2) 两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; 如左图12::S S a b = b a S 2S 1 D C B A (3) 夹在一组平行线之间的等积变形,如右上图ACD BCD S S =△△; 反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD . (4) 等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形); (5) 三角形面积等于与它等底等高的平行四边形面积的一半; (6) 两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的 高之比. 板块二 鸟头模型 两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比. 如图在ABC △中,,D E 分别是,AB AC 上的点如图 ⑴(或D 在BA 的延长线上,E 在AC 上), 则:():()ABC ADE S S AB AC AD AE =??△△