2011-2012学年西城初二上册数学(A卷)期末试题及答案(北区)
- 格式:doc
- 大小:1.13 MB
- 文档页数:15

北京市西城区2011–2012学年度第一学期期末试卷(北区)八年级数学(A 卷) 2012.1一、精心选一选(本题共30分,每小题3分) 1.下列四个汽车标志图中,不是..轴对称图形的是( ).A .B .C .D .2.计算33-的结果是( ).A .9-B .27-C .271 D .271- 3.下列说法中,正确的是( ).A .16的算术平方根是4-B .25的平方根是5C .1的立方根是1±D .27-的立方根是3- 4.下列各式中,正确的是( ).A .2121+=++a b a b B .21422-=--a a a C . 22)2(422--=-+a a a a D .a b a b --=--11 5.下列关于正比例函数5y x =-的说法中,正确的是( ).A .当1x =时,5y =B .它的图象是一条经过原点的直线C .y 随x 的增大而增大D .它的图象经过第一、三象限 6.如右图,在△ABC 中,∠C =90°,AB 的垂直平分线MN 分别交AC ,AB 于点D ,E . 若∠CBD : ∠DBA=3:1, 则∠A 为( ).A.18°B .20°C .22.5°D .30°7.如下图,在边长为a 的正方形中,剪去一个边长为b 的小正方形(b a >),将余下部分剪开后拼成一个梯形,根据两个图形阴影面积的关系,可以得到一个关于a ,b 的恒等式为( ).E D C BANM aA .2222)(b ab a b a +-=-B .2222)(b ab a b a ++=+ C .))((22b a b a b a -+=- D .)(2b a a ab a +=+ 8.下列条件中,不能..判定两个直角三角形全等的是( ). A .两锐角对应相等 B .斜边和一条直角边对应相等 C .两直角边对应相等 D .一个锐角和斜边对应相等 9.若一次函数y kx b =+不等式0≥+b kx 的解集为( ). A .0≥x B .1≥x C .2≥x D .2≤x 10.在直线2121+=x y 上,且到坐标轴距离为A .4个 B .3个 C .2个 二、细心填一填(本题共16分,每小题2分)11.在54,11-,∙7.0,π2,38.12.函数1+=x y 中,自变量x 的取值范围是______________.13.如右图,△ABC 为等边三角形,DC ∥AB ,AD ⊥CD 于D .若△ABC 的周长为12 cm ,则CD =________ cm .14.点(1-,2)关于x 轴对称的点的坐标为___________________.15.如右图,在△ABC 中,AC = BC ,D 是BC 边上一点,且AB =AD =DC ,则∠C =_________°.16.若将直线)0(≠=k kx y 的图象向下平移1个单位长度后经过点(1,5),则平移后直线的解析式为______________________.17.如右图,在△ABC 中,∠C =90°,BD 平分∠CBA交AC 于点D .若AB =a ,CD =b ,则△ADB 的面 积为______________ .18.下列图案均是用长度相同的小木棒按一定的规律拼搭而成:拼搭第1个图案需4根小木棒,拼搭第2个图案需10根小木棒,拼搭第3个图案需18根小木棒,……,依此规律,拼搭第8个图案需__________根小木棒.ABCA D CBC DAB第1个 第2个 第3个 第4个 ……三、耐心算一算(本题共19分,第19题6分,第20题3分,第21、22题各5分) 19.因式分解:(1)2225a b -; (2)2816ax ax a -+. 解: 解:20.计算:23259-+-.解:21.先化简,再求值:21)21441(22++÷++++x x x x x x ,其中x =3. 解:22.解分式方程:45251=+-++xx x . 解:四、认真做一做(本题共17分,第23题6分,第24题5分,第25题6分) 23.已知:如图,CB =DE ,∠B =∠E ,∠BAE =∠CAD .求证:∠ACD =∠ADC .证明:E A B CD……24.已知:如图1,长方形ABCD 中,AB =2,动点P 在长方形的边BC ,CD ,DA 上沿AD C B →→→的方向运动,且点P 与点A ,B 都不重合.图2是此运动过程中,△ABP 的面积y 与点P 经过的路程x 之间的函数图象的一部分. 请结合以上信息回答下列问题:(1)长方形ABCD 中,边BC 的长为________;(2)若长方形ABCD 中,M 为CD 边的中点,当点P 运动到与点M 重合时,x =________,y =________;(3)当106<≤x 时,y 与x 之间的函数关系式是___________________; (4)利用第(3)问求得的结论,在图2中将相应的y 与x 的函数图象补充完整. 图125.已知:直线321+-=x y 与x (1)分别求出A ,B (2)过A 点作直线AP 与y 轴交于点P ,且使OP =2OB , 求△ABP 的面积.解:(1)(2)五、仔细想一想(本题共18分,每小题6分)26.已知:如图,在△ABC 中,AB =AC ,∠BAC =30°.点D为△ABC 内一点,且DB =DC ,∠DCB =30°,点E 为BD 延长线上一点,且AE =AB . (1)求∠ADE 的度数;(2)若点M 在DE 上,且DM =DA ,求证:ME =DC . CMBDAE27.有一个装有进水管和出水管的容器,水管的所有阀门都处于关闭状态.初始时,打开容器的进水管,只进水;到5分钟时,打开容器的出水管,此时既进水又出水; 到15分钟时,关闭容器的进水管,只出水; 到t 分钟时,容器内的水全部排空.已知此容器每分钟的进水量与出水量均为常数,容器内的水量y (单位:升)与时间x (单位:分)之间的函数关系如图所示,请根据图象回答下列问题: (1)此容器的进水管每分钟进水______升;(2)求515x ≤≤时,容器内的水量y 与时间x 的函数关系式; (3)此容器的出水管每分钟出水多少升?t 的值为多少? 解:(2)28.已知:△ABC 中,AD 平分∠BAC 交BC 于点D ,且∠ADC =60°.问题1:如图1,若∠ACB =90°,AC =m AB ,BD =nDC , 则m 的值为_________,n 的值为__________.问题2:如图2,若∠ACB 为钝角,且AB >AC ,BD >DC . (1)求证:AC AB DC BD -<-;(2)若点E 在AD 上,且DE =DB ,延长CE 交AB 于点F ,求∠BFC 的度数. 证明:(1) 图1ABCA BCEF北京市西城区2011 — 2012学年度第一学期期末试卷(北区)八年级数学(A 卷)参考答案及评分标准二、细心填一填(本题共16分,每小题2分)11.11-,π2;(答对1个给1分) 12.x ≥1-; 13.2; 14.(1-,2-); 15.36; 16.16-=x y ; 17.ab 21; 18.88.三、耐心算一算(本题共19分,第19题6分,第20题3分,第21、22题每题5分) 19.(1)解:2225b a -=)5)(5(b a b a -+. -----------------------------------------------------------------2分(2)解:a ax ax 1682+-=)168(2+-x x a ---------------------------------------------------------------------4分 =2)4(-x a . ---------------------------------------------------------------------------6分20.解:23259-+-=23253-+- ----------------------------------------------------------------------1分 =23253-+- -----------------------------------------------------------------------2分 =266-. --------------------------------------------------------------------------------3分21.解:21)21441(22++÷++++x x x x x x=21])2(1)2(1[2++÷+++x x x x x=21)2(222++÷++x x x x x ----------------------------------------------------------------------2分 =2(1)2x x ++⋅=222x x+. ---------------------------------------------------------------------------------4分当3=x 时,原式=22323+⨯=152. --------------------------------------------------5分22.解:方程两边同乘(5)x +,得 20421+=-+x x . --------------------------------2分 解得 7-=x . ---------------------------------------------------------------------------4分 检验:7-=x 时50x +≠,7-=x 是原分式方程的解. ---------------------5分四、认真做一做(本题共17分,第23题6分,第24题5分,第25题6分)23.证明:如图1.∵∠BAE =∠CAD , ∴∠BAE -∠CAE =∠CAD -∠CAE ,即∠BAC =∠EAD . -------------------------------------1分在△ABC 和△AED 中, ∠BAC =∠EAD ,∠B =∠E ,BC =ED ,∴△ABC ≌△AED . ------------------------------------------------------------------4分 ∴AC =AD . -----------------------------------------------------------------------------5分 ∴∠ACD =∠ADC . -------------------------------------------------------------------6分24.解:(1)4; -------------------------------------------1分 (2)5,4;(每空1分) ---------------------3分 (3)10+-=x y ; -----------------------------4分 (4)如图2. --------------------------------------5分25.解:(1)令0=y ,则6=x ;∴点A 的坐标为A (6,0); 令0=x ,则3=y ;∴点B 的坐标为B (0,3). (2)如图3.∵OB =3,且OP =2OB , ∴OP =6.∵点P 在y 轴上,∴点P 的坐标为(0,6)或(0,6-).(两个坐标各1分) ------4分 若点P 的坐标为(0,6),E A B C D 图1则OA BP S ABP ⋅=∆21=6)36(21⨯-⨯=9; --------------------------------5分 若点P 的坐标为(0,6-),则OA BP S ABP ⋅=∆21=6)63(21⨯+⨯=27. -------------------------------6分∴△ABP 的面积为9或27.五、仔细想一想(本题共18分,每小题6分) 26.解:(1)如图4.∵△ABC 中,AB =AC ,∠BAC =30°,∴∠ABC =∠ACB =2)30180(÷- =75°.∵DB =DC ,∠DCB =30°, ∴∠DBC =∠DCB =30°. ∴∠1=∠ABC -∠DBC =75°-30°=45°.∵AB =AC ,DB =DC ,∴AD 所在直线垂直平分BC . ∴AD 平分∠BAC .∴∠2=21∠BAC =3021⨯=15°. -----------------------------------------------2分 ∴∠ADE =∠1+∠2 =45°+15°=60°. -----------------------------------------3分证明:(2)证法一:取BE 的中点N ,连接AN .(如图5)∵△ADM 中,DM =DA ,∠ADE =60°, ∴△ADM 为等边三角形. -----------------4分∵△ABE 中,AB =AE ,N 为BE 的中点,∴BN =NE ,且AN ⊥BE . ∴DN =NM . -----------------------------------5分∴BN -DN =NE -NM , 即 BD =ME .∵DB =DC ,∴ME = DC . ---------------------------------------------------------------------6分证法二:如图6.∵△ADM 中,DM =DA ,∠ADE =60°, ∴△ADM 为等边三角形. ------------------4∴∠3=60°. ∵AE =AB , ∴∠E =∠1=45°.∴∠4=∠3-∠E =60°-45°=15°. ∴∠2=∠4. 在△ABD 和△AEM 中,∠1 =∠E , AB =AE , ∠2 =∠4,∴△ABD ≌△AEM . ------------------------------------------------------------5分 ∴BD =EM . B BB∴ME = DC . ---------------------------------------------------------------------6分阅卷说明:其他正确解法相应给分.27.解:(1) 8 ; ----------------------------------------------------------------------------------1分(2)设当5≤x ≤15时,函数解析式为(0)y kx b k =+≠.∵点(5,40),(15,60)在此线段上,则 4056015.k b k b =+⎧⎨=+⎩,-----------------------------------------------------------------2分解得 230.k b =⎧⎨=⎩,∴230y x =+. --------------------------------------------------------------------3分 ∴当5≤x ≤15时,230y x =+.(3)由(1)知容器的进水管每分钟进水8升,则它的出水管每分钟出水量为: 8(6040)(155)--÷-=(升). ------------------------------------------4分15分钟后排空容器内的水所需时间为:60610÷=(分) -------------5分则 151025t =+=(分). -----------------------------------------------------6分 答:此容器的出水管每分钟出水6升,t 的值为25.28.解:问题1:21,2 ;(每空1分) -------------------------------------------------------2分 问题2:(1)在AB 上截取AG ,使AG =AC ,连接GD .(如图7) ∵AD 平分∠BAC ,∴∠1=∠2. 在△AGD 和△ACD 中, AG =AC ,∠1 =∠2, AD =AD ,∴△AGD ≌△ACD .∴DG =DC . -------------------------------------------------------------------------3分 ∵△BGD 中,BD -DG <BG , ∴BD -DC <BG .∵BG = AB -AG = AB -AC ,∴BD -DC <AB -AC . ------------------------------------------------------------4分(2)∵由(1)知△AGD ≌△ACD ,∴GD =CD ,∠4 =∠3=60°. ∴∠5 =180°-∠3-∠4=180°-60°-60°=60°. ∴∠5 =∠3.图7 7654321GF EDC B ADB =DE,∠5 =∠3,DG=DC,∴△BGD≌△ECD.--------------------------------------------------------------5分∴∠B =∠6.∵△BFC中,∠BFC=180°-∠B-∠7 =180°-∠6-∠7 =∠3,∴∠BFC=60°.---------------------------------------------------------------------6分阅卷说明:其他正确解法相应给分.。
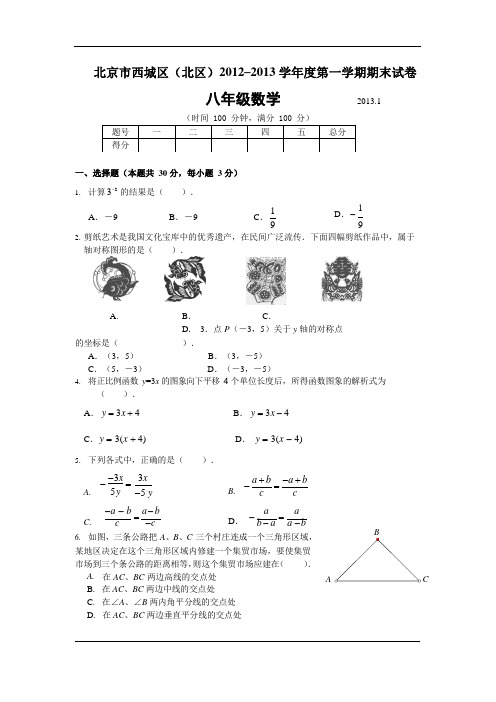
北京市西城区(北区)2012–2013 学年度第一学期期末试卷八年级数学2013.1(时间 100 分钟,满分 100 分)一、选择题(本题共30 分,每小题 3 分)1.计算3-2 的结果是().A.-9 B.-9 C.19D.-192.剪纸艺术是我国文化宝库中的优秀遗产,在民间广泛流传.下面四幅剪纸作品中,属于轴对称图形的是().A.B.C.D.3.点P(-3,5)关于y 轴的对称点的坐标是().A.(3,5)B.(3,-5)C.(5,-3)D.(-3,-5)4.将正比例函数y=3x 的图象向下平移4 个单位长度后,所得函数图象的解析式为().A.y = 3x + 4 B.y = 3x - 4C.y= 3(x + 4) D. y = 3(x - 4)5.下列各式中,正确的是().--3x=A. 5 y3x-5 y-a +b=-a +bB. c c-a -b=a -b-a=aC. c -c D. b -a a -b6.如图,三条公路把A、B、C 三个村庄连成一个三角形区域,B某地区决定在这个三角形区域内修建一个集贸市场,要使集贸市场到三个条公路的距离相等,则这个集贸市场应建在().A.在AC、BC 两边高线的交点处 A CB.在AC、BC 两边中线的交点处C.在∠A、∠B 两内角平分线的交点处D.在AC、BC 两边垂直平分线的交点处题号一二三四五总分得分7.估计的值在().142PA .1 与 2 之间B .2 与 3 之间C .3 与 4 之间D .4 与 5 之间8. 一次函数 y = mx + m (m 为常数且 m ≠0),若 y 随 x 增大而增大,则它的图象经().A .第一、二、三象限B .第一、二、四象限C .第一、三、四象限D .第二、三、四象限9. 如图,在等腰直角三角形 ABC 中,∠BAC =90°,A 在 BC 上截取 BD =BA ,作∠ABC 的平分线与 AD 相交于点 P ,连结 PC ,若△ABC 的面积为2cm 2 ,则 △BPC 的面积为( ).A. 0.5cm 2C .1.5cm 2 B. 1cm 2 BCD . 2cm 210. 小华、小明两同学在同一条长为 1100 米的直路上进行跑步比赛,小华、小明跑步的平均速度分别为 3 米/秒和 5 米/秒,小明从起点出发,小华在小明前面 200 米处出发,两人同方向同时出发,当其中一人到达终点时,比赛停止.设小华与小明之间的距离 y (单位:米),他们跑步的时间为 x (单位:秒),则表示 y 与 x 之间的函数关系的图象是 ( ).A.B .C .D . 二、填空题(本题共 24 分,第 13 题 4 分,第 18 题 2 分,其余各题每小题 3 分)11. 在函数 y =1x - 2 中,自变量 x 的取值范围是 . 12.在0.1&4&, 11 , - ,π, 7这五个实数中,无理数的是 .13. 一次函数 y = 2x -1 的图象与 x 轴的交点坐标为,与 y 轴的交点坐标为 .14. 如图,在 Rt △ABC 中,∠ACB =90°,∠A =15°,AB 的垂直平分线与 AC 交于点 D ,与 AB 交于点 E ,连结 BD .若 AD =12cm ,则 BC 的长为 cm .15.若 x 2 = 9 , y 3 = -8 ,则 x +y =.16. 某校组织学生到距离学校 15 千米的西山公园秋游,先遣车队与学生车队同时出发,先遣车队比学生车队提前半小时到达公园以便提前做好准备工作.已知先遣车队的速是学3 -273 3 16 E生队车速度的 1.2 倍, 若设学生车队的速度为 x 千米/ 时, 则列出的方程是.17.如图,在△ABC 中,AB =AC ,D 为 BC 边上一点,且∠BAD =30°,若 AD =DE ,∠EDC =33°,则∠DAE 的度 数为°.18. 如果满足条件“∠ABC =30°,AC =1, BC =k (k >0)”的△ABC 是唯一的,那么 k 的取值范围是.三、解答题(本题共 28 分,第 19、20 题每小题 5 分,第 21~23 题每小题 6 分) 19.计算: 2( -1) + - + .20. 先化简,再求值: (1 + m - 3 1 ) ÷ m + 3 2mm 2 - 6m + 9,其中m = 9 .21. 解方程:x - x -1 3 x +1= 1 . 22. 已知:如图, A 、B 、C 、D 四点在同一直线上, AB =CD ,AE ∥BF 且 AE =BF .F求证:EC =FD . 证明:AB C D23.如图,直线 y = kx + b 经过点 A (0,5),B (1,4).(1) 求直线 AB 的解析式;(2) 若直线 y = 2x - 4 与直线 AB 相交于点 C ,求点 C 的坐标; (3) 根据图象,写出关于 x 的不等式 2x -4≥kx +b 的解集. 解:(1)(2)(3)关于 x 的不等式 2x -4≥kx +b 的解集是 . 四、解答题(本题共 12 分,第 24 题 5 分,第 25 题 7 分) 24. 阅读下列材料:木工张师傅在加工制作家具的时候,用下面的方法在木板上画直角:如图 1,他首先在需要加工的位置画一条线段 AB ,接着分别以点 A 、点 B 为圆心,以大于 1AB 的适当长为半径画弧,两弧相交于点 C ,再以 C 为圆心,以同样长为半径画弧2交 AC 的延长线于点 D (点 D 需落在木板上),连接 DB .则∠ABD 就是直角. 木工张师傅把上面的这种作直角的方法叫做“三弧法.EF图 1图 2解决下列问题:(1) 利用图 1 就∠ABD 是直角作出合理解释(要求:先写出已知、求证,再进行证明);(2) 图 2 表示的一块残缺的圆形木板,请你用“三弧法”,在木.板.上.画出一个以 EF 为一条直角边的直角三角形 EFG (要求:尺规作图,不写作法,保留作图痕迹).25. 已知:一次函数 y =1x + 3 的图象与正比例函数 y = kx 的图象相交于点2A (a ,1).(1) 求 a 的值及正比例函数 y = kx 的解析式;(2) 点 P 在坐标轴上(不与点 O 重合),若 PA =OA ,直接写出 P 点的坐标; (3) 直线 x = m 与一次函数的图象交于点 B ,与正比例函数图象交于点 C ,若△ABC 的面积记为 S ,求 S 关于 m 的函数关系式(写出自变量的取值范围).DCA五、解答题(本题 6 分)26.在△ABC 中,AD 是△ABC 的角平分线.(1)如图1,过C 作CE∥AD 交BA 延长线于点E,若F 为CE 的中点,连结AF,求证:AF⊥AD;(2)如图2,M 为BC 的中点,过M 作MN∥AD 交AC 于点N,若AB=4,AC=7,求NC 的长.图1 图2北京市西城区(北区)2012–2013 学年度第一学期期末试卷八年级数学附加题2013.1一、填空题(本题共 6 分)1.在平面直角坐标系xOy 中,横、纵坐标都为整数的点称为整点.已知一组正方形的四个顶点恰好落在两坐标轴上,请你观察每个正方形四条边上的整点的个数的变化规律.回答下列问题:(1)经过x 轴上点(5,0)的正方形的四条边上的整点个数是;,图1 图2(2)经过x 轴上点(n,0)(n 为正整数)的正方形的四条边上的整点个数记为m,则m 与n 之间的函数关系是.二、解答题(本题共14 分,第 2 题8 分,第 3 题 6 分)2.在平面直角坐标系xOy 中,直线y =x + 6 与x 轴交于点A,与y 轴交于点B.(1)求∠BAO 的度数;(2)如图1,P 为线段AB 上一点,在AP 上方以AP 为斜边作等腰直角三角形APD.点Q 在AD 上,连结PQ,过作射线PF⊥PQ 交x 轴于点F,作PG⊥x 轴于点G.求证:PF=PQ ;(3)如图2,E 为线段AB 上一点,在AE 上方以AE 为斜边作等腰直角三角形AED.若P 为线段EB 的中点,连接PD、PO,猜想线段PD、PO 有怎样的关系?并说明理由.图1 图23.在Rt△ABC 中,∠ACB=90°,∠A=30°,BD 是△ABC 的角平分线,DE⊥AB 于点E.(1)如图 1,连接EC,求证:△EBC 是等边三角形;(2)点M 是线段CD 上的一点(不与点C,D 重合),以BM 为一边,在BM 的下方作∠BMG=60°,MG 交DE 延长线于点G.请你在图2 中画出完整图形,并直接写出MD,DG 与AD 之间的数量关系;(3)如图 3,点N 是线段AD 上的一点,以BN 为一边,在BN 的下方作∠BNG=60°,NG 交DE 延长线于点G.试探究ND,DG 与AD 数量之间的关系,并说明理由.3 3 3北京市西城区(北区)2012 — 2013 学年度第一学期期末试卷八年级数学参考答案及评分标准2013.1题号 1 2 3 45 6 7 8 9 10 答案CDABDCCABD11 12 13 14x ≠ 2- 2 , π( 1,0 ),( 0, -1) 2每空 2 分6 15161718-5 或 115 - 15 = 1x 1.2x 272k = 2或 0<k ≤1 每个结果 1 分三、解答题(本题共 28 分,第 19,20 题,每小题 5 分,第 21~23 题,每小题 6 分) 19.解: 2( -1) + - += 2 3 - 2 + + 4 ································ ··········································3 分= 3 3 + 2 . ································ ································ ·················· 5 分20. 解: (1+ m - 3 1 ) ÷m + 3 2m m 2 - 6m + 9= 2m ⋅(m - 3)2 ································ ··································· 3 分 (m - 3)(m + 3) 2m =m - 3.····················································································· 4 分 m + 3当 m = 9 时,原式=9 - 3 = 1. ································ ·························5 分9 + 3 221. 解:方程两边同乘(x -1)(x +1) ,得x (x +1) - 3(x -1) = (x -1)(x +1) . ································ ························· 2 分化简,得 x - 3x + 3 = -1 . ····················· 4 分 解得 x = 2 . ································································ ················· 5 分检验:当 x = 2 时, (x -1)(x +1) ≠ 0 , ∴ x = 2 是原分式方程的解. ····························································· 6 分16⎨⎩22.解:(1)∵AE ∥BF ,∴∠A =∠FBD . ······················· 1 分 又∵AB = CD ,∴AB +BC = CD +BC . 即 AC =BD . ······························ 3 分在△AEC 和△BFD 中,⎧ AE = BF , ⎪∠A = ∠FBD , ⎪ AC = BD ,∴△AEC ≌△BFD (SAS ). ································ ······················5 分∴EC =FD . ································ ··········································· 6 分23.解:(1)∵直线 y = -kx + b 经过点 A (5,0)、B (1,4),⎧5k + b = 0, ∴ ⎨⎩k + b = 4. ································ ································ ·········· 1 分⎧k = -1,解方程得 ⎨ ⎩b = 5.································································2 分 ∴直线 AB 的解析式为 y = -x + 5. ································ ·················3 分(2)∵直线 y = 2x - 4 与直线 AB 相交于点 C ,⎧y = - x + 5,∴解方程组⎨⎩y = 2 x - 4.⎧x = 3, 得⎨ ⎩y = 2.∴点 C 的坐标为(3,2). ································ ························5 分(3) x ≥3. ································ ·················································6 分四、解答题(本题共 12 分,第 24 题 5 分,第 25 题 7 分) 24.(1)已知:在△ABD 中,AC =BC =CD . 求证: ∠ABD = 90︒ . 证明:∵AC=BC ,∴ ∠1 = ∠2 . ∵BC=CD , ∴ ∠3 = ∠4 . ···················· 1 分在△ABD 中, ∠1+ ∠2 + ∠3 + ∠4 = 180︒ .∴ ∠1 + ∠4 = 90︒ .34 21即∠ABD = 90︒ . ································································ 3 分(2)如图,△EFG 为所求作的三角形 .E F································ ································ ································ ············· 5 分25. 解:(1)∵一次函数 y = 1x + 3 的图象与正比例函数 y = kx 的图象相交于点2A (a ,1),1∴ a + 3 = 1. 2解得a = -4 . ······················· 1 分∴A (-4 ,1). ∴ -4k = 1 .解得 k =- 1.4∴正比例函数的解析式为 y =- 1x . ································ ·········2 分4(2)P 1(-8 ,0)或 P 2(0 ,2); ································ ··············· 4 分阅卷说明:每个结果 1 分(3)依题意,得点 B 的坐标为(m , 1 m + 3 ),点C 的坐标为(m , - 1 m ).2 4作 AH ⊥BC 于点 H ,H 的坐标为(m ,1). ································5 分以下分两种情况: (ⅰ)当 m <-4 时,BC = -1 1 m - ( 4 23m + 3) = - m - 3 .4AH = -4 - m . 则 S ∆ABC = 1BC ⋅ AH2 = 1 (-3 m - 3)(-4 - m )2 4Gx=my = 1x + 32CHABy =- 1x4BC = 1 1 = 3 .( m + 3) + m 2 4 m + 3 4 AH = m + 4 .则 S ∆ABC= 1 BC ⋅ AH 2 = 1 3( m + 3)(m + 4) 2 4 = 3m 2 + 3m + 6 . 8综上所述, S∆ABC = 3 m 2+ 3m + 6 (m ≠-4).············ 7 分 8五、解答题(本题 6 分)26. 证明:∵AD 为△ABC 的角平分线,∴ ∠1 = ∠2 .(1)∵CE ∥AD ,∴ ∠1 = ∠E , ∠2 = ∠3 . ∴ ∠E = ∠3 . ∴AC =AE . ···························· 1 分∵F 为 EC 的中点,∴AF ⊥BC .∴ ∠AFE = ∠FAD = 90︒ .∴A F ⊥A D .···························2 分BDA51 2N43 DM⎨ ⎩(2) 延长 BA 与 MN 延长线于点 E ,过 B 作 BF ∥AC 交 NM 延长E 线于点F ········· 3 分 ∴ ∠3 = ∠C , ∠F = ∠4 .∵M 为 BC 的中点 ∴BM =CM .在△BFM 和△CNM 中,⎧∠F = ∠4, BC⎪∠3 = ∠C , ⎪BM = C M , F∴△BFM ≌△CNM (AAS ). ································ ························ 4 分∴BF =CN .∵MN ∥AD ,∴ ∠1 = ∠E , ∠2 = ∠4 = ∠5 . ∴ ∠E = ∠5 = ∠F . ∴AE =AN ,BE =BF .设 CN =x ,则 BF =x , AE =AN =AC -CN =7-x ,BE =AB +AE =4+7-x . ∴4+7-x =x . 解得 x =5.5.∴CN =5.5. ··············································································6 分北京市西城区(北区)2012 — 2013 学年度第一学期期末试卷八年级数学附加题参考答案及评分标准2013.1一、填空题(本题 6 分)1.(1)20;································ ·····························································3 分(2) m = 4n . ································································ ······················· 3 分二、解答题(本题共 14 分,第 2 题 8 分,第 3 题 6 分) 2.解:(1)直线 y = x + 6 与 x 轴交于点 A ,与 y 轴交于点 B .∴A (-6,0),B (0,6).∴O A =O B .································∴ ∠BAO = ∠ABO在△AOB 中, ∠AOB = 90︒ . ∴ ∠BAO = ∠ABO = 45︒ . ································ ·········································································· 1 分2 分(2) 在等腰直角三角形 APD 中,∠PDA = 90︒ ,DA =DP , ∠1 = ∠APD = 45︒ .∴DP ⊥AD 于 D .由(1)可得∠BAO = 45︒ . ∴ ∠BAO = ∠1 .又∵PG ⊥x 轴于 G , ∴PG = PD . ································ ································∴ ∠AGP = ∠PGF = ∠D = 90︒ .y··········· 3 分1 xA G F O⎨⎩⎨⎩⎨⎩∴ ∠4 + ∠APD = ∠DPG =90︒ . 即∠3 + ∠GPQ = 90︒ . 又∵PQ ⊥PF , ∴ ∠2 + ∠GPQ = 90︒ . ∴ ∠2 = ∠3 . ················· 4 分在△PGF 和△PDQ 中,⎧∠PGF = ∠D , ⎪PG = PD , ⎪∠2 = ∠3,∴△PGF ≌△PDQ (ASA). ∴PF =PQ . ································································ ············· 5 分(3) 答:OP ⊥DP ,OP =DP .证明:延长 DP 至 H ,使得 PH =PD .∵P 为 BE 的中点, ∴PB =PE .在△PBH 和△PED 中,⎧PB = PE , ⎪∠1 = ∠2, ⎪PH = PD , ∴△PBH ≌△PED (SAS ). ∴BH =ED . ························· 6 分∴ ∠3 = ∠4 . ∴BH ∥ED .在等腰直角三角形 ADE 中, AD =ED , ∠DAE = ∠DEA = 45︒ .∴AD =BH , ∠DAE + ∠BAO = ∠DAO = 90︒ . 图 2∴DE ∥x 轴,BH ∥x 轴, BH ⊥y 轴. ∴ ∠DAO = ∠HBO = 90︒ . 由(1)可得OA =OB . 在△DAO 和△HBO 中,⎧ AD = BH , ⎪∠DAO = ∠HBO , ⎪OA = OB ,∴△DAO ≌△HBO (SAS ). ∴OD =OH ,∠5=∠6. ································ ··························· 7 分∵ ∠AOB = ∠5 + ∠DOB = 90︒ , ∴ ∠DOH = ∠6 + ∠DOB = 90︒ . ∴在等腰直角三角形△DOH 中, ∵DP =HP ,∴OP ⊥DP , ∠7 = 1∠DOH = 45︒ .2M DE ⎨⎩∴ ∠ODP = ∠7 . ∴O P =P D .···········································································8 分3.(1)证明:在Rt △ABC 中,∠ACB =90°,∠A =30°,∴ ∠ABC = 60︒ , BC = 1AB .2 ∵BD 平分∠ABC ,∴ ∠1 = ∠DBA = ∠A = 30︒ . ∴DA =DB .∵DE ⊥AB 于点 E . ∴AE =BE = 1AB .2 A图 1∴BC =BE . ································ ································ ··········1 分 ∴△BCE 是等边三角形. ························································C2 分(2)结论:AD = DG +DM .A································ ································ ································ (3)结论:AD = DG -DN . 理由如下: BG图 2············ 3 分延长 BD 至 H ,使得 DH =DN . ································ ························· 4 分由(1)得 DA =DB , ∠A = 30︒ . ∵DE ⊥AB 于点 E .∴ ∠2 = ∠3 = 60︒ . ∴ ∠4 = ∠5 = 60︒ .∴△NDH 是等边三角形. ∴NH =ND , ∠H = ∠6 = 60︒ . ∴ ∠H = ∠2 . ∵ ∠BNG = 60︒ , ∴ ∠BNG + ∠7 = ∠6 + ∠7 . 即∠DNG = ∠HNB . 在△DNG 和△HNB 中,G⎧DN =HN , 图 3⎪∠DNG =∠HNB , ⎪∠H =∠2,∴△DNG ≌△HNB (ASA ). ∴DG =HB .∵HB =HD +DB =ND +AD , ∴DG = ND +AD .∴AD = DG-ND.············································································· 6 分。

北京市西城区(南区)2011-2012学年第一学期期末考试(八年级)一、选择题(每题4分)1.实数-5,-0.1,√3,21中为无理数的是( )A.21 B.-0.1 C.√3 D.-5 2.下列二次根式中,最简二次根式是( )A.5 B. 5.0 C. 51 D.50 3.计算111---a a a 的结果是( )A. 11-+a a B. 1--a a C. -1 D.a - 4.下列事件中,为必然事件的是( )A. 购买一张彩票,中奖B. 打开电视,正在播放广告C. 抛掷一枚硬币,正面朝上D.一个袋中只装有5个黑球,从中摸出一个球是黑球5.如图,已知21∠=∠,则不一定能使ACD ABD ∆≅∆的条件是( )A. BD=CDB. AB=ACC. C B ∠=∠D.CDA BDA ∠=∠6.如图,在0030390=∠==∠∆B AC C ABC ,,中,,点P 是BC 边上的动点,则AP 长不可能是( )A. 3.5B. 4.2C. 5.8D.77.如图,在ABC ∆中,AD 平分外角EAC ∠,且BC AD //,则ABC ∆一定是( )A. 任意三角形B.等边三角形C. 等腰三角形D.直角三角形8.下列命题的逆命题正确的是( )A. 全等三角形的面积相等B.全等三角形的对应角相等C. 直角三角形D.等边三角形的三个角都等于0609.如图,六边形ABCDEF 是轴对称图形,CF 所在的直线是它的对称轴,若0150=∠+∠BCF AFC 则BCD AFE ∠+∠的大小是( )A. 0150B. 0300C. 0210D.033010.如图,在ABC ∆中,分别以点A 和点B 为圆心,大于AB 21的长为半径画弧,两弧相交于点M,N ,作直线MN ,交BC 于点D ,连接AD ,若AD C ∆的周长为10,AB=7,则ABC ∆的周长为( )A. 7 B. 14 C. 17 D.2011.实数a 在数轴上的位置如图所示,则22)11()4(-+-a a 化简后为( )A.7 B 。

北京市西城区2011-2012学年第一学期期末(数学)北区一、选择题(32分,每题4分)1. 抛物线1)1(2+-=x y 的顶点坐标为 A.(1,1) B.(1,-1) C.(-1,1) D.(-1,-1) 2.若相交两圆的半径分别为4和7,则它们的圆心距可能是 A.2 B. 3 C.6 D.113.在RT △ABC 中,∠C=90 º,若BC=1,AB=5则tanA 的值为A. 55 B. 552 C.21 D.24.如图,在O Θ中,直径AB CD 弦⊥于E ,连接BD ,若2300==∠BD D ,,则AE 的长为 A.2 B.3 C.4 D.55.若正六边形的边长等于4,则它的面积等于A. 348B. 324C. 312D. 346.如图,以D 为位似中心,作△ABC 的一个位似三角形111C B A , C B A ,,的对应点分别 为111C B A ,DA DA 与1的比值为k ,若两个三角形的顶点及点D 均在如图所示的格点上,则k 的值和点1C 的坐标分别为A.2,(2,8)B.4,(2,8)C. 2,(2,4)D. 2,(4,4)7.如图,抛物线c bx axy ++=2经过点(-1,0),对称轴为x=1,则下列结论中正确的是A.a>0B.当x>1时,y 随x 的增大而增大C.c<0D.x=3是一元二次方程02=++c bx ax的一个根8.如图,在平面直角坐标系xoy 中,A(2,0),B(0,2), C Θ上的一个动点,线段DA 与y 轴交于点E ,则△ABE 面积的最大值是 A. 2 B.38 C. 222+D. 222-二、填空题(16分,每题4分)9.如图O Θ是△ABC 的外接圆,若=∠=∠A OCB ,则04010.将抛物线2x y =先向下平移1个单位长度后,再向右平移1个单位长度,所得抛物线的解析式11.如图,在RT △ABC 中,4,30,900==∠=∠AB B ACB ,以斜边AB 的中点D 为旋转中点,把△ABC 按逆时针方向旋转α角(0<α<1200)当点A 的对应点与点C 重合时,B,C 两点的对应点分别记为E,F ,EF 与AB 的交点为G ,此时α等于 ,△DEG 的面积是 12.已知二次函数x xy +-=221,(1)它的最大值为 (2)若存在实数m ,n 使得当自变量x 的取值范围是n x m ≤≤时,函数值y 的取值范围恰好是n y m 33≤≤,则m= n= 三、解答题(本题30分,每题5分) 13.计算:0245sin260tan 330cos -+14.已知关于x 的方程03222=-+-k x x 有两个不相等的实数根 (1)求k 的取值范围 (2)若k 为符合条件的最大整数,求此方程的根15.已知抛物线542-+=x x y(1)直接写出它与x 轴、y 轴的交点的坐标 (2)用配方法将542-+=x x y 化成k h x a y +-=2)(的形式16.已知:如图,在菱形ABCD 中,E 为BC 边上一点,B AED ∠=∠ (1)求证:DEA ABE ∆∆∽; (2)若AB=4,求DE AE ⋅的值17.学校要围一个矩形花圃,花圃的一边利用足够长的墙,另三边用总长为36米的篱笆恰好围成(如图所示),设矩形的一边AB 的长为x 米(要求AB<AD ),矩形ABCD 的面积为S 平方米(1)求S 与x 之间的函数关系式,并直接写出自变量x 的取值范围 (2)要想使花圃的面积最大,AB 边的长应为多少米?18.如图,在RT △ABC 中,090=∠C ,AB 的垂直平分线与BC 、AB 的交点分别为D,E(1)若54sin 10=∠=ADC AD ,,求AC 的长和βtan 的值(2)若AD=1,α=∠ADC ,参考(1)的计算过程直接写出2tan α的值四、解答题(20分,每题5分)19.如图所示,在平面直角坐标系xoy 中,正方形PABC 的边长为1,将其沿x 轴的正方向连续滚动,即先以顶点A 为旋转中心将正方形PABC 顺时针旋转900得到第二个正方形,再以顶点D 为旋转中心将第二个正方向顺时针旋转900得到第三个正方形,依次方法继续滚动下去得到第四个正方形,…第n 的正方形,设滚动过程中的点P 的坐标 为(x ,y )(1) 画出第三个和第四个正方形的位置,并直接写出第三个正方形中的点P 的坐标(2) 画出点P(x,y)运动的曲线(0)4≤≤x ,并直接写出该曲线与x 轴所围成区域的面积20.已知函数)0(2≥++=x c bx x y ,满足当x=1时,y=-1,且当x=0时与x=4时的函数值相等 (1)求函数)0(2≥++=x c bx x y 的解析式并画出它的图像(2)若f (x )表示自变量x 相对应的函数值,且⎩⎨⎧<-≥++=)0(2)0()(2x x c bx xx f 又已知关于x 的方程k x x f +=)(有三个不相等的实数根,请利用图像直接写出实数k 的取值范围21.已知:如图,AB 是O Θ的直径,BAC ∠的平分线与O Θ的交点为D ,AC DE ⊥,与AC 的延长线交于点E (1)求证:直线DE 是O Θ的切线(2)若OE 与AD 交于点F ,AFDF BAC 求,54cos =∠的值22.阅读下列材料题目:已知实数a ,x 满足a>2且x>2,试判断ax 与a+x 的大小关系,并加以说明思路:可用:求差法,比较两个数的大小,先列出ax 与a+x 的差)(x a ax y --=,再说明y 的符号即可 现给出如下利用函数解决问题的方法:简解:可将y 的代数式整理成a x a y --=)1(。

北京市西城区2011—2012学年度第一学期期末试卷(南区)九年级数学 2012.1考生须知1.本试卷共6页,共五道大题,25道小题,满分120分。
考试时间120分钟。
2.试题答案一律填涂或书写在答题纸上,在试卷上作答无效。
3.在答题纸上,选择题、作图题用2B 铅笔作答,其他试题用黑色字迹签字笔作答。
一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个..是符合题意的. 1.抛物线2(1)1y x =-+的顶点坐标为A .(1,1)B .(1,1)-C .(1,1)-D .(1,1)--2.若相交两圆的半径分别为4和7,则它们的圆心距可能是A .2B .3C . 6D .113.在Rt △ABC 中,∠ C =90°,若BC =1,AB 5tan A 的值为A 5B 25C .12D .24. 如图,在⊙O 中,直径AB ⊥弦CD 于E ,连接BD ,若∠D =30°, BD =2,则AE 的长为 A .2 B .3 C .4 D .55.下列图形中,中心对称图形有A .4个B .3个C .2个D .1个6.抛掷一枚质地均匀的正方体骰子,出现大于3点的概率为 A .21 B .31 C .41 D .617.如图,抛物线2y ax bx c =++经过点(-1,0),对称轴为x =1,则下列结论中正确的是A .0>aB .当1>x 时,y 随x 的增大而增大C .0<cD .3x =是一元二次方程20ax bx c ++=的一个根8.如图,在平面直角坐标系xOy 中,(2,0)A ,(0,2)B ,⊙C 的圆心为点(1,0)C -,半径为1.若D 是⊙C 上的一个动点,线段DA 与y 轴交于E 点,则△ABE 面积的最大值是 A .2 B . 83C .2+D . 2-二、填空题(本题共16分,每小题4分)9.如图,⊙O 是△ABC 的外接圆,若∠OCB =40°,则∠A= °.10.将抛物线2y x =先向下平移1个单位长度后,再向右平移1个单位长度,所得抛物线的解析式是 .11.如图,在Rt △ABC 中,∠ACB =90°,∠B =30°,AB =4.以斜边AB 的中点D 为旋转中心,把△ABC 按逆时针方向旋转 α角(0120α︒<<︒),当点A 的对应点与点C 重合时,B ,C 两点的对应点分别记为E ,F ,EF 与AB 的交点为G ,此时 α等于 ° ,△DEG 的面积为 .12.已知二次函数212y x x =-+,(1)它的最大值为 ;(2)若存在实数m , n 使得当自变量x 的取值范围是m ≤x ≤n 时,函数值y 的取值范围恰好是3m ≤y ≤3n ,则m= ,n= .13.计算:2cos30602sin 45︒+︒-︒.14.如图,网格中每个小正方形的边长均为1,且点A ,B ,C ,P 均为格点.(1) 在网格中作图:以点P 为位似中心,将△ABC 的各边长放大为原来的两倍,A ,B ,C 的对应点分别为A 1 ,B 1 ,C 1;(2) 若点A 的坐标为(1,1),点B 的坐标为(3,2),则(1)中点C 1的坐标为 .15.已知抛物线245y x x =+-.(1)直接写出它与x 轴、y 轴的交点的坐标;(2)用配方法将245y x x =+-化成2()y a x h k =-+的形式.16.如图,三角形纸片ABC 中,∠BCA =90°,∠A =30°,AB =6, 在AC 上取一点 E ,沿BE 将该纸片折叠,使AB 的一部分 与BC 重合,点A 与BC 延长线上的点D 重合,求DE 的长.17.学校要围一个矩形花圃,花圃的一边利用足够长的墙,另三边用总长为36米的篱笆恰好围成(如图所示). 设矩形的一边AB 的长为x 米(要求AB <AD ),矩形 ABCD 的面积为S 平方米.(1)求S 与x 之间的函数关系式,并直接写出自变量x 的取值范围; (2)要想使花圃的面积最大,AB 边的长应为多少米?18.如图,在Rt △ABC 中,90C ∠=︒,AB 的垂直平分线与BC ,AB 的交点分别为D ,E . (1)若AD =10,4sin 5ADC ∠=,求AC 的长和tan B 的值;(2)若AD=1,ADC ∠=α,参考(1)的计算过程直接写 出tan 2α的值(用sin α和cos α的值表示).19.如图所示,在平面直角坐标系xOy 中,正方形PABC 的边长为1,将其沿x 轴的正方向连续滚动,即先以顶点A 为旋转中心将正方形PABC 顺时针旋转90°得到第二个正方形,再以顶点D 为旋转中心将第二个正方形顺时针旋转90°得到第三个正方形,依此方法继续滚动下去得到第四个正方形,…,第n 个正方形.设滚动过程中的点P 的坐标为(,)x y .(1)画出第三个和第四个正方形的位置,并直接写出第三个正方形中的点P 的坐标; (2)画出点(,)P x y 运动的曲线(0≤x ≤4),并直接写出该曲线与x 轴所围成区域的面积.20.已知函数2y x bx c =++(x ≥ 0),满足当x =1时,1y =-,且当x = 0与x =4时的函数值相等. (1) 求函数2y x bx c =++(x ≥ 0)的解析式并 画出它的图象(不要求列表);(2)若()f x 表示自变量x 相对应的函数值,且2 (0),() 2 (0),x bx c x f x x ⎧++≥=⎨-<⎩ 又已知关于x 的 方程()f x x k =+有三个不相等的实数根,请利用图象直接写出实数k 的取值范围.21.已知:如图,AB 是⊙O 的直径,AC 是弦,∠BAC 的平分线与⊙O 的交点为D ,DE ⊥AC ,与AC 的延长线交于 点E .(1)求证:直线DE 是⊙O 的切线; (2)若OE 与AD 交于点F ,4cos 5BAC ∠=,求DF AF 的值.22.阅读下列材料:题目:已知实数a ,x 满足a >2且x >2,试判断ax 与a x +的大小关系,并加以说明. 思路:可用“求差法”比较两个数的大小,列出ax 与a x +的差()y ax a x =-+再说明y 的符号即可.现给出如下利用函数解决问题的方法:简解:可将y 的代数式整理成(1)y a x a =--,要判断y 的符号可借助函数(1)y a x a =--的图象和性质解决.参考以上解题思路解决以下问题:已知a ,b ,c 都是非负数,a <5,且 2220a a b c ---=,2230a b c +-+=. (1)分别用含a 的代数式表示4b ,4c ; (2)说明a ,b ,c 之间的大小关系.五、解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23.已知抛物线2(2)2y kx k x =+--(其中0k >).(1)求该抛物线与x 轴的交点及顶点的坐标(可以用含k 的代数式表示); (2)若记该抛物线顶点的坐标为(,)P m n ,直接写出n 的最小值; (3)将该抛物线先向右平移12个单位长度,再向上平移1k个单位长度,随着k 的变化,平移后的抛物线的顶点都在某个新函数的图象上,求新函数的解析式(不要求写自变量的取值范围).24.已知:⊙O 是△ABC 的外接圆,点M 为⊙O 上一点.(1)如图,若△ABC 为等边三角形,BM =1,CM =2, 求AM 的长;(2) 若△ABC 为等腰直角三角形,∠BAC =90︒,BM a =,CM b =(其中b a >),直接写出AM 的长(用含有a ,b 的代数式表示).25. 已知:在如图1所示的平面直角坐标系xOy 中,A ,C 两点的坐标分别为(2,3)A ,(,3)C n -(其中n >0),点B 在x 轴的正半轴上.动点P 从点O 出发,在四边形OABC 的边上依次沿O —A —B —C 的顺序向点C 移动,当点P 与点C 重合时停止运动.设点P 移动的路径的长为l ,△POC 的面积为S ,S 与l 的函数关系的图象如图2所示,其中四边形ODEF 是等腰梯形.(1)结合以上信息及图2填空:图2中的m = ; (2)求B ,C 两点的坐标及图2中OF 的长;(3)在图1中,当动点P 恰为经过O ,B 两点的抛物线W 的顶点时, ① 求此抛物线W 的解析式;② 若点Q 在直线1y =-上方的抛物线W 上,坐标平面内另有一点R ,满足以B ,P ,Q ,R 四点为顶点的四边形是菱形,求点Q 的坐标.北京市西城区2011 — 2012学年度第一学期期末试卷(南区)九年级数学参考答案及评分标准2012.1 一、选择题(本题共32分,每小题4分)阅卷说明:第10题写成2(1)1y x=--不扣分;第11题每空各2分;第12题第(1)问2分, 第(2)问每空各1分.三、解答题(本题共30分,每小题5分)13.解:原式= 222⨯…………………………………………………3分= 22+.……………………………………………………………………5分14.解:(1)…………………………………………3分(2)点C1的坐标为(2,8). ……………………………………………………5分图115.解:(1)抛物线与x 轴的交点的坐标为(5,0) (1,0)-和. …………………………2分抛物线与y 轴的交点的坐标为(05)-,. …………………………………3分 (2)245y x x =+-2(44)9x x =++-…………………………………………………………4分2(2)9x =+-. …………………………………………………………5分 16.解: 在RtΔACB 中,∠ACB =90°,AB =6, ∠A =30°,(如图2) ∴ 362121=⨯==AB BC . ………………………1分 ∵ 沿BE 将ΔABC 折叠后,点A 与BC 延长线上的点D∴ BD=AB=6,∠D =∠A =30°.……………………3分∴CD=BD -BC =6-3=3. ……………………………4分在RtΔDCE 中,∠DCE =90°,CD =3, ∠D =30°,∴3223330cos ===CD DE . ………………………………………………5分17.解:(1)∵ 四边形ABCD 是矩形,AB 的长为x 米, ∴ CD=AB=x (米).∵ 矩形除AD 边外的三边总长为36米,∴ 362BC x =-(米).………………………………………………………1分 ∴ 2(362)236S x x x x =-=-+. ……………………………………………3分 自变量x 的取值范围是012x <<. …………………………………………4分 ( 说明:由0<x <36-2x 可得012x <<.)(2)∵222362(9)162S x x x =-+=--+,且9x =在012x <<的范围内 ,∴ 当9x =时,S 取最大值.即AB 边的长为9米时,花圃的面积最大.…………………………………5分18.解:(1)在Rt △ACD 中,90C ∠=︒, AD =10,4sin 5ADC ∠=,(如图3) ∴ 4sin 1085AC AD ADC =⋅∠=⨯=.……1分3cos 1065CD AD ADC =⋅∠=⨯=. ∵ DE 垂直平分AB ,∴ 10BD AD ==.……………………………2分 ∴ 16BC CD BD =+=. ……………………3分 在Rt △ABC 中,90C ∠=︒,∴ 81tan 162AC B BC ===.……………………………………………………4分 (2)sin tan 21cos ααα=+.(写成1cos sin αα-也可) ……………………………………5分四、解答题(本题共20分,每小题5分) 19.解:(1)第三个和第四个正方形的位置 如图4所示.……………………2分 第三个正方形中的点P 的坐标为 (3,1). …………………………3分(2)点(,)P x y 运动的曲线(0≤x ≤4)如图4所示. …………………………4分它与x 轴所围成区域的面积等于1π+. ……………………………………5分20.解:(1)∵ 函数2y x bx c =++(x ≥0)满足当x =1时,1y =-, 且当x = 0与x =4时的函数值相等,∴ 11,2.2b c b ++=-⎧⎪⎨-=⎪⎩解得 4b =-,2c =.…………………………………………………………2分 ∴ 所求的函数解析式为242y x x =-+(x ≥0). …………………………3分 它的函数图象如图5所示.……………………………………………………4分(2)k 的取值范围是22k -<≤.(如图6)……………………………………………5分 21.(1)证明:连接OD .(如图7) ∵ AD 平分∠BAC ,∴ ∠1=∠2.…………………………………………………………………1分 ∵ OA =OD , ∴ ∠1=∠3. ∴ ∠2=∠3.∴ OD ∥AE .∵ DE ⊥AC , ∴ ∠AED =90°.∴ 18090ODE AED ∠=︒-∠=︒.∴ DE ⊥OD . ……………………………2分 ∵ OD 是⊙O 的半径,∴ 直线DE 是⊙O 的切线. ………………………………………………3分(2)解:作OG ⊥AE 于点G .(如图7) ∴ ∠OGE =90°.∴ ∠ODE =∠DEG =∠OGE =90°. ∴ 四边形OGED 是矩形.∴ OD =GE .……………………………………………………………………4分 在Rt △OAG 中, ∠OGA =90°,4cos 5BAC ∠=,设AG =4k ,则OA =5k . ∴ GE =OD =5k . ∴ AE =AG +GE =9k . ∵ OD ∥GE , ∴ △ODF ∽△EAF . ∴59DF OD AF AE ==.……………………………………………………………5分 22.解:(1)∵ 2220a a b c ---=,2230a b c +-+=,∴ ⎪⎩⎪⎨⎧+=--=+.322,222a b c a a c b消去b 并整理,得243c a =+.………………………1分消去c 并整理,得2423b a a =--. ………………2分(2)∵ ()()()411332422--=+-=--=a a a a a b , 将4b 看成a 的函数,由函数24(1)4b a =--的性质结合它的图象(如图8所示),以及a ,b 均为非负数得a ≥3.又 ∵ a <5,∴ 3≤a <5.……………………………………………………………………3分∵ 224()63(3)12b a a a a -=--=--,将4()b a -看成a 的函数,由函数24()(3)12b a a -=--的性质结合它的图象(如图9所示)可知,当3≤a <5时,4()0b a -<.∴ b <a . ……………………………………………4分∵ 24()43(1)(3)c a a a a a -=-+=--,a ≥3,∴ 4()c a -≥0.∴ c ≥a .∴ b <a ≤c . ………………………………………5分阅卷说明:“b <a ,b <c ,a ≤c ”三者中,先得出其中任何一个结论即可得到第4分,全写对得到5分.五、解答题(本题共22分,第23题7分,第24题7分,第25题8分)23.解:(1)令0y =,得方程 2(2)20kx k x +--=.整理,得 (1)(2)0x kx +-=.解得 11x =-,22x k= . ∴ 该抛物线与x 轴的交点坐标为(1,0)-,2(,0)k. ………………………2分 抛物线2(2)2y kx k x =+--的顶点坐标为2244(,)24k k k k k-++-. ………3分 (2)|n |的最小值为 2 . …………………………………………………………4分 (3)平移后抛物线的顶点坐标为214(,)4k k k k+-.…………………………………5分由1,14x k k y ⎧=⎪⎪⎨⎪=--⎪⎩可得 114y x =-- . ∴ 所求新函数的解析式为114y x=--. …………………………………7分 24.解:(1)因AB =AC 且∠BAC=60°,故将△ABM 绕点A 逆时针旋转60︒得△ACN ,则△ABM ≌△ACN ,(如图10)………………………………………………1分∴ ∠BAM =∠CAN ,∠ABM =∠ACN ,AM =AN ,BM =CN .∵ 四边形ABMC 内接于⊙O ,∴ ∠ABM +∠ACM =180︒.∴ ∠ACN +∠ACM =180︒.∴ M ,C ,N 三点共线.……………………2分∵ ∠BAM =∠CAN ,∴ ∠BAM +∠MAC =∠CAN +∠MAC =60︒, 即∠MAN =60︒. ………………………………………………………………3分∵ AM =AN ,∴ △AMN 是等边三角形.……………………………………………………4分 ∴ AM =MN =MC +CN =MC +BM =2+1=3. ……………………………………5分(2)AM)b a -)b a +.……………………………………………7分 25.解:(1)图2中的m1分(2)∵ 图11(原题图2)中四边形ODEF 是等腰梯形,点D 的坐标为(,12)D m ,∴ 12E D y y ==,此时原题图1中的点P 运动到与点B 重合,∴ 1131222BOC C S OB y OB ∆=⨯⨯=⨯⨯=. 解得 8OB =,点B 的坐标为(8,0). ……………………………………2分此时作AM ⊥OB 于点M ,CN ⊥OB 于点N .(如图12).∵ 点C 的坐标为(,3)C n -,∴ 点C 在直线3y =-上.又由图11(原题图2)中四边形ODEF 是等腰梯形可知图12中的点C 在过点O 与AB 平行的直线l 上,∴ 点C 是直线3y =-与直线l 的交点,且ABM CON ∠=∠.又∵ 3A C y y ==,即AM= CN ,可得△ABM ≌△CON .∴ ON=BM=6,点C 的坐标为(6,3)C -.……………………………………3分 ∵ 图12中AB ==∴ 图11中DE =,2D OF x DE =+= …………………4分(3)①当点P 恰为经过O ,B 两点的抛物线W 的顶点时,作PG ⊥OB 于点G .(如图13)∵ O ,B 两点的坐标分别为(0,0)O ,(8,0)B ,∴ 由抛物线的对称性可知P 点的横坐标为4,即OG=BG=4.由3tan 6AM PG ABM BM BG∠===可得PG=2. ∴ 点P 的坐标为(4,2)P .………………5分设抛物线W 的解析式为(8)y ax x =-(a ≠0).∵ 抛物线过点(4,2)P ,∴ 4(48)2a -=. 解得 18a =-. ∴ 抛物线W 的解析式为218y x x =-+.…………………………………6分 ②如图14.i )当BP 为以B ,P ,Q ,R 四点为顶点的菱形的边时,∵ 点Q 在直线1y =-上方的抛物线W 上, 点P 为抛物线W 的顶点,结合抛物线的对称性可知点Q 只有一种情况,点Q 与原点重合,其坐标为1(0,0)Q .……………………………………………………………………7分 ii )当BP 为以B ,P ,Q ,R 四点为顶点的菱形的对角线时,可知BP 的中点的坐标为(6,1),BP 的中垂线的解析式为211y x =-.∴ 2Q 点的横坐标是方程212118x x x -+=-的解.将该方程整理得28880x x +-=.解得4x =-± 由点Q 在直线1y =-上方的抛物线W 上,结合图14可知2Q 点的横坐标为4.∴ 点2Q 的坐标是219)Q . …………………………8分综上所述,符合题意的点Q 的坐标是1(0,0)Q ,219)Q .。

北京市西城区2010–2011学年度第一学期期末试卷(北区)八年级数学(B 卷)一、精心选一选(本题共30分,每小题3分) 1.计算24-的结果是( ).A .8-B .18-C .116- D .116 2.下列说法中,正确的是( ).A .5是25的算术平方根B .9-的平方根是3-C .4±是64的立方根D .9的立方根是3 3.下列四个交通标志中,轴对称图形是( ).A .B .C .D .4.当0b <时,函数y x b =-+的图象不经过...( ). A .第一象限 B .第二象限 C .第三象限 D .第四象限 5.下列各式中,正确的是( ).A .1a b b ab b ++= B .22x y x y-++=- C . 23193x x x -=-- D .222()x y x y x y x y --=++ 6.在△ABC 和△A′B′C′中,已知∠A=∠A′,AB=A′B′,添加下列条件中的一个, 不能..使△ABC≌△A′B′C′一定成立的是( ). A .AC =A′C ′ B .BC=B ′C ′ C .∠B =∠B ′ D .∠C =∠C ′ 7.点A (11y -,)和B (22y ,)都在直线3y x =-上,则1y 与2y 的关系是( ).A .12y y <B .12y y =C .12y y >D .212y y =8.如图,在△ABC 中,D 是BC 边上一点,且AB=AD=DC ,∠BAD=40°,则∠C 为( ).A .25°B .35°C .40°D .50° 9.已知一次函数y kx b =+的图象如图所示,当0x >时,y 的取值范围是( ).A .1y <B .1y >C .2y <-D .2y >-10.如图所示,长方形ABCD 中,AB=4,E是折线段A —D —C 上的一个动点(点E 与点A 不重合),点P 是点A 关于BE 的对称点.在点E 运动的过程中,能使△PCB 为等腰三角形.....的点E 的位置共有( ).A .2个B .3个C .4个D .5个二、细心填一填(本题共16分,每小题2分) 11.当x __________时,分式11x-有意义. 12.如图,△ABC 是等边三角形,D 是BC 边的中点,点 E 在AC 的延长线上,且∠CDE=30°.若则DE=_________. 13.在0.6,27,π-_______________. 14.如图,在Rt △ABC 中,∠C=90°,∠B=30°,AD 平分∠CAB 交BC 于D ,DE ⊥AB 于E .若DE=1cm , 则BC =_______ cm .15.如图,MN 是正方形ABCD 的一条对称轴,点P 是直线MN 上的一个动点,当PC+PD 最小时,ABCDAB CDEPDAEBC DCBAEDAM∠PC D=_________°.16.已知直线(0)y kx b k =+≠与直线2y x =-平行,且经过点(1,1),则直线(0)y kx b k =+≠可以看作由直线2y x =-向_______平移_______个单位长度而得到.17.如图,在△ABC 中,AB=AC ,∠A=40°,AB 的垂直平分线MN 交AC 于点D ,则∠DBC=_________°.18. 用长为4cm 的n 根火柴可以拼成如图1所示的x 个边长都为4cm 的平行四边形,还可以拼成如图2所示的2y 个边长都为4cm 的平行四边形,那么用含x 的代数式表示y ,得到______________________.三、耐心算一算(本题共19分,第19题6分,第20题3分,第21、22题每题5分)19.因式分解:(1)224x y -; (2)22363a ab b ++.解: 解:20+解:图1 图2 DAMNB C ………21.先化简,再求值:22211121x x x x x -÷+--+,其中5x =. 解:22.解分式方程:21155x x x x =+++. 解:四、认真做一做(共3个小题,第23、24题各6分,第25题5分,共17分) 23.已知:如图,点A 、E 、F 、C 在同一条直线上,AD=CB ,∠B=∠D ,AD∥BC.求证: AE=CF . 证明:F D C B AE24.已知:平面直角坐标系xOy 中,直线b kx y +=(0k ≠)与直线mx y =(0m ≠)交于点A (2,4-).(1)求直线mx y =(0m ≠(2)若直线b kx y +=(0k ≠直线x y 2=交于点B ,且点B 的横坐标为求△AB O 的面积. 解:(1)(2)25.如图,已知△ABC ,求作一点P ,使P 到∠A 的两边的距离相等,且PA =PB .要求:尺规..作图,并保留作图痕迹.(不要求写作法)五、仔细想一想(共3个小题,每小题6分,共18分)26.已知:2x y +=,求22222()8()x y x y --+的值.解:C BA27.王鹏和李明沿同一条路同时从学校出发到图书馆查阅资料,学校与图书馆的路程是4千米.王鹏骑自行车,李明步行.当王鹏从原路回到学校时,李明刚好到达图书馆.图中折线O-A-B-C和线段OD分别表示两人离学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系,请根据图象回答下列问题:(1) 王鹏在图书馆查阅资料的时间为_________分钟,王鹏返回学校的速度为___________千米/分钟;(2) 请求出李明离开学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系式;(3) 当王鹏与李明迎面相遇时,他们离学校的路程是多少千米?解:(2)(3)28.已知:如图,在△ABC 中,AB=AC ,∠BAC=α,且60°<α<120°.P 为△ABC 内部一点,且PC=AC ,∠PCA=120°—α.(1)用含α的代数式表示∠APC ,得∠APC =_______________________; (2)求证:∠BAP=∠PCB ;(3)求∠PBC 的度数.证明:(2)解:(3)北京市西城区2010 — 2011学年度第一学期期末试卷(北区)八年级数学(B 卷)参考答案及评分标准 2011.1分,每小题B CPA三、耐心算一算(本题共19分,第19题6分,第20题3分,第21、22题每题5分)19.(1)解:224x y -=(2)(2)x y x y +-.----------------2分 (2)解:22363a ab b ++=223(2)a ab b ++ ----------------2分=23()a b +. ----------------4分20+----------------2分=. ----------------3分 21.解:22211121xx x x x -÷+--+ =221(1)1(1)(1)x x x x x--⨯++- =211(1)x x x x --++ ----------------2分 =2(1)(1)x x x x --+=1x. ----------------4分 当5x =时,原式=1x =15. ----------------5分22.解:去分母,得 5255x x x =++. ----------------2分移项,合并得 25x =-. 系数化为1,得 52x =-. ----------------4分 经检验,52x =-是原方程的解. ----------------5分 所以,原方程的解为52x =-.四、认真做一做(本题共17分,第23、24题每题6分,第25题5分) 23.证明:如图1.∵ AD ∥BC , ∴∠A=∠C . ----------------1分 在△ADF 与△CBE 中, ∠A=∠C ,AD=CB , ∠D=∠B ,∴△ADF ≌△CBE . ----------------4分 ∴ AF=CE. ----------------5分 ∴ AF -EF=CE -EF .∴AE=CF. ----------------6分 24.解:(1)∵点A (2,4-)在直线mx y =(0m ≠)上,∴m 24-=2-=m .∴x y 2-=. ----------------2分(2)解法一:作AM⊥y 轴于M ,BN⊥y 轴于N ∵点B 在直线x y 2=上,且点B 的横坐标为-∴点B 的坐标为B )84(--,.∵MN BN)AM (21S ABNM⋅+=梯形 1(24)(48)2=⨯+⨯+36=,FD CBA E 图1MO AM 21S AOM ⋅=∆=44221=⨯⨯, NO BN 21S BON⋅=∆=168421=⨯⨯, ------------5分 ∴BO N A O M A BN M A BO S S S S ∆∆∆--=梯形16436--=16=. ------------6分解法二:设直线b kx y +=(0k ≠)与x 轴交于点C (如图3). ∵点B 在直线x y 2=上,且点B 的横坐标为-∴点B 的坐标为B )84(--,.∵直线b kx y +=(0k ≠)经过点A (2,4-)和点B )84(--,, ∴⎩⎨⎧+-=-+-=.48,24b k b k 解得⎩⎨⎧==.16,6b k∴166+=x y .令0=y ,可得38-=x . ∴点C 的坐标为C )038(,-. ------------5分 ∴BO C A O C A BO S S S ∆∆∆+=8382143821⨯⨯+⨯⨯=16=. ------------6分阅卷说明:其他正确解法相应给分.25.答案如图4所示.阅卷说明:(1)画出∠CAB 的平分线AD ; ------------2分 (2)画出AB 垂直平分线MN ; ------------4分 (3)标出射线AD 与直线MN 的交点P .------------5分五、仔细想一想(本题共18分,每小题6分)D图326.解法一:22222()8()x y x y --+)(8)()(2222y x y x y x +--+=. ------------1分∵2=+y x ,∴原式)(8)(4222y x y x +--= ------------2分 222288)2(4y x y xy x --+-=22484y xy x ---= ------------3分 2)(4y x +-= ------------5分 224⨯-=16-=. ------------6分解法二:由2=+y x ,得x y -=2. ------------1分 则原式])2([8])2([22222x x x x -+---= ------------2分 )442(8)44(22+---=x x x ------------4分 32321616321622-+-+-=x x x x16-=. ------------6分27.(1)15,154. (每空1分) ------------2分 (2)解:设线段OD 所在直线为)0(≠=k kt s . ∵点D (45,4)在此直线上, 则k 454=454=k . ∴t s 454=. ------------3分∴当045t ≤≤时,t s 454=. (3)解:设线段BC 所在直线为)0(11≠+=k b t k s .∵点B (30,4)和点C (45,0)在此直线上,则⎩⎨⎧+=+=.450,30411b k b k 解得⎪⎩⎪⎨⎧=-=.12,1541b k∴12154+-=t s . ------------4分 ∴当3045t ≤≤时,12154+-=t s .由(2)知线段OD 所在直线为t s 454=, 由 ⎪⎪⎩⎪⎪⎨⎧+-==.12154,454t s t s 解得⎪⎩⎪⎨⎧==.3,4135s t ------------5分∴直线OD 与BC 的交点坐标为)3,4135(. 答:当王鹏与李明迎面相遇时,他们离学校的路程是3千米.------------6分28.(1)∠APC 230α+=. ------------1(2)证明:如图5.∵CA=CP , ∴∠1=∠2=230α+.∴∠3=∠BAC -∠1=)230(αα+-=302-α. ------------2分∵AB=AC ,∴∠ABC=∠ACB=2180α- =290α-.∴∠4=∠ACB -∠5=)120()290(αα---=302-α.∴∠3=∠4.即∠BAP=∠PCB . ------------3分(3)解法一:在CB 上截取CM 使CM=AP ,连接PM (如图6).------------4分 ∵PC=AC ,AB=AC , ∴PC=AB .在△ABP 和△CPM 中,AB=CP , ∠3=∠4, AP=CM , ∴△ABP ≌△CPM .∴∠6=∠7, BP=PM . ∴∠8=∠9.∵∠6=∠ABC-∠8,∠7=∠9-∠4,∴∠ABC-∠8=∠9-∠4. 即(290α-)-∠8=∠9-(302-α).∴ ∠8+∠9=60. ∴2∠8=60. ∴∠8= 30.即∠PBC= 30. ------------6分解法二:作点P 关于BC 的对称点N ,连接PN 、AN 、BN 和CN (如图7). ------------4分 则△PBC 和△NBC 关于BC 所在直线对称. ∴△P BC ≌△NBC . ∴BP=BN ,CP=CN , ∠4=∠6=302-α,∠7=∠8.∴∠ACN=∠5+∠4+∠6=)302(2)120(-⨯+-αα= 60.∵PC=AC ,∴AC=NC .21645378CNBAP图74521CP AB63987图6∴△CAN 为等边三角形. ∴AN=AC ,∠NAC=60. ∵AB=AC ,∴AN=AB .∵∠PAN=∠PAC -∠NAC=(230α+)-60=302-α,∴∠PAN=∠3.在△ABP 和△ANP 中, AB=AN , ∠3=∠PAN , AP=AP ,∴△ABP ≌△ANP .∴PB=PN .∴△PBN 为等边三角形. ∴∠PBN=60. ∴∠7=21∠PBN =306021=⨯. 即∠PBC=30. ------------6分阅卷说明:其他正确解法相应给分.。
北京市西城区(南区)2011-2012学年度第一学期期末质■检测-■选择■(谓将答案写在下列表格中.本大JH共12小毎小題3分・共36分)越号123456789101112)I.实tt-5. -0.1.民 +中为无理数的是(2. H•列二次根式中.处简二次根式绘(D. /5O戈计算占•角的结壮<八年级数学(共8页)第1页八年级教学2012-1C. J3A. 75A~f4.下列卒件P.为必然爭件的是(D.A.购买一张彩泉.中奖B.打开电视.正在揭放广吿C・枪拠一枚傩币.正it向上D. 一个袋中只發有5个煞球,从中損出一个球足黑球5.如图.已知乙2乙2.则不一定能便△ ABDMACD的条件是(♦• ・A. HD CDB.AH^ACD. Z BOA = Z CDA6.如图.在厶A8C中.乙090°. M = 乙。
•点F圧“C边上的动点,则肿长于可能見()♦•A. 3.5B. 4.2 C 18 D. 7第5題图第6凹吊第7越图7.如史.隹AABC中.AD 4-分外^/.EAC. LUO力8C.则△人8(:—定是()A.任意三角形B-笹边三角形a等腰三角形 D.直角三危形8.下列命题的逆命BJiE備的足(儿全等三角形的廊枳相霎 B.金铮三角形的对应佝相等C.在倫祁相等D.等边二角形的三个角郁等J 60。
9・如图.六边形ABCDEE轴对称图形.CF所在的氏线是它的对秣轴•若乙AFUCF = 150°.则厶AFE *厶RC"的大小是()于点队N、作茂缄吓.交肌•于点6连结" 若△初C的周K为IO. 43".则△肪C的周长为(>A. 7B. 14 G 17 D. 2011.宾数a在数轴上的位置刻图所示.则&7石化简后为< }1 -------- 丄■」> 0 5 a ioMI1JK 图A. 7B.・7C. 2a・15D.无法确定12.关于x的方程工*2层"-1“的根的壻况描述正犢的是()A.左为任何实数.方凰郝没冇实歡根B-上为任何实数.力程部有曲个不相粵的实8(根C.&为任何实数•方稈邯有两个相簣的实枚根D.根据*的取伍不同.厅稈根的悄况分为没有实数根、有两个不相咎的实数祀和右凹个相等的实数根三种八年级数学f共8贞)第2页二、填空題(请将答秦写在横线上.本大IS共8小题,毎小16 3分,共24分)13.等99二饰形的两&长分別为4 rm和9cm・則它的周长为14.当,_________ 时,庄二T冇童义.15.-次救学活动课上,小龜埒一型三角板按图中方式叠放,则乙a等F _________ . ・16.如图,学校右•決氏方形花制・(少数人为raff拐角走••燧径”,住花勉内走岀『一条“路“ •他门仅仅少走了_________步路(假设2步为1米).却踩伤了花草.17.在一只不透期的口袋中放人只和魏色不同的白球6个.黑球4 个,黄球/»个,搅匀后随机从中模取一个恰好是黄珠的可能性为卜则放入的黄球总数" *168图18-已知为対个连续的整数.且“<、%VA•则_______________________ 19.已知关于*的一兀二次方桂3・1)/・2(卄2)八"0有实根.则。
八年级数学第一学期期末试卷试卷满分:100分,考试时间:100分钟一、选择题(本题共24分,每小题3分)下面各题均有四个选项,其中只有一个..是符合题意的. 1.下列各式中,最简二次根式是( ).A .5.0B .12C .2xD . 12+x2.下列汽车标志中,不是..轴对称图形的是( ).3.下列因式分解结果正确的是( ).A .3221055(2)a a a a a +=+B .249(43)(43)x x x -=+-C .2221(1)a a a --=-D .256(6)(1)x x x x --=-+ 4.下列各式中,正确的是( ). A .212+=+a b a b B . 22112236d cd cd cd++= C .a b a b c c-++=- D . 22)2(422--=-+a a a a5.如图,将三角形纸片ABC 沿直线DE 折叠后,使得点B 与点A 重合,折痕分别交BC ,AB 于点D ,E .如果AC =5cm ,△ADC 的周长为17cm ,那么BC 的长为( ).A .7cmB .10cmC .12cmD .22cm6.某园林公司增加了人力进行园林绿化,现在平均每天比原计划多植树50棵,现在植树600棵所需的时间与原计划植树450棵所需的时间相同,如果设原计划平均每天植树x 棵,那么下面所列方程中,正确的是( ). A .x x 45050600=- B .x x 45050600=+ C .50450600+=x x D .50450600-=x x 7.如果132x y x +=,那么x y的值为( ).A .21 B .32C .31D . 528.如图1,将长方形纸片先沿虚线AB 向右..对折,接着将对折后的纸片沿虚线CD 向下..对折,然后剪下一个小三角形,再将纸片打开,那么打开后的展开图是( ).二、填空题(本题共24分,每小题3分)9.如果分式32x x -+的值为0,那么x 的值为_________. 10.如果12-x 在实数范围内有意义,那么x 的取值范围是_________. 11.下列运算中,正确的是_______.(填写所有..正确式子的序号) ①2612a a a ⋅=;②329()x x =;③33(2)8a a =;④22242(5)255a b a b ab -=--. 12.如图是两个全等三角形,图中的字母表示三角形的边长,那么根据图中提供的信息可知1∠的度数为 . 13.计算:1111x x --+= .14.计算:432(68)(2)x x x -÷-= .15.如图,∠AOB=60︒,OC 平分∠AOB ,如果射线OA 上的点E 满足△OCE 是等腰三角形,那么∠OEC 的度数为 .16.如图,动点P 从(0,3)出发,沿所示的方向运动,每当碰到长方形的边时反弹,反弹时反射角等于 1(3,0)P .入射角,第一次碰到长方形的边时的位置为(1)画出点P 从第一次到第四次碰到长方形的边的全过程中,运动的路径;(2)当点P 第2014次碰到长方形的边时,点P 的坐标为 .三、解答题(本题共35分,第17、19题各10分,其余每题5分)17.(1)先化简,再求当2a =,1b =时,代数式(3)()(2)a b a b a a b +-+-的值. 解:(2)计算:1(83)642+⨯-. 解:18.已知:如图,AB= AC ,∠DAC=∠EAB ,∠B=∠C .求证:BD = CE . 证明:19.(1)因式分解:232448m m -+. 解:(2)计算:422222222a a b a ab b a ab b b a-+÷⋅-+.解:20.解分式方程:31122x x x +=--.解:21.尺规作图:已知:如图,线段a和h.求作等腰三角形ABC,使底边BC=a,底边上的高AD=h.(保留作图痕迹并写出相应的作法.)作法:四、解答题(本题6分)22.(1)阅读理解:我们知道,只用直尺和圆规不能解决的三个经典的希腊问题之一是三等分任意角,但是这个任务可以借助如图所示的一边上有刻度的勾尺完成,勾尺的直角顶点为P,“宽臂”的宽度.........,..=PQ=QR=RS (这个条件很重要哦!)勾尺的一边MN满足M,N,Q三点共线(所以PQ⊥MN).∠为例说明利用勾尺三等分锐角的过程:下面以三等分ABC第一步:画直线DE使DE∥BC,且这两条平行线的距离等于PQ;第二步:移动勾尺到合适位置,使其顶点P落在DE上,使勾尺的MN边经过点B,同时让点R ∠的BA边上;落在ABC第三步:标记此时点Q和点P所在位置,作射线BQ和射线BP.∠的三等分线是射线、.请完成第三步操作,图中ABC∠的主要证明过程:(2)在(1)的条件下补全三等分...ABC∵,BQ⊥PR,∴BP=BR.(线段垂直平分线上的点与这条线段两个端点的距离相等)∴∠=∠.∵PQ⊥MN,PT⊥BC,PT=PQ,∴∠=∠.(角的内部到角的两边距离相等的点在角的平分线上)∴ ∠ =∠ =∠ .(3)在(1)的条件下探究: 13A B S A B C∠=∠是否成立?如果成立,请说明理由;如果不成立,请在下图中 ABC ∠的外部..画出13ABV ABC ∠=∠(无需写画法,保留画图痕迹即可).解:五、解答题(本题共11分,第23题5分,第24题6分) 23.已知:如图,在平面直角坐标系xOy 中,(2,0)A -,(0,4)B ,点C 在第四象限,AC ⊥AB , AC=AB . (1)求点C 的坐标及∠COA 的度数;(2)若直线BC 与x 轴的交点为M ,点P 在经过点C 与 x 轴平行的直线上,直接写出BOM POM S S ∆∆+的值.解:(1)(2)BOM POM S S ∆∆+的值为 .24.已知:如图,Rt △ABC 中,∠BAC=90︒. (1)按要求作图:(保留作图痕迹) ①延长BC 到点D ,使CD=BC ; ②延长CA 到点E ,使AE=2CA ;③连接AD ,BE 并猜想线段 AD 与BE 的大小关系;考试结束后,请尝试自制一把“勾尺”实践一下!(2)证明(1)中你对线段AD 与BE 大小关系的猜想. 解:(1)AD 与BE 的大小关系是 . (2)证明:八年级数学附加题试卷满分:20分一、阅读与思考(本题6分)我们规定:用[]x 表示实数x 的整数部分,如[]3.143=,82⎡⎤=⎣⎦,在此规定下解决下列问题:(1)填空:1236⎡⎤⎡⎤⎡⎤⎡⎤++++⎣⎦⎣⎦⎣⎦⎣⎦= ;(2)求1234+49⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤++++⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦的值.解:二、操作与探究(本题6分)取一张正方形纸片ABCD 进行折叠,具体操作过程如下:第一步:先把纸片分别对折,使对边分别重合,再展开, 记折痕MN ,PQ 的交点为O ;再次对折纸片使AB 与PQ 重合, 展开后得到折痕EF ,如图1;第二步:折叠纸片使点N 落在线段EF 上,同时使折痕 GH 经过点O ,记点N 在EF 上的对应点为N ,如图2.解决问题:(1)请在图2中画出(补全)纸片展平后的四边形CHGD 及相应MN ,PQ 的对应位置;(2)利用所画出的图形探究∠POG 的度数并证明你的结论.解:(1)补全图形. (2)∠POG = °. 证明:三、解答题(本题8分)已知:如图,∠MAN 为锐角,AD 平分∠MAN ,点B ,点C 分别在射线AM 和AN 上,AB =AC . (1)若点E 在线段CA 上,线段EC 的垂直平分线交直线AD 于点F ,直线BE 交直线 AD 于点G ,求证:∠EBF =∠CAG ;(2)若(1)中的点E 运动到线段CA 的延长线上,(1)中的其它条件不变,猜想 ∠EBF 与∠CAG 的数量关系并证明你的结论. (1)证明: (2)图2备用图1备用图2。
北京市西城区2010-2011学年度第一学期期末试卷(北区)八年级数学(B 卷)一、精心选一选(本题共30分,每小题3分)1.计算24-的结果是( )A .8-B .18- C .116- D .1162.下列说法中,正确的是( ) A .5是25的算术平方根 B .9-的平方根是3- C .4±是64的立方根 D .9的立方根是3 3.下列四个交通标志中,轴对称图形是( )A .B .C .D . 4.当0b <时,函数y x b =-+的图象不经过...( ) A .第一象限 B .第二象限 C .第三象限D .第四象限 5.下列各式中,正确的是( )A .1a b b ab b ++=B .22x y x y -++=-C .23193x x x -=-- D .()222x y x y x y x y --=++ 6.在ABC △和A B C '''△中,已知A A '∠=∠,AB AB ''=,添加下列条件中的一个,不能..使ABC A B C '''△≌△一定成立的是( )A .AC A C ''=B .BC B C ''= C .B B '∠=∠D .C C '∠=∠ 7.点()11A y -,和()22B y ,都在直线3y x =-上,则1y 与2y 的关系是( )A .12y y <B .12y y =C .12y y >D .212y y =8.如图,在ABC △中,D 是BC 边上一点,且AB AD DC ==,40BAD ∠=°,则C ∠为( )A .25°B .35°C .40°D .50°9.已知一次函数y kx b =+的图象如图所示,当0x >时,y 的取值范围是( )A .1y <B .1y >C .2y <-D .2y >-10.如图所示,长方形ABCD 中,4AB =,BC =,点E 是折线段A D C --上的一个动点(点E 与点A 不重合),点P 是点A 关于BE 的对称点,在点E 运动的过程中,能使PCB △为等腰三角形.....的点E 的位置共有( )DCBAPEDCB AA .2个B .3个C .4个D .5个 二、细心填一填(本题共16分,每小题2分)11.当x 时,分式11x-有意义.12.如图,ABC △是等边三角形,D 是BC 边的中点,点E 在AC 的延长线上且30CDE ∠=°,若AD =DE = .EDCBA13.在0.6,,27,π-这五个实数中,无理数是 .1 14.如图,在Rt ABC △中,90C ∠=°,30B ∠=°,AD 平分CAB ∠交BC 于D ,DE AB ⊥于E ,若1cm DE =,则BC = cm .EDCBA15.如图,MN 是正方形ABCD 的一条对称轴,点P 是直线MN 上的一个动点,当PC PD +最小时,PCD ∠= .NMPDCBA16.已知直线y kx b =+()0k ≠与直线2y x =-平行,且经过点()11,,则直线()0y kx b k =+≠可以看作由直线2y x =-向 平移 个单位长度而得到.17.如图,在ABC △中,AB AC =,40A ∠=°,AB 的垂直平分线MN 交AC 于点D ,则D B C ∠= .NMDCBA18.用长为4cm 的n 根火柴可以拼成如图1所示的x 个边长都为4cm 的平行四边形,还可以拼成如图图1… 图2……三、耐心算一算(本题共19分,第19题6分,第20题3分,第21、22题每题5分)19.因式分解: (1)224x y -(2)22363a ab b ++20+21.先化简,再求值:22211121xx x x x -÷+--+,其中5x =,22.解分式方程:21155x x x x =+++.四、认真做一做(本题共17分,第23、24题每题6分,第25题5分)23.已知:如图,点A 、E 、F 、C 在同一条直线上,AD CB =,B D ∠=∠,AD BC ∥.求证:AE CF =.FEDC BA24.已知:平面直角坐标系xOy 中,直线()0y kx b k =+≠与直线()0y mx m =≠交于点()24A -,. (1)求直线()0y mx m =≠的解析式;(2)若直线()0y kx b k =+≠与另一条直线2y x =交于点B ,且点B 的横坐标为4-,求ABO △的面积.25.如图,已知ABC △,求作一点P ,使P 到A ∠的两边的距离相等,且PA PB =.要求:尺规..作图,并保留作图痕迹.(不要求写作法)CBA五、仔细想一想(本题共18分,每小题6分)26.已知:2x y +=,求()()222228x y x y --+的值.27.王鹏和李明沿同一条路同时从学校出发到图书馆查阅资料,学校与图书馆的路程是4千米.王鹏骑自行车,李明步行.当王鹏从原路回到学校时,李明刚好到达图书馆.图中折线O A B C ---和线段OD 分别表示两人离学校的路程s (千米)与所经过的时间t (分钟)之间的函数关系,请根据图象回答下列问题:(1)王鹏在图书馆查阅资料的时间为 分钟,王鹏返回学校的速度为 千米/分钟; (2)请求出李明离开学校的路程s (千米)与所经过的时间t (分钟)之间的函数关系式; (3)当王鹏与李明迎面相遇时,他们离学校的路程是多少千米?李明王鹏(分钟)28.已知:如图,在ABC △中,AB AC =,BAC α∠=,且60120α<<°°.P 为ABC △内部一点,且PC AC =,120PCA α∠=-°.(1)用含α的代数式表示APC ∠,得APC ∠= ; (2)求证:BAP PCB ∠=∠; (3)求PBC ∠的度数.PCBA北京市西城区2010-2011学年度第一学期期末试卷(北区)八年级数学(B 卷)参考答案及评分标准2011.1二、细心填一填(本题共16分,每小照2分)11.≠1;1213.,π-(答对一个给1分);14.3;15.45;16.上,3(每空1分); 17.30;18.3155y x =-三、耐心算一算(本题共19分,第19题6分,第20题3分,第21、22题每题5分)19.(1)解:224(2)(2)x y x y x y -=+-………………2分(2)解;22363a ab b ++223(2)a ab b =++…………2分 23(12)b =+………………4分20+2分=3分21.解: 22211121xx x x x -÷+--+ ()21211(1)(1)x x x x x -=-⨯++- 211(1)x x x x -=-++…………2分 2(1)(1)x x x x --=+1x=.………………4分 当x =5时,原式11.5x ==………………5分22.解:去分母,得5255x x x =++…………2分 移项,台并得25x =-.系数化为1,得52x =-⋅………………4分经检验,52x =-是原方程的解.…………5分分所以,原方程的解为52x =-.四、认真做一做(本题共17分,第23、24题每题6分,第25题5分) 23.证明:如图1. ∵AD BC ∥∴A C ∠=∠…………1分 在△ADF 与△CBE 中, A C AD CB D B ∠=∠⎧⎪=⎨⎪∠=∠⎩∴ADF CBE △≌△…………4分 ∴.AF CE =…………5分 ∴.AF EF CE EF -=- ∴.AE CF =…………6分 24.解:(1)∵点(24)A -,在直线(0)y mx m =⋅=/上, ∴42m =- 2m =-∴2y x =-………………2分(2)解法一:作AM y ⊥轴于M ,BN y ⊥轴于N (如图2) ∵点B 在直线y =2x 上,且点B 的横坐标为4-. ∴点B 的坐标为B (4-,8-)…………3分∵1()2ABNM S AM BN MN =+⋅梯形1(24)(48)362=⨯+⨯+=…………4分 1124422AOM S AM MO =⋅=⨯⨯=△11481622BON S BN NO =⋅=⨯⨯=△………………5分∴ABO AOM BON ABNM S S S S =--△△△梯形3641616=--=…………6分 解法二:设直线(0)y kx b k =+=/与x 轴交于点C (如图3). ∵点B 直线y =2x 上,且点B 的横坐标为4-. ∴点B 的坐标为B (4-,8-)………………3分 ∵直线()0y kx b k =+≠经过点A (2-,4) 和点B (4-,8-), ∴4284k b k b =-+⎧⎨-=-+⎩,616k b =⎧⎨=⎩∴616.y x =+…………4分令y =0.可得83x =-∴点C 的坐标为803C ⎛⎫- ⎪⎝⎭,…………5分∴181848162323ABO AOC BOC S S S =+=⨯⨯+⨯⨯=△△△.…………6分问卷说明:其他正确解法相应给分.25.答案如图4所示. 阅卷说明:(1)画出CAB ∠的平分线AD .………………2分 (2)画出AB 垂直平分线MN ;………………4分 (3)标出射线AD 与直线MN 的交点P .…………5分 五、仔细想一想(本题共18分,每小题6分)26.解法一:()()222222x y x y --+()()()22222x y x y x y =+---。
[初二数学]北京市西城区2010-2011学年度第一学期期末试卷北区八年级数学B卷北京市西城区2010-2011学年度第一学期期末试卷(北区)八年级数学(B 卷)一、精心选一选(本题共30分,每小题3分)1.计算24-的结果是( )A .8-B .18- C .116- D .1162.下列说法中,正确的是( )A .5是25的算术平方根B .9-的平方根是3-C .4±是64的立方根D .9的立方根是33.下列四个交通标志中,轴对称图形是( )A .B .C .D .4.当0b <时,函数y x b =-+的图象不经过...( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限5.下列各式中,正确的是( )A .1a b b ab b ++=B .22x y x y -++=-C .23193x x x -=-- D .()222x y x y x y x y --=++6.在ABC △和A B C '''△中,已知A A '∠=∠,AB A B ''=,添加下列条件中的一个,不能..使ABC A B C '''△≌△一定成立的是( )A .AC A C ''=B .BC B C ''= C .B B '∠=∠D .C C '∠=∠7.点()11A y -,和()22B y ,都在直线3y x =-上,则1y 与2y 的关系是( )A .12y y <B .12y y =C .12y y > D .212y y = 8.如图,在ABC △中,D 是BC 边上一点,且AB AD DC ==,40BAD ∠=°,则C ∠为( )A .25°B .35°C .40°D .50°9.已知一次函数y kx b =+的图象如图所示,当0x >时,y 的取值范围是( )-21O yxA .1y <B .1y >C .2y <-D .2y >-10.如图所示,长方形ABCD 中,4AB =,43BC =E是折线段A D C --上的一个动点(点E 与点A 不重合),点P 是点A 关于BE 的对称点,在点E 运动的过程中,能使PCB △为等腰三角形.....的点E 的位置共有( ) PEDCBAA .2个B .3个C .4个D CB AD .5个二、细心填一填(本题共16分,每小题2分)11.当x 时,分式11x-有意义. 12.如图,ABC △是等边三角形,D 是BC 边的中点,点E 在AC 的延长线上且30CDE ∠=°,若3AD =DE = .EDCBA13.在0.6,3527,π-36是 .114.如图,在Rt ABC △中,90C ∠=°,30B ∠=°,AD 平分CAB∠交BC 于D ,DE AB ⊥于E ,若1cm DE =,则BC = cm .EDCBA15.如图,MN 是正方形ABCD 的一条对称轴,点P 是直线MN 上的一个动点,当PC PD +最小时,PCD ∠= .NMPDCBA16.已知直线y kx b =+()0k ≠与直线2y x =-平行,且经过点()11,,则直线()0y kx b k =+≠可以看作由直线2y x =-向 平移 个单位长度而得到.17.如图,在ABC △中,AB AC =,40A ∠=°,AB 的垂直平分线MN 交AC 于点D ,则DBC ∠= .NMDCBA18.用长为4cm 的n 根火柴可以拼成如图1所示的x 个边长都为4cm 的平行四边形,还可以拼成如图图1… 图2……三、耐心算一算(本题共19分,第19题6分,第20题3分,第21、22题每题5分)19.因式分解: (1)224x y -(2)22363a ab b ++20.计算:3525+21.先化简,再求值:22211121xx x x x -÷+--+,其中5x =,22.解分式方程:21155x xx x =+++.四、认真做一做(本题共17分,第23、24题每题6分,第25题5分)23.已知:如图,点A 、E 、F 、C 在同一条直线上,AD CB =,B D ∠=∠,AD BC ∥.求证:AE CF =.FED CBA24.已知:平面直角坐标系xOy 中,直线()0y kx b k =+≠与直线()0y mx m =≠交于点()24A -,.(1)求直线()0y mx m =≠的解析式;(2)若直线()0y kx b k =+≠与另一条直线2y x =交于点B ,且点B 的横坐标为4-,求ABO △的面积.-3-4-5-6-7-8-8-7-6-5-4-2-1-3-2-13214321Oy x25.如图,已知ABC △,求作一点P ,使P 到A ∠的两边的距离相等,且PA PB =.要求:尺规..作图,并保留作图痕迹.(不要求写作法)CBA五、仔细想一想(本题共18分,每小题6分)26.已知:2x y +=,求()()222228x y x y --+的值.27.王鹏和李明沿同一条路同时从学校出发到图书馆查阅资料,学校与图书馆的路程是4千米.王鹏骑自行车,李明步行.当王鹏从原路回到学校时,李明刚好到达图书馆.图中折线O A B C ---和线段OD 分别表示两人离学校的路程s (千米)与所经过的时间t (分钟)之间的函数关系,请根据图象回答下列问题:(1)王鹏在图书馆查阅资料的时间为 分钟,王鹏返回学校的速度为 千米/分钟;(2)请求出李明离开学校的路程s (千米)与所经过的时间t (分钟)之间的函数关系式;(3)当王鹏与李明迎面相遇时,他们离学校的路程是多少千米?李明王鹏45301542(分钟)DC BAO28.已知:如图,在ABC △中,AB AC =,BAC α∠=,且60120α<<°°.P 为ABC △内部一点,且PC AC =,120PCA α∠=-°.(1)用含α的代数式表示APC ∠,得APC ∠= ; (2)求证:BAP PCB ∠=∠; (3)求PBC ∠的度数.PCBA北京市西城区2010-2011学年度第一学期期末试卷(北区)八年级数学(B 卷)参考答案及评分标准2011.1一、精心选一选(本题共30分,每小题3分)题号1 2 3 4 5 6 7 8 90 答案D A B A D A C B D 二、细心填一填(本题共16分,每小照2分)11.≠1;12.313.35-,π-(答对一个给1分);14.3;15.45;16.上,3(每空1分); 17.30;18.3155y x =- 三、耐心算一算(本题共19分,第19题6分,第20题3分,第21、22题每题5分)19.(1)解:224(2)(2)x y x y x y -=+-………………2分 (2)解;22363a ab b ++ 223(2)a ab b =++…………2分 23(12)b =+………………4分 203525+ 5325=+2分 353=3分 21.解: 22211121xx x x x -÷+--+()21211(1)(1)x x x x x-=-⨯++- 211(1)x x x x -=-++…………2分 2(1)(1)x x x x --=+1x =.………………4分当x =5时,原式11.5x ==………………5分 22.解:去分母,得5255x x x =++…………2分移项,台并得25x =-.系数化为1,得52x =-⋅………………4分 经检验,52x =-是原方程的解.…………5分分 所以,原方程的解为52x =-. 四、认真做一做(本题共17分,第23、24题每题6分,第25题5分)23.证明:如图1.∵AD BC ∥∴A C ∠=∠…………1分在△ADF 与△CBE 中,A C AD CBD B ∠=∠⎧⎪=⎨⎪∠=∠⎩∴ADF CBE △≌△…………4分∴.AF CE =…………5分∴.AF EF CE EF -=-∴.AE CF =…………6分24.解:(1)∵点(24)A -,在直线(0)y mx m =⋅=/上,∴42m =-2m =-∴2y x =-………………2分(2)解法一:作AM y ⊥轴于M ,BN y ⊥轴于N (如图2)∵点B 在直线y =2x 上,且点B 的横坐标为4-.∴点B 的坐标为B (4-,8-)…………3分 ∵1()2ABNM S AM BN MN =+⋅梯形 1(24)(48)362=⨯+⨯+=…………4分 1124422AOM S AM MO =⋅=⨯⨯=△ 11481622BON S BN NO =⋅=⨯⨯=△………………5分∴ABO AOM BON ABNM S S S S =--△△△梯形3641616=--=…………6分解法二:设直线(0)y kx b k =+=/与x 轴交于点C(如图3). ∵点B 直线y =2x 上,且点B 的横坐标为4-.∴点B 的坐标为B (4-,8-)………………3分∵直线()0y kx b k =+≠经过点A (2-,4)和点B (4-,8-),∴4284k b k b =-+⎧⎨-=-+⎩,616k b =⎧⎨=⎩∴616.y x =+…………4分令y =0.可得83x =- ∴点C 的坐标为803C ⎛⎫- ⎪⎝⎭,…………5分 ∴181848162323ABO AOC BOC SS S =+=⨯⨯+⨯⨯=△△△.…………6分问卷说明:其他正确解法相应给分.25.答案如图4所示.阅卷说明:(1)画出CAB ∠的平分线AD .………………2分(2)画出AB 垂直平分线MN ;………………4分(3)标出射线AD 与直线MN 的交点P .…………5分五、仔细想一想(本题共18分,每小题6分)26.解法一:()()222222x y x y --+()()()22222x y x y x y =+---。